迄今为止,小行星探测器对小行星的探测大多采用飞掠探测或一触即离的方式,只能得到表层的信息和样本[1-9]。获取小行星的深层样本需要探测器可靠地锚固在小行星表面[10],在各锚固方案中,通过钻机钻进实现几何力封闭的锚固方式具有较高的可靠性和较好的地质适应性。传统的钻机需要施加较大的钻压力和力矩,消耗功率大,探测器较难满足这些条件[11],超声波钻工作时钻压力小、功耗小,几乎不对机架产生附加力矩,并且能够适应地外空间的工作环境,适合应用在探测器的钻进锚固工作中。
超声波钻基于超声波换能器的逆压电效应工作,换能器工作时需要使驱动信号位于谐振频率区间[12-13],否则换能器未处于谐振状态时端面振幅过小,无法实现冲击钻进,因此需要对换能器的谐振频率进行辨识。此外,换能器的电品质因数较高,谐振频率经常受到温度、湿度等环境参数的影响而漂移[14-15],在工作过程中需要对谐振频率进行跟踪。在超声波应用常见的频率跟踪算法中,锁相控制有良好的稳定性,对扰动信号的抗干扰能力较强[16],但是需要让换能器谐振点的相角不发生变化,而超声波钻在工作时温度的变化会使谐振点的相角发生改变,并且换能器的阻抗特性参数对负载较敏感,因此锁相控制不适合应用于超声波钻的谐振控制中。扫频控制能够较可靠地跟踪谐振点,但是工作过程中需要对区间不断扫描,影响了频率跟踪速度和超声波钻的工作效率[17-18]。极值搜索控制能够自适应地跟踪于换能器的特性参数极值点,具有良好的鲁棒性、收敛速度快等优点[19]。本文利用超声波钻的谐振点与最小阻抗点的对应关系,研究超声波钻的谐振控制算法,高效稳定驱动超声波钻,并通过试验进行验证。
1 超声波钻锚固方案及工作特性分析 1.1 超声波钻钻进锚固方案利用超声波钻进行交叉钻进的锚固方案如图 1所示,超声波钻安装小行星探测器着陆腿上,在探测器提供较低的钻压力作用下,超声波钻对星岩进行交叉钻进,形成几何力封闭的锚固形式,使探测器锚固在小行星表面。

|
图 1 超声波钻锚固方案 Fig. 1 Anchoring scheme with ultrasonic drill |
超声波钻的结构如图 2所示,超声波钻由超声波换能器和钻具组成,超声波换能器由后盖板、压电陶瓷、前盖板和变幅杆构成,前、后盖板通过螺纹连接压紧压电陶瓷;钻具由钻杆、预紧装置、回复弹簧、自由质量块和钻套构成,预紧装置通过回复弹簧将钻杆和自由质量块压在换能器端面,通过紧钉螺钉固定预紧装置,避免在工作时旋出。

|
图 2 超声波钻结构 Fig. 2 Structure of ultrasonic drill |
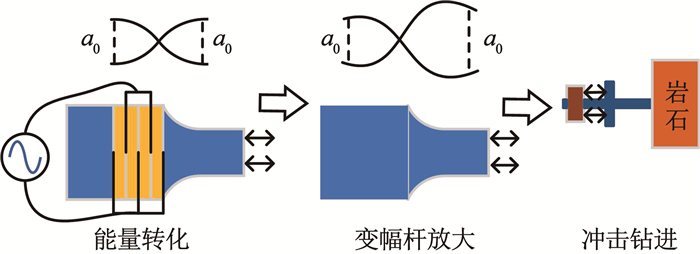
超声波钻的工作原理如图 3所示,基于压电陶瓷的逆压电效应,将激励交流信号转化为高频机械振动,变幅杆将振幅进一步放大,换能器的端面振动冲击自由质量块,自由质量块在换能器和钻杆间往复运动,使钻杆冲击岩石实现钻进。
|
图 3 超声波钻工作原理 Fig. 3 Working principle of ultrasonic drill |
基于BVD等效模型建立超声波换能器的等效电路模型如图 4所示,静态支路的静态电容C0由换能器自身品质决定,动态支路由动态电感L1、动态电容C1和动态电阻R1构成,分别表示换能器工作时的惯性、弹性和能量损耗。

|
图 4 超声波换能器等效电路模型 Fig. 4 Equivalent circuit model of ultrasonic transducer |
超声波换能器的电压-速度传递函数Y为
| $ Y=\frac{p}{\mathrm{j}\left(\omega L_1-1 / \omega C_1\right)+R_1} $ | (1) |
式中:p为超声波换能器的机电耦合系数,ω为驱动信号角频率。
为了使钻进速率最大化,驱动信号的频率应使Y最大,则最优驱动频率fs为
| $ f_{\mathrm{s}}=\frac{1}{2 \pi \sqrt{L_1 C_1}} $ | (2) |
此时驱动频率为换能器的串联谐振频率,动态支路呈现纯阻性,受到静态电容的影响,换能器整体呈现容性。通过阻抗分析仪分析发现换能器的最小阻抗频率与串联谐振频率基本相符,以此建立超声波钻最小阻抗点与最优工作点的对应关系。
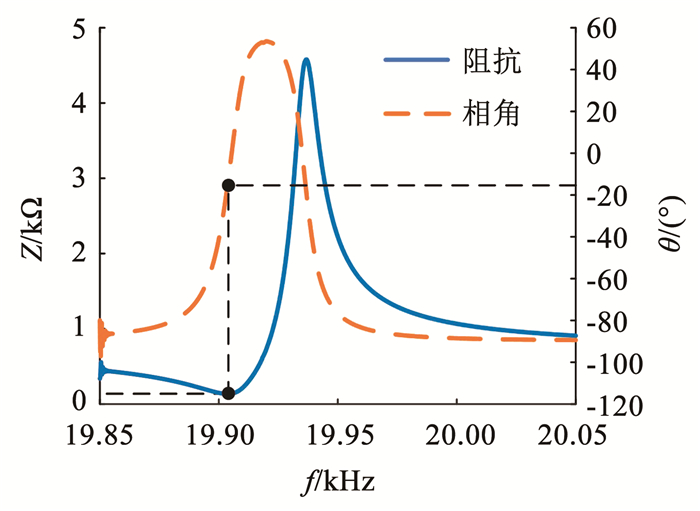
1.4 换能器负载特性分析超声波换能器在空载状态下的阻抗特性曲线如图 5所示,最小阻抗值为139.44 Ω,对应的驱动频率为19.905 kHz,对应相角为-16.662°。空载下的阻抗曲线作为负载变化后的参考曲线,研究负载对换能器阻抗特性的影响。
|
图 5 空载时换能器阻抗曲线 Fig. 5 Impedance curve of transducer without load |
对超声波换能器端面分别施加12 N和24 N的负载,阻抗曲线分别如图 6(a)、6(b)所示,负载为12 N时,最小阻抗值为223.93 Ω,对应的驱动频率为20.057 kHz,对应相角为-33.153°;负载为24 N时,最小阻抗值为292.04 Ω,对应的驱动频率为20.201 kHz,对应相角为-42.715°。

|
图 6 带载时换能器阻抗曲线 Fig. 6 Impedance curve of transducer with load |
对比空载和负载时换能器的阻抗曲线可以看出,当负载增大时,换能器的阻抗增大,谐振频率增大,对应的相角值增大。超声波钻在工作时自由质量块对换能器端面的冲击使换能器的负载变化剧烈,并且负载变化无规律。在对超声波钻的谐振频率进行跟踪时,由负载变化导致的阻抗特性参数变化应通过滤波处理去除。
1.5 换能器温度特性分析超声波钻在工作时自身的发热会导致换能器温度上升,需要研究温度变化对换能器特性参数的影响。利用高低温实验箱在-60~120 ℃温度范围内每隔30 ℃设置一次工作环境,测试不同温度下超声波钻工作时换能器的特性参数,测试结果见表 1,从测试结果可以看出,当换能器的温度上升时,谐振频率减小,阻抗值和相角值增大,工作性能下降。为了使换能器工作时处于相对较好的谐振状态,应对温度变化引起的谐振频率漂移进行跟踪。
| 表 1 不同温度下换能器特性参数 Tab. 1 Transducer characteristic parameters at different temperatures |
超声波钻的组成中存在机械系统,工作过程中阻抗特性曲线存在滞后特性,若在对谐振频率进行跟踪时忽略这一特性,容易使超声波钻长时间工作在低效率状态,导致钻进速率不理想。
装上钻具后利用阻抗分析仪预先得到谐振频率值,以此设定频率扫频的区间,在该区间内,分别以频率减小和频率增大的方向进行频率扫频,得到两个方向的阻抗曲线如图 7所示,以最小阻抗点为谐振频率,从图 7(a)可以看出,两个频率变化方向的谐振频率不同,以相角跳变点为换能器失去和进入谐振状态的判定依据从图 7(b)可以看出,频率减小方向失去谐振状态的频率点和频率增大方向进入谐振状态的频率点不同。

|
图 7 换能器滞后特性曲线 Fig. 7 Hysteresis characteristic curve of transducer |
以频率减小方向得到的最小阻抗值更小,可以取得更好驱动效果,所以在实际控制时应该以频率减小的方向进入谐振状态。
2 超声波钻谐振控制算法设计为使超声波钻获得最佳驱动状态,需要设计相应的谐振控制算法,识别超声波钻的谐振频率并在工作过程中对变化的谐振频率进行跟踪。
2.1 谐振控制整体方案设计设计超声波钻谐振控制整体方案流程图如图 8所示,启动驱动电源时,初始化起始参数,通过对最小阻抗点的识别判断初始状态下的谐振频率。钻进过程中,为了实现对谐振频率的跟踪,采集换能器的阻抗参数信号,经过信号处理后通过谐振频率跟踪算法进行判定决策输出频率变化量。

|
图 8 超声波钻谐振控制流程 Fig. 8 Flow chart of ultrasonic drill resonance control |
自由质量块对换能器端面的冲击性负载会影响阻抗特性参数,使谐振点附近的阻抗曲线存在较多的局部最小值,在识别超声波钻的谐振频率时,采用频率扫描算法对预设定区间内的频率进行遍历,记录区间内的最小阻抗点对应的频率为初始状态下的谐振频率。对谐振频率进行跟踪时,在对阻抗极值点的跟踪原理上提出了基于递归最小二乘估计的谐振频率跟踪算法和基于模糊控制的谐振频率跟踪算法,通过试验对两种算法的实际跟踪效果进行对比后选择跟踪效果更好的控制算法。
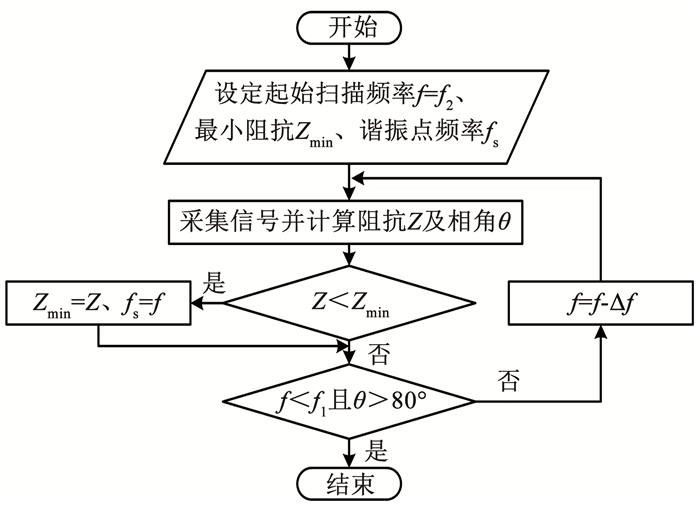
2.2 谐振频率识别算法设计频率扫描算法的工作流程如图 9所示,在阻抗分析仪的分析基础上设定频率扫描区间[f1, f2],由换能器的滞后特性可知以频率下降的方向进入谐振状态可以获得更好驱动效果,因此将f2作为起始驱动频率,每个采样周期采集驱动频率对应的换能器阻抗值并将驱动频率减小Δf,当换能器阻抗值接近最小阻抗值时,减小频率变化步长以获得更精确的谐振频率值,当驱动频率小于f2且当前换能器相角值大于80°时,认为已经对谐振区间完成扫描,以频率扫描区间内最小阻抗点对应的驱动频率为初始状态的谐振频率。
|
图 9 频率扫描算法工作流程 Fig. 9 Flow chart of frequency scanning algorithm |
在工作过程中超声波钻受工况和温升的影响谐振频率会发生漂移,在频率扫描算法识别出超声波钻的谐振频率后,还需设计频率跟踪算法实时跟踪谐振频率。
2.3.1 基于递归最小二乘估计的频率跟踪算法基于递归最小二乘估计的频率跟踪算法主要包含爬山算法和递归最小二乘法两部分,其工作流程图如图 10所示,在频率扫描算法给定起始驱动频率之后,由爬山算法继续对谐振频率进行跟踪并在谐振点两侧振荡,在爬山算法控制驱动频率阶段,输出的驱动频率值和采样反馈的阻抗值将作为递归最小二乘估计算法的输入,对谐振点邻域阻抗曲线的局部数学模型进行参数辨识,当估计收敛后,由递归最小二乘估计算法控制驱动频率,并不断更新估计算法的输入以实现对谐振频率的精确跟踪。

|
图 10 基于递归最小二乘估计的频率跟踪算法 Fig. 10 Frequency tracking algorithm based on RLS |
爬山算法工作时,需要设定步进方向和步长大小。考虑爬山算法并不用于精确跟踪谐振频率,步长大小采用定步长的方式;步进方向由当前控制周期和上一控制周期的阻抗值大小关系决定,当前周期阻抗值比上一周期小时,说明步进方向正确,继续按当前方向改变驱动频率,当前周期阻抗值比上一周期大时,步进方向错误,反向改变驱动频率。
递归最小二乘法对谐振频率的辨识需要建立换能器阻抗曲线的数学模型,爬山算法在工作时驱动频率在谐振频率周围振荡,因此只需建立换能器在谐振点周围的局部数学模型:
| $ Z(t)=Z_0+a\left(f(t)-f_0\right)^2 $ | (3) |
式中:Z(t)、Z0、a、f(t)、f0分别为换能器阻抗、最小阻抗点阻抗值、二次项系数、驱动频率、谐振频率,其中Z(t)、f(t)为输入量,Z0、a、f0需要进行辨识。
其中为避免估计过程中常数项Z0在估计过程中有效位数带来的数值问题,同时减少需要估计的参数量,将模型改为增量形式:
| $ y(t)=-2 a f_0 \Delta f(t)+a \Delta f^2(t) $ | (4) |
式中
记φ(k)为数据向量,θ为待估计参数向量
| $ \left\{\begin{array}{l} \boldsymbol{\varphi}(t)=\left[\begin{array}{ll} \Delta f(t) & \Delta f^2(t) \end{array}\right]^{\mathrm{T}} \\ \boldsymbol{\theta}=\left[\begin{array}{ll} -2 a f_0 & a \end{array}\right]^{\mathrm{T}} \end{array}\right. $ | (5) |
对于L次观测的代价函数J为
| $ J=\sum\limits_{t=1}^L \lambda^{L-t}\left[y(t)-\boldsymbol{\varphi}^{\mathrm{T}}(t) \hat{\boldsymbol{\theta}}\right]^2 $ | (6) |
式中: λ为遗忘因子,
推导得到参数估计的递推公式为
| $ \left\{\begin{array}{l} \hat{\boldsymbol{\theta}}(t)=\hat{\boldsymbol{\theta}}(t-1)+K(t)\left[y(t)-\boldsymbol{\varphi}^{\mathrm{T}}(t) \hat{\boldsymbol{\theta}}(t-1)\right] \\ K(t)=\frac{P(t-1) \boldsymbol{\varphi}(t)}{\lambda+\boldsymbol{\varphi}^{\mathrm{T}}(t) P(t-1) \boldsymbol{\varphi}(t)} \\ P(t)=\frac{1}{\lambda}\left[I-K(t) \boldsymbol{\varphi}^{\mathrm{T}}(t)\right] P(t-1) \end{array}\right. $ | (7) |
则谐振频率的估计量为
| $ \hat{f}_0(t)=-\frac{\theta_1(t)}{2 \theta_2(t)} $ | (8) |
为了在工作过程中持续对谐振频率进行辨识,需要不断获取估计算法的输入数据,因此在输出驱动频率时需要在估计量基础上加上一个小扰动激励信号fpert,例如幅值较小的正弦信号,则实际输出的驱动频率值fout为
| $ f_{\text {out }}(t+1)=f_0(t)+f_{\text {pett }}(t+1) $ | (9) |
从换能器的滞后特性分析中可以总结出超声波钻的滞回曲线如图 11所示,fs为最小阻抗点,处于相角的跳变位置,在工作过程中容易受到负载变化的影响而使相角发生跳变,从而让超声波钻失去谐振状态,为保证超声波钻工作的稳定性,在对目标跟踪点的选取时,应该使目标点ftgt偏置于最小阻抗频率一定值,图 11中fbias为频率偏置量。当超声波钻失去谐振状态时,应根据图 11中的滞回曲线,设计相应的决策快速回到谐振状态。

|
图 11 超声波钻滞回曲线 Fig. 11 Hysteresis curve of ultrasonic drill |
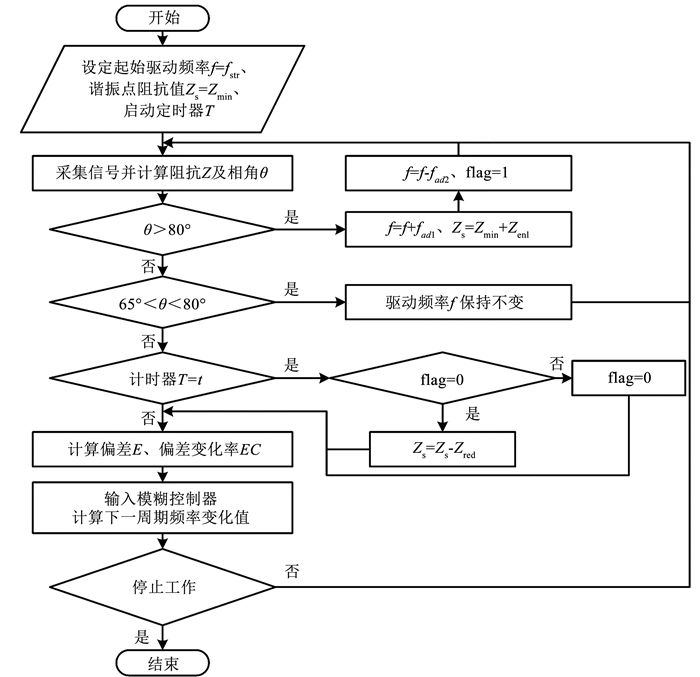
根据超声波钻的滞后特性,提出基于模糊控制的谐振频率跟踪算法,其工作流程如图 12所示,通过频率扫描算法设定初始状态的驱动频率和目标阻抗值,采集换能器信号并计算阻抗及相角值,当相角大于80°时,说明已经失去谐振状态,此时应根据阻抗滞回曲线将驱动频率增加一定值后再减小,使超声波钻快速回到谐振状态,同时增大目标阻抗值,以提升驱动的稳定性;当65°<θ<80°时,超声波钻处于临近失谐状态,若再改变驱动频率容易导致超声波钻失去谐振状态,应使驱动频率保持不变;若超声波钻在计时器计时到t的过程中都没有失去谐振状态,认为驱动状态已经比较稳定,使目标阻抗值降低一定值获得更好驱动效果;相角小于65°时,驱动频率处于谐振区间,为跟踪驱动效果较好的谐振频率,以当前控制周期的阻抗值和目标阻抗值的偏差以及偏差的变化率为模糊控制器的输入,输出驱动频率的变化量,对目标阻抗值进行跟踪,使换能器保持在较低的阻抗值。
|
图 12 基于模糊控制的频率跟踪算法 Fig. 12 Frequency tracking algorithm based on fuzzy control |
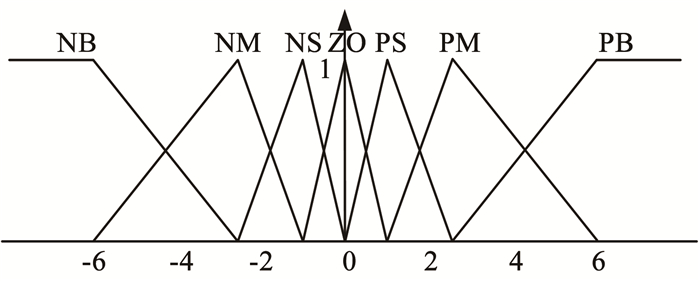
分析换能器在谐振点邻域的阻抗变化范围、阻抗和频率变化的比值、驱动频率的变化范围确定模糊控制器输入和输出的基本论域,设计模糊子集的论域为[-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6],设计模糊语言集合为[NB, NM, NS, ZO, PS, PM, PB],根据实际试验数据设计输入输出的隶属函数如图 13、14所示。

|
图 13 E/df隶属函数 Fig. 13 E/df membership function |
|
图 14 EC隶属函数 Fig. 14 EC membership function |
根据实际试验数据设计模糊控制规则(见表 2),采用Mamdani决策法,解模糊采用加权平均法。
| 表 2 模糊控制规则 Tab. 2 Fuzzy control rules |
记基于递归最小二乘估计的频率跟踪算法为控制方案1、基于模糊控制的频率跟踪算法为控制方案2,对两种频率跟踪算法的控制效果进行对比,结果如图 15所示,两种控制算法都可以对最小阻抗点进行跟踪,但是控制方案1跳变幅度较大,控制方案2跟踪稳定性更好,因此选择控制方案2作为谐振频率跟踪算法。

|
图 15 频率跟踪效果对比 Fig. 15 Frequency tracking effect comparison |
超声波换能器的端面振幅和其两端电流的大小成正比,为了使实现超声波钻更加稳定驱动,研究了恒电流控制算法。采集换能器的电流信号,与参考电流之做差得到电流偏差值,通过PID算法实现恒电流控制。
超声波钻的驱动电源主控芯片为现场可编程门阵列芯片(field programmable gate array,FPGA),需要将连续系统的PID转化为离散形式。
连续系统PID为
| $ u(t)=k_{\mathrm{p}}\left[e(t)+\frac{1}{T_{\mathrm{i}}} \int_0^t e(t) \mathrm{d} t+T_{\mathrm{d}} \frac{\mathrm{d} e(t)}{\mathrm{d} t}\right] $ | (10) |
式中: u(t)、e(t)、kp、Ti、Td分别为输出量、偏差值、比例系数、积分时间常数、微分时间常数。
在采样周期T的条件下,积分项和微分项做如下处理:
| $ \left\{\begin{array}{l} \int_0^t e(t) \mathrm{d} t \approx \sum\limits_{i=0}^k T e(i) \\ \frac{\mathrm{d} e(t)}{\mathrm{d} t} \approx \frac{e(k)-e(k-1)}{T} \end{array}\right. $ | (11) |
得到离散后PID公式为
| $ u(k)=k_{\mathrm{p}} e(k)+k_{\mathrm{i}} \sum\limits_{i=0}^k e(i)+k_{\mathrm{d}}[e(k)-e(k-1)] $ | (12) |
式中: ki=kpT/Ti,kd=kpTd/T。
为了优化驱动程序的存储资源占用,将式(12)改写为增量形式:
| $ u(k)=u(k-1)+k_0 e(k)+k_1 e(k-1)+k_2 e(k-2) $ | (13) |
式中: k0=kp+ki+kd,k1=-kp-2kd,k2=kd。
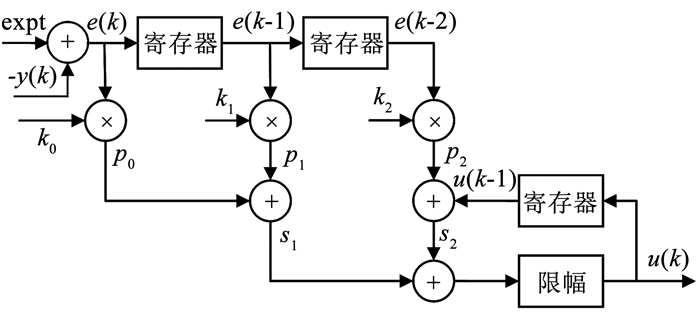
采用并行设计的思想构建增量式PID结构如图 16所示,3个乘法器和4个加法器同时工作,提高了算法的计算速度。
|
图 16 增量式PID结构 Fig. 16 Incremental PID structure |
设计驱动程序在超声波钻驱动电源中实现设计的控制算法,并通过试验对控制效果进行验证。
3.1 试验装置与条件超声波钻的钻进试验在如图 17所示的钻进实验台上进行,实验台由底座、导轨支架和砝码组成,岩石被切割为100 mm×100 mm×50 mm的立方体通过螺钉固定在实验台一侧,超声波钻安装在支架上,通过导轨滑块与底座相连,由砝码拉动支架提供钻进时的钻压力。

|
图 17 超声波钻钻进实验台 Fig. 17 Ultrasonic drilling test bench |
超声波钻的钻进试验环境如图 18所示,通过设计的驱动电源驱动超声波钻工作,上位机用于设计驱动程序烧录至驱动电源并对驱动电源上传的采样信号进行处理,可调电源为驱动电源提供28 V直流电,通过示波器测试驱动电源的输出激励信号。

|
图 18 超声波钻钻进试验环境 Fig. 18 Ultrasonic drilling test environment |
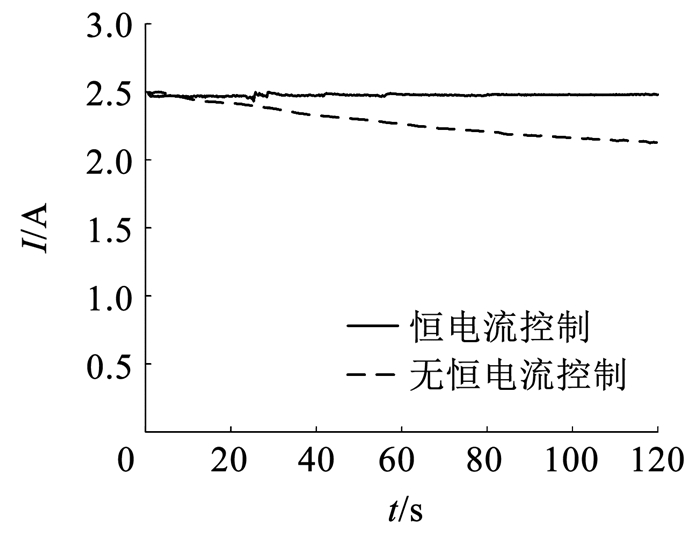
在对谐振频率跟踪的前提下,对恒电流控制的控制效果进行试验验证,试验结果如图 19所示,在没有恒定电流控制时,即使驱动电源跟踪于谐振频率,超声波换能器在工作过程中状态发生改变,导致换能器两端电流下降,恒电流控制可以使换能器两端电流保持相对稳定,电流变化范围小于0.06 A。
|
图 19 换能器电流对比 Fig. 19 Transducer current comparison |
在有恒电流控制和没有恒电流控制的条件下分别测试换能器的端面振幅,试验结果如图 20所示,对试验结果进行分析计算,恒电流控制可以抑制换能器端面振幅26.7%的衰减。

|
图 20 换能器端面振幅对比 Fig. 20 Amplitude comparison of transducer end face |
为了验证谐振频率跟踪算法的跟踪效果,分别采用固定驱动频率和频率跟踪的驱动方法进行钻进试验。固定驱动频率的方法是在谐振频率识别算法识别初始状态的谐振频率之后在工作过程中保持驱动频率值不变, 钻进试验中钻进对象为硬砂岩,其抗压强度为80~100 MPa,钻压力为5 N,超声波钻钻杆材料为钨钢,钻杆直径为3 mm。
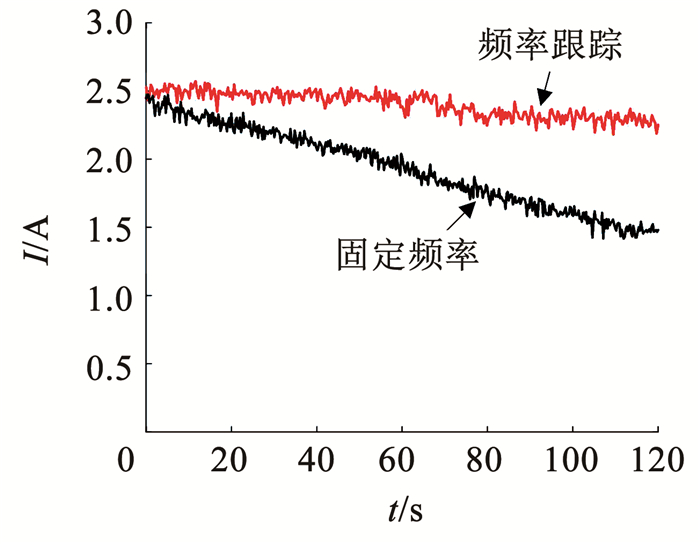
两种驱动方法在工作过程中换能器的阻抗变化曲线和电流变化曲线如图 21、22所示。当固定驱动频率时,工作过程中随着换能器状态的变化,换能器阻抗上升、两端电流下降,导致驱动效果变差;频率跟踪的控制方法可以使换能器阻抗保持在低点,降低电流衰减的幅度,保持良好的驱动状态。

|
图 21 换能器阻抗变化曲线 Fig. 21 Impedance curve of transducer |
|
图 22 换能器电流变化曲线 Fig. 22 Current curve of transducer |
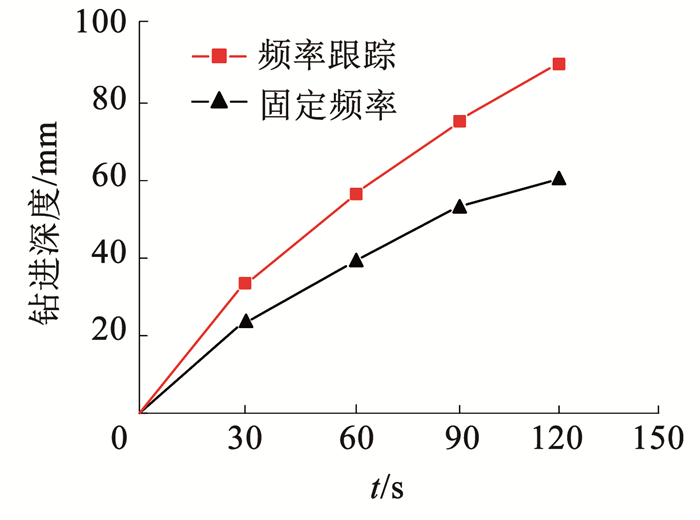
用固定频率的驱动方法和频率跟踪的驱动方法分别驱动超声波钻进行3次钻进试验,对3次试验取平均值得到钻进结果如图 23所示,采用频率跟踪的驱动方法时,钻进速度明显大于固定频率的驱动方法,取得更好钻进效果。
|
图 23 钻进速度对比 Fig. 23 Drilling speed comparison |
为了验证超声波钻驱动电源的驱动能力和对不同钻进对象的适应性,分别对如图 24所示的不同岩石样本进行钻进试验。

|
图 24 岩石样本 Fig. 24 Rock samples |
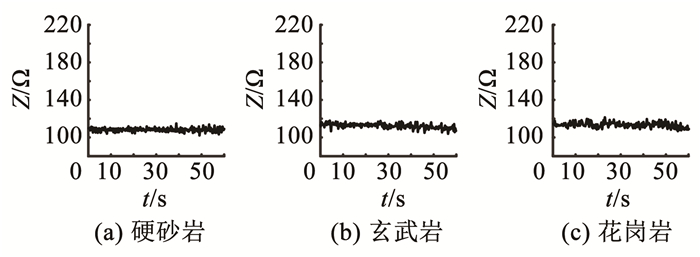
在对不同岩石的钻进过程中换能器的阻抗变化如图 25所示,从阻抗变化曲线可以看出在对不同的岩石进行钻进时,谐振控制算法都能够让换能器工作在驱动效果较好的谐振频率,让换能器的阻抗维持在低点。
|
图 25 钻进不同岩石的换能器阻抗曲线 Fig. 25 Impedance curves of transducers for drilling different rocks |
对每个岩石样本进行3次钻进试验并取平均值得到钻进速率(见表 3),所设计的谐振控制算法能够驱动超声波钻对不同的钻进对象稳定钻进,钻进速率随着钻进岩石的抗压强度增加而减小。
| 表 3 对不同岩石的钻进速率 Tab. 3 Drilling rate for different rocks |
考虑航天应用的极端温度环境,进行高低温环境下的钻进试验,搭建试验环境如图 26所示,由高低温箱提供试验温度环境,在-60~120 ℃温度范围内以30 ℃为温度变化步长进行钻进试验。

|
图 26 超声波钻高低温钻进试验 Fig. 26 High/low temperature drilling test of ultrasonic drill |
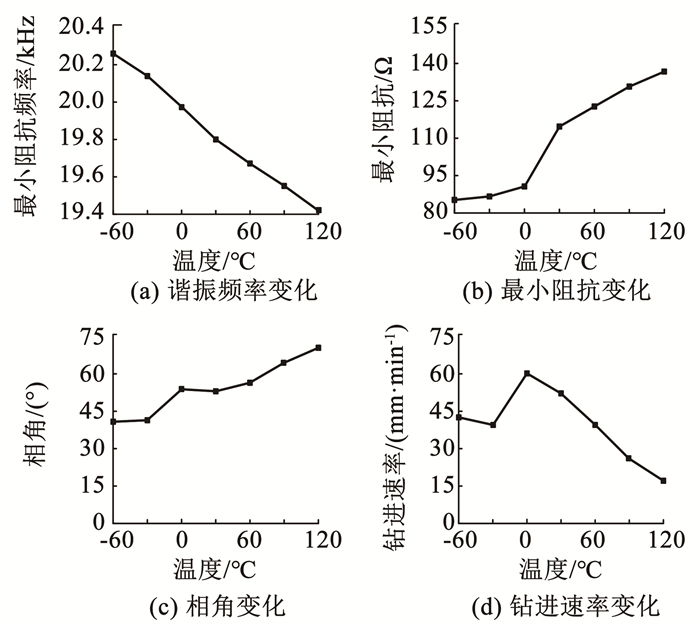
试验结果如图 27所示,随着温度的上升,换能器初始状态的谐振频率向下漂移,阻抗上升,相角上升。在高温环境下,换能器自身的工作性能较差,使得钻进速率下降,在低温环境时钻进试验台的滑轨阻力增大,一定程度上影响了钻进速度。谐振控制算法使换能器在每个温度环境下都维持在该温度的阻抗低点,保持稳定的驱动状态。
|
图 27 高低温环境钻进试验结果 Fig. 27 Drilling test results in high/low temperature environment |
1) 建立了超声波换能器的等效电路模型,分析了换能器的阻抗特性、负载特性、温度特性和滞后特性。
2) 在特性分析的基础上设计了超声波钻的谐振控制算法,采用频率扫描算法实现初始状态谐振频率的识别,在频率跟踪算法研究中,对比分析了基于递归最小二乘估计的频率跟踪算法和基于模糊控制的频率跟踪算法,后者实现了更稳定的驱动和跟踪效果,设计了恒电流控制算法增加控制的稳定性。
3) 通过试验验证了谐振控制算法的驱动效果,恒电流控制使换能器的电流波动稳定在0.06 A内,减小了26.7%的换能器端面振幅衰减,整体谐振控制算法驱动超声波钻适应于不同的钻进对象和温度环境,常温常压环境下对硬砂岩的钻进速率保持在50 mm/min以上。
| [1] |
王冠, 武小琴. 小天体探测任务统计与分析[J]. 国际太空, 2017(7): 23. WANG Guan, WU Xiaoqin. Statistics and analysis of small body exploration mission[J]. Space International, 2017(7): 23. |
| [2] |
VEVERKA J, FARQUHAR B, ROBINSON M, et al. The landing of the NEAR-Shoemaker spacecraft on asteroid 433 Eros[J]. Nature, 2001, 413(6854): 390. DOI:10.1038/35096507 |
| [3] |
SAIKI T, TAKEI Y, TAKAHASHI T, et al. Overview of Hayabusa2 asteroid proximity operation planning and preliminary results[J]. Transactions of the Japan Society of Aeronautical and Space Sciences, Aerospace Technology Japan, 2021, 19(1): 52. DOI:10.2322/TASTJ.19.52 |
| [4] |
KIMURA S, SAWADA H, SAIKI T, et al. Deep space in situ imaging results of commercial off-the-shelf visual monitoring system aboard the Hayabusa2 spacecraft[J]. IEEE Aerospace and Electronic Systems Magazine, 2021, 36(3): 16. DOI:10.1109/MAES.2020.3043068 |
| [5] |
YEOMANS D K, CHODAS P W, KEESEY M S, et al. Targeting an asteroid-The Galileo spacecraft's encounter with 951 Gaspra[J]. The Astronomical Journal, 1993, 105: 1547. DOI:10.1086/116534 |
| [6] |
LAURETTA D S, BALRAM-KNUTSON S S, BESHORE E, et al. OSIRIS-REx: Sample return from asteroid (101955) bennu[J]. Space Science Reviews, 2017, 212(1): 925. DOI:10.1007/s11214-017-0405-1 |
| [7] |
BIERHAUS E B, CLARK B C, HARRIS J W, et al. The OSIRIS-REx spacecraft and the touch-and-go sample acquisition mechanism (TAGSAM)[J]. Space Science Reviews, 2018, 214(7): 107. DOI:10.1007/s11214-018-0521-6 |
| [8] |
LI Mengxue, TANG Dewei, QUAN Qiquan, et al. Investigation of influence on the asteroid triple-drill anchoring force[J]. Powder Technology, 2023, 418: 118324. DOI:10.1016/j.powtec.2023.118324 |
| [9] |
WITTE L, ROLL R, BIELE J, et al. Rosetta lander Philae-Landing performance and touchdown safety assessment[J]. Acta Astronautica, 2016, 125: 149. DOI:10.1016/j.ACTAASTRO.2016.02.001 |
| [10] |
KAWAGUCHI J, UESUGI T, FUJIWARA A, et al. The MUSES-C, world's first sample and return mission from near Earth asteroid: NEREUS[J]. Acta Astronautica, 1996, 39(1/2/3/4): 15. DOI:10.1016/S0094-5765(96)00118-X |
| [11] |
ALDRICH J, SHERRIT S, BAO Xiaoqi, et al. Extremum-seeking control for an ultrasonic/sonic driller/corer (USDC) driven at high power[C]//Smart Structures and Materials 2006: Modeling, Signal Processing, and Control, SPIE Proceedings. San Diego, CA: SPIE, 2006: 616618. DOI: 10.1117/12.658872
|
| [12] |
KANBE N, AOYAGI M, HIROSE S, et al. Impedance-type equivalent circuits of the piezoelectric vibrator for applications to ultrasonic motors and actuators[J]. Journal of the Acoustical Society of Japan(E), 1993, 14(4): 235. DOI:10.1250/ast.14.235 |
| [13] |
SHI Weijia, ZHAO Hui, ZHAO Bo, et al. Extended optimum frequency tracking scheme for ultrasonic motor[J]. Ultrasonics, 2018, 90: 63. DOI:10.1016/j.ultras.2018.06.003 |
| [14] |
CHENG Lichen, KANG Yichen, CHEN C L. A resonance-frequency-tracing method for a current-fed piezoelectric transducer[J]. IEEE Transactions on Industrial Electronics, 2014, 61(11): 6031. DOI:10.1109/TIE.2014.2308156 |
| [15] |
KUANG Y, JIN Y, COCHRAN S, et al. Resonance tracking and vibration stablilization for high power ultrasonic transducers[J]. Ultrasonics, 2014, 54(1): 187. DOI:10.1016/j.ultras.2013.07.001 |
| [16] |
DONG Huijuan, WU Jian, ZHANG Guangyu, et al. An improved phase-locked loop method for automatic resonance frequency tracing based on static capacitance broadband compensation for a high-power ultrasonic transducer[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2012, 59(2): 205. DOI:10.1109/TUFFC.2012.2180 |
| [17] |
KYODO Y. New control method of ultrasonic motor-constant current drive and equivalent circuit[C]//Proceedings of the 41st SICE Annual Conference. SICE. Osaka, Japan: IEEE, 2003: 944
|
| [18] |
ZHANG Hongjie, WANG Fujun, ZHANG Dawei, et al. A new automatic resonance frequency tracking method for piezoelectric ultrasonic transducers used in thermosonic wire bonding[J]. Sensors and Actuators A: Physical, 2015, 235: 140. DOI:10.1016/j.sna.2015.09.040 |
| [19] |
ARIYUR K B, KRSTIĆ M. Real-time optimization by extremum-seeking control[M]. Hoboken, New Jersey: Wiley, 2003. DOI:10.1002/0471669784
|
 2024, Vol. 56
2024, Vol. 56


