对人眼开展仿生学研究,是机器视觉领域的一项重要内容,将使机器具备更为有效、高级的智能感知和认知能力。仿人眼双目图像能够模拟人左、右眼注视同一目标获取的两幅图像,在场景三维重建、仿人机器人等领域具有广阔的应用前景。
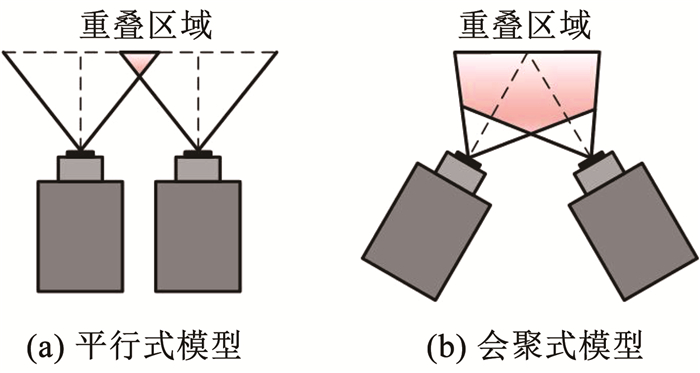
在常规的双目模型中,两相机平行放置,如图 1(a)所示。此时,处于重叠区域的某点在成像面上仅存在距离差。而人眼在观察物体时,双眼会形成会聚,使视线聚焦于同一点。图 1(b)为简化的仿人眼双目模型,与平行式模型相比,具有更大的视野重叠区域。两相机间不仅存在距离差,还存在视向差,这使得仿人眼双目图像间的变换关系变得更为复杂,图像特征匹配的准确性受到极大挑战。
|
图 1 双目相机模型 Fig. 1 Binocular camera model |
国内外研究学者针对图像特征点提取与匹配准确性问题作了很多研究,提出了一系列算法。例如,Lowe[1]提出尺度不变特征变换(scale-invariant feature transform, SIFT)算法,通过提取特征点邻域内的梯度信息构建描述向量,对多种图像变换都具有良好的稳定性。在此基础上,Bay等[2]提出快速鲁棒特征(speeded up robust features, SURF)算法,对扇形滑动窗口内的图像计算Haar小波,并对小波模板的响应进行统计,生成64维描述子,极大提高了计算效率。但该方法在视角变化下的匹配准确性低于SIFT[3]。近年来,Dong等[4]对特征点所属的尺度空间再次进行采样,通过池化生成DSP-SIFT描述子,提高了对多种图像变换的稳定性。Aguilera等[5]在Gabor滤波器的基础上改进传递函数,得到的LGHD描述子对图像光照变化具有良好的适应性。Cao等[6]利用递增的同心方形窗口描述特征点,得到的描述子维数较小,提高了匹配效率,但也丢失了部分可判别性。何显辉等[7]结合颜色和纹理信息,改进SURF描述子,能够在视角变化的图像上取得较高的匹配精度,但得到的匹配点对数量较少。
上述方法提取的匹配特征点对多位于图像的非边缘处,而人眼更加关注图像边缘信息[8],这意味着边缘匹配点对的准确与否将极大影响人眼对图像匹配准确性的整体感观,因此需要提取更多的边缘特征点并对其进行准确匹配,以满足在机器上实现仿人视觉特性的要求。此外,由于仿人眼双目图像存在显著的视点和视角差异,匹配点在两幅图像上的邻域像素信息会发生较大改变,增加特征点准确匹配的难度,而人眼的中心视力和周边视力能够以多种分辨率感知特征点邻域信息[9],提高对准确匹配点对的识别能力。因此,人眼对边缘信息敏感和多分辨率感知的特性能准确对应两幅差异较大图像的公共特征,本文根据该原理提出了一种仿人眼双目图像特征点提取与匹配方法,该方法能产生较多的边缘特征点对, 提高匹配准确性,对光照变化也具有良好的适应性。
1 方法 1.1 边缘特征点提取获得边缘匹配点对的前提是提取到足够的边缘特征点。作为一种边缘特征点检测算法,SUSAN算子提取的特征能较为完整地描述物体轮廓信息[10],如图 2所示。因此,本文选择SUSAN算子作为特征检测器,模拟人眼注重边缘信息的视觉特性。

|
图 2 SUSAN检测器的特征点提取效果 Fig. 2 Feature point extraction effect of SUSAN detector |
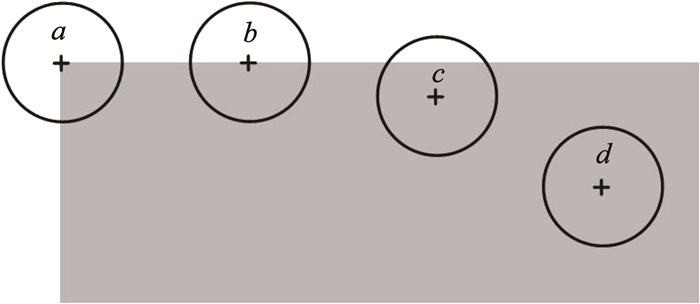
SUSAN算子采用一个圆形模板对输入图像的像素依次进行处理,通过计算模板内像素点的灰度值与模板中心灰度值的差异,将与模板中心灰度值相似的像素点归类为同一区域,该区域称为核值相似区。判断候选点是否为角点的过程如图 3所示,其中灰色区域为图像表面,a~d分别为圆形模板在图像中的不同位置。如图 3中的a,当圆形模板位于角点位置时,核值相似区面积最小;当圆形模板靠近图像表面时,如图 3中的b或c,核值相似区面积逐渐增大;当圆形模板完全处于图像内部时,如图 3中的d,核值相似区面积最大。
|
图 3 核值相似区面积示意 Fig. 3 Diagram of SUSAN area |
判断像素点是否属于核值相似区的公式为
| $ C\left(r, r_0\right)= \begin{cases}1, & \left|I(r)-I\left(r_0\right)\right| \leqslant t \\ 0, & \left|I(r)-I\left(r_0\right)\right|>t\end{cases} $ | (1) |
式中:I(r)为圆形模板中非核像素的灰度值,I(r0)为核的像素值,t为相似度阈值。对模板中每个像素都进行比较后,I(r0)处的核值相似区面积为
| $ n\left(r_0\right)=\sum\limits_{i=1}^{\max } C\left(r_i, r_0\right) $ | (2) |
在得到每个像素点的核值相似区面积后,将其与几何阈值g进行比较,若小于g,则该点被认为是一个角点。角点响应可表示为
| $ R\left(r_0\right)= \begin{cases}g-n\left(r_0\right), & n\left(r_0\right) <g \\ 0, & n\left(r_0\right) \geqslant g\end{cases} $ | (3) |
不同的g值可以检测出不同的特征,如角点、边缘等。本文将g值设定为24,以便同时提取角点和边缘特征点,使这些特征点能较为完整地描述物体轮廓信息,模拟人眼对边缘信息更加敏感的视觉特性。
1.2 多尺度描述子构建SIFT描述子对仿射变换、光照变化和噪声变化等具有良好的适应性[11]。由于仿人眼双目图像存在显著的视点和视角差异,因此本文对SIFT进行改进,与人眼中心视力与周边视力的多分辨率感知特性相结合,通过图像金字塔结构产生多尺度信息,并采用平方根核度量梯度信息之间的相似性,构建一种更为可靠的多尺度特征描述子。
SIFT算法在构建特征描述子时以特征点为中心,取16×16的邻域并将其划分为4×4的子区域,在每个子区域统计8方向的梯度直方图,形成4×4×8=128维的特征向量,如图 4(a)所示。由于仿人眼双目图像对之间存在较大的视点和视角差异,同一特征点在左、右目图像中的相对位置会发生改变,导致其周围场景发生变化。考虑到这一问题,本文首先缩小特征点的邻域大小,以特征点为中心取8×8的邻域并将其划分为2×2的子区域,然后将每个子区域划分为8个方向并进行梯度幅值统计,利用圆形模板对梯度幅值进行加权处理,进一步提高靠近关键点的梯度信息对匹配的贡献度。所使用的高斯加权函数为
| $ w_{i, j}=\mathrm{e}^{\frac{-\left(i^2+j^2\right)}{2 \times 1.5^2}} $ | (4) |

|
图 4 邻域改进示意 Fig. 4 Diagram of improved neighborhood area |
式中i、j为样本点与关键点之间的相对位置。最后形成2×2×8=32维的特征向量,如图 4(b)所示。
改进的32维描述子摒弃远离特征点的梯度信息,减少因视点和视角差异带来的梯度信息变化,能够提高后续准确匹配的抗干扰能力。SIFT描述子在单一尺度上计算梯度信息、生成特征向量,对靠近关键点的梯度信息利用有限。为进一步提高特征点的信息描述能力,增强同名特征的匹配稳定性,本文结合人眼中心视力的高分辨率与周边视力的低分辨率感知特性,在4层图像金字塔的每一层图像上对同名特征点计算改进的32维描述子,并按照尺度大小进行拼接,生成4×32=128维, 具有多尺度信息的特征描述子,获取的特征点描述信息更加全面,能够提高对主要梯度信息的利用率。两种描述子的构建方式如图 5所示。

|
图 5 构建多尺度描述子 Fig. 5 Multi-scale descriptor construction |
此时得到的描述子以欧式距离作为相似性度量,而用平方根核比较梯度相似性时得到的匹配效果更好[12]。因此本文使用平方根核衡量多尺度特征向量之间的相似性。其基本思想是对特征向量的每个元素进行L1范式归一化,并开平方根,以达到用平方根核替代原先的特征向量的目的。
设x和y是具有欧式距离规范的n维特征向量,则x、y之间的欧式距离为
| $ d_E(\boldsymbol{x}, \boldsymbol{y})^2=2-2 S_E(\boldsymbol{x}, \boldsymbol{y}) $ | (5) |
式中SE(x, y)=xTy,表示x和y之间的欧拉距离与它们的相似性。x和y的平方根核定义为
| $ H(\boldsymbol{x}, \boldsymbol{y})=\sum\limits_{i=1}^n \sqrt{x_i y_i} $ | (6) |
设m和n为多尺度描述子的特征向量,首先对m、n进行L1规范化,再对每个元素求平方根,即
| $ S_E(\sqrt{\boldsymbol{m}}, \sqrt{\boldsymbol{n}})=\sqrt{\boldsymbol{m}}^{\mathrm{T}} \sqrt{\boldsymbol{n}} $ | (7) |
故有
| $ d_E(\sqrt{\boldsymbol{m}}, \sqrt{\boldsymbol{n}})^2=2-2 H(\boldsymbol{m}, \boldsymbol{n}) $ | (8) |
采用双向匹配的方式对得到的多尺度描述子进行初步匹配,具体步骤为:
Step 1 将仿人眼左、右目图像中提取的特征点集合分别记为P、Q。
Step 2 首先将P作为基准集合,遍历其中所有的点,以欧氏距离作为相似性准则,找到Q中与其对应的匹配点,记为集合Z{P→Q}。
Step 3 然后采用相同的策略,以Q作为基准集合,遍历其中所有的点,搜索其在P中的对应匹配点,记为集合W{Q→P}。
Step 4 比较集合Z和W中的所有匹配点对,若某匹配点对在两个集合中存在相同的对应关系,则这两点被认为是一对正确匹配点对。
此时得到的初步匹配点集中仍会不可避免地存在部分误匹配对,因此本文采用随机抽样一致算法(RAndom SAmple consensus, RANSAC)[13]对匹配点对再次进行筛选。RANSAC算法通过迭代计算的方式在初步匹配点集中寻找满足某一正确模型对应的最大内点集,能够有效地剔除误匹配点对。
2 实验与分析为充分说明本文算法在提高匹配准确率和匹配精度方面的优势,对提出的多尺度描述子和整体算法分别进行评价。首先将多尺度描述子与SIFT、SURF、Root-SIFT[12]、LGHD以及BEBLID[14]描述子进行对比分析; 然后在不同光照变化的仿人眼双目图像上对多尺度描述子的适应性进行验证;最后对整体算法进行单应性估计实验(homography estimation),并与GMS[15]、RIFT[16]、SuperGlue[17]和DFM[18]算法进行对比。所有实验均在Windows 10, 64位操作系统,基于Intel Core i5-6300HQ、16 G内存的测试环境下进行。
2.1 描述子对比实验为体现多尺度描述子的匹配性能,将其与SIFT、SURF、Root-SIFT、LGHD以及BEBLID描述子进行性能比较。SIFT算法通过统计邻域梯度信息生成描述向量。SURF算法通过计算水平和垂直方向的Haar小波响应获取描述信息,这两种描述子因对多种图像变换都具有良好的鲁棒性而得到广泛应用。Root-SIFT算法使用海林格距离替代欧式距离以比较SIFT描述子之间的相似性,能够产生更多的准确匹配点对。LGHD算法通过构建多尺度和多方向的Log-Gabor滤波器计算频率和空间信息来描述特征点邻域信息,对光照变化具有良好的适应性。BEBLID算法作为近年来先进的机器学习算法之一[19],利用积分图像计算平均灰度值之差,能够显著提高图像匹配精度。
2.1.1 评价指标为进行定量比较,本文采用文献[20-21]中的评价指标对多尺度描述子的性能进行量化比较,具体如下。
1) 假定匹配率(putative match ratio, PMR)为初步匹配点对数量与左、右目图像中提取较少特征点数量的比值,表示算法的选择性,假定匹配率越低说明算法的限制性越强,即
| $ P_p=\frac{N_m}{\min \left(N_{\text {left }}, N_{\text {right }}\right)} $ | (9) |
式中:Pp为假定匹配率,Nm为初步匹配点对数量,Nleft、Nright分别为左、右目图像中提取的特征点数量。
2) 正确匹配数(number of correct matches, NCM)表示最终得到的匹配点对数量。本文以经过RANSAC算法筛选后得到的匹配点对数量作为正确匹配点对数量,即
| $ N_c=N_r $ | (10) |
式中:Nc为正确匹配点对数量,Nr为经过RANSAC算法筛选后得到的匹配点对数量。
3) 可重复率(repeatability, REP)为正确匹配点对数量与左、右目图像中提取较少特征点数量的比值,可重复率越高说明算法的准确率越高,即
| $ P_r=\frac{N_c}{\min \left(N_{\text {left }}, N_{\text {right }}\right)} $ | (11) |
式中Pr为可重复率。
2.1.2 实验过程实验选取6组仿人眼双目图像进行特征提取与匹配,测试图像如图 6所示,图 6中的圆圈表示仿人眼双目视线会聚点。其中: 第1、2组实验图像分别表示平面场景和三维场景, 第3、4组实验图像分别表示近距离场景和远距离场景, 第5、6组实验图像分别表示简单场景和复杂场景。为充分体现描述子的匹配性能,在特征提取阶段均采用SUSAN检测器,匹配方式和筛选过程均保持一致,图 7展示了不同描述子对比的实验结果。

|
图 6 仿人眼双目图像 Fig. 6 Humanoid-eye binocular image |

|
图 7 不同描述子的性能比较结果 Fig. 7 Performance comparison results of different descriptors |
从图 7可以看出,本文算法的假定匹配率略低,却能取得最高的可重复率,说明本文提出的多尺度描述子能够有效增强对特征点描述的独特性,降低不相似特征点间的误匹配率,从而减少误匹配点对数量。这主要是由于在构建描述子时结合人眼中心视力与周边视力的多分辨率感知特性,采用多尺度结构计算特征点邻域梯度信息,得到的信息量更加全面,并能充分利用特征点周围的主要梯度信息,提高特征点初始匹配时的抗干扰能力,限制不可靠特征点之间的匹配能力,以达到有效剔除误匹配点对的目的。从图 7(b)可以看出,本文提出的多尺度描述子在6组实验图像上取得的平均可重复率为11.31%,比SIFT描述子高出5.62%,比第2位的LGHD描述子和第3位的Root-SIFT描述子分别高出2.88%、5.03%,表明多尺度描述子在SIFT描述子的基础上能够显著提高匹配准确率,较其他算法相比同样具有明显优势。
为验证本文提出的多尺度描述子在光照变化下具有一定的适应能力,选取了5组存在3种光照强度的仿人眼双目图像进行实验,如图 8所示,图 8中的圆圈表示仿人眼双目视线会聚点。图 9展示了其中一组图像的正确匹配和误匹配结果。

|
图 8 3种光照强度变化下的仿人眼双目图像 Fig. 8 Humanoid-eye binocular images under three kinds of illumination intensity changes |

|
图 9 3种光照强度变化下不同描述子的匹配效果 Fig. 9 Matching effect of different descriptors under three kinds of illumination intensity variations |
由图 9可知,SURF算法和BEBLID算法在图像存在较大的视点和视角差异时易出现误匹配。SIFT算法和Root-SIFT算法对视点和视角变化具有一定的鲁棒性,但随着光照强度减弱,其重复率也会随之降低,说明其对图像光照变化的适应能力较差。LGHD作为一种适用于非线性强度变化图像之间的特征点匹配算法,能够在图像存在光照变化时保持较为稳定的重复率,但得到的正确匹配点对的数量有限。相较于上述算法,本文算法能够取得数量最多的正确匹配点对,并且在光照强度降低时仍能保持较为稳定的重复率,说明对图像光照变化具有良好的适应性。
为了在图像存在光照强度变化时对算法进行定量比较,对正确匹配数和可重复率这两种直接反映算法匹配性能的指标在不同光照强度下的实验结果进行平均化,计算结果见表 1。
| 表 1 光照强度变化下6种算法的平均计算结果 Tab. 1 Average calculation results of six algorithms under illumination intensity variations |
由表 1可知,在不同光照强度变化下,本文算法可取得数量最多的正确匹配点对和最高的可重复率。与SIFT算法相比,本文算法得到的正确匹配点对数量增加60.14%,可重复率提高5.66%,说明本文提出的多尺度描述子与SIFT描述子相比具有更强的光照变化适应能力。相较于第2位的LGHD算法和第3位的Root-SIFT算法,本文算法得到的正确匹配点对数量分别增加10.10%、51.66%,可重复率分别提高1.28%、5.18%,说明本文算法不仅能提高存在视点和视角差异图像的匹配准确率,而且对图像光照变化具有良好的适应性。
最后,本文对不同描述子的运行效率进行了对比分析,表 2为6种描述子在图 6所示的仿人眼双目图像上的平均运行时间。
| 表 2 6种算法的平均运行时间 Tab. 2 Average running time of six algorithms |
由表 2可知,SURF、LGHD和BEBLID算法的运行时间较短,但其产生的正确匹配点对数量较少、可重复率也较低。而与本文描述子维数相同的SIFT和Root-SIFT算法的匹配效果远低于本文算法。与这两种算法相比,本文算法的运行时间花费略高,这是由于SIFT和Root-SIFT算法只在单一尺度上构建描述子,而本文则在4个不同尺度上构建描述子,这会不可避免地增加匹配耗时。
2.2 总体算法对比实验为进一步说明本文算法在图像存在视点和视角差异下的匹配准确性,将所提出的总体算法与GMS、RIFT、SuperGlue和DFM算法进行对比。GMS算法以运动估计为基础,是一种具有代表性的特征匹配过滤算法,在实验中采用其默认的ORB算法进行特征点提取与匹配。RIFT算法使用相位一致性替代图像强度来检测特征点,并通过Log-Gabor滤波器构建用于特征描述的最大索引图,不仅提高了特征检测的稳定性,也克服了梯度信息对特征描述的限制性。SuperGlue和DFM是两种先进的基于深度学习的特征匹配算法,前者利用图神经网络对特征点进行匹配,在实验中采用其默认的SuperPoint算法提取特征点及其描述子;后者使用预训练的VGG网络提取特征点,对待匹配图像应用由粗到细的策略实现特征点对的准确匹配。
2.2.1 评价指标本文对上述算法进行了单应性估计实验以比较各自的匹配性能。采用文献[21]中的精确率作为评价指标,表示准确估计值与所有估计值的比值。具体来说,本文利用RANSAC算法推导出仿人眼双目图像对之间的变换模型,并将其与真实投影模型进行比较,若误差小于3像素,则认为该单应性估计准确。
2.2.2 实验过程选取5组仿人眼双目图像进行单应性估计实验,实验结果见表 3。
| 表 3 仿人眼双目图像单应性估计的定量比较 Tab. 3 Quantitative comparison of homography estimation in humanoid-eye binocular images |
由表 3可知,本文算法在除图组1外的4个图组中均取得了97.00%以上的精确率。与其他4种算法相比,本文算法的平均精确率最高,比第2位的RIFT算法和第3位的DFM算法分别高出2.97%、13.30%,说明本文算法相较于其他4种常规算法和基于深度学习的特征点匹配算法在匹配准确性方面具有明显的优势。
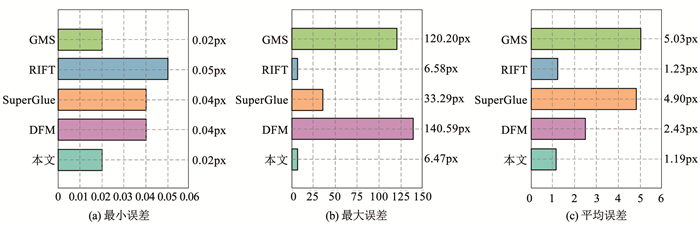
为了对具体的投影误差进行量化比较,实验过程中对相关算法的单应性估计误差的最小值、最大值以及平均值进行比较,图 10展示了这3种距离误差在5个图组中的平均计算结果。可以看出,本文算法的最小误差、最大误差和平均误差均低于其他4种算法,这表明本文算法能够取得较为准确的匹配结果,提高对存在视点和视角变化图像的匹配稳定性。
|
图 10 5种算法的平均单应性估计误差 Fig. 10 Average estimated homography error of five algorithms |
1) 结合人眼对边缘信息敏感和多分辨率感知的特性,以平方根核作为相似性度量,构建了一种多尺度描述子。
2) 实验结果表明:与相关描述子相比,多尺度描述子的可重复率至少提高2.88%,对光照强度变化也具有良好的适应性;与相关总体算法相比,本文算法的匹配精确率至少提高2.97%,并能使距离误差达到最小。
3) 本文算法能够提取较多的边缘特征点对,增强描述子的独特性,限制不可靠特征之间的匹配能力,实现视点和视角差异较大的仿人眼双目图像的准确匹配。这对于推动仿生视觉技术在智能机器上的应用具有重要的意义。
| [1] |
LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91. DOI:10.1023/B:VISI.0000029664.99615.94 |
| [2] |
BAY H, ESS A, TUYTELAARS T, et al. Speeded-up robust features (SURF)[J]. Computer Vision and Image Understanding, 2008, 110(3): 346. DOI:10.1016/j.cviu.2007.09.014 |
| [3] |
LUO Juan, GWUN O. A comparison of SIFT, PCA-SIFT and SURF[J]. International Journal of Image Processing, 2009, 3(4): 143. |
| [4] |
DONG Jingming, SOATTO S. Domain-size pooling in local descriptors: DSP-SIFT[C]//2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Boston, MA: IEEE, 2015: 5097. DOI: 10.1109/CVPR.2015.7299145
|
| [5] |
AGUILERA C A, SAPPA A D, TOLEDO R. LGHD: A feature descriptor for matching across non-linear intensity variations[C]//2015 IEEE International Conference on Image Processing (ICIP). Quebec City, QC, Canada: IEEE, 2015: 178. DOI: 10.1109/ICIP.2015.7350783
|
| [6] |
CAO Yu, PANG Bo, LIU Xin, et al. An improved Harris-SIFT algorithm for image matching[C]//International Conference on Advanced Hybrid Information Processing. Cham: Springer, 2018: 56. DOI: 10.1007/978-3-319-73317-3_8
|
| [7] |
何显辉, 王凯, 张平, 等. 融合颜色和纹理的多特征匹配算法[J]. 激光杂志, 2022, 43(3): 87. HE Xianhui, WANG Kai, ZHANG Ping, et al. Multi feature matching algorithm integrating color and texture[J]. Laser Journal, 2022, 43(3): 87. DOI:10.14016/j.cnki.jgzz.2022.03.087 |
| [8] |
徐翰文, 张闯, 陈苏婷. 基于视觉显著性的图像特征提取算法[J]. 计算机应用, 2022, 42(Sup.2): 72. XU Hanwen, ZHANG Chuang, CHEN Suting. Image feature extraction algorithm based on visual saliency[J]. Journal of Computer Applications, 2022, 42(Sup.2): 72. DOI:10.11772/j.issn.1001-9081.2022040574 |
| [9] |
STEWART E E M, VALSECCHI M, SCHÜTZ A C. A review of interactions between peripheral and foveal vision[J]. Journal of Vision, 2020, 20(12): 2. DOI:10.1167/jov.20.12.2 |
| [10] |
SMITH S M, BRADY J M. SUSAN: A new approach to low level image processing[J]. International Journal of Computer Vision, 1997, 23(1): 45. DOI:10.1023/A:1007963824710 |
| [11] |
丁国绅, 乔延利, 易维宁, 等. 基于光谱图像空间的改进SIFT特征提取与匹配[J]. 北京理工大学学报, 2022, 42(2): 192. DING Guoshen, QIAO Yanli, YI Weining, et al. Improved SIFT feature extraction and matching based on spectral image space[J]. Transactions of Beijing Institute of Technology, 2022, 42(2): 192. DOI:10.15918/j.tbit1001-0645.2020.024 |
| [12] |
ARANDJEIOVIĆ R, ZISSERMAN A. Three things everyone should know to improve object retrieval[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Providence, RI: IEEE, 2012: 2911. DOI: 10.1109/CVPR.2012.6248018
|
| [13] |
FISCHLER M A, BOLLES R C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography[M]. Amsterdam: Elsevier, 1987: 726. DOI:10.1016/b978-0-08-051581-6.50070-2
|
| [14] |
SUÁREZ I, SFEIR G, BUENAPOSADA J M, et al. BEBLID: Boosted efficient binary local image descriptor[J]. Pattern Recognition Letters, 2020, 133: 366. DOI:10.1016/j.patrec.2020.04.005 |
| [15] |
BIAN Jiawang, LIN Wenyan, LIU Yun, et al. GMS: Grid-based motion statistics for fast, ultra-robust feature correspondence[J]. International Journal of Computer Vision, 2020, 128(6): 1580. DOI:10.1007/s11263-019-01280-3 |
| [16] |
LI Jiayuan, HU Qingwu, AI Mingyao. RIFT: Multi-modal image matching based on radiation-variation insensitive feature transform[J]. IEEE Transactions on Image Processing: A Publication of the IEEE Signal Processing Society, 2019, 29: 3296. DOI:10.1109/TIP.2019.2959244 |
| [17] |
SARLIN P E, DETONE D, MALISIEWICZ T, et al. SuperGlue: Learning feature matching with graph neural networks[C]//2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Seattle, WA: IEEE, 2020: 4937. DOI: 10.1109/CVPR42600.2020.00499
|
| [18] |
EFE U, INCE K G, AYDIN ALATAN A. DFM: A performance baseline for deep feature matching[C]//2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW). Nashville, TN: IEEE, 2021: 4279. DOI: 10.1109/CVPRW53098.2021.00484
|
| [19] |
MATALOV D P, LIMONOVA E E, SKORYUKINA N S, et al. Memory efficient local features descriptor for identity document detection on mobile and embedded devices[J]. IEEE Access, 2022, 11: 1104. DOI:10.1109/ACCESS.2022.3233463 |
| [20] |
WANG Zhengbing, FENG Xugang, XU Guili, et al. A robust visible and infrared image matching algorithm for power equipment based on phase congruency and scale-invariant feature[J]. Optics and Lasers in Engineering, 2023, 164: 107517. DOI:10.1016/j.optlaseng.2023.107517 |
| [21] |
XIA Yifan, JIANG Jie, LU Yifan, et al. Robust feature matching via progressive smoothness consensus[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2023, 196: 502. DOI:10.1016/j.isprsjprs.2023.01.016 |
 2024, Vol. 56
2024, Vol. 56


