2. 福州大学 机械工程及自动化学院, 福州 350108;
3. 上海中研仪器制造有限公司, 上海 201411
2. School of Mechanical Engineering and Automation, Fuzhou University, Fuzhou 350108, China;
3. Shanghai Zhongyan Instrument Manufacturing Co., Ltd., Shanghai 201411, China
金属材料硬度[1]、弹性模量[2]和屈服强度是工程应用中重要的力学性能参数。硬度对微观组织结构和加工工艺敏感,是弹性模量和屈服强度的综合反映,基于压痕法获得材料的力学性能适用于小试样,较传统测试方法具有实验过程简便且对试样破坏小的优点,对材料力学性能的快速检测和降低测试成本有重要意义。努氏硬度HK和维氏硬度HV广泛应用于各种材料的表征,如涂层、薄膜、生物材料、陶瓷和金属玻璃等。同一种材料在相同载荷下,努氏压痕比维氏压痕深度浅,对试样破坏更小,测量精度高。由于维氏压痕两条对角线长度相等,对材料的弹性回复不敏感,无法定量表征材料的弹性回复,使得维氏硬度及其压痕对角线不能用于表征材料的弹性模量。Marshall等[3]根据努氏压痕短对角的弹性回复求解得到了玻璃和陶瓷等脆性材料的弹性模量E。基于努氏硬度表征弹性模量的方法对于压痕短对角线处堆积不太明显的材料较适合(如陶瓷、玻璃、光学晶体和热喷涂层),在较大载荷下同样适用于聚合物,但不适合短对角线处堆积较严重的金属材料。Conway[4]也提出了一种利用努氏压痕弹性回复计算弹性模量的方法,应用于玻璃、陶瓷和热障涂层。金属材料的名义硬度H可以衡量材料抗滑移性能,预估屈服强度σy[5]。基于HK可以获得金属玻璃的E和σy[6], 对于理想塑性材料,其H与σy直接相关;对于非理想塑性材料,H和σy之间有线性关系(例如σy≈H/3)[7],并会受到材料(例如E和泊松比v)和压头(例如等效圆锥半顶角θ)的影响[8]。金属、陶瓷、玻璃、聚合物等材料的显微硬度存在压痕尺寸效应,即随着载荷的增加硬度值有下降的趋势:金属材料显微硬度的尺寸效应可以用Meyer定律[9]、弹塑性变形模型[10]、Hays-Kendll模型[11]和比例试样阻力模型[12]等解释。材料的弹性模量可以被仪器化压入方法有效表征。仪器化压入具有试样制备简单和测试分辨率高等优点,广泛应用于表征各类材料(比如金属、高分子、陶瓷、玻璃和薄膜等)在微小区域的力学性能(比如压入硬度、结合强度、拉伸性能、断裂韧度、残余应力和黏弹塑性等)。分析仪器化压入载荷-位移曲线的加载[13]或卸载阶段都可以获得材料的弹性模量和硬度。仪器化压入过程的复杂应力使得通过载荷-位移曲线很难求解材料的屈服强度和硬化指数,并且单种压头下结果不唯一[14],需要结合有限元和机器学习[15]和基于能量等效原理[16]等才能表征弹塑性本构力学参数。
本文首次利用努氏硬度表征金属材料的弹性模量和屈服强度。在考虑金属材料压痕短对角线堆积和压痕尺寸效应影响下,利用金属材料的努氏硬度建立了快捷估算材料弹性模量和屈服强度的修正模型,有助于降低实验成本,开拓了努氏硬度在金属材料力学性能表征的应用。
1 努氏硬度和仪器化压入试验对35种金属材料进行多级水磨,随后进行机械抛光去掉试样表面划痕,最终达到镜面效果,最后依次在丙酮、无水乙醇和超纯水中进行10 min的超声清洗,除油去污,用高纯氮气吹干后放入干燥恒温箱中密封保存备用。35种金属材料的弹性模量文献报道值Eref(下标“ref”表示由文献报道)见表 1。利用上海中研仪器制造有限公司的HVST系列显微硬度计进行努氏硬度测试。努氏压头是两棱间半夹角分别为θ1=86.25°,θ2=65.00°的金刚石四棱锥压头[6], 实验载荷为0.245~9.800 N。为使压痕不超过屏幕显示范围,软材料的最大测试载荷较小,各种材料测试的最大载荷见表 1。每种载荷测试5次取平均值, 保载时间为15 s,卸载后分别测量努氏压痕两条对角线的长度。努氏硬度HK为实验载荷P与卸载后压痕投影面积AP的比值[17]为
| $ H_{\mathrm{K}}=\frac{P}{A_{\mathrm{P}}}=\frac{2 P}{d^2} \cdot \frac{\tan \theta_1}{\tan \theta_2}=14.229 \cdot \frac{P}{d^2} $ | (1) |
| 表 1 35种金属材料的力学性能(Eref、υ、σyref)[21-22]、努氏硬度测试的最大载荷、最大载荷下努氏压痕长对角线d、b/d和努氏硬度HK Tab. 1 Mechanical properties of 35 metals (Eref, υ, σyref)[21-22], Knoop hardness HK, long diagonal d, and b/d under maximum load |
式中d为努氏压痕长对角线长度。
采用Anton Paar公司型号为NHT2的仪器化纳米压入仪在大气环境下采用载荷控制模式将金刚石三棱锥Berkovcih压头垂直压入试样表面测试金属材料的弹性模量EIT。仪器化压入载荷-位移(F-h)曲线的卸载段可以用幂函数拟合[18]:
| $ \frac{F}{F_{\text {max }}}=\left(\frac{h-h_{\mathrm{p}}}{h_{\text {max }}-h_{\mathrm{p}}}\right)^m $ | (2) |
式中:Fmax、hmax分别为最大载荷和最大位移,残余接触位移hp、m(大多数材料的m范围为1.2~1.7[17]) 为拟合参数。
接触刚度S在卸载初始(即最大位移hmax)处确定:
| $ S=\left.\frac{\mathrm{d} F}{\mathrm{~d} h}\right|_{h_{\max }}=\frac{m F_{\max }}{h_{\max }-h_{\mathrm{p}}} $ | (3) |
弹性模量EIT可由缩减模量Er获得, 即
| $ \begin{aligned} & \frac{1}{E_{\mathrm{r}}}=\frac{1-v^2}{E_{\mathrm{IT}}}+\frac{1-v_{\mathrm{i}}^2}{E_{\mathrm{i}}} \\ & E_{\mathrm{r}}=\frac{\sqrt{\pi}}{2 \beta} \frac{S}{\sqrt{A_{\mathrm{p}}\left(h_{\mathrm{c}}\right)}} \\ & h_{\mathrm{c}}=h_{\max }-\varepsilon \frac{F_{\max }}{S} \end{aligned} $ | (4) |
式中:υ为被测材料的泊松比(见表 1),Ei=1 141 GPa和υi=0.07分别为金刚石压头的弹性模量和泊松比,β=1.034[19]为Berkovich压头的形状修正因子, 接触投影面积Ap(hc)为接触深度hc(在hmax处确定)的函数,通过对弹性模量和泊松比已知的标准材料(如熔融石英)进行仪器化压入试验获得若干hc下的Ap,利用B-样条插值拟合得到[19], 常数ε与压头几何形状有关,同时取决于拟合指数m[20]。
2 微米努氏硬度尺寸效应分析 2.1 努氏硬度的Meyer定律[9]Meyer定律中压痕的实验载荷P与努氏压痕长对角线d之间满足:
| $ $$ P=A_0 d^n, \ln P=\ln A_0+n \ln d $$ $ | (5) |
式中A0和材料有关,指数n可以衡量微米硬度的尺寸效应:n=2时无尺寸效应,此时硬度不随载荷的增加而变化;n < 2时材料有正尺寸效应,此时硬度随着载荷的增加而降低;n>2时材料有逆压痕尺寸效应,此时硬度随着载荷的增加而增加。图 1显示了硬度尺寸效应的示意图,尺寸效应在小载荷下较为显著,在大载荷下硬度近似为常数,尺寸效应可以忽略,所以在大载荷下测量得到的硬度更接近材料的真硬度。

|
图 1 压痕尺寸效应曲线 Fig. 1 Schematic illustration of indentation size effect |
压头尖端的钝化和卸载后压痕的弹性回复等都会对测量结果产生影响[10],因此努氏压痕长对角线d和载荷P有如下关系:
| $ P=A_1\left(d+d_0\right)^2, P^{1 / 2}=A_1^{1 / 2} d_0+A_1^{1 / 2} d $ | (6) |
式中:d0受压头钝化及压痕弹性回复综合影响,A1与材料有关。式(6)两侧同时除以d2可得
| $ \frac{P}{d^2}=A_1\left(1+\frac{d_0}{d}\right)^2 $ | (7) |
式中可以解释努氏硬度随载荷下降。随着载荷的增加d0/d和P/d2都逐渐减小,d0/d趋近于0,P/d2趋近于A1。与载荷无关的真硬度为
| $ H_{\mathrm{K}, \mathrm{EPD}}=14.229 \frac{P}{\left(d+d_0\right)^2}=14.229 A_1 $ | (8) |
材料发生塑性变形时对应一个临界载荷W,施加的载荷大于W时材料才会发生塑性变形,否则只会发生弹性变形。努氏压痕长对角线d与载荷P满足如下关系:
| $ P=W+A_2 d^2, \frac{P}{d^2}=\frac{W}{d^2}+A_2 $ | (9) |
式中A2与材料有关,而与载荷无关。W/d2随载荷的增大而降低,趋近于0,使得P/d2趋近于A2,因此硬度随着载荷增加而降低,趋于常数。与载荷无关的真硬度为
| $ H_{\mathrm{K}, \text { Hays }}=14.229 \frac{P-W}{d^2}=14.229 A_2 $ | (10) |
Li等[12]提出了比例试样模型来解释材料的压痕尺寸效应:
| $ P=A_3 d+A_4 d^2, \frac{P}{d^2}=\frac{A_3}{d}+A_4 $ | (11) |
式中A3、A4分别为与材料的弹性和塑性性能相关的常数。随着载荷的增大,A3/d逐渐减小,使得P/d2趋近于A4,因此硬度逐渐变小,趋于常数。材料的真硬度为
| $ H_{\mathrm{K}, \mathrm{PSR}}=\frac{P-A_3 d}{A_{\mathrm{P}}}=14.229 A_4 $ | (12) |
图 2显示60Si2Mn、HT150、Q235和T2紫铜4种典型材料的努氏硬度随载荷的增加而降低,最后趋于稳定,有正压痕尺寸效应,其他材料具有相同的变化趋势。金属材料的维氏硬度[23]和压入硬度也有相同的现象。
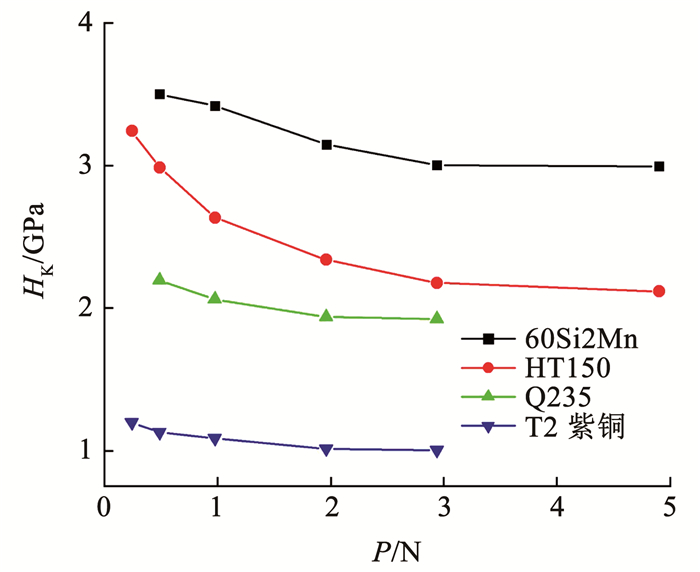
|
图 2 不同载荷下的努氏硬度 Fig. 2 Variation of Knoop hardness with load |
利用4种模型对努氏硬度的尺寸分析分别如图 3(a)~3(d)所示,4种模型拟合效果都很好,置信度R2均大于0.99,拟合参数见表 2。35种金属材料在Meyer定律中的n在1.73~1.98之间(在1.60~ 2.00之间,属于软材料特性),都表现出正压痕尺寸效应。Meyer定律能直接反映材料的压痕尺寸效应,但不能解释压痕尺寸效应的原因。对于弹塑性变形模型,d0在0.50~16.00 μm之间,较大的d0其他文献也有报道。对于Hays-Kendall模型,W的值在11.00~272.00 mN之间,说明不同材料加载时需要克服的最小弹性载荷不同。对于比例试样模型,A3在0.488~3.750 mN/μm之间,不同材料加载至相同深度时需要克服的弹性性能不同。虽然d0、W和A3都和材料的弹性性能相关,然而通过分析表 1、2中的数据并没发现这些参数与弹性模量E或HK/E之间的关系,因此各模型中参数的物理意义还有待于进一步深入研究。

|
图 3 努氏硬度尺寸效应分析 Fig. 3 Analysis of size effect of Knoop hardness |
| 表 2 压痕尺寸效应分析结果 Tab. 2 Analysis results of indentation size effect |
图 4显示了4种模型的拟合参数之间的关系。d0随n的增大有线性减小的趋势,这是因为材料的正压痕尺寸效应越明显时,n会越小或d0会越大。A3随W的增大有线性增大的趋势,这是由于发生塑性变形的最小载荷变大时,A3和W都会变大。
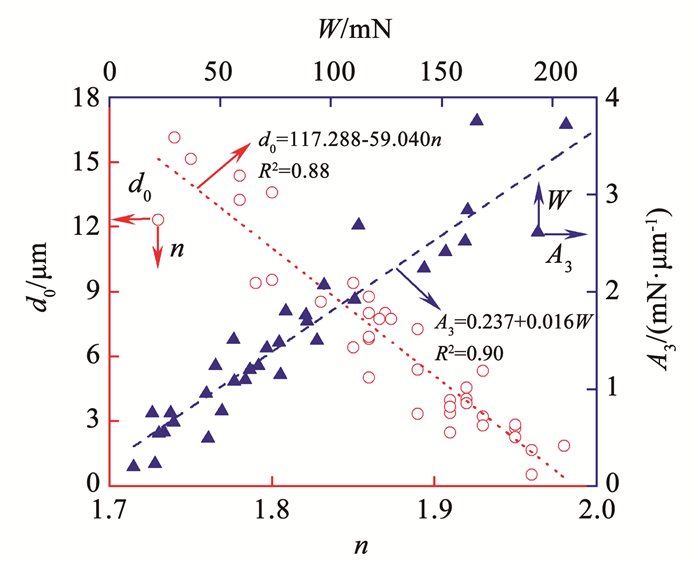
|
图 4 4种压痕尺寸模型拟合参数之间的关系A3、W和d0、n Fig. 4 Relationships among fitting parameters of the 4 models for indentation size effect: A3, W and d0, n |
图 5比较了不同模型计算的真硬度(HK, EPD、HK, Hays和HK, PSR,见表 2)和趋于稳定的努氏硬度(即最大载荷下的硬度值,见表 1),3个模型(EPD、Hays-Kendoll、PSR)计算的真硬度与趋于稳定的HK大体一致,可以用大载荷下的努氏硬度值表示材料的真硬度,因此本文均采用大载荷下趋于稳定的努氏硬度值(见表 1)来表征材料的弹性模量和屈服强度。小载荷下材料的微观组织对努氏硬度有较大影响,应选用大载荷下的硬度值作为真硬度,此时,压痕尺寸远大于晶粒尺寸,努氏硬度受材料的各向异性和微观不均匀性的影响可忽略。

|
图 5 3种压痕尺寸模型得到的真硬度(HK, EPD、HK, Hays和HK, PSR)与努氏硬度HK的比较 Fig. 5 Comparison between true hardness (HK, EPD, HK, Hays, and HK, PSR) by 3 indentation size models and Knoop hardness HK |
图 6(a)~6(d)分别为纯W、H13模具钢、T2紫铜和AZ61镁合金的仪器化压入载荷-位移曲线以及压痕光学图像。不同Fmax下加载曲线基本重合,压痕清晰,无裂纹。纯W和H13模量钢的压痕可以观察到材料堆积;T2紫铜有较明显的堆积,所以大部分金属材料的b/d>1/7.11,见表 2;AZ61镁合金的压痕出现了明显的沉陷现象,所以镁合金的b/d < 1/7.11。4种材料的弹性模量EIT(下标“IT”为由仪器化压入测得)随Fmax的变化如图 6(e)所示。大部分材料的EIT基本不随Fmax变化,例如H13模具钢、T2紫铜和AZ61镁合金的EIT可近似为常数。少数材料的EIT在大载荷下缓慢下降,只有在小载荷下可近似为常数,比如纯W的EIT在小载荷下(Fmax < 200 mN) 可近似为常数,而在大载荷时(Fmax> 200 mN)缓慢下降,这是因为纯W脆性较大,在大载荷下引起材料损伤,这时小载荷下的平均值才是材料真实的弹性模量。35种金属材料的EIT在稳定区间(一般是大载荷,硬脆材料是小载荷)的平均值见表 1。图 6(f)比较了35种金属材料由仪器化压入得到的弹性模量EIT和文献报道值Eref(见表 1)。EIT和Eref近似成比例,EIT略大于Eref,这是由于Eref通常是由宏观拉伸试验获得,受材料的各种缺陷影响较大,然而仪器化压入只测试微小局部区域,缺陷较少,所以由仪器化压入测得的弹性模量一般比宏观测试结果略大。

|
图 6 利用仪器化压入表征金属材料的弹性模量:4种典型金属的力和位移曲线,弹性模量随加载力的变化;35种金属材料利用仪器化压入测得的弹性模量EIT与文献结果Eref的比较 Fig. 6 Characterization of elastic modulus of metals by instrumented indentation: indentation load-displacement curves and variation of elastic modulus with applied load for 4 representative metals, and comparison of elastic modulus EIT measured by instrumented indentation and Eref reported in the literature of 35 metals |
图 7(a)、7(b)分别为W18Cr4V和T2紫铜的努氏压痕光学形貌。b′、d′分别为在最大载荷时努氏压头与材料接触投影面的长对角线和短对角线(不考虑材料堆积或者压痕沉陷,由压头的几何形状可知b′/d′=1/7.11[6]);b、d分别为在卸载之后残余压痕投影面的长对角线和短对角线。对于玻璃和陶瓷等脆性材料:压痕是沉陷(sink-in)的,不会发生材料堆积(pile-up);卸载后努氏压痕长对角线的弹性回复可以忽略不计,即d≈d′;但压痕短对角线发生明显弹性回复,使得b < b′,所以b/d < 1/7.11。Marshall等[3]提出可以利用卸载后努氏压痕的短对角线b与长对角线d的比值(b/d)计算弹性模量E为
| $ \frac{b}{d}=\frac{b^{\prime}}{d^{\prime}}-\alpha \frac{H_{\mathrm{K}}}{E} \approx \frac{1}{7.11}-\alpha \frac{H_{\mathrm{K}}}{E} $ | (13) |
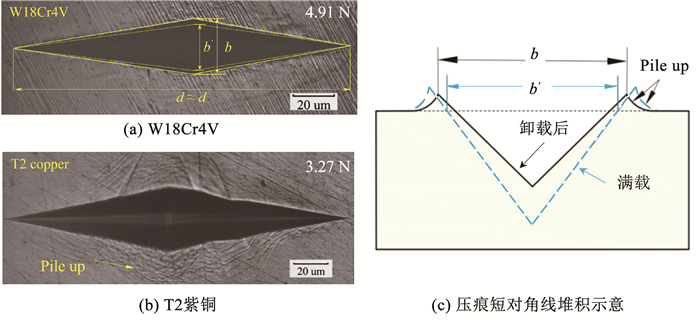
|
图 7 努氏残余压痕形貌和努氏压痕短对角线堆积示意 Fig. 7 Residual morphologies of Knoop imprints and schematic diagram of pile-up around short-diagonal of Knoop imprint |
式中: α为与材料有关的常数(对于陶瓷等脆性材料α=0.450,对于牙齿α=0.370,对于聚合物α=0.473,对于大块金属玻璃α随b/d线性增加[6]);HK应选用大载荷下趋于稳定的努氏硬度值(见表 1)。
Conway[4]对努氏压痕进行了分析,结果表明当压痕周围无明显堆积和沉陷时,通过分析压痕短对角线的弹性回复可以确定材料的弹性模量E为
| $ \left(\frac{b}{b^{\prime}}\right)^2=\left(7.11 \frac{b}{d}\right)^2=1-2\left(1-v^2\right) \tan \gamma\left(\frac{H_{\mathrm{K}}}{E}\right) $ | (14) |
式中: υ为材料泊松比(见表 1),γ=75°为努氏压头的等效半角,b′=d′/7.11=d/7.11。
Marshall模型和Conway模型主要用于硬脆材料,压痕周围无明显的堆积或沉陷,并且b/d < 1/7.11,可以利用压痕短对角线的弹性回复来计算弹性模量。利用有限元对金属材料的努氏压痕进行模拟,发现当材料的屈服强度和缩减模量之比σy/Er < 0.032时,满载下压痕短对角线处有较大的堆积,虽然卸载后压痕的短对角线会有一定的弹性回复,但短对角线处仍然有较为严重的材料堆积,使得b>b′,如图 7(c)所示;而长对角线基本无堆积且弹性回复量可以忽略不计,仍然有d′=d[24],于是残余压痕形貌的短对角线和长对角线的比值b/d>1/7.11。35种金属材料在最大载荷下的b/d见表 1,对于大部分金属材料b/d>1/7.11(≈0.14),Marshall模型和Conway模型不适用(适用条件需满足b/d < 1/7.11),需要对模型进行修正。
对于Marshall模型,根据已知的弹性模量EIT(由仪器化压入测得),系数α可以由式(13)计算:
| $ \alpha=E_{\mathrm{IT}}\left(\frac{1}{7.11}-\frac{b}{d}\right) / H_{\mathrm{K}} $ | (15) |
35种材料的α随b/d的变化如图 8(a)所示。大部分材料的b/d>1/7.11,所以α为负数,这是由于金属材料有严重的堆积,导致利用努氏硬度表征弹性模量只能应用于硬脆材料,还不能应用于金属材料;金属材料的α是b/d的二次函数,对Marshall模型进行修正,首次利用努氏硬度表征金属的弹性模量为
| $ E_\alpha=\frac{\left[-2+117(b / d)-725(b / d)^2\right] H_{\mathrm{K}}}{1 / 7.11-(b / d)} $ | (16) |

|
图 8 Marshall和Conway模型中系数的变化 Fig. 8 Variations of the empirical parameters of Marshall and Conway models |
对Conway模型引入修正系数β,并认为:
| $ \left(7.11 \frac{b}{d}\right)^2=\beta\left[1-2\left(1-v^2\right) \tan \gamma\left(\frac{H_{\mathrm{K}}}{E_{\mathrm{IT}}}\right)\right] $ | (17) |
由式(14)和已知的弹性模量EIT可以计算出β为
| $ \beta=\frac{(7.11 b / d)^2}{1-2\left[\left(1-v^2\right) \tan \gamma\right]\left(H_{\mathrm{K}} / E_{\mathrm{IT}}\right)} $ | (18) |
35种金属的β随b/b′的变化如图 8(b)所示,随着压痕短对角线比值的平方(7.11b/d)2的增加,β有线性增加的趋势(Ti6Al4V除外),适用于金属材料的Conway修正模型为
| $ E_\beta=\frac{2\left(1-v^2\right) \tan \gamma H_{\mathrm{K}}}{1-\frac{(7.11 b / d)^2}{0.07+(7.11 b / d)^2}} $ | (19) |
根据修正后的Marshall模型和Conway模型,见式(16)和式(19),可分别计算得到35种金属材料的弹性模量Eα、Eβ,如图 9(a)所示,大部分材料的Eα、Eβ和仪器化压入测得的弹性模量EIT一致(Ti6Al4V的弹性模量会被高估),置信度R2不低于0.94。图 9(b)放大展示了图 9(a)中低硬度材料(HK < 1.00 GPa)的结果:两修正模型计算的3种AZ系列镁合金的弹性模量与EIT基本相等,但会低估硬度较小的Sn(HK=0.08 GPa)的弹性模量。
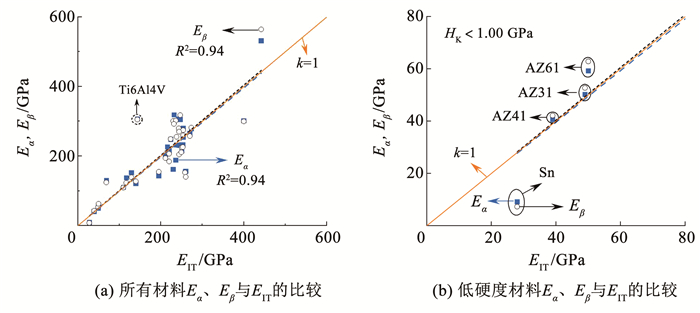
|
图 9 金属弹性模量比较:Marshall和Conway的修正模型计算的Eα、Eβ与仪器化压入得到的EIT Fig. 9 Comparison between Eα, Eβ, and EIT obtained by modified Marshall model, modified Conway model, and instrumented indentation, respectively |
利用硬度表征材料屈服强度的模型首先是基于圆锥压头提出的,也适用于维氏压头(可通过等效圆锥半顶角等效为圆锥压头)。因为努氏硬度与维氏硬度相关性很强[25],所以可以利用努氏硬度表征材料的屈服强度。相比于维氏压头,努氏压头长对角线远大于短对角线,如图 7(a)所示,对材料的各向异性较为敏感[26],大载荷下的结果更能代表金属材料宏观的屈服强度[27]。
Schuh等[28]研究金属材料的塑性变形时发现不同形状压头下屈服强度σy和名义硬度H呈线性关系:
| $ {\sigma _{\rm{y}}} = \frac{{\sqrt 3 H}}{{1.41 + 2.72\theta }}, H = \frac{P}{{{A_{\rm{c}}}}} = 12.873\frac{P}{{{d^2}}} $ | (20) |
式中:对于努氏压头取θ=77.64°×π/180°,P为最大载荷,Ac为最大压入深度下压头和材料的接触投影面积。
Yu等[29]发现屈服强度σy和名义硬度H之间满足:
| $ \begin{gathered} {\sigma _{\rm{y}}}=\frac{\left(1-v^2\right) E_{\mathrm{r}} \cot \theta}{2 C_\theta} \tanh ^{-1}\left(\frac{2 H}{\left(1-v^2\right) E_{\mathrm{r}} \cot \theta}\right) \\ C_\theta=\frac{2}{\sqrt{3}}\left[2.845-2.3757 \times 10^{-2}\left(\frac{\pi}{2}-\theta\right)\right] \\ 52.5^{\circ} \leqslant \theta \leqslant 90.0^{\circ} \end{gathered} $ | (21) |
Zhang等[7]在分析膨胀腔模型时发现材料的屈服强度σy、名义硬度H、弹性模量E和泊松比υ之间满足:
| $ \frac{H}{\sigma_{\mathrm{y}}}=\frac{2}{3}\left\{1+\ln \left[\frac{E}{3(1-v) \sigma_{\mathrm{y}}}\right]\right\} $ | (22) |
Fornell等[8]基于膨胀腔模型得到新的表达式为
| $ \frac{H}{\sigma_{\mathrm{y}}}=\frac{2}{3}\left(2+\ln \frac{E \cot \theta}{3 \sigma_{\mathrm{y}}}\right) $ | (23) |
Vandeperre等[30]考虑了弹性表面变形的影响,提出另一种表达式:
| $ \begin{gathered} \frac{H}{\sigma_{\mathrm{y}}}=\frac{2}{3}\left(1+\frac{1}{1-2 \lambda} \ln \frac{3+2 \mu}{6 \lambda+3 \mu-2 \lambda \mu}\right) \\ \lambda=(1-2 v) \frac{\sigma_{\mathrm{y}}}{E} \\ \mu=(1+v) \frac{\sigma_{\mathrm{y}}}{E} \end{gathered} $ | (24) |
根据式(20)~(24),当材料的名义硬度H、弹性模量E(即仪器化压入测试的弹性模量EIT,见表 1)、泊松比υ(见表 1)和压头的等效圆锥半顶角θ已知时,可以求得材料的屈服强度σy。式(20)、(21)可直接计算材料的屈服强度σy,式(22)~(24)可采用牛顿迭代法计算,初始迭代点可采用σy≈H/3。由式(1)和式(20)可知名义硬度H和努氏硬度HK成比例, H=0.905HK。将不同模型的名义硬度H替换为大载荷下趋于稳定的努氏硬度HK(见表 1),可计算得到35种金属屈服强度,与文献报道值(见表 1)的比较如图 10(a)所示,除60Si2Mn弹簧钢外,不同模型计算的屈服强度和文献报道值近似成比例,可以引入修正系数k来对模型进行修正,k表示文献值与原模型计算值的比值(拟合时未考虑偏离线性趋势较远的60Si2Mn弹簧钢)。60Si2Mn弹簧钢具有较高的弹性极限,并且其屈服强度与抗拉强度十分接近,与普通金属材料差异显著,所以适用于普通金属的公式不适合60Si2Mn弹簧钢。Vandeperre和Marsh两个模型的k值近乎等于1,模型不需要修正。基于k值,同时把名义硬度H替换成努氏硬度HK,对其他3个模型(Lockett、Johnson和Yu)进行了修正,修正前、后的模型仅仅差一个系数,即Lockett的修正模型为
| $ \sigma_{\mathrm{ym}}=\frac{\sqrt{3} H_{\mathrm{K}}}{2.21+4.27 \theta} $ | (25) |
3个修正模型计算出的35种金属屈服强度σym(下标“ym”表示修正模型计算值)与文献报道值σyref(见表 1)的比较如图 10(b)所示,修正后模型计算的屈服强度与文献报道值一致,置信度R2不低于0.90,说明修正后的模型可以准确预测大部分金属材料的屈服强度,偏差主要是由于金属材料的屈服强度受加工过程等因素影响,使得金属的屈服强度是一个范围,见表 1。图 10(c)放大展示了图 10(b)中低硬度材料(HK < 1.00 GPa)的结果:修正后的模型计算的低硬度材料的σym与σyref基本一致,说明修正后模型也适用于硬度较低的金属。Marsh、Johnson、Vandeperre模型需要利用牛顿迭代法解方程来计算材料的屈服强度σy,Lockett、Yu模型可直接计算σy,由于Lockett形式更简单,所以当努氏硬度容易测量时,推荐式(25)计算金属材料的屈服强度。大塑性变形得到的硬度还与材料的硬化指数有关[25],而本文中的模型均未考虑硬化指数的影响,因此适用于硬化指数对大变形影响不大的金属材料,从而为工程实践中基于努氏硬度评估金属材料的屈服强度提供简便方法。

|
图 10 35种材料屈服强度的计算值和文献值σyref比较 Fig. 10 Comparison between values of yield strength calculated by different models and σyref reported in the literature |
1) 对35种金属材料进行努氏硬度试验,发现金属材料的努氏硬度存在正压痕尺寸效应,大载荷下的硬度值区域稳定,并与弹塑性变形模型(EDP)、Hays-Kendall模型和比例试样模型(PSR)各自计算的真硬度值一致。
2) 首次考虑金属材料在努氏压痕短对角线处材料堆积的影响,利用最大载荷下的努氏硬度值计算金属材料的弹性模量和屈服强度,将Marshall模型中原有的常参数α修正为b/d(努氏压痕短对角线与长对角线的比值)的二次函数;将Conway模型乘以与b/d的平方呈线性关系的修正系数β。除Ti6Al4V和Sn外,修正模型与仪器化压入测得的弹性模量一致,置信度R2不低于0.94。
3) 通过比较文献值与Lockett、Yu、Marsh、Johnson和Vandeperre模型计算的屈服强度,引入修正系数k(文献值与原模型计算值的比值),首次建立了基于努氏硬度表征金属材料屈服强度的模型。除60Si2Mn弹簧钢外,修正模型计算值与文献值一致,置信度R2不低于0.90。
| [1] |
杨浩志, 辛艳青, 郑小龙, 等. 结构调制高硬度TiCu/TiN-Cu纳米多层复合膜制备及其机械性能[J]. 哈尔滨工业大学学报, 2021, 53(8): 56. YANG Haozhi, XIN Yanqing, ZHENG Xiaolong, et al. Preparation and mechanical properties of structure modulated TiCu/TiN-Cu nano-composite multilayer films[J]. Journal of Harbin Institute of Technology, 2021, 53(8): 56. DOI:10.11918/202001059 |
| [2] |
刘晓立, 曹建国, 柴雪婷, 等. 变弹性模量对高强钢辊弯成型回弹预测的影响[J]. 哈尔滨工业大学学报, 2018, 50(7): 137. LIU Xiaoli, CAO Jianguo, CHAI Xueting, et al. Springback prediction of DP980 steel considering nonlinear elastic modulus in cold roll forming[J]. Journal of Harbin Institute of Technology, 2018, 50(7): 137. DOI:10.11918/j.issn.0367-6234.201707163 |
| [3] |
MARSHALL D B, NOMA T, EVANS A G. A simple method for determining elastic-modulus-to-hardness ratios using Knoop indentation measurements[J]. Journal of the American Ceramic Society, 1982, 65(10): c175. DOI:10.1111/j.1151-2916.1982.tb10357.x |
| [4] |
CONWAY J C Jr. Determination of hardness to elastic modulus ratios using Knoop indentation measurements and a model based on loading and reloading half-cycles[J]. Journal of Materials Science, 1986, 21(7): 2525. DOI:10.1007/BF01114301 |
| [5] |
LAWN B R, MARSHALL D B. Hardness, toughness, and brittleness: An indentation analysis[J]. Journal of the American Ceramic Society, 1979, 62(7/8): 347. DOI:10.1111/j.1151-2916.1979.tb19075.x |
| [6] |
刘明, 郑强, 高诚辉. 基于努氏硬度表征大块金属玻璃的力学性能[J]. 固体力学学报, 2021, 42(4): 376. LIU Ming, ZHENG Qiang, GAO Chenghui. Characterization of mechanical properties of bulk metallic glasses based on Knoop hardness[J]. Chinese Journal of Solid Mechanics, 2021, 42(4): 376. DOI:10.19636/j.cnki.cjsm42-1250/o3.2021.002 |
| [7] |
ZHANG H W, SUBHASH G, JING X N, et al. Evaluation of hardness-yield strength relationships for bulk metallic glasses[J]. Philosophical Magazine Letters, 2006, 86(5): 333. DOI:10.1080/09500830600788935 |
| [8] |
FORNELL J, CONCUSTELL A, SURIÑACH S, et al. Yielding and intrinsic plasticity of Ti—Zr—Ni—Cu—Be bulk metallic glass[J]. International Journal of Plasticity, 2009, 25(8): 1540. DOI:10.1016/j.ijplas.2008.11.002 |
| [9] |
CAI Jun, LI Fuguo, LIU Taiying, et al. Microindentation study of Ti—6Al—4V alloy[J]. Materials & Design, 2011, 32(5): 2756. DOI:10.1016/j.matdes.2011.01.003 |
| [10] |
CHENG W L, PARK S S, TANG W N, et al. Influence of alloying elements on microstructure and microhardness of Mg-Sn-Zn-based alloys[J]. Transactions of Nonferrous Metals Society of China, 2010, 20(12): 2246. DOI:10.1016/S1003-6326(10)60636-X |
| [11] |
FAGHIHI D, VOYIADJIS G Z. Determination of nanoindentation size effects and variable material intrinsic length scale for body-centered cubic metals[J]. Mechanics of Materials, 2011, 44: 189. DOI:10.1016/j.mechmat.2011.07.002 |
| [12] |
LI Hong, HAN Y H, BRADT R C. Knoop microhardness of single crystal sulphur[J]. Journal of Materials Science, 1994, 29(21): 5641. DOI:10.1007/BF00349959 |
| [13] |
龚江宏, 刘明. 一种确定纳米压入接触面积的简便方法[J]. 中国科学: 物理学力学天文学, 2023, 53(1): 87. GONG Jianghong, LIU Ming. A simple method for the determination of contact area for nanoindentation tests[J]. Scientia Sinica (Physica, Mechanica & Astronomica), 2023, 53(1): 87. DOI:10.1360/SSPMA-2022-0208 |
| [14] |
陈辉, 蔡力勋, 包陈. 双锥度压入的FAT迭代法获取材料的力学性能[J]. 核动力工程, 2015, 36(5): 101. CHEN Hui, CAI Lixun, BAO Chen. FAT iterative method based on dual conical indentation to obtain properties of materials[J]. Nuclear Power Engineering, 2015, 36(5): 101. DOI:10.13832/j.jnpe.2015.05.0101 |
| [15] |
龙旭, 申子怡, 贾啟普, 等. 纳米压痕下单/多层薄膜弹塑性本构的无量纲分析[J]. 中国科学: 物理学力学天文学, 2023, 53(1): 55. LONG Xu, SHEN Ziyi, JIA Qipu, et al. Dimensionless analysis of the elastoplastic constitutive properties of single/multilayered filmsunder nanoindentation[J]. Scientia Sinica (Physica, Mechanica & Astronomica), 2023, 53(1): 55. DOI:10.1360/SSPMA-2022-0203 |
| [16] |
张志杰, 郑鹏飞, 陈辉, 等. 基于能量等效原理的金属材料硬度预测方法[J]. 工程力学, 2021, 38(3): 17. ZHANG Zhijie, ZHENG Pengfei, CHEN Hui, et al. The method for hardness prediction of metal materials based on energy equivalence principle[J]. Engineering Mechanics, 2021, 38(3): 17. DOI:10.6052/j.issn.1000-4750.2020.04.0249 |
| [17] |
LIU Ming, XU Zhitong, FU Renli. Micromechanical and microstructure characterization of BaO—Sm2O3—5TiO2 ceramic with addition of Al2O3[J]. Ceramics International, 2022, 48(1): 992. DOI:10.1016/j.ceramint.2021.09.184 |
| [18] |
GAO Chenghui, YAO Ligang, LIU Ming. Berkovich nanoindentation of borosilicate K9 glass[J]. Optical Engineering, 2018, 57(3): 034104. DOI:10.1117/1.OE.57.3.034104 |
| [19] |
GAO Chenghui, LIU Ming. Instrumented indentation of fused silica by Berkovich indenter[J]. Journal of Non-Crystalline Solids, 2017, 475: 151. DOI:10.1016/j.jnoncrysol.2017.09.006 |
| [20] |
YANG Fuqian, LIU Ming. Analysis for the indentation with a flat indenter on an elastic-perfectly plastic thin film[J]. Journal of Computational and Theoretical Nanoscience, 2014, 11(1): 265. DOI:10.1166/jctn.2014.3347 |
| [21] |
张雪, 程赫明, 李建云, 等. T10钢经常压高速气雾淬火工艺处理后组织及性能的研究[J]. 热加工工艺, 2015, 44(6): 219. ZHANG Xue, CHENG Heming, LI Jianyun, et al. Study on microstructure and mechanical properties of T10 steel quenched by atomized water with nitrogen gas[J]. Hot Working Technology, 2015, 44(6): 219. DOI:10.14158/j.cnki.1001-3814.2015.06.066 |
| [22] |
罗少强, 舒林森, 王波, 等. 1 mm厚304 L不锈钢冷轧板的低周疲劳性能分析[J]. 陕西理工大学学报(自然科学版), 2019, 35(2): 6. LUO Shaoqiang, SHU Linsen, WANG Bo, et al. Analysis of low cycle fatigue properties of 1 mm thick 304 L stainless steel cold rolled sheet[J]. Journal of Shaanxi University of Technology (Natural Science Edition), 2019, 35(2): 6. DOI:10.3969/j.issn.1673-2944.2019.02.002 |
| [23] |
刘松. 金属材料显微硬度压痕尺寸效应分析及其试验研究[J]. 失效分析与预防, 2019, 14(4): 225. LIU Song. Size effect analysis and experimental study of microhardness indentation of metal materials[J]. Failure Analysis and Prevention, 2019, 14(4): 225. DOI:10.3969/j.issn.1673-6214.2019.04.002 |
| [24] |
GIANNAKOPOULOS A E, ZISIS T. Analysis of Knoop indentation[J]. International Journal of Solids and Structures, 2011, 48(1): 175. DOI:10.1016/j.ijsolstr.2010.09.014 |
| [25] |
LIU Ming, ZHENG Qiang, WANG Xin, et al. Characterization of distribution of residual stress in shot-peened layer of nickel-based single crystal superalloy DD6 by nanoindentation technique[J]. Mechanics of Materials, 2022, 164: 104143. DOI:10.1016/j.mechmat.2021.104143 |
| [26] |
AMITAY-SADOVSKY E, WAGNER H D. Hardness and Young's modulus of transcrystalline polypropylene by vickers and Knoop microindentation[J]. Journal of Polymer Science Part B: Polymer Physics, 1999, 37(6): 523. DOI:10.1002/(sici)1099-0488(19990315)37:6<523:aid-polb4>3.0.co;2-2 |
| [27] |
MURUGESAN G, KALAINATHAN S. Experimental and theoretical modelling of Vickers, Knoop microhardness and laser damage threshold studies on Ca0.9Nd0.1Ti0.9Al0.1O3 single crystals grown by optical floating zone technique[J]. Journal of Alloys and Compounds, 2016, 677: 121. DOI:10.1016/j.jallcom.2016.03.178 |
| [28] |
SCHUH C A, ARGON A S, NIEH T G, et al. The transition from localized to homogeneous plasticity during nanoindentation of an amorphous metal[J]. Philosophical Magazine, 2003, 83(22): 2585. DOI:10.1080/1478643031000118012 |
| [29] |
YU Weiping, BLANCHARD J P. An elastic-plastic indentation model and its solutions[J]. Journal of Materials Research, 1996, 11(9): 2358. DOI:10.1557/JMR.1996.0299 |
| [30] |
VANDEPERRE L J, GIULIANI F, CLEGG W J. Effect of elastic surface deformation on the relation between hardness and yield strength[J]. Journal of Materials Research, 2004, 19(12): 3704. DOI:10.1557/JMR.2004.0473 |
 2024, Vol. 56
2024, Vol. 56


