工业机器人是智能制造系统的核心设备之一,其关节部位广泛采用RV减速器传动。RV减速器有体积小、精度高、寿命长等诸多优点,但由于实际加工、服役过程中,主轴承得不到充分润滑或在润滑条件下不能及时监测预警,导致传动机构极其容易发生摩擦磨损破坏。为此,以RV减速器E系列中重要的传动机构—主轴承为研究对象,对主轴承中滚珠与内外圈之间的润滑性能进行详细的研究分析,来改善RV减速器的传动精度、传动效率以及使用寿命[1]。
近年来,国内外学者研究了RV减速器摆线针轮传动机构的修形等因素对混合润滑性能的影响[2-4]。但是,关于RV减速器主轴承机构的弹流润滑研究甚少,主轴承机构滚珠和滚道之间是以点接触形式存在。针对点接触弹流润滑问题。Hamrock等[5]首先将弹性方程和雷诺方程进行联立,求解了点接触等温弹流润滑数学模型,对其使用的数值求解方法适用场合进行了说明。之后,翟文杰等[6]利用粗网格的结果作为细网格初值求解了点弹流润滑数值模型。Meng等[7]进一步构建了考虑轴承滑移和相互作用的多椭球体接触弹流润滑,分析了润滑油初始黏度、径向间隙等因素对轴承润滑性能的影响。同样是基于轴承点接触弹流润滑分析,李静等[8]建立了中介轴承弹流润滑接触模型,描述了双转子系统的动力学特性。
然而,实际加工零件表面存在缺陷性,粗糙度不容忽视,考虑零件表面粗糙程度对于研究机构润滑特性更具合理性。近些年,张丽静等[9]分析了轴承表面横向粗糙度、波长等对塑料轴承表面润滑性能的影响。随后,魏波等[10]考虑接触载荷和真实表面粗糙度等因素建立了瞬态点接触混合润滑理论模型,研究了不同载荷以及转速对膜厚的影响。此外,路遵友等[11]建立并求解了粗糙度影响下的角接触球轴承弹流润滑数值模型,考虑了不同内圈转速和滑滚比等因素对润滑特性的影响。最近,Li等[12]利用W-M函数表征了直线滚动导轨平面的表面形貌,建立了点接触弹流润滑数值模型,研究了分形粗糙度参数对接触润滑性能的影响。
上述模型考虑了接触副表面粗糙度对弹流润滑的影响,忽略了当润滑剂为润滑脂时,非牛顿特性对机构润滑特性的影响。在点接触弹流润滑的基础上,黄平等[13]建立了非牛顿流体的点接触弹流润滑模型,研究了润滑剂的非牛顿特性、载荷、卷吸速度等参数对压力以及润滑膜厚分布的影响。之后,张翔等[14]基于润滑剂的非牛顿性和吸附膜对热弹流润滑性能的影响。他们在研究非牛顿流体对弹流润滑特性的影响方面做出较大贡献,但未论述表面粗糙度的影响。最近,吴正海等[15]将微凸体接触模型应用到点接触副混合润滑模型中,模拟了构件考虑粗糙表面形貌参数时,不同稠度润滑脂对润滑特征的影响。该工作在理论研究方面探究了诸多因素对润滑性能的影响,但未能具体到工程对象上,并且只针对于混合润滑模型。
针对上述研究存在的问题,本文考虑分形粗糙表面以及非牛顿流体特性的综合影响,将其影响加入到RV减速器主轴承的点接触弹流润滑分析中,建立了脂润滑下点接触弹流润滑数值新模型,通过多重网格法和多重网格积分法,计算得到脂膜压力以及脂膜厚度相关润滑特性的收敛解,在此基础之上,基于主轴承表面光滑和表面粗糙,分析了流变指数、分形维数、卷吸速度、载荷和润滑脂黏度等不同工况因素对润滑性能的影响。
1 弹流润滑模型构建 1.1 几何模型结构尺寸和受力分析RV减速器E系列主轴承几何模型如图 1所示,以主轴承中心为原点O,建立坐标系xoz。滚珠在轨道内滚动,注入足够数量的润滑脂到主轴承中,以此确保滚珠在运行情况下得到充分的润滑,故可不考虑乏脂的影响。因此,该模型处于EHL工况下工作。

|
图 1 主轴承几何模型 Fig. 1 Geometric model of main bearing |
RV减速器主轴承相关结构尺寸如下:外圈直径D0=145 mm,内圈直径Di=124 mm,节圆直径dm=132 mm,滚珠直径Dw=10 mm,滚珠数量Z=40。RV减速器主轴承工作时承载多种力,尤其滚珠的受力较为复杂,滚珠与滚道受法向载荷wi(i=1, 2, 3, …, 40)最为明显,因此忽略其他复杂力影响,主要考虑法向载荷作用[16],如图 1所示。
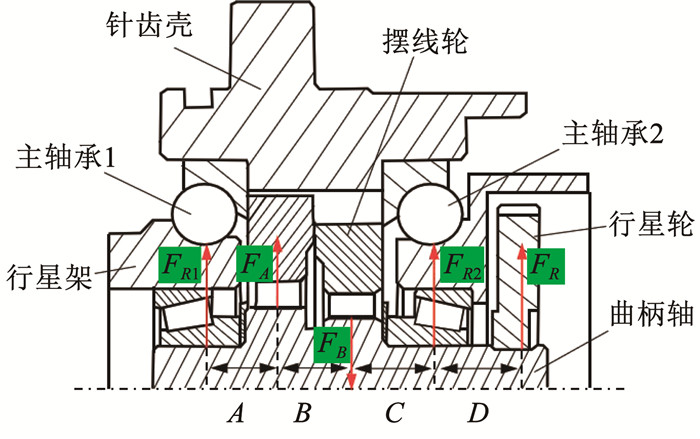
RV减速器曲柄轴受到摆线轮和行星轮的径向力FA、FB和FR作用后,从而对主轴承1、2产生了竖直方向的径向力FR1和FR2,如图 2所示。根据文献[17]可以求得作用在曲柄轴上的径向力FA、FB和FR,再以主轴承1的位置为研究点,规定箭头向上为正方向,建立主轴承的力平衡和力矩平衡,表达式如下:
| $ \left\{\begin{array}{l} F_{R 1}+F_A+F_{R 2}+F_R-F_B=0 \\ F_R(A+B+C+D)+F_{R 2}(A+B+C)- \\ F_B(A+B)+F_A A=0 \end{array}\right. $ | (1) |
|
图 2 主轴承受力分析 Fig. 2 Analysis of load distribution in bearing force |
式中:A、B、C、D分别为曲柄轴和主轴承上各力之间的距离,其值为12、12、12、22 mm。
求解式(1)可以得到主轴承1、2的总径向力合力分别为FR1、FR2,在此研究主轴承1的一组滚珠和滚道的受力情况,其法向载荷的表达式如下:
| $ w=\frac{F_{R 1}}{Z \cos \alpha} $ | (2) |
式中:α为主轴承的接触角,取α=10°;Z为滚珠个数。减速器运转时,曲柄轴带动摆线轮旋转,法向载荷w受曲柄轴转角和摆线轮转角的影响不断发生变化,根据各时段转角不同取得法向载荷w分别为1、2、5 N。
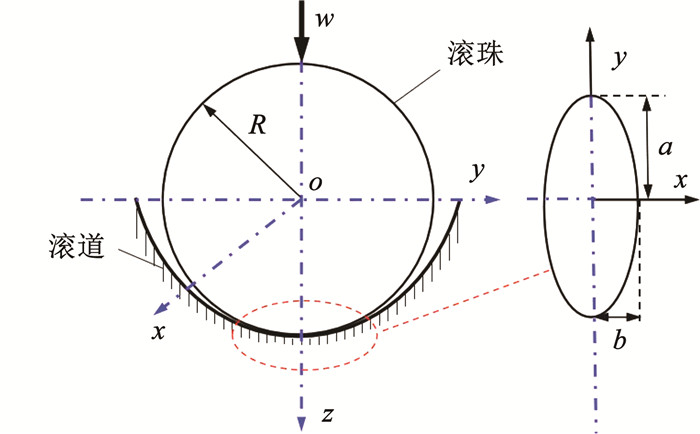
1.2 几何模型尺寸关系通过对RV减速器主轴承相关结构尺寸的测量以及规定,进而建立主轴承结构之间的尺寸关系。根据Hertz接触理论[18],当载荷w施加在滚珠上时,主轴承的滚珠与内、外圈相互接触,在接触面上会产生应力以及弹性变形,接触区域的形状为椭圆形,椭圆长、短半轴的长度为a、b[12],由于内圈和外圈的法向载荷w是一对相互作用力,它们的几何模型构建和研究方法类似,本文只选取了滚珠和外圈代表性的接触模型作为研究试样,如图 3所示。
|
图 3 滚珠-外圈接触 Fig. 3 Ball-outer race contact |
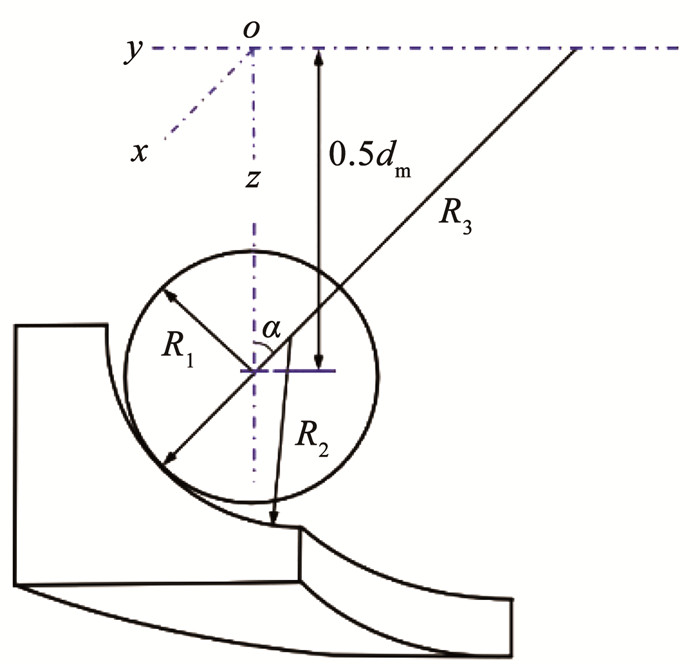
图 4为滚珠与外圈接触结构尺寸示意图,对于滚珠在xoz平面和yoz平面的主曲率半径都为R1,可表示为
| $ R_1=\frac{D_w}{2} $ | (3) |
|
图 4 滚珠-外圈接触尺寸示意 Fig. 4 Ball-outer race contact size diagram |
式中Dw为滚珠直径。
对于外圈在yoz平面的主曲率半径为R2,可表示为
| $ R_2=f D_w $ | (4) |
式中f为曲率半径系数,即滚珠与外圈曲率比。主要是描述滚珠与外圈滚道的接触程度,其值的大小会影响主轴承的传动精度,为保持较好的运行条件设定f=0.55[17]。
对于外圈在xoz平面的主曲率半径为R3,可表示为
| $ R_3=\frac{d_m / 2+D_w \cos \alpha / 2}{\cos \alpha} $ | (5) |
下式中Rx、Ry分别表示滚珠在x方向和y方向上的综合曲率半径,由滚珠和外圈的主曲率半径决定[19],即
| $ R_x=\frac{R_1 \cdot R_3}{R_1+R_3}, \quad R_y=\frac{R_1 \cdot R_2}{R_2-R_1} $ | (6) |
根据图 1和主轴承几何尺寸关系,实际工况下主轴承装配于RV减速器的行星架和针齿壳之间,其对输出法兰起到了支撑作用,反之,输出法兰带动主轴承旋转,则主轴承转速与额定输出转速相同,由于减速器允许最大输出转速为100 r/min,因此取主轴承转速N分别为28、55、83 r/min进行相关探究。
根据速度和转速的关系可得外圈表面沿x方向的速度为
| $ u_1=2 {\rm{ \mathsf{ π} }} R_3 N $ | (7) |
滚珠表面沿x方向的速度为
| $ u_2=2 {\rm{ \mathsf{ π} }} R_1 N $ | (8) |
则滚珠和外圈之间的卷吸速度为
| $ u=\frac{u_1+u_2}{2} $ | (9) |
式中,根据给定的主轴承转速求得主轴承卷吸速度分别为0.2、0.4、0.6 m/s。
通过简化模型可以将图 4滚珠与外圈接触等效为椭球体与平面之间的接触,如图 5所示。椭球体沿着x的方向以一定的速度运动时,椭球体和平面之间形成薄膜,进而对主轴承进行润滑保护。

|
图 5 椭球体-平面接触 Fig. 5 Ellipsoid-plane contact |
RV减速器所用润滑脂属于非牛顿流体,具有流变特性且遵循Ostwald模型[20],表征方程为
| $ \tau=\phi \dot{\gamma}^n $ | (10) |
式中:τ为润滑脂的剪切力,
主轴承旋转过程中,假设主轴承所用润滑脂流动属于层流,没有湍流和涡流,忽略与导轨空间垂直y方向上的速度、润滑介质的能量变化、惯性力和体积力的影响,根据Ostwald模型推导出点接触稳态脂润滑弹流润滑Reynolds方程[13]:
| $ \frac{\partial(\rho A)}{\partial x}+\frac{\partial(\rho B)}{\partial y}=\frac{2^{\frac{n+1}{n}}(2 n+1)}{n} \frac{\partial(\rho u h)}{\partial x} $ | (11) |
式中:
| $ \left\{\begin{array}{l} p\left(x_{\text {in }}, y\right)=0 \\ p\left(x_{\text {out }}, y\right)=0 \\ p\left(y_{\text {in }}\right)=p\left(y_{\text {out }}\right)=0 \end{array} \quad \partial p\left(x_{\text {out }}, y\right) / \partial x=0\right. $ | (12) |
式中:xin、xout、yin、yout分别为计算域沿x、y方向的起点和终点坐标。
2.2 膜厚方程滚珠和外圈相互接触会发生弹性变形,并且考虑滚珠和外圈在加工后的表面粗糙度,脂膜厚度方程可以表示为
| $ h(x, y)=h_0+\frac{x^2}{2 R_x}+\frac{y^2}{2 R_y}+v(x, y)+\delta(x, y) $ | (13) |
式中:δ(x, y)为表面粗糙度高度,v(x, y)为弹性变形,计算公式表示为
| $ v(x, y)=\frac{2}{{\rm{ \mathsf{ π} }} E^{\prime}} \iint\limits_{\mathit{\Omega }} \frac{p\left(x^{\prime}, y^{\prime}\right)}{\sqrt{\left(x-x^{\prime}\right)^2+\left(y-y^{\prime}\right)^2}} \mathrm{~d} x^{\prime} \mathrm{d} y^{\prime} $ | (14) |
式中:Ω为计算区域, E′为滚珠和滚道材料的等效弹性模量,2/E′=(1-υ12)/E1+(1-υ22)/E2, 其中:E1、E2分别为滚珠和外圈接触表面的弹性模量, υ1、υ2为两接触表面的泊松比;x′、y′用来区分x、y的坐标值,分别为横坐标和纵坐标。
2.3 润滑脂黏压方程、密压方程润滑脂的黏压、密压关系假定与润滑油一致。黏压关系使用Roelands[21]经验公式,密压关系通过Dowson等[22]推出的关系式表示,即
| $ \phi=\phi_0 \exp \left\{\left(\ln \phi_0+9.67\right)\left[\left(1+p / p_0\right)^{z_0}-1\right]\right\} $ | (15) |
| $ z_0=\frac{\alpha^{\prime}}{5.1 \times 10^{-9}\left(\ln \phi_0+9.67\right)} $ | (16) |
| $ \rho=\rho_0\left[1+\frac{0.6 \times 10^{-9} p}{1+1.7 \times 10^{-9} p}\right] $ | (17) |
式中:ϕ0、ρ0分别为环境压力下润滑脂的黏度和密度,z0为润滑脂定义的罗德参数,z0根据Barus黏压系数α′来确定,对于不同压力状态下其值恒定,取值为0.68。
2.4 载荷平衡方程忽略主轴承转动过程中,接触压力随接触位置的变化而变化,在滚珠与外圈接触的某一位置对应的接触压力和外载荷平衡,计算公式为
| $ \iint\limits_{\mathit{\Omega }} p(x, y) \mathrm{d} x \mathrm{~d} y=w $ | (18) |
磨削加工后的主轴承表面轮廓具有多尺度特征和自相似性,可以用三维分形几何理论来表征整个滚珠和外圈啮合面的粗糙表面形貌,三维分形粗糙面的函数表达式为[23]
| $ \begin{array}{l} \delta(x, y)=& L\left(\frac{G}{L}\right)^{(D-2)} \sqrt{\frac{\ln \gamma^{\prime}}{M}} \sum\limits_{m=1}^M \sum\limits_{n=0}^{n_{\max }}\left(\gamma^{\prime}\right)^{(D-3) n}\left\{\cos \phi_{m, n}-\right. \\ & \cos \left[\frac{2 {\rm{ \mathsf{ π} }}\left(\gamma^{\prime}\right)^n\left(x^2+y^2\right)^{1 / 2}}{L} \times\right. \\ & \left.\left.\cos \left(\tan ^{-1}\left(\frac{y}{x}\right)-\frac{{\rm{ \mathsf{ π} }} m}{M}\right)+\phi_{m, n}\right]\right\} \end{array} $ | (19) |
式中:L为样本长度,L=1.0×10-3 m;D为取值范围在(2, 3)的分形维数, G为分形粗糙度系数,其值为1×10-10 m;γ′为空间频率,通常γ′取1.5;nmax为最大频率指数,nmax=int[log(L/Ls)/log γ′];Ls为截断长度,Ls=1.5×10-9 m;M为峰值数量,M取值为15;ϕm, n为在(0, 2π)范围内的随机相位。
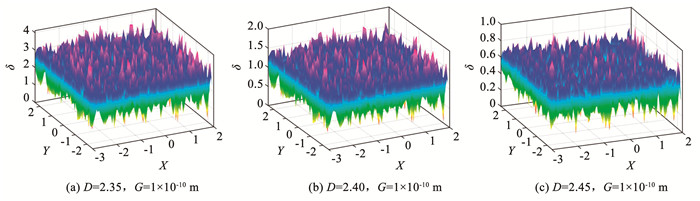
为研究分形参数D对主轴承三维粗糙表面形貌的影响,基于式(19),控制分形粗糙度系数G一定,得出不同分形维数下滚珠和外圈的分形表面粗糙度δ的分布情况,如图 6所示。由图 6可知,粗糙表面的三维轮廓由随机分布的波峰和波谷构成,且波峰和波谷代表了光滑程度。随着分形维数从2.35~ 2.45,粗糙表面波峰和波谷增加,但幅度减小,因而表面粗糙度逐渐减小,表面轮廓变得更加光滑。
|
图 6 不同分形维数的分形表面粗糙度 Fig. 6 Fractal surface roughness of different fractal dimensions |
文中的数值计算过程均利用VS编程软件求解,点接触弹流润滑数学模型求解域的横、纵坐标范围为X=-3.0~2.0,Y=-2.5~2.5,计算网格密度为65×65。收敛判据为载荷和压力的相对精度小于等于1×10-3。表 1中给出了数值计算参数。
| 表 1 数值计算参数 Tab. 1 Numerical calculation parameters |
本文采用迭代法联合求解方程(11)、(13)、(15)、(17)、(18),获得未知参数ϕ、ρ、P和H,求解流程如图 7所示,具体的求解过程详见如下步骤。

|
图 7 数值计算流程 Fig. 7 Numerical calculation flow chart |
Step1 将脂弹流润滑控制方程中的方程(11)、(13)、(15)、(17)、(18)进行无量纲化,具体参数为P=p/pH,H=hRx/ab,X=x/b,Y=y/a,ρ*=ρ/ρ0,ϕ*=ϕ/ϕ0,U=ϕ0u/(E′Rx),W=w/(E′Rx2)。其中: P为无量纲化压力,H为无量纲化膜厚,ρ*、ϕ*分别为无量纲化密度和黏度,U、W分别为无量纲化速度和载荷参数。对基本控制方程(11)和边界条件(12)进行无量纲化处理,再通过有限差分法对无量纲化后的控制方程进行离散化处理[24]。
Step2 给定等效弹性模量、初始黏度、载荷以及速度等已知参数,对网格层数和节点数进行设置,取网格层数为5层,节点数为65×65个节点。
Step3 合理假设接触区脂膜压力P以及脂膜厚度H的初始迭代值。
Step4 采用多重网格积分法[25]求解弹性变形,得到变形量v。采用多重网格法[26]求解脂膜压力P,将H0、ϕ0和ρ0等已知参数代入无量纲化后的方程(13)、(15)和(17)中,求解出接触变形后的脂膜厚度H、黏度ϕ、密度ρ。
Step5 判断求得脂膜压力是否满足给定的误差要求,再判断脂膜压力和载荷是否同时满足给定的误差要求。
Step6 判断是否满足误差要求即收敛判据为前、后两次迭代的压力差小于或等于相对精度1×10-3,迭代结束;否则继续执行Step3~Step6,直到满足收敛条件为止。
Step7 最后,输出脂膜压力以及脂膜厚度。
4 仿真结果与分析仿真中取流变指数为0.85,卷吸速度为0.6 m/s,轴承所受载荷为2.0 N,润滑脂黏度为0.16 Pa·s,分形维数D为2.40。通过软件编程计算,得到了求解域内润滑脂膜压力、脂膜厚度的分布情况,如图 8所示。图 8(a)、8(b)分别为未考虑粗糙度和考虑粗糙度下脂膜压力p的分布情况,图 8(c)、8(d)分别为未考虑粗糙度和考虑粗糙度下脂膜厚度h的分布情况。由图 8可知,受表面粗糙度的影响,脂膜压力和脂膜厚度在数值上出现了很多的凹凸拐点,与未计入表面粗糙度时明显不同。

|
图 8 脂膜压力、脂膜厚度分布情况 Fig. 8 Distribution of grease film pressure and thickness |
采用数值方法的求解步骤和表 1所示的数值计算参数,对本文方法在求解域网格17×17、33×33和65×65上进行网格无关性验证,验证过程中取脂膜厚度三维图纵坐标Y=0,分别得到不同网格密度下的脂膜厚度二维变化图,如图 9所示。由图 9可知,本文方法在不同网格密度下,脂膜厚度变化曲线基本重合。相同横坐标下,各网格密度之间的数值结果误差都保持在2%左右,从整体上看,膜厚计算结果对网格密度变化不再敏感。综上所述,对于本文选取的计算网格密度65×65可以满足数值求解的精度要求。
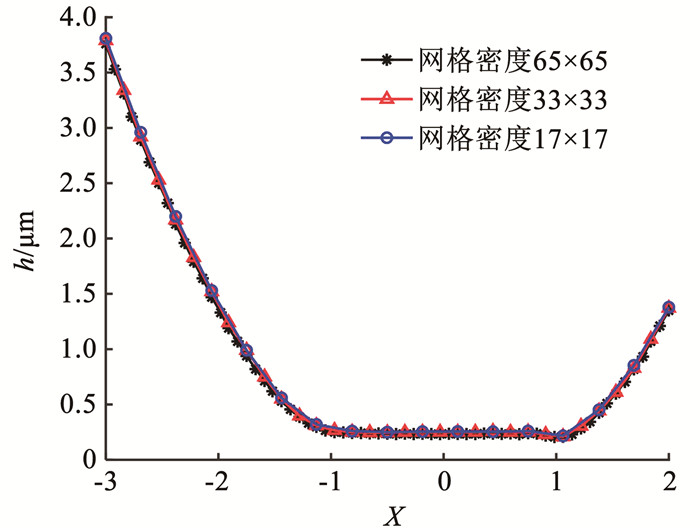
|
图 9 不同网格密度下的脂膜厚度对比 Fig. 9 Comparison of grease film thickness under different grid densities |
为验证本文弹流润滑数值分析模型的正确性,将新模型与黄平等[13]建立的点接触弹流分析模型和所搭建的弹流润滑实验台得到的结果[15]进行了对比。为了保证模型的一致性,新模型选取的相关计算参数与黄平等[13]所建模型和实验工况均相同。
图 10表示流变指数为0.62,载荷为2 N,同一卷吸速度下和流变指数为0.62,卷吸速度为0.4 m/s,同一载荷下,各模型的脂膜厚度的变化规律。由图 10可知,在中心膜厚区域脂膜呈现马蹄凹陷形状特征,在出口区脂膜出现明显的颈缩现象,最小脂膜厚度位置相对一致,将新模型与实验模型和其他模型的脂膜厚度进行对比,各模型对脂膜厚度影响趋势一致,且本文模型更加接近实验分析结果,从而验证了本文模型在求解弹流脂润滑理论方面的正确性。误差分析:从图 10(a)可见,新模型和实验模型脂膜在厚度上有略微偏差,这可能因为实验模型的钢球和玻璃盘的几何位置误差导致。从图 10(b)可观察到,新模型和实验模型脂膜的形状区别主要是中心膜厚区域的宽度不同,这可能由于实验载荷受振动的等外界因素影响不能使载荷恒定为1 N所致,载荷发生变化,接触区域宽度也会改变。
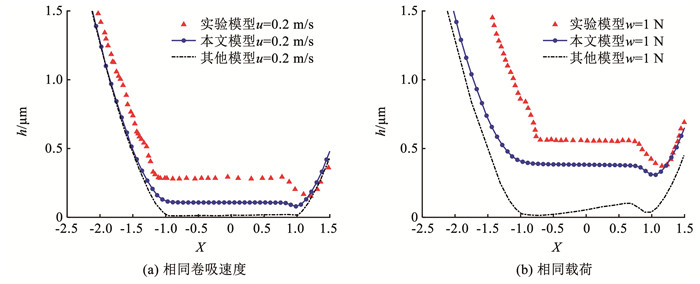
|
图 10 相同卷吸速度和载荷下各模型的脂膜厚度比较 Fig. 10 Comparison of grease film thickness of each model at same entrainment velocity and loads |
图 11研究了流变指数在3种状态即0.65、0.85、1.00下考虑粗糙度和未考虑粗糙度脂膜压力p和脂膜厚度h的分布情况。特别说明当流变指数为1.00时润滑脂的非牛顿性最弱此时为润滑油。
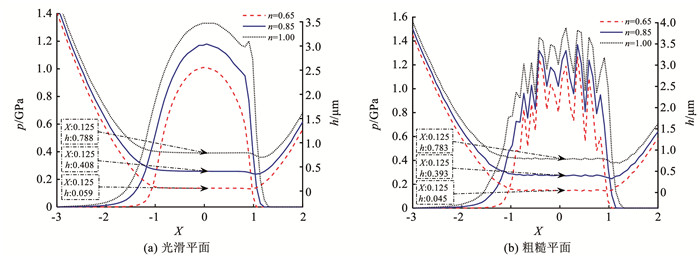
|
图 11 不同流变指数下脂膜压力和脂膜厚度的分布情况 Fig. 11 Distribution of grease film pressure and thickness under different rheological indexes |
从图 11(a)可以看出,随着流变指数减小,即非牛顿特性增强,脂膜厚度逐渐减小且颈缩现象愈加不明显,二次压力峰值逐渐减小,越靠近接触区脂膜压力越符合Hertz压力分布。这是因为入口处存在润滑脂的非剪切行为,流变指数越小则非牛顿特性越明显,剪切变稀的能力变强,润滑脂的黏度随剪应变率增大而减小,润滑脂流速变快,容量减小导致脂膜厚度减小,颈缩现象不明显,压力峰值降低。
从图 11(b)可以看出,在流变指数为0.65时,最大脂膜压力相对较小,最小脂膜厚度相对较小,而在流变指数为1.00时,最大脂膜压力相对较大,最小脂膜厚度相对较大。随着流变指数变化,粗糙平面的脂膜压力、脂膜厚度上下幅动,且与光滑平面脂膜压力及脂膜厚度的变化趋势相同,尤其在出口区域有二次压力峰,脂膜厚度也出现较为明显的颈缩现象。对比同一横坐标X=0.125条件下,脂膜厚度的具体数值,在考虑表面粗糙度时,接触区润滑脂的膜厚更小,极易受到破坏导致摩擦磨损。
4.3 分形维数对脂膜压力和脂膜厚度分布的影响图 12揭示了卷吸速度为0.6 m/s,轴承载荷为2.0 N,不同分形维数下脂膜压力p和脂膜厚度h的分布情况。可以看出,分形维数D为2.45时,最大脂膜压力相对较小,最小脂膜厚度相对较大; 而分形维数D为2.35时,最大脂膜压力相对较大,最小脂膜厚度相对较小。随着分形维数D减小,脂膜压力、膜厚上下波动范围变大,最大脂膜压力增大,最小脂膜厚度减小。这是由于分形维数D减小,表面微凸体越明显,表面越粗糙,这种情况下,滚珠和外圈表面多以微凸体之间相互接触,真实接触面积变小,导致局部脂膜压力增大,从而对将要流入间隙的润滑脂起到阻碍作用,润滑脂流动变慢,使得在Hertz接触区域的部分脂膜厚度减小。因此在计入粗糙度的情况下,脂膜厚度往往比光滑表面的膜厚更小,往往达不到更好润滑的目的,对润滑脂膜的产生起到了负作用。考虑表面粗糙度的影响对于研究主轴承润滑特性更具合理性。

|
图 12 不同分形维数下脂膜压力和脂膜厚度的分布情况 Fig. 12 Distribution of grease film pressure and thickness under different fractal dimension |
图 13比较了载荷为2 N,卷吸速度在3种状态即0.2、0.4、0.6 m/s下考虑粗糙度和未考虑粗糙度脂膜压力p和脂膜厚度h的分布情况。从图 13(a)可以看出,随着卷吸速度的增大,脂膜压力变化不大,膜厚增加,二次压力峰越明显,且逐渐远离出口区域。这是由于随着卷吸速度的增大,接触区上下界面润滑脂相对速度增大,被滚珠带入接触区的润滑脂增多,使得脂膜厚度增大,这说明在实际工况中也可以适当增大转速以达到利于润滑的目的。

|
图 13 不同卷吸速度下脂膜压力和脂膜厚度的分布情况 Fig. 13 Distribution of grease film pressure and thickness at different entrainment velocity |
从图 13(b)看出,最大脂膜压力相比较不太明显,但是在卷吸速度为0.2 m/s时,最小脂膜厚度相对较小,而在卷吸速度为0.6 m/s时,最小脂膜厚度相对较大。对于粗糙平面的脂膜压力以及膜厚分布,其压力值、膜厚值由于表面结构的不平整,变化幅度明显,且粗糙表面的脂膜压力和脂膜厚度具有更大或更小的极值,在实际中,受粗糙度影响主轴承更加容易缺脂,并同时存在干摩擦和流体动压润滑两种状态即混合润滑状态,从而极大可能发生摩擦和磨损破坏,所以有必要考虑粗糙度影响,对卷吸速度适当提高,改善润滑。
4.5 载荷对脂膜压力和脂膜厚度分布的影响图 14探讨了卷吸速度为0.6 m/s,载荷在3种状态即1、2、5 N下光滑和粗糙平面脂膜压力p和脂膜厚度h的分布情况。图 14(a)可以看出,载荷增大对脂膜压力影响不大但对脂膜厚度影响较大。随载荷的逐渐增大,脂膜厚度逐渐减小,润滑脂出口附近的二次压力峰逐渐降低,颈缩现象越来越不明显。这是因为较大的载荷对轴承间隙挤压作用加强,接触区上下界面润滑脂被挤压,接触区的润滑脂流失,使得脂膜厚度减小,因为脂膜厚度减小,所以接触区域内外压力差较难形成,压力峰值降低和颈缩现象愈加不明显。
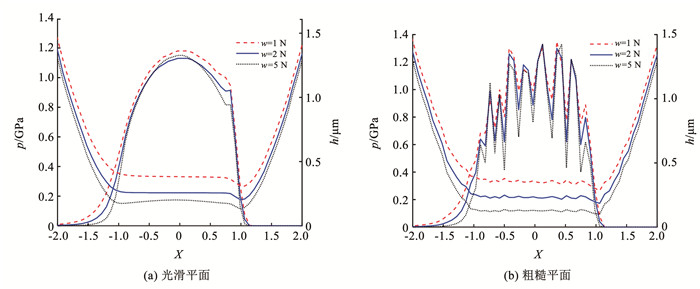
|
图 14 不同载荷下脂膜压力和脂膜厚度的分布情况 Fig. 14 Distribution of grease film pressure and thickness under different loads |
从图 14(b)可以看出,在载荷为5 N时,最大脂膜压力不做比较,最小脂膜厚度相对较小,而在载荷为1 N时,最小脂膜厚度相对较大。在润滑脂出口区域压力有聚增,颈缩现象也较为明显且和光滑平面二次压力峰以及颈缩变化规律保持高度一致。通过对光滑和粗糙平面形成脂膜厚度大小的判断,分析出适当减小载荷有利于润滑。
4.6 润滑脂黏度对脂膜压力和脂膜厚度分布的影响图 15探究了载荷为2 N,卷吸速度为0.6 m/s,润滑脂黏度在3种状态即0.05、0.08、0.16 Pa·s下光滑和粗糙平面脂膜压力p和脂膜厚度h的分布情况。图 15(a)可以看出,黏度变化对脂膜压力影响变化不大,随着黏度的增加,脂膜厚度逐渐增大,二次压力峰值逐渐增大,脂膜颈缩现象越来越明显。这是由于随着润滑脂黏度的增大,接触区界面润滑脂流动性会变差,导致接触区的润滑脂缓出滞留,使得脂膜厚度逐渐增大。因为脂膜厚度的增加,接触区域内外容易形成压力差,导致在出口区域的压力峰值增加和颈缩现象明显。

|
图 15 不同润滑脂黏度下脂膜压力和脂膜厚度的分布情况 Fig. 15 Distribution of grease film pressure and thickness under different grease viscosity |
从图 15(b)可以看出,在润滑脂黏度为0.05 Pa·s时,最大脂膜压力不做比较,最小脂膜厚度相对较小,而在润滑脂黏度为0.16 Pa·s时,最小脂膜厚度相对较大。粗糙平面与光滑平面相比,除脂膜压力、脂膜厚度有上下幅度变化外,总体趋势相同,且在润滑脂出口处同样出现二次压力峰和颈缩现象但不明显。光滑和粗糙平面的脂膜厚度都随润滑脂黏度增大而增大,因此适当增大润滑脂黏度有利于润滑。
5 结论1) 三维分形函数对主轴承实际加工表面形貌进行表征。受粗糙度影响的三维脂膜压力分布呈现多个压力峰值,二次压力峰和脂膜颈缩现象不再明显。考虑粗糙度的三维脂膜压力值比未考虑粗糙度的值大;相反,三维脂膜厚度值小。考虑粗糙度和润滑脂非牛顿性的点接触弹流润滑分析更贴近实际。
2) 流变指数越小,主轴承润滑脂的非牛顿特性越明显,润滑脂膜的剪切稀化行为越强,脂膜厚度减小;分形维数越小,主轴承表面越粗糙,真实接触面积减小,脂膜厚度也减小;主轴承的卷吸速度和润滑脂黏度越大,润滑脂堆积容量增加,脂膜厚度增大;主轴承法向载荷越大,接触间隙变小,脂膜厚度减小。
3) 脂膜厚度决定主轴承润滑效果。在流变指数较小、分形维数较小、重载、低转速和低黏度的润滑工况下,润滑脂膜厚度偏低,主轴承润滑效果越差,极易导致接触表面从流体动压润滑过渡为混合润滑状态。
| [1] |
SHI Xiujiang, SUN Wen, LU Xiqun, et al. Three-dimensional mixed lubrication analysis of spur gears with machined roughness[J]. Tribology International, 2019, 140: 105864. DOI:10.1016/j.triboint.2019.105864 |
| [2] |
BAHK C J, PARKER R G. Analytical investigation of tooth profile modification effects on planetary gear dynamics[J]. Mechanism and Machine Theory, 2013, 70: 298. DOI:10.1016/j.mechmachtheory.2013.07.018 |
| [3] |
WANG Hui, SHI Zhaoyao, YU Bo, et al. Transmission performance analysis of RV reducers influenced by profile modification and load[J]. Applied Sciences, 2019, 9(19): 4099. DOI:10.3390/app9194099 |
| [4] |
SUN Zhangdong, ZHU Caichao, LIU Huaiju, et al. Study on starved lubrication performance of a cycloid drive[J]. Tribology Transactions, 2016, 59(6): 1005. DOI:10.1080/10402004.2015.1129569 |
| [5] |
HAMROCK B J, DOWSON D. Isothermal elastohydrodynamic lubrication of point contacts: Part 1—theoretical formulation[J]. Journal of Lubrication Technology, 1976, 98(2): 223. DOI:10.1115/1.3452801 |
| [6] |
翟文杰, 张鹏顺. 点接触弹性流体动力润滑的数值求解[J]. 哈尔滨工业大学学报, 1993, 25(6): 80. ZHAI Wenjie, ZHANG Pengshun. Numerical calculation of elastohydrodynamic lubrication atpoint contact[J]. Journal of Harbin Institute of Technology, 1993, 25(6): 80. |
| [7] |
MENG Fanming, ZHENG Yong, LIU Yu, et al. Multi-ellipsoid contact elastohydrodynamic lubrication performance for deep groove ball bearing[J]. Tribology International, 2020, 150: 106367. DOI:10.1016/j.triboint.2020.106367 |
| [8] |
李静, 曹树谦, 郭虎伦, 等. 考虑中介轴承弹流润滑时双转子系统振动特性[J]. 哈尔滨工业大学学报, 2021, 53(6): 138. LI Jing, CAO Shuqian, GUO Hulun, et al. Vibration performance of dual rotor systems considering elastohydrodynamic lubrication of intershaft bearings[J]. Journal of Harbin Institute of Technology, 2021, 53(6): 138. DOI:10.11918/201909168 |
| [9] |
张丽静, 王优强. 海水润滑塑料轴承的微观热弹流润滑分析[J]. 中国机械工程, 2013, 24(1): 90. ZHANG Lijing, WANG Youqiang. Thermal micro-elastohydrodynamic lubrication analysis of seawater-lubricated plastic bearing[J]. China Mechanical Engineering, 2013, 24(1): 90. DOI:10.3969/j.issn.1004-132X.2013.01.018 |
| [10] |
魏波, 王家序, 周广武, 等. RV减速器主支撑角接触球轴承混合润滑分析[J]. 摩擦学学报, 2015, 35(4): 454. WEI Bo, WANG Jiaxu, ZHOU Guangwu, et al. Mixed lubrication analysis of the main supporting angular contact ball bearing of RV reducer[J]. Tribology, 2015, 35(4): 454. DOI:10.16078/j.tribology.2015.04.014 |
| [11] |
路遵友, 吕延军, 张永芳, 等. 考虑热弹性变形的角接触球轴承微观热弹流分析[J]. 摩擦学学报, 2018, 38(3): 299. LU Zunyou, LÜ Yanjun, ZHANG Yongfang, et al. Micro thermal elastohydrodynamic lubrication analysis of angular contact ball bearing considering thermal elastic deformation[J]. Tribology, 2018, 38(3): 299. DOI:10.16078/j.tribology.2018.03.007 |
| [12] |
LI Linlin, YANG Jiajun. Surface roughness effects on point contact elastohydrodynamic lubrication in linear rolling guide with fractal surface topographies[J]. Industrial Lubrication and Tribology, 2018, 70(4): 589. DOI:10.1108/ilt-04-2017-0092 |
| [13] |
黄平, 袁佳福. 非牛顿流体的点接触弹流润滑理论与实验研究[J]. 华南理工大学学报(自然科学版), 2019, 47(3): 37. HUANG Ping, YUAN Jiafu. Theoretical and experimental research on elastohydrodynamic lubrication of non-newtonian fluids in point contact[J]. Journal of South China University of Technology (Natural Science Edition), 2019, 47(3): 37. DOI:10.12141/j.issn.1000-565X.180252 |
| [14] |
张翔, 刘晓玲, 孙文东, 等. 计入表面吸附膜的热弹流润滑体系建模及分析[J]. 表面技术, 2022, 51(3): 57. ZHANG Xiang, LIU Xiaoling, SUN Wendong, et al. Modeling and analysis of thermal EHL system considering adsorption film on surfaces[J]. Surface Technology, 2022, 51(3): 57. DOI:10.16490/j.cnki.issn.1001-3660.2022.03.005 |
| [15] |
吴正海, 徐颖强, 刘楷安, 等. 脂润滑点接触副混合润滑模型研究[J]. 机械工程学报, 2022, 58(1): 145. WU Zhenghai, XU Yingqiang, LIU Kaian, et al. The study on grease mixed-lubrication model of point contact pair[J]. Journal of Mechanical Engineering, 2022, 58(1): 145. DOI:10.3901/JME.2022.01.145 |
| [16] |
黄健, 李朝阳, 陈兵奎. RV减速器用新型交错滚子主轴承承载能力分析与试验研究[J]. 机械工程学报, 2021, 57(7): 68. HUANG Jian, LI Chaoyang, CHEN Bingkui. Analysis and experimental study on static load capacity of a new radial-axial roller bearing integrated in RV reducer[J]. Journal of Mechanical Engineering, 2021, 57(7): 68. DOI:10.3901/JME.2021.07.068 |
| [17] |
张益铭, 杨荣松, 孙少强. RV减速器主轴承接触刚度及有限元分析[J]. 机械设计与制造, 2018(Sup.2): 1. ZHANG Yiming, YANG Rongsong, SUN Shaoqiang. The RV reducer main bearing contact stiffness and finite element analysis[J]. Machinery Design & Manufacture, 2018(Sup.2): 1. DOI:10.19356/j.cnki.1001-3997.2018.s2.001 |
| [18] |
HAN Kunpeng, ZHANG Dinghua, YAO Changfeng, et al. Analytical modeling of through depth strain induced by deep rolling[J]. The Journal of Strain Analysis for Engineering Design, 2022, 57(4): 279. DOI:10.1177/03093247211027081 |
| [19] |
卢宪玖, 王优强, 刘昺丽, 等. 考虑动态特性的角接触球轴承微观热弹流分析[J]. 机械工程学报, 2014, 50(23): 104. LU Xianjiu, WANG Youqiang, LIU Bingli, et al. Analysis of micro-elastohydrodynamic lubrication of angular contact ball bearing considering dynamic characteristics[J]. Journal of Mechanical Engineering, 2014, 50(23): 104. DOI:10.3901/JME.2014.23.104 |
| [20] |
温诗铸, 黄平, 田煜, 等. 摩擦学原理[M]. 5版. 北京: 清华大学出版社, 2018. WEN Shizhu, HUANG Ping, TIAN Yu, et al. Principles of Tribology[M]. 5th Ed. Beijing: Tsinghua University Press, 2018. |
| [21] |
ROELANDS C J A. Correlational aspects of the viscosity-temperature-pressure relationship of lubricating oils[D]. The Netherlands: Technische Hogeschool Delft, 1966
|
| [22] |
DOWSON D, HIGGINSON G R. Lubrication of rigid cylinders[M]//Elasto-Hydrodynamic Lubrication. Amsterdam: Elsevier, 1977: 30. DOI: 10.1016/b978-0-08-021302-6.50009-6
|
| [23] |
李玲, 裴喜永, 史小辉, 等. 混合润滑状态下结合面法向动态接触刚度与阻尼模型[J]. 振动工程学报, 2021, 34(2): 243. LI Ling, PEI Xiyong, SHI Xiaohui, et al. Normal dynamic contact stiffness and damping model of joint surfaces in mixed lubrication[J]. Journal of Vibration Engineering, 2021, 34(2): 243. DOI:10.16385/j.cnki.issn.1004-4523.2021.02.004 |
| [24] |
CHU Liming, CHANG Y P, LIN J R. Effects of elastic ball and coating on pure squeeze EHL motion for constant load with couple stresses using FDM method[J]. MATEC Web of Conferences, 2017, 123: 00007. DOI:10.1051/matecconf/201712300007 |
| [25] |
BRANDT A, LUBRECHT A A. Multilevel matrix multiplication and fast solution of integral equations[J]. Journal of Computational Physics, 1990, 90(2): 348. DOI:10.1016/0021-9991(90)90171-V |
| [26] |
JI Jinghu, BI Qinsheng, FU Yonghong. Hydrodynamic lubrication of conformal contacting surfaces with parabolic grooves[J]. Journal of Tribology, 2012, 134(1): 011701-1. DOI:10.1115/1.4005518 |
 2024, Vol. 56
2024, Vol. 56


