2. 流体及动力机械教育部重点实验室(西华大学),成都 610039;
3. 四川航天烽火伺服控制技术有限公司,成都 611130
2. Key Laboratory of Fluid and Power Machinery, Ministry of Education (Xihua University), Chengdu 610039, China;
3. Sichuan Aerospace Fiberhome Servo Control Technology Co. Ltd., Chengdu 611130, China
微流控系统是20世纪90年代由Manz[1]教授提出,自提出后一直保持着研究热度,更是被Forbes杂志和Business2.0杂志分别评价为“影响人类未来15件最主要的发明”和“改变世界的7种技术之一”。现阶段,微流控系统已在体育竞技、体外诊断、医疗诊断、司法和航空航天领域展现了重要而广泛的应用场景[2-6]。微泵作为微流控系统的执行元件,担任着微量流体快速、精准传输和控制作用,被誉为微流控系统的心脏,也是微流控系统发展的重要标志[7-8]。随着各领域与微流控系统的结合日益紧密,这些领域在高速发展的同时对微泵的性能提出了进一步要求,微型化、高度集成化、流速范围宽、流速稳定性高成为微泵发展的必然趋势。而目前存在的机械式或非机械式微泵[9],如压电微泵[10]、静电微泵[11]、电磁微泵[12]、气压微泵[13]、电渗微泵[14]等,都存在着加工困难或者无法避免的焦耳热问题。相比之下,铁磁流体微泵具有结构简单、泵送可靠性高、产热低、便于集成化等优点,其优越的性能与微泵发展趋势十分吻合,因此工程领域和学术领域对于推动铁磁流体微泵的发展给予高度重视。
铁磁流体是一种兼具磁响应特性和流动特性的新型智能材料,自1960年美国阿波罗登月计划中使用其成功实现宇航服和宇宙飞船可动部分的密封以及失重状态下燃料供给问题后,受到广泛关注,并迅速得到发展[15-16]。1973年,Miller[17]率先提出利用铁磁流体的磁-流二相性实现流体驱动,随后Greivell等[18]和Park等[19-20]相继使用电磁铁成功制成磁吸管和磁制动器,但由于体积和质量均较大,且应用领域较少,并没有得到推广。2001年,Hatch等[21]开创性的提出应用永磁体进行无侵入式控制磁流体运动,并设计了微结构的环形泵腔,极大的缩小了磁流体微泵的体积和质量,使磁流体微泵的性能逐渐与微流控的发展方向吻合。后来更多的科研工作者致力于将其应用在微流控系统中,如Ashouri等[22]提出了一种直线式往复运动的磁流体泵。Lee等[23]提出了一种双活塞驱动的磁流体泵。Qi等[24]提出了一种旋转多级的磁流体泵。由此可见,磁流体泵的结构开始趋于多样化,驱动原理和相应的理论基础也逐渐成熟,但随着进一步的研究和应用,也暴露出一些缺陷,因回流引起的流量不稳定和内部流动结构不稳定以及铁磁流体的融合、分离过程难以精确控制等问题阻碍了铁磁流体泵的发展。针对该问题,Kumamaru等[25]应用收缩-扩散管结构两端口的阻力系数不同,减少回流发生。沈忱[26]通过在泵腔结构中增设阻流挡板,通过磁流体绕流挡板,堵塞回流通道,抑制回流发生。Ashouri等[27]在微泵结构出口处增设了被动阻流阀。数据表明,这些结构上的改变对于减缓回流均起到了较好效果,但增加了制造困难,且可能诱导出口流速的不稳定,因此没有得到推广。
综上所述,目前铁磁流体微泵的研究及扩展,主要基于Hatch提出的微泵结构,但Hatch微泵结构中存在着磁流体融合、分离过程,对于外磁场的精准控制提出了极大要求[21],且对于磁流体微泵的回流问题均是以机械加工的手段增加主动、被动阀结构,实现抑制回流,从制造成本和能源利用角度而言,并没有从根本上解决因流动结构引起的回流问题。本文基于离心泵的工作原理,结合铁磁流体的磁学行为和泵送介质流体的流体力学行为,提出离心式铁磁流体微泵,在保留体积小、低产热、质量轻、结构简单特点的同时,抑制了微泵内部回流的产生,且新型磁流体微泵不存在磁流体融合和分离过程,因此在一定程度上提高了泵送可靠性及稳定性。
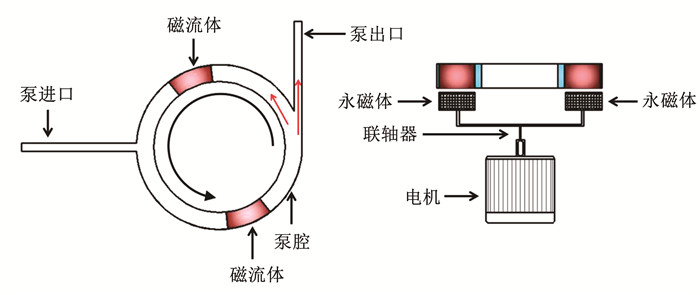
1 理论分析图 1展示了离心式铁磁流体微泵的基本结构。图 1中离心式铁磁流体微泵由电机、永磁体、联轴器、铁磁流体、泵腔5部分组成。两段铁磁流体呈180°放置。电机作为原动力,通过刚性连接的联轴器带动黏附在联轴器端部的永磁体进行周期圆周运动,铁磁流体受外磁场控制和固体壁面约束,无滞后的跟随永磁体进行圆周运动,因此,两段铁磁流体的夹角稳定在180°,并将整个圆环泵腔分割为两部分,靠近进口端的泵腔称为进液腔,靠近出口端的泵腔称为出液腔。当不考虑因界面不稳定引起的两相流体质量扩散、磁性颗粒自由度引起的流动性质变化等问题,并假设铁磁流体的磁化强度与密度正相关,其流动控制方程可以表示为
| $ \boldsymbol{f}+\mu_0 M \nabla H-\frac{1}{\rho_{\mathrm{f}}} \nabla p+\nu \nabla^2 \boldsymbol{v}=\frac{\mathrm{d} \boldsymbol{v}}{\mathrm{d} t} $ | (1) |
|
图 1 离心式铁磁流体微泵示意 Fig. 1 Schematic diagram of centrifugal ferrofluid micropump |
式中: f为铁磁流体所受的除磁场力以外的体积力,N;μ0为真空磁导率,值为4π×10-7 H/m; M为铁磁流体的磁化强度,A/m;H为外磁场强度,A/m; ρf为铁磁流体的密度,kg/m3;p为流体压力,Pa;υ为铁磁流体的运动黏度,m2/s;v为流体速度矢量,m/s;t为时间,s。
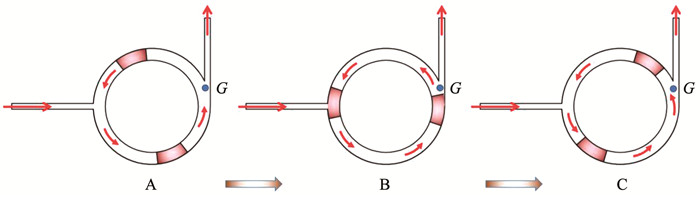
图 2为泵送过程示意图,磁性颗粒磁偶极矩与外磁场响应产生磁彻体力作用于铁磁流体,并通过两相耦合界面将磁能转化为泵送介质流体动能,泵送介质流体在铁磁流体推动和泵腔壁面约束的共同作用下,沿固体壁面做圆周运动,当运动到点G处(泵腔隔舌),速度矢量与圆环相切,在失去泵腔壁面约束后,惯性力促使泵送介质流体沿速度矢量方向运动,发生离心现象,介质流体流出腔体,实现泵送效果。在泵送过程中,不存在铁磁流体的融合、分离过程,因此在一定程度上提高了泵送可靠性和稳定性。
|
图 2 离心式铁磁流体微泵驱动过程 Fig. 2 Driving process of centrifugal ferrofluid micropump |
在该过程中,认为泵送介质流体的克努森数(Knudsen number)远小于1[28],流场分子自由行程的距离远小于宏观特征尺度,其流动过程遵循质量守恒方程和动量守恒方程[29-30]:
| $ \frac{\partial \rho}{\partial t}+\nabla(\rho v)=0 $ | (2) |
| $ f_x-\frac{1}{\rho} \frac{\partial p}{\partial x}+\eta \nabla^2 v_x=\frac{\partial v_x}{\partial t}+v_x \frac{\partial v_x}{\partial x}+v_y \frac{\partial v_x}{\partial y}+v_z \frac{\partial v_x}{\partial z} $ | (3) |
| $ f_y-\frac{1}{\rho} \frac{\partial p}{\partial y}+\eta \nabla^2 v_y=\frac{\partial v_y}{\partial t}+v_x \frac{\partial v_y}{\partial x}+v_y \frac{\partial v_y}{\partial y}+v_z \frac{\partial v_y}{\partial z} $ | (4) |
| $ f_z-\frac{1}{\rho} \frac{\partial p}{\partial z}+\eta \nabla^2 v_z=\frac{\partial v_z}{\partial t}+v_x \frac{\partial v_z}{\partial x}+v_y \frac{\partial v_z}{\partial y}+v_z \frac{\partial v_z}{\partial z} $ | (5) |
式中:fx、fy、fz分别为介质流体在x、y、z方向上的质量力分量, vx、vy、vz分别为介质流体沿x、y、z方向的速度分量, ρ为泵送介质流体的密度,kg/m3;η为泵送介质流体运动黏度,m2/s。
当忽略磁场力传递过程中的能量损失和重力作用时,质量力可表示为:
| $ f_x=\mu_0 M \nabla H \cos \theta_1 $ | (6) |
| $ f_y=\mu_0 M \nabla H \cos \theta_2 $ | (7) |
| $ f_z=\mu_0 M \nabla H \cos \theta_3 $ | (8) |
式中:θ1、θ2、θ3分别为磁场力与笛卡尔坐标系x、y、z轴之间的夹角。
在泵送过程中,两段铁磁流体始终使泵腔进口和泵腔出口处于隔断状态,因此阻断了出口外界流体与进口外界流体的质量交换。该结构设计为泵腔进口宽度小于圆环腔体宽度,使泵腔进口处的流动阻力系数大于圆环腔体的阻力系数,并设计进口与圆环腔体垂直相连,在阻力系数和流动特征的共同作用下,防止了进液腔流体的回流,从而实现整个泵送过程抑制回流发生。
2 模型参数与数值方法随着计算机技术与图像处理技术的发展,CFD(computational fluid dynamics)逐渐成为处理复杂流体流动的重要手段,其基本思想是将原来在时间域和空间域上连续的物理场通过有限个离散点物理量的集合来代替,具有周期短、投资少、流动可视化等优点[31]。本文应用Fluent软件对提出的离心式铁磁流体微泵结构进行数值分析,验证该结构的可行性。
表 1展示了铁磁流体微泵的尺寸参数,图 3为尺寸标注图。考虑到铁磁流体与介质流体多场、多相耦合过程的复杂性和铁磁流体在磁场作用下的磁流变效应,本文提出应用重叠网格和动网格耦合方法对铁磁流体驱动过程进行数值计算[32],将铁磁流体的圆周运动简化为组件网格(component mesh)的圆周运动,并以6DOF(six degrees of freedom)动网格技术控制其运动规律,泵腔结构作为背景网格(background mesh),实现铁磁流体驱动介质流体的泵送效果。因结构性网格具有更好的计算稳定性和收敛性[33],采用了ICEM划分结构性网格进行数值计算,网格模型如图 4所示。
| 表 1 铁磁流体微泵的尺寸参数 Tab. 1 Size parameters of ferrofluid micropump |

|
图 3 尺寸标注图 Fig. 3 Dimensioning drawing |
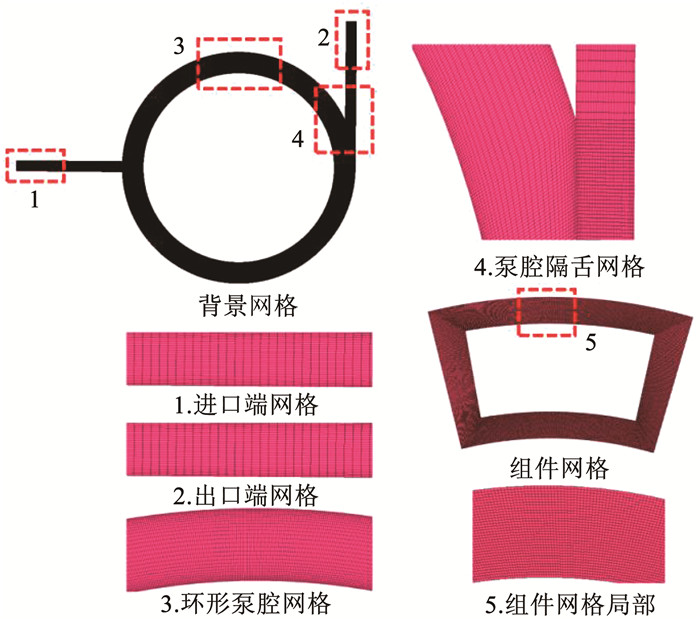
|
图 4 网格模型图 Fig. 4 Grid model diagram |
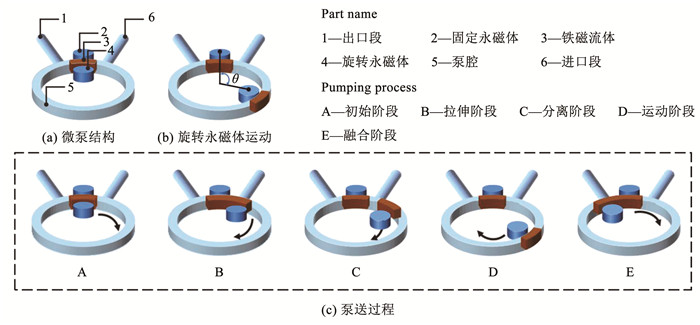
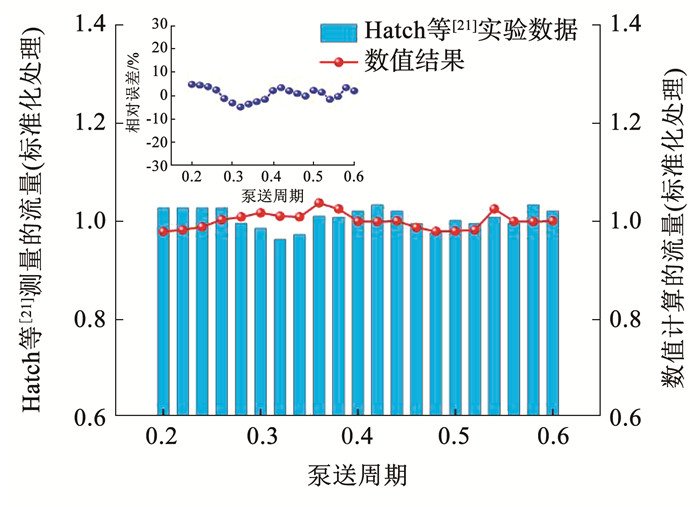
为验证重叠网格和动网格耦合方法模拟铁磁流体微泵运行过程的适用性,利用该方法对Hatch等[21]提出的铁磁流体微泵结构进行数值计算,Hatch等[21]结构主要由进口段、固定永磁体、铁磁流体、旋转永磁体、泵腔和出口段6部分组成,泵送过程分为初始、拉伸、分离、运动、融合5个阶段,如图 5所示,该结构一部分铁磁流体被固定永磁体固定在泵腔结构中,一部分铁磁流体随旋转永磁体运动,伴随两股铁磁流体相对运动,不断挤压泵腔内部的泵送流体,实现泵送过程。但在铁磁流体挤压泵送介质流体时,会产生界面不稳定现象,容易发生铁磁流体与介质流体的混合,同时对两股铁磁流体的融合、分离过程精准控制的难度较大,因此泵送可靠性低,且会发生泵腔内部回流。但该结构是铁磁流体微泵的典型结构,且具有较为完整的实验结果。本文基于Hatch等[21]实验测量的流量曲线,与数值计算的流量曲线进行对比,结果如图 6所示。由图 6可知,在主要泵送周期区间内,Hatch等[21]的实验结果与数值结果的趋势存在一定误差,主要原因在于Hatch等[21]的实验结果基于光学的研究方法,而在微尺寸的透明结构中,利用光学测量方法难免会产生折射、反射等现象,实验结果可能会存在系统误差。并且由于微机械加工技术的限制,在实际实验中,微管道内部的粗糙度难以控制,而在数值计算中,假设了无滑移壁面,从而产生了一定的误差,但二者的流量值较为接近,相对误差ζ在5%以内,可验证数值方法的可行性(标准化处理为瞬时流量与平均流量的比值,定义泵送一个周期所需的时间为T)。
|
图 6 数值结果与实验结果对比 Fig. 6 Comparison between numerical and experimental results |
泵腔隔舌处流体流动复杂,且对出口流量的影响较大,为细腻捕捉泵腔隔舌处的流动特性,对于隔舌处网格进行局部加密。同时为减小网格数量对计算结果的影响,进行了网格无关性验证,研究了一个泵送周期内,不同网格数量与出口周期净流量Qp的关系,Qp的计算方法为
| $ Q_{\mathrm{p}}=\int_t^{t+T} Q_{\mathrm{m}} \mathrm{d} t $ | (9) |
式中:T为泵送周期时长,Qm为微泵出口质量流量。
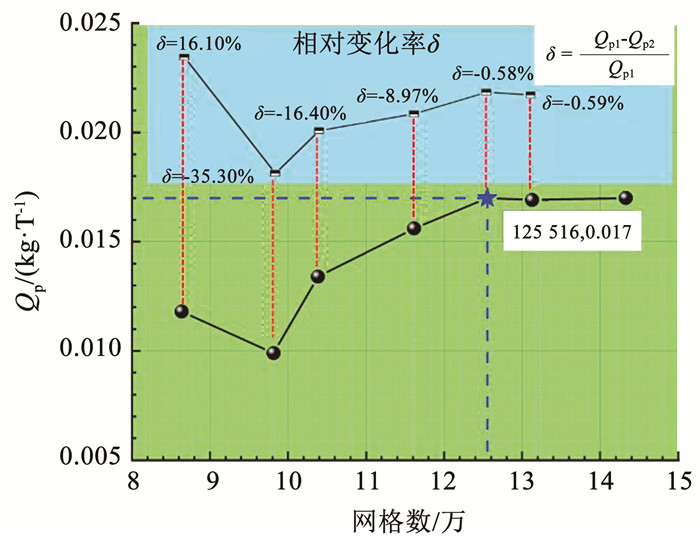
如图 7所示,随网格数量上升,Qp逐渐趋于稳定,当网格大于125 516时,继续增加网格数对于计算结果的影响小于1%,因此最终确定网格数量为125 516。计算基于压力求解器的Coupled算法,对于Gradient离散采用Least Squares Cell Based(基于网格单元的最小二乘法梯度),Pressure离散采用Second Order,Momentum离散采用Second Order Upwind,Transient Formulation离散采用First Order Implicit(图中Qp1为当前网格数下的周期净流量值,Qp2为下一个网格数下的周期净流量值)。
|
图 7 网格无关性验证 Fig. 7 Grid independence verification |
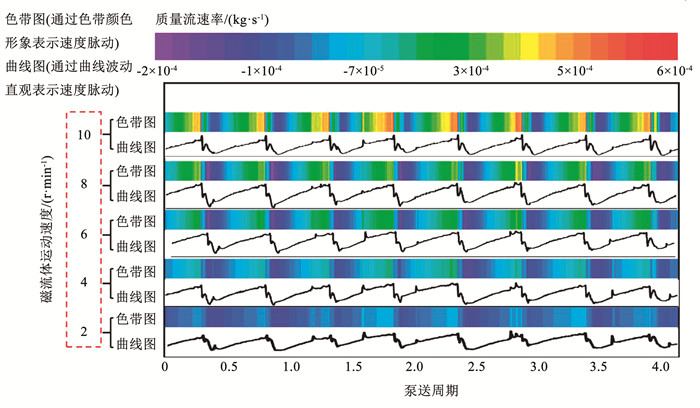
图 8为不同转速下,4个泵送周期内的离心式铁磁流体微泵出口流量曲线图,图 8中色带图表示流量幅值大小,曲线图进一步表示流量的波动规律(铁磁流体起始位置如图 3所示)。如图 8可知,随着铁磁流体的推动,出口处的流量逐渐增大,并在G点处流量达最大,之后介质流体依靠惯性进行滑行,受黏性阻力的影响,其速度开始缓慢下降,动能转化为压能,使部分滑行的流体压力大于圆环腔体内部压力,发生出口回流,但回流的介质流体受到两个铁磁流体的阻断,回流流体被束缚在出液腔,不会对进液腔内的流体流动特性产生影响。
|
图 8 离心式铁磁流体微泵出口流量曲线 Fig. 8 Outlet flow curve of centrifugal ferrofluid micropump |
回流的介质流体受到主流流体的撞击,产生强烈的动能交换,导致速度重新分布,并再次朝向出口运动,流量曲线开始上升。由于两个铁磁流体交替作用,出口流量曲线在泵送周期内进行周期性波动,出现两次波峰和波谷,波动周期与泵送周期相同。
流体在单位时间内受到的合外力F等于流体的动量变化量,这在流体力学中被称为流体的动量定理,如下式所示[35]。当铁磁流体的转速增加后,两相界面施加给介质流体更大的相互作用力,促使其产生更大的动量变化,因此高转速工况下出口具有较大流量值,且具有更大的波峰、波谷及其差值。
| $ \sum F=\frac{\mathrm{d} m v}{\mathrm{~d} t} $ | (10) |
表 2给出了Qp与转速n的关系。介质流体由G点向泵腔出口流动过程中,需要克服流体层与流体层和流体层与壁面之间的黏性阻力。当n为2 r/min时,介质流体的动能较小,其所具有的能量全部转化为黏性耗散,因此Qp趋于0。随着转速的增加,介质流体在分离点G处拥有更多的动能,支持其克服黏性耗散并保持一定的流速继续运动,因此在转速大于4 r/min之后,Qp随转速增加而逐渐增大,当n为10 r/min时,此时介质流体惯性力远大于流体的黏滞力,因此在该转速下,Qp有了明显的提升。
| 表 2 不同转速下的周期净流量值 Tab. 2 Cycle net flow at different rotational speeds |
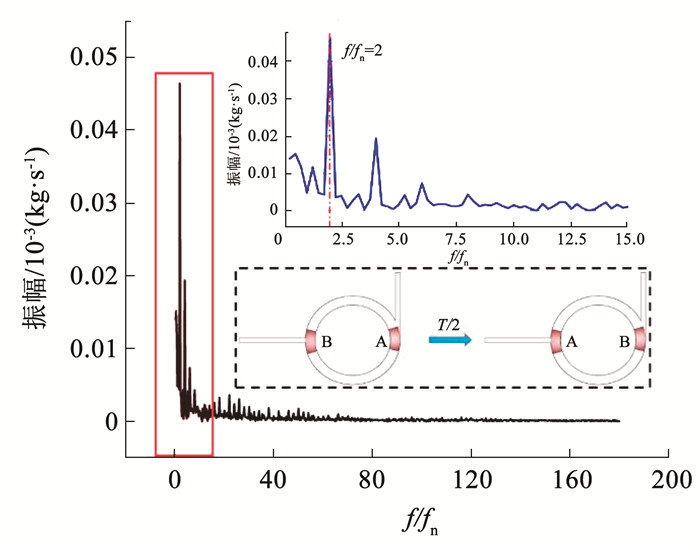
为进一步确定诱导出口流量波动的关键因素,对出口流量的流量-时间函数进行快速傅里叶变换(fast Fourier transform,FFT)[36],得到出口流量振幅与频率的关系。图 9为转速n在2 r/min时出口流量的频域特性,横坐标为相对频率值(f/fn,特征频率/轴频),纵坐标为相对频率值对应的流量脉动能量幅值。由图 9可知,脉动的主要能量振幅处于0~1低频范围,第一主频出现在2倍轴频处。
|
图 9 转速为2 r/min时流量曲线频域特性 Fig. 9 Frequency domain characteristics of flow curve at 2r/min |
下式给出了轴频fn和铁磁流体运动频率ff的表达式:
| $ f_{\mathrm{n}}=n / 60 $ | (11) |
| $ f_{\mathrm{f}}=Z n / 60 $ | (12) |
式中Z为铁磁流体个数,本文中为双铁磁流体结构,因此铁磁流体运动频率为2倍轴频,说明出口流量波动主要因铁磁流体周期性扫过隔舌导致,在大型旋转机械中,将这种诱导流场波动的现象称为动静干涉。
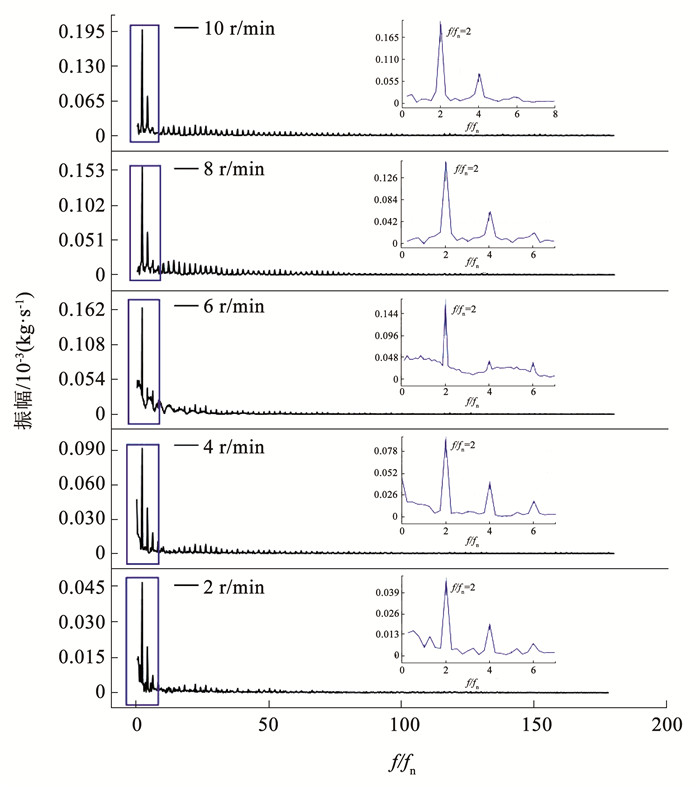
图 10为不同转速下的流量曲线频域特性,可以看出,在不同转速下的第一主频均为铁磁流体运动频率。说明在不同转速下,铁磁流体周期性扫过隔舌均是诱导出口流量脉动的主要因素。转速越高,流动越容易出现高频脉动,如在转速为2 r/min时,在相对频率为75时,频域曲线基本为直线; 而在转速为10 r/min时,在相对频率为75时,频域曲线仍具有明显的锯齿形。在高转速下,泵腔内部流体流动开始变的复杂,在流动分离点G处,部分流体受离心力作用朝向出口运动,还有部分流体撞击在泵腔隔舌处,反弹回环形泵腔内部,进行下一阶段的流体泵送。在该过程中,流体与泵腔隔舌的撞击将产生压力波,压力波一部分传给腔体内做圆周运动的流体,一部分传递给泵腔出口段流体,从而诱导出口流量的小幅度轻微脉动,压力波产生的频率与流动分离的频率相关,即与铁磁流体的运动频率相关。尽管存在脉动,在小尺度效应的加持下,泵腔内部及出口处流体的最大Re仍远小于圆管层流Re阈值(在2~10 r/min转速下,Re < 1),因此流动仍处于层流状态。
|
图 10 不同转速下的流量曲线频域特性 Fig. 10 Frequency domain characteristics of flow curves at different speeds |
式(13)~(15)为流体速度偏导数的等价变化,将式(13)~(15)分别代入到式(3)~(5)后,结合dx=vxt进行联立求解,可得到式(16),式(16)中U为质量力势函数,P为压力函数,wf为黏滞力做功,dl为微元线段长度,(∂v/∂t)dl为流体瞬时惯性力对流体所做的功,即介质流体在流动分离点G处所具有的惯性能。当流体在分离点G分离后,作用在流体上的质量力只有重力,而由于小尺寸效应,重力对于水平方向的流动影响可以忽略,即质量力势函数项可以省略,当流动分离点G处流体的总能量EG与出口处流体总能量EO的关系满足式(17)时,可实现泵送过程。
| $ \begin{gathered} \frac{\partial}{\partial x}\left(\frac{v^2}{2}\right)=\frac{1}{2} \frac{\partial\left(v_x^2+v_y^2+v_z^2\right)}{\partial x}= \\ v_x \frac{\partial v_x}{x}+v_y \frac{\partial v_y}{x}+v_z \frac{\partial v_z}{x} \end{gathered} $ | (13) |
| $ \begin{gathered} \frac{\partial}{\partial y}\left(\frac{v^2}{2}\right)=\frac{1}{2} \frac{\partial\left(v_x^2+v_y^2+v_z^2\right)}{\partial y}= \\ v_x \frac{\partial v_x}{y}+v_y \frac{\partial v_y}{y}+v_z \frac{\partial v_z}{y} \end{gathered} $ | (14) |
| $ \begin{gathered} \frac{\partial}{\partial z}\left(\frac{v^2}{2}\right)=\frac{1}{2} \frac{\partial\left(v_x^2+v_y^2+v_z^2\right)}{\partial z}= \\ v_x \frac{\partial v_x}{z}+v_y \frac{\partial v_y}{z}+v_z \frac{\partial v_z}{z} \end{gathered} $ | (15) |
| $ \mathrm{d}\left(U-P-\frac{v^2}{2}-w_{\mathrm{f}}\right)=\frac{\partial v}{\partial t} \mathrm{~d} l $ | (16) |
| $ \begin{gathered} E_{\mathrm{G}}=P_{\mathrm{G}}+\frac{v_{\mathrm{G}}^2}{2}+\frac{\partial v}{\partial t} \mathrm{~d} l>E_0= \\ P_{\mathrm{b}}+P_2+w_{\mathrm{f}}+e \end{gathered} $ | (17) |
式中: Pb为铁磁流体微泵出口背压,P2为出口处流体本身的压能,wf为流体在出口段处的黏性摩擦损失,e为出口段部分回流流体与主流流体撞击所产生的能量损失。
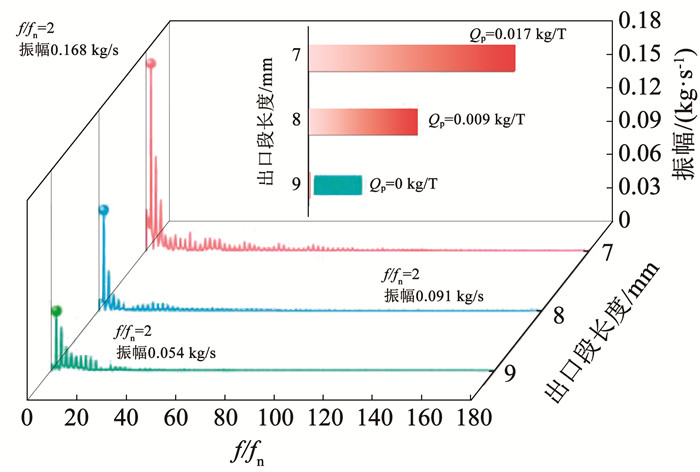
图 11为在转速n=4 r/min时,出口段长度l2分别为7、8、9 mm时出口流量的频谱图。如图 11可知,不同l2值下的出口流量脉动的主频值均在相对频率为2倍处,即产生流量波动的主要因素仍为铁磁流体与泵腔隔舌的动静干涉作用。随着出口段长度的增加,动静干涉所产生的波动信号沿出口段方向逐渐减弱,主频所对应的振幅值逐渐减小,并在相对频率20之后,振幅趋于平稳,因不良流动引起的轻微波动也逐渐消失,从该方面看,对离心式铁磁流体微驱动器的平稳泵送产生了有益的效果。
|
图 11 不同出口段长度的出口流量频域特性 Fig. 11 Frequency domain characteristics of outlet flow with different outlet length |
但出口段长度的增加,介质流体层与介质流体层和介质流体层与壁面之间的摩擦损失增加,由Capillary number定义可知,黏性力与界面力不受尺寸约束,而根据Reynolds number定义可知,惯性力与特征尺寸成线性关系,因此在小尺度下的离心式铁磁流体微泵,惯性动能较小,即使是微小的尺寸增加也会产生较大的泵送阻力,该结论可通过对比7、8、9 mm l2下的Qp进行验证。表 3给出了Capillary number和Reynolds number的定义,表 3中L为特征长度,gc为几何常数,σ为界面力[37]。
| 表 3 量纲一的数定义 Tab. 3 Definition of dimensionless numbers |
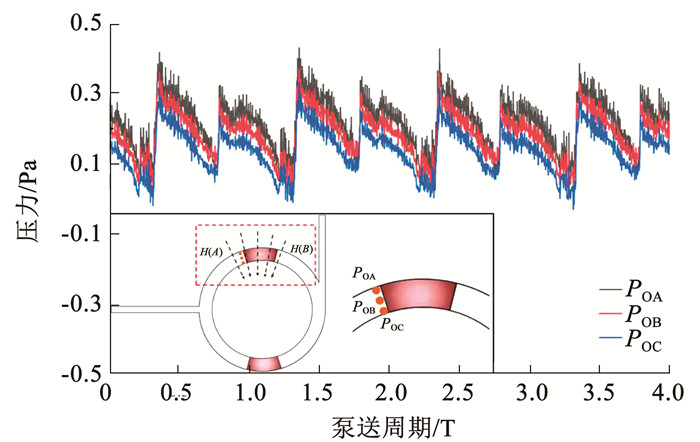
在铁磁流体驱动介质流体泵送过程中,两相界面的稳定性是实现泵送效果的关键,多数研究表明,两相界面的压力波动是引起铁磁流体界面失稳、乳化的重要因素[38-39],因此,本文通过用户自定义相对坐标系(user define reference frame),在两相界面上设置动态监测点,监测点的运动速度与铁磁流体(前景网格)的运动速度保持一致,监测点位置如图 12所示。
|
图 12 转速4 r/min时两相界面不同位置上的压力波动 Fig. 12 Pressure fluctuations at different positions of two-phase interface at the speed of 4 r/min |
图 12展示了两相界面不同位置上的压力波动。由图 12可知,界面上的压力波动展现出较好的周期性,并且不同位置上的压力脉动规律一致,其只有小程度上的幅值差异(差值小于0.1 Pa)。在一个泵送周期内(初始位置如图 3所示),监测点所在位置为进液腔,进液腔内残留的压力势能顺着进口流道传递向外界,因此界面上的压力呈现逐渐减小的趋势。当铁磁流体靠近进口流道处时,由于铁磁流体与泵腔缺口处的碰撞,将产生新的压力波,促使界面上压力突增,随后进液腔转化为出液腔,新的压力波顺着介质流体沿泵腔出口传向外界,因此界面上的压力再次呈现逐渐下降的趋势。之后铁磁流体运动到出口流道附近的隔舌处,因动静干涉作用产生新的压力波,并且同时出液腔转换为进液腔,重复上述的压力波传递过程。
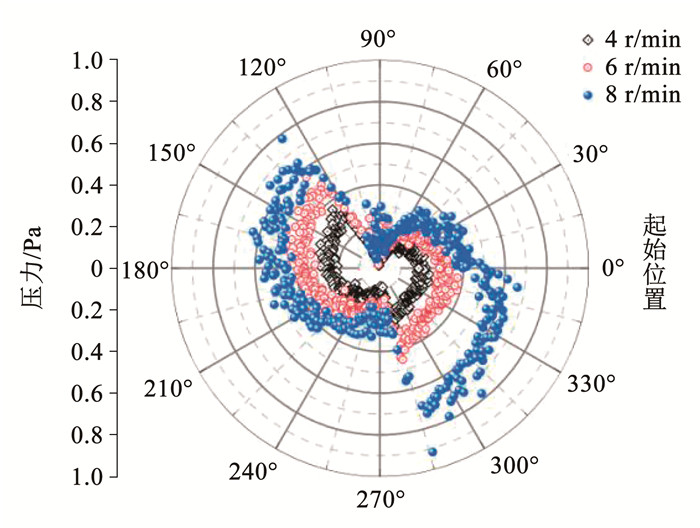
图 13展示了不同转速下在两相界面POB处的压力波动,由图 13可知,在高转速下的压力脉动幅值有了明显的上升,但尽管如此,其压力值仍处于非常小的量级(小于1 Pa),在这种小量级的压力波动下,不会加剧铁磁流体界面层的乳化现象,从铁磁流体界面稳定性方面验证了离心式铁磁流体微驱动器的可行性。
|
图 13 不同转速下相界面POB处的压力波动 Fig. 13 Pressure fluctuation at POB of phase interface at different rotational speeds |
为进一步研究离心式铁磁流体微泵的自密封性能,通过Maxwell软件对微泵的磁场分布特性进行研究,在保证基本模型参数不变的条件下,增加永磁体模型,永磁体位于铁磁流体正上方0.1 mm处,表 4展示了永磁体的基本结构和物理参数,计算边界条件设置为Zero Tangential H Field。
| 表 4 永磁体基本参数 Tab. 4 Basic parameters of permanent magnet |
铁磁流体的自密封性能公式可根据铁磁流体的伯努力方程推导得出[40-41]
| $ \Delta p=\mu_0 \int_{H(\mathrm{~A})}^{H(\mathrm{~B})} M_{\mathrm{s}} \mathrm{d} H $ | (18) |
式中: Δp为密封压差,H(A)、H(B)分别为铁磁流体两端的磁场强度最小值和最大值, Ms为铁磁流体的饱和磁化强度,取39.62 kA/m[42]。
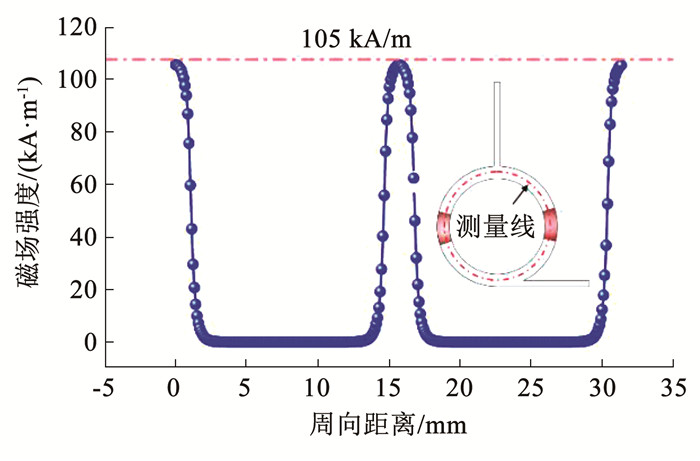
图 14为泵腔结构中磁场强度分布曲线,由图 14可知,因两段铁磁流体需要两块永磁体诱导其做圆周运动,因此在泵腔中的磁场强度分布曲线中出现两个峰值,峰值位置为永磁体所在位置,并且受外界非磁性材料的影响,由永磁体辐射出的磁场在强磁阻的作用下迅速下降,趋向于0 kA/m,由式(18)可计算出,单个铁磁流体在泵腔中的自密封性能为5 227 Pa,该值远大于两相界面的压力波动的正峰值,因此该结构在自密封性能和铁磁流体与泵送介质流体的界面稳定性方面是可行的。
|
图 14 泵腔中磁场强度分布曲线 Fig. 14 Magnetic field intensity distribution curve in pump chamber |
1) 离心式铁磁流体微泵基于铁磁流体的外场控制和磁流变效应给予介质流体初始动能,并在泵腔壁面的约束下促使介质流体圆周运动,应用其圆周运动时具有的切向惯性动能为驱动力,实现介质流体泵送。
2) 离心式铁磁流体微泵具有双铁磁流体结构,且两股铁磁流体呈180°角度放置,并交替作用阻断泵腔进口和出口的质量交换,抑制结构内部回流。
3) 离心式铁磁流体微泵的出口流量存在脉动现象,铁磁流体与泵腔固定结构之间的动静干涉造成的压力波是诱导出口流量脉动的主要原因。随转速增加,微泵具有更大的流量输出,并且有着更加复杂的流动过程,引起宽频脉动,但流动的Re < 1,因此流动仍保持层流状态。
4) 离心式铁磁流体微泵的泵送特性对泵腔出口段长度十分敏感,产生该现象的原因主要是在不可压缩牛顿流体且来流速度不变的情况下,惯性力与特征长度成一次正比关系,而黏滞力却不受特征长度影响,因此在设计时出口段长度应该尽量缩短。
5) 离心式铁磁流体微泵在转速8 r/min以下时,铁磁流体与泵送介质流体的相界面之间的压力脉动峰值相比于其自密封的最大压力值而言非常小,相差3个数量级,因此该结构在自密封性能和铁磁流体的界面稳定性角度而言是可行的。
| [1] |
MANZ A, GRABER N, WIDMER H M. Miniaturized total chemical analysis systems: A novel concept for chemical sensing[J]. Sensors and Actuators B: Chemical, 1990, 1(1/2/3/4/5/6): 244. DOI:10.1016/0925-4005(90)80209-I |
| [2] |
KOH A, KANG D, XUE Yeguang, et al. A soft, wearable microfluidic device for the capture, storage, and colorimetric sensing of sweat[J]. Science Translational Medicine, 2016, 8(366): 366ra165. DOI:10.1126/scitranslmed.aaf2593 |
| [3] |
CHAIMAYO C, KAEWNAPHAN B, TANLIENG N, et al. Rapid SARS-CoV-2 antigen detection assay in comparison with real-time RT-PCR assay for laboratory diagnosis of COVID-19 in Thailand[J]. Virology Journal, 2020, 17(1): 177. DOI:10.1186/s12985-020-01452-5 |
| [4] |
ADAMPOUREZARE M, DEHGHAN G, HASANZADEH M, et al. Application of lateral flow and microfluidic bio-assay and biosensing towards identification of DNA-methylation and cancer detection: Recent progress and challenges in biomedicine[J]. Biomedicine & Pharmacotherapy, 2021, 141: 111845. DOI:10.1016/j.biopha.2021.111845 |
| [5] |
SULTANA N, GUNNING S, FURST S J, et al. Direct analysis of textile dyes from trace fibers by automated microfluidics extraction system coupled with Q-TOF mass spectrometer for forensic applications[J]. Forensic Science International, 2018, 289: 67. DOI:10.1016/j.forsciint.2018.05.020 |
| [6] |
GOLOZAR M, CHU W K, CASTO L D, et al. Fabrication of high-quality glass microfluidic devices for bioanalytical and space flight applications[J]. Methods X, 2020, 7: 101043. DOI:10.1016/j.mex.2020.101043 |
| [7] |
POTHURI C, AZHARUDEEN M, SUBRAMANI K. Rapid mixing in microchannel using standing bulk acoustic waves[J]. Physics of Fluids, 2019, 31(12): 122001. DOI:10.1063/1.5126259 |
| [8] |
ABOELKASSEM Y. Pumping flow model in a microchannel with propagative rhythmic membrane contraction[J]. Physics of Fluids, 2019, 31(5): 051902. DOI:10.1063/1.5092295 |
| [9] |
LEI Jiechao, CHANG C C, WANG Changyi. An analysis of bi-directional Stokes micropump comprising a periodic array of moving belts[J]. Physics of Fluids, 2022, 34(12): 122005. DOI:10.1063/5.0128944 |
| [10] |
GAZARYAN A V, VASILKOV S A, CHIRKOV V A. Simple in fabrication and high-performance electrohydrodynamic pump[J]. Physics of Fluids, 2022, 34(12): 123604. DOI:10.1063/5.0124657 |
| [11] |
FOROUZANDEH F, ALFADHEL A, AREVALO A, et al. A review of peristaltic micropumps[J]. Sensors and Actuators A: Physical, 2021, 326: 112602. DOI:10.1016/j.sna.2021.112602 |
| [12] |
RUSLI M Q A, CHEE P S, ARSAT R, et al. Electromagnetic actuation dual-chamber bidirectional flow micropump[J]. Sensors and Actuators A: Physical, 2018, 282: 17. DOI:10.1016/j.sna.2018.08.047 |
| [13] |
BOTT H, LEONHARDT R, LAERMER F, et al. Employing fluorescence analysis for real-time determination of the volume displacement of a pneumatically driven diaphragm micropump[J]. Journal of Micromechanics and Microengineering, 2021, 31(7): 075003. DOI:10.1088/1361-6439/ac00c9 |
| [14] |
DEHGHAN MANSHADI M K, KHOJASTEH D, MOHAMMADI M, et al. Electroosmotic micropump for lab-on-a-chip biomedical applications[J]. International Journal of Numerical Modelling: Electronic Networks, Devices and Fields, 2016, 29(5): 845. DOI:10.1002/jnm.2149 |
| [15] |
LI Wangxu, LI Zhenggui, HAN Wei, et al. Measured viscosity characteristics of Fe3O4 ferrofluid in magnetic and thermal fields[J]. Physics of Fluids, 2023, 35(1): 012002. DOI:10.1063/5.0131551 |
| [16] |
LI Wangxu, LI Zhenggui, QIN Zhao, et al. Influence of the solution pH on the design of a hydro-mechanical magneto-hydraulic sealing device[J]. Engineering Failure Analysis, 2022, 135: 106091. DOI:10.1016/j.engfailanal.2022.106091 |
| [17] |
MILLER C W. Magnetic fluids: Magnetic forces and pumping mechanisms[R]. Ithaca, NY: Cornell University, 1973
|
| [18] |
GREIVELL N E, HANNAFORD B. The design of a ferrofluid magnetic pipette[J]. IEEE Transactions on Bio-Medical Engineering, 1997, 44(3): 129. DOI:10.1109/10.554759 |
| [19] |
PARK G S, PARK S H. Design of magnetic fluid linear pump[J]. IEEE Transactions on Magnetics, 1999, 35(5): 4058. DOI:10.1109/20.800754 |
| [20] |
PARK G S, PARK S H. New structure of the magnetic fluid linear pump[J]. IEEE Transactions on Magnetics, 2000, 36(5): 3709. DOI:10.1109/20.908948 |
| [21] |
HATCH A, KAMHOLZ A E, HOLMAN G, et al. A ferrofluidic magnetic micropump[J]. Journal of Microelectromechanical Systems, 2001, 10(2): 215. DOI:10.1109/84.925748 |
| [22] |
ASHOURI M, BEHSHAD SHAFⅡ M, MOOSAVI A. Theoretical and experimental studies of a magnetically actuated valveless micropump[J]. Journal of Micromechanics and Microengineering, 2017, 27(1): 015016. DOI:10.1088/0960-1317/27/1/015016 |
| [23] |
LEE C Y, LEONG J C, WANG Yaonan, et al. A ferrofluidic magnetic micropump for variable-flow-rate applications[J]. Japanese Journal of Applied Physics, 2012, 51(4R): 047201. DOI:10.1143/jjap.51.047201 |
| [24] |
QI Chao, SHINSHI T. A disposable bidirectional micropump with three diaphragms driven by a rotating multi-pole magnet[C]//2021 IEEE 30th International Symposium on Industrial Electronics (ISIE). Kyoto, Japan: IEEE, 2021: 1. DOI: 10.1109/ISIE45552.2021.9576266
|
| [25] |
KUMAMARU H, OKAMOTO S, ARIMOTO K, et al. Experimental study on micropump using reciprocating motion of magnetic ball covered with magnetic fluid[J]. Physics Procedia, 2010, 9: 238. DOI:10.1016/j.phpro.2010.11.053 |
| [26] |
沈忱. 无阀磁流体驱动微泵的设计及实验研究[D]. 北京: 北京工业大学, 2021 SHEN Chen. Design and experimental study of valveless Magnetic Fluid driven micropump[D]. Beijing: Beijing University of Technology, 2021. DOI: 10.26935/d.cnki.gbjgu.2021.000505 |
| [27] |
ASHOURI M, SHAFⅡ M B, MOOSAVI A, et al. A novel revolving piston minipump[J]. Sensors and Actuators B: Chemical, 2015, 218: 237. DOI:10.1016/j.snb.2015.04.104 |
| [28] |
IBÁÑEZ G, CUEVAS S. Entropy generation minimization of a MHD (magnetohydrodynamic) flow in a microchannel[J]. Energy, 2010, 35(10): 4149. DOI:10.1016/j.energy.2010.06.035 |
| [29] |
PAN Shiyang, WANG Jun, TAN Qingpeng, et al. Analysis and numerical simulation of claw vacuum pumps with novel three-claw rotors[J]. Vacuum, 2021, 192: 110442. DOI:10.1016/j.vacuum.2021.110442 |
| [30] |
WANG Jun, HAN Yi, PAN Shiyang, et al. Design and development of an oil-free double-scroll air compressor used in a PEM fuel cell system[J]. Renewable Energy, 2022, 199: 840. DOI:10.1016/j.renene.2022.08.154 |
| [31] |
谭善文, 何海宾, 师波. 一种基于尺度分解的湍流计算新方法[J]. 中国科技论文在线精品论文, 2022, 15(4): 488. TAN Shanwen, HE Haibin, SHI Bo. A new turbulence model based on scale decomposition[J]. Highlights of China Sciencepaper Online, 2022, 15(4): 488. |
| [32] |
郝博, 代浩, 吕超. 高速射弹入水过程弹道与流体动力特性研究[J]. 兵器装备工程学报, 2020, 41(12): 21. HAO Bo, DAI Hao, LYU Chao. Research on water entry trajectory and hydrodynamic characteristics of high-speed projectiles[J]. Journal of Ordnance Equipment Engineering, 2020, 41(12): 21. DOI:10.11809/bqzbgcxb2020.12.004 |
| [33] |
王绮帆, 李正贵, 王维军, 等. 空化对分流叶片式航空燃油泵性能的影响研究[J]. 热能动力工程, 2021, 36(4): 21. WANG Qifan, LI Zhenggui, WANG Weijun, et al. Research on the effect of cavitation on the performance of a split-vane aviation fuel pump[J]. Journal of Engineering for Thermal Energy and Power, 2021, 36(4): 21. DOI:10.16146/j.cnki.rndlgc.2021.04.004 |
| [34] |
LI Wangxu, LI Zhenggui, HAN Wei, et al. Pumping-velocity variation mechanisms of a ferrofluid micropump and structural optimization for reflow inhibition[J]. Physics of Fluids, 2023, 35(5): 052005. DOI:10.1063/5.0149130 |
| [35] |
陈卓如, 王洪杰, 刘全忠, 等. 工程流体力学[M]. 3版. 北京: 高等教育出版社, 2013. CHEN Zhuoru, WANG Hongjie, LIU Quanzhong, et al. Engineering fluid mechanics[M]. 3rd ed. Beijing: Higher Education Press, 2013. |
| [36] |
胡波, 张双全, 孙志翔. 导叶进口边相对位置对混流泵压力脉动的影响[J]. 排灌机械工程学报, 2021, 39(1): 16. HU Bo, ZHANG Shuangquan, SUN Zhixiang. Influence of relative position of diffuser leading edge on pressure pulsation in mixed-flow pump[J]. Journal of Drainage and Irrigation Machinery Engineering, 2021, 39(1): 16. DOI:10.3969/j.issn.1674-8530.19.0226 |
| [37] |
SHUI Lingling, EIJKEL J C T, VAN DEN BERG A. Multiphase flow in microfluidic systems: Control and applications of droplets and interfaces[J]. Advances in Colloid and Interface Science, 2007, 133(1): 35. DOI:10.1016/j.cis.2007.03.001 |
| [38] |
李新锐. 液体环境中磁流体密封失效机制与密封性能研究[D]. 成都: 西华大学, 2022 LI Xinrui. Study on failure mechanism and sealing performance of magnetic fluid seal in liquid environment[D]. Chengdu: Xihua University, 2022. DOI: 10.27411/d.cnki.gscgc.2022.000324 |
| [39] |
LI Zhenggui, LI Wangxu, WANG Qifan, et al. Effects of medium fluid cavitation on fluctuation characteristics of magnetic fluid seal interface in agricultural centrifugal pump[J]. International Journal of Agricultural and Biological Engineering, 2021, 14(6): 85. DOI:10.25165/j.ijabe.20211406.6718 |
| [40] |
SZCZECH M. Experimental study on the pressure distribution mechanism among stages of the magnetic fluid seal[J]. IEEE Transactions on Magnetics, 2018, 54(6): 4600507. DOI:10.1109/TMAG.2018.2816567 |
| [41] |
ZHAO Meng, ZOU Jibin, HU Jianhui. An analysis on the magnetic fluid seal capacity[J]. Journal of Magnetism and Magnetic Materials, 2006, 303(2): e428. DOI:10.1016/j.jmmm.2006.01.060 |
| [42] |
李望旭. 离心泵磁液密封界面动力学特性及密封装置优化[D]. 成都: 西华大学, 2022 LI Wangxu. Dynamic characteristics of magnetic fluid sealing interface of centrifugal pump and optimization of sealing device[D]. Chengdu: Xihua University, 2022. DOI: 10.27411/d.cnki.gscgc.2022.000247 |
 2024, Vol. 56
2024, Vol. 56