2. 河南省高等级公路检测与养护技术重点实验室,河南 新乡 453003
2. Henan Key Laboratory of High·grade Highway Detection and Maintenance Technology, Xinxiang 453003, Henan, China
就地热再生技术能实现100%回收旧沥青路面材料,已被广泛应用于沥青路面再生养护中[1-2]。热风加热均匀性好,层间温度梯度小,路面表层不易焦化,国内外75%的就地热再生设备采用热风加热[3]。沥青路面温度场分布是衡量就地热再生路面养护质量的重要指标,因此,构建准确的热风加热沥青路面模型,研究不同加热参数下路面温度场分布,对提高沥青路面热风加热效果具有重要的意义。
准确建立沥青路面传热模型是探究热传递机理的关键。文献[4]建立了热风加热沥青路面二维瞬态导热数学模型,得到了路面温度理论解。文献[5]建立了热风加热沥青路面的温度控制方程,得到了路面温度解析解。文献[6]建立了多层路面温度场数学模型,研究了路面表层辐射产生的热量输出。文献[7]建立了热风循环式加热沥青路面传热模型,研究了通风管参数对路面内部温度分布的影响。上述研究均建立了沥青路面内部的导热模型,但对热风加热路面的对流换热过程研究甚少,而就地热再生中对流换热和导热是同时进行,因此研究两者的共轭传热才能获得更准确的温度场分布。
现有求解对流换热模型常用有限差分法[4]和有限元法[8]。有限差分法仅考虑各网格点之间的数值变化,在计算中对网格点的数据处理较为简单;有限元法引入变分算法,选择逼近函数对计算域积分,但对计算资源要求高且计算周期长。有限容积法将求解区域划分为许多控制容积域,并引入网格内的插值函数,即使采用较粗的网格密度,也能保证离散化后所有控制容积内的各计算节点均满足守恒定律。因此,采用有限容积法求解热风冲击射流对流换热模型,将进一步扩宽其应用范围。
对于提高热风加热沥青路面的加热效果,文献[9]提出往复间隙加热工艺比单向连续加热效果好。文献[10]提出了连续变功率加热工艺,可提高路面热量吸收效率。文献[11]提出了多步法加热工艺,避免了路表层焦化现象。文献[12]提出了恒温加热方法,提高了热再生质量和施工效率。文献[13]提出了热风红外协同加热方法,研究了加热距离对热吸收率的影响。文献[14]研究了加热机组不同作业工序对沥青路面再生效率的影响。文献[15]研究了机组不同行进速度对沥青路面传热效果的影响。上述文献均侧重研究加热工艺对加热效果的影响,而加热参数与路面加热效果关系密切[16]。因此有必要研究热风加热参数对加热效果的影响。
本文基于热风冲击射流对流换热和沥青路面内部导热的共轭传热过程,建立热风加热沥青路面的冲击射流共轭传热理论模型,采用有限容积法研究不同热风参数下的路面温度场分布,讨论加热参数对路面加热效果的影响。
1 热风加热沥青路面共轭传热理论模型 1.1 假设条件黏性气体不可压缩性判据[17]为
| $ 2 v^2 / v_{\mathrm{p}}^2 \ll 1 $ | (1) |
式中:v为气体速度, vp为气体分子的最可几速率。vp的计算为
| $ v_{\mathrm{p}}=\sqrt{\frac{2 k T_{\mathrm{k}}}{m}} $ | (2) |
式中:k为玻耳兹曼常量,取1.381× 10-23 J/K;Tk为气体热力学温度, m为单个分子的质量。
空气平均相对分子质量为29,得到空气平均单个分子质量m=4.817×10-26 kg,取较大热风流速v=20 m/s,较低热风温Tk=573.15 K,计算出热风气体最可几速率vp=573.2 m/s,有2v2/vp=0.002 4≪1。因此,可认为热风具有不可压缩性,即热风气流密度不随压强变化。基于此,假设热风射流为稳定层流,不考虑热风温度对热风密度、黏度和导热系数等参数的影响,同时忽略质量力的影响。
图 1为热风加热沥青路面示意图,热风从喷嘴喷出后冲击路面的共轭传热过程分为热风冲击沥青路面的对流换热(S1)和热量从沥青路面表层沿深度方向的导热(S2)两部分,分别建立传热理论模型。
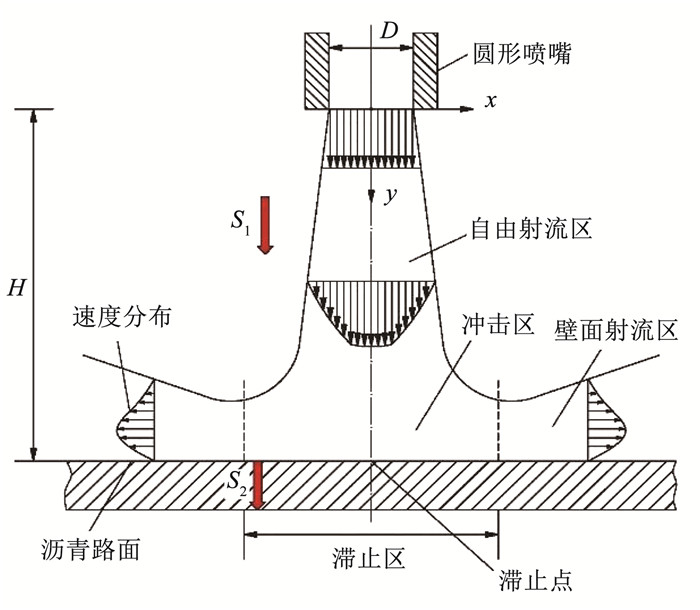
|
图 1 热风加热沥青路面示意 Fig. 1 Schematic diagram of asphalt pavement heated by hot air |
热风喷嘴为圆形,稳定状态时其流场和温度场分布关于轴线对称,因此取过轴线的一个截面,此截面上流场同时满足连续性方程、动量守恒方程以及能量守恒方程,这样将三维热风冲击射流对流换热过程简化为二维轴对称传热问题,建立热风冲击射流对流换热二维模型为
| $ \left\{\begin{array}{l} \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0 \\ \frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y}=-\frac{1}{\rho} \frac{\partial p}{\partial x}+\nu\left(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}\right) \\ \frac{\partial v}{\partial t}+u \frac{\partial v}{\partial x}+v \frac{\partial v}{\partial y}=-\frac{1}{\rho} \frac{\partial p}{\partial x}+\nu\left(\frac{\partial^2 v}{\partial x^2}+\frac{\partial^2 v}{\partial y^2}\right) \\ \frac{\partial T}{\partial t}+u \frac{\partial T}{\partial x}+v \frac{\partial T}{\partial y}=\frac{\lambda}{\rho c_p}\left(\frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}\right) \end{array}\right. $ | (3) |
式中:x为热风流场横坐标,y为热风流场纵坐标,t为时间,u为热风流场内x方向速度,v为热风流场内y方向速度,p为压强,T为温度,ρ为热风密度,λ为热风导热系数,ν为热风运动黏度, cp为热风比定压热容。
1.3 沥青路面导热模型热量到达沥青路面后,以热传导的方式沿轴线向沥青路面深处传递,这个导热过程仅受温差和沥青路面热物性参数的影响[18]。建立沥青路面导热二维模型为
| $ \frac{\partial T}{\partial t}=\frac{\lambda^{\prime}}{\rho^{\prime} c_p^{\prime}}\left(\frac{\partial^2 T}{\partial x^2}+\frac{\partial^2 T}{\partial y^2}\right) $ | (4) |
式中:ρ′为沥青路面密度,λ′为沥青路面导热系数,c′p为沥青路面比定压热容。
2 模型求解为求解冲击射流对流换热模型和导热模型,需要对式(3)、(4)进行离散化处理。由于冲击射流对流换热模型中存在速度场和压力场的耦合,引入基于压力耦合的半隐式算法(SIMPLE)进行解耦[19],得到速度场后再迭代计算温度场。
2.1 方程离散化处理图 2为求解域内采用正方形网格划分后的控制容积图,阴影部分为某网格点P的控制容积,N、S、W、E点分别为P点的北、南、西、东侧相邻网格点,n、s、w、e分别为控制容积的4个边界。
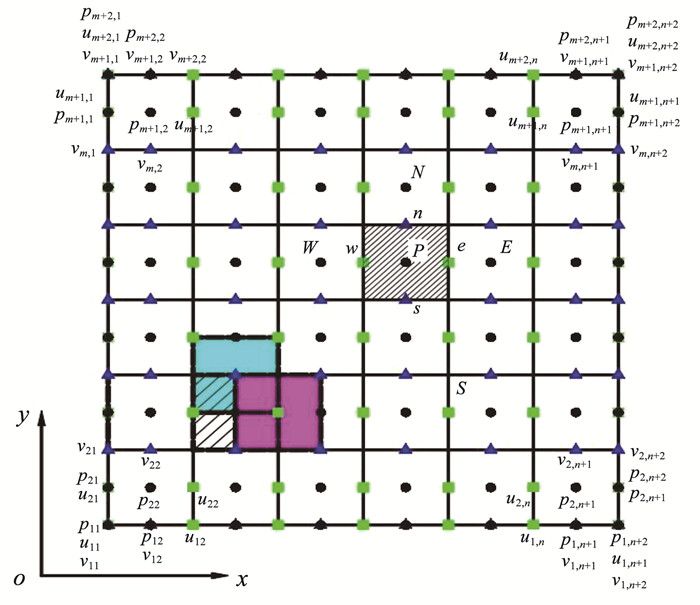
|
图 2 有限容积法网格划分 Fig. 2 Grid division diagram of finite volume method |
为了避免求解中得到“棋盘形”压力场和速度场的失真解,采用图 2所示的交错式网格结构,其中圆形为压力场网格点,其与求解域网格点重合;方形和三角形分别表示速度场分量u和v网格点,分别沿x和y坐标方向偏移半个网格长度。
将式(3)、(4)写成通用格式:
| $ \frac{\partial(\rho \mathit{\Phi })}{\partial t}+\frac{\partial}{\partial x}\left(\rho u \mathit{\Phi }-\mathit{\Gamma } \frac{\partial \mathit{\Phi }}{\partial x}\right)+\frac{\partial}{\partial y}\left(\rho v \mathit{\Phi }-\mathit{\Gamma } \frac{\partial \mathit{\Phi }}{\partial y}\right)=S $ | (5) |
式中:
| 表 1 通用方程各参数意义 Tab. 1 Parameter meanings of general equations |
记x和y方向对流—扩散总通量密度分别为
| $ \frac{\partial(\rho \mathit{\Phi })}{\partial t}+\frac{\partial J_x}{\partial x}+\frac{\partial J_y}{\partial y}=S $ | (6) |
在控制容积P内对式(6)两边进行时间域和空间域的积分,假设:
1) 以
2) 总通量密度Jx和Jy在控制体各界面上是均匀的,即有
| $ \begin{aligned} {\int\limits_s}^n {\int\limits_w}^e \frac{\partial J_x}{\partial x} \mathrm{~d} x \mathrm{~d} y= & {\int\limits_s}^n\left(J_x^e-J_x^w\right) \mathrm{d} y \cong \\ & \left(J_x^e-J_x^w\right) \Delta y=J_e-J_w \end{aligned} $ | (7) |
式中:Jxe、Jxw分别为x方向上e和w界面的单位面积转移量,Je、Jw分别为总面积Δy上的转移量。
3) 源项S可以表示为ΦP的线性函数,即:S=SC+SPΦP(SP≤0),其中SC、SP分别为常数项和正比例项系数。
那么,得到积分后的方程为
| $ \begin{gathered} \frac{(\rho \mathit{\Phi })_P-(\rho \mathit{\Phi })_P^0}{\Delta t} \Delta V+\left(J_e-J_w\right)+\left(J_n-J_s\right)= \\ \left(S_{\mathrm{C}}+S_{\mathrm{P}} \mathit{\Phi }_P\right) \Delta V \end{gathered} $ | (8) |
式中,ΔV=ΔxΔy为控制容积的体积。
界面总通量表达式为[20]
| $ \left\{\begin{array}{l} J_e=\left(a_E+F_e\right) \mathit{\Phi }_P-a_E \mathit{\Phi }_E \\ J_n=\left(a_N+F_n\right) \mathit{\Phi }_P-a_N \mathit{\Phi }_N \\ J_w=a_W \mathit{\Phi }_W-\left(a_W+F_w\right) \mathit{\Phi }_P \\ J_s=a_S \mathit{\Phi }_S-\left(a_S+F_s\right) \mathit{\Phi }_P \end{array}\right. $ | (9) |
将式(9)代入式(8),得到通用离散方程:
| $ a_P \mathit{\Phi }_P=a_E \mathit{\Phi }_E+a_W \mathit{\Phi }_W+a_N \mathit{\Phi }_N+a_S \mathit{\Phi }_S+b $ | (10) |
其中:
式中:贝克来数Pi=Fi/Di(i=e,w,n,s),对流项
| 表 2 对流强度Fi和扩散强度Di取值表 Tab. 2 Values of convection intensity Fi and diffusion intensity Di |
在求解域上,速度场和压力场的边界条件完全相反[21],图 3为整个求解域边界示意图。图中OA:u=u0,v=0,p=p0,T=T0;AB:u=0,v=0,p=0,T=Tf;OC:∂u/∂x=0,v=0,∂p/∂x=0,∂T/∂x=0;BD:u=0,∂v/∂x=0,p=0,T=Tf;CD:u=0,v=0,∂p/∂x=0;CE:∂T/∂x=0;DF:T=T1;EF:T=T1。
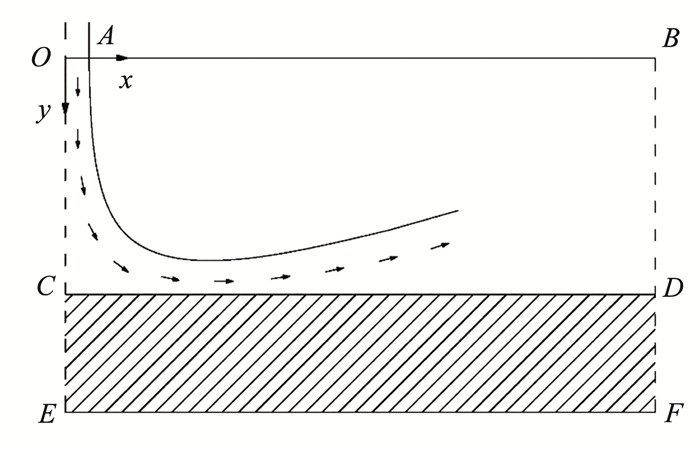
|
图 3 求解域边界示意 Fig. 3 Boundary diagram of solution domain |
热风以一定的热流密度对流固耦合界面CD加热,外部流场和路面内部温度场之间相互影响。相比于沥青路面内部温度场的平衡时间,外部流场达到平衡状态的时间很短,可忽略不计[22]。本文采用松耦合法[23]对流固耦合界面进行处理,即假设外部流场达到稳定状态后不再发生变化,在流固耦合界面CD处利用两侧热流密度相等的条件,以稳定状态下的外部流场对沥青路面内部导热模型进行迭代求解。
2.3 计算过程采用SIMPLE算法对速度-压力耦合方程进行解耦计算,速度u、v和压强p分别表示为估计值u*、v*、p*与修正值u′、v′、p′之和,即u= u*+ u′,v=v*+v′,p=p*+ p′,得到流固耦合界面的速度值,将此速度值代入离散方程(10),得到压力修正方程:
| $ a_P p_P^{\prime}=a_E p_E^{\prime}+a_W p_W^{\prime}+a_N p_N^{\prime}+a_S p_S^{\prime}+b $ | (11) |
式中:aE=ρdeΔy,aW=ρdwΔy,aN=ρdnΔx,aS=ρdsΔx;de=Δy/ae,dw=Δy/aw,dn=Δx/an,ds=Δx/as;aP=aE+aW+aN+aS, b=(ρuw-ρue)Δy+(ρvs-ρvn)Δx, ae,aw,an,as为动量方程中4个界面位置对应的aP值。
速度修正方程为
| $ \left\{\begin{array}{l} u_e^{\prime}=d_e\left(p_P^{\prime}-p_E^{\prime}\right) \\ u_w^{\prime}=d_w\left(p_W^{\prime}-p_P^{\prime}\right) \\ v_n^{\prime}=d_n\left(p_P^{\prime}-p_N^{\prime}\right) \\ v_s^{\prime}=d_s\left(p_S^{\prime}-p_P^{\prime}\right) \end{array}\right. $ | (12) |
具体计算过程为:假设初始压力场p*,在整个求解域上求解式(10),计算出图 2所示的交错网格界面速度u*和v*,将u*和v*代入方程(11),得到修正压力p′和修正后的压力p=p*+p′,再由方程(12)计算界面修正速度u′、v′及修正后的界面速度u=u*+u′和v=v*+v′。至此,完成一次速度与压力耦合方程的解耦计算。计算程序流程如图 4所示。
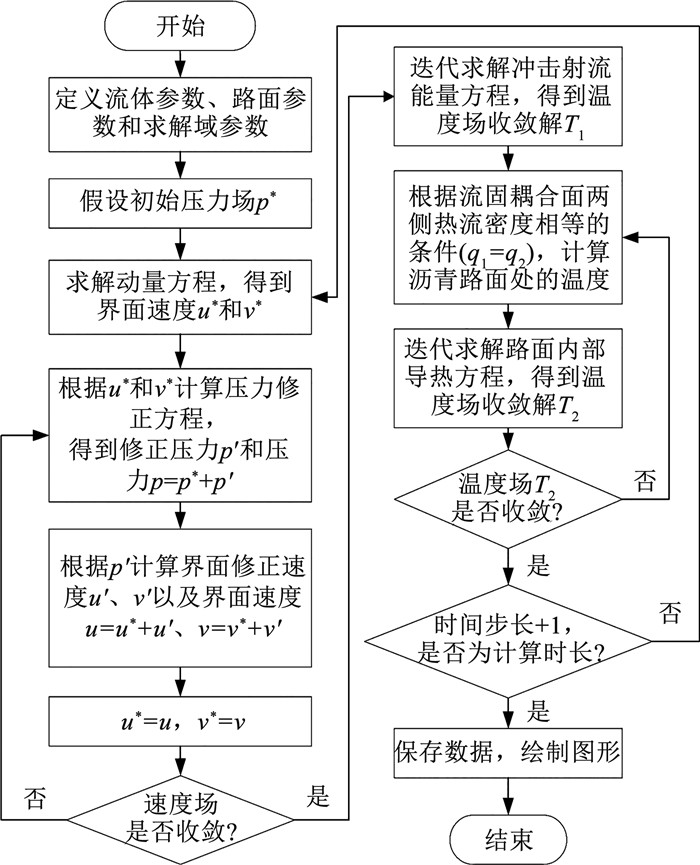
|
图 4 计算程序 Fig. 4 Calculation program diagram |
若速度场未收敛,将得到的压力场和速度场作为初始场重复迭代计算;若速度场已收敛,求解式(10)后重复迭代计算,得到温度场收敛解T1。令流固耦合面两侧的热流密度相等(q1=q2),求解由式(10)得到的路面内部导热的离散能量方程。若路面内部温度场T2未收敛,则重复利用流固耦合面两侧热流密度相等的条件继续迭代;若路面内部温度场T2已收敛,得到了一个时间步长的速度和温度。时间步长递进,直至计算完所需的计算时长,绘制求解时间内的速度场和温度场分布。
3 模型计算结果分析 3.1 计算参数选取计算热风加热沥青路面传热模型,输入的参数有热物性参数和工况参数。工况参数包括喷口处热风初始温度T0、初始流速v0、喷口距沥青路面高度H、喷口直径D等;热物性参数包括热风密度ρ、运动黏度ν、导热系数λ和比定压热容cp以及沥青路面密度ρ′、导热系数λ′和比定压热容c′p等。这些热物性参数的取值与环境因素密切相关。
表 3为采用插值法得到的标准大气压下标准烟气热物理性质参数[24]。假设沥青路面材料均匀、各向同性,表 4为沥青路面试件AC-13上面层试样块的热物理性质参数[10],选取表中参数进行数值计算。
| 表 3 标准大气压下标准烟气的热物理性质表 Tab. 3 Thermophysical properties of standard flue gas under standard atmospheric pressure |
| 表 4 试件AC-13上面层的热物理性质表 Tab. 4 Thermophysical properties of upper layer for AC-13 |
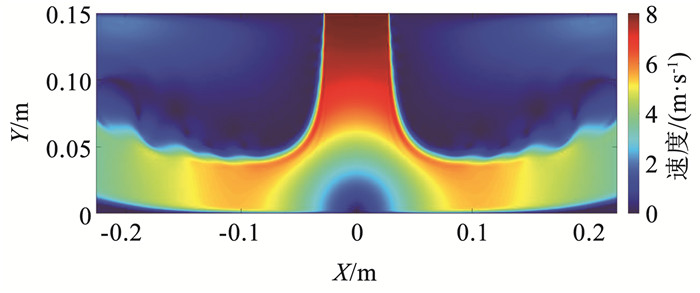
利用MATLAB编制程序求解热风加热沥青路面传热模型,取对称求解域长度0.45 m,喷口直径0.055 m,喷口高度0.15 m,出口热风速度8 m/s,出口热风温度500 ℃,取距原点0.05 m范围的平均温度作为计算指标。计算得到5 s流场达到稳定状态,稳定速度场分布如图 5所示。4 cm处平均温度达到100 ℃的时间为43.3 min,该时刻整个求解域温度场分布如图 6所示。图 6中Y向坐标在0.1 m以上区域为流场域,0.1 m以下为沥青路面区域。
|
图 5 速度场分布图 Fig. 5 Velocity field distribution |

|
图 6 温度场分布图 Fig. 6 Temperature field distribution |
从图 5可以看出,速度场沿着喷口轴线方向有一段自由射流区,在此区域内射流不断卷吸周围气体进行动量交换,使得射流截面宽度不断扩张。在Y向坐标0.07 m附近,速度场发生显著弯曲,射流进入冲击区。驻点区的速度受壁面冲击的影响而急剧下降,射流沿沥青路面表层向两侧发展,进入壁面射流区。射流在黏性和密度的作用下沿壁面产生一定的偏转角,沿弧线偏离壁面。
如图 6所示,壁面驻点区的温度达到最高,沿两侧逐渐降低,在沥青路面内部,仅存在导热作用,壁面驻点区附近的温度较高,温度梯度较大,因此路面内部驻点区附近的热量传递最快,温度也最高。通过分析,速度场和温度场分布均符合冲击射流换热的理论规律。
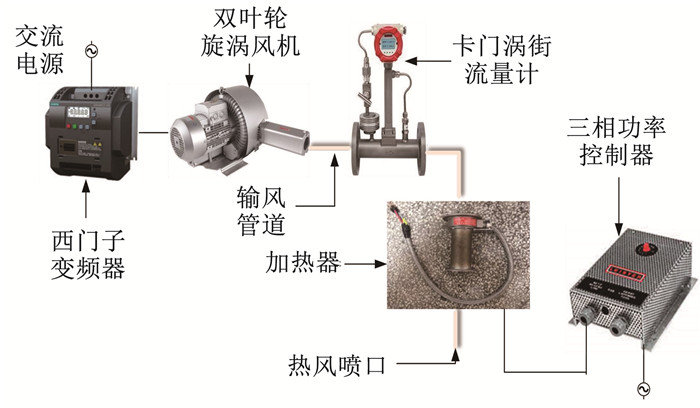
4 实验研究 4.1 实验平台组成为了验证所建模型计算的正确性,搭建了热风加热沥青试样块的冲击射流试验台。热风供给系统如图 7所示。鼓风机将恒定流量的冷风输送到管道中,冷风经加热器加热后形成高温热风,通过喷口以一定流速射向沥青试样块。
|
图 7 热风供给系统结构图 Fig. 7 Structural diagram of hot air supply system |
热风供给系统具备准确调节喷口的热风温度和热风速度的功能。鼓风机型号为RB-72S-4双叶轮旋涡风机,具有变频驱动和气体压力损失小的优点。西门子V20变频器,通过改变变频器工作频率对风机转速进行控制,以获得实验需求的热风速度。输风管道上安装有DN50卡门涡街流量计,可以测量管道中的冷风流量;加热器DF-5000R对管道内的空气进行加热;改变DSE三相功率控制器的功率对加热器输出功率进行无级调节,实现对喷口处热风温度控制。
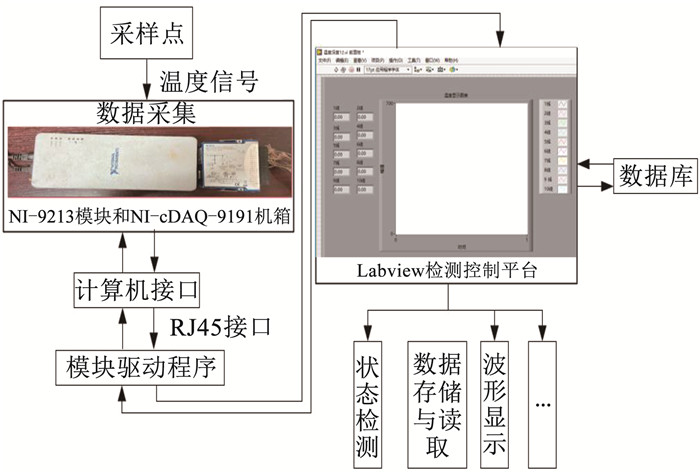
试验台配置了沥青试样块温度采集系统,如图 8所示。NI-9213温度输入模块对温度信号进行采集,通过RJ45网络接口,利用NI-cDAQ-9191机箱将NI-9213温度输入模块的数据同步至计算机,基于模块驱动程序,将计算机所得数据输送到Labview温度采集平台,Labview程序对数据进一步存储和处理,在界面上实时绘制数据曲线。
|
图 8 温度采集系统工作原理图 Fig. 8 Working principle of temperature acquisition system |
搭建的室内实验平台如图 9所示,AC-13上面层沥青试样块(厚度8 cm),其深度0 cm和4 cm的横截面上分别嵌入3个热电偶(如图 10所示),每个截面的温度是3个热电偶的平均值。实验选用测量精度较高的GG-K-36-SLE型热电偶作为温度传感器测量沥青路面温度,其温度测量范围为0~1 250 ℃,精度±0.4%,响应时间小于0.3 s。

|
图 9 试验台结构图 Fig. 9 Structural diagram of test bench |

|
图 10 沥青试样块及热电偶分布图 Fig. 10 Asphalt sample and thermocouple distribution |
调节喷嘴距沥青试样块表面的高度为0.15 m,加热温度为500 ℃,热风风速为8 m/s,进行加热实验,当沥青试样块4 cm处平均温度达到100 ℃时停止加热。
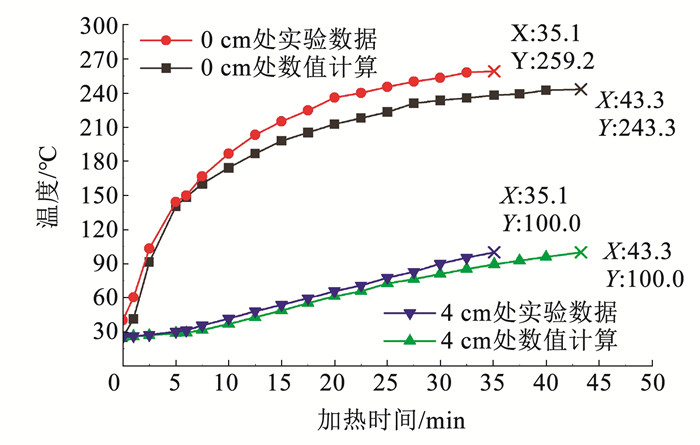
从图 11可以看出,路面表层温度和4 cm处温度的模型数值计算与试验结果吻合度高。在前7 min,路面表层温度的试验结果与数值模型计算结果接近一致,而7 min之后试验结果所测温度略高于模型计算温度。这是由于实验中为了防止加热的沥青试验块热量快速散逸到周围空气中,在试样块周围包裹了一圈保温棉,加强了热量沿深度方向传递,使实验中路层4 cm达到100.0 ℃的时间比仿真时间短,实验所测温度也略高。路面4 cm处达到100.0 ℃的时间为43.3 min,此时路面表层温度为243.3 ℃;实验时路层4 cm处达到100.0 ℃的时间为35.1 min,此时路面平均温度为259.2 ℃,两者温度的平均误差为8.4%。数值计算与实验的温度场变化趋势相似,因此,热风加热沥青路面冲击射流的数值模型可以用来评价热风加热沥青路面的温度场。
|
图 11 数值计算与试验结果对比图 Fig. 11 Comparison between numerical calculation and experimental results |
热流密度和换热系数是反映路面对热量吸收效果的重要指标。平均热流密度q由式(13)计算,反映了热量进入沥青路面的强度。平均换热系数h反映了热风从喷口到沥青路面间的热能利用率,平均换热系数越大,加热过程的能量利用率也越大,其通过式(14)计算。
| $ q=-\lambda^{\prime} \frac{\partial T}{\partial y} $ | (13) |
| $ h=q /\left(T_{\mathrm{f}}-T_{\mathrm{w}}\right) $ | (14) |
式中:Tf为热风出口温度与沥青路面温度的均值, Tw为沥青路面温度。
热风出口速度和热风出口温度是实现沥青路面高效加热的关键,为了分析热风出口速度和热风出口温度对沥青路面加热效果的影响程度,热风出口速度取6、8、10 m/s,热风出口温度取400、450、500 ℃,分别计算表 5中9组参数组合下数值和实验的平均热流密度和平均换热系数。
| 表 5 数值计算与实验实测结果 Tab. 5 Numerical calculation and experimental measurement results |
图 12为平均热流密度和平均换热系数变化曲线图。可以看出,平均热流密度和换热系数随加热时间的增加逐渐减小。在加热初期,两者数值较大,随着加热过程的进行,平均热流密度和平均换热系数均呈下降趋势,但下降幅度逐渐减小。因为加热前期,热流密度大,但沥青路面温度较低,与热风间的温差大,沥青路面表面换热强度大。随着加热的进行,沥青路面温度逐渐升高,路面与热风的温差减小,换热强度减弱,热流密度和换热系数逐渐减小,路面温升趋于平缓。
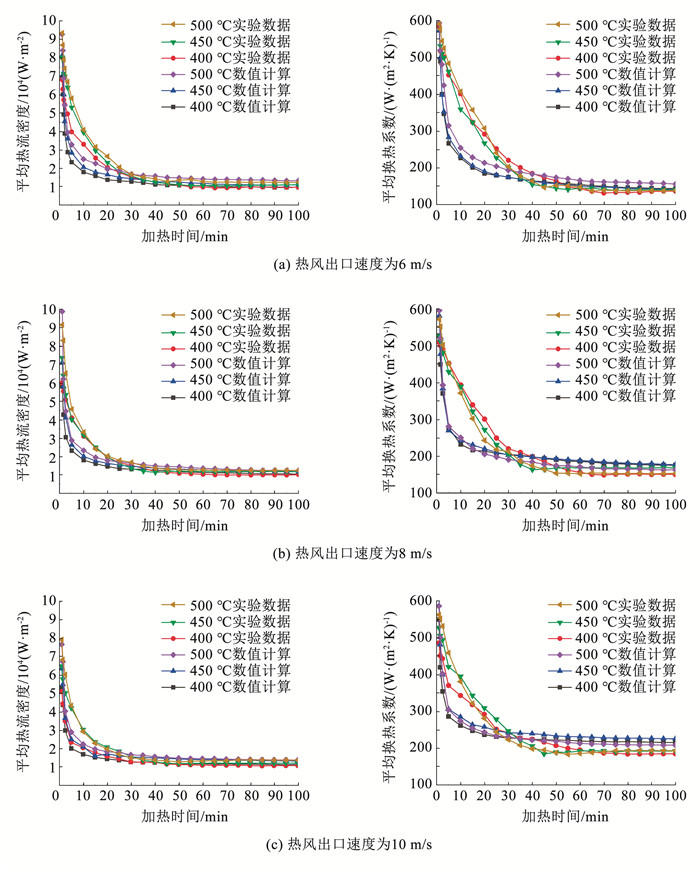
|
图 12 平均热流密度和换热系数变化曲线 Fig. 12 Change curve of average heat flux and heat-transfer coefficient |
正交试验法是一种利用数理统计学与正交性原理,建立正交表来研究多因素多水平优化问题的方法,具有均匀分散性和齐整可比性的特点,在许多领域的研究中得到了广泛应用。为分析热风出口速度和热风出口温度对沥青路面加热效果的影响程度,选取路面温度场达到稳态时的平均热流密度q和平均换热系数h为指标,A、B分别为热风出口速度和热风出口温度的两个因素,每个因素水平依次为k1、k2、k3,采用L9(34)正交试验表进行正交试验。
正交试验计算结果见表 6,采用极差R和方差F分析法确定各因素对指标的影响程度,极差值R越大,对应因素对指标的影响越大。选取置信度为0.05,若F>F0.05,对应因素对指标影响较大,反之,对应因素对指标影响不显著。
| 表 6 正交试验数值计算结果分析 Tab. 6 Numerical calculation results in orthogonal test |
从表 6中的极差和方差结果可知,热风出口速度和热风出口温度对平均热流密度q都有显著影响,其中热风出口温度对平均热流密度q的影响更为显著;热风出口速度对平均换热系数h有显著影响,而热风出口温度对平均换热系数h的影响相较于平均热流密度q指标表现为不显著。
随着热风出口速度的增大,热风射流能保持较长的速度核心区,边界层变薄,换热强度增强,因此,平均热流密度和换热系数均增大。热风出口温度增大,传递到路面的热量增加,热流密度随之增大,路面温升加快,热风与沥青路面间的温差逐渐减小,换热强度随之减弱,因此热风出口温度对平均换热系数的影响相较于平均热流密度指标表现为不显著。
6 结论1) 基于传热学理论,建立了热风冲击射流对流换热和沥青路面内部导热的共轭传热理论模型,采用有限容积法得到了沥青路面加热的通用离散方程,选取SIMPLE算法得到了整个求解域内温度场分布。理论模型得到的温度场分布与试验结果趋势吻合度高,两者平均误差为8.4%,验证了模型的正确性,表明有限容积法和SIMPLE算法用于沥青路面温度场计算的可靠性。
2) 9组沥青路面加热效果的仿真与试验结果表明, 在加热初期,平均的热流密度和换热系数均从最大值急剧下降,随后下降幅度逐渐减小至趋于平衡,两者试验与仿真结果的平均误差分别为6.4%和7.8%。因此,选取平均的热流密度和换热系数反映热风出口速度和热风出口温度对沥青路面加热效果的影响是有效的。
3) 正交试验表明, 热风出口速度和热风出口温度对平均热流密度有显著影响,热风出口速度对平均换热系数有显著影响,热风出口温度对平均换热系数的影响相较于平均热流密度指标表现为不显著。
| [1] |
交通运输部. 2020年交通运输行业发展统计公报[J]. 交通财会, 2021(6): 92. Ministry of Transport of the People's Republic of China. Statistical bulletin on the development of transportation industry in 2020[J]. Finance & Accounting for Communications, 2021(6): 92. DOI:10.3969/j.issn.1005-9016.2021.06.025 |
| [2] |
周艳. 道路工程施工新技术[M]. 徐州: 中国矿业大学出版社, 2013. ZHOU Yan. New technology of road engineering construction[M]. Xuzhou: China University of Mining & Technology Press, 2013. |
| [3] |
魏国忠, 刘文杰, 王善伟. 热风式再生修补车在高速公路路面养护中的应用[J]. 科技创新与应用, 2013(2): 169. WEI Guozhong, LIU Wenjie, WANG Shanwei. Application of hot air regenerative repair vehicle in expressway pavement maintenance[J]. Technology Innovation and Application, 2013(2): 169. |
| [4] |
WANG Dong, ROESLER J R, GUO Dazhi. Analytical approach to predicting temperature fields in multilayered pavement systems[J]. Journal of Engineering Mechanics, 2009, 135(4): 334. DOI:10.1061/(asce)0733-9399(2009)135:4(334) |
| [5] |
李雪毅, 邹晓翎, 吁新华. 热风循环式就地热再生沥青路面温度场[J]. 中外公路, 2018, 38(2): 69. LI Xueyi, ZOU Xiaoling, YU Xinhua. Asphalt pavement temperature field of hot air circulation heating method on hot in-ploce recycling[J]. Journal of China & Foreign Highway, 2018, 38(2): 69. DOI:10.14048/j.issn.1671-2579.2018.02.015 |
| [6] |
BAGDAT T, ELENA S. Freezing characteristics of a highwaysubgrade[J]. Sciences in Cold and Arid Regions, 2017, 9(3): 325. DOI:10.3724/SP.J.1226.2017.00325 |
| [7] |
夏悠杨, 何志勇. 热风循环式加热机关键结构参数对沥青路面加热性能影响分析[J]. 建筑机械, 2020(8): 40. XIA Youyang, HE Zhiyong. Performance and impact analysis of key structural parameters of hot air circulation heater using on asphalt road[J]. Construction Machinery, 2020(8): 40. DOI:10.14189/j.cnki.cm1981.2020.08.002 |
| [8] |
MALLICK R B, CHENBaoliang, DANIEL J S, et al. Heating and its effect on hot in-place recycling of asphalt pavements with rejuvenator[J]. International Journal of Pavement Research and Technology, 2012, 5(6): 347. DOI:10.6135/ijprt.org.tw/2012.5(6).347 |
| [9] |
HUANG Kai, XU Tao, LIGuofen, et al. Heating effects of asphalt pavement during hot in-place recycling using DEM[J]. Construction and Building Materials, 2016, 115: 62. DOI:10.1016/j.conbuildmat.2016.04.033 |
| [10] |
张珲. 沥青路面加热过程中的传热分析与试验研究[D]. 西安: 长安大学, 2017 ZHANG Hui. Analysis and experiment study on heat transfer in the asphalt pavement heating process[D]. Xi'an: Chang'an University, 2017 |
| [11] |
梁奉典. 沥青路面加热过程中的热能传输效率研究[D]. 西安: 长安大学, 2018 LIANG Fengdian. The Research of heat transfer efficiency in the asphalt pavement heating process[D]. Xi'an: Chang'an University, 2018 |
| [12] |
XU Xinxin, GU Hairong, DONG Qiangzhu, et al. Quick heating method of asphalt pavement in hot in-place recycling[J]. Construction and Building Materials, 2018, 178: 211. DOI:10.1016/j.conbuildmat.2018.05.091 |
| [13] |
马登成, 姚锦涛, 曹雨轩. 加热距离与风速对协同加热沥青路面的影响[J]. 华中科技大学学报(自然科学版), 2020, 48(11): 67. MA Dengcheng, YAO Jintao, CAO Yuxuan. Influence of heating distance and wind speed on coupling heating asphalt pavement[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2020, 48(11): 67. DOI:10.13245/j.hust.201111 |
| [14] |
程根源. 基于热风加热技术特征的沥青路面再生工艺和专用机械设备[J]. 公路交通科技(应用技术版), 2019, 15(1): 146. CHENG Genyuan. Asphalt pavement regeneration technology and special mechanical equipment based on hot air heating technology characteristics[J]. Journal of Highway and Transportation Research and Development, 2019, 15(1): 146. |
| [15] |
段宝东, 韩东东, 赵永利. 基于最小能耗的沥青路面就地热再生加热机组优化控制[J]. 公路交通科技, 2021, 38(1): 19. DUAN Baodong, HAN Dongdong, ZHAO Yongli. Optimization control of heating equipment in hot in-place recycling of asphalt pavement based on minimizing energy consumption[J]. Journal of Highway and Transportation Research and Development, 2021, 38(1): 19. DOI:10.3969/j.issn.1002-0268.2021.01.003 |
| [16] |
杨婧, 王小军, 杨祺. 冲击射流换热研究进展[J]. 真空与低温, 2018, 24(4): 217. YANG Jing, WANG Xiaojun, YANG Qi. Advances in jet impinging heat transfer[J]. Vacuum and Cryogenics, 2018, 24(4): 217. DOI:10.3969/j.issn.1006-7086.2018.04.001 |
| [17] |
储继国. 粘滞气体不可压缩性的适用条件探讨[J]. 真空科学与技术, 1997, 17(1): 66. CHU Jiguo. Criteria of incompressibility of viscous gases[J]. Vacuum Science and Technology, 1997, 17(1): 66. DOI:10.13922/j.cnki.cjovst.1997.01.012 |
| [18] |
潘贵璠, 赵欣林. 基于MATLAB对不可压缩粘性流体在流管中的研究[J]. 广西物理, 2018, 39(2/3): 17. PAN Guipan, ZHAO Xinlin. Study on incompressible viscous fluid in flow tube based on MATLAB[J]. Guangxi Physics, 2018, 39(2/3): 17. |
| [19] |
张琰, 白云, 王常莲, 等. 基于SIMPLE算法的大型浮顶油罐温度场数值模拟[J]. 石油工业技术监督, 2015, 31(9): 39. ZHANG Yan, BAI Yun, WANG Changlian, et al. Numerical simulation of temperature field of large floating roof oil tank based on SIMPLE algorithm[J]. Technical Supervision in Petroleum Industry, 2015, 31(9): 39. DOI:10.3969/j.issn.1004-1346.2015.09.013 |
| [20] |
陶文铨. 数值传热学[M]. 2版. 西安: 西安交通大学出版社, 2001. TAO Wenquan. Numerical heat transfer[M]. 2nd ed. Xi'an: Xi'an Jiaotong University Press, 2001. |
| [21] |
李鹏飞, 吴颂平. 一种新的界面处理方法在气固耦合传热中的应用[J]. 北京航空航天大学学报, 2010, 36(9): 1071. LI Pengfei, WU Songping. New interface boundary condition method for coupled thermal simulations[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(9): 1071. DOI:10.13700/j.bh.1001-5965.2010.09.013 |
| [22] |
夏刚, 刘新建, 程文科, 等. 钝体高超声速气动加热与结构热传递耦合的数值计算[J]. 国防科技大学学报, 2003, 25(1): 35. XIA Gang, LIU Xinjian, CHENG Wenke, et al. Numerical simulation of coupled aeroheating and solid heat penetration for a hypersonic blunt body[J]. Journal of National University of Defense Technology, 2003, 25(1): 35. DOI:10.3969/j.issn.1001-2486.2003.01.008 |
| [23] |
孟繁超, 董素君, 江泓升, 等. 长时间流固耦合传热过程的快速算法[J]. 北京航空航天大学学报, 2017, 43(6): 1224. MENG Fanchao, DONG Sujun, JIANG Hongsheng, et al. A fast algorithm for long-term fluid-solid conjugate heat transfer process[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(6): 1224. DOI:10.13700/j.bh.1001-5965.2016.0447 |
| [24] |
杨世铭, 陶文铨. 传热学[M]. 3版. 北京: 高等教育出版社, 1998. YANG Shiming, TAO Wenquan. Heat transfer[M]. 3rd ed. Beijing: Higher Education Press, 1998. |
 2024, Vol. 56
2024, Vol. 56


