2. 上海卫星工程研究所,上海 201109
2. Shanghai Institute of Satellite Engineering, Shanghai 201109, China
在轨航天器过境时通常需要多次连续对多个区域进行观测,连续姿态机动过程对航天器的敏捷性和高稳定度提出高需求[1]。控制力矩陀螺(control moment gyroscopes, CMGs)是一种大力矩输出的角动量交换装置,是实现快速机动理想的执行机构[2]。然而,CMGs存在奇异性和力矩分辨率小的问题[3]。因此,文献[4-5]提出了CMGs与飞轮(reaction wheels, RWs)组成混合执行机构的姿控方案,但是该方法提高了系统复杂度。近年来,学者广泛研究内转子可以调速的变速控制力矩陀螺(variable speed control moment gyroscopes, VSCMGs),使混合控制集成到单一执行机构逐渐成为可能。增加了飞轮转速自由度的VSCMGs同时具有CMGs与RWs两种工作模式[6]。通过设计两种工作模式切换策略,既能使航天器在姿态机动过程中采用CMGs模式输出大力矩,又能在姿态稳定及载荷工作时,将框架角锁定采用RWs模式输出精细的小力矩,同时满足了机动过程的快速性和稳定性。
目前,VSCMGs操纵律主要的研究集中于CMGs模式和RWs模式的切换策略以及各类不同功能零运动的设计方法。文献[7]设计了加权矩阵带零运动的操纵律,仅由奇异量度对指令力矩进行加权分配,并设计基于框架角和转速反馈的零运动,该方法能主动规避奇异。文献[8]基于姿态误差阈值设计了VSCMGs的模式直接切换策略。然而,该种缺少过渡段的切换方式可能使得姿态存在瞬态激励,引起帆板振动等不良影响。文献[9]对VSCMGs分离成CMGs与RWs两部分设计各自的操纵律,根据指令力矩方向与VSCMGs力矩方向之间的关系设计两个模式间切换条件。文献[10]基于VSCMGs模式调度操纵律,设计了一种末态框架角反馈的零运动,对末态框架角选型进行详细分析,但没有考虑挠性帆板影响。文献[11]建立了VSCMGs的挠性卫星姿态动力学模型,设计了输出反馈控制算法,但未对VSCMGs框架角与转子转速操纵律进行设计。文献[12]从刚体卫星动态扫描成像任务的角度对使用VSCMGs的控制器进行设计。文献[13]基于PSO粒子群优化方法寻找VSCMGs最优平滑切换参数。文献[14-15]针对VSCMGs为建模不确定性情况下的姿态跟踪控制问题,前者通过归一化神经网络补偿模型未知项的影响,后者采用鲁棒自适应律估计未知参数。两者的控制器未对VSCMGs操纵律详细设计。文献[16]给出了一种自适应估计未知姿态扰动的方法,并设计了力矩分配、奇异回避和轮速平衡的VSCMGs操纵律。该控制器未考虑挠性和惯量不确定,而且VSCMGs缺少末态框架角定位的功能。文献[17-18]利用内转子加减速实现飞轮的储能,设计了姿控/储能一体化操纵律。该类控制律目前工程实现较难,在解决了轴承摩擦及电子元件损耗问题后有较大前景。上述文献均属于单次机动,未对变速控制力矩陀螺在连续姿态机动过程中的操纵律使用进行详细规划。因此,VSCMGs的框架角与转速无法从当次姿态机动的复位到下次机动初始状态,应进一步研究机动过程中操纵律在机动不同阶段的使用方案,而且上述研究未考虑姿态控制中精确惯量未知的约束。
针对大角度姿态机动,目前工程中常使用路径规划和前馈补偿结合的方法,这能提高姿态机动的快速响应能力。文献[19]指出精确计算挠性航天器机动过程中的前馈补偿力矩存在两大困难,需要获得惯量信息和挠性模态信息:①航天器在轨运行中,由于燃料消耗或者机构运动,会导致转动惯量发生变化。因此,可以先完成航天器惯量参数辨识,然后再进行航天器控制[20],但这增加了在轨任务量。近年来,随着以自适应控制为代表的智能算法发展,学者们研究在精确惯量未知情况下,直接进行航天器姿态控制。通过设计自适应律对惯量参数在轨估计,控制器中将无需精确惯量信息,降低了模型不确定对控制性能的影响[21]。②如今航天器逐渐向大挠性发展,通常携带大型太阳帆板、大型薄膜天线、长伸杆机构等部件。在快速机动过程中,挠性部件激发的振动会影响姿态控制性能,因此必须在姿态快速机动过程中采取必要的振动抑制策略。振动抑制中分为主动抑制和被动抑制。其中,主动抑制又分为基于压电材料的主动振动抑制和基于挠性动力学特性的主动振动抑制[22]。前者需要航天器配置额外的敏感器和作动器来抑制挠性部件机动过程中的振动[23-24],后者无需额外的部件,仅从姿态控制算法层面抑制或补偿挠性振动对航天器平台的干扰。与自适应算法类似,设计仅需姿态信息的模态观测器,实时估计不可测的挠性模态和模态速度信息,从而估计出振动对航天器平台的干扰力矩,作为姿态控制器的前馈补偿力矩[25-26]。
现有的VSCMGs应用到航天器控制中的研究大多是刚体航天器,而且未考虑惯量信息不确定约束。VSCMGs操纵律缺少与姿态机动路径规划结合,算法缺少工程适用性。本文针对挠性航天器在轨姿态连续机动控制问题,采用VSCMGs作为执行机构,提出了一种基于观测器的挠性航天器鲁棒控制算法。在采用VSCMGs进行快速机动时,由于CMGs模式的输出力矩较大,引起挠性部件振动激励。控制律中将模态观测器和自适应控制结合,实时估计不可测的模态信息和惯量信息,精确计算姿控的前馈补偿力矩,用于补偿振动对平台的影响。设计的VSCMGs的操纵律根据其不同模式的功能,将多个零运动部署至姿态机动的不同阶段。设计的算法既能实现姿态机动到姿态稳定过程中的平滑切换,又能在不同阶段实现不同功能,使得在两次姿态机动之间框架角和转子转速实现复位。姿态控制律中规划了的三段式正弦型路径和稳定过程,对应不同的VSCMGs操纵律,以满足执行机构不同的功能需求。控制律中延长减速段时间既有利于让VSCMGs框架角复位,又降低进入稳态时的帆板激励。操纵律中的平滑切换策略减少了机动过程中对挠性干扰的补偿大小。因此,本文将姿态控制律与VSCMGs操纵律有机结合到一个方案规划中,使整个控制策略同时适用于高精度和高机动的姿态控制场合。
1 数学模型 1.1 挠性航天器姿态动力学模型本文考虑带N个挠性附件的航天器姿态动力学,由本体姿态动力学方程和挠性附件的振动方程组成:
| $ \mathit{\boldsymbol{J}} \dot{\mathit{\boldsymbol{\omega}}}+\mathit{\boldsymbol{\omega}}^{\times}(\mathit{\boldsymbol{J}} \mathit{\boldsymbol{\omega}}+\mathit{\boldsymbol{H}})+\sum\limits_{i=1}^{N} \mathit{\boldsymbol{B}}_{i} \ddot{\mathit{\boldsymbol{\eta}}}_{i}=\mathit{\boldsymbol{T}} $ | (1) |
| $ \ddot{\mathit{\boldsymbol{\eta}}}_{i}+2 \xi_{i} \mathit{\boldsymbol{ \boldsymbol{\varLambda}}}_{i} \dot{\mathit{\boldsymbol{\eta}}}_{i}+\mathit{\boldsymbol{ \boldsymbol{\varLambda}}}_{i}^{2} \mathit{\boldsymbol{\eta}}_{i}+\mathit{\boldsymbol{B}}_{i}^{\mathrm{T}} \dot{\mathit{\boldsymbol{\omega}}}=0 $ | (2) |
式中:J∈R3×3为正定对称的转动惯量矩阵, ω∈R3为本体坐标系相对惯性坐标系的角速度, H∈R3为轮控执行机构的角动量, T∈R3为轮控执行机构作用在航天器上的三轴力矩, Bi∈R3×m为转动刚柔耦合矩阵, ηi∈Rm为第i个挠性附件的模态坐标, Λi∈Rm×m为挠性附件的模态频率矩阵,其中i =1, 2, …, N,m为模态阶数, ξi∈R为挠性附件的阻尼比, ω×∈R3×3为叉乘矩阵,表示为
| $ \mathit{\boldsymbol{\omega}}^{\times}=\left[\begin{array}{ccc} 0 & -\omega_{z} & \omega_{y} \\ \omega_{z} & 0 & -\omega_{x} \\ -\omega_{y} & \omega_{x} & 0 \end{array}\right] $ | (3) |
姿态机动过程的运动学由四元数表示:
| $ \dot{\mathit{\boldsymbol{q}}}=\left[\begin{array}{l} \dot{q}_{0} \\ \dot{\mathit{\boldsymbol{q}}}_{\mathrm{v}} \end{array}\right]=\frac{1}{2}\left[\begin{array}{c} -\mathit{\boldsymbol{q}}_{\mathrm{v}}^{\mathrm{T}} \\ \mathit{\boldsymbol{q}}_{\mathrm{v}}^{\times}+q_{0} \mathit{\boldsymbol{I}}_{3} \end{array}\right] \mathit{\boldsymbol{\omega}} $ | (4) |
式中:q∈R4为姿态四元数,其矢量部分为qv∈R3,标量部分为q0∈R,In∈Rn×n为单位矩阵。
注1 式(1)中
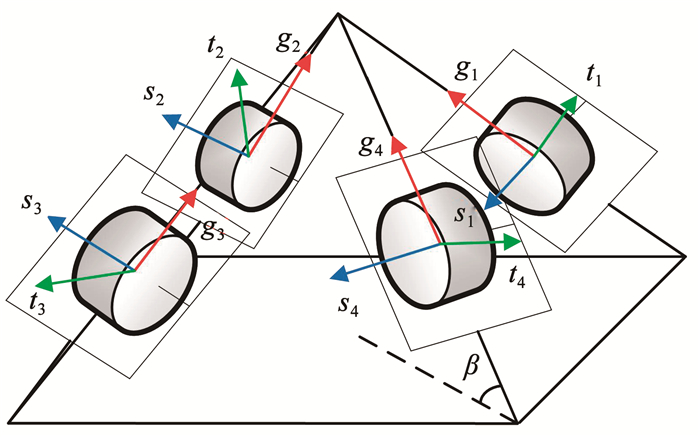
本文采用4个VSCMGs组成金字塔构型作为轮控执行机构,即N=4,侧倾角β=53.17°,如图 1所示。定义第i个VSCMGs的框架轴方向向量为gi∈R3,角动量轴方向向量为si∈R3,框架力矩输出轴方向向量为ti∈R3,框架角为δi,转子转速为Ωi,Is为转子转动惯量。若初始时刻时框架轴和角动量轴方向为gi, 0和si, 0,由几何关系可知:
| $ \mathit{\boldsymbol{g}}_{i}=\mathit{\boldsymbol{g}}_{i, 0}, \mathit{\boldsymbol{s}}_{i}=\mathit{\boldsymbol{C}}_{i}\left(\mathit{\boldsymbol{g}}_{i}, \delta_{i}\right) \mathit{\boldsymbol{s}}_{i, 0}, \mathit{\boldsymbol{t}}_{i}=\mathit{\boldsymbol{g}}_{i} \times \mathit{\boldsymbol{s}}_{i} $ | (5) |
|
图 1 金字塔构型VSCMGs Fig. 1 Pyramid configuration VSCMGs system |
式中:Ci(gi, δi)=cos δiI3+(1-cos δi)gigiT+sin δigi为定轴旋转余弦矩阵。VSCMGs系统的角动量为
| $ \mathit{\boldsymbol{H}}=\sum\limits_{i=1}^{4} \mathit{\boldsymbol{I}}_{\mathrm{s}} \mathit{\boldsymbol{ \boldsymbol{\varOmega}}}_{i} \mathit{\boldsymbol{s}}_{i}=\mathit{\boldsymbol{I}}_{\mathrm{s}} \mathit{\boldsymbol{A}}_{\mathrm{s}} \mathit{\boldsymbol{ \boldsymbol{\varOmega}}} $ | (6) |
对角动量求导可得执行机构作用在星体上的力矩为
| $\begin{array}{l} \mathit{\boldsymbol{T}}=-\dot{\mathit{\boldsymbol{H}}}=-\frac{\partial \mathit{\boldsymbol{H}}}{\partial \mathit{\boldsymbol{ \boldsymbol{\varOmega}}}} \dot{\mathit{\boldsymbol{ \boldsymbol{\varOmega}}}}-\frac{\partial \mathit{\boldsymbol{H}}}{\partial \mathit{\boldsymbol{\delta}}} \dot{\mathit{\boldsymbol{\delta}}}=-\sum\limits_{i=1}^{4} \mathit{\boldsymbol{I}}_{\mathrm{s}} \dot{\mathit{\boldsymbol{ \boldsymbol{\varOmega}}}}_{i} \mathit{\boldsymbol{s}}_{i}-\\ \;\;\;\;\;\;\;\; \sum\limits_{i=1}^{4} \mathit{\boldsymbol{I}}_{\mathrm{s}} \mathit{\boldsymbol{ \boldsymbol{\varOmega}}}_{i} \dot{\mathit{\boldsymbol{\delta}}}_{i} \mathit{\boldsymbol{t}}_{i}=-\mathit{\boldsymbol{I}}_{\mathrm{s}} \mathit{\boldsymbol{A}}_{\mathrm{s}} \dot{\mathit{\boldsymbol{ \boldsymbol{\varOmega}}}}-\mathit{\boldsymbol{I}}_{\mathrm{s}} \mathit{\boldsymbol{A}}_{\mathrm{t}} \operatorname{diag}(\mathit{\boldsymbol{ \boldsymbol{\varOmega}}}) \dot{\mathit{\boldsymbol{\delta}}}=-[\mathit{\boldsymbol{D}} \mathit{\boldsymbol{E}}] \mathit{\boldsymbol{y}} \end{array} $ | (7) |
式中:Ω=[Ω1 Ω2 Ω3 Ω4]T为转子转速向量,δ=[δ1 δ2 δ3 δ4]T为构型框架角向量,As=[s1 s2 s3 s4]T为角动量方向矩阵,At=[t1 t2 t3 t4]T为框架力矩方向矩阵,diag(Ω)=diag(Ω1, Ω2, Ω3, Ω4)为对角矩阵,D=IsAs为RWs模式力矩矩阵,E=IsAtdiag(Ω)为CMGs模式力矩矩阵,y=
注2 由式(7)可知T被分为精细的小力矩
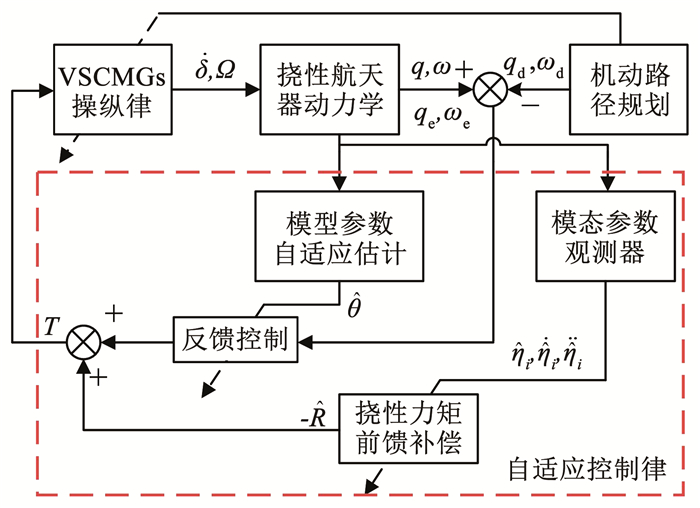
本文控制对象为式(1)~(3)的动力学模型。本文的控制问题为设计带精确前馈的姿态控制律和执行机构操纵律,输出VSCMGs框架与转子控制指令,使得航天器在VSCMGs作用下,在挠性振动干扰和模型参数不确定约束下,仍能跟踪规划好的机动路径,实现挠性航天器的连续姿态机动与稳定。控制器设计的关键问题可分为:1)无惯量信息下的姿控问题;2)无模态敏感器时的挠性干扰力矩精确前馈;3)VSCMGs操纵律在连续机动的不同阶段实现不同功能。基于VSCMGs的挠性航天器姿态机动自适应控制系统结构如图 2所示。
|
图 2 基于VSCMGs的挠性航天器姿态机动自适应控制系统结构 Fig. 2 System structure of flexible spacecraft attitude maneuver adaptive control based on VSCMGs |
从图 2中可知:
1) 针对转动惯量未知的情况,控制器设计中不能直接使用转动惯量真实值J,而需要经过变换由其参数估计值
2) 考虑挠性航天器动力学特性,需要精确计算前馈力矩补偿挠性附件对星体干扰作用,受限于模态信息ηi需要额外敏感器测得,故本文设计了模态观测器获得挠性模态估计值
3) 针对连续姿态机动的工况,为充分发挥VSCMG两种模式各自优点,操纵律需要实现4点基本功能。①力矩分配。VSCMGs比传统CMGs多了一个自由度,其操纵律设计本质是CMGs模式与RWs模式力矩分配设计,需要结合机动路径规划实现平滑切换两种模式。②奇异应对策略。发生奇异时,由RWs模式补偿CMGs奇异时的力矩。虽然,VSCMGs系统数学上可证明无奇异,但在实际硬件约束下操纵律仍需考虑规避CMGs模式奇异。③轮速平衡设计。由于转子转速可变,需要在进入CMGs模式时保证轮速尽可能维持一致,避免零奇异。此外,维持转子高转速运动可避免转子转速过零。④末态框架角定位。考虑到奇异性以及力矩输出同向性与框架角组合有关,特别是在姿态稳定控制段,框架锁定后框架组合直接影响RWs模式力矩输出方向。因此,需要对初始和末态框架角进行选取,要求在机动结束后框架锁定在期望的框架角组合附近。
3 基于模态观测器的姿态机动自适应控制律本文先将挠性航天器姿态动力学模型转换为跟踪误差模型,分离出惯量参数。随后设计模态观测器和自适应控制律,通过Lyapunov方法证明系统闭环稳定性。
3.1 模型转换设规划的期望姿态四元数为qd,则误差四元数为qe=qd-1⊗q,误差角速度为ωe=ω-Cωd。对ωe求导代入式(1)中可得
| $ \mathit{\boldsymbol{J}} \dot{\mathit{\boldsymbol{\omega}}}_{\mathrm{e}}=\mathit{\boldsymbol{\tau}}+\sum\limits_{i=1}^{N} \mathit{\boldsymbol{B}}_{i} \mathit{\boldsymbol{B}}_{i}^{\mathrm{T}}\left(\mathit{\boldsymbol{C}} \dot{\mathit{\boldsymbol{\omega}}}_{\mathrm{d}}-\mathit{\boldsymbol{\omega}}_{\mathrm{e}}^{\times} \mathit{\boldsymbol{C}} \mathit{\boldsymbol{\omega}}_{\mathrm{d}}\right)+\mathit{\boldsymbol{T}} $ | (8) |
式中:τ=-ω×Jω-ω×H+Jωe×Cωd-
| $ \dot{\mathit{\boldsymbol{q}}}_{\mathrm{e}}=\left[\begin{array}{l} \dot{\mathit{\boldsymbol{q}}}_{0, \mathrm{e}} \\ \dot{\mathit{\boldsymbol{q}}}_{\mathrm{v}, \mathrm{e}} \end{array}\right]=\frac{1}{2}\left[\begin{array}{c} -\mathit{\boldsymbol{q}}_{\mathrm{v}, \mathrm{e}}^{\mathrm{T}} \\ \mathit{\boldsymbol{q}}_{\mathrm{v}, \mathrm{e}}^{\times}+\mathit{\boldsymbol{q}}_{0, \mathrm{e}} \mathit{\boldsymbol{I}}_{3} \end{array}\right] \mathit{\boldsymbol{\omega}}_{\mathrm{e}} $ | (9) |
若ωe与qv, e均收敛至零则表明姿态跟踪上期望的规划路径,姿态机动控制转化为误差镇定问题。通常在忽略挠性力矩时,设计PD控制器[27]为
| $ \mathit{\boldsymbol{T}}=-\mathit{\boldsymbol{K}}_{\mathrm{w}} \mathit{\boldsymbol{\omega}}_{\mathrm{e}}-\mathit{\boldsymbol{K}}_{\mathrm{e}} \mathit{\boldsymbol{q}}_{\mathrm{v}, \mathrm{e}}-\mathit{\boldsymbol{\tau}} $ | (10) |
式中Ke、Kw分别为正定的PD增益矩阵。上述控制器除了使用可测的状态外,还使用了模型参数J,在精确惯量信息未知的情况时并不适用,而且未补偿挠性干扰对星体的作用。因此需要对误差动力学进行转换,分离出惯量参数,便于后续自适应律设计。
首先,对于任意的三维向量a∈R3定义矩阵算子F(a)∈R3×6为
| $ \mathit{\boldsymbol{F}}(\mathit{\boldsymbol{a}})=\left[\begin{array}{cccccc} a_{1} & 0 & 0 & 0 & a_{3} & a_{2} \\ 0 & a_{2} & 0 & a_{3} & 0 & a_{1} \\ 0 & 0 & a_{3} & a_{2} & a_{1} & 0 \end{array}\right] $ | (11) |
J可以写成θ∈R6的形式,θ=[J11 J22 J33 J23 J13 J12]T,则对任意三维向量a有Ja=F(a)θ恒成立。故非线性项可表示为
| $ \mathit{\boldsymbol{\tau}}=\mathit{\boldsymbol{Y}} \mathit{\boldsymbol{\theta}}-\mathit{\boldsymbol{\omega}}^{\times} \mathit{\boldsymbol{H}} $ | (12) |
式中, Y=-ω×F(ω)+F(ωe×Cωd)-
| $ \overline{\mathit{\boldsymbol{J}}} \dot{\mathit{\boldsymbol{\omega}}}_{\mathrm{e}}=\mathit{\boldsymbol{Y}} \mathit{\boldsymbol{\theta}}+\mathit{\boldsymbol{R}}+\mathit{\boldsymbol{T}}-\mathit{\boldsymbol{\omega}}^{\times} \mathit{\boldsymbol{H}} $ | (13) |
式中:J=J-
| $ \mathit{\boldsymbol{R}}=\sum\limits_{i=1}^{N} \mathit{\boldsymbol{B}}_{i}\left(2 \xi_{i} \mathit{\boldsymbol{ \boldsymbol{\varLambda}}}_{i} \dot{\mathit{\boldsymbol{\eta}}}_{i}+\mathit{\boldsymbol{ \boldsymbol{\varLambda}}}_{i}^{2} \mathit{\boldsymbol{\eta}}_{i}\right)+\mathit{\boldsymbol{B}}_{i} \mathit{\boldsymbol{B}}_{i}^{\mathrm{T}}\left(\mathit{\boldsymbol{C}} \dot{\mathit{\boldsymbol{\omega}}}_{\mathrm{d}}-\mathit{\boldsymbol{\omega}}_{\mathrm{e}}^{\times} \mathit{\boldsymbol{C}} \mathit{\boldsymbol{\omega}}_{\mathrm{d}}\right) $ | (14) |
注3 J由两项构成:1)J为航天器整体未发生弹性变形时的转动惯量; 2)BiBiT为挠性部件转动耦合系数的乘积。BiBiT数值近似为挠性部件的转动惯量,近似误差可作为挠性部件模态截断的准则。两者相减后,J的物理意义为航天器中心刚体部分的转动惯量矩阵[28],故J是正定的。
注4 由式(12)所示,τ被参数分离为惯量信息θ和不含惯量Y的两项,可由θ的自适应估计值
由式(12)可设计姿态控制律设计为
| $ \mathit{\boldsymbol{T}}=-\mathit{\boldsymbol{K}}_{\mathrm{w}} \mathit{\boldsymbol{\omega}}_{\mathrm{e}}-\mathit{\boldsymbol{K}}_{\mathrm{e}} \mathit{\boldsymbol{q}}_{\mathrm{v}, \mathrm{e}}-\hat{\mathit{\boldsymbol{Y}} \mathit{\boldsymbol{\theta}}}-\hat{\mathit{\boldsymbol{R}}}+\mathit{\boldsymbol{\omega}}^{\times} \mathit{\boldsymbol{H}} $ | (15) |
式中:
| $ \mathit{\boldsymbol{\psi}}_{i}=\dot{\mathit{\boldsymbol{\eta}}}_{i}+\mathit{\boldsymbol{B}}_{i}^{\mathrm{T}} \mathit{\boldsymbol{\omega}}_{i} $ | (16) |
对式(16)求导并代入式(2),有
| $ \dot{\mathit{\boldsymbol{\psi}}}_{i}=\ddot{\mathit{\boldsymbol{\eta}}}_{i}+\mathit{\boldsymbol{B}}_{i}^{\mathrm{T}} \dot{\mathit{\boldsymbol{\omega}}}=-\mathit{\boldsymbol{ \boldsymbol{\varLambda}}}_{i}^{2} \mathit{\boldsymbol{\eta}}_{i}-2 \xi_{i} \mathit{\boldsymbol{ \boldsymbol{\varLambda}}}_{i} \mathit{\boldsymbol{\psi}}_{i}+2 \xi_{i} \mathit{\boldsymbol{ \boldsymbol{\varLambda}}}_{i} \mathit{\boldsymbol{B}}_{i}^{\mathrm{T}} \mathit{\boldsymbol{\omega}}_{i} $ | (17) |
故联立式(16)、(17),可写为线性系统的矩阵形式:
| $ \dot{\mathit{\boldsymbol{x}}}_{i}=\mathit{\boldsymbol{A}}_{i} \mathit{\boldsymbol{x}}_{i}+\mathit{\boldsymbol{b}}_{i} $ | (18) |
其中:
| $ \mathit{\boldsymbol{x}}_{i}=\left[\begin{array}{l}\mathit{\boldsymbol{\eta}}_{i} \\ \mathit{\boldsymbol{\psi}}_{i}\end{array}\right], \mathit{\boldsymbol{A}}_{i}=\left[\begin{array}{cc}\mathit{\boldsymbol{0}}_{m} & \mathit{\boldsymbol{I}}_{m} \\ -\mathit{\boldsymbol{ \boldsymbol{\varLambda}}}_{i}^{2} & -2 \xi_{i} \mathit{\boldsymbol{ \boldsymbol{\varLambda}}}_{i}\end{array}\right], \mathit{\boldsymbol{b}}_{i}=\left[\begin{array}{c}-\mathit{\boldsymbol{I}}_{m} \\ 2 \xi_{i} \mathit{\boldsymbol{ \boldsymbol{\varLambda}}}_{i}\end{array}\right] \mathit{\boldsymbol{B}}_{i}^{\mathrm{T}} \mathit{\boldsymbol{\omega}}_{i} $ |
将
| $ \dot{\hat{\mathit{\boldsymbol{x}}}}_{i}=\mathit{\boldsymbol{A}}_{i} \hat{\mathit{\boldsymbol{x}}}_{i}+\mathit{\boldsymbol{b}}_{i}+\mathit{\boldsymbol{P}}_{i}^{-1}\left[\begin{array}{ll} \mathit{\boldsymbol{ \boldsymbol{\varLambda}}}_{i}^{2} & 2 \xi_{i} \mathit{\boldsymbol{ \boldsymbol{\varLambda}}}_{i} \end{array}\right]^{\mathrm{T}} \mathit{\boldsymbol{B}}_{i}^{\mathrm{T}}\left(\mathit{\boldsymbol{K}}_{\mathrm{e}}^{-1}\right)^{\mathrm{T}} \mathit{\boldsymbol{\omega}}_{\mathrm{e}} $ | (19) |
式中:Pi∈R2m为对称正定矩阵,由Lyapunov方程AiTPi+PiAi=-2Qi计算得到,其中Qi∈R2m为对称正定矩阵。因此,将式(16)代入式(14),可以基于观测器得到挠性作用项估计值
| $ \begin{array}{l} \hat{\mathit{\boldsymbol{R}}}=\sum\limits_{i=1}^{N} \mathit{\boldsymbol{B}}_{i}\left(2 \xi_{i} \mathit{\boldsymbol{ \boldsymbol{\varLambda}}}_{i} \hat{\mathit{\boldsymbol{\psi}}}_{i}+\mathit{\boldsymbol{ \boldsymbol{\varLambda}}}_{i}^{2} \hat{\mathit{\boldsymbol{\eta}}}_{i}-2 \xi_{i} \mathit{\boldsymbol{ \boldsymbol{\varLambda}}}_{i} \mathit{\boldsymbol{B}}_{i}^{\mathrm{T}} \mathit{\boldsymbol{\omega}}_{i}\right)+\\ \;\;\;\;\;\;\;\; \mathit{\boldsymbol{B}}_{i} \mathit{\boldsymbol{B}}_{i}^{\mathrm{T}}\left(\mathit{\boldsymbol{C}} \dot{\mathit{\boldsymbol{\omega}}}_{\mathrm{d}}-\mathit{\boldsymbol{\omega}}_{\mathrm{e}}^{\times} \mathit{\boldsymbol{C}} \mathit{\boldsymbol{\omega}}_{\mathrm{d}}\right) \end{array} $ | (20) |
设计
| $ \dot{\hat{\mathit{\boldsymbol{\theta}}}}=\mathit{\boldsymbol{G}} \mathit{\boldsymbol{Y}}^{\mathrm{T}}\left(\mathit{\boldsymbol{K}}_{\mathrm{e}}^{-1}\right)^{\mathrm{T}} \mathit{\boldsymbol{\omega}}_{\mathrm{e}} $ | (21) |
式中G∈R6×6为正定的自适应增益矩阵。
3.3 系统稳定性证明定理1 在由式(9)、(13)描述的挠性航天器姿态误差动力学系统中,给定规划后的期望姿态信息,在精确转动惯量未知和挠性模态不可测的条件下,在基于观测器的自适应控制律式(15)、式(19)~ (21)作用下,闭环控制系统渐进稳定,姿态跟踪误差ωe与qv, e和模态观测误差
证明 记
| $ \begin{array}{l} V=\frac{1}{2} \mathit{\boldsymbol{\omega}}_{\mathrm{e}}^{\mathrm{T}} \mathit{\boldsymbol{K}}_{\mathrm{e}}^{-1} \overline{\mathit{\boldsymbol{J}}} \mathit{\boldsymbol{\omega}}_{\mathrm{e}}+\mathit{\boldsymbol{q}}_{\mathrm{v}, \mathrm{e}}^{\mathrm{T}} \mathit{\boldsymbol{q}}_{\mathrm{v}, \mathrm{e}}+\left(1-q_{0, \mathrm{e}}\right)^{2}+\\ \;\;\;\;\;\;\;\; \frac{1}{2} \tilde{\mathit{\boldsymbol{\theta}}}^{\mathrm{T}} \mathit{\boldsymbol{G}}^{-1} \tilde{\mathit{\boldsymbol{\theta}}}+\frac{1}{2} \sum\limits_{i=1}^{N} \tilde{\mathit{\boldsymbol{x}}}_{i}^{\mathrm{T}} \mathit{\boldsymbol{P}}_{i} \tilde{\mathit{\boldsymbol{x}}}_{i} \end{array} $ | (22) |
对式(22)求导并代入式(9)、式(13),可得
| $ \begin{array}{l} \dot{V}=\mathit{\boldsymbol{\omega}}_{\mathrm{e}}^{\mathrm{T}} \mathit{\boldsymbol{K}}_{\mathrm{e}}^{-1} \overline{\mathit{\boldsymbol{J}}} \dot{\mathit{\boldsymbol{\omega}}}_{\mathrm{e}}+\mathit{\boldsymbol{q}}_{\mathrm{v}, \mathrm{e}}^{\mathrm{T}} \mathit{\boldsymbol{\omega}}_{\mathrm{e}}+\tilde{\mathit{\boldsymbol{\theta}}}^{\mathrm{T}} \mathit{\boldsymbol{G}}^{-1} \dot{\tilde{\mathit{\boldsymbol{\theta}}}}+\sum\limits_{i=1}^{N} \tilde{\mathit{\boldsymbol{x}}}_{i}^{\mathrm{T}} \mathit{\boldsymbol{P}}_{i} \dot{\tilde{\mathit{\boldsymbol{x}}}}_{i}=\\ \;\;\;\;\;\;\;\; \mathit{\boldsymbol{\omega}}_{\mathrm{e}}^{\mathrm{T}} \mathit{\boldsymbol{K}}_{\mathrm{e}}^{-1}(\mathit{\boldsymbol{Y}} \mathit{\boldsymbol{\theta}}+\mathit{\boldsymbol{R}}+\mathit{\boldsymbol{T}})+\mathit{\boldsymbol{q}}_{v, \mathrm{e}}^{\mathrm{T}} \mathit{\boldsymbol{\omega}}_{\mathrm{e}}-\tilde{\mathit{\boldsymbol{\theta}}}^{\mathrm{T}} \mathit{\boldsymbol{G}}^{-1} \dot{\hat{\mathit{\boldsymbol{\theta}}}}+\\ \;\;\;\;\;\;\;\; \sum\limits_{i=1}^{N} \tilde{\mathit{\boldsymbol{x}}}_{i}^{\mathrm{T}} \mathit{\boldsymbol{P}}_{i}\left(\dot{\mathit{\boldsymbol{x}}}_{i}-\dot{\hat{\mathit{\boldsymbol{x}}}}_{i}\right) \end{array} $ | (23) |
将控制律式(15)、式(19)~(21)代入式(23),可得
| $ \dot{V}=\mathit{\boldsymbol{\omega}}_{\mathrm{e}}^{\mathrm{T}} \mathit{\boldsymbol{K}}_{\mathrm{e}}^{-1}\left[\mathit{\boldsymbol{Y}} \tilde{\mathit{\boldsymbol{\theta}}}+\sum\limits_{i=1}^{N} \mathit{\boldsymbol{B}}_{i}\left(2 \xi_{i} \mathit{\boldsymbol{ \boldsymbol{\varLambda}}}_{i} \tilde{\mathit{\boldsymbol{\psi}}}_{i}+\mathit{\boldsymbol{ \boldsymbol{\varLambda}}}_{i}^{2} \tilde{\mathit{\boldsymbol{\eta}}}_{i}\right)-\right.\\ \;\;\;\;\;\;\;\; \left.\mathit{\boldsymbol{K}}_{\mathrm{w}} \mathit{\boldsymbol{\omega}}_{\mathrm{e}}-\mathit{\boldsymbol{K}}_{\mathrm{e}} \mathit{\boldsymbol{q}}_{{\rm{v}}, \mathrm{e}}\right]+\mathit{\boldsymbol{q}}_{{\rm{v}}, \mathrm{e}}^{\mathrm{T}} \mathit{\boldsymbol{\omega}}_{\mathrm{e}}-\tilde{\mathit{\boldsymbol{\theta}}}^{\mathrm{T}} \mathit{\boldsymbol{Y}}^{\mathrm{T}}\left(\mathit{\boldsymbol{K}}_{\mathrm{e}}^{-1}\right)^{\mathrm{T}} \mathit{\boldsymbol{\omega}}_{\mathrm{e}}+\\ \;\;\;\;\;\;\;\; \sum\limits_{i=1}^{N} \tilde{\mathit{\boldsymbol{x}}}_{i}^{\mathrm{T}} \mathit{\boldsymbol{P}}_{i}\left(\mathit{\boldsymbol{A}}_{i} \tilde{\mathit{\boldsymbol{x}}}_{i}-\mathit{\boldsymbol{P}}_{i}^{-1}\left[\begin{array}{ll}\mathit{\boldsymbol{ \boldsymbol{\varLambda}}}_{i}^{2} & 2 \xi_{i} \mathit{\boldsymbol{ \boldsymbol{\varLambda}}}_{i}\end{array}\right]^{\mathrm{T}} \mathit{\boldsymbol{B}}_{i}^{\mathrm{T}}\left(\mathit{\boldsymbol{K}}_{\mathrm{e}}^{-1}\right)^{\mathrm{T}} \mathit{\boldsymbol{\omega}}_{\mathrm{e}}\right)=\\ \;\;\;\;\;\;\;\; -\mathit{\boldsymbol{\omega}}_{\mathrm{e}}^{\mathrm{T}} \mathit{\boldsymbol{K}}_{\mathrm{e}}^{-1} \mathit{\boldsymbol{K}}_{\mathrm{w}} \mathit{\boldsymbol{\omega}}_{\mathrm{e}}+\mathit{\boldsymbol{\omega}}_{\mathrm{e}}^{\mathrm{T}} \mathit{\boldsymbol{K}}_{\mathrm{e}}^{-1} \sum\limits_{i=1}^{N} \mathit{\boldsymbol{B}}_{i}\left[\begin{array}{ll}\mathit{\boldsymbol{ \boldsymbol{\varLambda}}}_{i}^{2} & 2 \xi_{i} \mathit{\boldsymbol{ \boldsymbol{\varLambda}}}_{i}\end{array}\right]^{\mathrm{T}} \tilde{\mathit{\boldsymbol{x}}}_{i}+\\ \;\;\;\;\;\;\;\; \sum\limits_{i=1}^{N} \tilde{\mathit{\boldsymbol{x}}}_{i}^{\mathrm{T}} \mathit{\boldsymbol{P}}_{i} \mathit{\boldsymbol{A}}_{i} \tilde{\mathit{\boldsymbol{x}}}_{i}-\sum\limits_{i=1}^{N} \tilde{\mathit{\boldsymbol{x}}}_{i}^{\mathrm{T}}\left[\begin{array}{ll}\mathit{\boldsymbol{ \boldsymbol{\varLambda}}}_{i}^{2} & 2 \\ & \xi_{i} \mathit{\boldsymbol{ \boldsymbol{\varLambda}}}_{i}\end{array}\right]^{\mathrm{T}} \mathit{\boldsymbol{B}}_{i}^{\mathrm{T}}\left(\mathit{\boldsymbol{K}}_{e}^{-1}\right)^{\mathrm{T}} \mathit{\boldsymbol{\omega}}_{\mathrm{e}}=\\ \;\;\;\;\;\;\;\; -\mathit{\boldsymbol{\omega}}_{\mathrm{e}}^{\mathrm{T}} \mathit{\boldsymbol{K}}_{\mathrm{e}}^{-1} \mathit{\boldsymbol{K}}_{\mathrm{w}} \mathit{\boldsymbol{\omega}}_{\mathrm{e}}+\sum\limits_{i=1}^{N} \tilde{\mathit{\boldsymbol{x}}}_{i}^{\mathrm{T}} \mathit{\boldsymbol{P}}_{i} \mathit{\boldsymbol{A}}_{i} \tilde{\mathit{\boldsymbol{x}}}_{i} $ | (24) |
对式(24)第2项转置,代入对称性Pi=PiT有
| $ \begin{array}{l} \tilde{\mathit{\boldsymbol{x}}}_{i}^{\mathrm{T}} \mathit{\boldsymbol{P}}_{i} \mathit{\boldsymbol{A}}_{i} \tilde{\mathit{\boldsymbol{x}}}_{i}=\left(\tilde{\mathit{\boldsymbol{x}}}_{i}^{\mathrm{T}} \mathit{\boldsymbol{P}}_{i} \mathit{\boldsymbol{A}}_{i} \tilde{\mathit{\boldsymbol{x}}}_{i}\right)^{\mathrm{T}}=\tilde{\mathit{\boldsymbol{x}}}_{i}^{\mathrm{T}} \mathit{\boldsymbol{A}}_{i}^{\mathrm{T}} \mathit{\boldsymbol{P}}_{i}^{\mathrm{T}} \tilde{\mathit{\boldsymbol{x}}}_{i}=\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;\;\;\; \tilde{\mathit{\boldsymbol{x}}}_{i}^{\mathrm{T}} \mathit{\boldsymbol{A}}_{i}^{\mathrm{T}} \mathit{\boldsymbol{P}}_{i} \tilde{\mathit{\boldsymbol{x}}}_{i} \end{array} $ | (25) |
Lyapunov方程取二次型
| $ \tilde{\mathit{\boldsymbol{x}}}_{i}^{\mathrm{T}} \mathit{\boldsymbol{P}}_{i} \mathit{\boldsymbol{A}}_{i} \tilde{\mathit{\boldsymbol{x}}}_{i}=\tilde{\mathit{\boldsymbol{x}}}_{i}^{\mathrm{T}} \mathit{\boldsymbol{A}}_{i}^{\mathrm{T}} \mathit{\boldsymbol{P}}_{i} \tilde{\mathit{\boldsymbol{x}}}_{i}=-\tilde{\mathit{\boldsymbol{x}}}_{i}^{\mathrm{T}} \mathit{\boldsymbol{Q}}_{i} \tilde{\mathit{\boldsymbol{x}}}_{i} $ | (26) |
将式(26)代入式(24)可得
| $ \dot{V}=-\mathit{\boldsymbol{\omega}}_{\mathrm{e}}^{\mathrm{T}} \mathit{\boldsymbol{K}}_{\mathrm{e}}^{-1} \mathit{\boldsymbol{K}}_{\mathrm{w}} \mathit{\boldsymbol{\omega}}_{\mathrm{e}}-\sum\limits_{i=1}^{N} \tilde{\mathit{\boldsymbol{x}}}_{i}^{\mathrm{T}} \mathit{\boldsymbol{Q}}_{i} \tilde{\mathit{\boldsymbol{x}}}_{i}<0 $ | (27) |
故闭环控制系统渐进稳定。证闭。
4 VSCMGs复合操纵律本文基于VSCMGs的不同功能设计模式切换算法和3种零运动,并将它们引入到姿态机动路径的各个环节中。
4.1 模式权值设计VSCMGs的操纵律需要实现两种模式力矩的分配功能。由加权广义逆理论得到带权值矩阵的伪逆操纵律为:
| $ \mathit{\boldsymbol{y}}=\left[\begin{array}{l}\dot{\mathit{\boldsymbol{ \boldsymbol{\varOmega}}}} \\ \dot{\mathit{\boldsymbol{\delta}}}\end{array}\right]=-\mathit{\boldsymbol{W}} \mathit{\boldsymbol{L}}^{\mathrm{T}}\left(\mathit{\boldsymbol{L}} \mathit{\boldsymbol{W}} \mathit{\boldsymbol{L}}^{\mathrm{T}}\right)^{-1} \mathit{\boldsymbol{T}}, \mathit{\boldsymbol{W}}=\left[\begin{array}{cc}\mathit{\boldsymbol{W}}_{\mathrm{s}} \mathit{\boldsymbol{I}}_{4} & \mathit{\boldsymbol{0}} \\ \mathbf{0} & \mathit{\boldsymbol{W}}_{\mathrm{g}} \mathit{\boldsymbol{I}}_{4}\end{array}\right] $ | (28) |
式中:L=[D E], W∈R8×8为待设计的权值分配矩阵, Ws为转子输出力矩权重, Wg为框架输出力矩权重。通过设计这两个值可以有效根据实际情况分配力矩大小:
| $ \left\{\begin{array}{l} \mathit{\boldsymbol{W}}_{\mathrm{g}}=\frac{1}{1+b^{-c\left\|\mathit{\boldsymbol{\varphi}}-\mathit{\boldsymbol{\varphi}}_{\mathrm{d}}\right\|}}\left(1-\mathrm{e}^{-d\operatorname{det}\left(\mathit{\boldsymbol{A}}_{\mathrm{t}} \mathrm{A}_{\mathrm{t}}^{\mathrm{T}}\right)}\right)\\ \mathit{\boldsymbol{W}}_{\mathrm{s}}=1-\frac{1}{1+b^{-c\left\|\mathit{\boldsymbol{\varphi}}-\mathit{\boldsymbol{\varphi}}_{\mathrm{d}}\right\|}}\left(1-\mathrm{e}^{-d\operatorname{det}\left(\mathit{\boldsymbol{A}}_{\mathrm{t}} \mathit{\boldsymbol{A}}_{\mathrm{t}}^{\mathrm{T}}\right)}\right) \end{array}\right. $ | (29) |
式中:φ为实际姿态角, φd为目标姿态角, b、c、d为正的设计参数。接近奇异时,奇异测度det(AtAtT)趋于零,Ws增大,由RWs模式代替CMGs模式输出力矩直至脱离奇异。通过姿态角误差可以判断航天器姿态机动情况,当||φ-φd||远离零时,此时航天器处于机动状态,增大Wg,使用CMGs模式输出大力矩;当接近零时,此时航天器接近稳定状态,增大Ws,使用RWs模式输出精细小力矩。由机动段到稳定段的模式能够自主平滑切换。大角度机动完成后航天器进入稳定控制阶段,框架角锁定,将权值置为Ws=1姿态稳定控制完全由内转子输出力矩。
4.2 避奇异策略为解决CMGs模式下奇异问题,采用基于奇异值分解(SDA)的操纵律,将E改写为ESDA,即
| $ \mathit{\boldsymbol{E}}_{\mathrm{SDA}}=\mathit{\boldsymbol{U}}\left[\operatorname{diag}\left(\sigma_{1}, \sigma_{2}, \left(\sigma_{3}^{2}+\alpha\right) / \sigma_{3}\right) \quad \mathbf{0}_{3}\right] \mathit{\boldsymbol{V}}^{\mathrm{T}} $ | (30) |
式中:U、V为E奇异值分解得到的酉矩阵,其中E=U[diag(σ1, σ2, σ3) 03×1]VT, σ1≥σ2≥σ3为E的奇异值。当发生CMGs模式奇异时,σ3趋于零。引入误差参数α=α0e-det(EET)后,接近奇异时det(EET)趋于零,可以保证ESDA最小奇异值始终大于零,避免落入奇异状态后解的溢出。将ESDA代入LSDA=[D ESDA],基于SDA加权伪逆操纵律为
| $ \mathit{\boldsymbol{y}}_{\mathrm{SDA}}=-\mathit{\boldsymbol{W}} \mathit{\boldsymbol{L}}_{\mathrm{SDA}}^{\mathrm{T}}\left(\mathit{\boldsymbol{L}}_{\mathrm{SDA}} \mathit{\boldsymbol{W}} \mathit{\boldsymbol{L}}_{\mathrm{SDA}}^{\mathrm{T}}\right)^{-1} \mathit{\boldsymbol{T}} $ | (31) |
VSCMGs系统通过添加零运动实现空转从而远离落入奇异的构型。零运动的操纵律表达式为
| $ \mathit{\boldsymbol{y}}_{\mathrm{N} 1}=K_{\mathrm{N} 1}\left(\mathit{\boldsymbol{I}}-\mathit{\boldsymbol{W}} \mathit{\boldsymbol{L}}^{\mathrm{T}}\left(\mathit{\boldsymbol{L}} \mathit{\boldsymbol{W}} \mathit{\boldsymbol{L}}^{\mathrm{T}}\right)^{-1} \mathit{\boldsymbol{L}}^{\mathrm{T}}\right) \mathit{\boldsymbol{W}}\left[\begin{array}{l} \mathbf{0}_{4} \\ \frac{\partial \kappa}{\partial \delta} \end{array}\right] $ | (32) |
式中:KN1为避奇异零运动参数, κ=σ1/σ3为雅可比矩阵条件数。
4.3 轮速平衡策略为了保证在处于CMGs模式时,各转子转速应尽可能保持平衡,避免个别转子转速过高或过低。轮速平衡操纵律设计充分利用VSCMGs力矩方程
| $ \dot{\mathit{\boldsymbol{ \boldsymbol{\varOmega}}}}_{\mathrm{N}}=K_{\mathrm{N} 2}\left(\mathit{\boldsymbol{ \boldsymbol{\varOmega}}}_{\mathrm{f}}-\mathit{\boldsymbol{ \boldsymbol{\varOmega}}}\right) $ | (33) |
式中:Ωf为期望转速, KN2为转速平衡零运动参数。转速收敛于期望转速Ωf时,必然会产生额外的力矩误差
| $ \dot{\mathit{\boldsymbol{\delta}}}_{\mathrm{N} 2}=-K_{\mathrm{N} 2} \mathit{\boldsymbol{D}}\left(\mathit{\boldsymbol{D}} \mathit{\boldsymbol{D}}^{\mathrm{T}}\right)^{-1} \mathit{\boldsymbol{E}}\left(\mathit{\boldsymbol{ \boldsymbol{\varOmega}}}_{\mathrm{f}}-\mathit{\boldsymbol{ \boldsymbol{\varOmega}}}\right) $ | (34) |
转速平衡零运动表示为
| $ \mathit{\boldsymbol{y}}_{\mathrm{N} 2}=K_{\mathrm{N} 2}\left[\begin{array}{c} \mathit{\boldsymbol{ \boldsymbol{\varOmega}}}_{\mathrm{f}}-\mathit{\boldsymbol{ \boldsymbol{\varOmega}}}\\ -\mathit{\boldsymbol{D}}\left(\mathit{\boldsymbol{D}} \mathit{\boldsymbol{D}}^{\mathrm{T}}\right)^{-1} \mathit{\boldsymbol{E}}\left(\mathit{\boldsymbol{ \boldsymbol{\varOmega}}}_{\mathrm{f}}-\mathit{\boldsymbol{ \boldsymbol{\varOmega}}}\right) \end{array}\right] $ | (35) |
本文姿态控制背景为连续机动,因此需要在机动前和机动完成后的稳定段,框架能定位在期望的组合上,既实现锁定状态RWs模式力矩输出同向性,又能实现CMGs模式减少奇异。故引入末态框架角反馈零运动为
| $ \mathit{\boldsymbol{y}}_{\mathrm{N} 3}=K_{\mathrm{N} 3}\left(\mathit{\boldsymbol{I}}-\mathit{\boldsymbol{W}} \mathit{\boldsymbol{L}}^{\mathrm{T}}\left(\mathit{\boldsymbol{L}} \mathit{\boldsymbol{W}} \mathit{\boldsymbol{L}}^{\mathrm{T}}\right)^{-1} \mathit{\boldsymbol{L}}^{\mathrm{T}}\right) \mathit{\boldsymbol{W}}\left[\begin{array}{c} \mathbf{0}_{4}\\ \mathit{\boldsymbol{\delta}}_{\mathrm{f}}-\mathit{\boldsymbol{\delta}} \end{array}\right] $ | (36) |
式中:KN3为末态框架角定位零运动参数, δf为后续设计的期望框架组合。
在三轴稳定整星零动量控制策略中,忽略干扰作用,机动开始与机动结束,VSCMGs系统有零动量约束,即AsIsΩ=0。另外希望框架角组合尽可能对称,保证RWs模式时有较对称的力矩包络。假设机动开始时转速已在式(35)作用下趋于一致,一种使VSCMGs系统角动量为零且对称的框架角组合为δf=[δF-δF δF-δF]T,彼此相对的框架角相同,相邻的框架角相反,从而保证系统角动量为零。
在机械机构学中,雅可比矩阵的条件数κ=σ1/σ3用作表征机构灵敏度的评价函数,本文中评价VSCMGs不同框架组合下力矩输出各向同性。极限情况时κ=1,机构处于最佳运动传递性能,力矩包络呈现各向同性的球形。当出现奇异κ→∞时,机构将无法输出奇异方向力矩。利用该特性,可以为框架角组合选择提供参考依据。At和As的条件数为κcmg与κrw,分别对应RWs模式与CMGs模式,图 3为条件数关于框架角的曲线。

|
图 3 雅可比矩阵条件数 Fig. 3 Jacobian matirx condition number |
如图 3所示,两种模式的条件数均以60°为一个周期呈周期性分布。两者峰值交替出现,κcmg呈现极小值时,κrw为极大值。综合两者,取曲线交点δF=15°+30k°, (k=±1, ±2, …, ±5)。既保证在姿态机动初始时刻CMGs模式远离奇异,又使机动结束进入的RWs模式有较好的力矩同向性。本文仅从奇异的方面选取期望框架角,可根据实际航天器构型及工程需要灵活调整。如长杆型的航天器在X、Y方向受到较大的重力梯度力矩,可以将δF调整到60°附近来吸收干扰力矩。
4.5 姿态机动路径规划中的VSCMGs操纵律VSCMGs操纵律为伪逆解和零运动解的线性组合y=ySDA+yN1+yN2+yN3。引入各操纵律需要结合姿态机动路径,需要进行更细致规划,如图 4所示。在机动准备阶段框架解锁, VSCMGs使用RWs模式,引入转速平衡的零运动使内转子的转速在机动开始时尽可能趋于一致。机动过程中使用VSCMGs加权伪逆操纵律,由权值矩阵根据机动不同阶段分配力矩大小,并引入避奇异零运动,机动前期主要处于CMGs模式。当姿态机动进入到减速段时,对k进行寻优搜索,||δ-δF(k)||的最小值对应的k代入到δF(k),即为期望的末态框架角组合,此时引入框架角反馈的零运动。机动末段时,随着欧拉角误差逐渐减少,VSCMGs将处于CMGs模式与到RWs模式过渡状态的混合模式。大角度机动完成后航天器进入稳定控制,框架角锁定,姿态稳定控制完全由内转子加减速输出力矩,VSCMGs处于RWs模式。

|
图 4 VSCMGs操纵律使用方案规划 Fig. 4 VSCMGs control law scheme in path planning |
注5 文献[10]通过三角形规划路径的仿真证明了延长减速段时间可增加VSCMG框架角反馈的持续时间,更有利于让框架角能定位在δF附近。本文为了在实现敏捷机动减小激发挠性附件振动,规划了三段式正弦机动路径。减小其中减速段的加速度,延长正弦式机动的减速段时间,如图 4所示。
5 仿真分析本文从挠性航天器连续姿态机动仿真来说明本文提出的姿态控制律和VSCMGs操纵律。航天器初始姿态欧拉角为[0°, 0°, 0°],共计4次姿态机动循环往复:首次机动至[30°, -30°, 180°],维持后机动至零姿态,然后机动至[30°, -30°, -40°],再次机动复位。路径规划中绕欧拉轴最大旋转角度为2.3(°)/s,最大旋转角加速度为0.36(°)/s2。转动惯量为
| $ \mathit{\boldsymbol{J = }}\left[ {\begin{array}{*{20}{c}} {1\;200}&5&{10}\\ 5&{1\;800}&{20}\\ {10}&{20}&{2\;300} \end{array}} \right]{\rm{kg \times }}{{\rm{m}}^2} $ | (37) |
挠性部件前4阶固有频率为Λ1=diag(0.457 34, 1.028 80, 1.893 30, 2.245 30)Hz,模态阻尼为ξ1=0.005,转动耦合系数矩阵为
| $ \mathit{\boldsymbol{B}}_{1}=\left[\begin{array}{cccc} 0 & 0 & -2.452\;8 & 0 \\ 16.629\;6 & 0 & 0 & 1.300\;8 \\ 0 & 17.184\;7 & 0 & 0 \end{array}\right] \sqrt{\mathrm{kg}} \cdot \mathrm{m} $ | (38) |
模态坐标初值为η1=[2, 0, 0, 0]×10-5。VSCMGs的转子惯量为Is=0.028 kg·m2,初始框架角为δ0=[23.0°, -18.6°, 17.6°, -24.4°],初始框架转速为Ω0=[2 000, 1 600, 1 700, 1 900]r/min。VSCMGs操纵律参数设置为KN1=0.50,KN2=0.35,KN3=10.0, b=1 808, c=2, d=1。控制器增益为Kp=diag(252.720 0, 243.381 2, 232.608 0),Kd=diag(620.7, 931.0, 1 189.7), 惯量自适应律参数为G=diag(107, 107, 107, 103, 103, 103), 模态观测器参数为Q1=103I8,用Matlab中lqr命令计算: A1TP1+P1A1=-2Q1求得P1。惯量估计初值
|
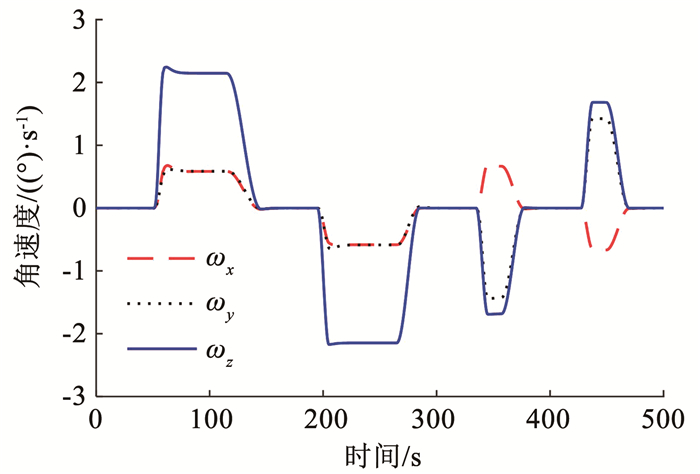
图 5 角速度 Fig. 5 Angular velocity |
|
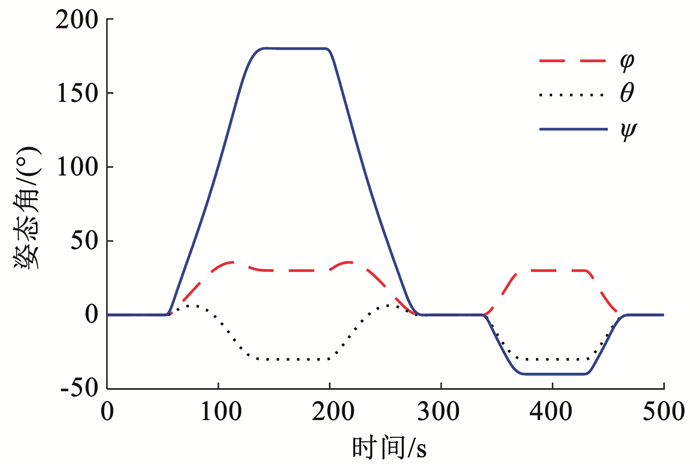
图 6 姿态角 Fig. 6 Euler angle |
|
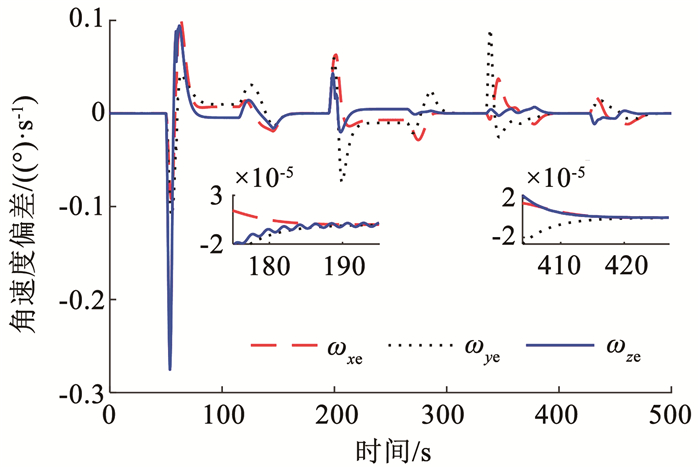
图 7 角速度跟踪误差 Fig. 7 Tracking error of angular velocity |
|
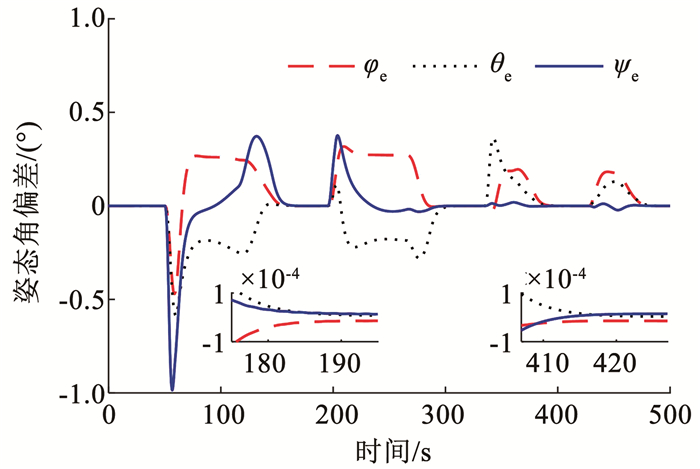
图 8 姿态角跟踪误差 Fig. 8 Tracking error of Euler angle |
|
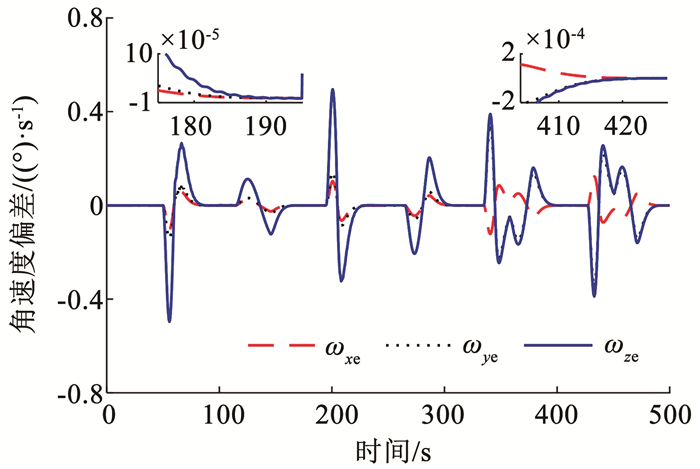
图 9 角速度跟踪误差(无自适应律与观测器) Fig. 9 Tracking error of angular velocity without adaptive law and observer |

|
图 10 姿态角跟踪误差(无自适应律与观测器) Fig. 10 Tracking error of Euler angle without adaptive law and observer |

|
图 11 RWs与CMGs模式权值 Fig. 11 Weight of RWs mode and CMGs mode |

|
图 12 VSCMGs奇异测度 Fig. 12 Singularity measurement of VSCMGs |

|
图 13 VSCMGs内转子转速 Fig. 13 Rotor speed of VSCMGs |
|
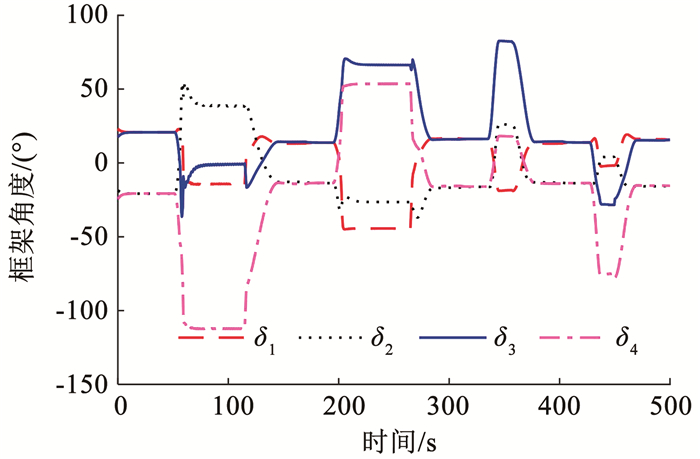
图 14 VSCMGs框架角 Fig. 14 Gimbal angle of VSCMGs |
|
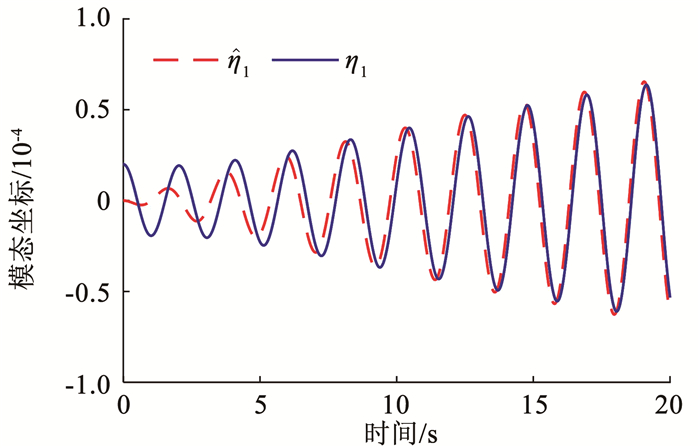
图 15 一阶模态坐标及观测值 Fig. 15 First mode coordinate and its estimation |

|
图 16 转动惯量估计值 Fig. 16 Estimation of inertia |
|
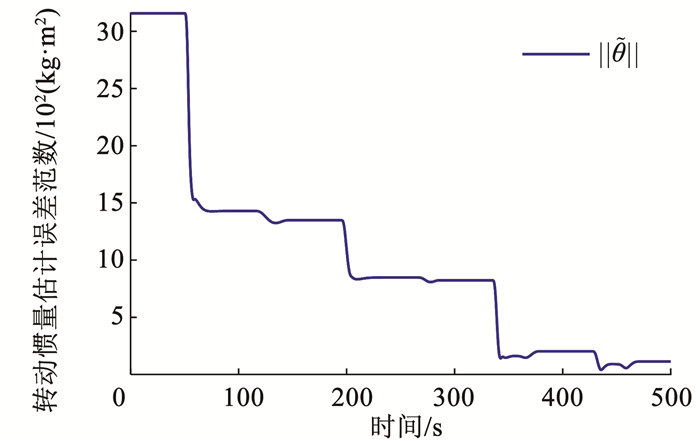
图 17 惯量估计误差范数 Fig. 17 Norm of estimation error of inertia |
姿态连续机动的角速度与姿态角如图 5、6所示,角速度与姿态角跟踪规划后正弦机动路的误差图 7、8可知。如图 7、8所示,每次机动开始的角速度偏差与角度偏差较大,稳态误差分别为2×10-5(°)/s和(10-4)°。在首次机动,由于惯量信息不准确,自适应律尚未估计完成,因此超调最大。作为对比实验,采用无惯量估计和无模态观测的普通PD反馈控制器式(10),仿真结果如图 9、10所示。显然,在没有任何挠性力矩补偿和不准确惯量的前馈力矩时,动态响应中超调量更大,进入稳态的时间更长,稳态的精度相比本文经过挠性抑制和惯量估计的控制器要低一个数量级。
图 11为模式权值曲线,反映了机动过程中模式切换及零运动引入过程。0 s时为机动准备阶段,VSCMGs处于RWs模式,此时开始转速平衡。50 s开始首次姿态机动,权值Wg>Ws,系统主要处于CMGs模式,主要由框架转动提供力矩。
如图 12的奇异测度曲线所示,在63 s处接近奇异,此时权值Ws减小,内转子变速由RWs模式补偿CMGs模式奇异力矩。在零运动的作用下,奇异测度快速增大,避开了奇异后,再次由CMGs模式提供力矩。115 s时进入减速段,引入末态框架角反馈零运动,使框架定位在期望框架角组合。机动末期,过渡为CMGs与RWs混合模式,RWs逐渐开始占主导,直至145 s机动结束。随着姿态角误差逐渐减小,Ws向1收敛,Wg向0收敛,最终进入姿态稳定控制置Wg=0,Ws=1,完全由转子变速提供力矩,等待下次姿态机动。图 13、14为VSCMGs的内转子转速和VSCMGs的框架角变化曲线。轮速平衡作用下,转子转速始终工作在1 800 r/min附近,既避免了稳态控制时转子转速过零,又使转子转速具有在姿态机动后复位的能力。进入稳态段后,由转子变速提供力矩,框架转速为零实现锁定。末态框架角定位的作用下,框架角能在每次姿态机动结束后锁定在至期望的角度[15°, -15°, 15°, -15°]附近。
图 15~17表示了模态观测器和惯量自适应估计器的辨识效果。图 15表明,模态观测器能在20 s内就跟踪上真实的模态坐标用于补偿挠性干扰力矩。图 16、17表明,在多次机动后,近似持续激励的辨识结果接近真实值,整体估计误差范数为150 kg·m2。通过调整估计增益矩阵G改变惯量估计的收敛速度,比较多组实验下最后一次姿态机动的仿真结果,从而分析不同惯量估计效果对控制品质的影响。如图 18、19所示,惯量估计误差||θe||越小,航天器进入稳态段的时间越短,快速稳定的能力越强;在相同的机动时间下,控制性能随估计精度的提高而提高。

|
图 18 角速度跟踪偏差与惯量估计误差的关系 Fig. 18 Angular velocity error related to inertial estimation error |

|
图 19 姿态角跟踪偏差与惯量估计误差的关系 Fig. 19 Euler angle error related to inertial estimation error |
1) 本文设计了一种适用于挠性卫星的敏捷机动和高稳定姿控场合的自适应控制器和VSCMGs复合操纵律。设计的模态观测器和惯量估计器用于辨识不可测的模态信息和惯量信息,这些辨识结果被用来精确估计挠性干扰前馈补偿力矩,使用Lyapunov方法证明了闭环控制系统的稳定性。
2) 设计的VSCMGs复合操纵律同时实现了4项重要功能:CMGs模式到RWs模式的平滑切换,规避CMGs模式奇异性,维持转子的轮速平衡以及在机动结束时将框架角复位到优选组合。
3) 本文算法有效降低了机动过程中挠性振动和转动惯量未知的不利影响,与无自适应控制律相比,姿态控制精度提高了一个数量级。调整自适应增益改变参数辨识效果,对比实验表明航天器快速稳定的能力随辨识误差减小而提升。
| [1] |
陈雪芹, 王峰, 耿云海, 等. 敏捷小卫星姿态控制律和操纵律一体化设计[J]. 哈尔滨工业大学学报, 2012, 44(1): 7. CHEN Xueqin, WANG Feng, GENG Yunhai, et al. Integrated attitude control algorithm and steering law for agile small satellites[J]. Journal of Harbin Institute of Technology, 2012, 44(1): 7. DOI:10.11918/j.issn.0367-6234.2012.01.002 |
| [2] |
WU Yunhua, HAN Feng, HUA Bing, et al. Review: A survey of single gimbal control moment gyroscope for agile spacecraft attitude control[J]. Journal of Harbin Institute of Technology (New Series), 2018, 25(6): 22. DOI:10.11916/j.issn.1005-9113.16225 |
| [3] |
LEVE F A. Evaluation of steering algorithm optimality for single-gimbal control moment gyroscopes[J]. IEEE Transactions on Control Systems Technology, 2014, 22(3): 1130. DOI:10.1109/TCST.2013.2259829 |
| [4] |
叶东, 孙兆伟, 刘一帆. 考虑安装偏差的联合执行机构自适应控制算法[J]. 哈尔滨工业大学学报, 2016, 48(11): 7. YE Dong, SUN Zhaowei, LIU Yifan. An adaptive control algorithm for hybrid actuator with installation deviation[J]. Journal of Harbin Institute of Technology, 2016, 48(11): 7. DOI:10.11918/j.issn.0367-6234.2016.11.002 |
| [5] |
王焕杰, 金磊, 贾英宏. 基于混合执行机构的敏捷卫星姿态机动控制[J]. 空间控制技术与应用, 2015, 41(6): 19. WANG Huanjie, JIN Lei, JIA Yinghong. Agile satellite attitude maneuver control using hybrid actuators[J]. Aerospace Control and Application, 2015, 41(6): 19. DOI:10.3969/j.issn.1674-1579.2015.06.004 |
| [6] |
LIU Feng, GAO Yang, ZHANG Weiwei. Large angle maneuver and high accuracy attitude pointing steering law for variable speed control momentum gyroscopes[J]. Journal of the Franklin Institute, 2021, 358(7): 3441. DOI:10.1016/j.jfranklin.2021.02.019 |
| [7] |
SCHAUB H, VADALI S R, JUNKINS J L. Feedback control law for variable speed control moment gyros[J]. The Journal of the Astronautical Sciences, 1998, 46(3): 307. DOI:10.1007/BF03546239 |
| [8] |
邢林峰, 孙承启, 汤亮. 高姿态稳定度敏捷卫星的VSCMGs操纵律研究[J]. 空间控制技术与应用, 2008, 34(6): 24. XING Linfeng, SUN Chengqi, TANG Liang. VSCMGs-based steering law design for a high attitude stability agile satellite[J]. Aerospace Control and Application, 2008, 34(6): 24. DOI:10.3969/j.issn.1674-1579.2008.06.005 |
| [9] |
杨雅萍, 吴忠. 变速控制力矩陀螺模式调度型操纵律设计[J]. 空间控制技术与应用, 2011, 37(3): 9. YANG Yaping, WU Zhong. Mode-scheduling steering law design for variable speed control moment gyroscope[J]. Aerospace Control and Application, 2011, 37(3): 9. DOI:10.3969/j.issn.1674-1579.2011.03.002 |
| [10] |
NANAMORI Y, TAKAHASHI M. Mode-scheduling steering law of VSCMGs for multi-target pointing and agile maneuver of a spacecraft[J]. International Journal of Advanced Computer Science and Applications, 2017, 8(5): 25. DOI:10.14569/ijacsa.2017.080504 |
| [11] |
刘军, 韩潮. 挠性航天器大角度机动的振动抑制控制[J]. 系统仿真学报, 2008, 20(7): 1880. LIU Jun, HAN Chao. Vibration suppression control of flexible spacecraft during large angle attitude maneuver[J]. Journal of System Simulation, 2008, 20(7): 1880. DOI:10.16182/j.cnki.joss.2008.07.005 |
| [12] |
赵波林, 刘昆, 张立. 基于VSCMG的卫星动态扫描成像姿态控制研究[C]//空天资源的可持续发展——第一届中国空天安全会议论文集. 北京: 科学出版社, 2016: 284 ZHAO Bolin, LIU Kun, ZHANG Li. Attitude control of satellite dynamic scanning imaging based on VSCMG[C]// The 1st Chinese Aerospace Safety Symposium (CASS). Beijing: China Science Publishing & Media Ltd., 2016: 284 |
| [13] |
杨楠, 郁丰, 马浩哲, 等. 基于聚类变异PSO优化的VSCMGs模糊平滑切换算法[J]. 哈尔滨工业大学学报, 2023, 55(10): 93. YANG Nan, YU Feng, MA Haozhe, et al. Fuzzy smooth switching algorithm for VSCMGs based on clustering-mutated PSO[J]. Journal of Harbin Institute of Technology, 2023, 55(10): 93. DOI:10.11918/202208117 |
| [14] |
黄喜元, 王青, 董朝阳. 基于归一化神经网络的航天器自适应姿态跟踪控制[J]. 宇航学报, 2010, 31(11): 2542. HUANG Xiyuan, WANG Qing, DONG Chaoyang. Adaptive attitude tracking control for spacecraft based on input normalized neural network[J]. Journal of Astronautics, 2010, 31(11): 2542. DOI:10.3873/j.issn.1000-1328.2010.11.017 |
| [15] |
刘军, 韩潮. 使用变速控制力矩陀螺的航天器鲁棒自适应姿态跟踪控制[J]. 航空学报, 2008, 29(1): 159. LIU Jun, HAN Chao. Spacecraft adaptive robust attitude tracking control with variable speed control moment gyroscopes[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(1): 159. |
| [16] |
刘向东, 辛星, 丛炳龙, 等. 以VSCMG为执行器的航天器姿态机动自适应动态滑模控制[J]. 宇航学报, 2012, 33(8): 1064. LIU Xiangdong, XIN Xing, CONG Binglong, et al. An adaptive dynamic sliding mode attitude maneuver control law for rigid body satellites using VSCMG actuator[J]. Journal of Astronautics, 2012, 33(8): 1064. DOI:10.3873/j.issn.1000-1328.2012.08.010 |
| [17] |
田林, 徐世杰. 带VSCMGs的航天器姿态稳定及功率补偿控制[J]. 北京航空航天大学学报, 2013, 39(2): 201. TIAN Lin, XU Shijie. Attitude stabilization and power compensation control for spacecraft with VSCMGs[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(2): 201. DOI:10.13700/j.bh.1001-5965.2013.02.017 |
| [18] |
张军, 徐世杰. 使用VSCMGs的IPACS的奇异性分析与操纵律设计[J]. 航空学报, 2008, 29(1): 123. ZHANG Jun, XU Shijie. Singularity analysis and steering law design of IPACS with VSCMGs[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(1): 123. DOI:10.3321/j.issn:1000-6893.2008.01.019 |
| [19] |
庞博, 李果, 黎康, 等. 一种带精确补偿的卫星姿态快速机动控制方法[J]. 宇航学报, 2020, 41(4): 464. PANG Bo, LI Guo, LI Kang, et al. Satellite attitude fast maneuver control method with accurate compensation[J]. Journal of Astronautics, 2020, 41(4): 464. DOI:10.3873/j.issn.1000-1328.2020.04.010 |
| [20] |
王首喆, 张庆展, 靳永强, 等. 带挠性附件航天器在轨质量特性辨识[J]. 航天控制, 2017, 35(5): 9. WANG Shouzhe, ZHANG Qingzhan, JIN Yongqiang, et al. Identification of mass property for on-orbit spacecrafts with flexible appendages[J]. Aerospace Control, 2017, 35(5): 9. DOI:10.16804/j.cnki.issn1006-3242.2017.05.002 |
| [21] |
袁国平, 史小平, 李隆. 航天器的自适应鲁棒姿态控制器设计[J]. 系统工程与电子技术, 2012, 34(12): 2524. YUAN Guoping, SHI Xiaoping, LI Long. Adaptive robust attitude maneuvering control for rigid spacecraft[J]. Systems Engineering and Electronics, 2012, 34(12): 2524. DOI:10.3969/j.issn.1001-506X.2012.12.21 |
| [22] |
孙延超, 李传江, 常雅杰, 等. 空间智能桁架的有限时间振动抑制控制[J]. 哈尔滨工业大学学报, 2018, 50(10): 27. SUN Yanchao, LI Chuanjiang, CHANG Yajie, et al. Finite-time vibration control of space intelligent truss[J]. Journal of Harbin Institute of Technology, 2018, 50(10): 27. DOI:10.11918/j.issn.0367-6234.201605018 |
| [23] |
BAZ A, POH S. Performance of an active control system with piezoelectric actuators[J]. Journal of Sound and Vibration, 1988, 126(2): 327. DOI:10.1016/0022-460x(88)90245-3 |
| [24] |
HU Qinglei, MA Guangfu. Spacecraft vibration suppression using variable structure output feedback control and smart materials[J]. Journal of Vibration and Acoustics, 2006, 128(2): 221. DOI:10.1115/1.2159039 |
| [25] |
DI GENNARO S. Output stabilization of flexible spacecraft with active vibration suppression[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(3): 747. DOI:10.1109/TAES.2003.1238733 |
| [26] |
DI GENNARO S. Output attitude tracking for flexible spacecraft[J]. Automatica, 2002, 38(10): 1719. DOI:10.1016/S0005-1098(02)00082-1 |
| [27] |
WIE B, WEISS H, ARAPOSTATHIS A. Quarternion feedback regulator for spacecraft eigenaxis rotations[J]. Journal of Guidance, Control, and Dynamics, 1989, 12(3): 375. DOI:10.2514/3.20418 |
| [28] |
屠善澄, 陈义庆, 严拱添, 等. 卫星姿态动力学与控制[M]. 北京: 中国宇航出版社, 2001. TU Shancheng, CHEN Yiqing, YAN Gongtian, et al. Satellite attitude dynamics and control[M]. Beijing: China Astronautic Publishing House, 2001. |
 2024, Vol. 56
2024, Vol. 56


