2. 信息融合技术教育部重点实验室(西北工业大学),西安 710072
2. Key Laboratory of Information Fusion Technology (Northwestern Polytechnical University), Ministry of Education, Xi'an 710072, China
在组合导航、目标跟踪、飞行器姿态控制、故障诊断等众多工程领域中, 系统的状态估计是关键问题。在状态估计方法中, 卡尔曼滤波器(Kalman filter, KF)因其简洁性、高效性与最优性被广泛应用于上述领域[1-6]。但是, 在实际应用中, 观测常常受到强未知干扰和仪器故障的影响, 系统本身也会受到随机和未建模干扰的侵蚀, 这些都容易造成未知异常值的出现。这种情况下, 过程与量测噪声往往是非高斯重尾分布, 这违背了KF的噪声是精确高斯的假设, 从而破坏了滤波器的准确性和可靠性[7-10]。对于这一问题, 许多优秀的研究者已经提出了很多鲁棒卡尔曼滤波器(robust Kalman filters, RKFs)。
虽然Huber-RKFs[11-12]和最大/最小相关熵准则RKFs[13-15]可以在一定程度上降低重尾噪声的负面影响, 但由于没有充分利用该噪声固有的重尾特性与不能适用于复杂的噪声环境限制了它们的性能。针对这一问题, 学生t KF(Student’s t KF,STKF)[16]和鲁棒学生t KF(robust Student’s t KF,RSTKF)[17]先后被提出, 其中状态后验的概率密度函数(probability density function, PDF)被建模为学生t分布, 并通过变分贝叶斯(variational Bayesian,VB)推理估计状态和噪声统计量。为进一步提高滤波器的鲁棒性能, 基于野值鲁棒学生t KF(outlier-robust Student’s t KF,ORSTKF)[18]和基于重尾混合分布的RKF(heavy-tailed mixture RKF,HTMRKF)[19]被设计。虽然上述提到的RKFs在平稳重尾噪声环境中表现良好,但是如果存在由动态异常值引起的非平稳重尾过程和测量噪声, 即噪声有时是高斯噪声, 有时是不同类型的重尾分布, 上述RKFs的性能会下降。例如在自主水下航行器协同定位中,由于传感器的离群值、声通道的多径效应以及水下环境的变化,实际状态和测量噪声可能是非平稳非高斯分布的[20]。还有在无人潜航器的惯性导航/多普勒组合导航实际实验中,也出现了类似的噪声环境[21]。因此在设计鲁棒滤波器时需考虑这样的噪声环境。
考虑到上述问题, 一种新的高斯-学生t混合分布(Gaussian-student’s t mixture distribution,GSTM)[22]被构造以建模非平稳重尾噪声, 该算法通过自适应学习高斯分布和学生t分布之间的混合概率来适应噪声的非平稳性。并通过引入伯努利随机变量,将所提出的GSTM分布表示为分层高斯形式,并在此基础上构造了新的分层线性高斯状态空间模型以推导一种新的基于GSTM分布的RKF(GSTMRKF),其中状态向量、辅助随机变量、伯努利随机变量和混合概率用VB方法联合推导。仿真结果表明,在非平稳重尾噪声情况下,该滤波器比现有的标准KF和ORSTKF具有更好的估计精度。这是由于混合参数克服了自由度参数自适应的困难,能更好地模拟非平稳重尾分布噪声。然而该滤波器的噪声尺度矩阵必须是预先已知的。在文献[22]工作的基础上, 基于两种高斯分布混合(mixture of two Gaussian distr-bution)的RKF(M2GRKF)[23]被提出。但实际上, 由于不同类型的异常值随机出现, 非平稳重尾噪声的特征是难以描述的, 这使得上述RKFs很难预先选择尺度矩阵和利用单个伽马分布的粗略先验信息来近似重尾特征。
本文以应对上述难题为目标, 提出了一种基于高斯-重尾切换分布的鲁棒卡尔曼滤波器(Gaussian-heavy-tailed switching distribution based robust Kalman filter,GHTSRKF)。所设计的GHTS分布可以通过在线调整高斯分布和新的重尾分布之间的切换概率来对非平稳重尾噪声进行建模。具有虚拟协方差的高斯分布用于处理协方差矩阵不准确的高斯噪声。重尾分布由高斯分布和混合伽马分布构成, 前者利用一个尺度参数来描述重尾噪声;后者可以根据精确先验对尺度参数进行建模, 所使用的精确先验是通过自适应学习混合概率向量从一组粗略的先验信息中提取的。本文首先建立一种新的GHTS分布对实际情况可能出现的非平稳重尾噪声进行建模。其次引入两个分别满足分类分布和伯努利分布的随机变量将GHTS分布PDF转换为分层高斯形式以便于算法的进一步推导。最后利用VB方法推导出GHTSRKF, 该滤波器中一步预测和测量似然PDFs被建模为GHTS分布, 并采用固定点迭代联合估计状态和模型参数。
1 问题描述离散时间状态空间模型如下:
| $ \left\{\begin{array}{l} \mathit{\boldsymbol{x}}_{t}=\mathit{\boldsymbol{F}}_{t-1} \mathit{\boldsymbol{x}}_{t-1}+\mathit{\boldsymbol{\omega}}_{t-1}\\ \mathit{\boldsymbol{z}}_{t}=\mathit{\boldsymbol{H}}_{t} \mathit{\boldsymbol{x}}_{t}+\mathit{\boldsymbol{v}}_{t} \end{array}\right. $ | (1) |
式中:xt∈Rnx、zt∈Rmz分别为状态向量与量测向量, Ft-1、Ht分别为状态转移矩阵与量测矩阵,ωt-1、υt分别为系统与量测噪声向量, 且协方差矩阵分别为Qt-1与Rt,同时, 假设状态与两种噪声相互独立。
KF可以根据给定的状态空间模型与量测z1∶ t估计出系统状态xt。在卡尔曼理论中, 当状态空间模型是线性的且系统与量测噪声是准确已知的高斯分布时, KF的估计是最优的。然而实际情况中, 系统本身与观测传感器由于变化的环境和自身的原因, 过程与量测中会出现未知的动态野值,导致系统的过程和测量噪声是非平稳重尾分布, 这违背了卡尔曼理论中精确高斯分布的假设, 严重影响到了滤波的估计精度和可靠性。
考虑到上述现实问题,本文以降低KF对精确先验噪声统计的依赖,并改善在复杂噪声,如重尾噪声、非平稳重尾噪声等环境下的状态估计性能为目标,研究一种应用更广、性能更好的鲁棒滤波器。
2 高斯-重尾切换分布(GHTS)本文首先引入了一种新的重尾分布, 也称为高斯-混合伽马(Gaussian-mixing Gamma,GMG)分布以建模重尾噪声[10]。基于混合概率向量ξ的服从GMG分布的随机向量y的PDF表示为
| $ p(\mathit{\boldsymbol{y}} \mid \mathit{\boldsymbol{\xi}})=N(\mathit{\boldsymbol{y}} ; \lambda, \mathit{\boldsymbol{ \boldsymbol{\varLambda}}} / \mathit{\boldsymbol{\kappa}}) \sum\limits_{m=1}^{M} \xi_{m} G\left(\kappa ; e_{m}, f_{m}\right) $ | (2) |
式中:N(·;λ, Λ)表示均值为λ和协方差矩阵为Λ的高斯分布, G(·;e, f)表示形状参数为e和速率参数为f的伽马分布,κ为尺度参数, ξm为第m个伽马分布的混合系数, M为伽马分布的数量,ξ=[ξ1, ξ2, …, ξM]为混合概率向量且
文献[24]考虑了贝叶斯框架下高斯混合分布的标准共轭先验,利用狄利克雷分布对混合系数进行建模。基于该方法,本文假定混合概率向量ξ服从如下狄雷克利分布:
| $ p(\mathit{\boldsymbol{\xi}})=\operatorname{Dir}(\mathit{\boldsymbol{\xi}} ; \mathit{\boldsymbol{w}}, m) $ | (3) |
式中, 向量w=[w1, w2, …, wm]且wm>0是狄利克雷分布的集中参数。
本文假设变量ξm的期望为wm=E[ξm],并利用式(2)、(3)可以将GMG分布表示为
| $\begin{array}{*{20}{c}} p(\mathit{\boldsymbol{y}})=\int p(\mathit{\boldsymbol{y}} \mid \mathit{\boldsymbol{\xi}}) p(\mathit{\boldsymbol{\xi}}) \mathrm{d} \mathit{\boldsymbol{\xi}}= \\ N(\mathit{\boldsymbol{y}} ; \lambda, \mathit{\boldsymbol{ \boldsymbol{\varLambda}}} / \kappa) \sum\limits_{m=1}^{M} \bar{w}_{m} G\left(\kappa ; e_{m}, f_{m}\right) \end{array} $ | (4) |
为准确描述非平稳重尾噪声, 设计了一种新的GHTS分布。服从该分布的随机向量y的PDF为
| $\begin{array}{*{20}{c}} p(\mathit{\boldsymbol{y}} \mid \mu)=\mu N(\mathit{\boldsymbol{y}} ; \lambda, \mathit{\boldsymbol{ \boldsymbol{\varLambda}}})+ \\ (1-\mu) \operatorname{GMG}(\mathit{\boldsymbol{y}}, \lambda, \mathit{\boldsymbol{ \boldsymbol{\varLambda}}}, e, f) \end{array} $ | (5) |
文献[10]设计了贝叶斯框架下实现了两种不同噪声分布之间的切换,并利用贝塔分布建模两种分布之间的切换概率。基于该结果,本文的切换概率μ也服从以下贝塔分布:
| $ p(\mu)=B(\mu ; v, 1-v) $ | (6) |
式中:B(·;v, 1-v)为形状参数为v∈[0, 1]的贝塔分布, v为先验切换概率, 则v=E[μ]。
根据式(5)、(6), GHTS的PDF表示为
| $ \begin{align*} p(\mathit{\boldsymbol{y}})= & \int p(\mathit{\boldsymbol{y}} \mid \mu) p(\mu) \mathrm{d} \mu=v N(\mathit{\boldsymbol{y}} ; \lambda, \mathit{\boldsymbol{ \boldsymbol{\varLambda}}})+ \\ & (1-v) \operatorname{GMG}(\mathit{\boldsymbol{y}}, \lambda, \mathit{\boldsymbol{ \boldsymbol{\varLambda}}}, e, f) \end{align*} $ | (7) |
引入一个伯努利参数ζ和一个服从分类分布的向量ρ=[ρ1, ρ2, …, ρM], 将GHTS分布的PDF表示为
| $ \begin{array}{*{20}{c}} {p(\mathit{\boldsymbol{y}})=\sum\limits_{\zeta=0}^{1} \iiiint_{0}^{+\infty}[N(\mathit{\boldsymbol{y}} ; \lambda, \mathit{\boldsymbol{ \boldsymbol{\varLambda}}})]^{\zeta} \times}\\ {[N(\mathit{\boldsymbol{y}} ; \lambda, \mathit{\boldsymbol{ \boldsymbol{\varLambda}}} / \kappa)]^{(1-\zeta)} \times \prod\limits_{m=1}^{M}\left[G\left(\kappa ; e_{m}, f_{m}\right)\right]^{\rho_{m}} \times}\\ p(\zeta \mid \mu) p(\mu) p(\mathit{\boldsymbol{\rho}} \mid \mathit{\boldsymbol{\xi}}) p(\mathit{\boldsymbol{\xi}}) \mathrm{d} \zeta \mathrm{d} \kappa \mathrm{d} \mu \mathrm{d} \mathit{\boldsymbol{\xi}}, \zeta \in\{0, 1\} \end{array} $ | (8) |
其中ζ、ρ的PDFs为
| $ \left\{\begin{array}{l} p(\zeta \mid \mu)=\operatorname{Bern}(\zeta ; \mu)=\mu^{\zeta}(1-\mu)^{1-\zeta} \\ p(\mathit{\boldsymbol{\rho}} \mid \mathit{\boldsymbol{\xi}})=\operatorname{Cat}(\mathit{\boldsymbol{\rho}} ; \xi, M) \end{array}\right. $ |
式中: Bern(·)为伯努利分布, Cat(·)为Categorical分布。式(8)中的混合概率向量ξ和切换概率μ已经在式(3) 和式(5)中被假设为狄利克雷和贝塔分布。
由于先验噪声统计不准确与野值干扰使得尺度矩阵Λ不太准确, 假设其服从[23]:
| $ p(\mathit{\boldsymbol{ \boldsymbol{\varLambda}}})=\operatorname{IW}(\mathit{\boldsymbol{ \boldsymbol{\varLambda}}} ; \mathit{\boldsymbol{V}}, \mathit{\boldsymbol{\sigma}}) $ | (9) |
式中IW(·;V, σ)为逆尺度矩阵V和自由度参数σ的逆威沙特分布。
利用式(3)~式(9)可将GHTS分布表示为
| $ \left\{ \begin{array}{l} \int p(\mathit{\boldsymbol{y}} \mid \zeta, \kappa, \mathit{\boldsymbol{ \boldsymbol{\varLambda}}})=[N(\mathit{\boldsymbol{y}} ; \mathit{\boldsymbol{\lambda}}, \mathit{\boldsymbol{ \boldsymbol{\varLambda}}})]^{\zeta}[N(\mathit{\boldsymbol{y}} ; \mathit{\boldsymbol{\lambda}}, \mathit{\boldsymbol{ \boldsymbol{\varLambda}}} / \kappa)]^{(1-\zeta)}\\ p(\mathit{\boldsymbol{\kappa}} \mid \mathit{\boldsymbol{\rho}})=\prod\limits_{m=1}^{M}\left[G\left(\mathit{\boldsymbol{\kappa}} ; e_{m}, f_{m}\right)\right]^{\rho_{m}}\\ p(\zeta \mid \mu)=\operatorname{Bern}(\zeta ; \mu)\\ p(\mathit{\boldsymbol{\rho}} \mid \mathit{\boldsymbol{\xi}})=\operatorname{Cat}(\eta ; \mathit{\boldsymbol{\xi}}, M)\\ p(\mathit{\boldsymbol{\xi}})=\operatorname{Dir}(\mathit{\boldsymbol{\xi}} ; \mathit{\boldsymbol{w}}, M)\\ p(\mu)=B(\mu ; v, 1-v)\\ p(\mathit{\boldsymbol{ \boldsymbol{\varLambda}}})=\operatorname{IW}(\mathit{\boldsymbol{ \boldsymbol{\varLambda}}} ; \mathit{\boldsymbol{V}}, \sigma) \end{array} \right. $ | (10) |
接下来, 基于式(10)和VB方法将推导出一种新的GHTSRKF。
注1 针对实际工程领域中可能因传感器故障、环境干扰等造成的野值引发的重尾噪声情形,文献[17-18]中的高斯伽马分布/学生t被广泛用于建模该类型噪声。进一步,为了更精确地建模该类型噪声,文献[10]中设计了一种高斯-混合伽马分布,即式(2)中的GMG分布来应对复杂的重尾噪声。它是基于多个不同参数的伽马分布的一组粗糙先验得到的精确先验来描述噪声尺度参数。因此本文利用GMG分布来描述重尾噪声。但考虑到GMG分布在无异常值情况下的性能受限,本文开发了如式(7)所示的GHTS分布,这可以扩展GMG的应用范围,提高其适用性与估计性能。
注2 在文献[23]中,设计了一种基于两个高斯分布混合的鲁棒滤波器,本文的GHTS分布与其相似。但相比于文献[23]中的M2G分布,在系统噪声与量测噪声是未知重尾分布时,GHTS分布中的混合伽马分布的设计能够预先提供一组粗略先验信息, 并通过混合概率向量的自适应学习提取出一个准确的先验, 这使得提出的滤波器能够对不同的重尾噪声进行更加准确描述, 鲁棒性也更强。而M2G分布中只能有一个协方差较大的高斯分布以应对重尾噪声,因此在应对重尾分布噪声时其性能略差于GHTS分布。这将在仿真中进一步验证。
注3 在式(2)中, 由于混合伽马分布中元素的数量直接决定了GHTS分布的性能,其选择应慎重。当M较小时,由于缺乏足够的先验噪声信息,滤波器的估计精度较差。随着M的增加,滤波器的估计精度会提高,而学习的参数越多,算法的计算量就越大。但是,如果M过大,对估计结果的影响将非常有限,甚至一个或多个混合元会陷入过拟合,这将大大降低估计的精度。而且,较大的M也会导致较大的计算复杂度,不利于算法的实时性估计。综上所述,在实际应用中,为了平衡估计精度和计算效率,混合数量M的设置应灵活适度。
3 基于GHTS分布的鲁棒卡尔曼滤波器(GHTSRKF) 3.1 分层高斯状态空间模型对于式(1)所示的状态空间模型, 当过程与量测噪声是非平稳重尾噪声时, 本文将一步预测与量测似然PDFs建模为GHTS分布:
| $ \left\{\begin{align*} p\left(\mathit{\boldsymbol{x}}_{t} \mid \mathit{\boldsymbol{z}}_{1: t-1}\right)= & \sum\limits_{y_{t}=0}^{1} \iiiint \int_{0}^{+\infty}\left[N\left(\mathit{\boldsymbol{x}}_{t} ; \hat{\mathit{\boldsymbol{x}}}_{t \mid t-1}, \mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}\right)\right]^{y_{t}} \times\left[N\left(\mathit{\boldsymbol{x}}_{t} ; \hat{\mathit{\boldsymbol{x}}}_{t \mid t-1}, \mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t} / \sigma_{t}\right)\right]^{1-y_{t}} \prod\limits_{i=1}^{I}\left[G\left(\sigma_{t} ; a_{0, i}, b_{0, i}\right)\right]^{\mathit{\boldsymbol{\varepsilon}}_{t, i}} \times \\ & \operatorname{Bern}\left(y_{t} ; \delta_{t}\right) B\left(\delta_{t} ; k_{0}, 1-k_{0}\right) \operatorname{Cat}\left(\mathit{\boldsymbol{\varepsilon}}_{t} ; \mathit{\boldsymbol{\theta}}_{t}, I\right) \times \operatorname{Dir}\left(\mathit{\boldsymbol{\theta}}_{t} ; \mathit{\boldsymbol{e}}_{t \mid t-1}, I\right) \operatorname{IW}\left(\mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t} ; s_{t \mid t-1}, \mathit{\boldsymbol{S}}_{t \mid t-1}\right) \mathrm{d} y_{t} \mathrm{~d} \sigma_{t} \mathrm{~d} \delta_{t} \mathrm{~d} \mathit{\boldsymbol{\theta}}_{t} \mathrm{~d} \mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t} \\ p\left(\mathit{\boldsymbol{z}}_{t} \mid \mathit{\boldsymbol{x}}_{t}\right)= & \sum\limits_{t_{k}=0}^{1} \iiiint \int_{0}^{+\infty}\left[N\left(\mathit{\boldsymbol{z}}_{t} ; \mathit{\boldsymbol{H}}_{t} \mathit{\boldsymbol{x}}_{t}, \mathit{\boldsymbol{R}}_{t}\right)\right]^{r_{t}} \times\left[N\left(\mathit{\boldsymbol{z}}_{t} ; \mathit{\boldsymbol{H}}_{t} \mathit{\boldsymbol{x}}_{t}, \mathit{\boldsymbol{R}}_{t} / \pi_{t}\right)\right]^{1-r_{t}} \prod\limits_{l=1}^{L}\left[G\left(\pi_{t} ; c_{0, l}, d_{0, l}\right)\right]^{\mathit{\boldsymbol{\eta}}_{t, l}} \times \\ & \operatorname{Bern}\left(r_{t} ; \lambda_{t}\right) B\left(\lambda_{t} ; h_{0}, 1-h_{0}\right) \times \operatorname{Cat}\left(\mathit{\boldsymbol{\eta}}_{t} ; \mathit{\boldsymbol{\tau}}_{t}, L\right) \times \operatorname{Dir}\left(\mathit{\boldsymbol{\tau}}_{t} ; \mathit{\boldsymbol{g}}_{t \mid t-1}, L\right) \operatorname{IW}\left(\mathit{\boldsymbol{R}}_{t} ; u_{t \mid t-1}, \mathit{\boldsymbol{U}}_{t \mid t-1}\right) \mathrm{d} r_{t} \mathrm{~d} \pi_{t} \mathrm{~d} \lambda_{t} \mathrm{~d} \mathit{\boldsymbol{\tau}}_{t} \mathrm{~d} \mathit{\boldsymbol{R}}_{t} \end{align*}\right. $ | (11) |
式中:yt、rt为伯努利变量, σt、πt为尺度参数, εt、ηt为分类分布向量, δt、λt为切换概率, θt、τt为混合概率向量, Σt、Rt为尺度矩阵, I、L为伽马分布的数量。
均值向量
| $ \hat{\mathit{\boldsymbol{x}}}_{t \mid t-1}=\mathit{\boldsymbol{F}}_{t} \hat{\mathit{\boldsymbol{x}}}_{t-1 \mid t-1} $ | (12) |
先验集中参数向量et|t-1、gt|t-1,先验自由度参数st|t-1、ut|t-1,先验逆尺度矩阵St|t-1、Ut|t-1分别为
| $ \left\{\begin{array}{l} \mathit{\boldsymbol{e}}_{t \mid t-1}=\rho \hat{\mathit{\boldsymbol{e}}}_{t-1 \mid t-1} \\ \mathit{\boldsymbol{g}}_{t \mid t-1}=\rho \hat{\mathit{\boldsymbol{g}}}_{t-1 \mid t-1} \\ s_{t \mid t-1}=m_{t} \\ \mathit{\boldsymbol{S}}_{t \mid t-1}=m \tilde{\mathit{\boldsymbol{P}}}_{t \mid t-1} \\ u_{t \mid t-1}=\rho \hat{u}_{t-1 \mid t-1} \\ \mathit{\boldsymbol{U}}_{t \mid t-1}=\rho \hat{U}_{t-1 \mid t-1} \end{array}\right. $ | (13) |
式中:ρ∈(0, 1]为遗忘因子, mt为调节参数, 这两个参数的作用将在后面分析,
| $ \tilde{\mathit{\boldsymbol{P}}}_{t \mid t-1}=\mathit{\boldsymbol{F}}_{t} \mathit{\boldsymbol{P}}_{t-1 \mid t-1} \mathit{\boldsymbol{F}}_{t}^{\mathrm{T}}+\tilde{\mathit{\boldsymbol{Q}}}_{t-1} $ | (14) |
式中
根据式(10)、(11), 一步预测与量测似然PDFs的分层高斯形式可以分别表示为
| $ \left\{ \begin{array}{l} p\left(\mathit{\boldsymbol{x}}_{t} \mid \mathit{\boldsymbol{z}}_{1: t-1}, y_{t}, \mathit{\boldsymbol{\varepsilon}}_{t}\right)=\left[N\left(\mathit{\boldsymbol{x}}_{t} ; \hat{\mathit{\boldsymbol{x}}}_{t \mid t-1}, \mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}\right)\right]^{y_{t}}\left[N\left(\mathit{\boldsymbol{x}}_{t} ; \hat{\mathit{\boldsymbol{x}}}_{t \mid t-1}, \mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t} / \sigma_{t}\right)\right]^{1-y_{t}} \times \\ \quad\quad\quad \prod\limits_{i=1}^{I}\left[G\left(\sigma_{t} ; a_{0, i}, b_{0, i}\right)\right]^{\mathit{\boldsymbol{\varepsilon}}_{t, i}} \\ p\left(\mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}\right)=\operatorname{IW}\left(\mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t} ; s_{t \mid t-1}, \mathit{\boldsymbol{S}}_{t \mid t-1}\right) \\ p\left(y_{t} \mid \delta_{t}\right)=\operatorname{Bern}\left(y_{t} ; \delta_{t}\right), p\left(\delta_{t}\right)=B\left(\delta_{t} ; k_{0}, 1-k_{0}\right) \\ p\left(\mathit{\boldsymbol{\varepsilon}}_{t} \mid \mathit{\boldsymbol{\theta}}_{t}\right)=\operatorname{Cat}\left(\mathit{\boldsymbol{\varepsilon}}_{t} ; \mathit{\boldsymbol{\theta}}_{t}, I\right), p\left(\mathit{\boldsymbol{\theta}}_{t}\right)=\operatorname{Dir}\left(\mathit{\boldsymbol{\theta}}_{t} ; \hat{\mathit{\boldsymbol{e}}}_{t \mid t-1}, I\right) \\ p\left(\mathit{\boldsymbol{z}}_{t} \mid \mathit{\boldsymbol{x}}_{t}, r_{t}, \mathit{\boldsymbol{\eta}}_{t}\right)=\left[N\left(\mathit{\boldsymbol{z}}_{t} ; \mathit{\boldsymbol{H}}_{t} \mathit{\boldsymbol{x}}_{t}, \mathit{\boldsymbol{R}}_{t}\right)\right]^{r_{t}}\left[N\left(\mathit{\boldsymbol{z}}_{t} ; \mathit{\boldsymbol{H}}_{t} \mathit{\boldsymbol{x}}_{t}, \mathit{\boldsymbol{R}}_{t} / \pi_{t}\right)\right]^{1-r_{t}} \times\\ \quad\quad\quad \prod\limits_{l=1}^{L}\left[G\left(\pi_{t} ; c_{0, l}, d_{0, l}\right)\right]^{\mathit{\boldsymbol{\eta}}_{t, l}}\\ p\left(\mathit{\boldsymbol{R}}_{t}\right)=\operatorname{IW}\left(\mathit{\boldsymbol{R}}_{t} ; u_{t \mid t-1}, U_{t \mid t-1}\right)\\ p\left(r_{t} \mid \lambda_{t}\right)=\operatorname{Bern}\left(r_{t} ; \lambda_{t}\right), p\left(\lambda_{t}\right)=B\left(\lambda_{t} ; h_{0}, 1-h_{0}\right)\\ p\left(\mathit{\boldsymbol{\eta}}_{t} \mid \mathit{\boldsymbol{\tau}}_{t}\right)=\operatorname{Cat}\left(\mathit{\boldsymbol{\eta}}_{t} ; \mathit{\boldsymbol{\tau}}_{t}, L\right), p\left(\mathit{\boldsymbol{\tau}}_{t}\right)=\operatorname{Dir}\left(\mathit{\boldsymbol{\tau}}_{t} ; \hat{\mathit{\boldsymbol{g}}}_{t \mid t-1}, L\right) \end{array} \right. $ | (15) |
式(12)~式(15)构成了一个分层高斯状态空间模型, 其模型如图 1所示。然后, 进一步利用VB方法推导出GHTSRKF。
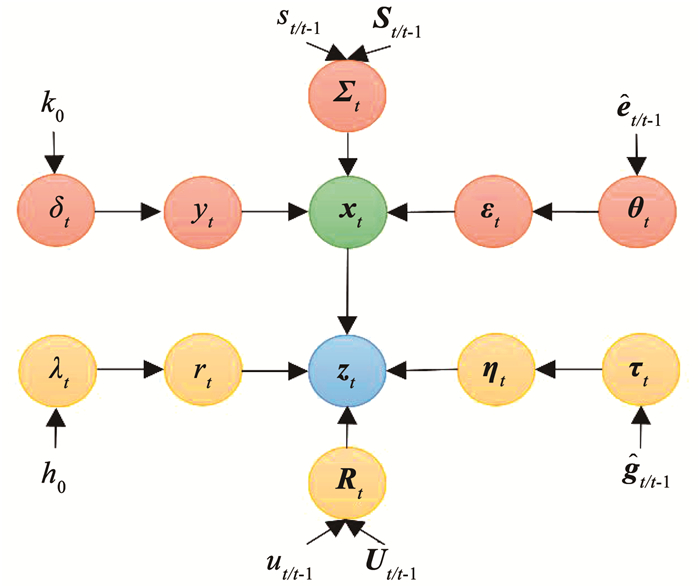
|
图 1 基于GHTS分布的分层高斯状态空间模型 Fig. 1 Graphical model for hierarchical Gaussian state-space model based on GHTS distribution |
正如式(15)所示, 由于模型参数与状态向量之间存在相互耦合关系, 通过解析的方式获取状态向量的后验估计是很麻烦的。因此为了估计变量集合Θ,本文利用VB方法通过最小化Kullback-Leibler发散代价函数实现对真实联合后验PDFp(Θ|z1:k)的最优近似[25]。使用的近似后验PDFq(Δ)满足:
| $ \log q(\Delta)=E_{\mathit{\boldsymbol{ \boldsymbol{\varTheta}}}^{-(\Delta)}}\left[\log p\left(\mathit{\boldsymbol{ \boldsymbol{\varTheta}}}, z_{1: t}\right)\right]+c_{\Delta} $ | (16) |
式中:E[·]为期望计算, 变量集合Θ={xt, σt, πt, yt, rt, δt, λt, εt, ηt, θt, τt, Σt, Rt}, Θ(-Δ)为Θ的一个子集,其满足{Δ}∪Θ(-Δ)=Θ, cΔ为独立于Δ的常数。
考虑到式(15)中变分参数之间的耦合, 本文采用固定点迭代法对式(16)进行迭代求解以计算q(Δ)。在(j+1)次更新时, 利用q(j)(Θ(-Δ))将q(Δ)更新为q(j+1)(Δ)。根据贝叶斯理论, 真实联合PDF分解为
| $ \begin{gather*} p\left(\mathit{\boldsymbol{ \boldsymbol{\varTheta}}}, \mathit{\boldsymbol{z}}_{1: t}\right)=p\left(\mathit{\boldsymbol{z}}_{1: t-1}\right) p\left(\mathit{\boldsymbol{x}}_{t} \mid \mathit{\boldsymbol{z}}_{1: t-1}, y_{t}, \mathit{\boldsymbol{\varepsilon}}_{t}\right) p\left(\mathit{\boldsymbol{z}}_{t} \mid \mathit{\boldsymbol{x}}_{t}, r_{t}, \mathit{\boldsymbol{\eta}}_{t}\right) \times \\ p\left(y_{t} \mid \delta_{t}\right) p\left(r_{t} \mid \lambda_{t}\right) p\left(\delta_{t}\right) p\left(\lambda_{t}\right) p\left(\mathit{\boldsymbol{\varepsilon}}_{t} \mid \mathit{\boldsymbol{\theta}}_{t}\right) p\left(\mathit{\boldsymbol{\eta}}_{t} \mid \mathit{\boldsymbol{\tau}}_{t}\right) p\left(\mathit{\boldsymbol{\theta}}_{t}\right) \times \\ p\left(\mathit{\boldsymbol{\tau}}_{t}\right) p\left(\mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}\right) p\left(\mathit{\boldsymbol{R}}_{t}\right) \end{gather*} $ | (17) |
对式(17)进行对数运算可得
| $ \log p\left(\mathit{\boldsymbol{ \boldsymbol{\varTheta}}}, \mathit{\boldsymbol{z}}_{1: t}\right)=-0.5 y_{t}\left[\log \left|\mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}\right|-\left(\mathit{\boldsymbol{x}}_{t}-\hat{\mathit{\boldsymbol{x}}}_{t \mid t-1}\right)^{\mathrm{T}} \mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}^{-1}\left(\mathit{\boldsymbol{x}}_{t}-\hat{\mathit{\boldsymbol{x}}}_{t \mid t-1}\right)\right]+\\ 0.5\left(1-y_{t}\right)\left[n_{x} \log \sigma_{t}-\log \left|\mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}\right|-\sigma_{t}\left(\mathit{\boldsymbol{x}}_{t}-\hat{\mathit{\boldsymbol{x}}}_{t \mid t-1}\right)^{\mathrm{T}} \mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}^{-1}\left(\mathit{\boldsymbol{x}}_{t}-\hat{\mathit{\boldsymbol{x}}}_{t \mid t-1}\right)\right]+\\ \sum\limits_{i=1}^{I}\left[\left(a_{0, i}-1\right) \log \sigma_{t}-b_{0, i} \sigma_{t}\right] \mathit{\boldsymbol{\varepsilon}}_{t, i}+\sum\limits_{i=1}^{I}\left(\mathit{\boldsymbol{\varepsilon}}_{t, i}+\hat{\mathit{\boldsymbol{e}}}_{t \mid t-1, i}-1\right) \log \mathit{\boldsymbol{\theta}}_{t, i}+\\ y_{t} \log \delta_{t}+\left(1-y_{t}\right) \log \left(1-\delta_{t}\right)+\left(k_{0}-1\right) \log \delta_{t}-k_{0} \log \left(1-\delta_{t}\right)-\\ 0.5\left(s_{t \mid t-1}+1\right) \log \left|\mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}\right|-0.5 \operatorname{tr}\left(\mathit{\boldsymbol{S}}_{t \mid t-1} \mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}^{-1}\right)-0.5 r_{t}\left[\log \left|\mathit{\boldsymbol{R}}_{t}\right|-\right.\\ \left.\left(\mathit{\boldsymbol{z}}_{t}-\mathit{\boldsymbol{H}}_{t} \mathit{\boldsymbol{x}}_{t}\right)^{\mathrm{T}} \mathit{\boldsymbol{R}}_{t}^{-1}\left(\mathit{\boldsymbol{z}}_{t}-\mathit{\boldsymbol{H}}_{t} \mathit{\boldsymbol{x}}_{t}\right)\right]+0.5\left(1-r_{t}\right)\left[n_{z} \log \pi_{t}-\log \left|\mathit{\boldsymbol{R}}_{t}\right|-\right.\\ \left.\pi_{t}\left(\mathit{\boldsymbol{z}}_{t}-\mathit{\boldsymbol{H}}_{t} \mathit{\boldsymbol{x}}_{t}\right)^{\mathrm{T}} \mathit{\boldsymbol{R}}_{t}^{-1}\left(\mathit{\boldsymbol{z}}_{t}-\mathit{\boldsymbol{H}}_{t} \mathit{\boldsymbol{x}}_{t}\right)\right]+\sum\limits_{l=1}^{L}\left[\left(c_{0, l}-1\right) \log \pi_{t}-\right.\\ \left.d_{0, l} \mathit{\boldsymbol{\pi}}_{t}\right] \mathit{\boldsymbol{\eta}}_{t, l}+\sum\limits_{l=1}^{L}\left(\mathit{\boldsymbol{\eta}}_{t, l}+\hat{\mathit{\boldsymbol{g}}}_{t|t-1, l}-1\right) \log \mathit{\boldsymbol{\tau}}_{t, l}+r_{t} \log \lambda_{t}+\left(1-r_{t}\right) \log \left(1-\lambda_{t}\right)+\\ \left(h_{0}-1\right) \log \lambda_{t}-h_{0} \log \left(1-\lambda_{t}\right)-0.5\left(u_{t \mid t-1}+1\right) \log \left|\mathit{\boldsymbol{R}}_{t}\right|-0.5 \operatorname{tr}\left(\mathit{\boldsymbol{U}}_{t \mid t-1} \mathit{\boldsymbol{R}}_{t}^{-1}\right) $ | (18) |
本文利用固定点迭代法对系统状态与模型参数的近似后验q(Δ)进行迭代求解[25]。
命题1 该命题是在噪声尺度参数、切换概率等未知参数与噪声协方差矩阵{σt, πt, yt, rt, δt, λt, εt, ηt, θt, τt, Σt, Rt}保持不变的情况下实现状态xt的后验估计,即在Δ=xt的同时将式(17)代入式(16),然后近似后验PDF q(j+1)(xt)可以被迭代更新为以下高斯分布:
| $ q^{(j+1)}\left(\mathit{\boldsymbol{x}}_{t}\right)=N\left(\mathit{\boldsymbol{x}}_{t} ; \hat{\mathit{\boldsymbol{x}}}_{t \mid t}^{(j+1)}, \mathit{\boldsymbol{P}}_{t \mid t}^{(j+1)}\right) $ | (19) |
式中, 后验状态向量
| $ \left\{\begin{array}{l} \mathit{\boldsymbol{K}}_{t}^{(j+1)}=\hat{\mathit{\boldsymbol{P}}}_{t \mid t-1}^{(j+1)} \mathit{\boldsymbol{H}}_{t}^{\mathrm{T}}\left(\mathit{\boldsymbol{H}}_{t} \mathit{\boldsymbol{P}}_{t \mid t-1} \mathit{\boldsymbol{H}}_{t}^{\mathrm{T}}+\hat{\mathit{\boldsymbol{R}}}_{t}^{(j+1)}\right)^{-1} \\ \hat{\mathit{\boldsymbol{x}}}_{t \mid t}^{(j+1)}=\hat{\mathit{\boldsymbol{x}}}_{t \mid t-1}+\mathit{\boldsymbol{K}}_{t}^{(j+1)}\left(\mathit{\boldsymbol{z}}_{t}-\mathit{\boldsymbol{H}}_{t} \hat{\mathit{\boldsymbol{x}}}_{t \mid t-1}\right) \\ \mathit{\boldsymbol{P}}_{t \mid t}^{(j+1)}=\left(\mathit{\boldsymbol{I}}_{n}-\mathit{\boldsymbol{K}}_{t}^{(j+1)} \mathit{\boldsymbol{H}}_{k}\right) \hat{\mathit{\boldsymbol{P}}}_{t \mid t-1}^{(j+1)} \end{array}\right. $ | (20) |
式中, 估计的状态预测误差协方差
| $ \left\{\begin{array}{l} \hat{\mathit{\boldsymbol{P}}}_{t \mid t-1}^{(j+1)}=\frac{\left\{\mathit{\boldsymbol{E}}^{(j)}\left[\mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}^{-1}\right]\right\}^{-1}}{\left(1-E^{(j)}\left[y_{t}\right]\right) E^{(j)}\left[\mathit{\boldsymbol{\sigma}}_{t}\right]+E^{(j)}\left[y_{t}\right]} \\ \hat{\mathit{\boldsymbol{R}}}_{t}^{(j+1)}=\frac{\left\{E^{(j)}\left[\mathit{\boldsymbol{R}}_{t}^{-1}\right]\right\}^{-1}}{\left(1-E^{(j)}\left[r_{t}\right]\right) E^{(j)}\left[\mathit{\boldsymbol{\pi}}_{t}\right]+E^{(j)}\left[r_{t}\right]} \end{array}\right. $ | (21) |
推导1 将式(16)代入式(18)有
| $\begin{array}{*{20}{c}} \log q^{(j+1)}\left(\mathit{\boldsymbol{x}}_{t}\right)=-0.5\left\{E^{(j)}\left[y_{t}\right]+\right.\\ \left.\left(1-E^{(j)}\left[y_{t}\right]\right) E^{(j)}\left[\sigma_{t}\right]\right\} \times\\ \left(\mathit{\boldsymbol{x}}_{t}-\hat{\mathit{\boldsymbol{x}}}_{t \mid t-1}\right)^{\mathrm{T}} \mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}^{-1}\left(\mathit{\boldsymbol{x}}_{t}-\hat{\mathit{\boldsymbol{x}}}_{t \mid t-1}\right)-\\ 0.5\left\{E^{(j)}\left[r_{t}\right]+\left(1-E^{(j)}\left[r_{t}\right]\right) \times\right.\\ \left.E^{(j)}\left[\mathit{\boldsymbol{\pi}}_{t}\right]\right\}\left(\mathit{\boldsymbol{z}}_{t}-\mathit{\boldsymbol{H}}_{t} \mathit{\boldsymbol{x}}_{t}\right)^{\mathrm{T}} \mathit{\boldsymbol{R}}_{t}^{-1}\left(\mathit{\boldsymbol{z}}_{t}-\mathit{\boldsymbol{H}}_{t} \mathit{\boldsymbol{x}}_{t}\right)+c_{\mathit{\boldsymbol{x}}_{t}} \end{array} $ | (22) |
由贝叶斯理论可以得到命题1中式(19)~式(21)。
命题2 该命题是在状态向量、伯努利参数等未知参数与噪声协方差矩阵{xt, yt, rt, δt, λt, εt, ηt, θt, τt, Σt, Rt}保持不变的情况下实现噪声尺度参数σt和πt的变分近似估计,分别使Δ=σt和Δ=πt并将式(17)代入式(16),然后近似后验PDFs q(j+1)(σt)和q(j+1)(πt)可以被迭代更新为以下伽马分布:
| $ \left\{\begin{array}{l} q^{(j+1)}\left(\sigma_{t}\right)=G\left(\sigma_{t} ; \hat{\alpha}_{1, t}^{(j+1)}, \hat{\alpha}_{2, t}^{(j+1)}\right) \\ q^{(j+1)}\left(\pi_{t}\right)=G\left(\pi_{t} ; \hat{\beta}_{1, t}^{(j+1)}, \hat{\beta}_{2, t}^{(j+1)}\right) \end{array}\right. $ | (23) |
式中估计的形状参数
| $ \left\{\begin{array}{l} \hat{\alpha}_{1, t}^{(j+1)}=0.5 n_{x}\left(1-E^{(j)}\left[y_{t}\right]\right)+E^{(j)}\left[\mathit{\boldsymbol{\varepsilon}}_{t}\right] a_{0}^{\mathrm{T}} \\ \hat{\alpha}_{2, t}^{(j+1)}=0.5\left(1-E^{(j)}\left[y_{t}\right]\right) \operatorname{tr}\left(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}}_{t}^{(j+1)} E^{(j)}\left[\mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}^{-1}\right]\right)+E^{(j)}\left[\mathit{\boldsymbol{\varepsilon}}_{t}\right] b_{0}^{\mathrm{T}} \\ \hat{\beta}_{1, t}^{(j+1)}=0.5 n_{z}\left(1-E^{(j)}\left[r_{t}\right]\right)+E^{(j)}\left[\mathit{\boldsymbol{\eta}}_{t}\right] c_{0}^{\mathrm{T}} \\ \hat{\beta}_{2, t}^{(j+1)}=0.5\left(1-E^{(j)}\left[r_{t}\right]\right) \operatorname{tr}\left(\mathit{\boldsymbol{ \boldsymbol{\varXi}}}_{t}^{(j+1)} E^{(j)}\left[\mathit{\boldsymbol{R}}_{t}^{-1}\right]\right)+E^{(j)}\left[\mathit{\boldsymbol{\eta}}_{t}\right] d_{0}^{\mathrm{T}} \end{array}\right. $ | (24) |
辅助矩阵Ψt(j+1)、Ξt(j+1)分别为
| $ \left\{\begin{array}{l} \mathit{\boldsymbol{ \boldsymbol{\varPsi}}}_{t}^{(j+1)}=E^{(j+1)}\left[\left(\mathit{\boldsymbol{x}}_{t}-\mathit{\boldsymbol{F}}_{t} \mathit{\boldsymbol{x}}_{t-1}\right)\left(\mathit{\boldsymbol{x}}_{t}-\mathit{\boldsymbol{F}}_{t} \mathit{\boldsymbol{x}}_{t-1}\right)^{\mathrm{T}}\right] \\ \mathit{\boldsymbol{ \boldsymbol{\varXi}}}_{t}^{(j+1)}=E^{(j+1)}\left[\left(\mathit{\boldsymbol{z}}_{t}-\mathit{\boldsymbol{H}}_{t} \mathit{\boldsymbol{x}}_{t}\right)\left(\mathit{\boldsymbol{z}}_{t}-\mathit{\boldsymbol{H}}_{t} \mathit{\boldsymbol{x}}_{t}\right)^{\mathrm{T}}\right] \end{array}\right. $ | (25) |
推导2 将式(16)代入式(18)有
| $ \left\{\begin{align*} \log q^{(j+1)}\left(\sigma_{t}\right)= & \left(0.5 n_{x}\left(1-E^{(j)}\left[y_{t}\right]\right)+E^{(j)}\left[\mathit{\boldsymbol{\varepsilon}}_{t}\right] a_{0}^{\mathrm{T}}-1\right) \times \\ & \log \sigma_{t}-0.5\left(1-E^{(j)}\left[y_{t}\right]\right) \operatorname{tr}\left(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}}_{t}^{(j+1)} E^{(j)}\left[\mathit{\boldsymbol{{\boldsymbol{\varSigma} }}}_{t}^{-1}\right]\right)+ \\ & E^{(j)}\left[\mathit{\boldsymbol{\varepsilon}}_{t}\right] b_{0}^{\mathrm{T}} \sigma_{t}+c_{\sigma_{t}}=\left(\hat{\alpha}_{1, t}^{(j+1)}-1\right) \log \sigma_{t}-\hat{\alpha}_{2, t}^{(j+1)} \sigma_{t}+c_{\sigma_{t}} \\ \log q^{(j+1)}\left(\pi_{t}\right)= & \left(0.5 n_{z}\left(1-E^{(j)}\left[r_{t}\right]\right)+E^{(j)}\left[\mathit{\boldsymbol{\eta}}_{t}\right] c_{0}^{\mathrm{T}}-1\right) \times \\ & \log \pi_{t}-0.5\left(1-E^{(j)}\left[r_{t}\right]\right) \operatorname{tr}\left(\mathit{\boldsymbol{ \boldsymbol{\varXi}}}_{t}^{(j+1)} E^{(j)}\left[\mathit{\boldsymbol{R}}_{t}^{-1}\right]\right)+ \\ & E^{(j)}\left[\mathit{\boldsymbol{\eta}}_{t}\right] d_{0}^{\mathrm{T}} \pi_{t}+c_{\pi_{t}}=\left(\hat{\beta}_{1, t}^{(j+1)}-1\right) \log \pi_{t}-\hat{\beta}_{2, t}^{(j+1)} \pi_{t}+c_{\pi_{t}} \end{align*}\right. $ | (26) |
对式(26)两边进行对数操作,并由伽马分布的定义可以得到命题2中的式(23)~式(25)。
命题3 该命题是在状态向量、噪声尺度参数等未知参数与噪声协方差矩阵{xt, σt, πt, δt, λt, εt, ηt, θt, τt, Σt, Rt}保持不变的情况下实现伯努利参数yt和rt的变分近似估计,分别使Δ=yt和Δ=rt并将式(17)代入式(16),近似后验PDFs q(j+1)(yt)和q(j+1)(rt)可以迭代更新为
| $ \left\{\begin{array}{l} q^{(j+1)}\left(y_{t}\right)=\left(\hat{\varphi}_{t}\right)^{y_{t}}\left(1-\hat{\varphi}_{t}\right)^{1-y_{t}}\\ q^{(j+1)}\left(r_{t}\right)=\left(\hat{\zeta}_{t}\right)^{r_{t}}\left(1-\hat{\zeta}_{t}\right)^{1-r_{t}} \end{array}\right. $ | (27) |
其中
| $ \left\{\begin{array}{l} \hat{\varphi}_{t}=\frac{\varphi_{1, t}^{(j+1)}}{\mathit{\boldsymbol{\varphi}}_{1, t}^{(j+1)}+\varphi_{2, t}^{(j+1)}} \\ \hat{\zeta}_{t}=\frac{\mathit{\boldsymbol{ \boldsymbol{\vartheta}}}_{1, t}^{(j+1)}}{\mathit{\boldsymbol{ \boldsymbol{\vartheta}}}_{1, t}^{(j+1)}+\mathit{\boldsymbol{ \boldsymbol{\vartheta}}}_{2, t}^{(j+1)}} \end{array}\right. $ |
中间参数分别由以下方程计算:
| $ \left\{\begin{align*} \varphi_{1, t}^{(j+1)}= & \exp \left\{E^{(j)}\left[\log \delta_{t}\right]-0.5 \operatorname{tr}\left(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}}_{t}^{(j+1)} E^{(j)}\left[\mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}^{-1}\right]\right)\right\} \\ \varphi_{2, t}^{(j+1)}= & \exp \left\{E^{(j)}\left[\log \left(1-\delta_{t}\right)\right]-0.5 n_{x} E^{(j+1)}\left[\log \sigma_{t}\right]-\right. \\ & 0.5 E^{(j+1)}\left[\sigma_{t}\right] \operatorname{tr}\left(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}}_{t}^{(j+1)} E^{(j)}\left[\mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}^{-1}\right]\right) \\ \mathit{\boldsymbol{ \boldsymbol{\vartheta}}}_{1, t}^{(j+1)}= & \exp \left\{E^{(j)}\left[\log \lambda_{t}\right]-0.5 \operatorname{tr}\left(\mathit{\boldsymbol{ \boldsymbol{\varXi}}}_{t}^{(j+1)} E^{(j)}\left[\mathit{\boldsymbol{R}}_{t}^{-1}\right]\right)\right\} \\ \mathit{\boldsymbol{ \boldsymbol{\vartheta}}}_{2, t}^{(j+1)}= & \exp \left\{E^{(j)}\left[\log \left(1-\lambda_{t}\right)\right]-0.5 n_{z} E^{(j+1)}\left[\log \pi_{t}\right]-\right. \\ & 0.5 E^{(j+1)}\left[\mathit{\boldsymbol{\pi}}_{t}\right] \operatorname{tr}\left(\mathit{\boldsymbol{ \boldsymbol{\varXi}}}_{t}^{(j+1)} E^{(j)}\left[\mathit{\boldsymbol{R}}_{t}^{-1}\right]\right) \end{align*}\right. $ | (28) |
推导3 将式(16)代入式(18)有
| $ \left\{ \begin{array}{l} \log q^{(j+1)}\left(y_{t}\right)=y_{t}\left\{E^{(j)}\left[\log \delta_{t}\right]-0.5 \operatorname{tr}\left(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}}_{t}^{(j+1)} E^{(j)}\left[\mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}^{-1}\right]\right)\right\}+\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left(1-y_{t}\right)\left\{E^{(j)}\left[\log \left(1-\delta_{t}\right)\right]-0.5 n_{x} E^{(j+1)}\left[\log \sigma_{t}\right]-\right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left.0.5 E^{(j+1)}\left[\sigma_{t}\right] \operatorname{tr}\left(\mathit{\boldsymbol{ \boldsymbol{\varPsi}}}_{t}^{(j+1)} E^{(j)}\left[\mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}^{-1}\right]\right)\right\}+c_{y_{t}}=\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; y_{t} \log \varphi_{1, t}^{(j+1)}+\left(1-y_{t}\right) \log \varphi_{2, t}^{(j+1)}+c_{y_{t}}\\ \log q^{(j+1)}\left(r_{t}\right)=r_{t}\left\{E^{(j)}\left[\log \lambda_{t}\right]-0.5 \operatorname{tr}\left(\mathit{\boldsymbol{ \boldsymbol{\varXi}}}_{t}^{(j+1)} E^{(j)}\left[\mathit{\boldsymbol{R}}_{t}^{-1}\right]\right)\right\}+\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left(1-r_{t}\right)\left\{E^{(j)}\left[\log \left(1-\lambda_{t}\right)\right]-0.5 n_{z} E^{(j+1)}\left[\log \pi_{t}\right]-\right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left.0.5 E^{(j+1)}\left[\pi_{t}\right] \operatorname{tr}\left(\mathit{\boldsymbol{ \boldsymbol{\varXi}}}_{t}^{(j+1)} E^{(j)}\left[\mathit{\boldsymbol{R}}_{t}^{-1}\right]\right)\right\}+c_{r_{t}}=\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; r_{t} \log \vartheta_{1, t}^{(j+1)}+\left(1-r_{t}\right) \log \vartheta_{2, t}^{(j+1)}+c_{r_{t}} \end{array} \right. $ | (29) |
对式(29)两边进行对数操作,并根据伯努利分布的定义可以得到命题3中的式(27)、(28)。
命题4 该命题是在状态向量、噪声尺度参数等未知参数与噪声协方差矩阵{xt, σt, πt, yt, rt, εt, ηt, θt, τt, Σt, Rt}保持不变的情况下实现切换概率δt和λt的变分近似估计,分别使Δ=δt和Δ=λt并将式(17)代入式(16),然后近似后验PDFs q(j+1)(δt)和q(j+1)(λt)可以被迭代更新为以下贝塔分布:
| $ \left\{\begin{array}{l} q^{(j+1)}\left(\delta_{t}\right)=B\left(\delta_{t} ; \hat{k}_{1, t}^{(j+1)}, \hat{k}_{2, t}^{(j+1)}\right)\\ q^{(j+1)}\left(\lambda_{t}\right)=B\left(\lambda_{t} ; \hat{h}_{1, t}^{(j+1)}, \hat{h}_{2, t}^{(j+1)}\right) \end{array}\right. $ | (30) |
其中形状参数
| $ \left\{\begin{array}{l} \hat{k}_{1, t}^{(j+1)}=k_{0}+E^{(j+1)}\left[y_{t}\right] \\ \hat{k}_{2, t}^{(j+1)}=2-E^{(j+1)}\left[y_{t}\right]-k_{0} \\ \hat{h}_{1, t}^{(j+1)}=h_{0}+E^{(j+1)}\left[r_{t}\right] \\ \hat{h}_{2, t}^{(j+1)}=2-E^{(j+1)}\left[r_{t}\right]-h_{0} \end{array}\right. $ |
推导4 将式(16)代入式(18)有
| $ \begin{array}{*{20}{c}} \log q^{(j+1)}\left(\delta_{t}\right)=\left(k_{0}+E^{(j+1)}\left[y_{t}\right]-1\right) \log \delta_{t}+\\ \left(1-E^{(j+1)}\left[y_{t}\right]-k_{0}\right) \log \left(1-\delta_{t}\right)+c_{\delta_{t}}=\\ \left(\hat{k}_{1, t}^{(j+1)}-1\right) \log \delta_{t}+\left(\hat{k}_{2, t}^{(j+1)}-1\right) \log \left(1-\delta_{t}\right)+\\ c_{\delta_{t}} \log q^{(j+1)}\left(\lambda_{t}\right)=\left(h_{0}+E^{(j+1)}\left[r_{t}\right]-1\right) \log \lambda_{t}+\\ \left(1-E^{(j+1)}\left[r_{t}\right]-h_{0}\right) \log \left(1-\lambda_{t}\right)+c_{\lambda_{t}}=\\ \left(\hat{h}_{1, t}^{(j+1)}-1\right) \log \lambda_{t}+\left(\hat{h}_{2, t}^{(j+1)}-1\right) \log \left(1-\lambda_{t}\right)+c_{\lambda_{t}} \end{array} $ | (31) |
对式(31)的两边进行对数操作,并根据贝塔分布的定义可以得到命题4中的式(30)。
命题5 该命题是在状态向量、噪声尺度参数等未知参数与噪声协方差矩阵{xt, σt, πt, yt, rt, δt, λt, θt, τt, Σt, Rt}保持不变的情况下实现分类分布参数εt和ηt的变分近似估计,分别使Δ=εt和Δ=ηt并将式(17)代入式(16),然后近似后验PDFs q(j+1)(εt)与q(j+1)(ηt) 可以被迭代更新为以下分类分布:
| $ \left\{\begin{array}{l} q^{(j+1)}\left(\mathit{\boldsymbol{\varepsilon}}_{t}\right)=\operatorname{Cat}\left(\mathit{\boldsymbol{\varepsilon}}_{t} ; \hat{\mathit{\boldsymbol{\omega}}}_{t}^{(j+1)}, I\right) \\ q^{(j+1)}\left(\mathit{\boldsymbol{\eta}}_{t}\right)=\operatorname{Cat}\left(\mathit{\boldsymbol{\eta}}_{t} ; \hat{\mathit{\boldsymbol{\varpi}}}_{t}^{(j+1)}, L\right) \end{array}\right. $ | (32) |
其中混合概率向量
| $ \left\{\begin{array}{l} \hat{\mathit{\boldsymbol{\omega}}}_{t}^{(j+1)}=\mathit{\boldsymbol{\omega}}_{t}^{(j+1)} / \sum\limits_{i=1}^{I} \mathit{\boldsymbol{\omega}}_{t, i}^{(j+1)} \\ \hat{\mathit{\boldsymbol{\varpi}}}_{t}^{(j+1)}=\mathit{\boldsymbol{\varpi}}_{t}^{(j+1)} / \sum\limits_{l=1}^{L} \mathit{\boldsymbol{\varpi}}_{t, l}^{(j+1)} \end{array}\right. $ |
辅助参数向量ωt, i(j+1)与ϖt, l(j+1)分别为
| $ \left\{\begin{align*} \mathit{\boldsymbol{\omega}}_{t, i}^{(j+1)}= & \exp \left\{\left(a_{0, i}-1\right) E^{(j+1)}\left[\log \sigma_{t}\right]-\right. \\ & \left.b_{0, i} E^{(j+1)}\left[\mathit{\boldsymbol{\sigma}}_{t}\right]+E^{(j)}\left[\log \mathit{\boldsymbol{\theta}}_{t, i}\right]\right\} \\ \mathit{\boldsymbol{\varpi}}_{t, l}^{(j+1)}= & \exp \left\{\left(c_{0, l}-1\right) E^{(j+1)}\left[\log \pi_{t}\right]-\right. \\ & \left.d_{0, l} E^{(j+1)}\left[\mathit{\boldsymbol{\pi}}_{t}\right]+E^{(j)}\left[\log \mathit{\boldsymbol{\tau}}_{t, l}\right]\right\} \end{align*}\right. $ | (33) |
推导5 将式(16)代入式(18)有
| $ \left\{ \begin{array}{l} \log q^{(j+1)}\left(\mathit{\boldsymbol{\varepsilon}}_{t}\right)= \sum\limits_{i=1}^{I} \mathit{\boldsymbol{\varepsilon}}_{t, i} \exp \left\{\left(a_{0, i}-1\right) \times E^{(j+1)}\left[\log \sigma_{t}\right]-\right. \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left.b_{0, i} E^{(j+1)}\left[\sigma_{t}\right]+E^{(j)}\left[\log \mathit{\boldsymbol{\theta}}_{t, i}\right]\right\}+ \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; c_{\mathit{\boldsymbol{\varepsilon}}_{t}}=\sum\limits_{i=1}^{I} \mathit{\boldsymbol{\varepsilon}}_{t, i} \mathit{\boldsymbol{\omega}}_{t, i}^{(j+1)}+c_{\mathit{\boldsymbol{\varepsilon}}_{t}}\\ \log q^{(j+1)}\left(\mathit{\boldsymbol{\eta}}_{t}\right)=\sum\limits_{l=1}^{L} \mathit{\boldsymbol{\eta}}_{t, l} \exp \left\{\left(c_{0, l}-1\right) \times E^{(j+1)}\left[\log \pi_{t}\right]-\right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \left.d_{0, l} E^{(j+1)}\left[\pi_{t}\right]+E^{(j)}\left[\log \mathit{\boldsymbol{\tau}}_{t, l}\right]\right\}+\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; c_{\mathit{\boldsymbol{\eta}}_{t}}=\sum\limits_{l=1}^{L} \mathit{\boldsymbol{\eta}}_{t, l} \mathit{\boldsymbol{\varpi}}_{t, l}^{(j+1)}+c_{\mathit{\boldsymbol{\eta}}_{t}} \end{array} \right. $ | (34) |
对式(34)的两边进行对数操作,并根据分类分布的定义可以得到命题5中的式(32)、(33)。
命题6 该命题是在状态向量、噪声尺度参数等未知参数与噪声协方差矩阵Θ={xt, σt, πt, yt, rt, δt, λt, εt, ηt, Σt, Rt}保持不变的情况下实现混合概率向量参数θt和τt的变分近似估计,分别使Δ=θt和Δ=τt并将式(17)代入式(16),然后近似后验PDFs q(j+1)(θt)和q(j+1)(τt)可以迭代更新为狄利克雷分布:
| $ \left\{\begin{array}{l} q^{(j+1)}\left(\mathit{\boldsymbol{\theta}}_{t}\right)=\operatorname{Dir}\left(\mathit{\boldsymbol{\theta}}_{t} ; \hat{\mathit{\boldsymbol{e}}}_{t \mid t}^{(j+1)}, I\right) \\ q^{(j+1)}\left(\mathit{\boldsymbol{\tau}}_{t}\right)=\operatorname{Dir}\left(\mathit{\boldsymbol{\tau}}_{t} ; \hat{\mathit{\boldsymbol{g}}}_{t \mid t}^{(j+1)}, L\right) \end{array}\right. $ | (35) |
其中后验集中参数向量
| $ \left\{\begin{array}{l} \hat{\mathit{\boldsymbol{e}}}_{t \mid t}^{(j+1)}=\mathit{\boldsymbol{e}}_{t \mid t-1}+E^{(j+1)}\left[\mathit{\boldsymbol{\varepsilon}}_{t}\right] \\ \hat{\mathit{\boldsymbol{g}}}_{t \mid t}^{(j+1)}=\mathit{\boldsymbol{g}}_{t \mid t-1}+E^{(j+1)}\left[\mathit{\boldsymbol{\eta}}_{t}\right] \end{array}\right. $ |
推导6 将式(16)代入式(18)有
| $ \left\{ \begin{array}{l} \log q^{(j+1)}\left(\mathit{\boldsymbol{\theta}}_{t}\right)=\sum\limits_{i=1}^{I}\left(\hat{\mathit{\boldsymbol{e}}}_{t \mid t-1, i}+E^{(j+1)}\left[\mathit{\boldsymbol{\varepsilon}}_{t, i}\right]-1\right) \log \mathit{\boldsymbol{\theta}}_{t, i}+c_{\mathit{\boldsymbol{\theta}}_{t}}\\ \log q^{(j+1)}\left(\mathit{\boldsymbol{\tau}}_{t}\right)=\sum\limits_{l=1}^{L}\left(\hat{\mathit{\boldsymbol{g}}}_{t \mid t-1, l}+E^{(j+1)}\left[\mathit{\boldsymbol{\eta}}_{t, l}\right]-1\right) \log \mathit{\boldsymbol{\tau}}_{t, l}+c_{\mathit{\boldsymbol{\tau}}_{t}} \end{array} \right. $ | (36) |
对式(36)两边进行对数操作,并根据狄利克雷分布的定义可以得到命题6中的式(35)。
命题7 该命题是在状态向量、噪声尺度参数等未知参数{xt, σt, πt, yt, rt, δt, λt, εt, ηt, θt, τt} 保持不变的情况下实现噪声协方差矩阵Σt和Rt的变分近似估计,分别使Δ=Σt和Δ=Rt并将式(17)代入式(16),然后近似后验PDFs q(j+1)(Σt)和q(j+1)(Rt)可以迭代更新为逆威沙特分布:
| $ \left\{\begin{array}{l} q^{(j+1)}\left(\mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}\right)=\operatorname{IW}\left(\mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t} ; \hat{s}_{t \mid t}^{(j+1)}, \hat{\mathit{\boldsymbol{S}}}_{t \mid t}^{(j+1)}\right) \\ q^{(j+1)}\left(\mathit{\boldsymbol{R}}_{t}\right)=\operatorname{IW}\left(\mathit{\boldsymbol{R}}_{t} ; \hat{u}_{t \mid t}^{(j+1)}, \hat{\mathit{\boldsymbol{U}}}_{t \mid t}^{(j+1)}\right) \end{array}\right. $ | (37) |
其中:后验自由度参数
| $ \left\{\begin{aligned} \hat{s}_{t \mid t}^{(j+1)}= & s_{t \mid t-1}+1 \\ \hat{u}_{t \mid t}^{(j+1)}= & u_{t \mid t-1}+1 \\ \hat{\mathit{\boldsymbol{S}}}_{t \mid t}^{(j+1)}= & \mathit{\boldsymbol{S}}_{t \mid t-1}+\left\{\left(1-E^{(j+1)}\left[y_{t}\right]\right) E^{(j+1)}\left[\sigma_{t}\right]+\right. \\ & \left.E^{(j+1)}\left[y_{t}\right]\right\} \mathit{\boldsymbol{ \boldsymbol{\varPsi}}}_{t}^{(j+1)} \\ \hat{\mathit{\boldsymbol{U}}}_{t \mid t}^{(j+1)}= & \mathit{\boldsymbol{U}}_{t \mid t-1}+\left\{\left(1-E^{(j+1)}\left[r_{t}\right]\right) E^{(j+1)}\left[\pi_{t}\right]+\right. \\ & \left.\mathit{\boldsymbol{E}}^{(j+1)}\left[r_{t}\right]\right\} \mathit{\boldsymbol{ \boldsymbol{\varXi}}}_{t}^{(j+1)} \end{aligned}\right. $ |
推导7 将式(16)代入式(18)有
| $ \left\{\begin{align*} \log q^{(j+1)}\left(\mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}\right)= & -0.5\left(s_{t \mid t-1}+n_{x}+2\right) \log \left|\mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}\right|- \\ & 0.5 \operatorname{tr}\left(\left(\mathit{\boldsymbol{S}}_{t \mid t-1}+\left\{\left(1-E^{(j+1)}\left[y_{t}\right]\right) E^{(j+1)}\left[\sigma_{t}\right]+\right.\right.\right. \\ & \left.\left.\left.E^{(j+1)}\left[y_{t}\right]\right\} \mathit{\boldsymbol{ \boldsymbol{\varPsi}}}_{t}^{(j+1)}\right) \mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}^{-1}\right)+c_{\mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}}=-0.5\left(\hat{s}_{t \mid t}^{(j+1)}+\right. \\ & \left.n_{x}+1\right) \log \left|\mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}\right|-0.5 \operatorname{tr}\left(\hat{\mathit{\boldsymbol{S}}}_{t \mid t}^{(j+1)} \mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}^{-1}\right)+c_{\mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}} \\ \log q^{(j+1)}\left(\mathit{\boldsymbol{R}}_{t}\right)= & -0.5\left(u_{t \mid t-1}+n_{z}+2\right) \log \left|\mathit{\boldsymbol{R}}_{t}\right|- \\ & 0.5 \operatorname{tr}\left(\left(\mathit{\boldsymbol{U}}_{t \mid t-1}+\left\{\left(1-E^{(j+1)}\left[r_{t}\right]\right) E^{(j+1)}\left[\pi_{t}\right]+\right.\right.\right. \\ & \left.\left.\left.E^{(j+1)}\left[r_{t}\right]\right\} \mathit{\boldsymbol{ \boldsymbol{\varXi}}}_{t}^{(j+1)}\right) \mathit{\boldsymbol{R}}_{t}^{-1}\right)+c_{\mathit{\boldsymbol{R}}_{t}}=-0.5\left(\hat{u}_{t \mid t}^{(j+1)}+\right. \\ & \left.n_{z}+1\right) \log \left|\mathit{\boldsymbol{R}}_{t}\right|-0.5 \operatorname{tr}\left(\hat{\mathit{\boldsymbol{U}}}_{t \mid t}^{(j+1)} \mathit{\boldsymbol{R}}_{t}^{-1}\right)+c_{\mathit{\boldsymbol{R}}_{t}} \end{align*}\right. $ | (38) |
对式(38)的两边进行对数操作,并根据逆威沙特分布的定义可以得到命题7中式(37)。
在式(19)~式(37)所示的近似后验PDF的迭代更新中, 涉及的模型参数期望可计算为
| $ \left\{\begin{array}{l} E^{(j+1)}\left[\sigma_{t}\right]=\hat{\alpha}_{1, t}^{(j+1)} / \hat{\alpha}_{2, t}^{(j+1)}\\ E^{(j+1)}\left[\mathit{\boldsymbol{\pi}}_{t}\right]=\hat{\beta}_{1, t}^{(j+1)} / \hat{\beta}_{2, t}^{(j+1)} \\ E^{(j+1)}\left[\log \sigma_{t}\right]=\psi\left(\hat{\alpha}_{1, t}^{(j+1)}\right)-\log \left(\hat{\alpha}_{2, t}^{(j+1)}\right) \\ E^{(i+1)}\left[y_{t}\right]=\hat{\varphi}_{t} \\ E^{(i+1)}\left[r_{t}\right]=\hat{\gamma}_{t} \\ E^{(j+1)}\left[\log \mathit{\boldsymbol{\pi}}_{t}\right]=\psi\left(\hat{\beta}_{1, t}^{(j+1)}\right)-\log \left(\hat{\beta}_{2, t}^{(j+1)}\right) \\ E^{(j+1)}\left[\log \delta_{t}\right]=\psi\left(\hat{r}_{1, t}^{(j+1)}\right)-\psi(2) \\ E^{(j+1)}\left[\log \lambda_{t}\right]=\psi\left(\hat{h}_{1, t}^{(j+1)}\right)-\psi(2) \\ E^{(j+1)}\left[\log \mathit{\boldsymbol{\theta}}_{t, i}\right]=\psi\left(\hat{n}_{t, i}^{(j+1)}\right)-\psi\left(\sum\limits_{i=1}^{I} \hat{n}_{t, i}^{(j+1)}\right) \\ E^{(j+1)}\left[\log \mathit{\boldsymbol{\tau}}_{t, l}\right]=\psi\left(\hat{\mathit{\boldsymbol{g}}}_{t, l}^{(j+1)}\right)-\psi\left(\sum\limits_{l=1}^{L} \hat{\mathit{\boldsymbol{g}}}_{t, l}^{(j+1)}\right) \\ E^{(j+1)}\left[\mathit{\boldsymbol{ \boldsymbol{\varSigma}}}_{t}^{-1}\right]=\hat{s}_{t \mid t}^{(j+1)}\left(\mathit{\boldsymbol{S}}_{t \mid t}^{(j+1)}\right)-1 \\ E^{(j+1)}\left[\mathit{\boldsymbol{R}}_{t}^{-1}\right]=\hat{u}_{t \mid t}^{(j+1)}\left(\hat{\mathit{\boldsymbol{U}}}_{t \mid t}^{(j+1)}\right)^{-1} \\ E^{(j+1)}\left[\mathit{\boldsymbol{\varepsilon}}_{t}\right]=\hat{\mathit{\boldsymbol{\omega}}}_{t}^{(j+1)} \\ E^{(j+1)}\left[\mathit{\boldsymbol{\eta}}_{t}\right]=\hat{\mathit{\boldsymbol{\sigma}}}_{t}^{(j+1)} \end{array}\right. $ | (39) |
根据式(12)~式(14)中的时间更新与式(19)- 式(39)所示的量测更新给出了如下的GHTSRKF的一次迭代的执行过程,其中算法输入为上一时刻的后验估计结果。
注4 在提出的GHTSRKF中,其一步状态预测PDF和量测似然PDF分别建模为式(11)中GHTS分布,通过标准高斯分布与重尾分布之间的自适应切换以适应非平稳重尾状态与量测噪声。然后对于两种PDFs中的状态向量、噪声协方差矩阵、噪声尺度参数、伯努利参数等未知参数根据VB理论实现式(16)中变分近似并利用式(19)~式(39)中固定点迭代方法进行近似估计。最后得到GHTSRKF算法如下,其通过时间更新与迭代量测更新过程实现了非高斯噪声条件下的状态估计。
算法: 提出的GHTSRKF
输入:
时间更新:
通过式(12)~式(14)计算先验参数。
量测更新:
利用式(39)计算初始参数期望。
for j=0 : J-1
由式(21)计算
根据式(19)更新q(j+1)(xt);
由式(26)~式(39)更新q(j+1)(Σt)、
q(j+1)(Rt);
end
输出:
首先分析了GHTSRKF与现有的滤波器之间的关联。当混合伽马分布的数量I=L=1时, 混合伽马分布会退化为单一伽马分布, 这时GHTSRKF几乎等同于M2GRKF[23]和噪声尺度矩阵未知情况下的GSTMRKF[20]的滤波框架。与此同时, 当先验形状参数k0=h0=1时, GHTSRKF会进一步退化为变分自适应KF[25];当k0=h0=0时, GHTS-RKF基本与现有的ORSTKF[18]的形式一样。从上述分析可知, 变分自适应KF, ORSTKF, GST-MRKF和M2GRKF是本文提出的滤波器的几种特殊形式, 这在一定程度上说明了所提出的滤波器性能更全面。
在文献[22]的GSTM分布和文献[23]的M2G分布中, 单一伽马分布被用来建模尺度参数以近似重尾噪声的特性, 但是动态野值特点是很复杂的, 单一伽马分布所包含先验信息在这样的情况下过于简单而不能准确的近似重尾特性。而在GHTS分布中, 本文构造的混合伽马分布可以提供一个粗略先验信息集合并通过自适应学习混合概率向量从该集合中提取一个准确先验用于建模尺度参数。因此理论上, 如此的GHTS分布可以更准确描述非平稳重尾噪声, 基于该分布的GHTSRKF的鲁棒性能将会更优越。
在一般的应用中, 考虑到大概率情况下噪声是不准确的高斯噪声, 因此有0 < 1-δt≪δt < 1和0 < 1-λt≪λt < 1且E[δt]=k0和E[λt]=h0,所以在本文中设先验形状参数k0=h0=0.85.对于尺度参数0 < σt≤1和0 < πt≤1,根据式(11)可以得到p(σt)=
对式(13)中的调节参数mt与遗忘因子ρ进行分析,联立式(13)、(21)、(37)可得
| $ \left\{\begin{array}{l} \hat{\mathit{\boldsymbol{P}}}_{t \mid t-1}^{(j+1)}=\frac{m_{t} \tilde{\mathit{\boldsymbol{P}}}_{t \mid t-1} / \mathit{\boldsymbol{ \boldsymbol{\varPhi}}}_{t}^{(j+1)}+\mathit{\boldsymbol{ \boldsymbol{\varPsi}}}_{t}^{(j+1)}}{m_{t}+1}\\ \hat{\mathit{\boldsymbol{R}}}_{t}^{(j+1)}=\frac{\rho \hat{\mathit{\boldsymbol{U}}}_{t-1 \mid t-1} \hat{\mathit{\boldsymbol{R}}}_{t-1} / \mathit{\boldsymbol{ \boldsymbol{\varOmega}}}_{t}^{(j+1)}+\mathit{\boldsymbol{ \boldsymbol{\varXi}}}_{k}^{(j+1)}}{\hat{\rho u_{t-1 \mid t-1}+1}} \end{array}\right. $ | (40) |
式中:
辅助参数Φt(j+1)、Ωt(j+1)分别为
| $ \left\{\begin{array}{l} {\mathit{\Phi}}_{t}^{(j+1)}=\left(1-E^{(j+1)}\left[y_{t}\right]\right) E^{(j+1)}\left[\sigma_{t}\right]+E^{(j+1)}\left[y_{t}\right]\\ {\mathit{\Omega}}_{t}^{(j+1)}=\left(1-E^{(j+1)}\left[r_{t}\right]\right) E^{(j+1)}\left[\pi_{t}\right]+E^{(j+1)}\left[r_{t}\right] \end{array}\right. $ | (41) |
由式(40)可知, 调节参数mt可视为一个用来平衡Ψt(j+1)与自适应校正项
对于固定点迭代数量J的选取需要平衡算法的估计精度与计算复杂度, 该参数对滤波器性能的影响在仿真中会被讨论。
对于一个动态系统来说,其系统不确定性主要有两个方面:噪声不确定性(系统与量测噪声)与系统参数不确定性(未知输入、失配的系统与量测矩阵)。本文提出的鲁棒滤波器主要是为降低系统与量测噪声的不确定所带来的负面影响,没有考虑系统参数的不确定所带的影响。受限于时间与现有的知识储备,在本文中没有针对系统参数的不确定问题进行研究,在下一步的研究中,结合本文方法对系统参数的不确定问题进行深入研究。
4 仿真与分析 4.1 设置本文使用文献[23]中的仿真实例来验证所提出的GHTSRKF的性能。该模型采用类似式(1)的状态空间模型来描述, 状态为xt=
考虑以下场景验证所提滤波器的性能。
场景1 时变高斯噪声为:
| $ \mathit{\boldsymbol{w}}_{t-1} \sim N\left(0, \mathit{\boldsymbol{Q}}_{t-1}\right), \mathit{\boldsymbol{v}}_{t} \sim N\left(0, \mathit{\boldsymbol{R}}_{t}\right) $ | (42) |
场景2 非平稳重尾噪声为
| $ \begin{cases}\mathit{\boldsymbol{w}}_{t-1} \sim q_{1} N\left(0, \mathit{\boldsymbol{Q}}_{t-1}\right)+\left(1-q_{1}\right) N\left(0, 100 \mathit{\boldsymbol{Q}}_{t-1}\right), t \in[201, 400] \\ \mathit{\boldsymbol{w}}_{t-1} \sim q_{2} N\left(0, \mathit{\boldsymbol{Q}}_{t-1}\right)+\left(1-q_{2}\right) N\left(0, 100 \mathit{\boldsymbol{Q}}_{t-1}\right), t \in[601, 800] \\ \mathit{\boldsymbol{w}}_{t-1} \sim N\left(0, \mathit{\boldsymbol{Q}}_{t-1}\right), & \text { 其他时间 } \\ \mathit{\boldsymbol{\nu}}_{t} \sim q_{1} N\left(0, \mathit{\boldsymbol{R}}_{t}\right)+\left(1-q_{1}\right) N\left(0, 200 \mathit{\boldsymbol{R}}_{t}\right), & t \in[201, 400] \\ \mathit{\boldsymbol{\nu}}_{t} \sim q_{2} N\left(0, \mathit{\boldsymbol{R}}_{t}\right)+\left(1-q_{2}\right) N\left(0, 200 \mathit{\boldsymbol{R}}_{t}\right), & t \in[601, 800] \\ \mathit{\boldsymbol{\nu}}_{t} \sim N\left(0, \mathit{\boldsymbol{R}}_{t}\right), & \text { 其他时间 }\end{cases} $ | (43) |
式中:q1=0.85、q2=0.95分别表示概率,真实的时变噪声协方差矩阵Qt-1、Rt分别为
| $ \left\{\begin{aligned} & \boldsymbol{Q}_{t-1}= {[6.5+0.5 \cos (\pi t / T)] \times } \\ &\;\;\;\;\;\;\;\; {\left[\begin{array}{cc} \left(\Delta t^3 / 3\right) \boldsymbol{I}_2 & \left(\Delta t^2 / 2\right) \boldsymbol{I}_2 \\ \left(\Delta t^2 / 2\right) \boldsymbol{I}_2 & \Delta t \boldsymbol{I}_2 \end{array}\right] } \\ & \boldsymbol{R}_t= {[0.1+0.05 \cos (\pi t / T)] \times } \\ & \;\;\;\;\;\;\;\;100\left[\begin{array}{cc} \Delta t & \left(\Delta t^2 / 2\right) \\ \left(\Delta t^2 / 2\right) & \Delta t \end{array}\right] \end{aligned}\right. $ | (44) |
仿真参数为
为了从统计意义上评估不同滤波器的估计性能, 本文将均方根误差(root mean square error, RMSE)和平均均方根误差(average root mean square error, ARMSE)作为性能指标, 分别定义为
| $ \left\{\begin{array}{l} R_{\mathrm{MSE}_{\mathrm{pos}}}=\\ \sqrt{\frac{\sum\limits_{m=1}^{m}\left(\left(x_{t}^{m}-\hat{x}_{t}^{m}\right)^{2}+\left(y_{t}^{m}-\hat{y}_{t}^{m}\right)^{2}\right)}{m}} \\ A_{\mathrm{RMSE}_{\mathrm{pos}}}= \\ \sqrt{\frac{\sum\limits_{t=1}^{T} \sum\limits_{m=1}^{m}\left(\left(x_{t}^{m}-\hat{x}_{t}^{m}\right)^{2}+\left(y_{t}^{m}-\hat{y}_{t}^{m}\right)^{2}\right)}{m T}} \end{array}\right. $ | (45) |
式中: RMSEpos、ARMSEpos分别为位置的均方根误差和平均均方根误差(其中RMSE、ARMSE分别为均方根误差和平均均方根误差, pos为位置), (xtm, ytm)、
首先, 在不准确时变高斯噪声的情况下, 分别来自现有的滤波器与提出的滤波器的位置与速度的估计结果在图 2中呈现。
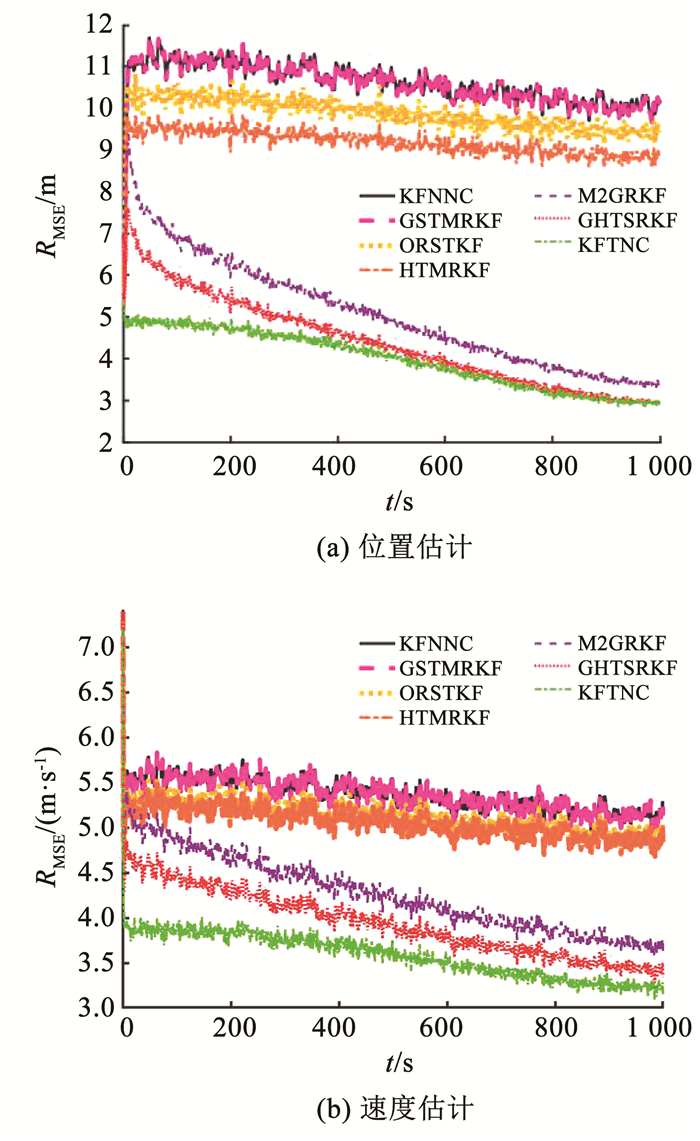
|
图 2 场景1中位置与速度的RMSEs Fig. 2 RMSEs of position and velocity in Case 1 |
由图 2可知, 所提出的GHTSRKF的精度优于其他RKFs, 它的RMSEs最接近噪声信息准确的KFTNC的RMSEs。由于不准确的时变噪声的影响, KFNNC的精度严重退化。GSTMRKF的估计结果与KFNNC类似, 虽然此滤波器设计时考虑了高斯噪声的情况, 但预选的噪声尺度矩阵不准确严重影响了GSTMRKF的性能。其次, 由于ORSTKF和HTMRKF只考虑了存在野值的情况, 因此它们估计效果不理想。M2GRKF受益于两个高斯分布混合框架, 在噪声是未知时变高斯的情况下依然取得了较好的估计结果。然而由于单一的粗糙先验信息, 现有的M2GRKF与提出的GHTSRKF相比并不占优势。因此可以得到结论, 当系统与量测噪声是未知时变高斯噪声时, 相比于现有的滤波器, GHTSRKF具有更好的估计性能。
然后, 非平稳重尾噪声情况下, 分别来自现有的滤波器与提出的滤波器的位置与速度RMSEs被展示在图 3中。
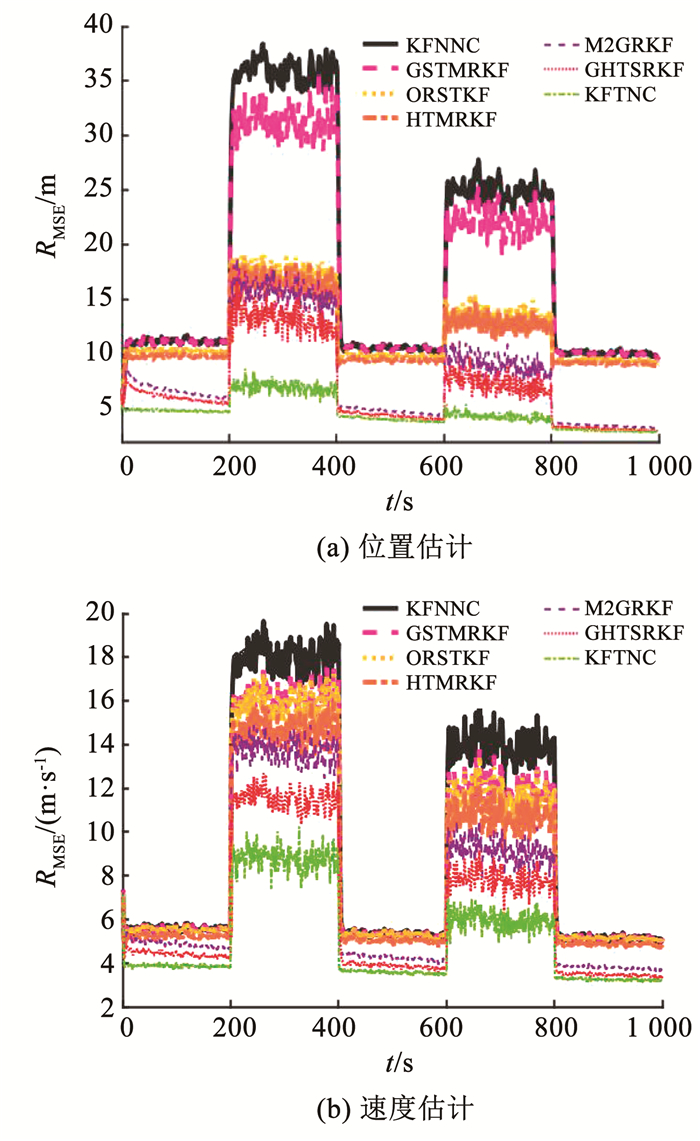
|
图 3 场景2中位置与速度的RMSEs Fig. 3 RMSEs of position and velocity in Case 2 |
由图 3可知, 提出的GHTSRKF在所有时段的位置与速度估计结果都明显优于现有的RKFs, 这证明了GHTS分布更适合对非平稳重尾噪声建模。在1~200、401~600、801~1 000 s 3个时间段内, 各滤波器的表现与图 1结果基本一致。在201~400、601~800 s时间段内不同的重尾噪声情况下, KFNNC的性能出现不同程度的恶化, 这也说明了发展与研究RKF的必要性。GSTMRKF表现出了一定的鲁棒性, 但由于承受着噪声尺度矩阵需要事先已知的限制, 鲁棒性能依然较差。ORSTKF和HTMRKF由于所构建的分层高斯状态模型而对这种情况有着不错的鲁棒性能, 并且HTMRKF受益于其采用的重尾混合分布在性能上以微弱优势赢得了ORSTKF。由于针对非平稳重尾噪声的设计, 现有的M2GRKF呈现出了更好的估计性能, 然而M2GRKF在估计精度方面比提出的GHTSRKF表现略差。本文猜测应该是混合伽马分布能够预先提供丰富的粗略先验信息, 并通过混合概率向量的自适应学习提取出一个准确的先验, 这使得提出的滤波器能够对不同的重尾噪声进行更加准确描述, 因此鲁棒性也更强。综合所有时间段的估计结果, 可以发现提出的滤波器受益于高斯和新设计的重尾分布的切换和多重伽马分布混合对尺度参数的建模, 其性能在非平稳重尾噪声情况下明显优于现有的RKFs。
除此之外,本文比较了所提出的滤波器与其他滤波器算法的每步迭代计算时间,结果见表 1。从表 1可以看出,在上述滤波器中,标准CKF的计算速度最快。由于状态和未知参数的VB迭代极大地增加了算法的计算负荷,各鲁棒滤波器算法每一步迭代时间明显增加。与RSTKF、GSTMRKF、HTMRKF和M2GRKF相比,本文滤波器的运行时间略有增加。这说明本文滤波器在略微增加计算负担的基础上实现了更高的状态估计精度。
| 表 1 各算法单次运行的时间 Tab. 1 Run times in a signal step from each algorithms |
本文分析了最大迭代数目J, 调节参数mt和伽马分布的混合数量I和L对所提出的滤波器性能的影响, 在场景2下该滤波器的位置与速度的ARMSEs分别展示在图 4~6中。
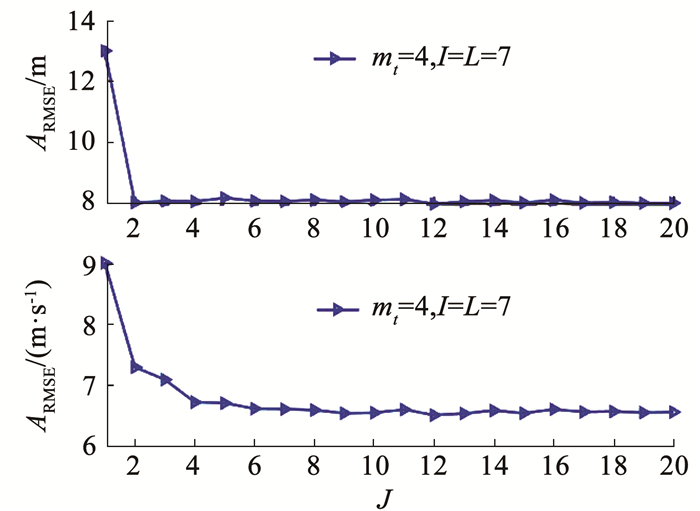
|
图 4 J=1, 2, …, 20时GHTSRKF的ARMSEs Fig. 4 ARMSEs of GHTSRKF with J=1, 2, …, 20 |
|
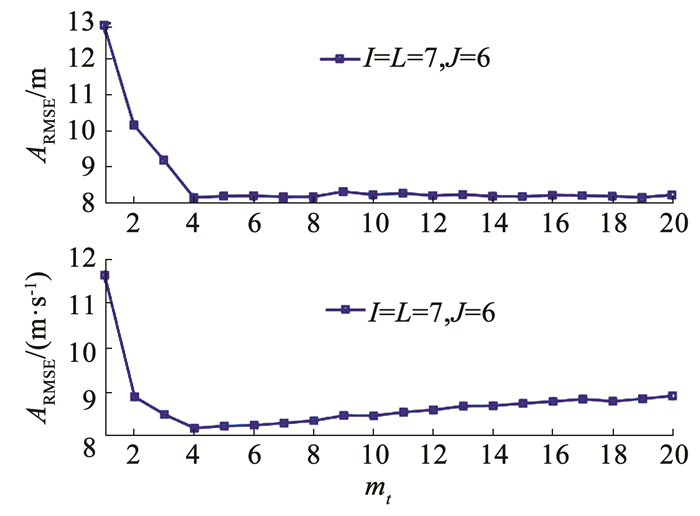
图 5 mt=1, 2, …, 20时GHTSRKF的ARMSEs Fig. 5 ARMSEs of GHTSRKF with mt=1, 2, …, 20 |
|
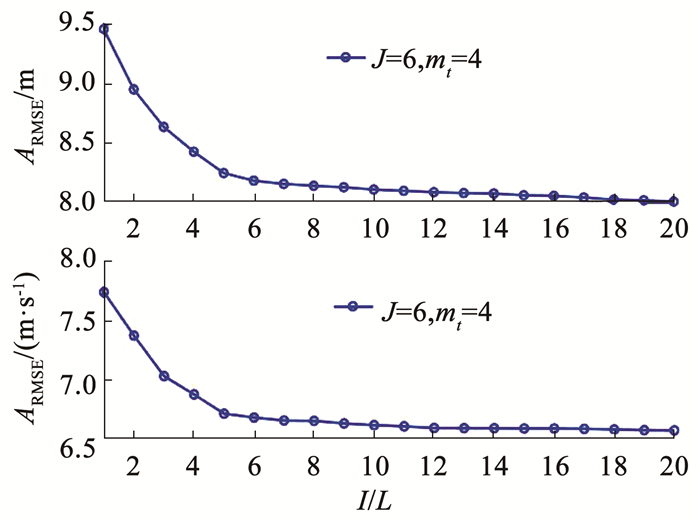
图 6 I=L=1, 2, …, 20时GHTSRKF的ARMSEs Fig. 6 ARMSEs of GHTSRKF with I=L=1, 2, …, 20 |
图 4显示了当迭代次数J≥6时, 滤波器收敛, 这说明本文的GHTSRKF具有满意的收敛速度。而且也说明了在满足估计精度的同时可以设定合理的固定点迭代数目以提升滤波器的计算效率。图 5呈现了当固定点迭代次数J∈[1, 20], 调节参数mt∈[1, 20]时提出的滤波器的位置与速度估计。结果显示, 当mt>4时, 调节参数对ARMSEs的影响是有限的,mt=4时估计精度相对最优, 从图 5中可得该参数选择的区间范围推荐为mt∈[3, 8]。
图 6呈现了当固定点迭代次数J在区间[1, 20]时, 伽马分布数量I=L∈[1, 20]时提出的滤波器的位置与速度估计,结果显示所提出的GHTSRKF的精度应随着伽马分布混合的数量I=L的增加而单调上升。然而, 当I=L≥7时, 滤波器的估计精度的提升很小, 因此通过仔细选择I和L的大小可以平衡算法的估计精度和计算复杂度。
4.4 初始状态影响本文分析了不同的初始状态对所提出的滤波器性能的影响, 设置5组不同的初始状态值,分别为
| $ \left\{\begin{array}{l} s_{1}: \hat{\mathit{\boldsymbol{x}}}_{0}=[0, 0, 0, 0]^{\mathrm{T}} \\ s_{2}: \hat{\mathit{\boldsymbol{x}}}_{0}=[100, 100, 10, 10]^{\mathrm{T}} \\ s_{3}: \hat{\mathit{\boldsymbol{x}}}_{0}=[500, 500, 100, 100]^{\mathrm{T}} \\ s_{4}: \hat{\mathit{\boldsymbol{x}}}_{0}=[-100, -100, 10, 10]^{\mathrm{T}} \\ s_{5}: \hat{\mathit{\boldsymbol{x}}}_{0}=[-500, -500, 100, 100]^{\mathrm{T}} \end{array}\right. $ | (46) |
在场景2下该滤波器的位置与速度的RMSEs展示在图 7中。
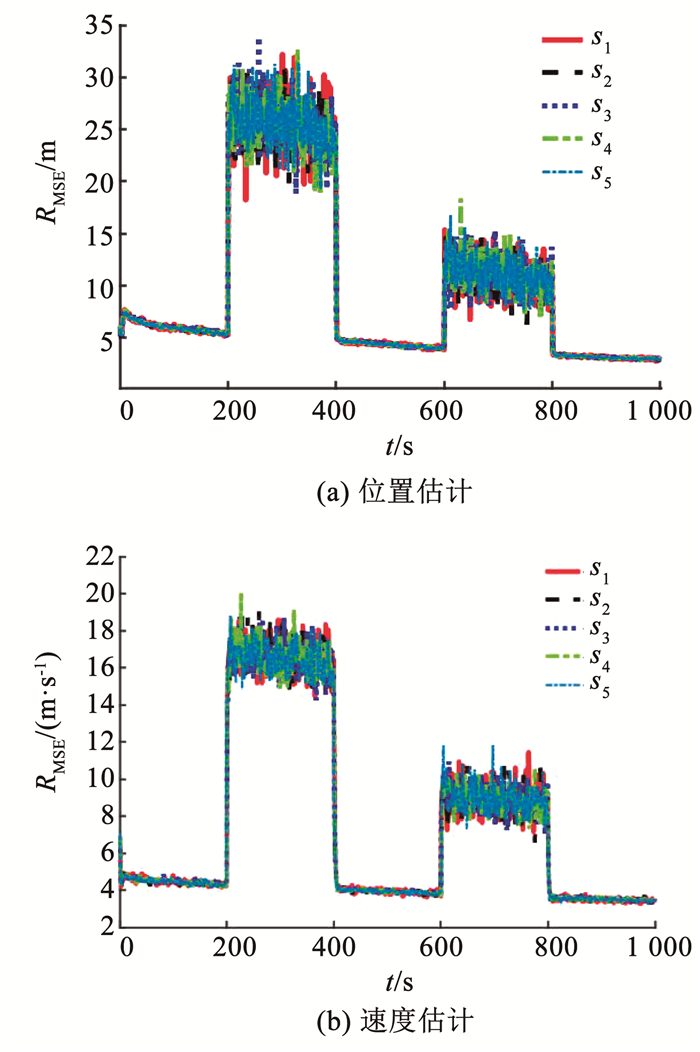
|
图 7 不同初始状态情况下GHTSRKF的估计 Fig. 7 Estimation of GHTSRKF with different initial states |
由图 7可知,所提出的GHTSRKF算法的估计精度对初始状态
1) 所提出的GHTSRKF算法的估计精度对初始状态的选取不敏感,其位置与速度的估计结果基本保持一致,因此可得初始状态对所提出算法的估计性能基本没有影响。
2) 所提出的GHTSRKF的精度优于其他RKFs, 它的RMSEs最接近噪声信息准确的KFTNC的RMSEs。
3) 当系统与量测噪声是未知时变高斯噪声时, 相比于现有的滤波器, GHTSRKF具有更好的估计性能,且该滤波器能够对不同的重尾噪声进行更加准确描述, 因此鲁棒性也更强。
| [1] |
SARGOLZAEI A, YAZDANI K, ABBASPOUR A, et al. Detection and mitigation of false data injection attacks in networked control systems[J]. IEEE Transactions on Industrial Informatics, 2020, 16(6): 4281. DOI:10.1109/TⅡ.2019.2952067 |
| [2] |
LI Haoqing, MEDINA D, VILÀ-VALLS J, et al. Robust variational-based Kalman filter for outlier rejection with correlated measurements[J]. IEEE Transactions on Signal Processing, 2020, 69: 357. DOI:10.1109/TSP.2020.3042944 |
| [3] |
潘泉, 胡玉梅, 兰华, 等. 信息融合理论研究进展: 基于变分贝叶斯的联合优化[J]. 自动化学报, 2019, 45(7): 1207. PAN Quan, HU Yumei, LAN Hua, et al. Information fusion progress: Joint optimization based on variational Bayesian theory[J]. Acta Automatica Sinica, 2019, 45(7): 1207. DOI:10.16383/j.aas.c180029 |
| [4] |
罗小元, 潘雪扬, 王新宇, 等. 基于自适应Kalman滤波的智能电网假数据注入攻击检测[J]. 自动化学报, 2022, 48(12): 2960. LUO Xiaoyuan, PAN Xueyang, WANG Xinyu, et al. Detection of false data injection attack in smart grid via adaptive Kalman filtering[J]. Acta Automatica Sinica, 2022, 48(12): 2960. DOI:10.16383/j.aas.c190636 |
| [5] |
HU Yumei, WANG Xuezhi, PAN Quan, et al. Variational Bayesian Kalman filter using natural gradient[J]. Chinese Journal of Aeronautics, 2022, 35(5): 1. DOI:10.1016/j.cja.2021.08.033 |
| [6] |
LI Ling, SONG Xinmin. State estimation for systems with packet dropping and state equality constraints[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2019, 66(9): 1572. DOI:10.1109/TCSⅡ.2018.2889047 |
| [7] |
WANG Jian, ZHANG Tao, JIN Bonan, et al. Student's t-based robust Kalman filter for a SINS/USBL integration navigation strategy[J]. IEEE Sensors Journal, 2020, 20(10): 5540. DOI:10.1109/JSEN.2020.2970766 |
| [8] |
HUANG Yulong, ZHANG Yonggang, XU Bo, et al. A new adaptive extended Kalman filter for cooperative localization[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(1): 353. DOI:10.1109/TAES.2017.2756763 |
| [9] |
ZHANG Junhao, LI Peng, JIN Congcong, et al. A novel adaptive Kalman filtering approach to human motion tracking with magnetic-inertial sensors[J]. IEEE Transactions on Industrial Electronics, 2020, 67(10): 8659. DOI:10.1109/TIE.2019.2946557 |
| [10] |
ZHU Hao, ZHANG Guorui, LI Yongfu, et al. An adaptive Kalman filter with inaccurate noise covariances in the presence of outliers[J]. IEEE Transactions on Automatic Control, 2022, 67(1): 374. DOI:10.1109/TAC.2021.3056343 |
| [11] |
WANG Guangcai, XU Xiaosu, ZHANG Tao. M-M estimation-based robust cubature Kalman filter for INS/GPS integrated navigation system[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 70: 9501511. DOI:10.1109/TIM.2020.3021224 |
| [12] |
QIU Zhenbing, GUO Lei. Improved cubature Kalman filter for spacecraft attitude estimation[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 9504213. DOI:10.1109/TIM.2020.3041077 |
| [13] |
FAN Xuxiang, WANG Gang, HAN Jiachen, et al. Interacting multiple model based on maximum correntropy Kalman filter[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2021, 68(8): 3017. DOI:10.1109/TCSⅡ.2021.3068221 |
| [14] |
CHEN Badong, LIU Xi, ZHAO Haiquan, et al. Maximum correntropy Kalman filter[J]. Automatica, 2017, 76: 70. DOI:10.1016/j.automatica.2016.10.004 |
| [15] |
CHEN Badong, DANG Lujuan, GU Yuantao, et al. Minimum error entropy Kalman filter[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(9): 5819. DOI:10.1109/TSMC.2019.2957269 |
| [16] |
TRONARP F, KARVONEN T, SÄRKKÄ S. Student's t-filters for noise scale estimation[J]. IEEE Signal Processing Letters, 2019, 26(2): 352. DOI:10.1109/LSP.2018.2889440 |
| [17] |
HUANG Yulong, ZHANG Yonggang, LI Ning, et al. A novel robust student's t-based Kalman filter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(3): 1545. DOI:10.1109/TAES.2017.2651684 |
| [18] |
HUANG Yulong, ZHANG Yonggang, XU Bo, et al. A new outlier-robust student's t based Gaussian approximate filter for cooperative localization[J]. IEEE/ASME Transactions on Mechatronics, 2017, 22(5): 2380. DOI:10.1109/TMECH.2017.2744651 |
| [19] |
BAI Mingming, HUANG Yulong, ZHANG Yonggang, et al. A novel heavy-tailed mixture distribution based robust Kalman filter for cooperative localization[J]. IEEE Transactions on Industrial Informatics, 2021, 17(5): 3671. DOI:10.1109/TⅡ.2020.3015001 |
| [20] |
BAI Mingming, HUANG Yulong, CHEN Badong, et al. A novel mixture distributions-based robust Kalman filter for cooperative localization[J]. IEEE Sensors Journal, 2020, 20(24): 14994. DOI:10.1109/JSEN.2020.3012153 |
| [21] |
XU Bo, GUO Yu, HU Junmiao. An improved robust Kalman filter for SINS/DVL tightly integrated navigation system[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 8502915. DOI:10.1109/TIM.2021.3079556 |
| [22] |
HUANG Yulong, ZHANG Yonggang, ZHAO Yuxin, et al. A novel robust gaussian - student's t mixture distribution based Kalman filter[J]. IEEE Transactions on Signal Processing, 2019, 67(13): 3606. DOI:10.1109/TSP.2019.2916755 |
| [23] |
ZHU Hao, ZHANG Guorui, LI Yongfu, et al. A novel robust Kalman filter with unknown non-stationary heavy-tailed noise[J]. Automatica, 2021, 127: 109511. DOI:10.1016/j.automatica.2021.109511 |
| [24] |
ZHU Hao, LEUNG H, HE Zhongshi. State estimation in unknown non-Gaussian measurement noise using variational Bayesian technique[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(4): 2601. DOI:10.1109/TAES.2013.6621839 |
| [25] |
HUANG Yulong, ZHANG Yonggang, WU Zhemin, et al. A novel adaptive Kalman filter with inaccurate process and measurement noise covariance matrices[J]. IEEE Transactions on Automatic Control, 2018, 63(2): 594. DOI:10.1109/TAC.2017.2730480 |
 2024, Vol. 56
2024, Vol. 56


