2. 空军预警学院 预警情报系, 武汉 430019;
3. 之江实验室, 杭州 311121
2. Dept. of Early Warning Intelligence, Air Force Early Warning Academy, Wuhan 430019, China;
3. Zhejiang Lab., Hangzhou 311121, China
随着信息技术的不断发展,网络化、体系化作战模式已经越来越成为未来战争的主要形式。具有高效互连、互通、互操作特性的作战体系网络能够为备战打赢提供有力保障,但也容易成为体系对抗时被打击的重点对象[1],造成“毁点断链瘫网”的严重后果。因此,如何提高作战体系网络在遭受打击时的鲁棒性,通过弹性作用适应破坏,并尽可能地恢复作战能力已成为当前研究的重难点问题[2]。
网络科学、复杂系统理论等交叉科学的发展为作战体系建模提供了有力的工具,将复杂多变的作战体系通过网络化手段转变成结构模型,从而方便体系的鲁棒性研究。总的来说,提高体系网络的鲁棒性主要分为预防、优化和恢复策略:预防主要针对关键部位,通过加强对节点和边的保护[3]、容量冗余等手段[4],在一定范围内延缓甚至阻止故障的传播,适用于事前场合;优化是通过优化算法对网络结构和工作流量进行改变[5],从而控制故障的传播,适用于事后场合;恢复也适用于事后场合,它是在故障发生后按照最优策略尽可能低成本地恢复系统的原始能力。预防有助于促进漏洞发现,优化能够实现灵活控制,但是这两种方法在实际中都具有一定的局限性,比如仍然无法避免灾难性事件的发生以及成本过高等;而恢复策略在其成本范围内不用考虑上述问题。因此,通过制定合理的恢复方法越来越成为提高鲁棒性的选择。
对于常见网络的恢复方法,学者们进行了广泛的研究,如蒋文君等[6]针对多层级联失效产生的影响,总结了应对网络失效的故障检测、保护节点和备份等预防策略,以及各种形式的节点和连边恢复策略;刘青霞等[7]也从指向性恢复和自发性恢复两个角度讨论了目前网络应对随机故障和蓄意攻击时的主要恢复方法;Danziger等[8]研究了多层网络中的恢复耦合关系,发现了大扰动后恢复的普遍非线性行为。
作战体系网络同层级网络类似,也具有层间耦合依存,相互级联作用的特点,因此学者们用相依网络对其建模并就鲁棒性开展了广泛研究[9-11]。老松杨等[9]从子网类型和数量、依赖模式、耦合强度等方面研究了不同攻击模式下相依网络的鲁棒性,但是研究对象都是一一对应的相依网络;邢积超等[10]通过构建加权相依网络,提出融合节点过载失效和过载修复的级联失效模型,并以演习数据为样本仿真了双层相依指挥信息系统网络的鲁棒性,但是仅用剩余节点比例来度量鲁棒性指标;Zhong等[11]基于负载依赖级联模型,研究了相依网络中不同耦合强度和拓扑结构在考虑修复资源、时间和负载容限情况下的鲁棒性,但也只考虑了一一对应的依赖方式。对于此类相依网络的恢复方法,Di Muro等[12]首次针对依赖网络提出了基于共同边界节点的恢复方法,通过随机恢复和级联失效过程的动态交替,有效地缓解了失效作用。考虑到随机恢复方法没有资源和时间的限制,吴佳键等[13]提出了基于依赖网络相连边的择优恢复算法,具有恢复能力好,起效快以及迭代次数少等优势,但是他们没有检验不同网络级联失效机制对该方法的适用性。对于现实中电网、通信网具有负载的现象,刘凤增等[14]设计了负载作用下相依网络级联失效择优恢复方法,较好地控制了失效传播,但依赖网络间的规模必须一致。在优化恢复层面,Moshiri等[15]利用被攻击网络的双曲几何和局部信息进行链路预测来发现冗余,以替换被攻击的链路。Almoghathawi等[16]提出了一个弹性驱动的多目标优化模型,在最小化总成本的同时尽可能加强恢复力度。Alkhaleel等[17]针对电网、水网、电话网、天然气网和运输网等相互依存的关键基础设施网络的失效问题,提出了两阶段平均风险随机恢复模型,利用混合整数规划来使综合恢复成本最小。考虑到链路预测以及优化算法计算量大且准确性依然欠佳,本文暂不考虑优化方法手段来研究作战网络恢复。
上述网络建模和修复等方面工作对作战体系网络的鲁棒性提升产生积极影响,但是目前作战网络的恢复研究依然存在以下问题:1)建模时没有考虑作战体系的异质特征,且鲁棒性能只是简单从拓扑结构进行评价;2)大部分研究没有考虑依赖的方向性,这与实际不太相符;3)择优恢复方法假定两个子网的节点数相同,并且网间依赖模式仅限于一对一的耦合关系,这种条件过于严格。基于此,本文针对作战体系中作战单元的异质性和依赖特征,建立群依赖作战网络模型。根据网络结构和动力学过程,设计作战网络非对称依赖失效、条件性群依赖失效、非连通失效和过载失效的级联失效过程,给出反映作战能力的鲁棒性指标。为研究鲁棒性与恢复操作之间的关系,构建了基于最大连通子图边界节点的择优恢复方法,利用节点容量和重要性优选节点。通过仿真实验验证了所提方法的可行性和有效性,结果表明所提方法相对其他方法具有效果更好,起效快和迭代少的优点。
1 群依赖作战网络模型用复杂网络进行建模时,作战体系中的单元和单元间的关系常被抽象成复杂网络的节点和连边。作战体系网络是由作战体系中的作战装备按照功能属性抽象成节点,装备之间的各种信息交互、能量影响等关系抽象成连边构成的复杂网络,为了方便以下简称为作战网络。由于作战体系的节点功能异质性和存在的依赖特性,从物理通信和逻辑功能两个方面出发,分别建立对应的子网模型。
对于物理子网,不同的作战装备在物理空间分散部署,承担以信息流为基础的能量流和物质流的流转任务,因而将具有通信功能的实体抽象成物理节点,组成物理子网。据此,各装备之间形成能够数据高度共享、信息快速交互、端口动态接入以及满足柔性组合要求的信息栅格。物理网络定义如下。
定义1 作战体系物理网络。假设网络GW= (V, Wa, E, Wb)为作战体系的物理网络,节点集合为V=(v1, v2, …, vNW),其中:NW为节点数,Wa为实体节点的属性,包括通信负载和容量等。边集合为E=(e1, e2, …, eMW),其中:MW为边数,边的存在性由隶属关系、任务需求及指挥组织等因素确定; Wb为通信链路的属性,表示带宽或者时延等。
为简单起见,认为物理网络没有方向性,并且Wb=1,所以不考虑其时延等因素。
对于功能子网,体系中的装备被描述成不同功能的作战单元,单元之间具有复杂的交互关系,形成组分异质、多点交互、多域融合和动态演化的网络结构,采用异质信息网络来进行建模。
定义2 作战体系异质功能网络。假设网络GG=(V, Wa, E, Wb; φ, ψ; VG, EG)为作战体系抽象出来的异质功能网络,节点集合为V=(v1, v2, …, vNG),其中:NG为节点数,Wa为节点业务属性,包括业务类别、业务负载和容量等。边集合为E=(e1, e2, …, eMG),其中:MG为边数,Wb为边的属性,表示业务信息的交互强度等。节点和边都拥有类型特征,节点类型集合为VG,存在映射函数φ∶V→VG满足φ(vi)∈VG。网络边类型集合为EG,存在映射函数ψ∶E→EG满足ψ(ei)∈EG。
另外,功能网依赖于物理网发挥效用。虽然从逻辑上说,情报信息及指控命令都是在功能网上流转,但节点之间的信息交互是需要通信单元的支撑来实现信息分发和传送的,如图 1所示。
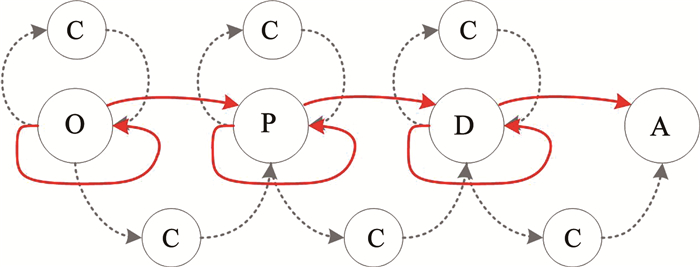
|
图 1 信息流转示意 Fig. 1 Information flow diagram |
所以除了功能网和物理网外,两者相互依存形成依赖网络。为了构建作战网络子网间的依赖关系,进行如下理想化处理:
1) 作战网络节点只具备单项功能,即情报获取节点O、情报处理节点P、指挥决策节点D、作战响应节点A和通信节点C的功能互不影响。
2) 不考虑物理网实际装备的空间和时间限制,即功能网依赖于物理网时不考虑连接限制,可任意相连。
于是,作战体系双层异质依赖网络定义如下。
定义3 作战体系双层异质依赖网络。假设作战体系的功能网和物理网的耦合关系为ED={EGW, EWG},若节点vGi依赖于vWj,有ED(vGi, vWj)=1(单向依赖,为了方便计算,假设ED(vGi, vWj)=1),相依节点和依赖边构成依赖网为GD,则三者构成双层异质依赖网络,记为
| $ G=\left(G_{\mathrm{G}}, G_{\mathrm{D}}, G_{\mathrm{W}}\right) $ | (1) |
作战网络的邻接矩阵表示为
| $ \boldsymbol{S}=\left[\begin{array}{cc} \boldsymbol{S}_{\mathrm{G}} & \boldsymbol{S}_{\mathrm{GW}} \\ \boldsymbol{S}_{\mathrm{WG}} & \boldsymbol{S}_{\mathrm{W}} \end{array}\right] $ | (2) |
式中:SG为对应功能网,SW为对应物理网,SWG、SGW为对应依赖关系。依赖网络表明两个子网络之间具有依赖关系,依赖网的节点产生依赖,被依赖网的节点受到依赖,两者构成了依赖网络这个整体。对于作战体系双层异质依赖网络,功能子网为依赖网,物理子网为被依赖网。
注1 双层异质依赖网络之间的依赖关系可以是一对一、一对多以及多对一等类型[18],一对多的依赖的形式叫做群依赖或者多重依赖,因此将具有一对多双层异质依赖关系的作战网络称为群依赖作战网络。
为了便于理解,给出所构建的群依赖作战网络模型示意图如图 2所示。
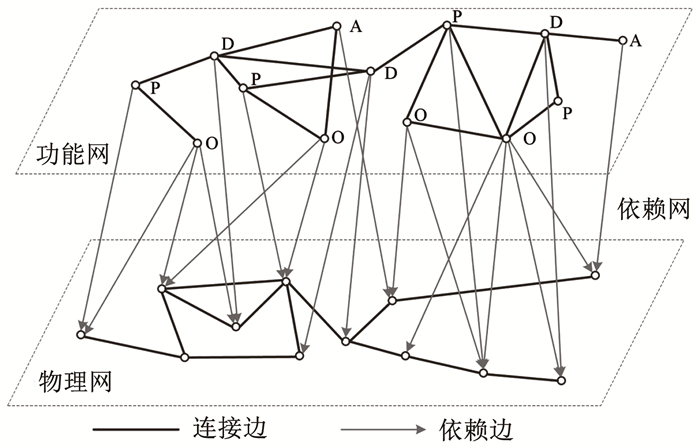
|
图 2 群依赖网络示意 Fig. 2 Schematic diagram of group-dependent network |
作战网络中功能网单向依赖于物理网,功能网的信息流只要能经过通信节点流转即可发挥效用,所以功能网节点是否失效对物理网节点不产生影响。为了建立作战网络的级联失效模型,分别从依赖失效和过载失效两个角度进行研究。
2.1 非连通失效与依赖失效非对称依赖网络即单向依赖网络,结合经典的相依网络失效模型[19],针对双层的单向依赖网络,部分节点遭受打击后的依赖失效规则为:对于依赖网节点,当其不在最大连通子图或者被依赖节点全失效时,该节点失效;对于被依赖网节点,当其不在最大连通子图时,该节点失效。上述失效规则默认为即有多重依赖时,只要还有部分依赖关系正常就不会发生依赖失效。基于此,提出一种群依赖情形下能够容忍部分被依赖节点失效的条件性群依赖失效模型:令条件性群依赖失效的容忍度为τ,当被依赖节点的失效比例大于τ时,依赖节点失效。给出一个例子如图 3所示。
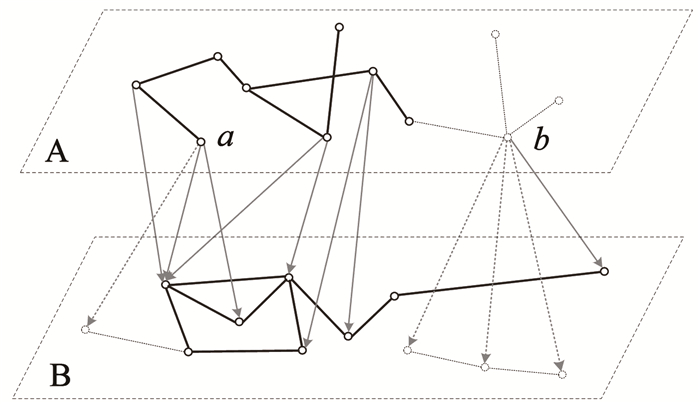
|
图 3 条件性群依赖失效示意 Fig. 3 Schematic diagram of conditional group-dependent failure |
图 3中子网A的节点单向群依赖于子网B,依赖的规模不尽相同。记条件性群依赖的容忍系数为τ,当τ=0.5时,节点a依赖的3个节点中的1个发生失效,失效比例为1/3,没有超过容忍系数τ,因此节点a不发生依赖失效;而节点b的失效比例为3/4,超过了容忍系数τ,所以节点b发生依赖失效,与其相邻的节点的其他连边全部被断开。
2.2 过载失效群依赖作战网络除了会发生依赖失效,还要进一步考虑其内部运行机制产生的其他问题,比如两类子网都会因为负载过高而失效。Motter等[20]提出了“容量-负载”模型来描述这种现象;彭兴钊等[21]进一步将这类级联失效模型结合到依赖失效模型上。基于此,针对物理网和功能网分别建立过载失效模型,并与依赖失效模型融合,形成多因素的级联失效模型。需要注意的是,对于物理网,负载可在整个子网中分配;而功能子网业务负荷的重分配仅限于同种类型的节点之间,两者的负载、容量和负载重分配方式模型都是一致的,以下用统一的形式表示。
2.2.1 初始负载初始负载可定义为节点度的指数幂,但Motter等[20]指出信息路径即介数的函数更合理。对大规模网络及非连通网络介数不易求解的情形,Wang等[22]根据局部信息计算节点负载,并证明了节点度和邻节点度的乘积和介数是正相关的。根据上述思想,初始负载为
| $ L_{i}(0)=\left(k_{i} \sum\limits_{j \in \varGamma_{i}} k_{j}\right)^{\kappa}, i=1, 2, \cdots, N $ | (3) |
式中:ki(kj)为节点度,表示节点与邻居节点的连边数量; κ为调节参数,用来控制节点初始负载的分布; Γi为节点vi邻居节点的下标集合。
2.2.2 节点容量由于成本的限制,负载作用下的节点容量具有上限。在大多数实际网络中,容量较小的节点通常却有较大的空闲容量,所以容量C和负载L并非简单的线性关系[23]。在作战网络中,若节点初始负载很大,则表明节点很重要,与其他节点的信息或者业务往来会更加频繁,其工作状态通常会接近满负荷,剩余容量(C-L)就小;反之不太重要的节点负载较小,有较多的空闲容量[24]。借鉴Kim等[23]的模型,容量可定义为
| $ C_{i}=L_{i}(0)+\lambda \cdot L(0)^{\gamma}, i=1, 2, \cdots, N $ | (4) |
式中:Li(0)为初始时刻节点vi的负载,λ>0、γ>0为负载调节参数。当γ=1时,退化为线性模型,可见非线性模型更具一般性。
2.2.3 失效状态判别在经典的“容量-负载”模型中,节点除了正常状态就是失效状态,郝羽成等[25]提出了一种考虑过载状态的失效模型。据此,可使节点按一定概率失效。当节点的负载超过容量时,在一定的承受范围μ内节点处于过载的临界状态,失效概率介于0~1之间。当重新分配负载后,可得更新负载的节点发生过载失效的概率为
| $ p_{i}(t)=\left(\begin{array}{ll} 0, & L_{i}(t) \leqslant C_{i} \\ \frac{L_{i}(t)-C_{i}}{\mu C_{i}}, & C_{i}<L_{i}(t) \leqslant(1+\mu) C_{i} \\ 1, & L_{i}(t)>(1+\mu) C_{i} \end{array}\right. $ | (5) |
节点失效后,其负载按一定方式进行传播,常见负载分配方式有局部分配[26]、全局分配[27]和平均分配[28]等。不同分配方法对网络鲁棒性的影响差别很大,考虑到通信传输一般按照最小跳数原则寻址,所以在负载重分配时也更倾向于局部分配的准则。另外,同时考虑静态和动态负载体现的节点重要性,则两者的分配比例分别为:
| $ Q_{i j}^{\mathrm{s}} =\frac{L_{j}(0)}{\sum\limits_{j \in \varGamma_{i}} L_{j}(0)} $ | (6) |
| $ Q_{i j}^{\mathrm{d}} =\frac{L_{j}(t)}{\sum\limits_{j \in \varGamma_{i}} L_{j}(t)} $ | (7) |
于是综合分配比例为
| $ Q_{i j}=\eta Q_{i j}^{\mathrm{s}}+(1-\eta) Q_{i j}^{\mathrm{d}} $ | (8) |
式中:η、1-η为分配比例混合时的权重,默认都为0.5。进而邻居节点的负载更新为
| $ L_{j}(t+1)=L_{j}(t)+\sum\limits_{j \in \varGamma_{i}} Q_{i j} L_{i}(t) $ | (9) |
式中加权和是因为邻居节点会受到其邻居节点负载重分配的影响。在整个网络中重分配就导致了加权和的结果。
3 作战网络恢复方法为了恢复作战网络,首先需要根据攻击方式确定作战网络的鲁棒性评价指标,以判断作战网络恢复的效果,然后在此基础上利用恢复方法进行择优恢复。
3.1 攻击方式对于作战体系网络的攻击模式一般分为随机攻击和蓄意攻击[29]。随机攻击任意选择节点使其失效,蓄意攻击按节点度指标排序进行优先攻击。现实中,作战网络的重要节点往往更容易遭受打击,因此选择对物理网的节点进行蓄意攻击。设初始攻击比例为f,则总攻击节点数为fNW,对于节点度相同的节点,按照随机原则进行选取,这里的节点度计算限于子网内部,不考虑依赖边。
3.2 鲁棒性评价指标大多数网络的鲁棒性指标主要从连通性角度进行刻画,比如最大连通子图规模、自然连通度等,着眼点在网络的拓扑结构。对于作战网络而言,除了要考虑体系结构的连通性,更要突出作战网络功能的发挥和实际作战意义,即形成快速完整的作战回路以获得对抗优势。综合考虑作战网络的结构和功能,结合作战循环理论[30],网络的鲁棒性评价将从两方面指标来设计。
1) 基于作战杀伤链的指标。采用从情报获取节点O到作战响应节点A所形成的杀伤链的数量来表示。杀伤链的类型见表 1。
| 表 1 作战体系中杀伤链的类型和意义 Tab. 1 Types and meanings of kill link in combat SOS |
在图 1中功能网信息流转需要依赖物理网的通信节点,所以计算杀伤链数量时也要将其融入,先计算整体可达矩阵
| $ \begin{align*} (\boldsymbol{S}+\boldsymbol{I})^{(1)} \neq & (\boldsymbol{S}+\boldsymbol{I})^{(2)} \neq \cdots \neq \\ & (\boldsymbol{S}+\boldsymbol{I})^{(r)}=(\boldsymbol{S}+\boldsymbol{I})^{(r+1)}=\tilde{\boldsymbol{S}} \end{align*} $ | (10) |
式中:I为单位阵,r为布尔幂乘法次数。然后令
| $ \begin{align*} \boldsymbol{S}_{\text {link }}(G)= & \operatorname{tr}\left\{\left[\boldsymbol{S}_{\mathrm{OP}} \wedge\left(\boldsymbol{S}_{\mathrm{OC}} \times \boldsymbol{S}_{\mathrm{CC}} \times \boldsymbol{S}_{\mathrm{CP}}\right)\right] \times\right. \\ & {\left[\boldsymbol{S}_{\mathrm{PD}} \wedge\left(\boldsymbol{S}_{\mathrm{PC}} \times \boldsymbol{S}_{\mathrm{CC}} \times \boldsymbol{S}_{\mathrm{CD}}\right)\right] \times } \\ & {\left[\boldsymbol{S}_{\mathrm{DA}} \wedge\left(\boldsymbol{S}_{\mathrm{DC}} \times \boldsymbol{S}_{\mathrm{CC}} \times \boldsymbol{S}_{\mathrm{CA}}\right)\right] \times \boldsymbol{S}_{\mathrm{AO}} } \} \end{align*} $ | (11) |
式中:SOC、SCP分别为功能节点和通信节点之间的可达矩阵,∧为布尔和运算。同理可得其他杀伤链的数量,所以7种杀伤链的数量为
| $ S_{\text {links }}(G)=\sum\limits_{i=1}^{7} S_{\text {link }_{i}}(G) $ | (12) |
2) 基于最大连通子图规模,表示为物理网和功能网最大连通子图规模之和,初始规模为
| $ S_{\text {huge }}=N_{\mathrm{W}}+N_{\mathrm{G}} $ | (13) |
对于未受打击的作战网络G,杀伤链数量为Slinks(G),最大连通子图规模为Shuge(G),令打击后的网络为G′,对应的指标分别变为Slinks(G′)和Shuge(G′),那么作战网络的鲁棒性指标为
| $ R=\left(\frac{S_{\text {links }}\left(G^{\prime}\right)}{S_{\text {links }}(G)}\right)^{\theta}\left(\frac{S_{\text {huge }}\left(G^{\prime}\right)}{S_{\text {huge }}(G)}\right)^{1-\theta} $ | (14) |
式中:θ、1-θ分别为杀伤链数量和最大连通子图规模这两个指标的比例参数,默认都为0.5。
3.3 择优恢复方法考虑到实际生活中资源和时间的限制,网络恢复策略的制定是有一定规律可循的。从恢复范围看,一般倾向于选择正常区域周边的节点,由近及远进行恢复操作;从恢复效果看,需要选择能对网络能力恢复有积极作用的节点,避免因为效果不佳而造成网络的反复失效和资源浪费;从恢复优先级看,选择能使网络能力提升增益大的节点进行恢复可以提高恢复的效率。根据该思想,吴佳键等[13]用相依网络的共同边界节点来选择恢复的范围,然后按照一定规则进行择优恢复。但是这类方法都是在一对一依赖的情形下运行的,对于异质依赖作战网络模型,群依赖的问题无法得到有效解决。针对该问题,考虑从边界节点出发研究异质群依赖作战网络恢复方法。
对于物理网,如图 4所示,灰色节点构成失效节点集,这些失效节点中,与最大连通子图距离为1的节点称为边界节点,于是进行节点恢复时,被恢复的节点就在边界节点集中选取。为了选择重要的边界节点进行恢复,考虑网络结构和失效的动力学模型来进行节点重要性分析。从网络结构看,物理网节点的主要功能是作为中间节点传递信息,因此通信节点为功能网担任中介次数(即外部度)越多,说明其在信息流转中发挥的作用越重要。另一方面,失效的边界节点与当前物理网最大连通子图的连边越多,在恢复后面临新的过载失效时负载重分配的压力就会越小,从而一定程度上缓解了失效传播;并且失效边界节点与其他失效节点的连边越多,则后续恢复中边界节点数量也越多,更有可能找到对网络能力提升大的节点,因此也可以将内部度作为网络结构的重要性指标。由于物理网只要保持连通即可,因此功能网与物理网的连通性比物理网之间的连通性更重要,为了简单而不失一般性,默认外部度和内部度的重要性比例为2。结合上述分析,对于物理网的节点vi,其归一化后的结构重要性指标为
| $ \tilde{k}_{i}=\frac{2 k_{i}^{\text {out }}}{k_{\max }^{\text {out }}}+\frac{k_{i}^{\text {in }}}{k_{\max }^{\text {in }}} $ | (15) |

|
图 4 物理网边界节点恢复模型 Fig. 4 Recovery model of boundary nodes of physical net |
式中:kiin、kiout分别为节点i的入度和出度,kmaxin、kmaxout分别为入度和出度中最大的度数。从失效的动力学模型来看,节点的容量越大,可承受的负载就越多,相应地在恢复后过载失效的概率就越小。优先对容量大的边界节点进行恢复,能更好地提高总体容量,降低过载失效的风险。因此,将边界节点的容量也作为重要性评价指标。对于物理网的节点vi,其归一化后的容量指标为
| $ \tilde{C}_{i}=\frac{C_{i}}{C_{\max }} $ | (16) |
根据上述结构重要性指标和容量指标,物理网边界节点的综合重要性指标可以表示为
| $ H_{i}=\beta \tilde{k}_{i}+(1-\beta) \tilde{C}_{i} $ | (17) |
式中:β为结构重要性指标和容量指标之间的比例参数,本文默认β为0.5。
对于功能网,根据物理网节点恢复的情况进行恢复,主要规则为:先恢复与优选的物理网边界节点有依赖关系的功能网节点和依赖边,然后将这些节点与功能网最大连通子图之间原有的连接关系恢复。物理网和功能网在恢复部分节点后,恢复节点的负载都为0。
综上所述,考虑边界节点容量和重要性的优先恢复方法(prior recovery based on capacity and importance, PRCI)过程为:首先从物理网的失效节点中选出边界节点;然后利用式(17)的综合重要性指标进行排序;接着按照物理网恢复比例α选择排名靠前的边界节点进行恢复;最后基于此按照功能网恢复规则恢复功能网节点。
3.4 恢复过程建立恢复方法后,将其加入作战网络级联失效的过程中,形成两个子网发生依赖失效、非连通失效、过载失效等级联失效和节点恢复有序交替的动态过程。n(n≥0)为迭代次数(number of iteration, NOI),表示在第n个阶段网络失效和恢复的状态过程,如图 5所示。
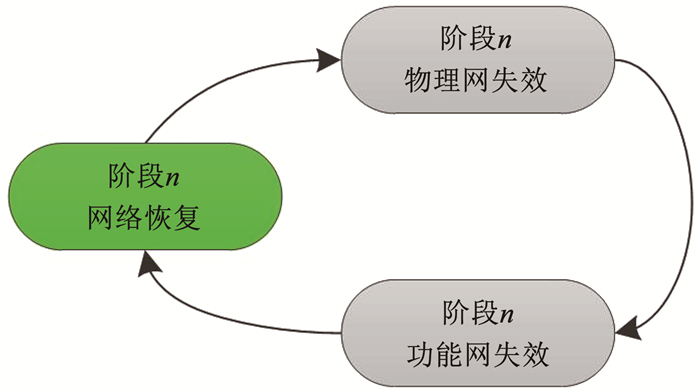
|
图 5 作战网络失效和恢复过程 Fig. 5 Failure and recovery process of combat network |
在初始阶段n=1,物理网的fNW个节点被打击,发生过载失效和非连通失效,失效传递给功能网,功能网发生依赖失效、非连通失效和过载失效;在失效范围进一步扩散前,通过节点恢复操作恢复部分失效节点,若部分恢复后失效并未停止,则进入下一轮“失效-恢复”循环。具体步骤为:
Ⅰ.第n阶段物理网失效过程。
Step1 若物理网节点vi发生过载,则节点vi失效。
Step2 脱离最大连通子图的节点都失效。
Step3 新失效节点的负载向周边扩散更新。
Ⅱ.第n阶段功能网失效过程。
Step4 若功能网节点vi依赖于物理网第n阶段失效节点的比例超过限度τ,则节点vi失效。
Step5 若功能网节点vi发生过载,则节点vi失效。
Step6 脱离最大连通子图的节点都失效。
Step7 新失效节点的负载向周边扩散引发新一轮过载和非连通级联失效,直到本阶段功能网无新增失效节点。
Ⅲ.第n阶段功能网恢复过程。
Step8 找出所有的失效节点,按照前文所述的规则进行恢复,物理网的恢复比例为α。所有被恢复的节点,原先存在的与当前正常节点的连边关系全部恢复。
Step9 重复执行Step1~Step8,直到网络达到没有新增失效节点的稳定状态或者完全崩溃状态。
为检验PRCI方法的效果,与3种基准方法进行对比[13]:随机恢复方法(random recovery, RR),按照恢复比例等概率在边界节点中随机选择节点恢复[12];度优先恢复方法(prior recovery based on degree, PRD),按照节点内部度降序排列优先选择度值大的边界节点进行恢复[31];局域中心性优先恢复方法(prior recovery based on local centrality, PRL),按照节点局域中心性指标降序排列优先选择靠前的边界节点进行恢复[32]。
4 仿真实验与分析为验证方法的可行性和有效性,基于模型网络开展仿真实验。分别选用ER随机网络[33]、参数可调的Goh无标度网络[34]和NW小世界网络[35]等模型网络作为功能子网和物理子网。功能网规模为NG=150,其中: NO=50,NP=40,ND=30,NA=30,物理网NW=100。对模型网络设置参数,ER网中不同节点之间的连接概率为fOO=0.02,fOP=0.03,fPP=0.05,fPD=0.03,fDD=0.05,fDA=0.03,fAA=0.03,fCC=0.07, Goh网络幂指数β=2.3,平均度〈k〉=6,不同功能类型节点之间按ER网的参数连接;NW网K=2,同种类型功能节点之间连接概率为fOO=0.08,fPP=0.10,fDD=0.14,fAA=0.14,fCC=0.05,不同类型之间连接概率同ER网的参数。功能网随机单向依赖于物理网,依赖群的规模统一设置为5。为了减小实验中的随机性,上述网络按照设定的参数各自重复生成500个。在进行仿真时,如果没有特别说明,统一采用如下默认参数:α=0.6, τ=0.6, κ=0.5, λ=1.0, γ=1.1, μ=0.3,节点的初始失效比例f为[0, 0.3]。
4.1 不同网络结构的恢复效果对于不同的子网结构,针对3种模型网络分别展开实验。图 6给出了RR、PRD、PRL和本文PRCI方法的恢复效果比较。从图 6(a)中可以看出,对物理网和功能网都是ER网时,PRL和PRD的恢复效果相近,PRL要略优于PRD,RR恢复效果在前期要优于PRD和PRL,但当f=0.09时,RR的效果不如这两种方法。PRCI的恢复效果在f<0.06时略优于RR,之后PRCI开始体现出明显优势。图 6(b)中,RR的恢复效果最差,择优方法效果明显更好。对于3种择优方法,总体来说效果比较相近,当f<0.16时,PRCI
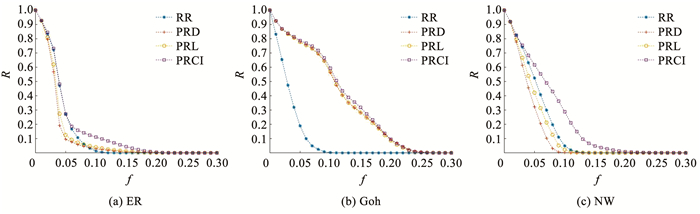
|
图 6 不同子网结构下4种方法的恢复效果比较 Fig. 6 Comparison of recovery performance among four methods with different topology |
图 7给出了不同网络结构下几种方法的平均迭代次数NOI。从图 7中可以看出,恢复效果越相近,迭代次数曲线的相似和重合程度就越高,且恢复效果越差,迭代次数越多。对于子网为ER网和NW网,由于恢复效果的趋势比较一致,迭代次数的形状也很相似,都是呈山峰状,根据恢复效果,PRCI、RR、PRL和PRD的迭代次数峰值点依次向右下方推移,进一步验证了恢复效果好的方法具有迭代少、起效快的特点。在失效比例较小和较大的时候迭代次数都很小,几乎为1,因为失效比例较小时,仅需一步恢复操作就可使作战网络维持稳定状态;而失效比例较大时,恢复不再起作用,作战网络能力已经完全丧失。

|
图 7 不同子网结构下4种方法的迭代次数比较 Fig. 7 Comparison of NOI among four methods with different topology |
由于4种恢复方法在NW网作为子网时区分最明显,因此在后续实验中,通过调节不同的参数来比较几种方法的恢复效果,设定都是单参数变化。对于群依赖失效的容忍系数,当τ在[0.4, 0.8]变化时,恢复效果如图 8所示。从图 8中可以看出,τ越大,作战网络能忍受失效的程度越高,鲁棒性越强,网络的恢复效果也越明显。比如τ=0.4时,PRCI作用下的Rf=0.1=0.049,其他方法几乎为0,而τ=0.8时,PRCI方法作用下的Rf=0.1=0.315,其他方法也有明显提升。随着τ的增大,PRCI方法相对于其他方法的优势逐渐扩大,说明该方法能更好地抑制级联失效。

|
图 8 不同容忍度下4种方法恢复效果比较 Fig. 8 Comparison of recovery performance among four methods with different tolerance |
对于不同的负载参数,令κ分别为0.3、0.5和0.7,恢复效果如图 9所示。从图 9中可以看出,随着κ增大,恢复效果逐渐减弱,用PRCI方法恢复后,在不同κ取值下的Rf=0.1分别为0.327、0.285和0.269,下降幅度为12.84%和5.61%。负载的增大使得网络更容易发生过载失效,导致级联反应更加剧烈,从而最终恢复的节点和连边数变少,恢复效果减弱。

|
图 9 不同负载参数κ下4种方法恢复效果比较 Fig. 9 Comparison of recovery performance among four methods with different κ |
对于不同的容量参数,图 10给出了λ= 0.5、0.9和1.3时4种方法恢复效果的比较结果,图 11给出了γ= 0.7、1.1和1.5时4种方法恢复效果的比较结果,从图 11中可以看出,随着容量参数的增大,作战网络发生失效的程度变低,用PRCI方法恢复后,在不同λ取值下的Rf=0.1分别为0.105、0.243和0.341,在不同γ取值下的Rf=0.1分别为0.121、0.291和0.322。提高容量参数能降低过载失效的概率,随着参数的增大,PRCI相对于其他方法的优势进一步扩大。
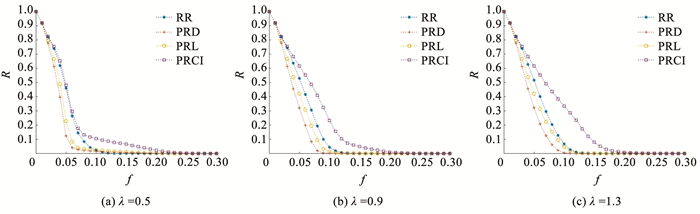
|
图 10 不同容量参数λ下4种方法恢复效果比较 Fig. 10 Comparison of recovery performance among four methods with different λ |
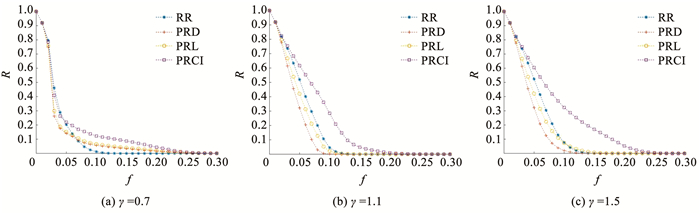
|
图 11 不同容量参数γ下4种方法恢复效果比较 Fig. 11 Comparison of recovery performance among four methods with different γ |
对于过载状态承受系数,图 12给出了μ变化时的恢复效果情况,当μ=0.3和μ=0.5时,图 12(a)、12(b)的曲线几乎没有差别,因为过载的程度过大,当μ在小范围波动时,对失效状态几乎没有影响;当μ取较大的3.0时,可以看出,失效的情况有所缓解,PRCI方法恢复后的Rf=0.1从原来的0.295提升至0.331。

|
图 12 不同参数μ下4种方法恢复效果比较 Fig. 12 Comparison of recovery performance among four methods with different μ |
对于不同的恢复比例,图 13给出了α= 0.4、0.6和0.8时4种方法恢复效果的比较结果。可以看出,随着恢复比例的增加,恢复效果有着明显的提升,PRL方法与RR方法的恢复效果差距进一步缩小,到α=0.8时,PRL方法在f >0.08后超越RR方法;而PRCI方法与其他方法的优势进一步增大,在f =0.30时,网络甚至还没有完全失效。
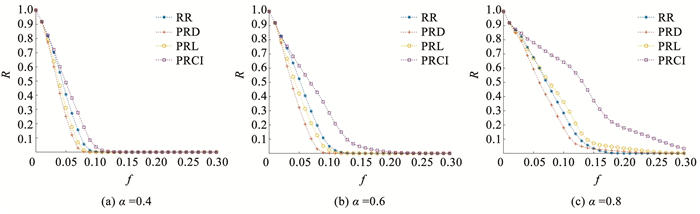
|
图 13 不同恢复比例下4种方法恢复效果比较 Fig. 13 Comparison of recovery performance among four methods with different recovery ratio |
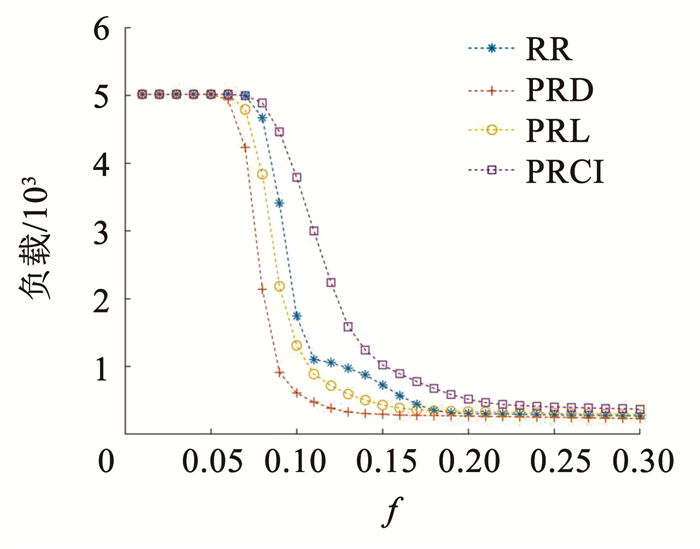
通过网络恢复操作后的作战网络会进入终态,此时的网络结构特性和节点负载能一定程度上反映不同方法的恢复效果的优劣,图 14、15分别给出了经过4种方法恢复后作战网络的节点平均度和负载的分布情况。

|
图 14 不同方法恢复后的网络平均度 Fig. 14 Average degree after recovery by different methods |
|
图 15 不同方法恢复后的负载 Fig. 15 Node load after recovery by different method |
从图 14、15中可以看出,PRCI、RR、PRL和PRD方法的平均度和负载依次递减,和前文所排列的恢复方法优劣次序一致。终态时作战网络节点的平均度越大,说明存活的节点越多,作战网络的能力越强,鲁棒性越好;留存的负载越多,说明网络所经受的损失越少,信息交互能力越好。结果表明, PRCI方法的恢复效果相比其他几种方法是最好的,当恢复资源有限时,可以优先选择PRCI方法进行节点恢复,增强作战网络的能力。
5 结论1) 考虑作战体系的异质特性,建立了符合实际特征的作战体系双层异质网络模型,并提出了具有作战意义的鲁棒性指标。
2) 通过提出条件性群依赖失效的方式,融合非连通失效和临界过载失效,设计了贴近实际的级联失效模型,突破了常见模型规模匹配和单一依赖等理想化限制。
3) 通过融合边界节点的容量和重要性等属性特征,提出了节点优先恢复方法,并仿真验证其有效性和可行性。该方法相对其他基线方法效果更好,具有恢复快、迭代少的特点,恢复后的节点平均度和负载更高,更好地保存了作战网络的能力。
4) 从实验结果看,恢复效果还与容忍度、容量参数、承受系数和恢复比例成正比,与负载参数成反比,研究结果对于作战体系运用与保护具有一定的指导意义。
| [1] |
康东, 李建华, 王哲, 等. 指挥信息系统相依网络模型弹性策略研究[J]. 电光与控制, 2021, 28(12): 22. KANG Dong, LI Jianhua, WANG Zhe, et al. Aresilience recovery strategy of double-layer interdependent network model of C4 KISR[J]. Electronics Optics & Control, 2021, 28(12): 22. DOI:10.3969/j.issn.1671-637X.2021.12.005 |
| [2] |
HOSSEINI S, BARKER K, RAMIREZ-MARQUEZ J E. A review of definitions and measures of system resilience[J]. Reliability Engineering & System Safety, 2016, 145: 47. DOI:10.1016/j.ress.2015.08.006 |
| [3] |
LIU Xing, FERRARIO E, ZIO E. Identifying resilient-important elements in interdependent critical infrastructures by sensitivity analysis[J]. Reliability Engineering & System Safety, 2019, 189: 423. DOI:10.1016/j.ress.2019.04.017 |
| [4] |
张震, 刘迪洋, 张进, 等. 基于节点冗余容量动态控制的复杂网络鲁棒性研究[J]. 电子与信息学报, 2021, 43(5): 1349. ZHANG Zhen, LIU Diyang, ZHANG Jin, et al. Research on the robustness of complex networks based on dynamic control of node redundancy capacity[J]. Journal of Electronics & Information Technology, 2021, 43(5): 1349. DOI:10.11999/JEIT200185 |
| [5] |
CHEN Junyuan, LIU Jing. A memetic algorithm for optimizing inter-links to enhance the robustness of interdependent networks against malicious attacks[C]//2021 IEEE Congress on Evolutionary Computation (CEC). Kraków, Poland: IEEE, 2021: 327. DOI: 10.1109/CEC45853.2021.9504787
|
| [6] |
蒋文君, 刘润然, 范天龙, 等. 多层网络级联失效的预防和恢复策略概述[J]. 物理学报, 2020, 69(8): 81. JIANG Wenjun, LIU Runran, FAN Tianlong, et al. Overview of precaution and recovery strategies for cascading failures in multilayer networks[J]. Acta Physica Sinica, 2020, 69(8): 81. DOI:10.7498/aps.69.20192000 |
| [7] |
刘青霞, 王邦. 网络弹性与恢复机制的研究综述[J]. 信息安全学报, 2021, 6(4): 44. LIU Qingxia, WANG Bang. Network resilience and recovery mechanism: A review[J]. Journal of Cyber Security, 2021, 6(4): 44. DOI:10.19363/J.cnki.cn10-1380/tn.2021.07.03 |
| [8] |
DANZIGER M M, BARABÁSI A-L. Recovery coupling in multilayer networks[J]. Nature Communications, 2022, 13(1): 955. DOI:10.1038/s41467-022-28379-5 |
| [9] |
老松杨, 王竣德, 白亮. 相依网络研究综述[J]. 国防科技大学学报, 2016, 38(1): 122. LAO Songyang, WANG Junde, BAI Liang. Review of the interdependent networks[J]. Journal of National University of Defense Technology, 2016, 38(1): 122. DOI:10.11887/j.cn.201601020 |
| [10] |
邢积超, 陈楚湘, 朱兆梁, 等. 双层相依网络化指挥信息系统级联失效研究[J]. 控制与决策, 2020, 35(12): 3017. XING Jichao, CHEN Chuxiang, ZHU Zhaoliang, et al. Cascading failure of double layer networked command information system[J]. Control and Decision, 2020, 35(12): 3017. DOI:10.13195/j.kzyjc.2019.0696 |
| [11] |
ZHONG Jilong, ZHANG Fengming, YANG Shunkun, et al. Restoration of interdependent network against cascading overload failure[J]. Physica A: Statistical Mechanics and Its Applications, 2019, 514: 884. DOI:10.1016/j.physa.2018.09.130 |
| [12] |
DI MURO M A, LA ROCCA C E, STANLEY H E, et al. Recovery of interdependent networks[J]. Scientific Reports, 2016, 6: 22834. DOI:10.1038/srep22834 |
| [13] |
吴佳键, 龚凯, 王聪, 等. 相依网络上基于相连边的择优恢复算法[J]. 物理学报, 2018, 67(8): 289. WU Jiajian, GONG Kai, WANG Cong, et al. Enhancing resilience of interdependent networks against cascading failures under preferential recovery strategies[J]. Acta Physica Sinica, 2018, 67(8): 289. DOI:10.7498/aps.67.20172526 |
| [14] |
刘凤增, 肖兵, 陈施思, 等. 负载作用下相依网络择优恢复方法研究[J]. 电子与信息学报, 2020, 42(7): 1694. LIU Fengzeng, XIAO Bing, CHEN Shisi, et al. A preferential recovery method of interdependent networks under load[J]. Journal of Electronics & Information Technology, 2020, 42(7): 1694. DOI:10.11999/JEIT190486 |
| [15] |
MOSHIRI M, SAFAEI F, SAMEI Z. A novel recovery strategy based on link prediction and hyperbolic geometry of complex networks[J]. Journal of Complex Networks, 2021, 9(4): cnab007. DOI:10.1093/comnet/cnab007 |
| [16] |
ALMOGHATHAWI Y, GONZÁLEZ A D, BARKER K. Exploring recovery strategies for optimal interdependent infrastructure network resilience[J]. Networks and Spatial Economics, 2021, 21(1): 229. DOI:10.1007/s11067-020-09515-4 |
| [17] |
ALKHALEEL B A, LIAO Haitao, SULLIVAN K M. Model and solution method for mean-risk cost-based post-disruption restoration of interdependent critical infrastructure networks[J]. Computers & Operations Research, 2022, 144: 105812. DOI:10.1016/j.cor.2022.105812 |
| [18] |
禹明刚, 余晓辉, 权冀川, 等. 面向任务与基于ANP的网络信息体系能力需求满足度分析方法[J]. 系统工程理论与实践, 2020, 40(3): 795. YU Minggang, YU Xiaohui, QUAN Jichuan, et al. Task-oriented and ANP-based requirement satisfactory degree analysis method for net-centric information system-of-systems[J]. Systems Engineering—Theory & Practice, 2020, 40(3): 795. DOI:10.12011/1000-6788-2018-2051-12 |
| [19] |
BULDYREV S V, PARSHANI R, PAUL G, et al. Catastrophic cascade of failures in interdependent networks[J]. Nature, 2010, 464(7291): 1025. DOI:10.1038/nature08932 |
| [20] |
MOTTER A E, LAI Yingcheng. Cascade-based attacks on complex networks[J]. Physical Review E: Statistical, Nonlinear & Soft Matter Physics, 2002, 66(6 Pt.2): 065102. DOI:10.1103/PhysRevE.66.065102 |
| [21] |
彭兴钊, 姚宏, 杜军, 等. 负荷作用下相依网络中的级联故障[J]. 物理学报, 2015, 64(4): 355. PENG Xingzhao, YAO Hong, DU Jun, et al. Load-induced cascading failure in interdependent network[J]. Acta Physica Sinica, 2015, 64(4): 355. DOI:10.7498/aps.64.048901 |
| [22] |
WANG Jianwei, RONG Lili. A model for cascading failures in scale-free networks with a breakdown probability[J]. Physica A: Statistical Mechanics and its Applications, 2009, 388(7): 1289. DOI:10.1016/j.physa.2008.12.067 |
| [23] |
KIM D H, MOTTER A E. Resource allocation pattern in infrastructure networks[J]. Journal of Physics A: Mathematical and Theoretical, 2008, 41(22): 224019. DOI:10.1088/1751-8113/41/22/224019 |
| [24] |
杨迎辉, 李建华, 沈迪, 等. 体系作战信息流转层级网络级联失效模型[J]. 计算机应用研究, 2017, 34(7): 2099. YANG Yinghui, LI Jianhua, SHEN Di, et al. Cascading failure model for systematic operations information flowing layered network[J]. Application Research of Computers, 2017, 34(7): 2099. DOI:10.3969/j.issn.1001-3695.2017.07.040 |
| [25] |
郝羽成, 李成兵, 魏磊. 考虑节点过载的复杂网络级联失效模型[J]. 系统工程与电子技术, 2018, 40(10): 2282. HAO Yucheng, LI Chengbing, WEI Lei. Cascading failure model of complex networks considering overloaded nodes[J]. Systems Engineering and Electronics, 2018, 40(10): 2282. DOI:10.3969/j.issn.1001-506X.2018.10.19 |
| [26] |
HONG Chen, ZHANG Jun, DU Wenbo, et al. Cascading failures with local load redistribution in interdependent Watts-Strogatz networks[J]. International Journal of Modern Physics C, 2016, 27(11): 1650131. DOI:10.1142/S012918311650131X |
| [27] |
SUN H J, ZHAO H, WU J J. A robust matching model of capacity to defense cascading failure on complex networks[J]. Physica A: Statistical Mechanics and Its Applications, 2008, 387(25): 6431. DOI:10.1016/j.physa.2008.07.028 |
| [28] |
MORENO Y, PASTOR-SATORRAS R, VÁZQUEZ A, et al. Critical load and congestion instabilities in scale-free networks[J]. Europhysics Letters(EPL), 2003, 62(2): 292. DOI:10.1209/epl/i2003-00140-7 |
| [29] |
GAO Yanli, CHEN Shiming, NIE Sen, et al. Robustness analysis of interdependent networks under multiple-attacking strategies[J]. Physica A: Statistical Mechanics and its Applications, 2018, 496: 495. DOI:10.1016/j.physa.2017.12.085 |
| [30] |
BOYD J R. A discourse on winning and losing[M]. Alabama: Air University Press, 2018: 383.
|
| [31] |
GAO Jiazi, YIN Yongfeng, LANCE F, et al. Recovery of coupled networks after cascading failures[J]. Journal of Systems Engineering and Electronics, 2018, 29(3): 650. DOI:10.21629/JSEE.2018.03.22 |
| [32] |
CHEN Duanbing, LÜ Linyuan, SHANG Mingsheng, et al. Identifying influential nodes in complex networks[J]. Physica A: Statistical Mechanics and its Applications, 2012, 391(4): 1777. DOI:10.1016/j.physa.2011.09.017 |
| [33] |
BOLLOBÁS B. The evolution of random graphs[J]. Transactions of the American Mathematical Society, 1984, 286(1): 257. DOI:10.1090/s0002-9947-1984-0756039-5 |
| [34] |
GOH K I, KAHNG B, KIM D. Universal behavior of load distribution in scale-free networks[J]. Physical Review Letters, 2001, 87(27Pt 1): 278701. DOI:10.1103/PhysRevLett.87.278701 |
| [35] |
NEWMAN M E J, WATTS D J. Renormalization group analysis of the small-world network model[J]. Physics Letters A, 1999, 263(4/5/6): 341. DOI:10.1016/s0375-9601(99)00757-4 |
 2024, Vol. 56
2024, Vol. 56


