2. 中国商用飞机责任有限公司 上海飞机设计研究院, 上海 201210
2. Commercial Aircraft Corporation of China Ltd., Shanghai Aircraft Design and Research Institute, Shanghai 201210, China
广布疲劳损伤是大型民用客机和运输机结构设计和适航验证必须考虑的问题[1-2],它指飞机的相同或相邻结构中广泛分布的裂纹达到了一定尺寸和密度之后,不再满足损伤容限剩余强度要求[1]。统计表明:因广布疲劳损伤而导致的飞机结构安全事故多达三十余起,涉及十几个机型[2]。著名的如1988年Aloha航空公司的波音737事故。广布疲劳损伤主要有两种形式:多位置损伤和多元件损伤。多位置损伤指同一结构的不同位置出现了一定数量的小裂纹,它们在服役过程中不断扩展、连通,最终形成长裂纹而导致结构破坏。因此,开展多位置损伤敏感结构的疲劳裂纹扩展分析方法研究对飞机安全具有重要意义。
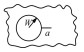
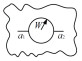
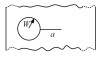
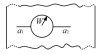
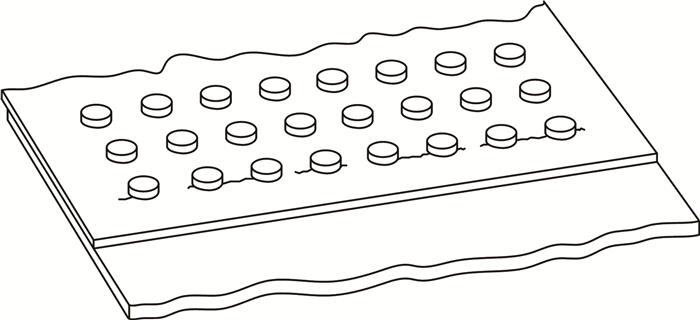
为研究多位置损伤,国内外开展了大量的试验和分析研究[3-5]。张健萍等[4]试验研究了多光孔平板的裂纹萌生寿命,提出了确定飞机结构多位置损伤平均行为的寿命升降法。李政鸿等[5]通过试验和分析研究了含8孔多裂纹平板的疲劳裂纹扩展行为。Newman等[6]研究了老龄飞机单列3铆钉搭接板的疲劳裂纹萌生和扩展寿命。Galatolo等[7]研究了多排铆钉搭接平板的设计方法,开展了裂纹萌生与扩展行为试验研究。图 1所示的多排铆钉搭接结构为典型多位置损伤敏感结构,由于其铆钉孔边裂纹个数、位置和大小随机多变,铆钉与平板间存在的复杂接触关系随裂纹扩展而发生变化,如何高效、准确地计算其应力强度因子是疲劳裂纹扩展分析预测的关键之一。
|
图 1 多排铆钉搭接结构的复杂裂纹构型 Fig. 1 Complex crack configurations in multi-rivet lap joint |
有限元法是处理复杂裂纹问题最常用的方法。Cope等[8]对搭接结构进行了简化,采用有限元法计算了孔边裂纹应力强度因子。陈跃良等[9-10]采用FRANC2D/L软件计算了多铆钉连接结构的应力强度因子。邹君等[11]基于ABAQUS软件,建立三维有限元模型,得到了含多位置损伤搭接结构的应力强度因子。有限元法分析复杂接触裂纹问题的计算效率低、收敛性差,且需开发专门网格自动划分程序以实现裂纹扩展。如采用有限元法完成图 1所示的铆钉孔边裂纹扩展分析需数百小时,进而在工程上难以得到广泛应用。除有限元法外,聂峰华等[12]采用了无网格方法来分析二维平面多裂纹问题,赵树力等[13]采用近场动力学分析了多裂纹的疲劳裂纹扩展行为。
相比于上述方法,权函数法计算精度和效率高,是另一种常用于分析裂纹体受复杂载荷下应力强度因子的方法。针对各类有限边界裂纹体问题,文献[14-16]建立了基于张开位移的正则化权函数法,给出了几十个裂纹构型的权函数。基于吴学仁-Carlsson规范化权函数法,Xu等[16-17]给出了典型平板多孔多裂纹和加筋板结构的应力强度因子解。值得指出的是,目前权函数法主要应用于单一简单结构,对于本文研究的铆钉搭接结构(组合结构),尚无对应的解析权函数可供直接使用。
为此,在已有的权函数法研究基础上[15],本文提出采用简单裂纹构型的权函数结合壳/三维铆钉无裂纹模型的应力分析,以获得铆钉孔边裂纹的应力强度因子。在此基础上,采用Paris裂纹扩展公式对铆钉搭接结构进行疲劳裂纹扩展分析并通过试验进行验证。研究结果表明, 采用本文方法计算的应力强度因子与完全采用有限元方法计算的应力强度因子的相对差别小于5%,只需约5 min便可获得与试验结果吻合良好的多铆钉孔边疲劳裂纹扩展行为,计算效率比完全采用有限元法快3个数量级,进而为多铆钉搭接结构孔边裂纹的应力强度因子和疲劳裂纹扩展分析提供了一个高效、可靠的方法。
1 铆钉搭接平板应力强度因子计算的权函数法及验证快速、准确获得图 1所示复杂裂纹构型的应力强度因子,对铆钉连接结构的多裂纹扩展分析具有关键作用。本文将给出并验证铆钉搭接结构孔边裂纹应力强度因子的权函数分析方法。
1.1 铆钉搭接板应力强度因子计算的权函数法根据权函数法,裂纹体受外载荷作用下的裂尖应力强度因子K可通过下式获得:
| $ K(a)=\int_{0}^{a} \sigma(x) \cdot m(a, x) \mathrm{d} x $ | (1) |
式中: a、x分别为裂纹长度和沿裂纹线上的坐标, σ(x)为没有裂纹存在时,受载结构在假想裂纹面上的应力分布,也称无裂纹应力; m(a, x)为权函数,其正则化形式由下式给出:
| $ m(\alpha, \xi)=\frac{1}{\sqrt{2 \pi \alpha}} \sum\limits_{i=1}^{5} \beta_{i}(\alpha) \cdot\left(1-\frac{\xi}{\alpha}\right)^{i-\frac{3}{2}} $ | (2) |
式中:α=a/W, ξ=x/W, α、ξ分别为量纲一的裂纹长度和裂纹面上量纲一的坐标; W为裂纹的特征尺寸,对于文章中需要分析的问题,W为铆钉孔的半径。为方便工程应用,文献[18]对式(2)中的βi作如式(3)的拟合, 并给出了孔边裂纹权函数的拟合系数bin。
| $ \beta_{i}(\alpha)=\sum\limits_{n=0}^{k} b_{i n} \cdot \alpha^{n} $ | (3) |
对于本文研究的如图 1所示的多铆钉搭接结构,在裂纹萌生及扩展过程中将出现复杂多样的裂纹构型,目前尚无相应的解析权函数。因此,本文对这些复杂裂纹构型进行简化等效处理,以应用简单裂纹构型的权函数求解应力强度因子。裂纹萌生初期长度较短,可处理为孔边裂纹,随着裂纹长度增长,需考虑裂纹间的相互影响。所有等效处理方式汇总见表 1。对于较短(a/W<2)的孔边单/双裂纹,采用孔边单裂纹[18]或孔边双裂纹的权函数[19];对于较长(a/W>2)的孔边单裂纹和双裂纹以及连通两孔的长裂纹,则将孔与裂纹等效为一条偏心长裂纹,有限边界板偏心裂纹的权函数由文献[20-21]给出;对于裂尖接近的连通长裂纹,则采用共线裂纹权函数,其权函数由文献[17]给出。
| 表 1 各种典型裂纹的简化方法 Tab. 1 Simplifications of different crack configurations |
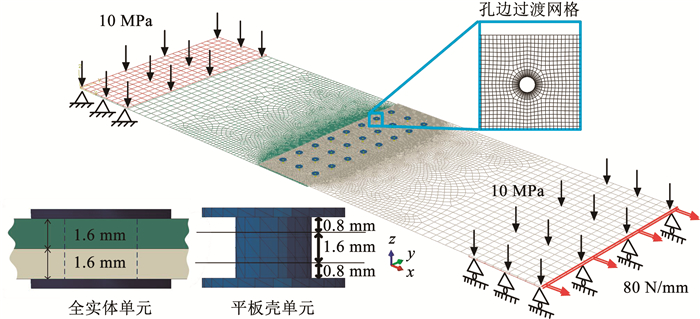
根据式(1),使用权函数法计算裂纹体受外载作用下的应力强度因子需无裂纹应力σ(x)。本文采用ABAQUS/Standard进行有限元分析,以获得搭接结构的无裂纹应力σ(x)。图 2给出了多铆钉搭接试件的有限元模型,其详细材料参数见文献[22]。为降低计算成本并提高收敛性,模型中的搭接板简化为壳单元。为保证孔边无裂纹应力σ(x)的精度,需准确模拟平板间、平板与铆钉间的接触关系。因此,铆钉使用C3D10实体单元模拟。平板为S4R壳单元,厚度为1.6 mm。单元全局尺寸为5 mm,平板铆钉孔边使用过渡网格,靠近孔边最小单元尺寸0.1 mm。
|
图 2 无裂纹搭接平板的有限元模型 Fig. 2 Finite element model for stress analysis without hole-edge cracks |
有限元模型的边界条件如图 2所示。左端夹持区的下表面固支,右端夹持区下表面仅允许x方向位移,两端夹持区上表面施加10 MPa的均布夹紧力。右端壳边缘施加80 N/mm的均布载荷。根据试件几何尺寸,载荷传递至搭接板后,远端截面应力为100 MPa。模型使用通用接触(general contact)定义所有接触部位。接触的法向行为为“硬”接触,切向设置滑动摩擦系数为0.33。
另一种获得无裂纹应力的建模方法是平板、铆钉均采用三维实体单元模拟。相比于壳单元,三维实体单元能够更准确地模拟平板间及平板与铆钉间的接触关系,但代价是计算量大。此外,如果采用该方法分析含裂纹搭接板,计算量更大且不易收敛。
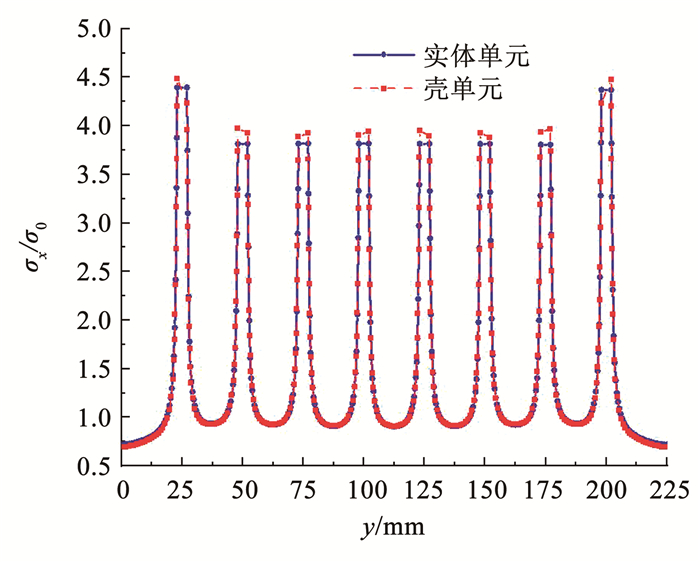
通过对上述两种模型进行线弹性有限元分析,可获得孔边应力分布。根据有限元结果,搭接板三排铆钉孔中,靠近夹持端的一排应力显著偏高,是疲劳损伤关键位置,其孔边应力分布如图 3所示,其中: σx为平板上、下表面x方向(拉伸方向)应力的均值,σ0=100 MPa为远端截面应力。为评估使用壳单元简化有限元模型的计算精度,图 3中也给出了使用三维实体单元建模的计算结果。从图 3中可以看出, 采用壳单元的模型可以得到准确的应力分布。计算效率上,采用壳单元比采用三维实体单元模拟平板的模型计算效率高10倍。
|
图 3 简化壳单元模型与3D实体单元模型的关键排孔边无裂纹应力分布对比 Fig. 3 Comparison of crack-free stress distributions from shell and 3D solid element models(row of holes close to the applied load) |
本文采用有限元法验证权函数法的精度。由于有限元软件的J积分计算结果在壳单元上与积分路径相关,本文根据裂尖应力场、位移场与应力强度因子的关系,采用应力外推法、位移外推法和虚拟裂纹闭合方法[23]计算铆钉孔边裂纹的Ⅰ型应力强度因子。
位移外推法使用下式计算应力强度因子:
| $ K_{i}=\frac{V_{i} \sqrt{2 \pi / r_{i}}}{G(1+k)}, K=\frac{\sum r_{i} \cdot \sum r_{i} K_{i}-\sum r_{i}^{2} \cdot \sum K_{i}}{\left(\sum r_{i}\right)^{2}-N \cdot \sum r_{i}^{2}} $ | (4) |
式中:Ki为裂纹线上第i个位置的名义应力强度因子,ri为该位置离裂尖的距离,Vi为该位置裂纹张开位移,G为材料剪切模量, k=(3-n)/(1+n),其中n为泊松比,K为应力强度因子,外推公式中N为数据点总个数。裂尖附近位置的Ki会有震荡趋势,外推时应剔除这些数据[23]。
应力外推法使用下式计算应力强度因子:
| $ K_{i}=\sigma_{i} \sqrt{2 \pi r_{i}}, K=\frac{\sum r_{i} \cdot \sum r_{i} K_{i}-\sum r_{i}^{2} \cdot \sum K_{i}}{\left(\sum r_{i}\right)^{2}-N \cdot \sum r_{i}^{2}} $ | (5) |
应力外推法使用裂纹张开应力计算Ki,式中σi为裂纹延长线上第i个位置的裂纹张开方向内应力(上、下表面平均)。由于本文采用的S4R线性单元不能准确描述应力奇异性,裂尖附近位置的Ki会有突变,外推时应剔除这些数据[23]。
虚拟裂纹闭合法使用下式计算应力强度因子:
| $ \frac{K^{2}}{E}=\frac{F_{1} \cdot V_{2}}{B \cdot r_{12}} $ | (6) |
式中:F1为裂尖节点(位置1)张开方向的节点力,V2为裂纹线上与裂尖相邻的节点对(位置2)的裂纹张开位移,B为壳单元厚度,r12为1位置和2位置的距离。
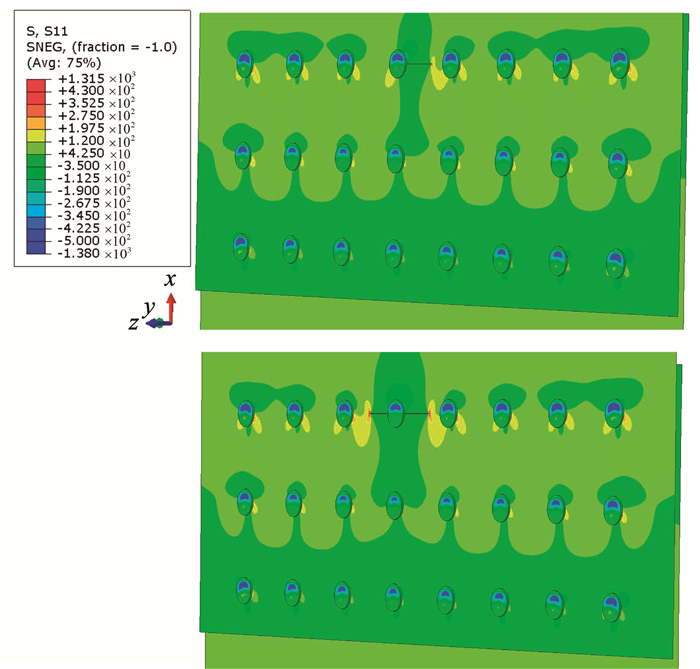
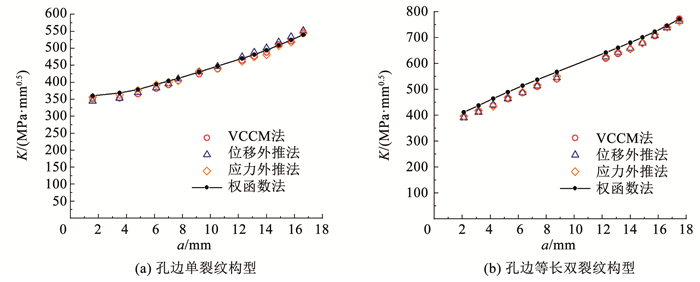
采用铆钉孔边单裂纹和等长双裂纹有限元模型进行对比验证,将裂纹引入铆钉搭接板应力强度因子计算的权函数法中的简化有限元模型进行分析,应力云图如图 4所示。铆钉孔边单裂纹的长度从1.57~16.62 mm,等长双裂纹的长度从2.1~17.5 mm,根据裂纹构型的不同,从表 1选择对应的权函数,把无裂纹应力σ(x)(如图 3所示)代入式(1)得到不同裂纹长度下的应力强度因子,图 5给出了权函数法与3种有限元法得到的应力强度因子。从图 5中可以看出, 3种有限元法的计算结果与权函数法差别均在5%以内。由于两种外推法数据点选择及这3种方法本身的原因,3种有限元法计算结果存在小的差别。权函数法与有限元法的计算结果在裂纹较短(a/W<2)时偏差相对较大,是由真实裂纹构型与等效构型的差别引起。图 5的对比结果表明,本文提出的权函数分析方法对复杂连接结构裂纹问题具有很高的精度。
|
图 4 铆钉孔边单裂纹和等长双裂纹的应力云图 Fig. 4 Stress distribution of a single and double hole-edge cracks |
|
图 5 采用权函数法和有限元计算两种裂纹构型的应力强度因子 Fig. 5 Comparison of SIFs obtained by WFM and FEM |
计算效率上,由于涉及复杂接触,即使采用壳单元建模,有限元法计算单个带裂纹算例仍需2 h; 而采用权函数法,计算图 5中所有算例仅需5 s。即,采用权函数法计算铆钉孔边裂纹应力强度因子的效率比有限元法快3个数量级。
2 搭接结构疲劳裂纹扩展试验多铆钉搭接结构是典型的多位置损伤敏感结构。其特点是存在大量疲劳关键细节(铆钉孔),服役过程中关键细节应力水平相近,进而易发生多位置损伤。为研究此类结构的疲劳裂纹扩展行为,设计了如图 6所示单板尺寸为225.0 mm×387.5 mm的搭接件。试件单板厚1.6 mm,材料为2024-T3铝合金。夹持端铆接同厚度支持板以减小应力并保证试验对中,从而避免试件在夹持端破坏。试件中部由3排铆钉连接,通过有限元分析发现:由于自由边和泊松效应的影响,图 6所示最左和最右两列铆钉孔的孔边应力明显高于中间孔(详细结果如图 3所示)。为避免疲劳裂纹过早萌生在这些位置,产生单一裂纹而没有达到研究多位置损伤的目的,最左和最右列紧固件采用高锁螺栓以提高孔边疲劳强度,中间6列采用铆钉连接以获得多条疲劳裂纹。高锁螺栓和铆钉直径均为4 mm。同排孔心距为25 mm,排间距为25 mm,外侧孔心距板边25 mm。

|
图 6 多铆钉搭接试件几何尺寸与疲劳试验装置 Fig. 6 Geometry dimensions and test setup of rivet joint panels |
为确保试验中应力均匀传递,板正反面对称位置贴有12枚应变片以便试验对中。正式试验前,采用20 MPa的拉伸载荷进行预实验,当对应位置应变的相对差别小于5%时,可进行正式试验。试验在室温下进行,应力比R=0.06,加载频率f=6 Hz。试件分为两类。其中1-6号为试件远端截面最大应力σmax=115 MPa,7-11号为试件的远端截面最大应力σmax=125 MPa。试验过程中使用高分辨率相机定时记录各试件孔边裂纹的裂尖位置。两种载荷下,所有试件均出现多条疲劳裂纹。图 7给出了一个典型的多裂纹连通与断裂照片,详细试验结果将在后续部分给出。

|
图 7 典型多裂纹连通与断裂现象 Fig. 7 Multiple hole-edge cracks link up and fracture |
本文将采用铆钉搭接平板应力强度因子计算的权函数法分析典型铆钉孔边裂纹的疲劳扩展,并采用搭接结构疲劳裂纹扩展的试验进行验证。
3.1 裂纹扩展分析方法为预测铆钉孔边疲劳裂纹的扩展,本文采用Paris公式结合铆钉搭接平板应力强度因子计算经过验证的权函数方法进行疲劳裂纹扩展分析:
| $ \frac{\mathrm{d} a}{\mathrm{~d} N}=C \cdot(\Delta K)^{m} $ | (7) |
式中: a为裂纹长度,mm;N为载荷循环数, C、m为材料参数,根据手册[24],C=2.34×10-8,m=3.427;ΔK为一个载荷循环内应力强度因子极差, MPa·m0.5。
一旦材料参数C和m通过试验确定,采用Paris公式分析预测裂纹扩展的核心便是获得裂纹尖端的应力强度因子。对于本文研究的铆钉连接结构,由于裂纹位置和个数不定,目前没有解析的应力强度因子解,不能解析积分式(7)获得裂纹扩展长度a与循环数N的关系。实际运算时,使用下式获得裂纹长度a与循环数N的关系:
| $ a(N)=\sum\limits_{n=0}^{n=N} C \cdot[\Delta K(a)]^{m} \Delta n $ | (8) |
式中Δn为循环数的计算步长。理论上,Δn=1,即每次循环均需更新裂纹长度。这种方法需计算数万次应力强度因子,计算量巨大。由于试件实际寿命通常在1万~10万循环之间,单个循环裂纹扩展很小,权衡计算效率与精度,本文取Δn=100。使用式(8),并结合权函数法得到每100个循环后各裂尖的ΔK,便可获得裂纹扩展过程中各裂纹长度a随循环数N的变化关系。
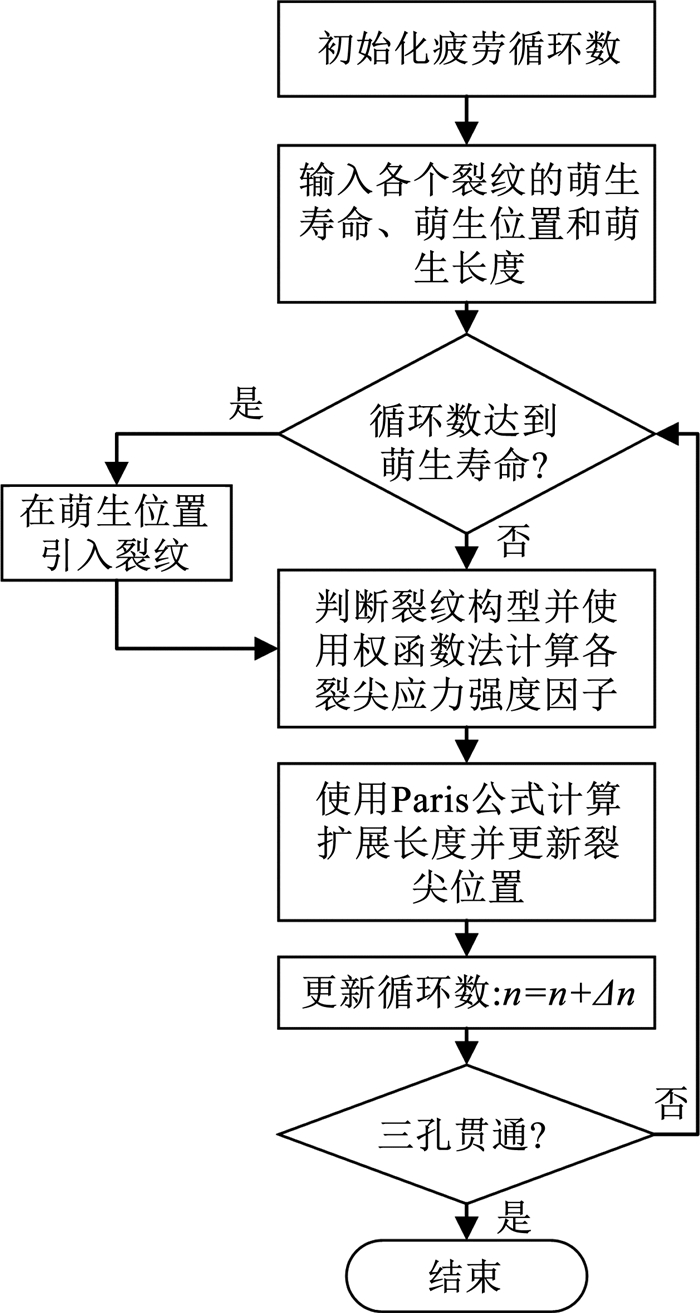
裂纹扩展分析的流程如图 8所示。试件在破坏前不久均发生相邻3个铆钉孔裂纹连通的现象,因此将其作为裂纹扩展分析的终止条件。
|
图 8 疲劳裂纹扩展分析流程 Fig. 8 Flow chat of fatigue crack growth analysis |
表 2给出了试件的试验结果与裂纹扩展寿命预测结果。其中试验得到的首条、第2条、第3条裂纹萌生寿命分别由N1st、N2nd、N3rd表示,结构疲劳寿命由Nfail表示,裂纹扩展寿命由Nfail-N1st表示。从表 2中可看出,使用本文方法进行疲劳裂纹扩展分析得到的裂纹扩展寿命与试验结果偏差在20%以内。
| 表 2 试件的疲劳寿命试验结果与扩展寿命预测结果 Tab. 2 Test result and crack growth life prediction results of specimens |
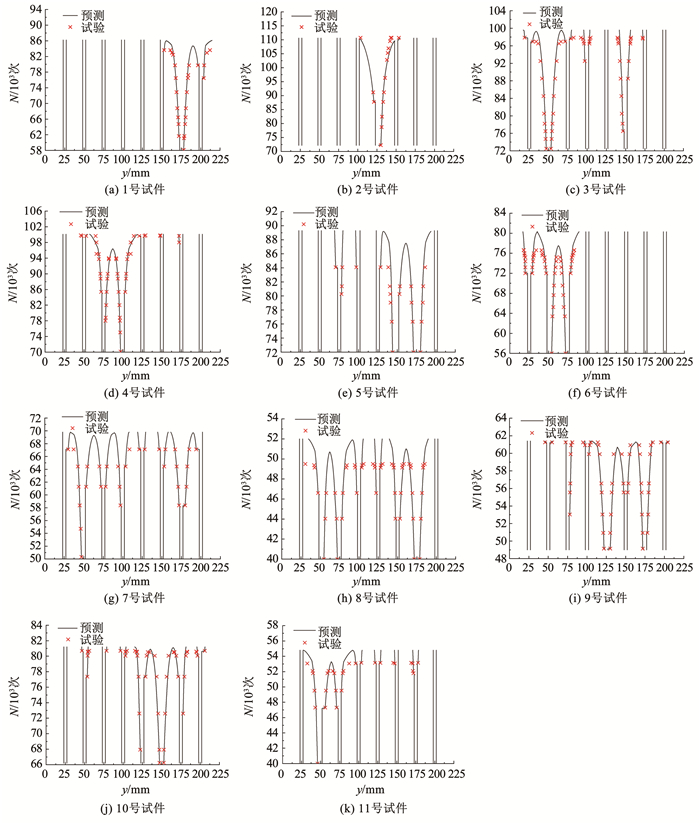
采用裂纹扩展分析方法中的分析方法,对搭接结构疲劳裂纹扩展介绍的搭接试件进行裂纹扩展分析,分析中初始裂纹长度为试验中铆钉孔边萌生多条目视可见裂纹的长度。图 9给出了搭接结构疲劳试验中各平板萌生多条裂纹的循环数以及疲劳裂纹扩展长度与循环数的关系(用“×”表示)。图 9中纵坐标表示循环数,横坐标表示孔边裂纹的裂尖位置。试验结果表明, 各试件萌生裂纹的寿命、数量和位置不同,2个或以上铆钉孔萌生疲劳裂纹后仍可经历几万次循环。分析获得的裂纹扩展长度与寿命的关系如图 9中实线所示,每个搭接件的疲劳裂纹扩展分析约需5 min完成。从图 9中可以看出,分析获得的裂纹扩展行为与试验结果吻合良好。
|
图 9 裂纹扩展分析结果与试验对比 Fig. 9 Comparison of predicted and experimental results |
1) 采用壳单元模拟搭接板和三维实体单元模拟铆钉的有限元建模方式,可高效、准确地获得铆钉孔边无裂纹情况下的应力分布。
2) 权函数法计算的应力强度因子与有限元法分析结果的相对差别小于5%。
3) 基于权函数法和Paris裂纹扩展公式分析预测的搭接板多裂纹扩展寿命与试验结果的相对差别在20%之内,裂纹扩展行为与试验吻合良好。
4) 在计算精度相当(相对差别小于5%)的条件下,权函数法计算应力强度因子的效率比有限元法快3个数量级。
| [1] |
王生楠, 郑晓玲. 运输类飞机防止广布疲劳损伤的新规章解读[J]. 航空学报, 2010, 31(9): 1758. WANG Shengnan, ZHENG Xiaoling. Study on proposed rules to preclude widespread fatigue damage for transport category aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(9): 1758. |
| [2] |
FAA. Aging airplane program: Widespread fatigue dam-age: FAA-2006-24281-2010[S]. Washington, DC: Federal Register, Rules and Regulations, 2010
|
| [3] |
PITT S, JONES R. Multiple-site and widespread fatigue damage in aging aircraft[J]. Engineering Failure Analysis, 1997, 4(4): 237. DOI:10.1016/s1350-6307(97)00020-4 |
| [4] |
张健萍, 时新红, 张建宇, 等. 确定飞机结构WFD平均行为的寿命升降法[J]. 北京航空航天大学学报, 2016, 42(1): 147. ZHANG Jianping, SHI Xinhong, ZHANG Jianyu, et al. Life up and down method for determining WFD average behavior of aircraft structures[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(1): 147. DOI:10.13700/j.bh.1001-5965.2015.0056 |
| [5] |
李政鸿, 徐武, 张晓晶, 等. 多孔多裂纹平板的疲劳裂纹扩展试验与分析方法[J]. 航空学报, 2018, 39(7): 221867-1. LI Zhenghong, XU Wu, ZHANG Xiaojing, et al. Experimental and analytical analyses of fatigue crack growth in sheets with multiple holes and cracks[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(7): 221867-1. DOI:10.7527/S1000-6893.2018.21867 |
| [6] |
NEWMAN J C Jr, RAMAKRISHNAN R. Fatigue and crack-growth analyses of riveted lap-joints in a retired aircraft[J]. International Journal of Fatigue, 2016, 82(2): 342. DOI:10.1016/j.ijfatigue.2015.04.010 |
| [7] |
GALATOLO R, LAZZERI R. Experiments and model predictions for fatigue crack propagation in riveted lap-joints with multiple site damage[J]. Fatigue & Fracture of Engineering Materials & Structures, 2016, 39(3): 307. DOI:10.1111/ffe.12354 |
| [8] |
COPE D, LACY T. Stress intensity determination in lap joints with mechanical fasteners[C]//Proceedings of the 41st Structures, Structural Dynamics, and Materials Conference and Exhibit. Reston, Virigina: AIAA, 2000: AIAA2000-1368. DOI: 10.2514/6.2000-1368
|
| [9] |
陈跃良, 郁大照, 杨茂胜, 等. 含多处损伤搭接结构应力强度因子有限元分析[J]. 航空学报, 2007, 28(3): 615. CHEN Yueliang, YU Dazhao, YANG Maosheng, et al. Finite element analysis of stress intensity factors of lap joint with multiple site damage[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(3): 615. DOI:10.3321/j.issn:1000-6893.2007.03.022 |
| [10] |
陈跃良, 杨茂胜, 张勇. 考虑微动影响的搭接结构应力强度因子有限元分析[J]. 失效分析与预防, 2011, 6(4): 199. CHEN Yueliang, YANG Maosheng, ZHANG Yong. Finite element analysis of stress intensity factors of single lap joint with under inching[J]. Failure Analysis and Prevention, 2011, 6(4): 199. DOI:10.3969/j.issn.1673-6214.2011.04.001 |
| [11] |
邹君, 张悦超, 冯振宇, 等. 含多部位损伤搭接结构应力强度因子三维有限元分析[J]. 南京航空航天大学学报, 2020, 52(4): 618. ZOU Jun, ZHANG Yuechao, FENG Zhenyu, et al. Three-dimensinal finite element analysis of stress intensity factors of lap joints with multiple site damage[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2020, 52(4): 618. DOI:10.16356/j.1005-2615.2020.04.013 |
| [12] |
聂峰华, 潘金虎, 李冬明, 等. 基于修正权函数的多裂纹无网格模拟[J]. 固体力学学报, 2022, 43(2): 208. NIE Fenghua, PAN Jinhu, LI Dongming, et al. Meshless simulation of multi-crack problems based on modified weight function[J]. Chinese Journal of Solid Mechanics, 2022, 43(2): 208. DOI:10.19636/j.cnki.cjsm42-1250/o3.2021.054 |
| [13] |
赵树力, 余音, 徐武. 疲劳多裂纹扩展的常规态型近场动力学分析[J]. 哈尔滨工业大学学报, 2019, 51(4): 19. ZHAO Shuli, YU Yin, XU Wu. Ordinary state-based peridynamics method for fatigue multi-crack propagation[J]. Journal of Harbin Institute of Technology, 2019, 51(4): 19. DOI:10.11918/j.issn.0367-6234.201709154 |
| [14] |
袁奎霖, 江燕, 赵峰, 等. 大深长比表面裂纹应力强度因子的二维权函数[J]. 船舶力学, 2020, 24(11): 1453. YUAN Kuilin, JIANG Yan, ZHAO Feng, et al. 2D weightfunction for stress intensity factor of semi-elliptical surface cracks with high aspect ratio[J]. Journal of Ship Mechanics, 2020, 24(11): 1453. DOI:10.3969/j.issn.1007-7294.2020.11.009 |
| [15] |
吴学仁, 徐武. 裂纹体分析的权函数理论与应用: 回顾和展望[J]. 力学进展, 2022, 52(3): 415. WU Xueren, XU Wu. Weight function theory and applications for crack analysis: A review and outlook[J]. Advances in Mechanics, 2022, 52(3): 415. DOI:10.6052/1000-0992-21-060 |
| [16] |
XU Wu, WU Xueren, YU Yin, et al. A weight function method for mixed modes hole-edge cracks[J]. Fatigue & Fracture of Engineering Materials & Structures, 2018, 41(1): 223. DOI:10.1111/ffe.12674 |
| [17] |
ZHANG Bo, XU Wu, WU Xueren, et al. Stress intensity factors and plastic zones of stiffened panels with multiple collinear cracks[J]. Theoretical and Applied Fracture Mechanics, 2020, 110: 102816. DOI:10.1016/j.tafmec.2020.102816 |
| [18] |
吴学仁, 童第华, 徐武, 等. 断裂力学的权函数理论与应用[M]. 北京: 航空工业出版社, 2019. WU Xueren, TONG Dihua, XU Wu, et al. Weight function methods in fracture mechanics: Theory and applications[M]. Beijing: Aviation Industry Press, 2019. |
| [19] |
ZHANG Bo, XU Wu, WU Xueren. Weight function method and stress intensity factor for two unsymmetric through-thickness and quarter-elliptical corner cracks at circular hole[J]. Engineering Fracture Mechanics, 2022, 264: 108361. DOI:10.1016/j.engfracmech.2022.108361 |
| [20] |
CHEN X, ALBRECHT P. Weight functions for eccentric cracks[M]//Fracture Mechanics: Twenty-Fourth Volumes. West Conshoho cken, PA: ASTM International, 1994: 581. DOI: 10.1520/stp13728s
|
| [21] |
HE Xiaofan, DONG Yinghao, YANG Boxiao, et al. A wide range stress intensity factor solution for an eccentrically cracked middle tension specimen with clamped ends[J]. Engineering Fracture Mechanics, 2018, 191: 461. DOI:10.1016/j.engfracmech.2018.01.007 |
| [22] |
饶聃钰, 徐武, 张博, 等. 飞机典型连接结构多位置损伤实验设计及验证[J]. 机械设计与研究, 2021, 37(5): 148. RAO Danyu, XU Wu, ZHANG Bo, et al. Experimental design and verification of typical aircraft joint structures with multiple site damage[J]. Machine Design & Research, 2021, 37(5): 148. |
| [23] |
解德, 钱勤, 李长安. 断裂力学中的数值计算方法及工程应用[M]. 北京: 科学出版社, 2009. XIE De, QIAN Le, LI Chang'an. Numerical calculation method in fracture mechanics and its engineering application[M]. Beijing: Science Press, 2009. |
| [24] |
《某型飞机设计用关键金属材料力学性能数据手册》编委会. 某型飞机设计用关键金属材料力学性能数据手册[M]. 北京: 航空工业出版社, 2016.
|
| [38] |
Editorial board of the Mechanical properties data manual of key metal materials for aircraft design. Mechanical properties data manual of key metal materials for aircraft design[M]. Beijing: Aviation Industry Press, 2016.
|
 2024, Vol. 56
2024, Vol. 56