2. 中国科学院复杂航天系统电子信息技术重点实验室(中国科学院国家空间科学中心), 北京 100190;
3. 中国科学院大学,北京 100049
2. Key Laboratory of Electronics and Information Technology for Space Systems (National space Science Center, Chinese Academy of Sciences), Beijing 100190, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
小行星探测以获取其资源成分、形态结构和运动特征等基本信息为目标,对于认识太阳系、研究生命起源和演化具有重大意义[1]。这些年,随着深空探测能力的逐渐提升,美国、日本、欧盟及俄罗斯已经实施了多次小行星探测着陆任务[2]。中国也将深空探测任务写入“十三五”规划,预期于2025年左右对近地小行星2016HO3和主带彗星133P进行探测。由于小行星形状各异,引力场分布不均匀,若事先没有关于所探测小行星的具体形状、引力分布等信息,则难以提前准确规划轨道及实现导航,在抵近详细观测后才能进行下一步工作。但由于多数探测目标距离地球较远,通讯的传输延迟长,因此要求探测器在接近目标天体时具备自主探测能力[3]。自主导航和表面建模是行星自主探测的主要关键技术,能实现获取航天器相对于小行星表面的位置、姿态、小天体自身运动参数、三维模型及引力场等基本信息[4]。
传统航天器导航的方式,一般基于累积误差不受控的惯性元件,或基于能耗较高、测量范围受限的激光雷达等主动传感器,在周期长、能耗有限的深空探测任务中应用效果有限[5]。因此,深空自主导航系统普遍采用能耗低且能获取丰富图像信息的视觉导航系统,它可以通过探测器上的摄像头拍摄一系列不同位置的图片,利用图片估计出探测器自身的位置信息,在此基础上进行探测器轨道规划及控制。从自主性的角度分析,现有的行星视觉导航方法需要前期对小行星进行长时间的绕飞观测,并且要求大量人工参与重建天体模型和标记路标特征,不适应未来自主探测导航的发展需求;从定位精度的角度分析,提前标记参考特征库的方法,容易受光照、尺度、视角变化影响,在探测器降落过程中特征提取和匹配中引入误差,进而影响导航定位精度[6]。因此需要在小行星探测任务中引入一种自主导航技术,以适应未来在未知无先验信息环境中进行探测的需求。
同时定位与地图构建(simultaneous localization and mapping,SLAM)是近年来导航方法的研究热点方向,该技术可以在未知环境中实现探测设备的相对定位,不依赖前期观测和现有特征。视觉SLAM算法主要在运动中利用相机连续拍摄图像对自身的位置和姿态进行估计,同时对环境进行增量式地地图构建,从而实现在未知场景中的路径规划、导航、避障等功能。视觉SLAM目前已经在地面自主机器人、自动驾驶等任务中取得显著成功。近些年也有学者将视觉SLAM应用在深空领域小行星探测研究中。文献[7]将基于SURF特征的单目视觉里程计与基于Rao-Blackwellized粒子过滤器的SLAM系统相结合,在绘制小行星地形的同时估计探测器的位置和姿态。文献[8]之后的研究在此基础上利用单目视觉SLAM框架进行近实时导航,研究了基于粒子滤波的小天体附近航天器状态估计。文献[9]用扩展卡尔曼滤波(extended kalman filter, EKF)来跟踪航天器的位置和速度,并利用轨道动力学来解析尺度。但是基于粒子滤波器和EKF等滤波算法存在鲁棒性不强、在大型场景中效率低等问题,而基于因子图优化的方式能通过关键帧建立多个节点和节点之间的变换关系,在保证精度同时提高效率[10]。文献[11]融合了姿态传感器、惯性传感器和单目摄像机的测量,通过图优化估计探测器和小天体的相对位置和姿态,以及小天体的质心和自转轴等特性,但使用SIFT特征提取方式无法实时运行且无回环检测消除累计误差,文献[12]则是直接使用小行星公开特征库进行路标提取,未考虑真实图像的特征问题,因此在2021年文献[13]使用DAWN探测任务中拍摄的真实图片建立了一套包括前端、后端及回环检测的完整视觉SLAM,通过星追器和地球相对辐射器完成初始化,实现了相对导航和小行星表面建图,但其精度有限,未考虑行星真实的引力场对其运动的约束。此外,也有部分小行星导航算法研究在探究探测器的在轨运动状态时考虑小行星引力场的影响,但由于只采用了简化的模型,不符合真实的小行星引力场,在探测器距小行星较近时误差较大[12, 14]。以上应用在小行星探测场景中初步验证了视觉SALM算法在未知环境自主导航的可行性,但仍存在精度较低、场景适应性较差等问题:一是一些研究使用因子图优化的方式提高计算精度和效率,但未引入回环检测模块导致难以约束累积误差;二是由于真实数据稀缺,仿真实验大多基于小行星特征库而不是真实图像;三是仍未有研究考虑真实场景物理约束对定位系统的影响,因此算法精度有限,与实际探测应用也存在差距。
针对以上问题,本文提出了一种融合轨道动力学的深空探测器自主视觉定位方法,能在缺乏表面先验信息、无人工手动标记的场景中利用纯视觉信息,实现实时定位,建立小行星表面三维模型,并创新性地将轨道动力学作为一种物理约束引入小行星探测导航中,融合轨道动力学的轨道改进技术能显著提高导航精度。首先,基于视觉SLAM对小行星表面的特征进行提取匹配,通过因子图优化算法估计探测器位姿,为修正视觉累积误差设计回环检测提高定位精度。其次,重构行星表面三维模型,实现基于多面体法的行星不规则引力场建模。最后,提出了一种基于轨道动力学的伪相对运动分析精确轨道优化算法,修正视觉定位累计误差。经UNREAL ENGINE仿真引擎生成的数据验证,本文提出的方法能改善初始定位结果,从而实现高精度导航。
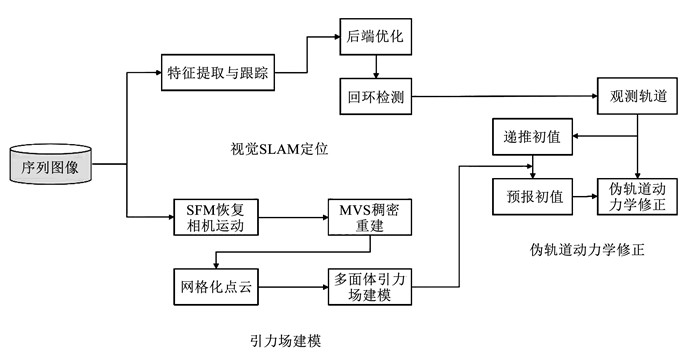
1 融合轨道动力学的行星探测器自主定位体系架构本文构建了融合轨道动力学的行星探测器自主定位体系架构,并针对视觉SLAM定位、引力场建模和伪轨道动力学修正算法开展了研究。小行星探测器在绕飞过程中通过单目相机拍摄表面图像,视觉SLAM定位算法对输入图像提取特征,并估计探测器的相对位姿;引力场建模算法根据输入图像通过多视角几何重建小行星表面三维结构,由此对引力场建模;伪轨道动力学修正算法结合视觉的初始定位结果和小行星引力场,修正累积误差,提高初定位精度。融合轨道动力学的行星探测器自主定位体系架构如图 1所示,根据功能主要分为3个部分。
|
图 1 融合轨道动力学的行星探测器自主定位体系架构 Fig. 1 Autonomous positioning architecture of planetary probes fused with orbital dynamics |
1) 视觉SLAM定位:对小行星表面的特征进行提取匹配与跟踪,通过因子图优化算法估计探测器位姿,利用回环检测修正视觉累积误差,提高定位精度。
2) 引力场建模:根据绕飞段的图像由SFM算法恢复相机运动并重构行星表面三维模型,通过MVS进行稠密重建,随后对点云进行网格化处理,再基于多面体法对不规则小行星引力场建模。
3) 伪轨道动力学修正算法:设计了一种基于轨道动力学的伪相对运动分析精确轨道优化算法,基于定位模块估计的探测器相对小行星位置姿态和引力场建模模块求解的行星不规则引力场,分析反演视觉初始定轨误差在轨道动力学中的传播过程,修正视觉定位累计误差,改善初始定位结果。
2 融合轨道动力学的行星探测器自主定位技术融合轨道动力学的行星探测器自主定位技术主要包括:视觉SLAM相对定位算法、小行星稠密建图及引力场建模算法、伪轨道动力学修正算法,本文分别针对3个算法进行详细介绍。
2.1 探测器导航相关坐标系定义定义小行星固连坐标系为{A},并以此作为世界坐标系,其中A为坐标系原点,通常是为小行星质心。探测器坐标系为{S},原点为探测器本体坐标系原点S,为了保证探测过程中小行星始终处于相机视野中,在绕飞时XS轴指向小行星质心,YS迹向方向,ZS为XS及YS叉乘结果。相机坐标系{C},在设定中相机位于探测器正前方,三轴与探测器坐标系{S}一致,像平面坐标系为{F}。
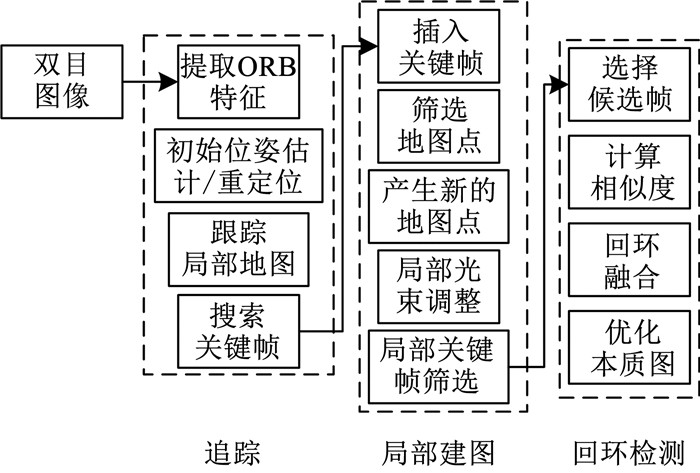
2.2 视觉SLAM相对定位算法视觉SLAM能根据提取到的路标特征实时计算自身相对于环境的位置和姿态,并建立环境地图。如图 2所示算法包括3个线程:追踪、局部建图和回环检测。追踪线程主要负责根据输入图像提取特征进行初始位姿估计,并建立关键帧。局部建图根据关键帧建立局部地图,回环检测线程通过词袋模型检测候选帧是否回环,最后优化全局地图并更新。
|
图 2 视觉SLAM流程 Fig. 2 Visual SLAM flow |
深空探测任务中,探测器在对行星表面进行特征提取时需要解决所获取图像随轨道高度变化而存在的尺度、角度和光照等变化问题,同时还需要考虑星上的算力限制。因此本文使用ORB(oriented FAST and rotated BRIEF)[15]算子进行特征提取,该方法具有尺度不变性和旋转不变性的特征点描述方法,能够利用增强的FAST(features from accelerated segment test)提取关键点,并使用方向归一化的BRIEF(binary robust independent elementary features)描述子表示关键点。根据ORB特征所构建的ORB-SLAM3[16]是如今公认综合性能最佳的视觉导航算法。
2.2.2 追踪追踪进程将输入的序列图像与地图点进行匹配计算相机位姿。当提取到ORB特征点之后,追踪进程主要将输入的序列图像与地图点进行匹配以计算相机的位姿信息。具体计算过程中,将第一帧图像的相机坐标系作为系统参考坐标系,通过序列图像的帧间匹配可以传递特征点的世界坐标,在帧间进行3D-3D对应估计可以求解参考坐标系与每帧图像对应的位姿关系。为了提高匹配精度降低误匹配,在前一帧追踪成功时,采用匀速运动模型或关键帧模型获得初始的位姿矩阵,再基于因子图优化模型最小化3D-2D重投影误差函数,迭代求解得到更优的位姿,其中优化函数为
| $ \left\{\begin{array}{l} \left\{\boldsymbol{R}_{\mathrm{Re}}^i, \boldsymbol{t}_{\mathrm{Re}}^i\right\}=\underset{\boldsymbol{R}_{\mathrm{Re}}^i, \boldsymbol{t}_{\mathrm{Re}}^i}{\operatorname{argmin}} \sum\limits_{j=1}^N \rho(E(i, j)) \\ E(i, j)=\left\|\left(u_j, v_j\right)-\operatorname{project}\left(\boldsymbol{R}_{\mathrm{Re}}^i \boldsymbol{X}^j+\boldsymbol{t}_{\mathrm{Re}}^i\right)\right\|_{\Sigma}^2 \end{array}\right. $ | (1) |
式中: RRei和tRei分别是系统参考坐标系相对于第i帧相机坐标系的旋转矩阵和平移向量; (uj, vj)为第j个特征点的像素坐标;N为匹配到的特征点总和;ρ为Huber损失函数;project()表示3D-2D重投影误差函数;Xj为第j个匹配点在参考坐标系中的x坐标;∑为协方差矩阵。
2.2.3 局部建图在对每帧影像进行以上操作的同时,采用局部建图线程负责在当前地图插入关键帧和筛选、产生新的地图点,实现实时地优化局部若干帧的位姿及相应3D点的位置,对误差进行修正。
2.2.4 回环检测由于视觉SLAM定位根据输入的序列图像增量式地进行帧间匹配并估计相机位姿,因此必然存在累积误差。回环检测负责检测轨迹是否闭环,并在检测到闭环后修正轨迹,对提高定位精度至关重要。探测器一旦再次回到之前抵达过的“关键帧”,就能通过“关键帧”的相互关联性进行有效的闭合回环,优化位姿、纠正累积误差。小行星绕飞轨迹大多为环形轨道,多次绕飞之后通过回环检测能实现将视觉定位的误差约束在一定范围内,也为下一步融合轨道动力学提供基础。为实现回环检测。本文使用词袋模型,将每张图像构建为一个词袋向量vi,通过相似度度量:
| $ \left(\boldsymbol{v}_i, \boldsymbol{v}_j\right) \triangleq 1-\frac{1}{2}\left|\frac{\boldsymbol{v}_i}{\left|\boldsymbol{v}_i\right|}-\frac{\boldsymbol{v}_j}{\left|\boldsymbol{v}_j\right|}\right| $ | (2) |
评价两幅图像的相似度得分,判断是否进行回环检测。
2.3 小行星稠密建图及引力场建模算法本文为实现小行星引力场建模,先通过多视角立体几何方法重建稠密地图,获得小行星表面三维点云和多面体模型,随后通过该模型对行星引力场进行多面体引力场建模。
2.3.1 小行星稠密三维重建虽然视觉SLAM算法也能在实现定位的同时进行建图,但是由ORB算法提取的特征较为稀疏,存在较多的空洞和重建不完全区域,而且由于受到视觉定位误差的影响导致建图精度较低,会影响后续引力场建模效果。一般小行星任务通过多视角立体几何方法重建小行星的稠密模型,主要包括从运动恢复结构(structure from motion,SFM)[17]结合多视角立体几何(multi-view stereo,MVS)[18]方法。多视角立体几何法相比于现有小行星任务常用的立体光度测量法[19](StereoPhotoclinometry, SPC),仅靠绕飞拍摄的图像数据即可实现三维重建,其结果稳定性强且精度较高,是未来小行星探测任务中表面重建的主要技术之一[20]。
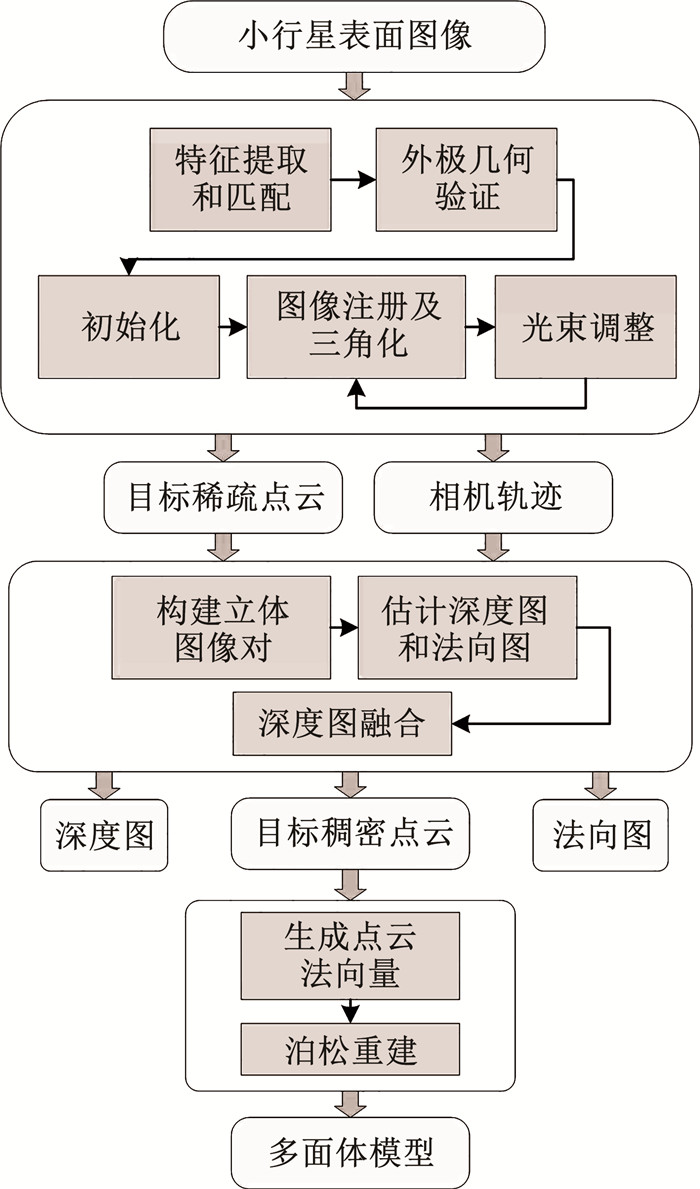
小行星稠密三维重建算法流程见图 3,在输入小行星表面序列图像之后,先通过SFM算法恢复相机运动信息和内外参,建立行星表面稀疏点云。
|
图 3 小行星稠密三维重建流程 Fig. 3 Flow of dense 3D reconstruction of asteroids |
1) 首先利用SIFT算法进行特征提取和匹配,其次对图像对进行几何验证即求解基础矩阵F并去除外点。
2) 随后在初始化时选择重叠度较高的两张图像,并增量式地依次添加新的图像和其特征点云坐标。
3) 为了减少误差,在每次添加图像之后使用光束平差法(bundle adjustment,BA)优化相机内外参和特征点云,并将此作为MVS算法的输入。其中光束平差法通过最小化重投影误差优化相机参数,定义n个空间点Pi=[Xi, Yi, Zi]T在像素平面的投影坐标为ui=[ui, vi]T,相机的旋转R和平移变换t的李群表示为T,K为相机内参矩阵,构建如式(3)所示的最小二乘问题,求解最优的相机位姿。
| $ \boldsymbol{T}^*=\arg \min _{\boldsymbol{T}} \frac{1}{2} \sum\limits_{i=1}^n\left\|\boldsymbol{u}_i-\frac{1}{s_i} \boldsymbol{K} \boldsymbol{T} \boldsymbol{P}_i\right\|_2^2 $ | (3) |
MVS稠密建图部分通过融合深度图实现。首先由立体匹配PatchMatch算法进行视差估计得到深度图,并对深度图进行融合和滤波处理。由于多面体法需要用到模型表面的三角面片,因此还需要进一步生成点云的法向量,并使用泊松重建方法进行表面重建。
2.3.2 引力场建模算法本文要对引力场进行建模,主要方法包括球谐函数法[21]、质点群法[22]和多面体法[23]。考虑到探测器高精度导航的需求,本文主要选择多面体法进行引力场重建,它是不规则小行星引力场建模的主要方法之一,目前理论分析中多以该方法所得结果为精确值,相对于其他建模方法,多面体法具有更高的精度。
多面体法计算得到的引力势能和引力加速度分别是:
| $ U(\boldsymbol{r})=\frac{1}{2} G \rho\left(\sum\limits_{\mathrm{e} \notin \text { edges }} \boldsymbol{r}_{\mathrm{e}}^{\mathrm{T}} E_{\mathrm{e}} \boldsymbol{r}_{\mathrm{e}} \cdot L_{\mathrm{e}}-\sum\limits_{\mathrm{f} \notin \text { faces }} \boldsymbol{r}_{\mathrm{f}}^{\mathrm{T}} F_{\mathrm{f}} \boldsymbol{r}_{\mathrm{f}} \cdot \omega_{\mathrm{f}}\right) $ | (4) |
| $ g(\boldsymbol{r})=\nabla U(\boldsymbol{r})=-G \rho\left(\sum\limits_{\mathrm{e} \notin \text { edges }} E_e \boldsymbol{r}_{\mathrm{e}} \cdot L_e-\sum\limits_{\mathrm{f} \notin \text { faces }} F_{\mathrm{f}} \boldsymbol{r}_{\mathrm{f}} \cdot \omega_{\mathrm{f}}\right) $ | (5) |
式中: U(r)表示引力势,U(r)对r求导获得引力加速度g(r),G表示万有引力常量,ρ是小行星密度,r表示在小行星固连坐标系{A}中任一点位置向量(x, y, z),re是该点到多面体上面A和面B多面体棱边上一点(x0, y0, z0)的向量,rf表示(x, y, z)到多面体平面内的任意一点(x1, y1, z1)的向量,Ee、Le、Ff和ωf的具体定义参考文献[22]。
2.4 伪轨道动力学修正算法为了进一步提升轨道精度,本文提出融合轨道动力学的航天器轨道改进方法,通过最大限度地挖掘航天器测量数据中的轨道信息,实现探测器定位精度的进一步提高。该改进方法的前提是航天器通过前述视觉SLAM技术的初定位基本完成,通过这些轨道信息并借助本文提出的处理方法,便可以实现定位的改进。
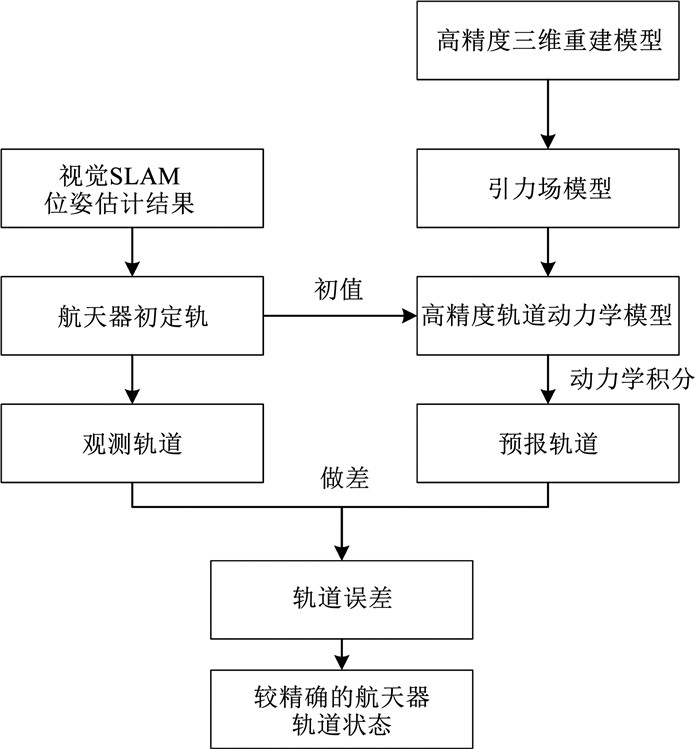
融合轨道动力学实现探测器轨道估计优化模块的算法流程见图 4,该算法一方面将视觉SLAM技术对小行星探测器的位姿估计结果作为航天器初定位结果,将其作为观测轨道;另一方面将基于视觉信息的小行星高精度三维重建模型通过多面体法完成小行星引力场建模,进而得到其高精度轨道动力学模型,再对视觉估计结果通过动力学积分得到预报轨道。将观测轨道和预报轨道分别输入基于“伪相对运动”的探测器轨道优化算法,通过求解目标函数得到相对运动方程中的相关系数,进而反向解算出相对初始位置和速度,最终得到更为精确的探测器轨道估计结果。
|
图 4 融合轨道动力学模块的算法流程 Fig. 4 Algorithm flow chart of fusion orbital dynamics module |
定义探测器在绕飞若干个周期之后,通过视觉SLAM估计的一系列状态结果为
在进行轨道预报时,主要考虑小天体本身的引力作用,引力加速度由式(5)给出。取某一时刻i的xV(i)作为输入,通过动力学方程可数值积分可递推出T时刻之后的状态xd(i+T)=d(xV(i), T),及以xV(i)为初值的一条“预报轨道”,由于其不真实存在,因此称为“伪轨道”。由于xV(i)相比于真实轨道该时刻的状态x(i)存在误差ΔU(i),且轨道递推的误差是随着时间i逐渐累积的,因此ΔU(i+T)>ΔU(i),通过不断迭代搜索合适的初值xV(i)使得减少i+T时刻附近的误差,就可以达到对xV(i)的进一步优化。
由于真实轨道是未知的,通过在真实轨道附近分布w(i)~N{0, δ}的视觉定位结果进行曲线拟合,获取符合运动学方程的精确轨道。选取xV(i)作为递推初值,在
| $ d\left(\boldsymbol{x}_V^{(i)}, \left[T-\frac{m}{2}, T+\frac{m}{2}\right]\right)=\left\{\boldsymbol{x}_d^{T-\frac{m}{2}}, \cdots, \boldsymbol{x}_d^{T+\frac{m}{2}}\right\} $ | (6) |
在得到递推结果后,对轨迹进行拟合以得到一条符合真实运动学方程的轨道。本文提出的方法以递推结果与视觉定位点误差和作为约束,通过迭代反演求解最优的xV(i),优化公式为
| $ \min \sum\limits_{j=T-\frac{m}{2}}^{T+\frac{m}{2}}\left\|\boldsymbol{x}_V^{(j)}-d^{(j)}\left(\boldsymbol{x}_V^{(j)}\right)\right\|^2 $ | (7) |
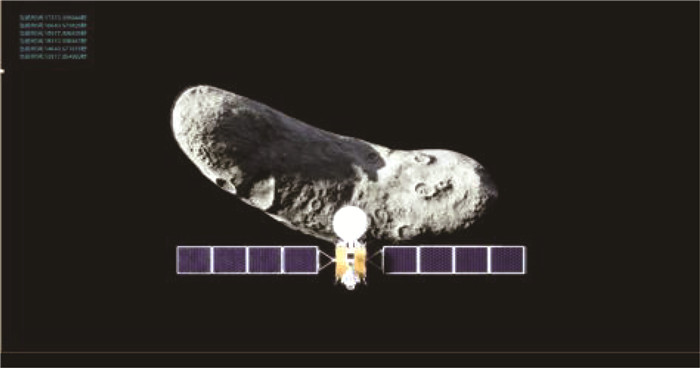
为了对本文方法进行仿真验证,采用NASA官方公布的小行星模型433 Eros[24],该模型最短轴13 km,最长轴33 km,平均密度为2 670 kg/m3。该模型包括小行星的三维结构,纹理信息采用Unreal Engine引擎中提供的小行星表面纹理,可视化效果见图 5。
|
图 5 探测器绕飞小行星的建模效果 Fig. 5 Modeling effect of the probe flying around the asteroid |
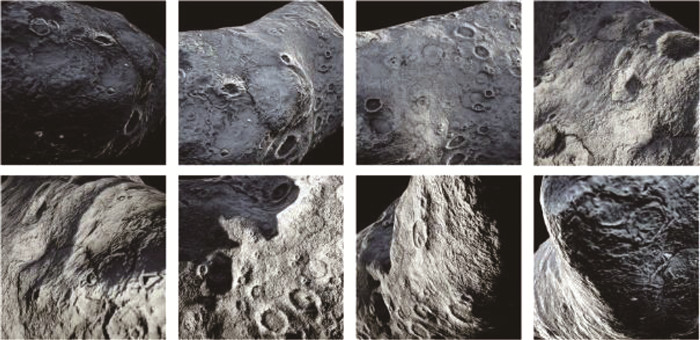
使用该小行星模型,并参考真实引力场通过轨道动力学模型生成仿真绕飞的探测轨道。此轨道距离小行星质心的最小距离为14.3 km,最大距离为26.4 km,轨道的时间间隔为50 s。通过程序控制摄像机按指定轨道绕飞小行星,可以实现小行星全部区域的探测而不产生盲区。在绕飞过程中探测器朝向始终保持对准小行星质心,同时视场相机拍摄行星表面图像,系统输出每张图像对应的时间戳、相机位置及旋转四元数,其可作为位姿估计精度评估过程中的真值(ground truth,GT)。最终在轨拍摄时间60 000 s,共生成1 201张图像,如图 6即为仿真引擎生成图像。相机分辨率为1 024×1 024,视场角为15°。
|
图 6 仿真引擎生成图像 Fig. 6 Images generated by the simulation engine |
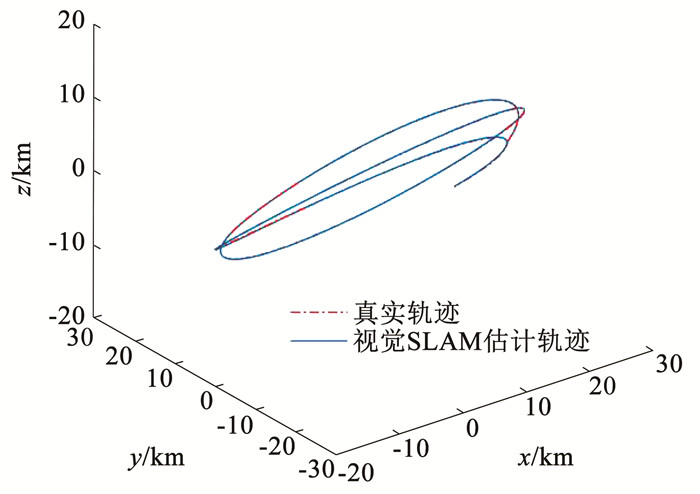
通过观测图像的提取ORB特征点并进行匹配,能实时获取探测器的相对位姿信息。由于视觉SLAM得到的是相机坐标系下的相对定位结果,为了对比分析算法精度,本文将相机坐标系转换到世界坐标系下。由图 7看出视觉定位结果与真实轨道基本一致。
|
图 7 视觉SLAM在433 Eros定位结果 Fig. 7 Visual SLAM positioning results in 433 Eros |
视觉的定位结果与真值误差对比如图 8曲线所示,图中分别对比了x、y、z三轴的定位误差和轨迹的定位误差,其中横坐标表示时间戳,单位是s,纵坐标表示定位误差,单位为km。

|
图 8 融合轨道动力学改进前、后位置误差对比 Fig. 8 Comparison of position errors before and after fusion orbit dynamics improvement |
在实际工程应用中,经常通过绝对轨迹误差AAPE(absolute pose error, APE)来评价算法的估计轨迹与真实轨迹的差异。假设系统真实轨迹为Tgt, i,估计的轨迹为Testi, i,其中i=1, 2, …, N,那么绝对轨迹误差则表征了每个时刻位姿李代数的均方根误差(root-mean-squared, RMSE),其数学定义如式(8)所示:
| $ A_{\mathrm{APE}}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^N\left\|\log \left(T_{\mathrm{g}, i}^{-1} T_{\mathrm{esti}, i}\right)^{\vee}\right\|_2^2} $ | (8) |
计算求解得到视觉定位的均方根误差116.97 m,误差最大值203.86 m,均值103.33 m。绕飞轨道大致可以认为环绕小行星飞行两圈,从图 8的三轴和总体的误差趋势也能看到定位误差所代表的曲线呈周期性变化,同时在30 000 s前后探测器又回到了初始点位置附近。由于回环检测算法在此匹配到之前的关键帧,累积误差被修正,整体误差在一个周期内呈现先变大后变小的趋势,这是因为随着时间的增加,误差会逐渐累积,校正后能将误差降低。该结果可以验证了自主视觉定位算法的有效性,并进一步肯定了视觉SLAM技术应用于小行星绕飞轨道估计的可行性,但误差仍有进一步提升空间。
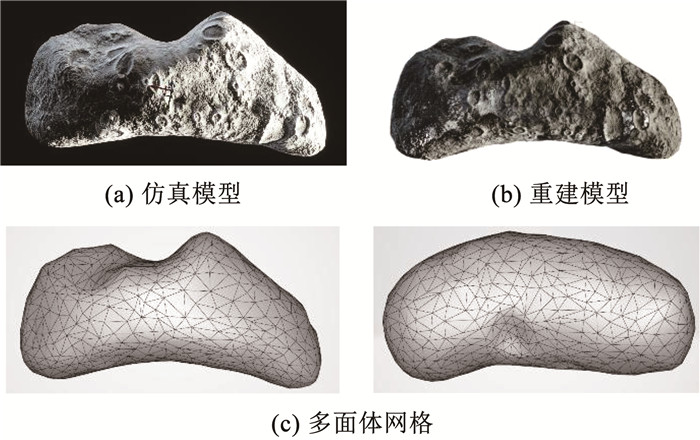
3.3 小行星稠密建图及引力场建模实验及分析根据输入的序列图像对小行星进行表面三维重建,得到图 9所示的稠密点云模型,总计1 687万个点,外形与Unreal仿真引擎中的小行星形态基本一致。
|
图 9 433 Eros的重建效果 Fig. 9 Reconstructed model of 433 Eros |
为了便于重建不规则小行星的引力场模型,考虑到引力场反演和轨道计算所需的时间,本文使用MeshLab工具将点云模型简化至902个点,并通过泊松重建算法对曲面进行重建,生成由1 800个三角面片构成的多面体网格。
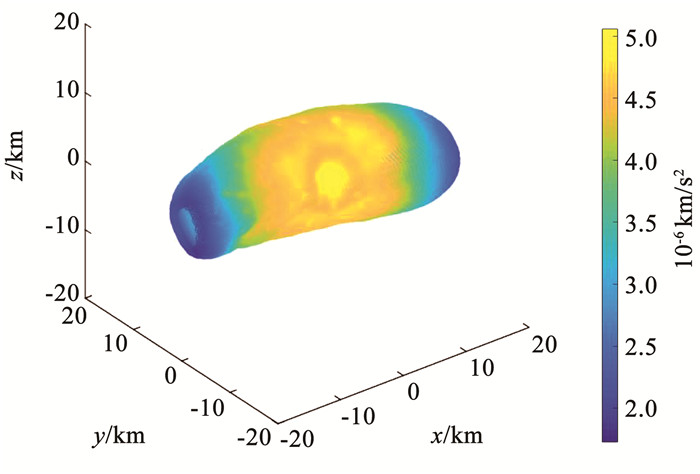
通过多面体法实现多面体网格的引力场重建,获得其重新建模的加速度精度,得到近地表面的引力加速度分布见图 10。
|
图 10 重建引力场 Fig. 10 Reconstructed gravitational field |
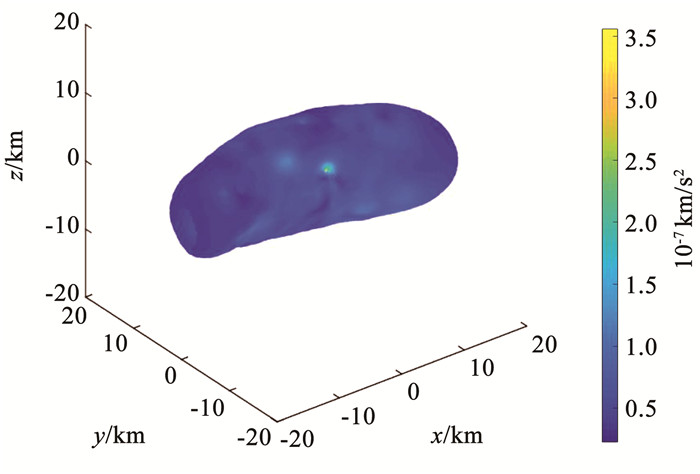
与真实引力场模型下的加速度进行对比,图 11计算得引力场误差均值为2.923 2×10-8 km/s2,最大值为3.654 9×10-7 km/s2,最小值为1.282 5×10-9 km/s2,相对误差为0.75%,最大不超过9.39%,引力场建模精度能满足任务需求。
|
图 11 重建引力场与真实引力场误差值 Fig. 11 Error value between reconstructed gravitational field and real gravitational field |
选取5 000 s处的纯视觉定位结果作为初值输入,在整体轨道60 000 s上间隔1 000 s均匀采样60个点作为约束,不断迭代优化,获得融合轨道动力学之后的结果,误差如图 8虚线所示,可以看出无论是各个分量的误差还是总体误差,皆比未优化前的精度要高。
根据表 1的统计结果,融合轨道动力学的改进方法将原先均值为103.33 m、均方根误差为116.97 m的视觉定位误差降低至均值为59.61 m,均方根误差为65.60 m的水平,精度提升43.92%,可以满足未来小行星自主探测任务中的定位要求。因此融合轨道动力学进行视觉轨道优化后的轨道误差能将视觉SLAM定位误差进一步降低。
| 表 1 视觉SLAM和融合轨道动力学后的定位误差对比 Tab. 1 Positioning error after visual SLAM and fusion of orbital dynamics |
提出了一种融合轨道动力学的深空探测器自主视觉定位方法,并进行了算法实现和实验验证。该方法先通过视觉SLAM估计探测器的位置和姿态,同时由多视角立体几何方法重建小行星表面三维模型,并在此基础上进行引力场建模,结合初始的视觉定位和引力场模型,融合轨道动力学获得精确的探测器定位结果。实验结果表明,所提出的方法能实现小行星探测器的自主视觉导航,并且融合轨道动力学之后能有效将视觉定位误差均值从116.97 m降低至65.60 m。本文工作能够为未来中国的深空探索提供有效技术支撑,符合未来更高自主性和更强适应性的探测需求。
| [1] |
顾逸东, 吴季, 陈虎, 等. 中国空间探测领域40年发展[J]. 空间科学学报, 2021, 41(1): 10. GU Yidong, WU Ji, CHEN Hu, et al. Review of the 40-year development of China space xploration[J]. Chinese Journal of Space Sciences, 2021, 41(1): 10. |
| [2] |
崔平远, 赵冬越, 朱圣英, 等. 小天体主动附着制导与控制技术研究进展[J]. 宇航学报, 2021, 42(9): 1057. CUI Pingyuan, ZHAO Dongyue, ZHU Shengying, et al. Research progress of guidance and control technologies for active landing on small celestial bodies[J]. Journal of Astronautics, 2021, 42(9): 1057. |
| [3] |
TURAN E, SPERETTA S, GILL E. Autonomous navigation for deep space small satellites: scientific and technological advances[J]. Acta Astronautica, 2022, 193: 56. DOI:10.1016/j.actaastro.2021.12.030 |
| [4] |
王大轶, 徐超, 黄翔宇. 深空探测着陆过程序列图像自主导航综述[J]. 哈尔滨工业大学学报, 2016, 48(4): 1. WANG Dayi, XU Chao, HUANG Xiangyu. Overview of autonomous navigation based on sequential images for planetary landing[J]. Journal of Harbin Institute of Technology, 2016, 48(4): 1. DOI:10.11918/j.issn.0367-6234.2016.04.001 |
| [5] |
张成渝, 梁潇, 吴奋陟, 等. 小行星探测下降着陆段光学导航技术发展综述[J]. 红外与激光工程, 2020, 49(5): 113. ZHANG Chengyu, LIANG Xiao, WU Fenzhi, et al. Overview of optical navigation for asteroid exploration descent and landing[J]. Infrared and Laser Engineering, 2020, 49(5): 113. |
| [6] |
崔平远, 贾贺, 朱圣英, 等. 小天体光学导航特征识别与提取研究进展[J]. 宇航学报, 2020, 41(7): 880. CUI Pingyuan, JIA He, ZHU Shengying, et al. Research progress on optical navigation feature recognition and extraction technologies for small body exploration[J]. Journal of Astronautics, 2020, 41(7): 880. |
| [7] |
COCAUD C, KUBOTA T. SURF-based SLAM scheme using octree occupancy grid for autonomous landing on asteroids[C]//Proceedings of the 10th International Symposium on Artificial Intelligence, Robotics and Automation in Space. Sappora: [s. n. ], 2010, 29: 275
|
| [8] |
COCAUD C, KUBOTA T. Probabilistic motion estimation for near real-time navigation and landing on small celestial bodies[J]. Journal of Aerospace Engineering, 2011, 4(3): 1. DOI:10.7446/jaesa.0403.01 |
| [9] |
VASSALLO C, TABIB W, PETERSON K. Orbital SLAM[C]//2015 12th Conference on Computer and Robot Vision. Halifax: IEEE, 2015: 305. DOI: 10.1109/CRV.2015.47
|
| [10] |
TWEDDLE B E, SAENZ-OTERO A, LEONARD J J, et al. Factor graph modeling of rigid-body dynamics for localization, mapping, and parameter estimation of a spinning object in space[J]. Journal of Field Robotics, 2015, 32(6): 897. DOI:10.1002/rob.21548 |
| [11] |
TAKEISHI N, YAIRI T. Visual monocular localization, mapping, and motion estimation of a rotating small celestial body[J]. Journal of Robotics & Mechatronics, 2017, 29(5): 856. DOI:10.20965/jrm.2017.p0856 |
| [12] |
RATHINAM A, DEMPSTER A G. Vision based state estimation using a graph-SLAM approach for proximity operations near an asteroid[C]//The 69th International Astronautical Congress. Bermen: IAF, 2018
|
| [13] |
DOR M, SKINNER K A, DRIVER T, et al. Visual SLAM for asteroid relative navigation[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE: 2021: 2066. DOI: 10.1109/CVPRW53098.2021.00235
|
| [14] |
朱圣英. 小天体探测器光学导航与自主控制方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2009 ZHU Shengying. Research on optical navigation and autonomous control method of small celestial detector[D]. Harbin: Harbin Institute of Technology, 2009 |
| [15] |
RUBLEE E, RABAUD V, KONOLIGEK, et al. ORB: an efficient alternative to SIFT or SURF[C]//IEEE International Conference on Computer Vision, ICCV 2011. Barcelona: IEEE, 2011. DOI: 10.1109/ICCV.2011.6126544
|
| [16] |
CAMPOS C, ELVIRA R, RODRIGUEZ JJ G, et al. ORB-SLAM3: an accurate open-source library for visual, visual-inertial, and multimap SLAM[J]. IEEE Transactions on Robotics, 2021, 37(6): 1874. DOI:10.1109/TRO.2021.3075644 |
| [17] |
SCHONBERGER J L, FRAHM J M. Structure-from-motion revisited[C]//IEEE Conference on Computer Vision & Pattern Recognition. IEEE, 2016: 4104. DOI: 10.1109/CVPR.2016.445
|
| [18] |
SCHNBERGER J L, ZHENG E, POLLEFEYS M, et al. Pixelwise view selection for unstructured multi-view stereo[C]//European Conference on Computer Vision (ECCV). Springer, Cham, 2016. DOI: 10.1007/978-3-319-46487-9_31
|
| [19] |
GASKELL R W, BARNOUIN-JHA O S, SCHEERES D J, et al. Characterizing and navigating small bodies with imaging data[J]. Meteoritics & Planetary Science, 2008, 43(6): 1049. DOI:10.1111/j.1945-5100.2008.tb00692.x |
| [20] |
KIKUCHI H, HEMMI R, KOMATSUG, et al. 3D mapping of structural features on Ryugu[C]//Lunar and Planetary Science Conference. Houston: Lunar and Planetary Institute, 2019(2132): 2409
|
| [21] |
VALLADO D A, MCCLAIN W D. Fundamentals of astrodynamics and applications[M]. [S. l. ]: Springer Science & Business Media, 2001
|
| [22] |
GEISSLER P, PETIT J M, DURDA D D, et al. Erosion and ejecta reaccretion on 243 Ida and its moon[J]. Icarus, 1996, 120(1): 140. DOI:10.1006/icar.1996.0042 |
| [23] |
WERNER R A, SCHEERES D J. Exterior gravitation of a polyhedron derived and compared with harmonic and mascon gravitation representations of asteroid 4769 Castalia[J]. Celestial Mechanics and Dynamical Astronomy, 1996, 65(3): 313. |
| [24] |
RAUGH A C. Near-a-5-collected-models-V1.0[EB/OL]. [2015-10-05]. http://sbn.psi.edu/pds/resource/nearbrowse.html
|
 2024, Vol. 56
2024, Vol. 56


