随着互联网和社交平台的快速发展,短视频作为一种新兴的多媒体形式,因具备时长短、内容丰富、制作简单、传播性强等特点而广受年轻人喜爱。数据显示,截至2021年12月,中国短视频用户规模达8.88亿人。在如此庞大的用户规模下产生了海量的短视频数据,因此对这些数据的研究迫在眉睫。
深度神经网络(deep neural network, DNN)是现代机器学习研究的一个领域,因为其在复杂预测任务[1-3]中表现突出而受到极大欢迎。但是在一些任务和领域中(如碰撞检测[4]、医学影像分类[5]等),单一的预测分数(即预测的准确性)是不够的。为此需要建立一个不确定度指标来对预测结果的可信度进行衡量。贝叶斯概率模型可以对数据进行观测,并在预测中获得可靠的不确定性估计。例如文献[4]利用贝叶斯联立方程模型来解决自行车碰撞时由于数据不完整而产生的不确定性。不确定度同样可以用来提高神经网络的性能。例如文献[5]利用贝叶斯深度学习中的不确定度来解决皮肤癌图像分类的问题。文献[6]在计算机视觉任务中提出了一个结合任意不确定性和认知不确定性的贝叶斯深度学习框架。本文则是引入了不确定度来更好的解决短视频事件检测任务。
短视频事件检测是对特定场景下所涉及的主体和对象的特征进行检测[7]。视频中出现的简单手势,如拍手、跑步、微笑,这些都被视为动作。在特殊场合下,如生日会、游行、婚礼等,发生的动作合集称为事件。现有事件检测研究主要集中在监控视频的异常事件检测[8]和传统视频的体育事件检测[9]。实际上,体育事件或异常事件定义更加明确,模式较为重复,如监控视频中的跑步[10]。短视频事件更为复杂,由多个对象、不同场景等元素组成[11]。文献[12] 采用循环压缩卷积网络来发现短视频中包括的大部分非事件视频的潜在事件模式。文献[13]采用长短期记忆网络来识别短视频中的多个事件。
短视频中的视觉模态信息与音频模态信息包含独立性与相关性,将这两种模态的互补性与一致性进行有效融合可以大大提高事件检测精度。例如: 对比笔在纸上的摩擦声,视觉上可以更好地分辨出是在写作还是绘画;声音可以比视觉上更好地分辨出说话和唱歌。为了更好地从多模态融合中获益,建立一个可靠的多模态不确定度分析模型是十分必要的。此外,主流数据集的缺少也限制了短视频事件检测的发展。
针对上述问题, 本文提出一种深度多模态不确定度的短视频事件检测方法,具体贡献如下:
1) 提出了一个深度多模态不确定度网络框架。利用构建数值与分布相联合的独立性和相关性损失来划分音频模态共、私有域网络以及视觉模态共、私有域网络。
2) 将变分层嵌入到划分的各个域网络中,通过变分推断获得包含不确定度的音频模态共、私有域预测分布以及视觉模态共、私有域预测分布。针对这些预测分布,提出了不确定度判别方法。利用不确定度对4个域的预测进行筛选,从而获得更准确的分类结果。
3) 构造了新的短视频事件检测数据集来解决该方向缺少主流数据集的问题。同时在该数据集和经典动作数据集UCF-101、HMDB51上进行了实验并与其他方法比较,验证了所提方法的有效性。
1 相关工作 1.1 贝叶斯神经网络贝叶斯神经网络(Bayesian neural network, BNN)是标准神经网络中的一种变体,可以有效解决DNN的缺少不确定度和过拟合问题[14]。BNN将标准神经网络中的确定性权重替换为分布来处理,即让网络中的参数从点估计变成分布估计。这可以将网络参数的不确定性转化为输出的不确定性,使预测结果带有不确定度。同时BNN不需要强制固定网络参数,这对过拟合有着很好的鲁棒性。
针对给定训练集
| $ p(\boldsymbol{w} \mid D)=\frac{p(D \mid \boldsymbol{w}) p(\boldsymbol{w})}{p(D)} $ | (1) |
式中w为模型权重。
后验分布需要计算神经网络中所有训练样本的预测值,这一点是难以做到的。为此文章采用变分推理[15]来解决这一问题。变分推理是贝叶斯深度学习中一个常见的研究方法。通过构造一个关于参数θ的简单分布qθ(w)来近似替代后验分布。通过优化θ来使qθ(w)逼近后验分布。具体公式为
| $ \begin{aligned} \boldsymbol{\theta}^*= & \arg \min _{\boldsymbol{\theta}} K L\left(q_{\boldsymbol{\theta}}(\boldsymbol{w}) \| p(\boldsymbol{w} \mid D)\right)= \\ & \arg \min _{\boldsymbol{\theta}} K L\left(q_{\boldsymbol{\theta}}(\boldsymbol{w}) \| p(\boldsymbol{w})\right)- \\ & E_{\boldsymbol{w} \sim q_\boldsymbol{\theta}(\boldsymbol{w})}[\log p(D \mid \boldsymbol{w})]+\log p(D) \end{aligned} $ | (2) |
预测分布可以在预测阶段对网络进行多次随机正向传递得到。利用蒙特卡洛估计从网络参数的后验分布中采样,对已训练好的神经网络中给定一个新输入x*可以得到对应的预测输出y*的分布,具体公式为
| $ \begin{gathered} p\left(\boldsymbol{y}^* \mid \boldsymbol{x}^*, D\right)=\int p\left(\boldsymbol{y}^* \mid \boldsymbol{x}^*, \boldsymbol{w}\right) q_{\boldsymbol{\theta}}(\boldsymbol{w}) \mathrm{d} \boldsymbol{w} \\ p\left(\boldsymbol{y}^* \mid \boldsymbol{x}^*, D\right) \approx \frac{1}{T} \sum\limits_{i=1}^T p\left(\boldsymbol{y}^* \mid \boldsymbol{x}^*, \boldsymbol{w}_i\right), \boldsymbol{w}_i \sim q_{\boldsymbol{\theta}}(\boldsymbol{w}) \end{gathered} $ | (3) |
式中T为蒙特卡洛采样次数。
1.2 多模态特征融合多模态特征融合是将来自多种不同模态的信息进行整合,用于分类或回归任务。短视频中常见的模态信息有视觉、音频和文本等。不同模态间存在着互补性与一致性。若能合理利用不同模态之间的互补性与一致性, 则可以有效提升模型性能。
多模态融合方法主要有早期特征融合、后期分类决策、子空间学习等。早期特征融合通常将不同模态特征直接拼接为一个全局特征,然后进行分类。例如文献[16]将音频特征与视频特征直接拼接为一个全局向量用于情感分析。后期分类决策通常是将几种不同模态的分类结果采取数学的方式进行加权平均或阈值筛选等操作。子空间学习的主要思想是不同模态特征会存在一个公共子空间。例如,典型相关性分析(canonical correlation analysis, CCA)[17], 将文本信息和图像信息在公共子空间相关度最大化,从而获得两个模态的共有信息,并称其为公共特征。除CCA之外, 利用深度学习的方法进行模态融合也是子空间学习的常见方法。例如文献[18]提出多模态多维信息融合的卷积神经网络算法,并应用在肿瘤图像中。文献[19]所提算法构造了域分离网络,将视觉信息和音频信息划分为音视频共有域特征与音视频私有域特征,最后将各个域特征拼接到一起进行分类。
受到子空间学习、后期分类决策以及域分离网络的启发,本文从不确定度的角度出发,将网络划分为包含不确定度的不同模态的私有域和共有域网络,再利用不确定度做最终分类决策。
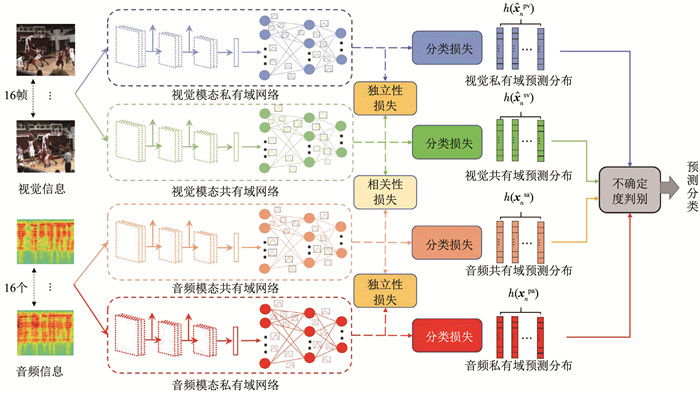
2 深度多模态不确定度事件检测方法 2.1 网络框架结构本文模型框架见图 1。模型采用I3D[20]卷积神经网络来提取视觉模态共、私有域特征以及音频模态共、私有域特征。为了同时获取各个域特征的不确定度信息,将I3D卷积网络的全连接层替换为BNN的变分层从而得到视觉模态私有域预测分布、音频模态私有域预测分布、音频模态共有域预测分布以及视觉模态共有域预测分布。
|
图 1 多模态不确定度短视频事件检测网络 Fig. 1 Micro-video event detection network with multimode uncertainty |
整个网络结构按照音频模态私有域网络、视觉模态私有域网络、音频模态共有域以及视觉模态共有域网络进行划分。利用损失函数来优化各个网络的参数,来获得更加真实的预测分布。整个损失函数由3部分组成:1)相关性损失LS,用来学习视觉模态共有域预测分布和音频模态共有域预测分布的相关性;2)独立性损失LD,用来学习视觉模态私有域预测分布和共有域预测分布以及音频模态共有域预测分布和私有域预测分布的独立性;3)分类损失LC,用来优化整个网络参数,并对预测分布进行分类。整个损失函数表示为
| $ L=\alpha L_{\mathrm{S}}+\beta L_{\mathrm{D}}+\gamma L_{\mathrm{C}} $ | (4) |
式中:α为整个损失中的相关性损失权重;β为整个损失中的独立性损失权重;γ为整个损失中的分类损失权重。
2.2 相关性损失视觉模态和音频模态共有域预测分布可由相关性损失获得。文章借鉴了孪生网络[21]以及域分离网络[19]中的相似性损失来探寻不同模态共有域预测分布之间的相关性。受孪生网络和相似性损失启发,本文从分布的角度出发,提出了不同模态下的预测分布近似的相关性损失。
不同模态间的分布近似可分为数值近似和不确定度近似两种。数值近似可表示为
| $ L_{\text {S_}\text {Siamese }}=\frac{1}{2 N} \sum\limits_{n=1}^N \sum\limits_{i=1}^T\left\|h\left(\hat{\boldsymbol{x}}_n^{\text {sa }}\right)_i-h\left(\hat{\boldsymbol{x}}_n^{\text {sv }}\right)_i\right\|_2^2 $ | (5) |
式中:N为训练一次的样本数;
模型参数的广泛分布意味着模型无法确定其真实值,具有较高的不确定度。反之,狭窄的参数分布则可以量化更低的不确定性[22]。BNN可以将参数分布转化为预测分布。利用贝叶斯不一致主动学习(Bayesian active learning by disagreement, BALD)[22-23]可以对预测分布中所包含的任意不确定度和认知不确定度信息进行量化。BALD公式为
| $ \begin{aligned} F_{\mathrm{BALD}}\left(\boldsymbol{y}^*, \boldsymbol{w} \mid \boldsymbol{x}^*, D\right)= & H\left(\boldsymbol{y}^* \mid \boldsymbol{x}^*, D\right)- \\ & E_{\boldsymbol{w}-q_\boldsymbol{\theta}(\boldsymbol{w})}\left[H\left(\boldsymbol{y}^* \mid \boldsymbol{x}^*, \boldsymbol{w}\right)\right] \approx \\ & -\sum\limits_{c=1}^c\left(\frac{1}{T} \sum\limits_{i=1}^r \hat{p}_c^i\right) \log \frac{1}{T} \sum\limits_{i=1}^r \hat{p}_c^i+ \\ & \frac{1}{T} \sum\limits_{c, i} \hat{p}_c^i \log \hat{p}_c^i \end{aligned} $ | (6) |
式中:
BALD可以对模型特征能否很好地体现模型参数进行评分,即量化不确定度[24]。将式(5)中的音频和视觉模态共有域预测经过Softmax归一化后分别带入式(6),计算出各自的不确定度。通过最小化不同模态间不确定度的差异,可以进一步提升不同模态预测分布的近似性。具体公式为
| $ \begin{aligned} L_{\mathrm{S} \_ \text {uncertainty }}= & \frac{1}{2 N} \sum\limits_{n=1}^N \| F_{\text {BALD }}\left(\hat{\boldsymbol{y}}_n^{\text {sa }}, \boldsymbol{w} \mid \hat{\boldsymbol{x}}_n^{\text {sa }}, D\right)- \\ & F_{\text {BALD }}\left(\hat{\boldsymbol{y}}_n^{\text {sv }}, \boldsymbol{w} \mid \hat{\boldsymbol{x}}_n^{\text {sv }}, D\right) \|_2^2 \end{aligned} $ | (7) |
式中:
最终的相关性损失为
| $ L_{\mathrm{S}}=L_{\mathrm{S}{\text {_Siamese}}}+L_{\mathrm{S}{\text {_uncertainty }}} $ | (8) |
独立性损失可用来衡量同一模态下私有域预测分布与共有域预测分布之间的离散程度。同一模态下的离散程度可分为数值离散性和分布离散性两种,其中数值离散性损失可表示为数值近似性损失的负数形式为
| $ \begin{gathered} L_{\mathrm{D}{\text {_difference }}}=-\frac{1}{2 N} \sum\limits_{n=1}^N \sum\limits_{i=1}^T\left[\left\|h\left(\hat{\boldsymbol{x}}_n^{\text {pa }}\right)_i-h\left(\hat{\boldsymbol{x}}_n^{\text {sa }}\right)_i\right\|_2^2+\right. \\ \left.\left\|h\left(\hat{\boldsymbol{x}}_n^{\mathrm{pv}}\right)_i-h\left(\hat{\boldsymbol{x}}_n^{\text {sv }}\right)_i\right\|_2^2\right] \end{gathered} $ | (9) |
式中:
分布离散性可体现为同一模态下的共有域预测分布与私有域预测分布没有很好的匹配。通过最大化同一模态下两个域特征的不确定度差异,可以进一步提升两个域预测的离散性。
| $ \begin{aligned} L_{\mathrm{D} \_ \text {uncertainty }}= & -\frac{1}{2 N} \sum\limits_{n=1}^N\left[\| F_{\text {BAL.D }}\left(\hat{\boldsymbol{y}}_n^{\text {sa }}, \boldsymbol{w} \mid \hat{\boldsymbol{x}}_n^{\text {sa }}, D\right)-\right. \\ & F_{\text {BALD }}\left(\hat{\boldsymbol{y}}_n^{\text {pa }}, \boldsymbol{w} \mid \hat{\boldsymbol{x}}_n^{\text {pa }}, D\right) \|_2^2+ \\ & \| F_{\text {BALD }}\left(\hat{\boldsymbol{y}}_n^{\text {sv }}, \boldsymbol{w} \mid \hat{\boldsymbol{x}}_n^{\text {sv }}, D\right)- \\ & \left.F_{\text {BALD }}\left(\hat{\boldsymbol{y}}_n^{\text {pv }}, \boldsymbol{w} \mid \hat{\boldsymbol{x}}_n^{\text {pv }}, D\right) \|_2^2\right] \end{aligned} $ | (10) |
式中:
最终的独立性损失为
| $ L_{\mathrm{D}}=L_{\text {D_difference }}+L_{\text {D_uncertaimy }} $ | (11) |
通过相关性损失和独立性损失,整个网络可以获得视觉模态共有域预测分布、视觉模态私有域预测分布、音频模态共有域预测分布、音频模态私有域预测分布。构建可以对整个网络参数进行优化的分类损失来实现分类任务。整个网络参数可分为BNN变分层和DNN确定层两部分。
2.4.1 变分层分类损失BNN权值分布的构建有多种形式,在本文中针对权值采用正态分布来建立模型。对于难以求解的后验分布p(w|D)利用变分推理通过构造近似分布qθ(w)=N(w|μ, σ2)来替代后验分布。其中θ=(μ, σ2),μ表示均值,σ2表示方差。变分层的网络参数的优化等价于最大化证据下界(evidence lower bound, ELBO),也即最小化ELBO的负数。
| $ \begin{gathered} L_{\mathrm{V}}=-E_{\boldsymbol{w} \sim q_\boldsymbol{\theta}(\boldsymbol{w})}[\log p(D \mid \boldsymbol{w})]+K L\left[q_{\boldsymbol{\theta}}(\boldsymbol{w}) \| p(\boldsymbol{w})\right] \approx \\ \sum\limits_{i=1}^T\left[\log q_{\boldsymbol{\theta}}\left(\boldsymbol{w}^{(i)}\right)-\log p\left(\boldsymbol{w}^{(i)}\right)-\log p\left(D \mid \boldsymbol{w}^{(i)}\right)\right], \\ \boldsymbol{\mu}^{m+1} \leftarrow \boldsymbol{\mu}^m-\eta \Delta_{\boldsymbol{\mu}} L_{\mathrm{V}}^m \quad \boldsymbol{\sigma}^{m+1} \leftarrow \boldsymbol{\sigma}^m-\eta \Delta_{\boldsymbol{\sigma}} L_{\mathrm{V}}^m \end{gathered} $ | (12) |
式中:m为训练次数,η为学习率, ΔμLV和ΔσLV是分别计算μ和σ2的梯度损失。
2.4.2 确定层分类损失确定层的参数可利用交叉熵损失进行优化,具体公式为
| $ L_{\text {crossentropy }}=-\sum\limits_{n=1}^N y_n \cdot \log _2 \hat{y}_n $ | (13) |
式中:yn为第n个标签;
整体的分类损失为
| $ L_{\mathrm{C}}=L_{\mathrm{V}}+L_{\text {crossentropy }} $ | (14) |
一个可靠的模型可以对预测正确结果提供较低的不确定度,对错误的预测结果提供更高的不确定度。为此设置一个不确定度阈值,用来区分不确定度的高低。同时本文引入准确率与不确定度(accuracy vs uncertainty, AvU)指标IAvU来评价模型。
| $ I_{\mathrm{AvU}}=\frac{n_{\mathrm{ac}}+n_{\mathrm{iu}}}{n_{\mathrm{ac}}+n_{\mathrm{iu}}+n_{\mathrm{au}}+n_{\mathrm{ic}}} $ | (15) |
式中:nac为事件预测正确且不确定度低于阈值的数量;niu为事件预测错误且不确定度高于阈值的数量;nau为事件预测正确且不确定度高于阈值的数量;nic为事件预测错误且不确定度低于阈值的数量。
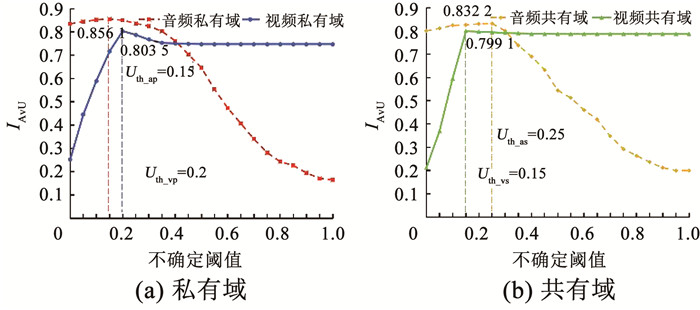
图 2所示,通过调节不确定度阈值来让模型获得更高的IAvU评分。IAvU评分最高时对应的不确定度阈值即为最优值Uth。实验表明视觉模态私有域网络的最优阈值Uth_vp为0.2;视觉模态共有域最优值Uth_vs为0.15;音频模态私有域最优值Uth_ap为0.15;音频模态共有域最优值Uth_as为0.25。
|
图 2 不确定度阈值与IAvU关系曲线 Fig. 2 Relationship between uncertainty threshold and IAvU |
从4个域输出分布中选取低于不确定度阈值的域输出作为最终预测结果。若有多个域的不确定度低于各自的阈值,则选取更低不确定度的输出作为预测结果。若4个域输出分布的不确定度均高于阈值,则对4个域的输出进行加权平均得到的输出作为最终预测结果。
3 数据集构建及实验分析 3.1 数据集构建现有的事件检测数据集主要针对的是视频监控和体育事件,在短视频方向上缺少可靠的主流数据集。Flickr是国外的一个资源开放的短视频网络平台。同时Flickr网站中的大部分短视频都含有上传者添加的标签,这可以更加便捷地批量下载短视频。针对上述特点,本文利用编写的爬虫脚本,从Flickr网站批量下载对应标签的视频数据。
在构建数据集时还需注意以下3点:1)所选视频的标签要能充分体现出复杂事件的特点; 2)视频长度要能体现出短视频的特点; 3)为了便于模型训练,每个标签都要有足够多的视频数量。针对上述问题, 作者从体育运动、生活技能、社交活动这3个方面对事件进行整理,共计得到20分类。为确保短视频的实际内容能与标签相符,将批量下载的短视频进行人工清洗。每一个视频都会被至少3个人观看,以避免主观因素的偏差对事件标注的影响。同时要求每个视频时长都在3~30 s之间,分辨率在428×320以上。最终共筛选出20 231个符合要求的短视频。短视频各事件数量见表 1。
| 表 1 20类事件及对应视频数量 Tab. 1 Twenty categories of events and number of corresponding videos |
在实际生活中,短视频的音频与视觉信息有时并不具备相关性,甚至会人为进行有意扰动,例如作者拍摄视频时添加背景音乐。进一步筛选发现构建的Flickr数据集中约有40%的视频满足音频和视觉的相关性,这满足音视频算法的音频和视觉信息要具备一定相关性的假设要求。
3.2 实验分析实验用到了公开数据集UCF-101、HMDB51和新建立的Flickr短视频事件检测数据集。其中新建立的数据集按照10∶ 2的比例划分为训练集和测试集。UCF-101和HMDB51是两个有关动作识别的公开数据集。UCF-101提供了来自101个动作类别的13 320个短视频。HMDB51共51个类别,包含6 766个短视频。这两个数据集均按照官方提供的第一种划分方式获得训练集和测试集。实验过程采用准确率ACC(accuracy)、平均精确率AP(average precision)、平均召回率AR(average recall)这3种指标来评价模型。
3.2.1 模型预处理与参数设置为了更好地获得音频模态和视觉模态时域上的信息,首先对短视频进行一些预处理。针对视觉模态,考虑到特征对齐问题,文章将不同时间长度的短视频按照等间隔的方式提取16帧作为视频帧序列;针对音频模态,首先将短视频中的声音部分转换为MP3格式的音频文件,再将音频文件按照等间隔的方式分为16个音频片段,最后将这16个音频片段转换为16个频谱图。利用频谱图来表达音频的变化规律。考虑到频谱图和视频帧序列具有时间上的关联性,采用I3D[20]网络来提取视觉模态共、私有域特征以及音频模态共、私有域特征。
实验在python3.6环境下完成,实验服务器CPU为Intel(R) Core(TM) i9-10920X CPU@3.5 GHz,GPU为RTX 3090,显存16 GB,采用PyTorch框架对模型进行训练。训练过程采用随机梯度下降SGD优化器,初始学习率为0.000 1,动量0.9。
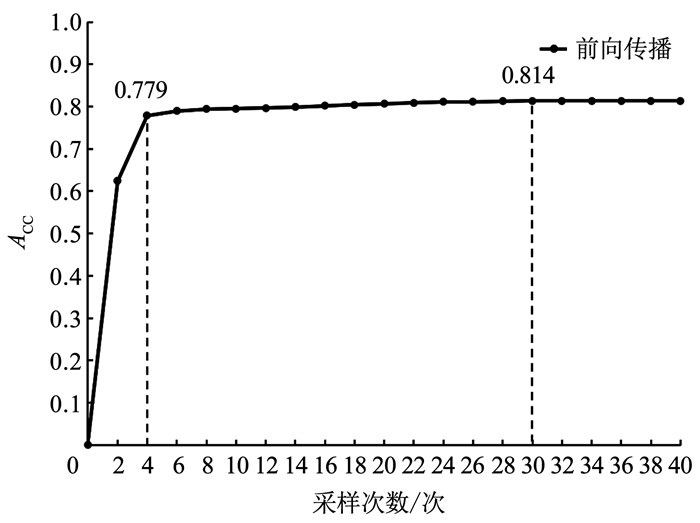
模型将I3D网络中最后用于分类的层替换为三层变分层,并把贝叶斯推断应用于变分层,对模型通过多次随机前向传递,并对权重后验分布进行蒙特卡洛采样,得到预测分布。在Flickr数据集中采样次数对模型准确率的影响见图 3。从图中可以看出前向传播达到4次时便可以取得较为理想性能,超过30次模型结果将不受影响。为了追求模型效果,本文将采样次数T设为30次。模型预测结果是将30次的前向传播得到的结果进行平均处理。
|
图 3 采样次数对模型性能影响 Fig. 3 Influence of sampling times on model performance |
为验证模型的有效性,在Flickr数据集下模型总损失和准确率随模型训练次数的结果见图 4。图 4(a)中验证了模型总损失随迭代次数增加而减少,从第70次迭代之后趋于稳定。图 4(b)中验证了视频私有域网络输出的准确率随迭代次数的增加而增加,同样在第70次迭代之后趋于平稳。上述可以证明模型具备收敛性,是有效的。

|
图 4 收敛性验证 Fig. 4 Convergence verification |
为了让模型效果达到最好,本文在Flickr数据集下寻找相关性损失权重α、独立性损失权重β、分类损失权重γ对模型性能影响的最优值。为了便于性能对比,本文采用控制变量法,即首先固定分类损失权重γ,然后寻找相关性损失权重α和独立性损失权重β对实验效果影响的最优值。最后再控制变量α和β,寻找γ的最优值。模型参数α、β和γ对模型准确率影响见图 5。从图 5中可以看出,在固定γ的条件下,α取值为0.6、β取值为0.4时模型效果最好。这说明相关性损失比独立性损失对模型影响影响更大。在固定α和β的情况下,γ取值为2.5时,模型效果达到最佳。

|
图 5 各参数对模型性能影响 Fig. 5 Influence of parameters on model performance |
为了验证实验的有效性以及各个域网络对实验效果的影响程度,在其他条件不变的情况下,分别对视觉私有域网络、视觉共有域网络、音频私有域网络、音频共有域网络、共有域网络以及私有域网络进行实验,实验结果见表 2。其中共有域网络的预测为视觉共有域和音频共有域网络经过不确定度判别后得到的结果,私有域网络得到的预测为视觉私有域和音频私有域网络经不确定度判别得到的结果。本文方法为视觉共、私有域与音频共、私有域网络共同经过不确定度判别得到的预测结果。实验结果发现:1)视觉模态信息的效果普遍都比音频效果要好,这说明短视频中视觉模态信息比音频模态信息更丰富; 2)私有域网络和共有域网络相比,共有域网络效果更好,这也间接证明了参数敏感性中相关性损失比独立性损失对模型的效果影响更大; 3)本文方法则是结合了共有域和私有域网络并将各个域的网络特征进行不确定度筛选,获得了更好的分类效果。
| 表 2 不同域网络的短视频事件分类性能对比 Tab. 2 Micro-video events classification performance comparison of different domain networks |
表 3对比了相关性损失S、独立性损失D和不确定度判别部分U对模型效果影响。其中S+D表示模型仅采用相关性和独立性损失,S+U表示模型采用相关性损失和不确定度判别,D+U表示模型采用独立性损失和不确定度判别。S+D+U为模型同时采用两种损失和不确定度判别。针对未使用不确定度判别部分的模型,文章将各个域特征拼接到一起再通过全连接层降维得到最终分类结果。实验结果发现:S+D的效果比S、D和U单独作用效果要好,证明了S和D的有效性。同时S+D+U的效果比S+D的效果好,证明了U的有效性。
| 表 3 相关性损失、独立性损失和不确定度判别对模型效果影响 Tab. 3 Influence of correlation loss, independence loss, and uncertainty discrimination on model effect |
为了探究音频与视觉的相关性对模型性能的影响,文章对Flickr数据集进一步筛选,筛选出音频与视觉相关的子集(约占总体的40%)以及不相关的扰动集(约占总体的60%)。
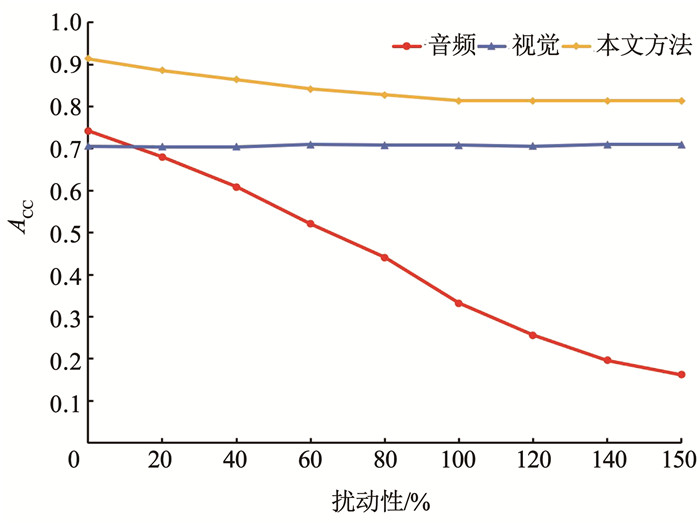
文章在Flickr的相关子集中分别加入不同数量的扰动集进行对比实验,对比结果见图 6。其中音频与视觉模态的单模态分类效果采用I3D网络获得。从图 6中可以看出在不添加扰动集,即音频与视觉全部相关的情况下,本文方法的效果最好, 可以达到0.914。随着扰动性的增加,音频的分类准确率会急剧下降,而视觉的准确率几乎不受影响。这是因为标签与视觉内容相符,音频的扰动性不会干扰到视觉模态。同时扰动性的增加会导致本文方法的效果下降,但是当扰动性达到100%以上时,即添加的扰动集数量大于等于相关子集数量时,本文方法的准确率将趋于稳定不变。这是因为本文方法的不确定度判别法则可以从不同域中筛选出有利的分类结果,当音频模态效果差时,则更加依赖视觉模态。
|
图 6 扰动性与准确率的关系 Fig. 6 Relationship between irrelevance and accuracy |
为探究在不同程度的音频扰动下多模态模型的性能变化,文章在Flickr的相关子集中分别添加轻度扰动(在原有样本基础上,从扰动集中选取相关集总数的40%的扰动视频并加入到相关集中)和重度扰动(添加相关集总数的120%的扰动视频) 来进行对比实验。对比多模态方法有C3D[26](multimodal)、I3D[20](multimodal)、TSN[29]、CTSN[30]。对比结果见表 4,从表中可以看出在扰动程度为0时各个方法的准确率最高,并且准确率随着扰动程度的增加而下降。此外本文方法无论是在相关、轻度扰动和重度扰动的情况下都有着更好的性能表现。
| 表 4 不同程度扰动下的不同网络的短视频事件分类性能对比 Tab. 4 Comparison of micro-video events classification performance of different networks under different degrees of disturbance |
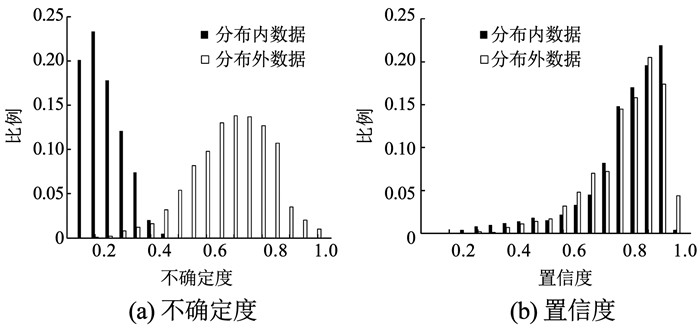
BNN可以获得包含不确定度的预测分布,采用BALD则可以捕捉这一不确定度。为了验证BNN不确定度相比于DNN置信度的优势,文章将Flickr数据集作为分布内样本并选取HMDB51中的20类数据作为分布外样本。在分布内样本的训练集进行训练,并在分布内样本的测试集和分布外样本上进行测试。文章所提的变分推断模型和采用全连接层模型在内外分布的测试结果见图 7。图 7(a)为采用变分层分类的模型,纵坐标为该不确定度下的预测数量占全部预测的比例。图 7(b)为采用全连接层分类的模型,因为全连接层无法提供不确定度,所以将全连接层的预测通过Softmax层归一化后得到的预测置信度作为评判标准。图中可以发现DNN全连接层模型得到的分布内和分布外的数据置信度都较高,而采用BNN变分推断模型得到的两个分布数据不确定度有明显的区分,且分布外数据不确定度普遍高于分布内数据,说明BNN能对数据来源的可靠性给出一个不确定性估计。
|
图 7 不确定度与置信度的对比关系 Fig. 7 Contrast of uncertainty and confidence |
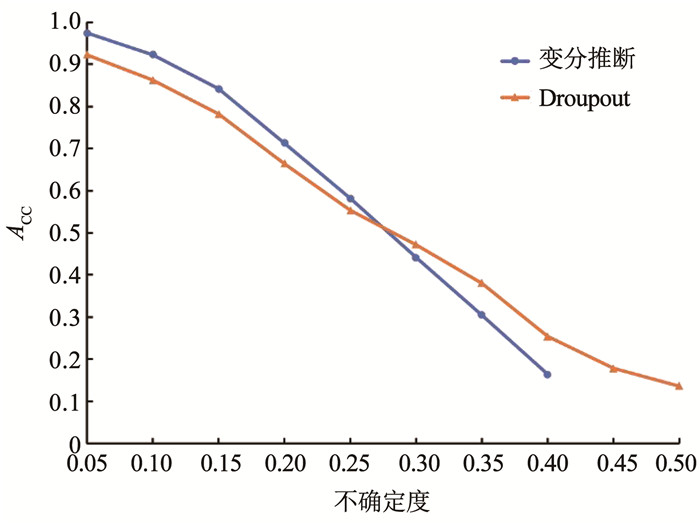
为了验证模型采用变分推断方式获得不确定度的效果,实验对比了经典贝叶斯推理中蒙特卡洛Dropout[25]方法。Dropout设置为0.5,前向传播次数设置为30次, 对比结果见图 8。从图中可以看出变分推断方法在低不确定度中的准确率明显高于蒙特卡洛Dropout方法。证明文章所提模型的不确定度效果更好。
|
图 8 不同方法下不确定度与准确率的关系 Fig. 8 Relationship between uncertainty and accuracy of different methods |
为证明本文所提方法的有效性,分别在Flickr、UCF-101和HMDB51这3个数据集中,将本文提出的方法与其他方法进行对比。
在新建立的Flickr数据集中采取对比的方法分为单模态和多模态两种,其中单模态方法有C3D[26]、GoogleNet[27]、I3D[20]、ResNet3D[28];多模态方法有C3D(multimodal)、I3D(multimodal)、TSN[29]、CTSN[30]。对比结果见表 5,从表中可以看出:1)在同一方法下,多模态效果比单模态要好,例如C3D(multimodal)与C3D;2)单模态中GoogleNet与C3D网络效果不如I3D网络,这可能是由于网络参数量太大而导致的过拟合问题; 3)多模态中CTSN网络效果较好,这可能是因为该网络结合了时间与空间信息,多帧密集光流也助于性能的提高; 4)本文方法的AR、AP和ACC指标分别达到了0.784、0.798和0.814,比其他方法效果更好,证明了本文方法在该数据集上的有效性。
| 表 5 Flickr数据集下的不同网络的短视频事件分类性能对比 Tab. 5 Micro-video events classification performance comparison of different networks in Flickr datasets |
为进一步验证模型在公共数据集上的有效性,模型将BNN变分层的最后一层网络维数分别调整为51和101,并采用相同的不确定度阈值在HMDB51和UCF-101数据集中重新进行上述训练并测试最终分类准确率。将分类结果与表 5中所提方法进行对比,对比结果见表 6。从表中可以看出本文所提方法在UCF-101和HMDB51数据集下的ACC指标达到了0.964和0.718,效果最好。证明了本文方法在公开数据集上的有效性。
| 表 6 UCF-101和HMDB51数据集下的不同网络的分类准确率对比 Tab. 6 Comparison of classification accuracy of different networks in UCF-101 and HMDB51 datasets |
从Flickr网站中构建了一个新的短视频事件检测数据集, 以弥补缺少相关数据集的问题。针对短视频事件检测研究,提出了一个深度多模态不确定度的短视频事件检测方法,该方法将I3D网络中的全连接层替换为BNN变分层,并利用独立性和相关性损失获得包含不确定度的音频视觉模态私有域与共有域预测,最后利用不确定度判别法则筛选出最后的分类结果。在新构建的数据集和公开数据集上进行实验,证明了该方法在提高分类准确率的同时,还可以对输出结果进行不确定度估计。
| [1] |
JING P G, SU Y T, NIE L, et al. Low-rank multi-view embedding learning for micro-video popularity prediction[J]. IEEE Transactions on Knowledge and Data Engineering, 2018, 30(8): 1519. DOI:10.1109/TKDE.2017.2785784 |
| [2] |
WEI Y, WANG X, GUAN W, et al. Neural multimodal cooperative learning toward micro-video understanding[J]. IEEE Transactions on Image Processing, 2020, 29(1): 1. DOI:10.1109/TIP.2019.2923608 |
| [3] |
LIU X, CHEN Z Z, LIU H Y, et al. User-video co-attention network for personalized micro-video recommendation[C]//[S. l. ]: Association for Computing Machinery, 2019: 3020. DOI: 10.1145/3308558.3313513
|
| [4] |
XU P, BAI L, PEI X, et al. Uncertainty matters: Bayesian modeling of bicycle crashes with incomplete exposure data[J]. Accident Analysis & Prevention, 2022, 165: 106518. DOI:10.1016/j.aap.2021.106518 |
| [5] |
ABDAR M, SAMAMI M, MAHMOODABAD S D, et al. Uncertainty quantification in skin cancer classification using three-way decision-based Bayesian deep learning[J]. Computers in Biology and Medicine, 2021, 135: 104418. DOI:10.1016/j.compbiomed.2021.104418 |
| [6] |
KENDALL A, GAL Y. What uncertainties do we need in Bayesian deep learning for computer vision?[J]. Advances in Neural information Processing Systems, 2017, 30. |
| [7] |
NIST. The TRECVID MED 2014 evaluation plan[EB/OL]. [2013-05-06]. http://nist.gov/itl/iad/mig/med14.cfm
|
| [8] |
YE O, DENG J, YU Z, et al. Abnormal event detection via feature expectation subgraph calibrating classification in video surveillance scenes[J]. IEEE Access, 2020, 8: 97564. DOI:10.1109/ACCESS.2020.2997357 |
| [9] |
YU J, LEI A, HU Y. Soccer video event detection based on deep learning[J]. Multi-Media Modeling, 2019, 11296: 8. |
| [10] |
SHYU M L, XIE Z, CHEN M, et al. Video semantic event/concept detection using a subspace-based multimedia data mining framework[J]. IEEE Trans Multimedia, 2008, 10(2): 252. DOI:10.1109/TMM.2007.911830 |
| [11] |
MA Z, CHANG X, XU Z, et al. Joint attributes and event analysis for multimedia event detection[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(7): 2921. DOI:10.1109/TNNLS.2017.2709308 |
| [12] |
LI P, XU X. Recurrent compressed convolutional networks for short video event detection[J]. IEEE Access, 2020, 8: 114162. DOI:10.1109/ACCESS.2020.3003939 |
| [13] |
LIU A A, SHAO Z, WONG Y, et al. LSTM-based multi-label video event detection[J]. Multimedia Tools and Applications, 2019, 78: 677. DOI:10.1007/s11042-017-5532-x |
| [14] |
DEODATO G. Uncertainty modeling in deep learning. Variational inference for Bayesian neural networks[D]. Turin: Politecnico di Torino, 2019
|
| [15] |
STEINBRENER J, POSCH K, PILZ J. Measuring the uncertainty of predictions in deep neural networks with variational inference[J]. Sensors, 2020, 20(21): 6011. DOI:10.3390/s20216011 |
| [16] |
DMELLO S K, KORY J. A review and meta-analysis of multimodal affect detection systems[J]. ACM Computing Surveys (CSUR), 2015, 47(3): 1. DOI:10.1145/2682899 |
| [17] |
HARDOON D R, SZEDMAK S, SHAWE-TAYLOR J. Canonical correlation analysis: an overview with application to learning methods[J]. Neural Computation, 2004, 16(12): 2639. DOI:10.1162/0899766042321814 |
| [18] |
洪炎佳, 孟铁豹, 黎浩江, 等. 多模态多维信息融合的鼻咽癌MR图像肿瘤深度分割方法[J]. 浙江大学学报(工学版), 2020, 54(3): 566. HONG Yanjia, MENG Tiebao, LI Haojiang, et al. Deep segmentation method of tumor boundaries from MR images of patients with nasopharyngeal carcinoma using multi-modality and multi-dimension fusion[J]. Journal of Zhejiang University: Engineering Science, 2020, 54(3): 566. DOI:10.3785/j.issn.1008-973X.2020.03.017 |
| [19] |
张丽娟, 崔天舒, 井佩光, 等. 基于深度多模态特征融合的短视频分类[J]. 北京航空航天大学学报, 2021, 47(3): 478. ZHANG Lijuan, CUI Tianshu, JING Peiguang, et al. Short video classification based on deep multi-modal feature fusion[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(3): 478. DOI:10.13700/j.bh.1001-5965.2020.0457 |
| [20] |
CARREIRA J, ZISSERMAN A. Quo vadis, action recognition? A new model and the kinetics dataset[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition(CVPR). Honolulu: 2017: 6299. DOI: 10.48550/arXiv.1705.07750
|
| [21] |
柳恩涵, 张锐, 赵硕, 等. 一种基于视频预测的红外行人目标跟踪方法[J]. 哈尔滨工业大学学报, 2020, 52(10): 192. LIU Enhan, ZHANG Rui, ZHAO Shuo, et al. An infrared pedestrian target tracking method based on video prediction[J]. Journal of Harbin Institute of Technology, 2020, 52(10): 192. DOI:10.11918/201910048 |
| [22] |
HOULSBY N, F HUSZAR, GHAHRAMANI Z, et al. Bayesian active learning for classification and preference learning[J]. Computer Science, 2011. DOI:10.48550/arXiv.1112.5745 |
| [23] |
TRAN T, DO T T, REID I, et al. Bayesian generative active deep learning[C]//International Conference on Machine Learning[S. l. ]: PMLR, 2019: 6295. DOI: 10.48550/arXiv.1904.11643
|
| [24] |
GAL Y, ISLAM R, GHAHRAMANI Z. Deep Bayesian active learning with image data[C]//International Conference on Machine Learning. Sydney: JMLR, 2017: 1183. DOI: 10.48550/arXiv.1703.02910
|
| [25] |
GAL Y, GHAHRAMANI Z. Dropout as a Bayesian approximation: representing model uncertainty in deep learning[C]//In International Conference on Machine Learning. New York: JMLR, 2016: 1050
|
| [26] |
TRAN D, BOURDEY L, FERGUS R, et al. Learning spatiotemporal features with 3D convolutional networks[C]//Proceedings of IEEE International Conference on Computer Vision. Santiago: IEEE, 2015: 4489. DOI: 10.1109/ICCV.2015.510
|
| [27] |
SZEGEDY C, LIU W, JIA Y, et al. Going deeper with convolutions[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Boston: IEEE, 2015: 1
|
| [28] |
HARA K, KATAOKA H, SATOH Y. Can spatiotemporal 3D CNNs retrace the history of 2D CNNs and image net?[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018: 6546. DOI: 10.48550/arXiv.1711.09577
|
| [29] |
WANG L, XIONG Y, WANG Z, et al. Temporal segment networks: towards good practices for deep action recognition[C]//Proceedings of European Conference on Computer Vision. The Netherlands: ECCV, 2016: 20. DOI: 10.1007/978-3-319-46484-8_2
|
| [30] |
FEICHTENHOFER C, PINZ A, ZISSERMAN A. Convolutional two-stream network fusion for video action recognition[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016: 1933
|
 2024, Vol. 56
2024, Vol. 56


