2. 中国矿业大学 力学与土木工程学院,江苏 徐州 221116;
3. 西南交通大学 土木工程学院,成都 610031
2. School of Mechanics and Civil Engineering, China University of Mining and Technology, Xuzhou 221116, Jiangsu, China;
3. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China
2022年2月,风暴“尤尼斯”席卷欧洲,伦敦千年穹顶的多处膜结构顶棚于膜面连接节点处出现撕裂后迅速扩展,从而形成整体膜面脱落。在膜结构服役过程期间,因风致残片冲击或者膜材内部缺陷,膜面会产生裂纹,且易出现在应力集中的膜面边界部位[1-3]。而膜面边界部位往往布置了一些连接构造措施,其中就包括需要人为开孔的节点板连接或者穿绳连接等。另外,已有研究表明孔洞的存在对材料裂纹扩展行为有显著影响,降低了裂尖的拉伸应力进而增大了裂纹的扩展韧度,间接延缓裂纹扩展和裂纹再次萌生[4-5]。因此亟需对含裂纹-孔洞膜材的破坏模式及撕裂机理展开研究。
撕裂强度作为表征膜材撕裂性能的主要指标[6-7],其测试方法有单、双舌撕裂法,中心撕裂法和梯形撕裂法等。织物类膜材作为一种纤维编织复合材料,主要通过各组分材料间的协同作用来抵抗撕裂荷载,其撕裂机理较为复杂[8-9]。现有研究多集中在膜材起裂韧性的表征参数(断裂韧性、断裂能释放率和J积分等)。其中文献[10]通过建立细观物理模型,指出纤维的断裂应变、弹性模量和织物密度等是撕裂强度的关键影响因素,并基于经典模型改进,提出适用于评估织物膜材撕裂性能的计算模型。文献[11]通过虚拟裂纹张合技术(VCCT)确定织物膜材的断裂韧性GIC并以此评估膜材的抗撕裂性。文献[12]通过单轴拉伸试验的荷载-位移曲线计算下降段的锯齿波面积,基于计算结果表征断裂韧性GIC以确定膜材撕裂强度。上述研究多为针对单裂缝膜材的撕裂行为开展的,而鲜有涉及孔洞对膜材裂纹扩展行为影响的验证。
本文进行了系列含裂纹-孔洞的PVC膜材中心撕裂试验,探究膜材撕裂扩展机理,讨论撕裂过程中膜面的应变分布规律,对比分析孔洞尺寸对膜材撕裂性能的影响,提出一种能够预测含裂纹-孔洞多缺陷下的撕裂模型。本文的研究成果能够为含多缺陷下织物类膜材的撕裂机理和撕裂强度预测提供理论指导。
1 材料与试验方法试验采用Serge Ferrari公司生产的PVC膜材(F702T),其基本材料参数见表 1。参考《膜结构检测标准》(DG/TJ 08-2019—2019)[13],选用矩形试样,尺寸为150 mm×200 mm,两端夹持长度为50 mm。
| 表 1 材料参数 Tab. 1 Material parameters |
参考实际工程中开孔形式(见图 1),孔洞形式选择以圆孔为主,同时考虑扁孔和竖缝,初始缺陷布置见图 2,具体初始缺陷尺寸见表 2,试样编号中字母代表孔洞类型,数字代表缺陷的横向尺寸。需要说明的是,试样S-0指在中心裂纹两侧布置竖缝缺陷,沿竖向切割4 mm裂纹。试验在Zwick Z202单轴拉伸试验机上进行,加载速率为10 mm/min。试验过程中以10 Hz频率采集拉力和位移数据。此外,为获取初始缺陷处的应变场,在试样中心区域设置了150 mm×60 mm的散斑,见图 3。试验中通过工业相机以1 Hz的频率采集该区域的整体变形,并结合Ncorr V12软件进行相关分析[14]。

|
图 1 膜面边界部位的连接构造措施(穿绳连接) Fig. 1 Connecting structural measures at membrane boundary (threading connection) |

|
图 2 试样尺寸(mm) Fig. 2 Dimension of specimens(mm) |
| 表 2 初始缺陷尺寸 Tab. 2 Dimension of initial crack |

|
图 3 散斑示意(mm) Fig. 3 Speckle diagram(mm) |
图 4分别为R-4试样和S-0试样的破坏形态。裂纹与孔洞连通前,裂纹沿垂直于荷载方向扩展。圆孔未改变裂纹扩展路径,断口较为整齐,而竖缝缺陷改变了裂纹扩展路径,新裂纹从竖缝两端的随机一侧沿垂直于荷载方向扩展。

|
图 4 中心撕裂破坏形态 Fig. 4 Central tear failure mode of specimen |
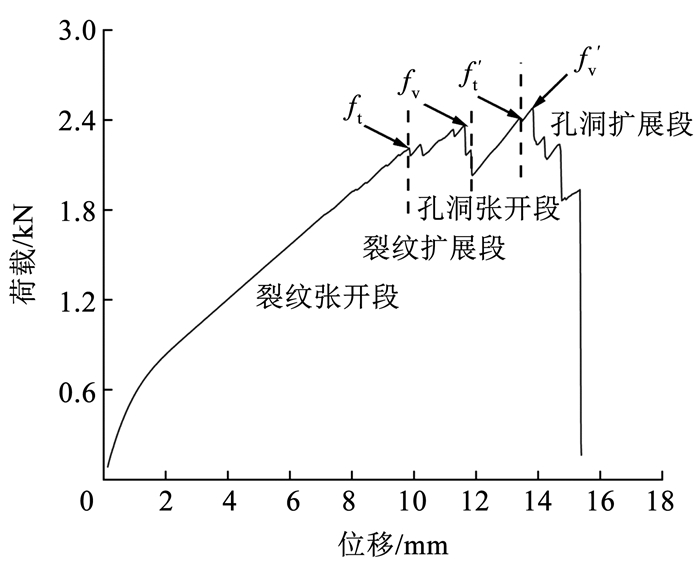
以R-4试样为例,图 5为含裂纹-孔洞多缺陷下的阶段破坏过程。结合撕裂模式,荷载-位移曲线可分为4个阶段(见图 6):1)裂纹张开段,中心裂纹尚未向两侧扩展,随着荷载逐渐增大,裂纹张开成纺锤形,圆孔被拉伸为椭圆形,中心裂纹处由于纤维断裂不受力而出现褶皱[15]。2)裂纹扩展段,越接近裂纹尖端的纤维束受力越大,将裂纹端部第一根纤维束断裂时的荷载记为裂纹端临界撕裂荷载ft,此时裂纹开始扩展。曲线中锯齿形的起伏变化是裂纹尖端纤维断裂释放应变能,新的纤维又快速存储应变能导致,将裂纹与孔洞连通前最大荷载记为裂纹端峰值撕裂荷载fv。3)孔洞张开段,在裂纹与孔洞连通前,裂纹尖端的应力由于应力集中远高于孔洞外侧纤维束的应力,当裂纹与孔洞连通瞬间,应变能释放造成曲线陡降,但由于孔洞缺陷处的应力集中程度低于裂纹尖端的应力集中程度,孔洞端部纤维束的应力还未达到断裂应力,所以膜材仍有承载能力,曲线出现上升直至孔洞裂纹尖端纤维束断裂,将此刻的荷载记为孔端临界撕裂荷载f′t。4)孔洞扩展段,裂纹随荷载增加迅速扩展直至破坏,记孔洞扩展撕裂过程中最大荷载为孔端峰值撕裂荷载f′v。

|
图 5 R-4试样的中心撕裂过程 Fig. 5 Central tear process of R-4 specimen |
|
图 6 多缺陷下中心撕裂的荷载-位移曲线 Fig. 6 Load - displacement curves of central tearing with multiple defects |
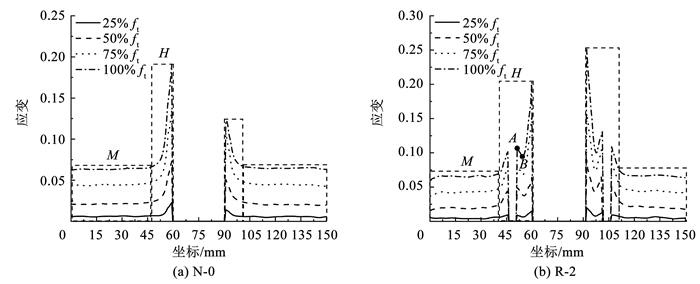
以R-2试样为例,试样在裂纹开始扩展时刻其位移量为8.63 mm,基于DIC技术计算得出该时刻最大位移量为8.51 mm,二者仅相差1.39%,因此DIC技术能精准地测量试样的全场应变。图 7为R-2试样受25%ft、50%ft、75%ft、100%ft时的应变场,裂纹与孔洞的存在和相互作用导致应变分布不均匀,裂纹尖端存在显著的应变集中。如图 7(d)所示可将应变场分为:低应变区(L)、中应变区(M)和高应变区(H)。图 8为N-0试样和R-2试样分别在25%ft、50%ft、75%ft、100%ft下裂纹中心线上的应变分布,零应变对应裂纹与孔洞区域。随着荷载的增大,M区与H区的应变大小同步增加。随着远离裂纹尖端,应变迅速降低至M区后保持稳定。由于孔洞的存在,R-2试样在孔洞两侧出现应变突增,在100%ft情况下,突增点A较局部最低点B分别提升了12.92%、30.79%。图 7中100%ft时的最大应变为裂纹端部首根纤维束的断裂应变,分别为0.190 8和0.251 1,二者差异较大是因为夹持试样难以实现理想对中状态,导致受荷不均;另一方面因纤维束具有一定宽度,在预制裂纹时无法精准切断整根纤维束,从而导致裂纹尖端应变峰值不一致。由表 3可以看出,R-2、R-4、R-6和R-8试样在100%ft下裂纹尖端的平均极限应变在0.26~0.28区间内浮动,这表明中心裂纹尖端极限应变值与孔洞尺寸无关。

|
图 7 不同载荷水平下的全场应变 Fig. 7 Full-field strain at different load levels |
|
图 8 不同荷载水平下裂纹中心线上的应变分布 Fig. 8 Strain disfribution along the crack centercine at different load levels |
| 表 3 中心裂纹尖端两侧极限应变 Tab. 3 Ultimate strain on both sides of the central crack |
图 9为各试样的荷载-位移曲线和强度指标,由图 9(a)可以看出,N-0试样承受荷载达裂纹端临界撕裂荷载ft后曲线随着中心裂纹的扩展出现锯齿形波动上升,达到裂纹端峰值撕裂荷载fv后,裂纹突然快速扩展卸载;而对于含有孔洞缺陷的试样,其中心裂纹扩展模式发生改变,裂纹扩展至与孔洞连通后膜面应力重分布,短时间内不再扩展,当膜面再一次达到极限承载力后,孔外侧形成新裂纹继而扩展破坏。

|
图 9 各试样的荷载-位移曲线和强度指标 Fig. 9 Load - displacement curves and strength indicators of each specimen |
各试样的强度指标变化趋势见图 9(b),对于含圆孔缺陷的试样,随着圆孔直径的增大,裂纹端临界撕裂荷载ft、裂纹端峰值撕裂荷载fv、孔端临界撕裂荷载f′t和孔端峰值撕裂荷载f′v均降低,其中f′t和f′v的下降趋势更显著,当孔径大于4 mm时,最大撕裂荷载fmax转由fv控制。这是因为随着孔径的增大,裂纹与孔洞连通后, 试件的整体缺陷尺寸和变形更大,从而导致孔端的纤维束更接近断裂应变。这一现象表明孔洞尺寸对试件在裂纹与孔洞连通后的撕裂性能影响更显著。
含竖缝缺陷和含扁孔缺陷的试样由于其特殊的孔洞形状,其强度指标变化趋势与含圆孔缺陷试样不同,整体呈递增趋势,表明竖缝和扁孔的应力集中程度小于圆孔,膜面应力在裂纹与孔洞连通后分布更均匀,从而导致试样所承受的荷载更大。值得注意的是,S-0试样的f′t和f′v近似相等,这意味着该试样在孔端产生新裂纹后就丧失继续承载的能力。对于F-2试样,由于孔洞纵向尺寸变大,纬纱剪切传力作用减弱,裂纹扩展后迅速与孔洞连通,fv较ft提升变小。
3 撕裂模型对于含中心裂纹和孔洞的试件,通过裂纹端临界撕裂应力σt和孔端临界撕裂应力σ′t评判膜材撕裂性能,见式(1)、(2):
| $ \sigma_{\mathrm{t}}=\frac{f_{\mathrm{t}}}{L-2\left(l_1+l_3\right)} $ | (1) |
| $ \sigma_{\mathrm{t}}^{\prime}=\frac{f_{\mathrm{t}}^{\prime}}{L-2\left(l_1+l_2+l_3\right)} $ | (2) |
式中:ft(N)为裂纹端临界撕裂荷载,f′t(N)为孔端临界撕裂荷载,L(mm)为试样宽度,l1(mm)为中心裂纹宽度的一半,l2(mm)为中心裂纹与孔洞之间的距离,l3(mm)为孔洞的横向尺寸。由于本文未将l1和l2作为变量进行试验,因此l1和l2为定值,l1=15 mm,l2=10 mm。
本文结合DIC测得的膜面应变场和含裂纹-孔洞下膜材的撕裂机理,提出以下撕裂模型以探究含裂纹-孔洞多缺陷下膜材的撕裂性能,模型做出以下假设:
1) 根据DIC所测得的膜面应变场,膜面A、B两区域的应力场分别呈二次函数和指数函数分布,见图 10(a);

|
图 10 初始缺陷端应力场分布 Fig. 10 Stress field distribution at the end of initial defect |
2) 当缺陷尖端纤维束应力达到极限抗拉强度σu时,裂纹开始扩展;
3) 根据试验结果,当达到裂纹端临界撕裂荷载ft时,孔洞两端的应变值最大相差为9.03%(见表 4),引入折减系数α=0.909 7表征孔洞两端应力关系;
| 表 4 中心裂纹开始扩展时孔洞两端的应变 Tab. 4 Strain at both ends of the hole when the central crack starts to expand |
4) 中心裂纹与孔洞引起的应力集中与缺陷处撕裂应力相平衡。
本文提出一种改进的应力场模型,分别预测裂纹端临界撕裂应力和孔端临界撕裂应力,基于假定1,A区应力场呈二次函数分布,B区应力场呈指数函数分布,表达式见式(3)、(4):
| $ \sigma_{(x)}^A=\left(\sigma_{\mathrm{u}}-\sigma_{\mathrm{c}}\right)(x+1)^2+A \cdot x+\sigma_{\mathrm{c}} \quad 0 \leqslant x \leqslant l_2 $ | (3) |
| $ \sigma_{(x)}^B=\left(\sigma_{\mathrm{m}}-\sigma_{\mathrm{c}}\right) \mathrm{e}^{-B\left(x-l_2-l_3\right)}+\sigma_{\mathrm{c}} \quad x \geqslant l_2+l_3 $ | (4) |
式中:x为横坐标,σ(x)A和σ(x)B为x坐标处的膜面应力,σu为抗拉强度,σc为临界撕裂应力,σm为孔洞两端应力,A和B为模型参数。当中心裂纹尖端第一根纤维束达到断裂荷载时,裂纹开始扩展,此时应力场分布见图 10(a)。基于假定3,其中σ(0)A=σu,σB(l2+l3)=ασA(l2)。经后文对比发现,α=0.909 7和α=1时的模型计算结果差距较小,为简化模型参数,以α=1推导公式,σm与σu和σc的关系见式(5):
| $ \sigma_{\mathrm{m}}=\left(\sigma_{\mathrm{u}}-\sigma_{\mathrm{c}}\right)\left(l_2+1\right)^2+A \cdot l_2+\sigma_c $ | (5) |
根据假定4,缺陷处纤维束原应承担的荷载应与裂纹与孔洞所引起的应力集中平衡,基于此得出:
| $ \begin{gathered} \int\left[\left(\sigma_{\mathrm{u}}-\sigma_{\mathrm{c}}\right)(x+1)^2+A x\right] \cdot \mathrm{d} x= \\ \frac{l_2^3+3 l_2^2+3 l_2}{3}\left(\sigma_{\mathrm{u}}-\sigma_{\mathrm{c}}\right)+\frac{A}{2} \cdot l_2^2 \end{gathered} $ | (6) |
| $ \begin{gathered} \int\left[\left(\sigma_{\mathrm{m}}-\sigma_{\mathrm{c}}\right) \mathrm{e}^{-B\left(x-l_2-l_3\right)}\right] \cdot \mathrm{d} x=\frac{\sigma_{\mathrm{m}}-\sigma_{\mathrm{c}}}{B}= \\ \frac{\left(l_2+1\right)^2\left(\sigma_{\mathrm{u}}-\sigma_{\mathrm{c}}\right)}{B}+\frac{A}{B} \cdot l_2 \end{gathered} $ | (7) |
通过简化,临界撕裂应力与中心裂纹和孔洞尺寸的关系见式(8):
| $ \sigma_c=\frac{\left[\left(l_2^3+3 l_2^2+3 l_2\right) / 3+\left(l_2+1\right)^2 / B_1\right] \sigma_{\mathrm{u}}+\left(A \cdot l_2^2\right) / 2+\left(A \cdot l_2\right) / B_1}{\left(l_2^3+3 l_2^2+3 l_2\right) / 3+\left(l_2+1\right)^2 / B_1+l_1+l_3} $ | (8) |
根据本文试验内容,将l3作为变量,l1和l2作为定量进行研究,其中l1=15 mm、l2=10 mm,拟合出参数A=-337.63、B1=11.09。当中心裂纹扩展至与孔洞相连时,A区应力场消失,此时应力场分布见图 10(b),其中σ(l2+l3)B=σu。同理,临界撕裂应力与裂纹尺寸的关系见式(9)、(10):
| $ \sigma_{\mathrm{c}} \cdot\left(l_1+l_2+l_3\right)=\frac{\sigma_{\mathrm{u}}-\sigma_{\mathrm{c}}}{B_2} $ | (9) |
| $ \sigma_{\mathrm{c}}=\frac{\sigma_u}{1+B_2 \cdot\left(l_1+l_2+l_3\right)} $ | (10) |
结合本文试验结果,拟合出参数B2=0.046。
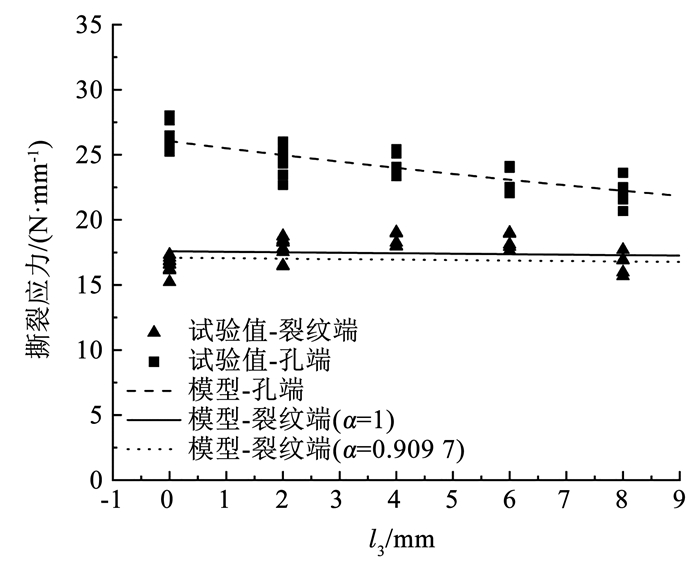
本文模型针对含裂纹-孔洞缺陷的试样,修改应力分布函数实现了分段预测。由式(8)和式(10)可知,中心裂纹尺寸、孔洞尺寸和孔与中心裂纹间距是影响裂纹端临界撕裂应力和孔端临界撕裂应力的主要因素。由图 11可以看出,孔端两侧应力相等的模型(α=1)与考虑孔洞两端应力折减的模型(α=0.909 7)差距不明显,这是因为在中心裂纹开始扩展时刻,裂纹尖端应力集中导致孔端应力远小于断裂应力,孔端应力对撕裂应力计算的贡献较小。孔洞尺寸对裂纹端撕裂应力影响较小,而随着孔洞尺寸的增大,孔端撕裂应力逐渐降低。通过试验数据可知,对于大于2 mm但小于6 mm的孔洞,裂纹端临界撕裂应力预测值偏小,对于其他尺寸范围的孔洞,预测值偏大,其中最大误差为5.37%;在预测孔端临界撕裂应力时,本文模型的预测结果在试验尺寸范围内与试验数据接近且拟合良好,最大误差为2.29%。综上所述,本文模型对裂纹端临界撕裂应力和孔端临界撕裂应力均具有良好的预测性能。
|
图 11 裂纹端临界撕裂应力和孔端临界撕裂应力的预测效果 Fig. 11 Prediction effect of critical tear stress at crack-end and hole-end |
1) 孔洞的存在削弱了膜材抗撕裂性能,裂纹扩展路径和模式随孔洞类型改变,圆孔缺陷与扁孔缺陷不会改变裂纹扩展路径,而新裂纹会在竖缝缺陷两端随机一侧产生并继续扩展。膜面应力在裂纹扩展至与孔洞连通后重分布,这种情况下裂纹扩展中断,膜材仍具有一定承载能力。
2) 当孔洞形状为圆孔时,孔端临界撕裂荷载均小于裂纹端峰值撕裂荷载,而形状为扁孔或竖缝时,孔端临界撕裂荷载较裂纹端峰值撕裂荷载大幅提升。当圆孔直径从4 mm增大到8 mm时,孔洞对缝孔连通后承载能力的削弱愈发显著,最大撕裂荷载变为裂纹端峰值撕裂荷载。值得注意的是,含竖缝缺陷试样的孔端临界撕裂荷载与孔端峰值撕裂荷载相等,孔端没有新裂纹扩展,表现为脆性破坏。
3) 缺陷端部应力场受孔洞影响呈二次函数和指数函数两段分布形式,本文提出了含裂纹-孔洞多缺陷膜材撕裂模型,预测精度良好,其中裂纹尺寸、孔洞尺寸和裂纹与孔洞间距离是影响膜材撕裂强度的主要因素。
| [1] |
武岳, 陈昭庆, 孙晓颖. 张拉膜结构风致动力灾变研究进展[J]. 哈尔滨工业大学学报, 2017, 49(6): 1. WU Yue, CHEN Zhaoqing, SUN Xiaoying. Advances on wind-induced dynamic disaster of tensioned membrane structures[J]. Journal of Harbin Institute of Technology, 2017, 49(6): 1. DOI:10.11918/j.issn.0367-6234.201606104 |
| [2] |
张营营, 赵玉帅, 徐俊豪, 等. PVC涂层织物撕裂破坏机理分析与强度预测模型[J]. 建筑结构学报, 2018(Sup.2): 336. ZHANG Yingying, ZHAO Yushuai, XU Junhao, et al. Analysis of tearing failure mechanism and strength predictive model of PVC coated fabrics[J]. Journal of Building Structures, 2018(Sup.2): 336. DOI:10.14006/j.jzjgxb.2018.S2.046 |
| [3] |
陈建稳, 张若男, 张阳, 等. 经编织物气囊蒙皮梯形撕裂行为及破坏机制[J]. 哈尔滨工业大学学报, 2022, 54(6): 28. CHEN Jianwen, ZHANG Ruonan, ZHANG Yang, et al. Trapezoid tearing behavior and damage mechanism of warp-knitted envelope fabrics[J]. Journal of Harbin Institute of Technology, 2022, 54(6): 28. DOI:10.11918/202012127 |
| [4] |
姜旭, 吕志林, 强旭红, 等. 高强螺栓止裂法修复含裂纹钢板疲劳受力性能[J]. 同济大学学报(自然科学版), 2021, 49(4): 476. JIANG Xu, LV Zhilin, QIANG Xuhong, et al. Fatigue performance of cracked steel plates repaired by high strength bolt stop-hole method[J]. Journal of Tongji University, 2021, 49(4): 476. DOI:10.11908/j.issn.0253-374x.20385 |
| [5] |
张召冉, 左进京, 郭义先. 爆炸载荷下空孔缺陷与爆生裂纹扩展行为研究[J]. 振动与冲击, 2020, 39(3): 111. ZHANG Zhaoran, ZUO Jinjing, GUO Yixian. Crack propagation behavior of empty hole defects under blast load[J]. Journal of Vibration and Shock, 2020, 39(3): 111. DOI:10.13465/j.cnki.jvs.2020.03.015 |
| [6] |
张旭波, 吴明儿, 包晗. 涂层织物类膜材的偏轴梯形撕裂行为[J]. 建筑材料学报, 2021, 24(1): 121. ZHANG Xubo, WU Minger, BAO Han. Off-axial trapezoid tearing behaviors of coated fabrics[J]. Journal of Building Materials, 2021, 24(1): 121. DOI:10.3969/j.issn.1007-9629.2021.01.017 |
| [7] |
曹帅, 刘龙斌, 孟军辉, 等. 杆模型的平流层飞艇蒙皮撕裂扩展分析[J]. 哈尔滨工业大学学报, 2015, 47(11): 58. CAO Shuai, LIU Longbin, MENG Junhui, et al. Tearing propagation of stratospheric airship envelope based on the link model[J]. Journal of Harbin Institute of Technology, 2015, 47(11): 58. DOI:10.11918/j.issn.0367-6234.2015.11.010 |
| [8] |
陈建稳, 周涵, 陈务军, 等. 双轴向经编类膜材PVDF8028偏轴强度及刚度特征[J]. 湖南大学学报(自然科学版), 2019, 46(9): 54. CHEN Jianwen, ZHOU Han, CHEN Wujun, et al. Mechanical characteristics of off-axis tensile strength and stiffness of biaxial warp-knitted fabric PVDF8028[J]. Journal of Hunan University(Natural Sciences), 2019, 46(9): 54. DOI:10.16339/j.cnki.hdxbzkb.2019.09.006 |
| [9] |
包晗, 张旭波, 吴明儿. PVC涂层聚酯纤维膜材撕裂性能试验研究[J]. 建筑材料学报, 2020, 23(3): 631. BAO Han, ZHANG Xubo, WU Minger. Experimental study on tearing behavior of PVC coated polyester fiber membrane[J]. Journal of Building Materials, 2020, 23(3): 631. DOI:10.3969/j.issn.1007-9629.2020.03.021 |
| [10] |
刘龙斌, 吕明云, 肖厚地. 含初始裂纹的平流层飞艇用蒙皮薄膜撕裂行为[J]. 复合材料学报, 2015, 32(2): 508. LIU Longbin, LV Mingyun, XIAO Houdi. Tear behavior of skin films for stratospheric airships with initial cracks[J]. Acta Materiae Compositae Sinica, 2015, 32(2): 508. DOI:10.13801/j.cnki.fhclxb.20140603.001 |
| [11] |
HE Rijin, SUN Xiaoying, WU Yue. Central crack tearing test and fracture parameter determination of PTFE coated fabric[J]. Construction and Building Materials, 2019, 208: 472. DOI:10.1016/j.conbuildmat.2019.03.046 |
| [12] |
BAO Han, WU Minger, ZHANG Xubo. Study on tearing tests and the determination of fracture toughness of PVC-coated fabric[J]. Journal of Industrial Textiles, 2022, 51(6): 977. DOI:10.1177/1528083721993943 |
| [13] |
上海市住房和城乡建设管理委员会. 膜结构检测标准: DG/TJ 08-2019—2019[S]. 上海: 同济大学出版社, 2020 Shanghai Municipal Commission of Housing and Urban-Rural Development. Standard for inspection of membrane structures: DG/TJ 08-2019—2019[S]. Shanghai: Tongji University Press, 2020 |
| [14] |
BLABER J, ADAIR B, ANTONIOU A. Ncorr: Open-Source 2D Digital Image Correlation Matlab Software[J]. Experimental Mechanics, 2015, 55: 1105. DOI:10.1007/s11340-015-0009-1 |
| [15] |
丁凯, 陈永霖, 陈亚飞, 等. 平流层飞艇蒙皮材料撕裂性能影响因素研究[J]. 空间结构, 2021, 27(3): 61. DING Kai, CHEN Yonglin, CHEN Yafei, et al. Study on factors influencing tearing properties of stratospheric airship envelope materials[J]. Spatial Structures, 2021, 27(3): 61. DOI:10.13849/j.issn.1006-6578.2021.03.061 |
 2024, Vol. 56
2024, Vol. 56


