2. 先进船舶通信与信息技术工业和信息化部重点实验室(哈尔滨工程大学),哈尔滨 150001
2. Key Laboratory of Advanced Ship Communication and Information Technology (Harbin Engineering University), Ministry of Industry and Information Technology, Harbin 150001, China
非线性量测下的机动目标跟踪问题是多目标跟踪(multi-target tracking,MTT) [1]领域的热点问题之一。一方面实际场景中常见的传感器,诸如雷达、声呐等,捕获到的目标量测信息均为非线性的,滤波时无法直接得到闭合形式的解;另一方面被跟踪的目标常具有机动性,单一运动模型无法描述目标的运动状态,易产生目标的漏估。因此需要对非线性量测下的机动多目标跟踪算法展开研究。
近几年,基于随机有限集(random finite set, RFS)[2]的MTT算法因避免了传统数据关联[3]算法中的NP问题,受到广泛的关注。经典的RFS多目标跟踪算法有:概率假设密度(probability hypothesis density, PHD)[4]、势概率假设密度(cardinalized probability hypothesis density, CPHD)[5]、多伯努利(multiple target multi-Bernoulli, MeMBer)[6]以及δ-广义标签多伯努利(δ-generalized labeled multi-Bernoulli, δ-GLMB) [7]滤波器。其中δ-GLMB能够利用标签信息准确的产生航迹,跟踪性能优异,被证明为最优贝叶斯滤波器,是本文研究的基础。
在非线性量测场景中,δ-GLMB算法一般通过扩展卡尔曼(extended Kalman filter, EKF)[8]、无迹卡尔曼(unscented Kalman filter, UKF)[9]、容积卡尔曼(cubature Kalman filter, CKF)[10]等线性化技术将非线性滤波问题转化为近似线性滤波问题,但这些技术的应用会使算法的计算复杂度大幅度增加。而另一类基于量测转换卡尔曼(converted measurement Kalman filter, CMKF)[11]的方法,可直接将非线性量测转化为线性量测,再使用卡尔曼求解,避免了此问题,却因转换有偏导致跟踪精度较低,应用较少。
另外,为了实现对机动多目标的跟踪,文献[12]引入了马尔科夫跳变系统(jump Markov system,JMS),推导了JMS-δ-GLMB高斯混合实现的闭式解,但其只能应用于线性高斯场景;文献[13]提出了无迹变换的马尔科夫多模型δ-GLMB(UKF-JMS-δ-GLMB)滤波器,实现了非线性场景的应用,但其在滤波阶段使用的分支真实密度以及UKF为近似先验分布所产生的点集,导致计算量过于庞大;文献[14]对分支密度进行合并,提出了交互多模型δ-GLMB(IMM-δ-GLMB)滤波器,降低了计算量,但其计算时间仍随着杂波率线性增加。
针对上述非线性量测下的机动多目标δ-GLMB算法计算复杂度较高、跟踪误差较大以及对杂波变化鲁棒性较差的问题,本文提出了一种采用去相关无偏量测转换(decorrelated unbiased converted measurement, DUCM)[15]和模糊算法[16]改进的多模型δ-GLMB (DUCM-FIMM-δ-GLMB)滤波器。该算法使用DUCM处理非线性量测,实现位置量测从极坐标系到笛卡尔坐标系的无偏转换,并通过预测值去除量测误差和其协方差的相关性造成的滤波估计偏差;然后基于量测关联新息和目标的机动约束构建联合波门,降低杂波环境中无效关联量测的数量;最后在IMM的基础上引入模糊算法,自适应改变运动模型的过程噪声,进一步提升对机动多目标的跟踪精度。仿真结果表明,所提算法与现有算法相比跟踪精度更高,计算时间更少,鲁棒性更强。
1 背景模型 1.1 状态模型在二维多目标运动场景中,假设k时刻有N个目标,则多目标状态RFS建模为Xk={x1, k, …, xN, k}, xi, k=[xi, k,
| $ \boldsymbol{x}_k=\boldsymbol{F} \boldsymbol{x}_{k-1}+\boldsymbol{w}_{k-1} $ | (1) |
式中: F为状态转移矩阵; wk-1为过程噪声,服从均值为零、标准差为σμ的高斯分布。
1.2 量测模型假设传感器在k时刻获取到M个量测信息Zkm={z1, km, …, zM, km}, zj, km=[γj, km, βj, km]T,其中γj, km、βj, km分别为目标的径向距离和方位角。目标状态和量测之间的关系可表示为
| $ \boldsymbol{z}_k^m=h\left(\boldsymbol{x}_k\right)+\boldsymbol{v}_k^m $ | (2) |
式中h(·) 为非线性函数,式(2)可写为
| $ \left[\begin{array}{c} \gamma_k^m \\ {\beta}_k^m \end{array}\right]=\left[\begin{array}{c} \sqrt{x_k^2+y_k^2} \\ \arctan \left(y_k / x_k\right) \end{array}\right]+\left[\begin{array}{c} \tilde{\gamma}_k^m \\ \tilde{{\beta}}_k^m \end{array}\right] $ | (3) |
式中
引入标签集,用标签l对状态 x进行扩维,则多目标状态X可由标签RFS表示为
| $ X=\left\{(\boldsymbol{x}, l)_1, (\boldsymbol{x}, l)_2, \cdots, (\boldsymbol{x}, l)_N\right\} $ | (4) |
式中:x ∈ X为目标状态矢量,l∈ L为其唯一对应标签;X⊆ X × L,X为状态空间,L为标签空间。
设k时刻的多目标概率密度πk|k(X)服从δ-GLMB分布,如下式所示:
| $ \pi_{k \mid k}(X)=\varDelta(X) \sum\limits_{(I, \vartheta) \in \mathcal{F}\left(\boldsymbol{L}_{k \mid k}\right) \times {\mathit{\Xi}}} w_{k \mid k}^{(I, \vartheta)} \delta_l(\mathcal{L}(X))\left[p_{k \mid k}^{(\vartheta)}\right]^X $ | (5) |
式中,
交互多模型(interactive multiple model, IMM)算法在单目标跟踪领域一直被认为是解决机动目标跟踪的有效手段,它采用多个运动模型来描述目标的运动状态,再通过加权融合估计,很好地克服了单模型估计误差较大的问题。在基于RFS的MTT领域,文献[17]最早使用IMM思想提出了一种新的多模型PHD滤波器; 文献[14]采用马尔科夫分支合并策略与δ-GLMB算法结合,提出了线性高斯的IMM-δ-GLMB,并证实了IMM在RFS领域同样具有优越性。本文在此基础上提出了用于非线性量测下机动多目标跟踪的DUCM-FIMM-δ-GLMB滤波器,算法流程见图 1。首先进行输入混合,通过混合每个航迹上一时刻所有模型滤波器的状态估计来获得与此航迹特定模型匹配的滤波器的初始条件;然后对每个模型进行并行预测;预测完成后,利用预测信息对非线性量测进行去相关无偏量测转换和杂波滤除;处理后的线性量测将用于并行滤波更新;最后,更新每个模型的概率,一方面将其作为模糊控制器的输入,用于改变运动模型的过程噪声系数,另一方面用于对每个模型滤波器的输出进行加权混合,得到最终的状态估计。

|
图 1 DUCM-FIMM-δ-GLMB流程 Fig. 1 DUCM-FIMM-δ-GLMB flow |
在JMS中,各模型之间的转移由马尔科夫概率转移矩阵 TPM确定,其中元素pij为目标从模型i转移到模型j的概率
| $ \boldsymbol{T}_{\mathrm{PM}}=\left[\begin{array}{ccc} p_{11} & \cdots & p_{1 j} \\ \vdots & & \vdots \\ p_{i 1} & \cdots & p_{i j} \end{array}\right] $ | (6) |
使用表征运动模型的离散变量对状态变量进行扩维,则增广状态 x =(ξ, μ),其中ξ为目标状态,μ∈
| $ p(\xi)=\int p(\xi, \mu) \mathrm{d} \mu=\sum\limits_{\mu \in {\cal{M}}} p(\mu) p(\xi \mid \mu) $ | (7) |
输入航迹l在k时刻所有模型的条件概率密度pk|kϑ(ξ, l|μi),其混合分布pk|k0, ϑ(ξ, μj, l)可由IMM混合分布原理得到
| $ p_{k \mid k}^{0, \vartheta}\left(\xi, \mu_j, l\right)=\sum _{i=1}^{|{\cal{M}}|} u_k^{i j} p_{k \mid k}^{\vartheta}\left(\xi, l \mid \mu_i\right) $ | (8) |
式中:
在高斯过程中,pk∣k0, ϑ(ξ, μj, l) 可由混合均值 mk|k0, μj和混合协方差 Pk|k0, μj表示成单一高斯项:
| $ p_{k \mid k}^{0, \vartheta}\left(\xi, \mu_j, l\right) =w_{k \mid k}^{0, \mu_j} \mathcal{N}\left(\xi ; \boldsymbol{m}_{k \mid k}^{0, \mu_j}, \boldsymbol{P}_{k \mid k}^{0, \mu_j}\right) $ | (9) |
| $ w_{k \mid k}^{0, \mu_j} =\sum\nolimits_{i=1}^{|{\cal{M}}|} u_k^{i j} w_{k \mid k}^{\mu_i} $ | (10) |
| $ \boldsymbol{m}_{k \mid k}^{0, \mu_j} =\sum\nolimits_{i=1}^{|{\cal{M}}|} u_k^{i j} \boldsymbol{m}_{k \mid k}^{\mu_i} $ | (11) |
| $ \boldsymbol{P}_{k \mid k}^{0, \mu_j}=\sum\nolimits_{i=1}^{|{\cal{M}}|} u_k^{i j} \times\left[\boldsymbol{P}_{k \mid k}^{\mu_i}+\left(\boldsymbol{m}_{k \mid k}^{0, \mu_j}-\boldsymbol{m}_{k \mid k}^{\mu_i}\right)\left(\boldsymbol{m}_{k \mid k}^{0, \mu_j}-\boldsymbol{m}_{k \mid k}^{\mu_i}\right)^{\mathrm{T}}\right] $ | (12) |
将式(5)中的单目标概率分布用式(7)近似,即
| $ \pi_{k+1| k}(X)={\mathit{\Delta}}(X) \sum\limits_{(I, \vartheta) \in \mathcal{F}\left(\boldsymbol{L}_{k+1| k}\right) \times {\mathit{\Xi}}} w_{k+1 \mid k}^{(I, \vartheta)} \delta_I(\mathcal{L}(X))\left[p_{k+1| k}^{(\vartheta)}\right]^X $ | (13) |
式中:
| $ \left\{\begin{array}{l} w_{k+1 \mid k}^{(I, \vartheta)}=w_{k+1| k, S}^{(\vartheta)}\left(I \cap \boldsymbol{L}_k\right) w_{k, b}\left(I \cap \boldsymbol{B}_k\right) \\ w_{k+1| k, S}^{(\vartheta)}=\left[\boldsymbol{\eta}_S^{(\vartheta)}\right]^L \sum\limits_{I \subseteq \boldsymbol{L}_k} 1_I(L)\left[1-\boldsymbol{\eta}_S^{(\vartheta)}\right]^{I-L} w_{k \mid k}^{(I, \vartheta)} \\ p_{k+1 \mid k}^{(\vartheta)}(\boldsymbol{x}, l)=\sum\nolimits_{j=1}^{|{\cal{M}}|}-\bar{c}_k^{\mu_j} p_{k+1 k}^{(0, \vartheta)}\left(\xi, \mu_j, l\right) \\ p_{k+1 \mid k}^{(0, \vartheta)}(\xi, \mu, l)=1_{\boldsymbol{L}_k}(l) p_{k+1 \mid k, S}^{(0, \vartheta)}(\xi, \mu, l)+1_{\boldsymbol{B}_k}(l) p_{k, b}(\xi, \mu, l) \\ p_{k+1 \mid k, S}^{(0, \vartheta)}(\xi, \mu, l)=\frac{\left\langle p_S(\cdot , \mu, l) \varphi(\xi \mid \cdot, \mu, l), p_{k \mid k}^{(0, \vartheta)}(\cdot, \mu, l)\right\rangle}{\eta_S^{(\vartheta)}(l)} \\ \eta_S^{(\vartheta)}(l)=\sum\limits_{\mu \in \mathcal{M}}\left\langle p_S(\cdot, \mu, l), p_{k \mid k}^{(0, \vartheta)}(\cdot , \mu, l)\right\rangle \end{array}\right. $ |
其中,预测标签空间 Lk+1|k= Lk∪ Bk,Bk为新生目标的标签空间。〈f, g〉为内积,1Y(X)为广义指示函数,也称包含函数。wk+1|k(I, ϑ)为预测假设分量的权重,表示存活和新生分量权重的乘积。pk+1|k(0, ϑ)(ξ, μ, l)表示运动模型为μ的单目标预测混合状态概率密度,由存活目标密度pk+1|k, S(0, ϑ)(ξ, μ, l)和新生目标密度pk, b(ξ, μ, l)组成,其高斯混合实现如下:
对于线性高斯模型,存活概率密度设为常数pS(ξ, μ, l)=pS,概率转移密度ϕ(ξk+1|ξk, μ, l)=(ξk+1; Fμξk, Qk(μ, l)),其中 Fμ为运动模型为μ的状态转移矩阵,Qk(μ, l)为相应的过程噪声协方差,由后续模糊算法得到。若单目标先验混合密度pk|k(0, ϑ)(ξ, μ, l)和新生目标密度pk, b(ξ, μ, l)均为高斯混合形式,那么预测密度pk+1|k(0, ϑ)(ξ, μ, l)也为高斯形式,则有:
| $ \begin{gathered} p_{k+1 \mid k}^{(0, \vartheta)}(\xi, \mu, l)=w_{k+1 \mid k}^{(0, \vartheta, \mu, l)} \subset \mathcal{N}\left(\boldsymbol{\xi} ; \boldsymbol{m}_{k+1 \mid k}^{(0, \vartheta, \mu, l)}, \boldsymbol{P}_{k+1 \mid k}^{(0, \vartheta, \mu, l)}\right)= \\ 1_{\boldsymbol{L}_k}(l) w_{k+1 \mid k, S}^{(0, \vartheta, \mu, l)}\left( \boldsymbol{\xi} ; \boldsymbol{m}_{k+1 \mid k, S}^{(0, \vartheta, \mu, l)}, \boldsymbol{P}_{k+1 \mid k, S}^{(0, \vartheta, \mu, l)}\right)+ \\ 1_{\boldsymbol{B}_k}(l) w_{k, b}^{(\mu, l)} \mathcal{N}\left(\xi ; \boldsymbol{m}_{k, b}^{(\mu, l)}, \boldsymbol{P}_{k, b}^{(\mu, l)}\right) \end{gathered} $ | (14) |
| $ \eta_S^{(0, \vartheta)}(l)=p_S $ | (15) |
式中:
| $ w_{k+1 \mid k, S}^{(0, \vartheta, \mu, l)}=p_S w_{k \mid k}^{(0, \vartheta, \mu, l)} $ | (16) |
| $ \boldsymbol{m}_{k+1 \mid k, S}^{(0, \vartheta, \mu, l)}=\boldsymbol{F}^\mu \boldsymbol{m}_{k \mid k}^{(0, \vartheta, \mu, l)} $ | (17) |
| $ \boldsymbol{P}_{k+1 \mid k, S}^{(0, \vartheta, \mu, l)}=\boldsymbol{F}^\mu \boldsymbol{P}_{k \mid k}^{(0, \vartheta, \mu, l)}\left(\boldsymbol{F}^\mu\right)^{\mathrm{T}}+\boldsymbol{Q}_k^{(\mu, l)} $ | (18) |
在滤波更新前,对量测信息进行预处理,可有效增加滤波精度。对于传感器捕获到的非线性量测信息,利用DUCM算法进行位置量测的无偏转换和量测转换误差的去相关。
k+1时刻的位置量测为 zk+1m=[γk+1m, βk+1m]T,传统量测转换 zk+1v及其数学期望为:
| $ \boldsymbol{z}_{k+1}^v=\left[\begin{array}{c} x_{k+1}^v \\ y_{k+1}^v \end{array}\right]=\left[\begin{array}{c} \gamma_{k+1}^m \cos \left({\beta}_{k+1}^m\right) \\ \gamma_{k+1}^m \sin \left({\beta}_{k+1}^m\right) \end{array}\right] $ | (19) |
| $ \begin{aligned} \boldsymbol{E}_{k+1}^v= & {\left[\begin{array}{l} E\left[x_{k+1}^v\right] \\ E\left[y_{k+1}^v\right] \end{array}\right]=} \\ & {\left[\begin{array}{l} E\left[\left(\gamma_{k+1}+\tilde{\gamma}_{k+1}^m\right) \cos \left(\beta_{k+1}+\tilde{\beta}_{k+1}^m\right)\right] \\ E\left[\left(\gamma_{k+1}+\tilde{\gamma}_{k+1}^m\right) \sin \left(\beta_{k+1}+\tilde{\beta}_{k+1}^m\right)\right] \end{array}\right]=} \\ & {\left[\begin{array}{l} \lambda_\beta \gamma_{k+1} \cos \left(\beta_{k+1}\right) \\ \lambda_\beta \gamma_{k+1} \sin \left(\beta_{k+1}\right) \end{array}\right] } \end{aligned} $ | (20) |
式中: γk+1、βk+1为真实量测; λβ=e-σβ2/2为偏差因子[18]。可知,当λβ≠1时,zk+1v转换有偏。因此,可用λβ-1作为补偿因子进行乘性去偏,则从极坐标系到笛卡尔坐标系的无偏转换为
| $ {\boldsymbol{z}}_{k + 1}^c = \left[ {\begin{array}{*{20}{c}} {x_{k + 1}^c}\\ {y_{k + 1}^c} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\rm{e}}^{\sigma _\beta ^2/2}}\gamma _{k + 1}^m\cos \left( {\beta _{k + 1}^m} \right)}\\ {{{\rm{e}}^{\sigma _\beta ^2/2}}\gamma _{k + 1}^m\sin \left( {\beta _{k + 1}^m} \right)} \end{array}} \right] $ | (21) |
无偏量测转换误差的均值为
| $ \boldsymbol{E}_{k+1}^c=E\left[\left(\tilde{x}_{k+1}^c \tilde{y}_{k+1}^c\right)^{\mathrm{T}}\right]=\mathbf{0}_{2 \times 1} $ | (22) |
传统量测转换算法基于量测值计算量测转换误差的协方差,这使得量测转换误差的协方差和量测噪声具有相关性,进而导致滤波估计偏差。为去除相关性,使用预测状态 mk+1|k和预测协方差 Pk+1|k推导量测转换误差的协方差 Rk+1c
| $ \boldsymbol{R}_{k+1}^c=\operatorname{cov}\left\{\left(\tilde{x}_{k+1}^c \tilde{y}_{k+1}^c\right)^{\mathrm{T}} \mid \gamma_t, {\beta}_t\right\}=\left[\begin{array}{ll} {R}_{k+1}^{x x} & {R}_{k+1}^{x y} \\ {R}_{k+1}^{y x} & {R}_{k+1}^{y y} \end{array}\right] $ | (23) |
其中:
| $ \left\{ {\begin{array}{*{20}{l}} {R_{k + 1}^{xx} = }&{\frac{1}{2}\left[ {\gamma _t^2 + \sigma _\gamma ^2 + \sigma _{{\gamma _t}}^2} \right]{{\rm{e}}^{\sigma _\beta ^2}}\left[ {1 + \cos \left( {2{\beta _t}} \right){{\rm{e}}^{ - 2\sigma _\beta ^2}}{{\rm{e}}^{ - 2\sigma _{{\beta _t}}^2}}} \right] - }\\ {}&{\frac{1}{2}\left[ {\gamma _t^2 + \sigma _{{\gamma _t}}^2} \right]\left[ {1 + \cos \left( {2{\beta _t}} \right){{\rm{e}}^{ - 2\sigma _{{\beta _t}}^2}}} \right]}\\ {R_{k + 1}^{yy} = }&{\frac{1}{2}\left[ {\gamma _t^2 + \sigma _\gamma ^2 + \sigma _{{\gamma _t}}^2} \right]{{\rm{e}}^{\sigma _\beta ^2}}\left[ {1 - \cos \left( {2{\beta _t}} \right){{\rm{e}}^{ - 2\sigma _\beta ^2}}{{\rm{e}}^{ - 2\sigma _{{\beta _t}}^2}}} \right] - }\\ {}&{\frac{1}{2}\left[ {\gamma _t^2 + \sigma _{{\gamma _t}}^2} \right]\left[ {1 - \cos \left( {2{\beta _t}} \right){{\rm{e}}^{ - 2\sigma _{{\beta _t}}^2}}} \right]}\\ {R_{k + 1}^{xy} = }&{R_{k + 1}^{yx} = \frac{1}{2}\left[ {\gamma _t^2 + \sigma _\gamma ^2 + \sigma _{{\gamma _t}}^2} \right]{{\rm{e}}^{\sigma _\beta ^2}}\left[ {\sin \left( {2{\beta _t}} \right){{\rm{e}}^{ - 2\sigma _\beta ^2}}{{\rm{e}}^{ - 2\sigma _{{\beta _t}}^2}}} \right] - }\\ {}&{\frac{1}{2}\left[ {\gamma _t^2 + \sigma _{{\gamma _t}}^2} \right]\left[ {\sin \left( {2{\beta _t}} \right){{\rm{e}}^{ - 2\sigma _{{\beta _t}}^2}}} \right]}\\ {\sigma _{{\gamma _t}}^2 = }&{\left( {{P_{xx}}y_t^2 - 2{P_{xy}} + {P_{yy}}x_t^2} \right)/\left( {x_t^2 + y_t^2} \right)}\\ {\sigma _{{\beta _t}}^2 = }&{\left( {{P_{xx}}y_t^2 - 2{P_{xy}}{x_t}{y_t} + {P_{yy}}x_t^2} \right)/{{\left( {x_t^2 + y_t^2} \right)}^2}} \end{array}} \right. $ |
式中: γt、βt为距离和角度的预测值; xt、yt为笛卡尔坐标系目标预测位置,可由 mk+1|k提取得到;σγt2、σβt2为距离和角度的预测误差方差,可由 Pk+1|k经计算得到。由pk+1|k(0, ϑ)(ξ, μ, l)可计算相应航迹转换后的量测噪声协方差 Rk+1c, μ, l。
2.4 联合波门杂波滤除转换后的量测需进行杂波滤除,多模型的滤波过程采用多个并行滤波器[19],这导致多模型δ-GLMB中目标假设航迹的数量大幅度增加,通过设置门限过滤杂波已经不能有效地减少无效航迹的数量。为此本文提出了一种适用于机动多目标跟踪的联合波门杂波滤除策略,如下:
预测航迹与量测的关联新息d[20]为
| $ \begin{gathered} d\left(x_{k+1 \mid k}^{\mu, l}, \boldsymbol{z}_{k+1}^{c, z_i}\right)= \\ \left(\boldsymbol{z}_{k+1}^{c, z_i}-\boldsymbol{H} \boldsymbol{x}_{k+1 \mid k}^{\mu, l}\right)^{\mathrm{T}}\left(\boldsymbol{W}_{k+1}^{\mu, l}\right)^{-1}\left(\boldsymbol{z}_{k+1}^{c, z_i}-\boldsymbol{H} \boldsymbol{x}_{k+1 \mid k}^{\mu, l}\right) \end{gathered} $ | (24) |
式中: H为线性观测矩阵,Wk+1μ, l为新息协方差。
| $ \boldsymbol{W}_{k+1}^{\mu, l}=\boldsymbol{H} \boldsymbol{F}^\mu \boldsymbol{P}_{k \mid k}^{\mu, l}\left(\boldsymbol{H} \boldsymbol{F}^\mu\right)^{\mathrm{T}}+\boldsymbol{H} \boldsymbol{Q}_k^{\mu, l} \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{R}_{k+1}^{c, \mu, l} $ | (25) |
预设关联门限,则预测航迹周围的量测
| $ \hat{{Z}}_{k+1}^{c, l, 1}=\left\{\boldsymbol{z} \mid d\left(\boldsymbol{x}_{k+1 \mid k}^{\mu, l}, \boldsymbol{z}_{k+1}^{c, z_i}\right)<{\varepsilon}, \boldsymbol{z}_{k+1}^{c, z_i} \in {Z}_{k+1}^c\right\} $ | (26) |
门限ε的选择可依据逆卡方分布确定,门限之外的量测被认为是杂波,不予考虑。然而在高杂波场景下,目标量测附近也密布杂波,且多模型的场景会有更多假设航迹,门限过滤的方法效果大打折扣。为进一步降低量测关联的复杂度,减少门限内的杂波量测对状态更新的影响,本文利用k时刻的目标后验信息对杂波进行二次处理:
θ为航迹标签到量测索引的映射函数,则θk(l)为航迹l在k时刻的关联量测索引,μ为模型索引,
| $ \boldsymbol{z}_k^{c, \mu, l}=\hat{Z}_k^c\left(\theta_k(l), \mu\right) $ | (27) |
航迹l符合机动约束的量测可由下式提取:
| $ \hat{{Z}}_{k+1}^{c, l, 2}=\left\{\boldsymbol{z} \mid d\left(\boldsymbol{z}_k^{c, \mu, l}, \boldsymbol{z}_{k+1}^{c, z_i}\right)<T_{k+1}^{\mu, l}, \boldsymbol{z}_{k+1}^{c, z_i} \in {Z}_{k+1}^c\right\} $ | (28) |
其中:
| $ d\left(\boldsymbol{z}_k^{c, \mu, l}, \boldsymbol{z}_{k+1}^{c, z_i}\right)=\left(\boldsymbol{z}_k^{c, \mu, l}-\boldsymbol{z}_{k+1}^{c, z_i}\right)^{\mathrm{T}}\left(\boldsymbol{R}_{k+1}^{c, \mu, l}\right)^{-1}\left(\boldsymbol{z}_k^{c, \mu, l}-\boldsymbol{z}_{k+1}^{c, z_i}\right) $ | (29) |
| $ T_{k+1}^{\mu, l}=\eta\left(\sqrt{\left(\dot{x}_{k+1 \mid k}^{\mu, l}\right)^2+\left(\dot{y}_{k+1 \mid k}^{\mu, l}\right)^2}+2 \sqrt{R_{k+1}^{\mu, l, x x}+R_{k+1}^{\mu, l, y y}}\right) $ | (30) |
门限Tk+1μ, l由目标的预测速度和量测噪声决定,η=(1+κ(Zk+1c)) 为调整因子,κ(Z)为杂波密度函数,在观测空间中服从均匀分布,每一帧量测产生的杂波数量服从期望为λ的泊松分布,可知η随着杂波的数量增加而增大。
综合式(26)、(28)得k+1时刻关联量测为
| $ \hat{{Z}}_{k+1}^c=\bigcup\limits_{l \in \boldsymbol{L}}\left(\hat{{Z}}_{k+1}^{c, l, 1} \cap \hat{{Z}}_{k+1}^{c, l, 2}\right) $ | (31) |
由于新生、漏检的目标在上一时刻无关联量测,所以新生航迹及漏检航迹仅使用式(26)椭圆波门保留关联量测,存活假设航迹使用式(31)联合波门保留关联量测。
2.5 更新假设经过量测转换和杂波滤除得到的线性量测集合为Zk+1,则更新后的多目标后验密度
| $ \begin{gathered} \pi_{k+1 \mid k+1}\left(X \mid Z_{k+1}\right)=\varDelta(X) \sum\limits_{(I, \vartheta) \in \mathcal{F}\left(\boldsymbol{L}_{k+1 \mid k+1}\right) \times {\mathit{\Xi}} }\sum\limits_{\theta \in \Theta(I)} \times \\ w_{k+1 \mid k+1}^{(I, \vartheta, \theta)}\left(Z_{k+1}\right) \delta_I(\mathcal{L}(X))\left[p_{k+1 \mid k+1}^{(\vartheta, \theta)}\left(\cdot \mid Z_{k+1}\right)\right]^X \end{gathered} $ | (32) |
其中:
| $ \left\{ \begin{array}{l} w_{k+1 \mid k+1}^{(I , \vartheta, \theta)}\left(Z_{k+1}\right)=\frac{\delta_{\theta^{-1}\left(\left\{0:\left|Z_{k+1}\right|\right\}\right)}(I)\left[\eta_{Z_{k+1}}^{(\vartheta, \theta)}\right]^I w_{k+1 \mid k}^{(I, \vartheta)}}{\sum\limits_{(I, \vartheta) \in \mathcal{F}\left(L_{k+1 \mid k+1}\right) \times {\mathit{\Xi}}}\sum\limits_ {\theta \in \Theta(I)} \delta_{\theta-1\left(\left\{0 ; \mid Z_{k+1}\right\}\right)}(I)[\eta_{Z_{k+1}}^{(\vartheta, \theta)}]^{I} w_{k+1 \mid k}^{(I, \vartheta)}.}\\ \begin{aligned} & \eta_{Z_{k+1}}^{(\vartheta, \theta)}(l)=\sum\limits_{\mu \in \mathcal{M}}\left\langle p_{k+1 \mid k}^{(0, \vartheta)}(\cdot, \mu, l), \varphi_{Z_{k+1}}(\cdot, \mu, l ; \theta)\right\rangle \\ & p_{k+1 \mid k+1}^{(\vartheta, \theta)}\left(x, l \mid Z_{k+1}\right)=\sum\limits_{\mu \in M} p_{k+1}(\mu, l) p_{k+1 \mid k+1}^{(\vartheta, \theta)}\left(\xi, \mu, l \mid Z_{k+1}\right) \\ & p_{k+1 \mid k+1}^{(\vartheta, \theta)}\left(\xi, \mu, l \mid Z_{k+1}\right)=\frac{p_{k+11 k}^{(0, \vartheta)}(\xi, \mu, l) \varphi_{Z_{k+1}}(\xi, \mu, l ; \theta)}{\eta_{Z_{k+1}}^{(\vartheta, \theta)}(l)} \end{aligned}\\ \varphi_{Z_{k+1}}(\xi, \mu, l ; \theta)= \begin{cases}\frac{p_D(\xi, \mu, l) g\left(z_{\theta(l)}^c \mid \xi, \mu, l\right)}{\kappa\left(z_{\theta(l)}^c\right)} & \theta(l)>0 \\ 1-p_D(\xi, \mu, l) & \theta(l)=0\end{cases} \end{array} \right. $ |
式中: Θ是k+1时刻的关联映射空间,代表所有映射关系θ的集合,Θ(I)为关联映射的子集。pD(ξ, μ, l) 是检测概率; φZk+1(ξ, μ, l; θ) 是伪量测似然函数,包含检测(θ(l)>0) 和漏检(θ(l)=0)两部分。wk+1|k+1(I, ϑ, θ)(Zk+1)为后验假设分量的权重,pk+1|k+1(ϑ, θ)(ξ, μ, l|Zk+1)是模型为μ的单目标后验概率密度,可由卡尔曼单目标更新得到,其高斯混合实现如下:
对于线性高斯模型,检测概率设为常数pD(ξ, μ, l)=pD,单目标量测似然函数g(z|ξ, μ, l)=
| $ p_{k+1 \mid k+1}^{(\vartheta, \theta)}(\xi, \mu, l \mid Z_{k+1})=w_{k+1 \mid k+1}^{(\vartheta, \theta, \mu, l)} \propto {\cal{N}}(\xi ; \boldsymbol{m}_{k+1 \mid k+1}^{(\vartheta, \theta, \mu, l)}, \boldsymbol{P}_{k+1 \mid k+1}^{(\vartheta, \theta, \mu, l)}) $ | (33) |
若目标未被检测到,即θ(l)=0,式中:
| $ \left\{\begin{array}{l} w_{k+1 \mid k+1}^{(\vartheta, \theta, \mu, l)}=\left(1-p_D\right) w_{k+1 \mid k}^{(0, \vartheta, \mu, l)} \\ \boldsymbol{m}_{k+1 \mid k+1}^{(\vartheta, \theta, \mu, l)}=\boldsymbol{m}_{k+1 \mid k}^{(0, \vartheta, \mu, l)} \\ \boldsymbol{P}_{k+1 \mid k+1}^{(\vartheta, \theta, \mu, l)}=\boldsymbol{P}_{k+1 \mid k}^{(0, \vartheta, \mu, l)} \end{array}\right. $ |
若目标被检测到,即θ(l)>0,式中:
| $ \left\{ \begin{array}{l} \begin{aligned} w_{k+1 \mid k+1}^{(\vartheta, \theta, \mu, l)} & =w_{k+1 \mid k}^{(0, \vartheta, \mu, l)} p_D q_{k+1}^{(\vartheta)}\left(\boldsymbol{z}_{\theta(l)}^c ; \mu, l\right) / \boldsymbol{\kappa}\left(\boldsymbol{z}_{\theta(l)}^c\right) \\ \boldsymbol{m}_{k+1 \mid k+1}^{(\vartheta, \theta, \mu, l)} & =\boldsymbol{m}_{k+1 \mid k}^{(0, \vartheta, \mu, l)}+G_{k+1}^{(0, \vartheta, \mu, l)}\left(\boldsymbol{z}_{\theta(l)}^c-\boldsymbol{H} \boldsymbol{m}_{k+1 \mid k}^{(0, \vartheta, \mu, l)}\right) \end{aligned}\\ \begin{aligned} & \boldsymbol{P}_{k+1, 1 k+1}^{(\vartheta, \theta, \mu)}=\left(\boldsymbol{I}-\boldsymbol{G}_{k+1}^{(0, \vartheta, \mu, l)} \boldsymbol{H}\right) \boldsymbol{P}_{k+1 \mid k}^{(0, \vartheta, \mu, l)} \\ & q_{k+1}^{(\vartheta)}\left(\boldsymbol{z}^c ; \mu, l\right)= \mathcal{N}\left(\boldsymbol{z}^c ; \boldsymbol{H} \boldsymbol{m}_{k+1 / k}^{(0, \vartheta, \mu, l)}, \boldsymbol{H} \boldsymbol{P}_{k+1 \mid k}^{(0, \vartheta, \mu, l)} \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{R}_{k+1}^{c, \mu, l}\right) \\ & \boldsymbol{G}_{k+1}^{(0, \vartheta, \mu, l)}=\boldsymbol{P}_{k+1 \mid k}^{(0, \vartheta, \mu, l)} \boldsymbol{H}^{\mathrm{T}}\left(\boldsymbol{H} \boldsymbol{P}_{k+1 \mid k}^{(0, \vartheta, \mu, l)} \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{R}_{k+1}^{(c, \mu, l)}\right)^{-1} \end{aligned} \end{array} \right. $ |
模型概率pk+1(μj, l)更新为
| $ \begin{array}{cc} p_{k+1}\left(\mu_j, l\right)= \\ \begin{cases}\bar{c}_k^{\mu_j}\left\langle p_{k+1 \mid k}^{(0, \vartheta)}\left(\cdot, \mu_j, l\right), \varphi_{Z_{k+1}}\left(\cdot, \mu_j, l ; \theta\right)\right\rangle / c_{k+1} & \theta(l)>0 \\ \bar{c}_k^{\mu_j} / c_{k+1} & \theta(l)=0\end{cases} \end{array} $ | (34) |
式中
量测更新后,可用k+1时刻的模型概率对每个滤波器的估计结果加权合并,输出混合,得到单目标航迹的后验估计pk+1|k+1(ϑ, θ)(x, l|Zk+1)。同时,将模型概率输入到模糊控制器,执行模糊算法。
2.6 模糊算法在目标跟踪中,算法的跟踪效果很大程度上依赖于运动模型的匹配程度,所建立的运动模型越符合目标真实运动轨迹,跟踪精度越高。但是,现实中的目标往往有一定的机动性,其轨迹是多模型的、易变的,因此无法建立与之完全匹配的运动模型。过程噪声一方面刻画了运动模型的不匹配程度,另一方面也为滤波过程提供了更大的缓冲空间。在滤波过程中,实时的调整过程噪声的大小可以有效增加滤波精度。文献[21]在单目标跟踪中引入模糊算法,将Kalman滤波器的新息及新息变化率的归一化值作为模糊系统的输入变量,来确定过程噪声的协方差,但其需要大量的先验信息,且需频繁调整归一化参数,不适用于多目标跟踪。本文在多目标跟踪中引入模糊算法,以每个航迹的模型概率为输入,相应的过程噪声协方差系数为输出,不需要归一化输入参数,且可自适应调整运动模型中的过程噪声,具体如下:
模糊系统的输入变量I1、I2、I3分别为k+1时刻航迹l的模型概率pk+1(μ1, l)、pk+1(μ2, l)、pk+1(μ3, l),输出变量U为过程噪声协方差系数。
1) 输入变量、输出变量的论域
| $ \left\{\begin{array}{l} I_1, I_2, I_3:[0, 1] \\ U:[0, 2] \end{array}\right. $ |
2) 输入变量、输出变量的模糊子集
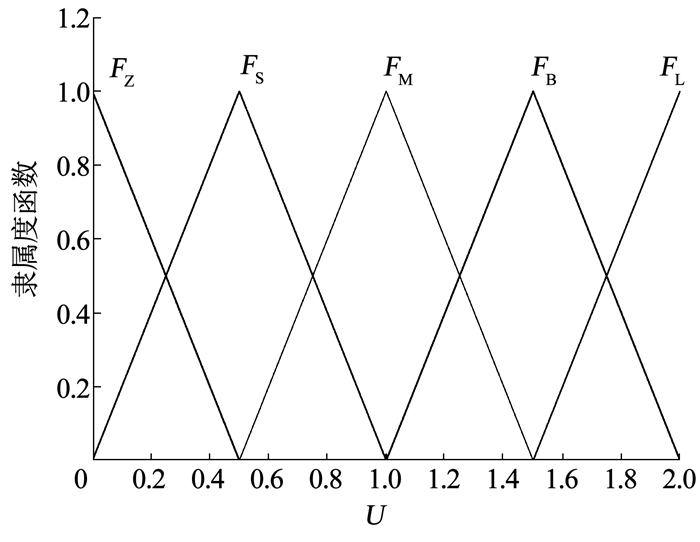
| $ \left\{\begin{array}{l} I_1, I_2, I_3:\left\{\text { 小 }\left(P_{\mathrm{S}}\right), \text { 中 }\left(P_{\mathrm{M}}\right), \text { 大 }\left(P_{\mathrm{B}}\right)\right\} \\ U:\left\{\begin{array}{l} \text { 极小 }\left(F_{\mathrm{Z}}\right), \text { 小 }\left(F_{\mathrm{S}}\right), \text { 中 }\left(F_{\mathrm{M}}\right) \\ \text { 大 }\left(F_{\mathrm{B}}\right), \text { 极大 }\left(F_{\mathrm{L}}\right) \end{array}\right\} \end{array}\right. $ |
3) 隶属度函数
4) 模糊规则的建立
文献[21]分析了单目标跟踪中,过程噪声的大小和跟踪精度的关系。当运动模型与真实目标轨迹匹配时,过程噪声越小跟踪精度越高;当运动模型与真实目标轨迹不匹配时,过程噪声越大跟踪精度越高。基于此推出模糊规律:当模型概率的分离度高时,减小过程噪声;当模型概率较为平均时,增大过程噪声。相应的模糊规则见表 1。

|
图 2 I1、I2、I3输入隶属度函数 Fig. 2 I1, I2, I3 input membership function |
|
图 3 输出隶属度函数 Fig. 3 Output membership function |
| 表 1 模糊规则表 Tab. 1 Fuzzy rules table |
使用重心法解模糊化,输出航迹l过程噪声协方差的系数U(l),由此可得k+1时刻的过程噪声协方差 Qk+1μ, l=U(l) Q0μ,可用于目标的预测和杂波滤除,来增加跟踪精度。
3 仿真分析为了评估所提算法的性能,本文在[0, 10 000]× [0, 10 000]m的非线性观测区域中,将所提非线性量测转换算法和EKF、UKF、CKF中精度最高、计算量最小的CKF比较。设置2个仿真场景:场景一在固定杂波率的情况下,比较了DUCM-FIMM-δ-GLMB滤波器与CKF-δ-GLMB[7]、CKF-JMS-δ-GLMB[13]及CKF-IMM-δ-GLMB[14]滤波器的性能;场景二根据杂波率的变化情况评估DUCM-FIMM-δ-GLMB滤波器的鲁棒性。
在这2种场景下,每个目标都可以在3种不同的运动模型下随机改变机动。模型一是匀速直线(CV)模型, 过程噪声标准差σCV=5 m/s;模型二是协同转弯(CT)模型,向左转动10(°)/s,过程噪声标准差σCT=5 m/s;模型三是协同转弯(CT)模型,向右转动10(°)/s,过程噪声标准差σCT=5 m/s。
CV、CT模型的状态转移矩阵,过程噪声初始协方差矩阵如下式:
| $ \boldsymbol{F}^{\mathrm{CV}}=\left[\begin{array}{llll} 1 & T & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & T \\ 0 & 0 & 0 & 1 \end{array}\right] $ | (35) |
| $ \boldsymbol{F}^{\mathrm{CT}}=\left[\begin{array}{cccc} 1 & (\sin (\theta T)) / \theta & 0 & -(1-\cos (\theta T)) / \theta \\ 0 & \cos (\theta T) & 0 & -\sin (\theta T) \\ 0 & (1-\cos (\theta T)) / \theta & 1 & (\sin (\theta T)) / \theta T \\ 0 & \sin (\theta T) & 0 & \cos (\theta T) \end{array}\right] $ | (36) |
| $ \boldsymbol{Q}_0^{\mathrm{CV}}=\sigma_{\mathrm{CV}}^2\left[\begin{array}{cccc} T^4 / 4 & T^3 / 2 & 0 & 0 \\ T^3 / 2 & T^2 & 0 & 0 \\ 0 & 0 & T^4 / 4 & T^3 / 2 \\ 0 & 0 & T^3 / 2 & T^2 \end{array}\right] $ | (37) |
| $ \boldsymbol{Q}_0^{\mathrm{CT}}=\boldsymbol{\sigma}_{\mathrm{CT}}^2\left[\begin{array}{cccc} T^4 / 4 & T^3 / 2 & 0 & 0 \\ T^3 / 2 & T^2 & 0 & 0 \\ 0 & 0 & T^4 / 4 & T^3 / 2 \\ 0 & 0 & T^3 / 2 & T^2 \end{array}\right] $ | (38) |
每个场景都有5个机动目标,为了使目标的机动轨迹显示得更加直观,这里采用笛卡尔坐标系表示,其初始位置、出生时刻、消亡时刻及机动情况见表 2。目标的真实运动轨迹和传感器位置见图 4。
| 表 2 目标初始状态表 Tab. 2 Initial states of targets |

|
图 4 目标真实运动航迹 Fig. 4 Real track of target |
目标出生时的初始模型分布概率p(μ)=[0.4, 0.3, 0.3],运动模型之间的切换由马尔科夫状态概率转移矩阵TPM给出
| $ \boldsymbol{T}_{\mathrm{PM}}=\left[\begin{array}{lll} 0.8 & 0.1 & 0.1 \\ 0.1 & 0.8 & 0.1 \\ 0.1 & 0.1 & 0.8 \end{array}\right] $ |
此外,采样周期T=1 s,方位角量测噪声σγ=0.1°,径向距离量测噪声σβ=10 m,目标存活概率Ps=0.99,目标检测概率PD=0.98,每次扫描中的杂波均匀分布在探测区域,数量服从期望为λ的泊松分布。最优子模型分配(optimal sub-pattern assignment,OSPA)的参数设定c=100,p=1。
1) 场景一。本场景为了评估DUCM-FIMM-δ-GLMB滤波器在杂波环境下对机动目标的跟踪性能。设置杂波率λ=30, CKF-JMS-δ-GLMB、CKF-IMM-δ-GLMB、DUCM-FIMM-δ-GLMB滤波器参数与上文所述完全一致,CKF-δ-GLMB滤波器始终认为目标符合CV模型,过程噪声标准差σ=30 m/s[12]。对权重大于10-2的GLMB分量所对应的假设航迹引入模糊算法。每个算法执行100次蒙特卡洛实验,具体结果见图 5。
|
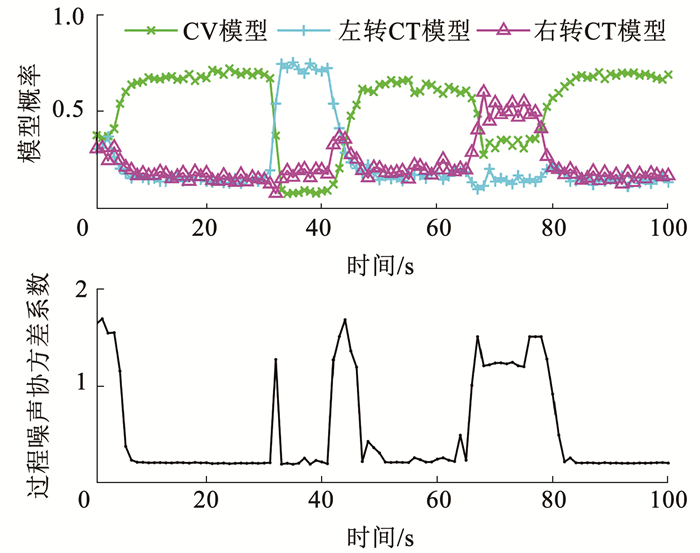
图 5 目标1的模型概率及过程噪声系数 Fig. 5 Model probability and process noise of object 1 |
图 5直观展示了模糊算法的作用,可以看出所提算法能实现对目标运动模型的实时估计,并由此自适应改变其过程噪声的大小。目标1在1~30 s、43~65 s、78~100 s做匀速直线运动,31~42 s左转,66~77 s右转,均能估计准确。当目标的运动模型保持稳定时,模型概率的分离度高,相应时刻的过程噪声系数变小;当目标转换运动模型时,模型概率的分离度低,相应时刻的过程噪声系数变大。
图 6、图 7为4种滤波器的目标数量估计和OSPA误差随时间的变化曲线,由图所示CKF-δ-GLMB、CKF-JMS-δ-GLMB、CKF-IMM-δ-GLMB都有一定程度的漏警,而DUCM-FIMM-δ-GLMB在目标数目估计中表现优异。另外,模糊算法的引入使得DUCM-FIMM-δ-GLMB在跟踪机动目标时可以根据运动模型概率的分离度而调整过程噪声的大小,增加了多模型滤波的包容性,因此DUCM-FIMM-δ-GLMB的跟踪精度最高,CKF-JMS-δ-GLMB、CKF-IMM-δ-GLMB的效果次之,CKF-δ-GLMB跟踪误差最大。由于δ-GLMB系列滤波器均采用多帧量测信息计算假设航迹,所以在检测目标的新生和消亡时,4种滤波器都有一定的滞后性,但DUCM-FIMM-δ-GLMB的表现更好。

|
图 6 不同滤波器目标数量估计对比 Fig. 6 Comparison of potential estimation for different filters |

|
图 7 不同滤波器OSPA误差对比 Fig. 7 Comparison of OSPA error for different filters |
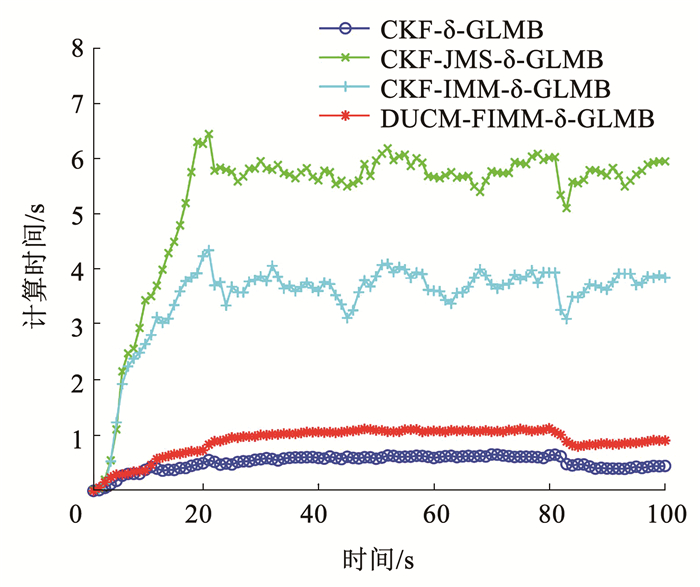
在量测处理方面,CKF-δ-GLMB、CKF-JMS-δ-GLMB、CKF-IMM-δ-GLMB滤波器均使用了式(26)过滤杂波,DUCM-FIMM-δ-GLMB滤波器采用了本文所提DUCM和联合波门过滤杂波算法,图 8、图 9、表 3为4种滤波器每帧的平均关联量测个数和计算时间。上述3种多模型算法均使用多个并行的滤波器,计算复杂度要高于采用单模型的CKF-δ-GLMB。另外,JMS算法在混合和更新阶段使用了分支真实密度,相比于IMM的合并分支密度,计算量更大,所以即使CKF-JMS-δ-GLMB相较于CKF-IMM-δ-GLMB关联量测数量更小,计算时间却更大。DUCM-FIMM-δ-GLMB一方面使用DUCM的方式,避免了UKF、CKF等算法采用多个离散采样点来近似随机变量的统计特性而造成的计算复杂度增加的问题,降低了计算量;另一方面,加入机动约束的联合波门杂波过滤算法显著降低了关联量测的个数,使得计算时间大幅度减少,相较于CKF-JMS-δ-GLMB下降了82.8%,相较于CKF-IMM-δ-GLMB降低了74.1%。

|
图 8 不同滤波器关联量测数量对比 Fig. 8 Comparison of correlation measurements number for different filters |
|
图 9 不同滤波计算时间对比 Fig. 9 Comparison of running time for different filters |
| 表 3 量测和时间对比 Tab. 3 Comparison of measurements and time |
2) 场景二。本场景主要为了评估所提DUCM-FIMM-δ-GLMB滤波器在不同杂波环境下的鲁棒性,设置杂波率λ=1、20、30、60、100,其他参数与场景一保持一致。每个杂波场景进行100次蒙特卡洛实验,评估了目标数量估计、OSPA误差、关联量测个数和计算时间等多项指标,具体结果见图 10、11。

|
图 10 不同杂波率目标数量估计对比 Fig. 10 Comparison of potential estimation for different clutter rates |

|
图 11 不同杂波率OSPA误差对比 Fig. 11 Comparison of OSPA error for different clutter rates |
由图 10、11所示,DUCM-FIMM-δ-GLMB滤波器在不同杂波环境下具有较好的鲁棒性。随着杂波率的上升,所提算法目标数量估计和OSPA误差变化并不明显,即使在杂波率λ=100,即远超常规情况的高杂波场景下[12],仍然可以实现准确的跟踪。可惜在目标数量变化时,虚警量测的增加会导致滤波器检测新生目标的时间更久。
由表 4可知,关联量测个数和计算时间成正比,杂波率的提高会使滤波器的关联量测个数和计算时间都有所增加。然而得益于所提联合波门杂波滤除算法,相较于杂波率的增加速度,关联量测个数和计算时间的增加都是更加平缓的。
| 表 4 不同杂波率参数对比 Tab. 4 Comparison of different clutter rates |
本文首先在标准δ-GLMB滤波器的基础上推导了IMM-δ-GLMB的预测和更新方程;其次,采用DUCM量测转换和联合波门杂波滤除策略,解决了多模型滤波器在非线性量测的杂波环境下计算速度下降和跟踪精度下降的问题;最后,将模糊算法引入到MTT领域,提出了DUCM-FIMM-δ-GLMB滤波器,自适应改变运动模型的过程噪声,进一步降低了OSPA误差,提高了目标跟踪的精度。
仿真结果表明,DUCM-FIMM-δ-GLMB滤波器在非线性量测的机动多目标跟踪场景下,跟踪精度比CKF-δ-GLMB、CKF-JMS-δ-GLMB、CKF-IMM-δ-GLMB滤波器更高,计算时间比CKF-JMS-δ-GLMB下降82.8%,比CKF-IMM-δ-GLMB下降74.1%。另外,所提滤波器对环境中杂波的变化具有较好的鲁棒性,无论在低杂波场景还是高杂波场景,滤波器的跟踪精度与目标数量估计都比较稳定。
| [1] |
GARCIA-FERNANDEZ A F, MORELANDE M R, GRAJAL J. Bayesian sequential track formation[J]. IEEE Transactions on Signal Processing, 2014, 62(24): 6366. DOI:10.1109/TSP.2014.2364013 |
| [2] |
RONALD P, MAHLER S. Statistical multisource-multitarget information fusion[M]. Norwood: Artech House, 2013: 1.
|
| [3] |
FORTMANN T E, BAR-SHALOM Y, SCHEFFE M. Sonar tracking of multiple targets using joint probabilistic data association[J]. IEEE Journal Oceanic Engineering, 1983, 8(3): 173. DOI:10.1109/JOE.1983.1145560 |
| [4] |
RONALD P, MAHLER S. Multitarget filtering via first-order multitarget moments[J]. IEEE Transactions Aerospace and Electronic Systems, 2003, 39(4): 1175. DOI:10.1109/TAES.2003.1261119 |
| [5] |
RONALD P, MAHLER S. PHD filters of higher order in target number[J]. IEEE Transactions Aerospace and Electronic Systems, 2007, 43(3): 1523. DOI:10.1109/TAES.2007.4441756 |
| [6] |
VO B T, VO B N, CANTONI A. The cardinality balanced multi-target multi-Bernoulli filter and its implementations[J]. IEEE Transactions on Signal Processing, 2009, 57(2): 409. DOI:10.1109/TSP.2008.2007924 |
| [7] |
VO B T, VO B N, PHUNG D. Labeled random finite sets and the Bayes multi-target tracking filter[J]. IEEE Transactions on Signal Processing, 2014, 62(24): 6554. DOI:10.1109/TSP.2014.2364014 |
| [8] |
JETTO L, LONGHI S, VENTURINI G. Development and experimental validation of an adaptive extended Kalman filter for the localization of mobile robots[J]. IEEE Transactions on Robotics and Automation, 1999, 15(2): 219. DOI:10.1109/70.760343 |
| [9] |
JULIER S, UHLMANN J K. Unscented filtering and nonlinear estimation[J]. Proceedings of IEEE, 2004, 92(3): 401. DOI:10.1109/JPROC.2003.823141 |
| [10] |
ARASARATNAM I, HAYKIN S. Cubature Kalman filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254. DOI:10.1109/TAC.2009.2019800 |
| [11] |
LERRO D, BAR-SHALOM Y. Tracking with debiased consistent converted measurements versus EKF[J]. IEEE Transactions on Aerospace & Electronic Systems, 1993, 29(3): 1015. DOI:10.1109/7.220948 |
| [12] |
WEI Yi, MENG Jiang, HOSEINNEZHAD R. The multiple model Vo-Vo filter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(2): 1045. DOI:10.1109/TAES.2017.2667300 |
| [13] |
PUNCHIHEWA Y, VO B T, VO B N. A generalized labeled multi-Bernoulli filter for maneuvering targets[C]//19th International Conference on Information Fusion. Heidelberg: IEEE, 2016: 980
|
| [14] |
辛怀声, 宋鹏汉, 曹晨. 多模型广义标签多伯努利滤波器[J]. 系统工程与电子技术, 2022, 44(12): 3603. XIN Huaisheng, SONG Penghan, CAO Chen. Multiple model based generalized labeled multi-Bernoulli filter[J]. Systems Engineering and Electronics, 2022, 44(12): 3603. DOI:10.12305/j.issn.1001-506X.2022.12.03 |
| [15] |
BORDONARO S, WILLETT P, BAR-SHALOMY. Decorrelated unbiased converted measurement Kalman filter[J]. IEEE Transactions on Aerospace & Electronic Systems, 2014, 50(2): 1431. DOI:10.1109/TAES.2014.120563 |
| [16] |
国强, 贺紫兰. 一种新的模糊控制多模型算法在目标跟踪中的应用[J]. 哈尔滨工业大学学报, 2016, 48(11): 123. GUO Qiang, HE Zilan. Application of a new fuzzy control multi model algorithm in target tracking[J]. Journal of Harbin Institute of Technology, 2016, 48(11): 123. DOI:10.11918/j.issn.0367-6234.2016.11.019 |
| [17] |
王晓, 韩崇昭. 用于机动目标跟踪的多模型概率假设密度滤波器[J]. 西安交通大学学报, 2011, 45(12): 1. WANG Xiao, HAN Chongzhao. A probability hypothesis density filter with multiple models for maneuvering target tracking[J]. Journal of Xi'an JiaoTong University, 2011, 45(12): 1. |
| [18] |
彭瀚, 程婷. 基于预测信息的量测转换序贯滤波目标跟踪[J]. 系统工程与电子技术, 2019, 41(3): 549. PENG Han, CHENG Ting. Measurement conversion sequential filtering target tracking based on prediction information[J]. System Engineering and Electronic Technology, 2019, 41(3): 549. DOI:10.3969/j.issn.1001-506X.2019.03.13 |
| [19] |
WAN Jian, REN Peiwen, GUO Qiang. Application of interactive multiple model adaptive five-degree cubature Kalman algorithm based on fuzzy logic in target tracking[J]. Symmetry, 2019, 11(6): 767. DOI:10.3390/SYM11060767 |
| [20] |
辛怀声, 曹晨. 基于交互多模型的分组δ-广义标签多伯努利算法[J]. 系统工程与电子技术, 2022, 44(4): 1128. XIN Huaisheng, CAO Chen. Interacting multiple model based grouping δ-generalized labeled multi-Bernoulli algorithm[J]. Systems Engineering and Electronics, 2022, 44(4): 1128. DOI:10.12305/j.issn.1001-506X.2202.04.08 |
| [21] |
DING Z, LEUNG H, CHAN K, et al. Model-set adaptation using a fuzzy Kalman filter[J]. Mathematical and Computer Modelling: An International Journal, 2001, 34(7): 799. DOI:10.1016/S0895-7177(01)00100-5 |
 2024, Vol. 56
2024, Vol. 56


