2. 北京空间飞行器总体设计部,北京 100094;
3. 华中科技大学 光学与电子信息学院,武汉 430074
2. Beijing Institute of Spacecraft System Engineering, Beijing 100094, China;
3. School of Optical and Electronic Information, Huazhong University of Science and Technology, Wuhan 430074, China
在中小型直流电能转换技术中,开关电源变换器因其电能转换效率高占有重要地位,其中DC-DC变换器以其体积小、功耗低、效率高等优点,在工业、航空、通信等领域得到广泛使用。变换器系统的稳定性以及可靠性是目前研究的重点。由于设备的长期运行,电路中的电感和电容等元器件会随时间老化,这会导致系统的输入和输出特性发生改变[1],使系统性能不断降低,影响工作效率和稳定性。因此,对变换器重要元器件进行在线估计具有重要研究意义。
近年来,许多学者对DC-DC变换器的参数估计方法进行了研究,可以分为离线估计技术和在线估计技术。对于离线参数估计,有故障诊断技术[2]、离散傅立叶变换[3]和遗传优化算法[4]等,通常需要大量计算得到。此外,由于元件参数会根据电路运行状态而变化,以上这些方法都存在无法实时跟踪参数和及时更新控制器参数的缺点,因此学者们提出了在线参数估计。
变换器在线参数估计主要分为单元件在线参数估计[5-10]和多元件在线参数估计[11-14]。由于电感和电容是变换器中最容易失效的器件,因此单元件参数估计一般是对电感或电容进行估计。在对电容进行在线估计的方法中,文献[15]提出了一种基于暂态充电分布的DC-DC升压变换器电容估计方案,在较低的采样频率下,可以实现电容估计误差小于3%。在对电感进行在线估计的研究中,文献[16]提出利用带遗忘因子的递推最小二乘法进行电感的参数辨识,辨识效果较好,但当遗忘因子取值过小时,会使辨识结果出现较大波动,降低参数辨识精度。
相对于单元件参数的在线辨识,多元件参数在线辨识方法的研究更具有现实意义和挑战性。文献[17]提出了一种基于模型参考自适应系统的在线电感和电容辨识算法,该算法辨识效果较好,但并未考虑实际电路中的各项寄生参数对电路的影响。文献[18]针对功率变换器的多参数在线辨识,提出了一种离散观测器算法,可以实现低采样频率下对多参数进行在线辨识,但电路中并未考虑到开关管导通压降,且电感寄生电阻的辨识效果不理想。为了同时估计电感和电容,文献[19]提出了基于模型观测器的Buck变换器状态监测方案。利用具有自适应反馈法的新型观测器重构元件状态参数,该算法需要导通和关断期间的电压和电流,且在一个开关周期内通过多次采样获得,所需的高频采样增加了电路设计的复杂性和成本。
为了在低采样频率下同时估计电感和电容,本研究提出了一种参考电压脉冲注入的方法。向参考电压中注入一个小幅度短脉冲信号,以建立瞬态和新稳态。瞬态时,根据基于电感伏秒特性和电容电荷平衡特性推导的精确离散变换器模型,在线估计电感和电容值。为了降低电感电流采样频率,提出了一种电感电流估计算法。根据电感电流的几何特性,采样峰值电感电流推导出需要的平均电感电流,将电流采样频率降低到每开关周期一次。此外,根据原稳态和新稳态获得的满秩状态模型,可以用于估计电感等效寄生电阻RL、二极管导通压降VD和负载电阻R,进一步提高了电感和电容估计的精度。该算法将采样频率降低到了开关频率,且估计过程无需迭代,易于实现,有效地降低了ADC采样模块和数字信号处理器等硬件的要求。
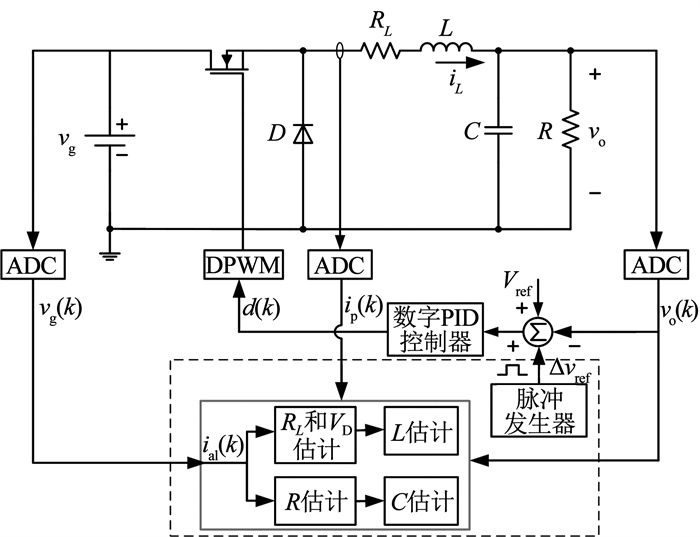
1 Buck变换器在线参数估计系统基于参考电压脉冲注入法进行在线电感和电容估计的Buck变换器结构图见图 1。为了保证系统稳定运行,给参数估计提供条件,采用数字PID控制器实现变换器的闭环控制。给参考电压注入一个小幅度的短脉冲信号,以建立瞬态过程和新稳态。通过采样不同状态下的输入电压、输出电压和电感电流,可以依次估计出RL、VD、R、L和C。对RL、VD和R进行估计是为了提高电感和电容的估计精度。
|
图 1 基于在线L和C估计算法的Buck变换器结构 Fig. 1 Structure of a Buck converter with proposed online L and C estimation algorithm |
虽然由于温度、老化和其他因素的影响,电气参数是时变的,但在参数估计过程中,它们的变化可以忽略不计。因此,电气参数可以视为常量。
2 基于参考电压注入的在线电感和电容估计 2.1 电感和电容估计图 2所示为小信号脉冲注入过程中的电感电流和输出电压波形。在一个开关周期起始时刻在参考电压Vref上施加脉冲激励,通过PID控制器调节,将电感电流和输出电压稳定在一个新稳态。Vref上的注入信号移除后,系统调节回初始稳定状态。整个信号注入过程对应的电感电流和输出电压波形见图 2,为电感和电容估计创造了瞬态和新稳态。由于变换器模型是参数估计的基础,本节首先研究基于电感伏秒特性和电容电荷平衡特性的精确离散时间变换器模型。

|
图 2 小信号注入过程中的电感电流和输出电压波形 Fig. 2 Inductor current and output voltage waveforms during signal injection process |
前缘调制下,一个开关周期内的电感电流和电容电压变化可分别表示为式(1)和(2):
| $ \begin{aligned} L \frac{i_{\mathrm{p}}(k+1)-i_{\mathrm{p}}(k)}{T}= & d(k) v_{\mathrm{g}}(k)- \\ & v_{\mathrm{o}}(k)-i_{\mathrm{al}}(k) R_L-d^{\prime}(k) V_D \end{aligned} $ | (1) |
| $ C \frac{v_{\mathrm{o}}(k+1)-v_{\mathrm{o}}(k)}{T}=i_{\mathrm{al}}(k)-\frac{v_{\mathrm{o}}(k)}{R} $ | (2) |
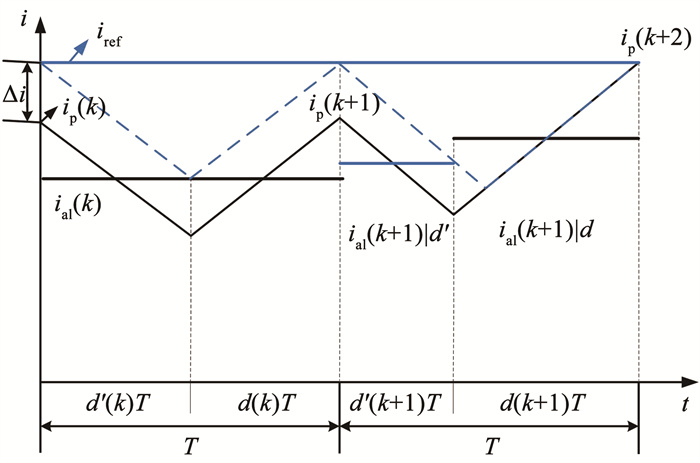
式中:d′(k)=1-d(k),d(k)是占空比; vg(k)和vo(k)分别是第k个周期的输入电压和输出电压; ip(k)为电感电流采样值,由于采样是在每个开关周期开始时刻进行的,因此它还表示电感电流的峰值。ial(k)表示第k个周期的平均电感电流,见图 3。
|
图 3 瞬态下的电感电流波形 Fig. 3 Inductor current waveform in transient state |
根据式(1)和(2)可以估计出L和C,其估计结果表示为LEST和CEST,如式(3)和(4)所示:
| $ L_{\mathrm{EST}}=\frac{d(k) v_{\mathrm{g}}(k)-v_{\mathrm{o}}(k)-i_{\mathrm{al}}(k) R_L-d^{\prime}(k) V_{\mathrm{D}}}{i_{\mathrm{p}}(k+1)-i_{\mathrm{p}}(k)} T $ | (3) |
| $ C_{\mathrm{EST}}=\frac{i_{\mathrm{al}}(k)-\frac{v_{\mathrm{o}}(k)}{R}}{v_{\mathrm{o}}(k+1)-v_{\mathrm{o}}(k)} T $ | (4) |
在稳态期间,相邻两个开关周期中的电感电流和输出电压相同,即ip(k+1)=ip(k)和vo(k+1)=vo(k),式(3)和(4)的计算结果为无穷大,估计结果不收敛。为了避免这个问题,L和C估计需要在瞬态下进行。
正如式(3)和(4)所示,估计电感和电容值需要知道平均电感电流ial(k)。它可以通过一个开关周期内多次采样电感电流获得,但这会大大增加采样频率,对硬件装置提出了更高的要求。为了降低采样频率,根据电感电流的几何特性,提出了一种平均电感电流估计算法:
| $ i_{\text {al }}(k)=d(k) i_{\text {al }}(k)\left|d+d^{\prime}(k) i_{\text {al }}(k)\right| d^{\prime} $ | (5) |
| $ i_{\mathrm{al}}(k) \left\lvert\, d^{\prime}=i_{\mathrm{p}}(k)-\frac{1}{2} M_2(k) d^{\prime}(k) T\right. $ | (6) |
| $ i_{\mathrm{al}}(k) \left\lvert\, d=i_{\mathrm{p}}(k+1)-\frac{1}{2} M_1(k) d(k) T\right. $ | (7) |
式中:ial(k)|d′和ial(k)|d分别为开关关断和导通期间的电感电流平均值。M1(k)是第k个开关周期中电感电流的上升斜率,M2(k)是同一开关周期中下降斜率的绝对值,分别如式(8)和(9)所示:
| $ M_1(k)=\frac{v_{\mathrm{g}}(k)-v_{\mathrm{o}}(k)-R_L i_{\mathrm{al}}(k) \mid d}{L} $ | (8) |
| $ M_2(k)=\frac{v_{\mathrm{o}}(k)+R_L i_{\mathrm{al}}(k) \mid d^{\prime}+V_{\mathrm{D}}}{L} $ | (9) |
将式(9)代入式(6),可以得到ial(k)|d′的表达式为
| $ i_{\mathrm{al}}(k) \left\lvert\, d^{\prime}=\frac{2 L i_{\mathrm{p}}(k)+\left[V_{\mathrm{D}}-v_{\mathrm{o}}(k)\right] d^{\prime}(k) T}{2 L+R_L d(k) T}\right. $ | (10) |
类似地,将式(8)代入式(7),得到ial(k)|d表达式为
| $ i_{\mathrm{al}}(k) \left\lvert\, d=\frac{2 L i_{\mathrm{p}}(k+1)+\left[v_{\mathrm{o}}(k)-v_{\mathrm{g}}(k)\right] d(k) T}{2 L-R_L d(k) T}\right. $ | (11) |
结合式(5)、(10)和(11),ial(k)可以近似地表示为
| $ \begin{aligned} i_{\mathrm{al}}(k)= & i_{\mathrm{p}}(k+1) d(k)+i_{\mathrm{p}}(k) d^{\prime}(k)+ \\ & \frac{\left[v_{\mathrm{o}}(k)-v_{\mathrm{g}}(k)\right] d^2(k)-v_{\mathrm{o}}(k) d^{\prime 2}(k)}{2 L} T \end{aligned} $ | (12) |
如式(12)所示,ial(k)可以从ip(k)中推导出来,因此每个开关周期只需要一次采样。实际应用时,只要将式(12)中的L设为初始值L0,即可根据式(3)和式(12)计算出实际电感值。此外,可以根据式(4)和式(12)获得实际电容值。
2.2 寄生参数和负载电阻估计根据式(3)和式(4)可以看出,为了准确估计L和C,应提前获得RL、VD和R。在实际应用中,这些元件参数随时间变化,因此有必要在线估计其实际值。稳态下,一个开关周期内的电感伏秒数和电容电荷数为零,式(1)和(2)可简化为:
| $ d(k) v_{\mathrm{g}}(k)-v_{\mathrm{o}}(k)-i_{\mathrm{al}}(k) R_L-d^{\prime}(k) V_{\mathrm{D}}=0 $ | (13) |
| $ i_{\mathrm{al}}(k)-\frac{v_{\mathrm{o}}(k)}{R}=0 $ | (14) |
根据式(14)可以估计出负载R的表达式为
| $ R=\frac{v_{\mathrm{o}}(k)}{i_{\mathrm{al}}(k)} $ | (15) |
由于欠秩问题的存在,仅用式(13)不足以推导出RL和VD,需要一个新稳态提供另一个稳态方程。如图 2所示,采用给参考电压注入激励可以得到一个新稳态,脉冲注入前后的两个稳态方程表示为
| $ \left\{\begin{array}{l} i_{\mathrm{al}}\left(k_0\right) R_L+d^{\prime}\left(k_0\right) V_{\mathrm{D}}=d\left(k_0\right) v_{\mathrm{g}}\left(k_0\right)-v_{\mathrm{o}}\left(k_0\right) \\ i_{\mathrm{al}}\left(k_1\right) R_L+d^{\prime}\left(k_1\right) V_{\mathrm{D}}=d\left(k_1\right) v_{\mathrm{g}}\left(k_1\right)-v_{\mathrm{o}}\left(k_1\right) \end{array}\right. $ | (16) |
式中:ial(k0)、vo(k0)、vg(k0)、d(k0)和d′(k0)是激励信号注入前测得的稳态值; ial(k1)、vo(k1)、vg(k1)、d(k1)和d′(k1)是新稳态下的测量值。由于占空比在稳态下保持不变,因此可以利用该特性来判断系统是否已进入稳态。
通过求解式(16),获得RL和VD的表达式:
| $ R_L=\frac{d^{\prime}\left(k_1\right) d\left(k_0\right) v_{\mathrm{g}}\left(k_0\right)-d^{\prime}\left(k_0\right) d\left(k_1\right) v_{\mathrm{g}}\left(k_1\right)-d^{\prime}\left(k_1\right) v_{\mathrm{o}}\left(k_0\right)+d^{\prime}\left(k_0\right) v_{\mathrm{o}}\left(k_1\right)}{d^{\prime}\left(k_1\right) i_{\mathrm{al}}\left(k_0\right)-d^{\prime}\left(k_0\right) i_{\text {al }}\left(k_1\right)} $ | (17) |
| $ V_{\mathrm{D}}=\frac{d\left(k_1\right) i_{\mathrm{al}}\left(k_0\right) v_{\mathrm{g}}\left(k_1\right)-d\left(k_0\right) i_{\mathrm{al}}\left(k_1\right) v_{\mathrm{g}}\left(k_0\right)-i_{\mathrm{al}}\left(k_0\right) v_{\mathrm{o}}\left(k_1\right)+i_{\mathrm{al}}\left(k_1\right) v_{\mathrm{o}}\left(k_0\right)}{d^{\prime}\left(k_1\right) i_{\mathrm{al}}\left(k_0\right)-d^{\prime}\left(k_0\right) i_{\mathrm{al}}\left(k_1\right)} $ | (18) |
利用式(15)、(17)和(18)的计算结果,可以提高L和C的估计精度。
2.3 算法流程整个参数估计的流程见图 4。测量并记录在t0、ts和t1时间段内的三组输入电压、输出电压、电感电流和占空比的值,用于参数估计。将电感L设置为初始值L0,根据式(12)计算平均电流ial(k)。根据计算的ial(k)、式(17)和(18)可以计算出RL和VD,将计算结果带回到式(3)估计出电感值LEST。利用RL、VD和LEST的估计结果来提高ial(k)的精度,然后可以根据式(15)计算出精确的负载R。最后,利用在ts时间间隔内测量的数据和式(4)估计出电容值CEST。

|
图 4 参数估计流程 Fig. 4 Parameter estimation flow |
为了验证参考电压脉冲注入估计算法的准确性,在Matlab/Simulink中搭建Buck变换器系统模型,其设计参数见表 1。电压和电感电流的采样频率与开关频率相同,即100 kHz。实际应用中,系统噪声和测量误差会降低估计精度。为了减弱这种影响,式(3)和(4)的分母应该相对较大。从式(1)和(2)可以看出,ip(k+1)-ip(k)和vo(k+1)-vo(k)与第k个开关周期中的占空比增量成正比,这表明增加d(k)可以提高L和C的估计精度。在脉冲激励信号注入之后,由于阶跃变化的影响,瞬态中第一个开关周期的占空比增量相对较大。因此,本文利用该周期的电压和电流测量值来估计L和C。
| 表 1 Buck变换器的设计参数 Tab. 1 Design parameters of Buck converters |
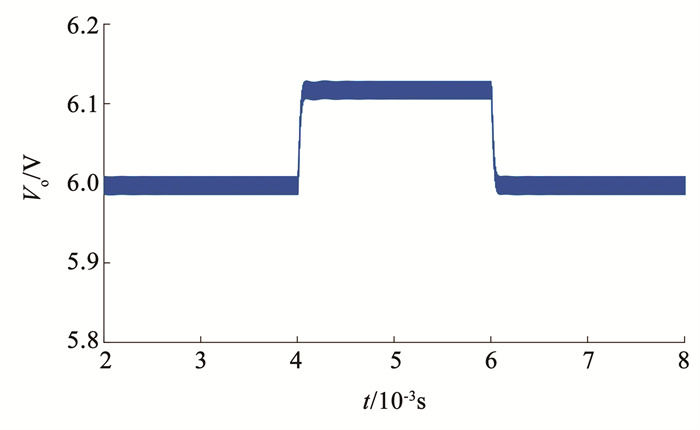
图 5所示为脉冲激励信号注入过程中的输出电压波形。注入脉冲时,最大电压扰动约为0.12 V,在标称参考电压的2%范围内;注入结束后输出电压恢复到6 V。脉冲宽度设置为2 ms,实际应用可设置为与稳定时间相等。在此期间,测量所需的电压和电感电流,然后进行参数估计。
|
图 5 脉冲激励信号注入期间的输出电压波形 Fig. 5 Output voltage waveform during excitation signal injection |
RL、VD、R、L和C的估计结果见表 2,分别为0.194 Ω、0.321 V、6.020 Ω、59.860 μH和22.060 μF。与表 1所列标称值相比,RL和VD的估计误差分别为3%和7%,R的估计误差小于0.4%,L和C的估计误差均小于0.3%。
| 表 2 参考电压脉冲注入算法下的参数估计 Tab. 2 Parameter estimation under the reference voltage pulse injection algorithm |
RL和VD的估计误差相对较大,这是因为仿真系统中还考虑了其他寄生参数(例如二极管串联电阻、电容寄生电阻等)导致RL和VD估计精度降低。但这并非坏事,由于其他寄生参数耦合到RL和VD的估计值中,利用该估计值计算平均电感电流、电感和电容,可以一定程度上弥补忽略其他寄生参数引入的估计误差。R、L和C估计结果的高精度证明RL和VD估计精度是足够的。
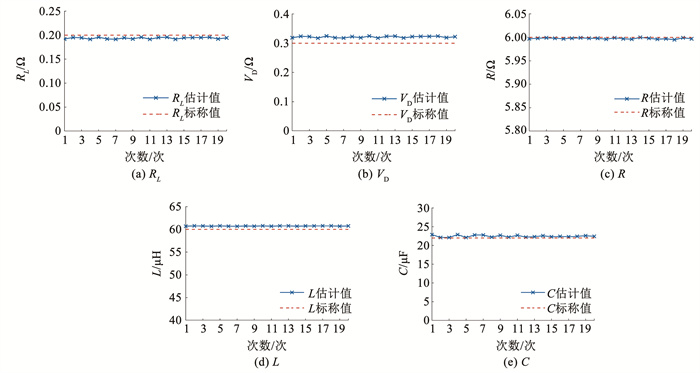
考虑到实际电路中存在噪声,例如ADC量化误差、EMI引起的输出电压噪声等,本文在仿真中使用电压源和电流源产生噪声并将其注入电路中。尽管这是真实噪声的简化模型,但这种方法适用于开关电源电路噪声敏感性的一般分析[20]。EMI引入的噪声,可以通过合理选择电感电流和输出电压采样点有效消除,因此本文重点考虑ADC和电感电流采样引入的噪声,如果采用10位ADC采样输出电压和电感电流,量化误差最大值约为额定值的0.098%。以此为参考在仿真系统的输出电压和电感电流采样处分别引入幅值在额定值±0.2%和±0.5%内变化的噪声,并对电感、电容等参数进行估计。RL、VD、R、L和C的估计结果见图 6,RL、VD和R的估计平均值分别为0.194 Ω、0.321 V和5.998 Ω。L和C的估计平均值分别为60.737 μH和22.467 μF,与标称值相比,误差分别为1.23%和2.12%。电感估计的最大值和最小值分别为60.780 μH和60.681 μH,最大估计误差不超过1.5%。电容估计的最大值和最小值分别为22.901 μF和22.132 μF,最大估计误差不超过4.1%。上述参数估计结果证明提出的算法具有较好的抗干扰能力,可以有效估计电感和电容值。
|
图 6 引入噪声的参考电压脉冲注入的参数估计 Fig. 6 Parameter estimation of reference voltage pulse injection introducing noise |
为了验证所提算法的跟踪性能,将电阻RS分别设置为0.05 Ω、0.1 Ω和0.2 Ω与电感串联,以模拟RL中的阶跃变化,参数估计结果见表 3。RL的估计结果分别为0.248 Ω、0.303 Ω和0.414 Ω,能够跟踪RL+RS的实际值0.25 Ω、0.3 Ω和0.4 Ω。与表 1标称值相比,VD的估计误差分别为7.33%、6.54%和5.96%,R的估计误差分别为0.4%、0.2%和1.7%,L和C的估计误差均小于1.1%。因此,RL的变化对其他参数估计的影响很小,电感和电容的估计精度仍然足够高。
| 表 3 参考电压脉冲注入算法RL变化下的参数估计 Tab. 3 Parameter estimation for the reference voltage pulse injection algorithm with RL variation |
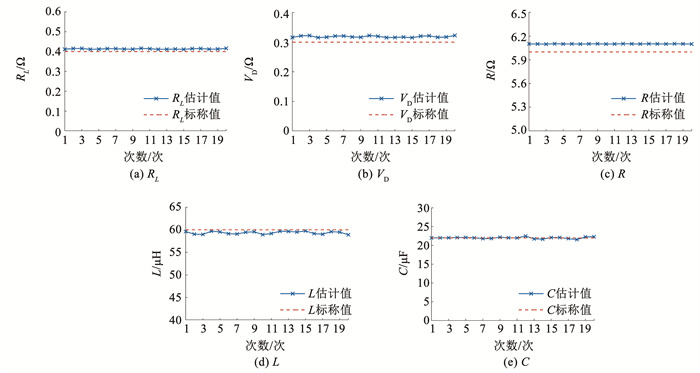
同样的,在系统中分别加入输出电压额定值±0.2%和电感电流额定值±0.5%内变化的噪声扰动模拟实际电路中的噪声。RL变化为100%的情况下,RL、VD、R、L和C的估计结果见图 7,RL和VD的最大估计误差都分别不超过1.8%和9%。而电感的最大估计误差均小于2%,电容的最大估计误差均未超过6.5%。VD的估计误差虽然相对较大,但足以满足电感和电容估计的需要。由上述仿真结果可以得出,当RL变化为100%的情况下,电路中其他参数的估计误差几乎没有影响,提出算法仍然具有较好的动态跟踪性能和抗干扰能力。
|
图 7 引入噪声后RL变化100% (RL=0.4 Ω)的参数估计结果 Fig. 7 Parameter estimation results of 100% change in RL after introducing noise (RL =0.4 Ω) |
为了验证参考电压脉冲注入估计算法的优势性,我们与最近在DC-DC变换器领域提出的其他参数估计方法进行了对比分析,见表 4。可以看出本文在引入噪声扰动以及RL动态变化下,仍可实现L和C的参数估计,且保持了较高的精度。因此,本文提出的估计算法不仅具有较高的电感电容辨识精度,且同比之下采样频率及成本更低。
| 表 4 不同算法的参数估计误差 Tab. 4 Estimation errors of different parameter estimation algorithms |
提出了一种基于参考电压小幅度脉冲注入的Buck变换器电感电容在线估计方法。作为参数估计的基础,首先提出了一种精确的离散时间变换器模型。利用小信号脉冲注入产生的瞬态,可以同时估计电感和电容。然后,提出了一种电感电流估计算法,以降低电流采样频率。与很多已发表的方法相比,采样频率要低得多。最后,推导了电路中寄生参数和负载电阻,以保证电感和电容的估计精度。仿真结果表明,该参数估计算法准确,采样频率低,对电感和电容的变化具有良好的跟踪性能,可以用于控制器的自动整定和在线故障诊断。
| [1] |
徐静. 基于自适应滑模观测器的DC-DC变换器故障诊断方法[D]. 吉林: 东北电力大学, 2021 XU Jing. DC-DC converter fault diagnosis method using adaptive sliding mode observer[D]. Jilin: Northeast Electric Power University, 2021 |
| [2] |
AMARAL A M R, CARDOSO A J M. Using Newton-Raphson method to estimate the condition of aluminum electrolytic capacitors[C]//Industrial Electronics. Vigo: IEEE International Symposium, 2007: 827
|
| [3] |
AMARAL A M R, CARDOSO A J M. A simple offline technique for evaluating the condition of aluminum-electrolytic-capacitors[J]. IEEE Transactions on Industrial Electronics, 2009, 56(8): 3230. DOI:10.1109/TIE.2009.2022077 |
| [4] |
BOSICH D, SULLIOI G, MOCANU E, et al. Medium voltage DC power systems on ships: an offline parameter estimation for tuning the controllers' linearizing function[J]. IEEE Transactions on Energy Conversion, 2017, 32(2): 748. DOI:10.1109/TEC.2017.2676618 |
| [5] |
王辉. 基于MRAS的感应电机参数辨识方法研究[D]. 北京: 北京交通大学, 2019 WANG Hui. Research oil parameter identification method of induction motor based on MRAS[D]. Beijing: Beijing Jiaotong University, 2019 |
| [6] |
魏念巍. 变工况DC-DC电路故障特征提取方法研究[D]. 淮南: 安徽理工大学, 2021 WEI Nianwei. Research on the method of fault feature extraction of DC-DC circuit under variable conditions[D]. Huainan: AnHui University of Science and Technology, 2021 |
| [7] |
张焕青, 雷鸣, 王汇, 等. 直流供电系统电容在线测量器的设计与应用[J]. 电网与清洁能源, 2018, 34(5): 19. ZHANG Huanqing, LEI Ming, WANG Hui, et al. Design and application of the capacitor on-line measuring instrument for DC power supply System[J]. Power System and Clean Energy, 2018, 34(5): 19. DOI:10.3969/j.issn.1674-3814.2018.05.004 |
| [8] |
赵朝阳. 连续负载瞬态DC-DC变换器的电容可靠性优化与最优瞬态轨迹控制研究[D]. 重庆: 重庆大学, 2020 ZHAO Chaoyang. Study on capacitor reliability optimization and optimal transient trajectory control of DC-DC converters with consecutive load transients[D]. Chongqing: Chongqing University, 2020 |
| [9] |
YAO Kai, TANG Weijie, HU Wenbin, et al. A current-sensorless online ESR and C identification method for output capacitor of buck converter[J]. IEEE Transactions on Power Electronics, 2015, 30(12): 6993. DOI:10.1109/TPEL.2014.2383436 |
| [10] |
ABDENNADHER K, VENET P, ROJAT G, et al. A real-time predictive-maintenance system of aluminum electrolytic capacitors used in uninterrupted power supplies[J]. IEEE Transactions on Industry Applications, 2010, 46(4): 1644. DOI:10.1109/TIA.2010.2049972 |
| [11] |
袁煜博. 四开关变换器控制技术研究[D]. 北京: 北京交通大学, 2021 YUAN Yibo. Control strategy of four-switch buck-boost converter[D]. Beijing: Beijing Jiaotong University, 2021 |
| [12] |
AL-HOSANI K, UTKIN V I. Parameters estimation using sliding mode observer with shift operator[J]. Journal of the Franklin Institute, 2012, 349(4): 1509. DOI:10.1016/j.jfranklin.2011.05.002 |
| [13] |
MA Xiaojun J, BI Chao. A technology for online parameter identification of permanent magnet synchronous motor[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(3): 237. DOI:10.30941/CESTEMS.2020.00029 |
| [14] |
LI B X, LOW K S. Low sampling rate online parameters monitoring of DC-DC converters for predictive-maintenance using biogeography-based optimization[J]. Nanjing University of Science and Technology, 2016, 31(4): 2870. DOI:10.1109/TPEL.2015.2472459 |
| [15] |
ZHAO Zhaoyang, DAVARI P, WANG Yaoqiang, et al. Online capacitance monitoring for DC/DC boost converters based on low-sampling-rate approach[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 1. DOI:10.1109/JESTPE.2021.3108420 |
| [16] |
姚家煊. 基于参数辨识的APF自适应预测电流控制方法研究[D]. 成都: 西南交通大学, 2020 YAO Jiaxuan. Adaptive predictive current control of active power filter based on parameter identification[D]. Chengdu: Southwest Jiaotong University, 2020 |
| [17] |
吕典, 熊彩含, 张宋泽, 等. 瞬态下基于MRAS的DC-DC转换器参数辨识[J]. 华中科技大学学报(自然科学版), 2017, 45(4): 97. LÜ Dian, XIONG Caihan, ZHANG Songze, et al. Parameter estimation for DC-DC converter based on MRAS under transient state[J]. Journal of Huazhong University of Science and Technology(Nature Science Edition), 2017, 45(4): 97. DOI:10.13245/j.hust.170418 |
| [18] |
吴杭举, 周雒维. 一种基于离散观测器的DC/DC变换器参数在线辨识方法[J]. 电源学报, 2017, 15(3): 30. WU Hangju, ZHOU Luowei. Online parameter estimation of DC/DC converters based on discrete-time observer[J]. Journal of Power Supply, 2017, 15(3): 30. DOI:10.13234/j.issn.2095-2805.2017.3.30 |
| [19] |
CEN Zhaohui, STEWART P. Condition parameter estimation for photovoltaic buck converters based on adaptive model observers[J]. IEEE Transactions on Reliability, 2017, 66(1): 148. DOI:10.1109/TR.2016.2618320 |
| [20] |
MELO J G M, TORRES F S. Noise analysis of integrated bulk current sensors for detection of radiation induced soft errors[C]//2015 16th Latin-American Test Symposium (LATS). [S. l. ]: IEEE, 2015: 1. DOI: 10.1109/LATW.2015.7102515
|
| [21] |
王友仁, 傅宏辉, 邵力为, 等. 基于电压检测与混杂模型的Buck电路参数辨识[J]. 电力电子技术, 2019, 53(6): 137. WANG Youren, FU Honghui, SHAO Liwei, et al. A novel method of parameter identification for Buck circuit based on voltage detection and hybrid models[J]. Power Electronics Technology, 2019, 53(6): 137. |
| [22] |
任磊, 龚春英. 基于修正混杂系统模型的Boost变换器LC参数辨识方法[J]. 中国电机工程学报, 2018, 38(22): 6647. REN Lei, GONG Chunying. LC parameter identification method of boost converter based on modified hybrid system model[J]. Chinese Society for Electrical Engineering, 2018, 38(22): 6647. DOI:10.13334/j.0258-8013.pcsee.170746 |
| [23] |
孙权, 王友仁, 姜媛媛, 等. 变温度下Boost变换器健康状态评估方法[J]. 电工技术学报, 2018, 33(6): 1364. SUN Quan, WANG Youren, JIANG Yuanyuan, et al. A novel approach of health condition assessment for boost converters under variable temperature conditions[J]. Journal of Electrotechnical Technology, 2018, 33(6): 1364. DOI:10.19595/j.cnki.1000-6753.tces.161651 |
 2024, Vol. 56
2024, Vol. 56


