2. 西安建筑科技大学 信息与控制工程学院,西安 710055;
3. 浙江中控技术股份有限公司, 杭州 310000
2. School of Information and Control Engineering, Xi'an University of Architecture and Technology, Xi'an 710055, China;
3. Zhejiang Supcon Technology Co.Ltd, Hangzhou 310000, China
锂电池与传统的镍氢、镍铬等电池相比,具有自重轻、能量密度高和循环寿命长等特点,被广泛应用于生活[1]。但由于外部环境复杂和内部电极损失等情况,锂电池会产生容量衰减、热稳定性下降等问题,增大了锂电池的使用风险。因此,对锂电池的健康监测已成为一项重要课题[2]。
锂电池的剩余使用寿命(remaining useful life, RUL)通常定义为在电池达到寿命阈值之前的充放电循环周期[3]。RUL预测是电池管理系统(battery management system, BMS)电池状态估计的重要组成部分,RUL的精确预测可以有效降低锂电池的使用风险,故RUL预测准确度的提升具有重要意义。针对锂电池RUL的预测,目前常用的方法大致分为基于模型、基于数据驱动和基于融合方法的预测方法[3]。
模型法分为退化机理模型、等效电路模型和经验退化模型[4-5]。退化机理模型通过电池内部的物理化学过程,建立电池老化模型。文献[6]提出一种控制导向单粒子模型,并基于最小二乘和递归参数法估计锂电池的老化参数。等效电路模型搭建由电气元件构成的模型来等效或近似电池内部工作原理。文献[7]基于改进的Randles等效电路模型,通过功率和容量衰减预测RUL。机理模型和等效电路模型复杂度高、难度大,因此较少使用。经验退化模型通过输入与输出之间的内在关联,建立逼近规律的统计模型[4]。经验模型通常与滤波算法结合进行RUL预测,常用的有卡尔曼滤波(Kalman filter, KF)、粒子滤波(particle filter, PF)等。文献[8]基于联合预测模型利用噪声状态信号和约束KF进行RUL预测。文献[9]基于单指数经验模型采用PF预测RUL。用经验模型建模预测RUL时,会增大对模型的依赖,导致鲁棒性降低。
数据驱动法不需要考虑电池内部运行及失效机制,仅需要大量数据集,分析其隐含的电池状态信息来预测RUL。常用的数据驱动法有支持矢量机(support vector machine,SVM)、相关矢量机(relevance vector machine,RVM)和人工神经网络(artificial neural network,ANN)等。文献[10]基于SVM在线监测电动汽车的电池退化情况。文献[11]基于RVM进行RUL预测。数据驱动法需要大量的训练数据,计算复杂度较高,对于SVM这样的人工智能算法,核的选择和参数设置对预测精度影响很大。
目前,基于融合方法的RUL预测逐渐成为热点。融合型算法可以分为模型与数据驱动的融合算法和不同数据驱动算法之间的互补或加权融合[4]。融合型预测方法可以结合不同算法的特点,发挥不同算法的优势,从而获得更好的预测精度和鲁棒性。文献[12]以PF为核心,以双指数模型作为状态方程,以ANN作为观测方程,估计得到电池容量退化曲线,进一步估计锂电池RUL,但作为PF观测方程的ANN引入了误差,增加了RUL预测误差。文献[13]提出PF和自回归模型相融合的RUL预测方法,但预测方法的动态更新能力不足。文献[14]将相关矢量回归得到的预测值和最新的真实残差值进行融合,构成具有时变权重的未来残差,再基于UKF对电池的RUL进行预测。文献[15]将自回归综合模型的预测值作为平方根容积KF的观测值,进而弱化了该滤波算法对经验模型的依赖性,提高了RUL的预测精度。文献[16]选取容量和等压降放电时间数据,训练出容量退化CNN-LSTM模型和等压降放电时间预测CNN-LSTM模型,最后结合这2个模型预测锂电池的RUL。
基于现有研究,本文采用融合型算法中的模型与数据驱动融合的算法,提出基于PF和门控循环单元(gated recurrent unit,GRU)神经网络融合的锂电池RUL预测方法。首先,利用训练数据分别建立锂电池经验退化双指数模型和GRU神经网络模型;然后,利用GRU神经网络获得预测值,并将其作为PF的观测值添加到容量退化模型中;最后,更新得到最终预测值。本文的贡献点总结为以下3点:1)采用GRU神经网络作为融合信息源之一,GRU具有结构简单、训练参数较少的特点,与跟其结构类似的长短期记忆网络(long short-term memory, LSTM)相比,GRU的训练复杂度和过拟合风险较低; 2)所提的PF和GRU融合的方法在训练数据较少的情况下,仍可以具有较高的长期预测精度; 3)对融合的2个模型采用带移动窗口的迭代式的训练机制,区别于许多现有研究中预测模型一成不变的状态,具有动态更新能力,能有效提高对电池长期性的容量预测的准确性。
1 锂电池RUL预测方法 1.1 粒子滤波(PF)PF算法是基于蒙特卡罗方法和递归贝叶斯估计的滤波方法。对于锂电池这样的非线性系统,PF算法具有良好的适用性,因此,PF是现阶段应用最广泛的RUL估计方法之一。PF算法如下[17]:
若已知非线性系统的状态空间方程为
| {xk=f(xk−1,ωk)yk=h(xk,γk) | (1) |
式中:xk为k时刻的系统状态值,yk为k时刻的观测值,f和h为系统状态方程和观测方程,ω和γ为系统过程噪声和观测噪声且相互独立。
1) 粒子初始化。根据先验分布p(x0)随机生成粒子集{x0i}i=1N,i=1, 2, …, N。
2) 重要性采样。根据xki~p(xki|xik-1)对每个粒子进行采样。
3) 计算权重。令q(xk|y1∶ k)=p(xk|xk-1),得到权值wk(i)的递归更新为
| w(i)k=w(i)k−1p(yk∣x(i)k)p(x(i)k∣x(i)k−1)q(x(i)k∣x(i)k−1,y1:k) | (2) |
式中p(yk|xk(i))是xk(i)的似然估计。
4) 权重归一化。对式(2)所得wk(i)进行归一化
| ˆw(i)k=w(i)k∑Ni=1w(i)k | (3) |
5) 重采样。根据归一化权重的大小,保留权重大的粒子,舍弃权重小的粒子,得到k时刻的新粒子集合{xki}i=1N,重新分配权值,使
6) 状态估计。见式(4):
| xk=∑Ni=1w(i)kx(i)k | (4) |
GRU神经网络源于循环神经网络(recurrent neural network, RNN),传统的RNN存在梯度消失问题,同时对时间距离长的数据特征信息的处理能力较弱。LSTM神经网络作为RNN的一种变体,可以学习长期依赖信息。GRU神经网络与LSTM神经网络类似,也是RNN的一种变体,同样可以有效保留时间序列数据中的长期依赖性。
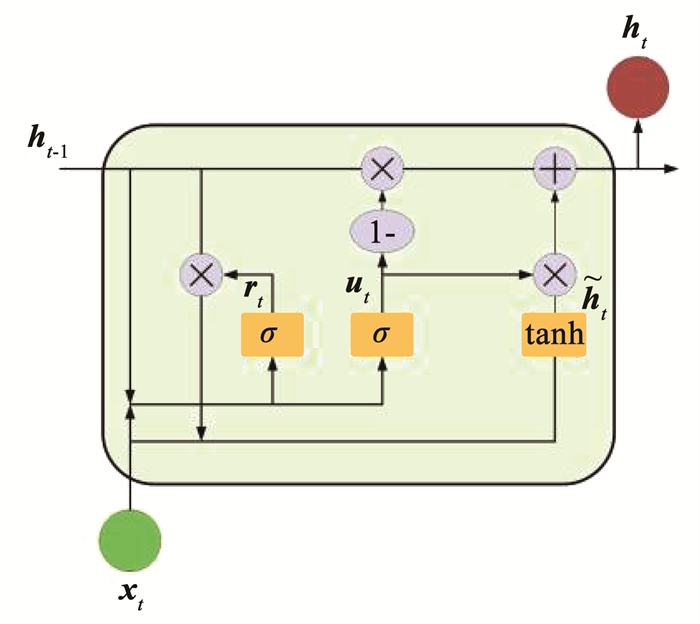
GRU神经网络的结构见图 1。图 1中,rt为重置门,ut为更新门,xt为t时刻的输入,ht为t时刻的输出,ht-1为前一时刻的隐藏状态。
|
图 1 GRU神经网络结构示意 Fig. 1 Schematic of GRU neural network structure |
1) 重置门。该门得到0~1之间的门控信号为
| rt=σ(Wrht−1+Wrxt) | (5) |
式中:ht-1为前一时刻的隐藏状态,xt为当前时刻的输入,Wr为其各自的权重,σ为sigmoid函数。
当得到门控信号之后,按式(6)计算,得到范围在-1~1之间的
| ˜ht=tanh[rt⊙(W′hht−1)+W′xxt] | (6) |
式中:W′h、W′x为 ht-1、xt各自可训练的权重; ⊙为Hadamard乘法;tanh为非线性激活函数。
2) 更新门。更新门和重置门的计算形式相同,但对每个门来说,权重矩阵与输入状态和隐藏状态相乘的结果都是唯一的,这表明每个门的最终矢量是不同的。具体为
| ut=σ(Wzht−1+Wzxt) | (7) |
式中Wz为更新门输出对应的权重矩阵。
然后,按式(8)合并输出ht为
| ht=ut⊙ht−1+(1−ut)⊙˜ht | (8) |
式中: ut为进行选择性的记忆,(1-ut)为进行选择性的遗忘。
GRU神经网络相较于LSTM神经网络的优势在于,GRU使用同一个门控ut便可以同时进行选择性的记忆和遗忘,而LSTM则需要多个门控。GRU的输入输出结构与标准的RNN相似,而其内部思想则与LSTM相似。与LSTM结构相比,GRU的内部少了一个“门控”,相关参数也比LSTM少,但却能够达到与LSTM相当的效果。故本文选择计算能力高且时间成本低的GRU神经网络作为融合方法的神经网络部分。
1.3 融合方法基于融合方法的锂电池RUL预测已经获得了越来越多研究者的关注,本文采用一种经验模型与数据驱动相融合的结构,提出一种迭代式的基于PF和GRU神经网络(PF-GRU)的锂电池RUL预测方法。该方法与现有融合方法相比,考虑了训练数据较少情况下的长期预测效果,且该方法的运算效率较高。
1.3.1 基于PF-GRU的融合方法对于PF-GRU的融合方法的锂电池RUL预测过程,需建立状态转移方程和观测方程:
| xk=[ak;bk;ck;dk] | (9) |
| {ak=ak−1+ωa,ωa∼N(0,σa)bk=bk−1+ωb,ωb∼N(0,σb)ck=ck−1+ωc,ωc∼N(0,σc)dk=dk−1+ωd,ωd∼N(0,σd) | (10) |
| Qk=ak∗exp(bk∗k)+ck∗exp(dk∗k)+γk,γk∼N(0,σQ) | (11) |
式中:a、b、c、d为电池的内部参数,也为状态量,电池容量作为观测量; k为电池的充放电循环周期; ω、γ分别为过程噪声和测量噪声, 它们都是高斯噪声; Qk是k循环周期的容量观测值,该状态估计问题的外部测量值yobs由GRU神经网络的预测值提供,即yobs=g(V, I, t); V、I、t分别为电池充电电压、放电电流和放电时间。本文在预测阶段的每一个预测周期中采用PF的滤波方法利用GRU神经网络的预测值对双指数经验模型的参数a、b、c、d进行更新,再利用更新后的参数计算新的容量预测值,从而实现GRU神经网络提供的预测信息与双指数经验模型提供的预测信息的融合。
在获得融合后的更新参数后,当电池达到所设置的寿命阈值EOL时,由式(12)便可得到充放电循环周期Lk
| EOL =ak∗exp(bk∗Lk)+ck∗exp(dk∗Lk) | (12) |
进一步可以确定在循环周期Lk时的RUL分布,见式(13),由此就可以预测电池的RUL
| P(Lk∣Q1k)≈∑Ni=1w(i)kδ(Lk−L(i)k) | (13) |
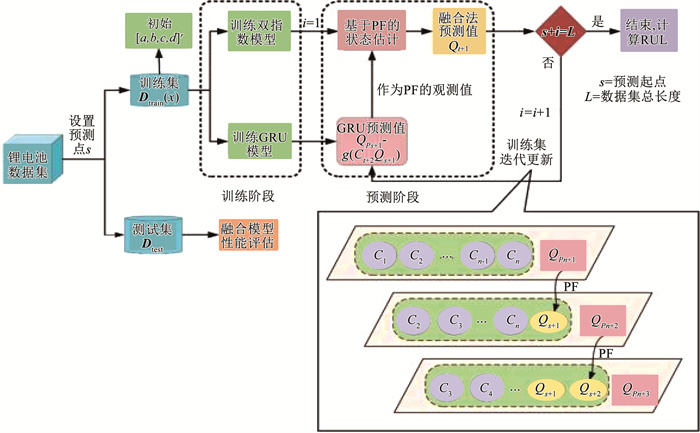
本文所提出的基于PF-GRU融合方法对锂电池的容量状态估计和RUL预测方法的流程见图 2。
|
图 2 PF-GRU融合方法流程 Fig. 2 Flow chart of PF-GRU fusion method |
PF-GRU算法分为训练阶段和预测阶段。为了描述方便,有如下定义:预测起点为s;Dtrain(s)是GRU模型训练的训练数据矢量,Dtest是GRU模型的测试数据矢量,根据实验电池的数据集总长度,#5、#6、#7电池的s设置为84,即#5、#6、#7电池的Dtrain(s)为各自的前84组数据,#18电池的s设置为66,即#18电池的Dtrain(s)为其前66组数据;在Dtrain(s)中,锂电池的充电电压、放电电流以及放电时间3个特征作为输入量,锂电池的容量作为输出量,1~s步周期的容量用C1,C2,C3,…,Cs表示;在预测阶段,GRU模型每个循环周期的输出为Qps+i,表示第s+i步的预测容量。
如图 2所示,基于PF-GRU的融合方法的详细步骤如下:
1) 从电池数据集中提取电池的充电电压、放电电流、放电时间数据和容量数据并进行预处理。
2) 设置预测起点s和寿命阈值。将循环容量数据集分为两部分,将循环周期1~s步的电池充电电压、放电电压、放电时间数据和容量数据作为GRU模型和双指数经验模型的训练数据集Dtrain(s)。
3) 训练阶段开始。用Dtrain(s)训练GRU模型,同时Dtrain(s)也用于建立双指数经验模型。
4) 预测阶段开始。在第s+1个循环周期,用GRU模型预测s+1循环周期时的电池容量,并命名为Qps+1。
5) 针对由式(9)、(10)组成的状态空间模型,将Qps+1作为PF中的测量值,利用PF算法估计模型状态[ak; bk; ck; dk],从而由此得到优化后的容量预测值Qs+1。
6) 使用优化的容量预测值Qs+1更新GRU模型的训练数据集 Dtrain,再利用新的训练数据集Dtrain重新训练GRU神经网络。
7) 重复执行步骤4至步骤5,直到预测步长达到数据集总长度,循环结束。最后外推至寿命阈值,得到锂电池容量退化曲线和RUL的分布。
1.3.2 GRU神经网络的迭代训练为提高融合方法的预测精度,在预测阶段对GRU模型采用了带移动窗口的迭代训练机制,能够使整个预测阶段的经验模型和GRU神经网络相互学习,保持动态更新。具体来说,本文将最新的融合信息插入GRU的训练数据集中,使之保持迭代更新。该方法的详细过程描述如下:
1) 对电池数据集进行预处理。
2) 设置预测起点s,得到的Dtrain(s)为电池前s组数据,即Dtrain(s)由C1,C2,…,Cs组成,剩下的Cs+1,Cs+2,…,C168作为测试集(以#5号电池数据集为例)。
3) 利用训练数据集Dtrain(s)对GRU模型进行训练,得到第s+1步GRU模型的预测值Qps+1。
4) 将Qps+1作为PF的观测值输入PF并进行滤波,得到第s+1步融合后的优化估计值Qs+1。
5) 将Qs+1加入GRU模型的Dtrain(s),生成新的训练数据集Dtrain(s+1)。更新后的Dtrain(s+1)由C2,C3,…,Cs,Qs+1组成。
6) 从第s+2步到第168步反复执行步骤3至步骤5,直到预测步长达到数据集总长度。
2 实验数据集和评价标准 2.1 实验数据集采用来自美国NASA的PCoE实验室的公开锂电池数据集,验证所提出方法预测锂电池RUL的准确性。选择标号为B0005、B0006、B0007、B0018的4块电池数据,本文使用#5、#6、#7、#18代表上述电池标号。对所获取的电池原始数据进行分析,原始数据集中的个别数据不是一次完整的充放电循环,存在缺失充电或放电状态数据的情况,对这些异常值进行删除,最终分别得到#5、#6、#7和#18电池的168、168、168和132个充放电循环容量数据。4块电池均为钴酸锂电池,额定容量均为2 Ah,且均在24 ℃的室温下进行实验。在1.5 A恒流状态下充电至电压达到4.2 V,然后保持恒压,直到电流降至20 mA;然后在2 A左右的恒流下进行放电至电池电压分别降至2.7、2.5、2.2和2.5 V;最后进行阻抗检测,完成一个充放电周期。重复上述过程,直到电池容量下降到电池寿命阈值时,实验停止。
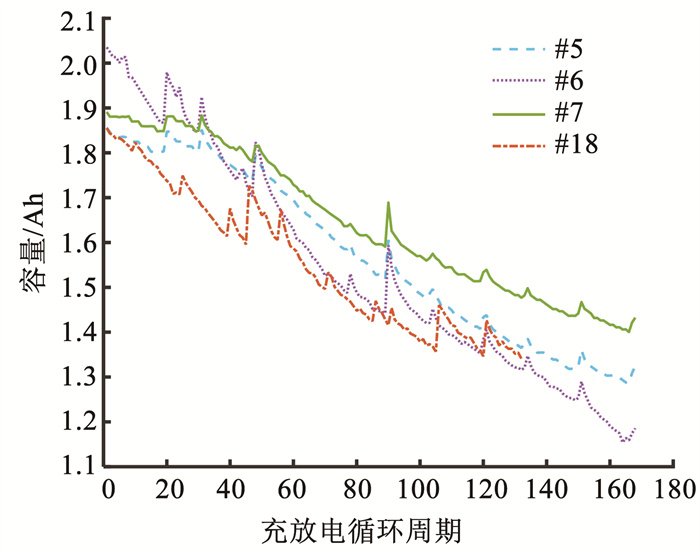
本次实验,#5、#6、#18电池寿命阈值定为额定容量的70%(即容量达到1.4 Ah),#7电池寿命阈值定为额定容量的72%(即容量达到1.44 Ah)。#5、#6、#7和#18电池容量随充放电循环的变化见图 3。
|
图 3 #5、#6、#7、#18电池容量退化曲线 Fig. 3 Capacity degradation curve of #5, #6, #7, #18 batteries |
为了更好地说明本文所提出的PF-GRU融合方法的准确性,通过评价指标预测误差PE和均方根误差RRMSEQ(root mean square error, RMSE)来评价模型精度。PE定义为预测得到的RUL和实际RUL差值的绝对值,见式(14):
| PE=|RRULpre −RRULreal | | (14) |
如式(15)所示,RRMSEQ反映了整个预测过程中对电池容量预测结果相对实验测量值的误差,数值越小,表示预测曲线与实际曲线越来越接近。
| RRMSE Q=√1N∑Ni=1(y(i)−ˆy(i))2 | (15) |
本文通过对#5、#6、#7、#18电池数据集分别进行4组仿真,其中每一组仿真都使用GRU、PF、PF-GRU(无移动窗口)和PF-GRU(有移动窗口)共4种方法对同一电池进行预测。4组仿真的粒子数量均设置为200。同一电池用PF、PF-GRU(无移动窗口)和PF-GRU(有移动窗口)预测时使用相同的初始粒子集,即模型初始参数和噪声保持一致。首先,利用MATLAB曲线拟合工具箱分别对#5、#6、#7和#18电池的训练数据集中的容量数据进行拟合,将目标函数选定为双指数函数,从而获得双指数模型的参数值,将该估计值作为PF估计的初始值。得到的初始参数拟合值见表 1。
| 表 1 PF初始参数 Tab. 1 Initial parameters of PF |
通过仿真调试,过程噪声σa、σb、σc、σd和测量噪声σQ取值设置见表 2。
| 表 2 噪声参数 Tab. 2 Noise parameters |
根据文献[3]对用4块电池的训练集数据对GRU模型进行训练。GRU神经网络由输入层、隐藏层和输出层组成,使用标准前馈神经网络。采用Adam优化器,学习率为0.000 5,为防止梯度爆炸,将梯度阈值设置为1。通过调整超参数进行重复训练,最终得到的GRU模型训练超参数见表 3。
| 表 3 GRU的训练超参数设置 Tab. 3 Training hyper parameter settings of GRU |
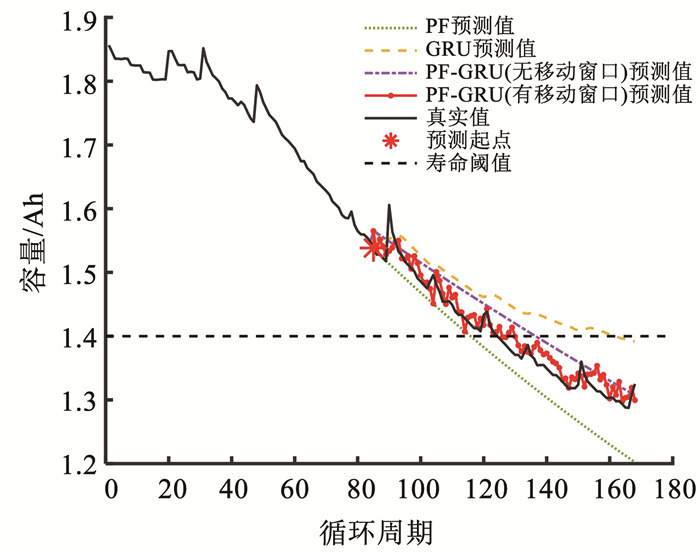
根据4块电池的有效数据量,#5、#6、#7电池的预测点设置为第84个周期,#18电池的预测点设置为第66个周期。由4种方法得到的锂电池容量退化的预测结果见图 4~7。
|
图 4 对#5电池容量的预测结果 Fig. 4 Prediction results of #5 battery capacity |
|
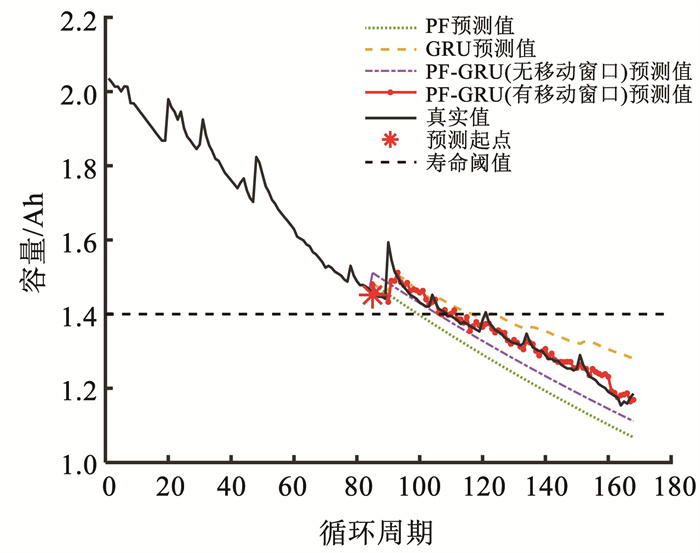
图 5 对#6电池容量的预测结果 Fig. 5 Prediction results of #6 battery capacity |
|
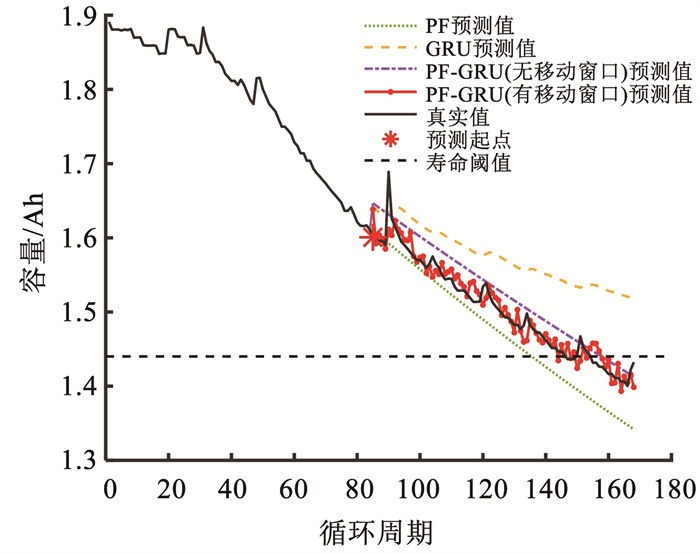
图 6 对#7电池容量的预测结果 Fig. 6 Prediction results of #7 battery capacity |
|
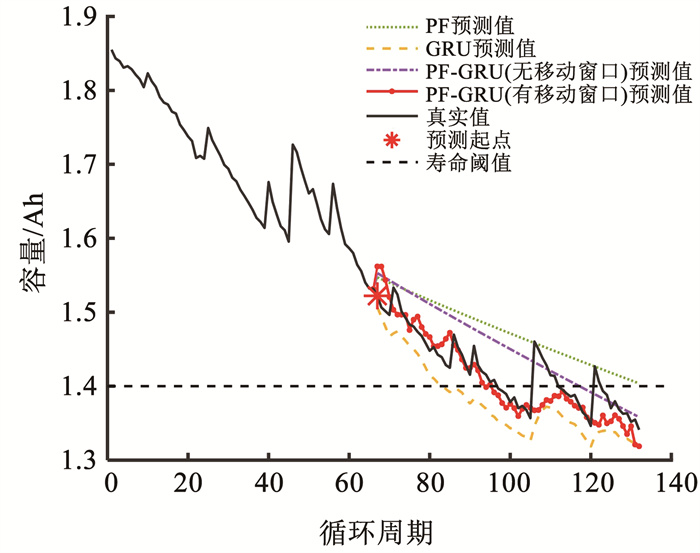
图 7 对#18电池容量的预测结果 Fig. 7 Prediction results of #18 battery capacity |
结合图 4~7以及表 5所列出的4种方法预测结果的RMSE可以看出,与PF、GRU、PF-GRU(无移动窗口)融合方法相比,本文所提出的PF-GRU(有移动窗口)融合方法可以更好地近似锂电池的真实退化过程,预测结果不仅最接近锂电池的真实容量值,而且预测出的容量值呈波动状态,更加接近真实容量值。由图 4~7可以观察到,虽然2种PF-GRU融合方法的预测精度都高于单个算法,但有移动窗口的融合方法明显比无移动窗口的融合方法预测效果更好。
同时,给出最后一个循环周期的双指数经验模型参数a、b、c、d更新值,见表 4。
| 表 4 最后一周期的经验模型参数值 Tab. 4 Parameter value of empirical model in the last cycle |
| 表 5 4种电池锂电池RUL预测结果 Tab. 5 RUL prediction results of four kinds of lithium batteries |
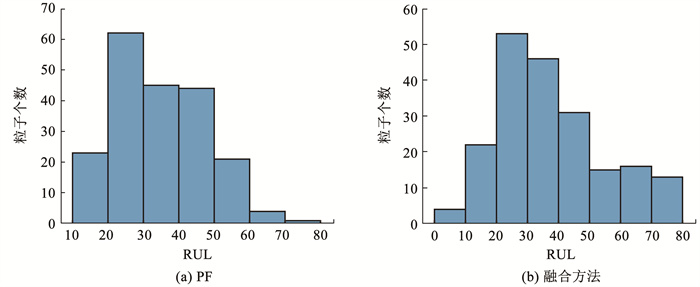
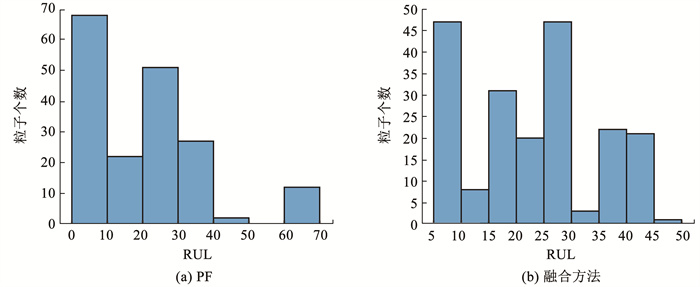
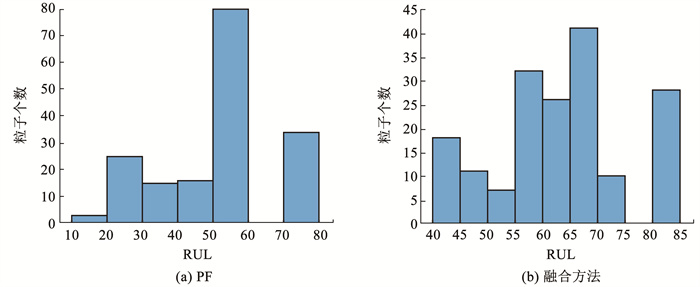
接下来,对于PF和PF-GRU(有移动窗口)融合预测方法,本文根据有效粒子所代表的参数值外推至寿命阈值,进行锂电池的RUL预测,绘制出的直方图见图 8~11。
|
图 8 #5电池RUL分布的预测 Fig. 8 RUL distribution prediction of #5 battery |
|
图 9 #6电池RUL分布的预测 Fig. 9 RUL distribution prediction of #6 battery |
|
图 10 #7电池RUL分布的预测 Fig. 10 RUL distribution prediction of #7 battery |

|
图 11 #18电池RUL分布的预测 Fig. 11 RUL distribution prediction of #18 battery |
4种预测方法之间的详细比较结果见表 5。
由表 5得出以下结论,首先从对电池RUL的预测结果上看,无论有无移动窗口,PF-GRU融合方法的预测误差都低于单个算法,同时有移动窗口的PF-GRU更进一步地缩小了预测误差,预测出的RUL最接近于真实值,而GRU在本次实验中未能对#7电池的RUL做出估计,其长期性的预测性能稳定性较低。其次,从对电池容量预测结果的RMSE上看,本文所提出的融合方法的预测精度明显高于其他方法。最后综合RUL和RMSE的预测结果来看,本文提出的预测算法的误差最小,精度最高,对锂电池RUL具有良好的预测性能。
3.3 不同算法预测所需时长对比仿真本部分以#5电池为研究对象,用本文仿真所用到的4种方法和同样采用带移动窗口迭代训练的PF-LSTM进行仿真,记录各自的预测所需时间以及容量和RUL的预测,结果见表 6。其中,预测所需时间是由5种方法各进行了10次训练,取10次仿真时间的平均值,见表 6第2列。
| 表 6 #5电池的预测精度和所需时间结果 Tab. 6 Prediction accuracy and required time results of #5 battery |
从表 6的对比结果看,可以得到以下结论:
1) 由于存在移动窗更新迭代机制,有移动窗的比无移动窗的平均预测时间长,但是RMSE和RUL显著提高。故相对于RMSE和RUL的预测结果精度的提高,由移动窗算法导致的预测时间的加长是可以接受的。
2) GRU比LSTM更高效,这是由于LSTM有3个不同的门,参数较多,收敛时间长,导致训练会消耗大量的时间,而GRU只含有2个门控,结构更为简单。
综上所述,本文提出的PF-GRU融合算法具有如下优点:1)运算效率高,一方面是由于GRU结构简单,训练参数较少,另一方面是由于PF对强非线性模型的状态估计有着很高的效率和精度。2)提出的融合方法可以在使用少样本数据集的情况下,仍可以达到进行长期预测并保证其精度。3)预测精度高,提出的带移动窗口的融合方法利用迭代训练机制在预测阶段对进行融合的2个模型迭代训练、动态更新,将2个模型的优势相结合,充分发挥其各自的优点,在保证了模型的准确性的同时,提高了预测精度。
4 结论本文为提高锂电池RUL的预测精度,提出了一种将PF和GRU神经网络相结合的锂电池RUL预测的融合方法。GRU作为一种神经网络,对时间序列预测问题具有良好的性能,同时,GRU采用门机制解决了传统RNN的梯度问题和长期记忆被覆盖问题,而且GRU比LSTM参数少,拥有更快的收敛速度,更少的收敛时间,可以加速迭代过程。PF算法能够处理非线性非高斯系统的滤波问题,对具有强非线性的锂电池经验模型的参数估计十分适用。而PF-GRU的融合方法集合了其所包含的2种方法的优点,为锂电池RUL的预测提供了新的可能性,另外,本文在训练阶段采用训练集迭代更新机制来实现GRU模型和经验模型的融合,根据最新预测的容量数据进行动态更新,保证2种模型的准确性。这种带移动窗口的迭代更新预测模型的方法较好地解决了现有方法对长期性的电池容量估计不准的问题,可以显著提高预测精度。通过美国NASA PCoE实验室提供的数据,采用PF、GRU神经网络、PF-GRU(无移动窗口)融合和PF-GRU(有移动窗口)融合方法来进行RUL预测性能验证,通过提出预测误差和均方根误差的评价指标,对4种算法的预测结果进行了比较和分析。最后得出,4块电池用本文所提方法与其他3种方法相比,预测误差显著降低,预测精度明显上升,从而进一步说明本文提出的融合方法可以更好地近似锂电池真实容量退化过程,明显提高对锂电池RUL的预测精度。RUL预测准确率的提升,有助于BMS提高电池能量利用率,降低电池热失控风险,并且对电池的维保具有重要意义。
| [1] |
朱丽群, 张建秋. 一种联合锂电池健康和荷电状态的新模型[J]. 中国电机工程学报, 2018, 38(12): 3613. ZHU Liqun, ZHANG Jianqiu. A new model of jointed states of charge and health for lithium batteries[J]. Proceedings of the CSEE, 2018, 38(12): 3613. DOI:10.13334/j.0258-8013.pcsee.172699 |
| [2] |
闫啸宇, 周思达, 卢宇, 等. 锂离子电池容量衰退机理与影响因素研究[J/OL]. 北京航空航天大学学报: 1. [2022-08-18]. DOI: 10.13700/j.bh.1001-5965.2021.0458 YAN Xiaoyu, ZHOU Sida, LU Yu, et al. Research on degradation mechanism and influencing factors on lithium-ion batteries[J/OL]. Journal of Beijing University of Aeronautics and Astronautics: 1. [2022-08-18]. DOI: 10.13700/j.bh.1001-5965.2021.0458 |
| [3] |
HU Xiaosong, YANG Xin, FENG Fei, et al. A particle filter and long short-term memory fusion technique for lithium-ion battery remaining useful life prediction[J]. Journal of Dynamic Systems, Measurement, and Control, 2021, 143(6). DOI:10.1115/1.4049234 |
| [4] |
戴海峰, 张艳伟, 魏学哲, 等. 锂离子电池剩余寿命预测研究[J]. 电源技术, 2019, 43(12): 2029. DAI Haifeng, ZHANG Yanwei, WEI Xuezhe, et al. Review of remaining useful life prediction for lithium ion battery[J]. Chinese Journal of Power Sources, 2019, 43(12): 2029. DOI:10.3969/j.issn.1002-087X.2019.12.032 |
| [5] |
刘大同, 周建宝, 郭力萌, 等. 锂离子电池健康评估和寿命预测综述[J]. 仪器仪表学报, 2015, 36(1): 1. LIU Datong, ZHOU Jianbao, GUO Limeng, et al. Survey on lithium-ion battery health assessment and cycle life estimation[J]. Chinese Journal of Scientific Instrument, 2015, 36(1): 1. DOI:10.19650/j.cnki.cjsi.2015.01.003 |
| [6] |
PRASAD G K, RAHN C D. Model based identification of aging parameters in lithium ion batteries[J]. Journal of Power Sources, 2013, 232: 79. DOI:10.1016/j.jpowsour.2013.01.041 |
| [7] |
PATTIPATI B, SANKAVARAM C, PATTIPATI K R. System identification and estimation framework for pivotal automotive battery management system characteristics[J]. IEEE Transactions on Human-Machine Systems, 2011, 41(6): 869. DOI:10.1109/tsmcc.2010.2089979 |
| [8] |
SON J, ZHOU Shiyu, SANKAVARAM C, et al. Remaining useful life prediction based on noisy condition monitoring signals using constrained Kalman filter[J]. Reliability Engineering and System Safety, 2016, 152: 38. DOI:10.1016/j.ress.2016.02.006 |
| [9] |
TIAN Ye, LU Chen, WAMG Zili, et al. Artificial fish swarm algorithm-based particle filter for Li-ion battery life prediction[J]. Mathematical Problems in Engineering, 2014, 2014: 1. DOI:10.1155/2014/564894 |
| [10] |
KLASS V, BEHM M, LINDBERGH G. A support vector machine-based state-of-health estimation method for lithium-ion batteries under electric vehicle operation[J]. Journal of Power Sources, 2014, 270: 262. DOI:10.1016/j.jpowsour.2014.07.116 |
| [11] |
ZHOU Yapeng, HUANG Miaohua, CHEN Yupu, et al. A novel health indicator for on-line lithium-ion batteries remaining useful life prediction[J]. Journal of Power Sources, 2016, 321: 1. DOI:10.1016/j.jpowsour.2016.04.119 |
| [12] |
QIN Wei, LV Huichun, LIU Chengliang, et al. Remaining useful life prediction for lithium-ion batteries using particle filter and artificial neural network[J]. Industrial Management & Data Systems, 2019, 120(2): 312. DOI:10.1108/imds-03-2019-0195 |
| [13] |
罗悦. 基于粒子滤波的锂离子电池剩余寿命预测方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2012 LUO Yue. Research on remaining useful life prediction of lithium-ion battery with particle filter[D]. Harbin: Harbin Institute of Technology, 2012 |
| [14] |
ZHENG Xiujuan, FANG Huajing. An integrated unscented Kalman filter and relevance vector regression approach for lithium-ion battery remaining useful life and short-term capacity prediction[J]. Reliability Engineering and System Safety, 2015, 144: 74. DOI:10.1016/j.ress.2015.07.013 |
| [15] |
王玉斐. 一种基于ARI模型和SRCKF的融合型算法的锂电池剩余寿命预测方法[J]. 舰船电子对抗, 2019, 42(4): 117. WANG Yufei. A prediction approach of lithium battery life based on ARI model and SRCKF fusion algorithm[J]. Shipboard Electronic Countermeasure, 2019, 42(4): 117. DOI:10.16426/j.cnki.jcdzdk.2019.04.026 |
| [16] |
陈赐阳, 陈德旺. 基于CNN-LSTM的锂电池剩余寿命(RUL)间接预测研究[J]. 电源技术, 2021, 45(5): 589. CHEN Ciyang, CHEN Dewang. Research on indirect prediction of lithium battery RUL based on CNN-LST-M[J]. Chinese Journal of Power Sources, 2021, 45(5): 589. DOI:10.3969/j.issn.1002-087X.2021.05.009 |
| [17] |
朱文超, 许德章. 一种基于人工萤火虫群优化的改进粒子滤波算法[J]. 计算机应用研究, 2014, 31(10): 2920. ZHU Wenchao, XU Dezhang. Improved particle filter algorithm based on artificial glowworm swarm optimization[J]. Application Research of Computers, 2014, 31(10): 2920. DOI:10.3969/j.issn.1001-3695.2014.10.008 |
| [18] |
王钋, 雷敏, 梁娇娇, 等. 基于IPSO-GRU的锂离子电池剩余使用寿命预测[J]. 湖南工业大学学报, 2022, 36(4): 23. WANG Po, LEI Min, LIANG Jiaojiao, et al. An IPSO-GRU-based prediction of remaining useful life of lithium-ion batteries[J]. Journal of Hunan University of Technology, 2022, 36(4): 23. |
 2024, Vol. 56
2024, Vol. 56



