人脸情感识别是极具挑战性的机器学习任务,图片完整程度、图片亮度、被拍摄者的肤色和种族以及拍照角度等因素的差异都会对情感识别形成干扰[1-2]。因此,如何提升情感识别的正确性是当前的国内外相关研究中的难点与重点。为了有效提升情感识别准确率,研究者多采用集成多基分类器的方式增强系统识别能力与鲁棒性[3-5]。然而,由于集成学习不可避免地引入了一些低识别率和冗余的基分类器,这些“低质量”的基分类器不仅会降低最终集成的性能,还会增加存储空间和运行时间的负担。因此,研究人员提出了集成剪枝方法[6-7],这类方法将弱分类器和冗余分类器从基分类器池中剔除,保留最优能力的基分类器进行集成。相比传统集成学习,集成剪枝不仅降低了算法的时空复杂度,还提升了最终的识别效果。例如,文献[4]提出了一种聚类软标签的方法进行样本选择,进而进行集成剪枝,这种方法有效地提高了人脸情感的识别性能并降低了算法整体的时空复杂度。然而,如何设计一种方法剔除弱分类器和冗余分类器仍是一个需要不断研究的问题。
集成剪枝旨在选择“好而不同”的基分类器,以构建高质量的基分类器子集,这就意味着,选择的基分类器不仅是高识别性能,而且还是低冗余的。在集成剪枝领域,基分类器高识别性能和低冗余分别用准确率和多样性来表示,它们的值越高,选择的基分类器子集识别性能越高、冗余度更低。文献[8]证明了同时考虑基分类器的准确率和多样性能够获得更优秀、泛化能力更强的基分类器子集,从而提高集成模型的效果。此外,文献[7]提出了一种将频谱聚类和结构稀疏性集成于一个回归联合框架中的方法,可以无监督地选择具有较低冗余度和良好识别性能的基分类器。然而,这些方法都没有考虑到分类器噪声和异常值对集成剪枝的影响,也没有充分考虑基分类器之间的冗余关系。为了解决上述问题,本文提出了一种基于回归的目标方程的方法,称为具有依赖分数的鲁棒性稀疏低冗余集成剪枝(robust sparse and low-redundancy ensemble pruning with dependencies score, RSLDS)。该方法使用l2, 1范数表示损失函数,以实现对基分类器进行鲁棒性选择。同时,它使用互信息和熵分别计算成对基分类器之间的依赖关系和优先级,并将它们结合起来,得到基分类器的依赖分数,从而更加准确地表示基分类器之间的依赖关系。此外,该方法使用内积化正则项来选择数量更少、更冗余的基分类器子集,从而进一步提高基分类器子集的识别性能和效率。
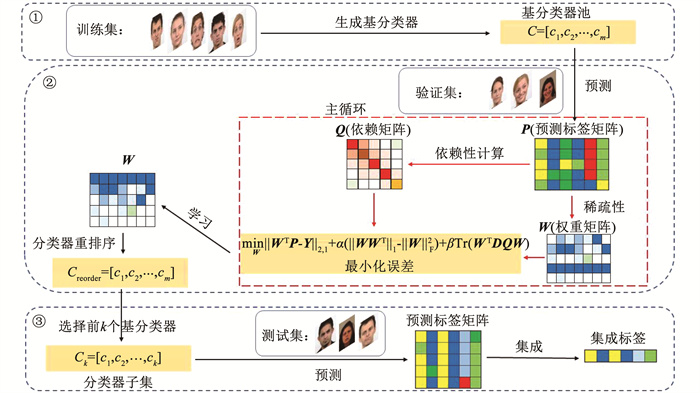
1 具有依赖分数的鲁棒稀疏低冗余集成修剪本文所提出的RSLDS方法框架见图 1。此方法主要可以分为3个部分。首先,RSLDS通过训练多个深度神经网络模型来创建集分类器池。其次,RSLDS设计了一种基于回归优化的集成剪枝方法,以平衡基分类器的准确率和多样性,并对分类器进行排序。最后,该方法从最新的基分类器序列中选择前k个基分类器,并使用多数投票对基分类器子集的预测标签进行集成,在测试集上测试该方法的效果。
|
图 1 RSLDS的框架 Fig. 1 Framework of RSLDS |
在整篇文章中向量Ai ·和A·j分别表示矩阵A的行和列,Aij表示矩阵A在i行j列的元素,方阵A的迹和转置分别表示为Tr(A)和AT,‖A‖1=
在本文中,用V={xi, yi}i=1n表示一组标签实例,X={x1, x2, …, xn}∈Rd×n是一个表示所有实例特征空间的d×n维的矩阵,P∈Rm×n表示m个基分类器对具有n个实例的预测标签矩阵。基本分类器ci是一个映射:X→Y从特征空间X到标签空间Y。集成剪枝生成一组基本分类器C={ci}i=1m,它们被集成以产生最终的预测。Y∈Rn×c表示c维标签空间中有n个实例的标签矩阵,其中当第i个实例与第j个标签相关联时,Yij表示1,否则Yij表示0。
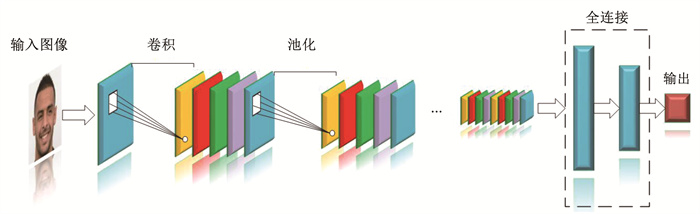
1.2 构建基分类器特征集成剪枝的有效性在很大程度上取决于基分类器的准确性和多样性。卷积神经网络在人脸情感识别中具有很强的识别效果[2],其结构框图见图 2。为了保证最终实验具有良好的识别性能,本文使用卷积神经网络作为基础分类器,通过修改卷积神经网络的参数和网络结构来构建一系列基分类器C={ci}i=1m。这些卷积神经网络模型的参数值范围见表 1。
|
图 2 卷积神经网络的结构框图 Fig. 2 Block diagram of structure of convolutional neural network |
| 表 1 生成的卷积神经网络模型参数范围 Tab. 1 Range of generated convolutional neural network model parameters |
基分类器对样本的预测结果更加能反映基分类器的学习能力[3],而不是样本的特征。因此,本文使用基分类器对样本的预测值作为基分类器的特征来进行分类器选择。本文用cj(xi)表示第j个分类器对第i个样本实例的一个预测值,则第m个基分类器对第n个样本实例的预测矩阵P∈Rm×n可以表达为
| $ \boldsymbol{P}=\left[\begin{array}{ccc} c_1\left(x_1\right) & \cdots & c_1\left(x_n\right) \\ \vdots & & \vdots \\ c_m\left(x_1\right) & \cdots & c_m\left(x_n\right) \end{array}\right] $ | (1) |
传统基于回归的集成剪枝的目标方程一般形式为
| $ \min\limits_{\boldsymbol{W}} J\left(\boldsymbol{W}^{\mathrm{T}} \boldsymbol{P}, \boldsymbol{Y}\right)+\alpha \mathit{\varOmega}(\boldsymbol{W}) $ | (2) |
式中:J(WTP, Y)是损失函数; W∈Rm×c是权重矩阵,Ω(W)是正则化项,迫使W行稀疏性,α≥0表示一般正则化项Ω(W)的正则化参数; c是类别的数量; Y=[y1, …, yn]∈{0, 1}c×n是热编码标签矩阵,其中,yi∈{0, 1}c表示样本实例xi的标签向量。
传统的方法对式(2)中的损失函数J(WTP, Y)采用了最小二乘回归模型,正则化项Ω(W)通常使用l2, 1范数[9],则式(2)可表示为
| $ \min\limits_{\boldsymbol{W}}\left\|\boldsymbol{W}^{\mathrm{T}} \boldsymbol{P}-\boldsymbol{Y}\right\|_{\mathrm{F}}^2+\alpha\|\boldsymbol{W}\|_{2, 1} $ | (3) |
此目标函数旨在找到最小化投影数据WTP和标签Y之间差异的分类器,同时通过对权重矩阵W施加l2, 1范数使W强制稀疏性,根据权重矩阵W判断基分类器优先级,从而实现基分类器子集的选择。使用最小二乘回归模型对噪声和异常值敏感,可能会导致选择错误的基分类器,文献[10]进一步证明了使用l2, 1范数的损失函数具有更强的鲁棒性。因此,本文将式(3)中的损失函数J(WTP, Y)改为l2, 1范数,提升基分类器选择的鲁棒性,从而增加基分类器子集的泛化性能。式(3)可以重新表达为
| $ \min\limits_{\boldsymbol{W}}\left\|\boldsymbol{W}^{\mathrm{T}} \boldsymbol{P}-\boldsymbol{Y}\right\|_{2, 1}+\alpha\|\boldsymbol{W}\|_{2, 1} $ | (4) |
为了进一步学习最优权重,考虑冗余的基分类器对集成剪枝的影响,互信息能够捕捉随机变量之间的非线性统计依赖[11],可采用互信息来评估分类器之间的依赖关系。依赖分类器又称为冗余分类器。2个分类器ci和cj的预测标签之间的互信息MI(ci, cj)定义为MI(ci, cj)=H(ci)+H(cj)-H(ci, cj),其中H(ci)=-ΣP(ci)logP(ci)是联合熵,它使用联合概率函数P(ci)来衡量ci中包含的信息。本文使用互信息来构建多分类器预测结果的依赖矩阵Q。此矩阵的每个元素定义为
| $ \boldsymbol{Q}_{i, j}= \begin{cases}\mathrm{MI}\left(c_i, c_j\right) & \text { if } i \neq j \\ \sum\limits_{k \neq i} \boldsymbol{Q}_{i, k} & \text { if } i=j\end{cases} $ | (5) |
将依赖矩阵Q合并到式(4)中,可得
| $ \min\limits_{\boldsymbol{W}}\left\|\boldsymbol{W}^{\mathrm{T}} \boldsymbol{P}-\boldsymbol{Y}\right\|_{2, 1}+\alpha\|\boldsymbol{W}\|_{2, 1}+\beta \operatorname{Tr}\left(\boldsymbol{W}^{\mathrm{T}} \boldsymbol{Q} \boldsymbol{W}\right) $ | (6) |
式中β>0也是一个正则化参数。对于式(6)的第3项,文献[12]发现了该表达式存在2个缺点。首先,当2个特征之间的互信息较高时,并不能保证它们的优先级较低,无法判断哪个特征更重要。其次,它平等地考虑了所有的特征。Tr(WTQW)可以表述为
| $ \begin{aligned} \operatorname{Tr}\left(\boldsymbol{W}^{\mathrm{T}} \boldsymbol{Q} \boldsymbol{W}\right)= & \operatorname{Tr}\left[\boldsymbol{W}^{\mathrm{T}} \operatorname{diag}(\boldsymbol{Q}) \boldsymbol{W}\right]+\operatorname{Tr}\left[\boldsymbol{W}^{\mathrm{T}} \operatorname{diag}(\boldsymbol{Q})^{\prime} \boldsymbol{W}\right]= \\ & \sum\limits_{i=1}^{m-1} \sum\limits_{j=i+1}^m\left(<\boldsymbol{W}_i, \boldsymbol{W}_i .>+<\boldsymbol{W}_j, \boldsymbol{W}_j .>\right) \operatorname{MI}\left(c_i, c_j\right)+\sum\limits_{i=1}^{d-1} \sum\limits_{j=i+1}^d 2<\boldsymbol{W}_i, \boldsymbol{W}_j .>\operatorname{MI}\left(c_i, c_j\right)= \\ & \sum\limits_{i=1}^{m-1} \sum\limits_{j=i+1}^m<\boldsymbol{W}_i .+\boldsymbol{W}_{j .}, \boldsymbol{W}_i .+\boldsymbol{W}_j .>\operatorname{MI}\left(c_i, c_j\right)=\sum\limits_{i=1}^{m-1} \sum\limits_{j=i+1}^m\left\|\boldsymbol{W}_i .+\boldsymbol{W}_j .\right\|_2^2 \mathrm{MI}\left(c_i, c_j\right) \end{aligned} $ | (7) |
式中:diag(Q)表示Q的对角线部分元素,而diag(Q)′表示Q的非对角线部分元素。用‖Wi · ‖2表示i维基分类器的重要性。根据式(7),当MI(ci, cj) 较大时,‖Wi · +Wj · ‖2较小,由于Wi · 和Wj · 都是向量,较小的‖Wi · +Wj · ‖2并不能保证Wi · 和Wj · 同时较小。因此,该方法存在次优解,为了增加冗余基分类器的优先级,将熵纳入式(7)中,新的优化问题为
| $ \begin{gathered} \min\limits_{\boldsymbol{W}}\left\|\boldsymbol{W}^{\mathrm{T}} \boldsymbol{P}-\boldsymbol{Y}\right\|_{2, 1}+\alpha\|\boldsymbol{W}\|_{2, 1}+\beta \sum\limits_{i=1}^{m-1} \sum\limits_{j=i+1}^m\left(\mathrm{H}\left(c_j\right)\left\|\boldsymbol{W}_i \cdot\right\|_2+\right. \\ \left.\mathrm{H}\left(c_i\right)\left\|\boldsymbol{W}_j \cdot\right\|_2\right) \mathrm{MI}\left(c_i, c_j\right) \end{gathered} $ | (8) |
该公式的第3项表明,如果ci和cj之间的互信息较大,那么ci和cj不应该同时重要。如果H(ci)更大,那么ci具有更多的不确定性或多样性,应该比cj更重要。式(8)不包含MI(ci, ci),因此MI(ci, ci)可以定义为0,式(8)的第3部分可以重写为
| $ \begin{aligned} & \sum\limits_{i=1}^{m-1} \sum\limits_{j=i+1}^m\left(\mathrm{H}\left(c_j\right)\left\|\boldsymbol{W}_i \cdot\right\|_2+\mathrm{H}\left(c_i\right)\left\|\boldsymbol{W}_j \cdot\right\|_2\right) \mathrm{MI}\left(c_i, c_j\right)= \\ & \frac{1}{2} \sum\limits_{i, j=1}^m\left(\mathrm{H}\left(c_j\right)\left\|\boldsymbol{W}_i \cdot\right\|_2+\mathrm{H}\left(c_i\right)\left\|\boldsymbol{W}_j \cdot\right\|_2\right) \mathrm{MI}\left(c_i, c_j\right)= \\ & \frac{1}{2}\left[\sum\limits_{i, j=1}^m \mathrm{H}\left(c_j\right)\left\|\boldsymbol{W}_i \cdot\right\|_2 \mathrm{MI}\left(c_i, c_j\right)+\sum\limits_{i, j=1}^m \mathrm{H}\left(c_i\right)\left\|\boldsymbol{W}_j \cdot\right\|_2 \mathrm{MI}\left(c_i, c_j\right)\right]= \\ & \frac{1}{2}\left[\sum\limits_{i, j=1}^m \mathrm{H}\left(c_j\right)\left\|\boldsymbol{W}_i \cdot\right\|_2 \mathrm{MI}\left(c_i, c_j\right)+\sum\limits_{j, i=1}^m \mathrm{H}\left(c_j\right)\left\|\boldsymbol{W}_i \cdot\right\|_2 \mathrm{MI}\left(c_i, c_j\right)\right]= \\ & \sum\limits_{i, j=1}^m \mathrm{H}\left(c_j\right)\left\|\boldsymbol{W}_i \cdot\right\|_2 \mathrm{MI}\left(c_i, c_j\right)=\sum\limits_{i=1}^m\left\|\boldsymbol{W}_i \cdot\right\|_2 \sum\limits_{j=1}^m \mathrm{H}\left(c_j\right) \mathrm{MI}\left(c_i, c_j\right)= \\ & \left.\sum\limits_{i=1}^m\left\|\boldsymbol{W}_i \cdot\right\|_2\left[\mathrm{H}\left(c_i\right) \mathrm{MI}\left(c_i ; c_i\right)+\sum\limits_{j \neq i}^m \mathrm{H}\left(c_j\right) \mathrm{MI}\left(c_i, c_j\right)\right)\right]= \\ & \sum\limits_{i=1}^m\left\|\boldsymbol{W}_i \cdot\right\|_2 \sum\limits_{j \neq i}^m \mathrm{H}\left(c_j\right) \mathrm{MI}\left(c_i ; c_j\right)=\operatorname{Tr}\left(\boldsymbol{W}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{Q} \boldsymbol{W}\right) \end{aligned} $ | (9) |
式中D∈Rm×m和Q∈Rm×m是对角矩阵,并且矩阵D和Q的ith对角元素分别为
| $ \min\limits_{\boldsymbol{W}}\left\|\boldsymbol{W}^{\mathrm{T}} \boldsymbol{P}-\boldsymbol{Y}\right\|_{2, 1}+\alpha\|\boldsymbol{W}\|_{2, 1}+\boldsymbol{\beta} \operatorname{Tr}\left(\boldsymbol{W}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{Q} \boldsymbol{W}\right) $ | (10) |
式(10)的第1项迫使本文选择识别性能好的基分类器,第2项使用l2, 1范数迫使权重矩阵W行稀疏性,而第3项使用互信息和熵表示基分类器依赖分数,进而评估分类器的冗余程度。3项约束条件同时作用于权重矩阵W,并且通过限制W中行的分布情况来进行基分类器的选择。然而,该式的第2项使用具有l2, 1范数约束的正则化项在基分类器选择过程中忽略了基分类器与高冗余信息基分类器之间的相关性,从而导致容易陷入次优解。文献[13]设计了一个新的范数,称为内积正则化项,它通过计算分类器特征系数向量内积的绝对值的和,从而选择数量更少和冗余度更低的基分类器子集。本文将这个范数应用于权重矩阵W上,内积正则化项的公式为
| $ \begin{gathered} \mathit{\varOmega}(\boldsymbol{W})=\sum\limits_{i=1}^m \sum\limits_{j=1, i \neq j}^m\left|<\boldsymbol{W}_{i \cdot}, \boldsymbol{W}_j .>\right|= \\ \sum\limits_{i=1}^m \sum\limits_{j=1}^m\left|<\boldsymbol{W}_{i \cdot}, \boldsymbol{W}_j .>\right|-\sum\limits_{i=1}^m\left|<\boldsymbol{W}_{i \cdot}, \boldsymbol{W}_j .>\right|= \\ \left\|\boldsymbol{W} \boldsymbol{W}^{\mathrm{T}}\right\|_1-\operatorname{Tr}\left(\boldsymbol{W} \boldsymbol{W}^{\mathrm{T}}\right)=\left\|\boldsymbol{W} \boldsymbol{W}^{\mathrm{T}}\right\|_1-\|\boldsymbol{W}\|_{\mathrm{F}}^2 \end{gathered} $ | (11) |
式中Ω(W)越小,去除的无效和冗余基分类器越多,即如果Wi ·和Wj ·之间的冗余足够高,则Wi ·和Wj ·之间的内积很大,在不考虑这部分冗余分类器后,使得Ω(W)更小。从而提高了正则化项的惩罚强度,保证了基分类器之间的低冗余度。将式(11)与式(10)结合可以得到
| $ \begin{gathered} \min\limits_{\boldsymbol{W}}\left\|\boldsymbol{W}^{\mathrm{T}} \boldsymbol{P}-\boldsymbol{Y}\right\|_{2, 1}+\alpha\left(\left\|\boldsymbol{W} \boldsymbol{W}^{\mathrm{T}}\right\|_1-\|\boldsymbol{W}\|_{\mathrm{F}}^2\right)+ \\ \beta \operatorname{Tr}\left(\boldsymbol{W}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{Q} \boldsymbol{W}\right) \end{gathered} $ | (12) |
为了解决式(12)中的第1项在求解时l2, 1范数难以计算的问题,本文引入了一个辅助变量K,式(12)被重新表述为
| $ \begin{gathered} \min\limits_{\boldsymbol{W}}\|\boldsymbol{K}\|_{2, 1}+\alpha\left(\left\|\boldsymbol{W} \boldsymbol{W}^{\mathrm{T}}\right\|_1-\|\boldsymbol{W}\|_{\mathrm{F}}^2\right)+ \\ \beta \operatorname{Tr}\left(\boldsymbol{W}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{Q} \boldsymbol{W}\right) \end{gathered} $ | (13) |
式中K=WTP-Y。这个公式是凸的,因此,可以使用ADMN[14]来解式(13),式(13)相应的增广拉格朗日方程为
| $ \begin{gathered} L(\boldsymbol{W}, \boldsymbol{K}, \boldsymbol{Y})=\|\boldsymbol{K}\|_{2, 1}+ \\ \alpha\left(\left\|\boldsymbol{W} \boldsymbol{W}^{\mathrm{T}}\right\|_1-\|\boldsymbol{W}\|_F^2\right)+\beta \operatorname{Tr}\left(\boldsymbol{W}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{Q} \boldsymbol{W}\right)+ \\ \operatorname{Tr}\left[\boldsymbol{E}^{\mathrm{T}}\left(\boldsymbol{K}-\boldsymbol{W}^{\mathrm{T}} \boldsymbol{P}+\boldsymbol{Y}\right)\right]+(\mu / 2)\left\|K-\boldsymbol{W}^{\mathrm{T}} \boldsymbol{P}+\boldsymbol{Y}\right\|_{\mathrm{F}}^2 \end{gathered} $ | (14) |
式中E和μ分别为拉格朗日乘子和惩罚项。
1.4.1 更新W式(14)相对于W的最小化表示为
| $ \begin{gathered} \min\limits_W \alpha\left(\left\|\boldsymbol{W} \boldsymbol{W}^{\mathrm{T}}\right\|_1-\|\boldsymbol{W}\|_{\mathrm{F}}^2\right)+ \\ \beta \operatorname{Tr}\left(\boldsymbol{W}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{Q} \boldsymbol{W}\right)+({\mu} / 2)\left\|\boldsymbol{K}-\boldsymbol{W}^{\mathrm{T}} \boldsymbol{P}+\boldsymbol{Y}-\boldsymbol{E} / \mu\right\|_{\mathrm{F}}^2 \end{gathered} $ | (15) |
当式(15)相对于W的导数设置为零时,可以得到
| $ \begin{gathered} 2 \alpha\left(\boldsymbol{I}_{d d} \boldsymbol{W}-\boldsymbol{W}\right)+2 \beta \boldsymbol{D} \boldsymbol{Q} \boldsymbol{W}-\mu \boldsymbol{P} \boldsymbol{K}^{\mathrm{T}}+ \\ \mu \boldsymbol{P} \boldsymbol{P}^{\mathrm{T}} \boldsymbol{W}-u \boldsymbol{P} \boldsymbol{Y}^{\mathrm{T}}+\boldsymbol{P} \boldsymbol{E}^{\mathrm{T}}=0 \end{gathered} $ | (16) |
从而有
| $ \begin{gathered} \boldsymbol{W}=\left[2 \alpha\left(\boldsymbol{I}_{d d}-1_{d d}\right)+\right. \\ \left.2 \beta \boldsymbol{D} \boldsymbol{Q}+\mu \boldsymbol{P} \boldsymbol{P}^{\mathrm{T}}\right]^{-1} \boldsymbol{P}\left(\mu \boldsymbol{K}^{\mathrm{T}}+\mu \boldsymbol{Y}^{\mathrm{T}}-\boldsymbol{E}^{\mathrm{T}}\right) \end{gathered} $ | (17) |
式(14)相对于K的最小化表示为
| $ \min\limits_{\boldsymbol{K}}\|\boldsymbol{K}\|_{2, 1}+(\mu / 2)\|\boldsymbol{K}-\boldsymbol{J}\|_{\mathrm{F}}^2 $ | (18) |
式中J=WTP-Y+E/μ。关于K的优化与关于W的优化相同。因此可以快速得到:
| $ \begin{gathered} 2 \boldsymbol{M} \boldsymbol{K}+\mu \boldsymbol{K}-\mu \boldsymbol{J}=0 \\ \Rightarrow \boldsymbol{K}=(2 \boldsymbol{M}+\mu \boldsymbol{I})^{-1} \mu \boldsymbol{J} \end{gathered} $ | (19) |
式中M是一个对角矩阵且对角元素为Mii=
在更新其他变量后,根据ADMN的规则和文献[10]更新拉格朗日乘数E和惩罚参数μ,即:
| $ \boldsymbol{E}=\boldsymbol{E}+\mu\left(\boldsymbol{K}-\boldsymbol{W}^{\mathrm{T}} \boldsymbol{P}+\boldsymbol{Y}\right) $ | (20) |
| $ \mu=\min \left(\rho \mu, \mu_{\max }\right) $ | (21) |
式中:ρ是收敛条件控制参数; μmax是最大惩罚参数,通常设置为106。
使用ADMN方法求解式(14)满足一般条件的收敛定理[14]。在优化RSLDS的目标函数时,最耗时的操作是计算矩阵W,时间复杂度为O(cmn)。RSLDS标准化过程的伪代码见算法1。
算法1: PSLDS
输入: 一组经过训练的基分类器C={ci(x)}i=1m; 验证集数据V={(xi, xj)}i=1n; 测试集数据T={(xi, xj)}i=1n; 选择基分类器的数量k
输出: k个基分类器,集成剪枝的准确率
1.初始化: W∈Rm×c, K∈Rc×n, D∈Rm×m, M∈Rc×c, E∈Rc×n, parameters: α, β, ρ, μ
2.使用式(1)生成验证集预测标签矩阵P∈Rm×n
3.生成验证集热编码标签矩阵Y∈Rc×n
4.使用
5.重复
6.K←(2M+μI)-1μ(WTP-Y+E/μ)
7.E←E+μ(K-WTP+Y)
8. μ←min (ρμ, μmax)
9.W←[2α(Imm-1mm)+2βDQ+μPPT]-1P(μKT+μYT-ET)
10. 检查收敛条件‖WTP-Y-E‖∞≤ε
11.直到收敛
12.通过计算‖Wi·‖2并按降序对所有基本分类器进行排序,选择排名前k个基本分类器在测试集中使用多数投票进行集成
由于本文主要研究基分类器的选择,因此分类器融合策略采用大多数投票方法。多数投票的过程可以表示如下:
| $ C_i=\arg \max\limits_e \sum\limits_{j=1}^k \varphi\left(c_j\left(x_i\right)=e\right) $ | (22) |
式中e=1, 2, …, 7;如果基分类器j对样本实例i的预测标签cj(xi)等于e, 则φ(·)=1, 否则, φ(·)=0。
为了更加清晰地展示集成剪枝在现实中是如何进行人脸情感识别,本文使用一个例子来进行说明。首先,在通用人脸情感数据集训练基分类器模型; 然后,使用RSLDS选择最优能力的基分类器子集; 其次,使用摄像头采集人物图片,再使用OpenCV等工具识别出相关人脸区域; 最后,基分类器子集对人脸图片进行情感识别,并使用多数投票对多个模型的预测进行集成从而得到最终预测的情感分类。当基分类器子集的大多数模型都预测错误时,就会导致最终集成的预测出现误差,因此可以使用识别能力更好的基分类器组建分类器池从而提高最终的分类性能。
2 实验结果和分析 2.1 实验环境与数据集本文所有实验均在Windows 10专业版下完成,电脑处理器为11th Gen Intel(R) Core(TM) i7-11800H@2.30 GHz 2.30 GHz,运行内存大小为16 GB,显卡为NVIDA GeForce RTX 3060 Laptop GPU,本文使用TensorFlow-GPU2.5完成神经网络的搭建,相关软件为Anaconda3.2、PyCharm2021.3和Matlab R2022b。
本文使用4个真实的人脸情感数据集进行实验,分别是FER2013[15]、JAFFE[3]、CK+[16]和KDEF[17]。本文使用Opencv工具识别图片中的人脸区域,并将其裁剪缩放为48×48,所有数据集的情感类别统一为7类,每种情感的详细信息见表 2。
| 表 2 上述4个数据集中每种情感的详细信息 Tab. 2 Detailed information of each emotion in four datasets |
FER2013数据集可分为训练集、验证集和测试集3个部分。本文使用训练集训练231个卷积神经网络基分类器,然后使用RSLDS方法在验证集中选择合适的基分类器子集,最后在测试集、JAFFE、CK+和KDEF上测试基分类器子集的效果。
本文使用准确率(Accuracy, Acc)和分类器子集的数量作为评价指标,其中,准确率Acc的计算公式为
| $ A_{\mathrm{cc}}=\left(\frac{1}{n} \sum\limits_{l=1}^n \frac{N_{\text {Correct }}}{N_{\text {All }}}\right) $ | (23) |
式中NCorrect和NAll分别表示为集成后正确预测样本实例和所有样本实例的数量。
2.3 参数敏感性分析和选择本文的方法需要2个正则化参数α和β,以及2个ADMN方法的参数ρ和μ。α控制矩阵W的稀疏性。理论上,α越大,强调W的稀疏性越大,而β控制冗余分类器数量的减少程度,较大的β强调更多冗余分类器的消除。
在选择α和β的最优参数时,根据文献[10]分别将ρ和μ的值临时设置为0.001和1.2。首先,本文通过网格搜索策略从{10-6, 10-5, …, 105, 106} 中选择参数α和β。RSLDS方法在不同α和β下的准确率见图 3,对于αβ不同数据集,分别选择最高准确率对应的α和β为最终参数。可以发现,相比于α,本文方法对β更加敏感,这说明考虑分类器之间的冗余是正确的。在α和β的值确定之后,再使用网格搜索的方法确定ρ和μ得最优参数,ρ的值范围为{10-5, 10-4, …, 1},μ的值范围为{0.2, 0.4, …, 1.8, 2}。RSLDS方法在不同ρ和μ下的准确率见图 4,同样选择最高准确率对应的参数为最终参数。

|
图 3 本文算法对参数α和β的敏感性分析 Fig. 3 Sensitivity analysis of parameters α and β in proposed algorithm |

|
图 4 本文算法对参数ρ和μ的敏感性分析 Fig. 4 Sensitivity analysis of paramaters ρ and μ in proposed algorithm |
参数确定之后,在上述最优参数下获得本文后续的所有实验结果。集成剪枝前后,基分类器子集的准确率分布情况见图 5。图形越宽表示在当前区间分别的基分类器数量越多,图形越长表示基分类器分布范围越广,结果表明,剪枝后,图形都变得短而小,这表明大多数冗余和弱分类器在集成修剪后被成功去除。

|
图 5 集成剪枝前后的基分类器分布 Fig. 5 Base classifier distribution before and after ensemble pruning |
为了分析不同改进点对集成剪枝性能的影响,以式(3)为基础方法,在此基础上分别考虑各个改进点的作用,式(3)考虑鲁棒性的表达式为
| $ \min\limits_{\boldsymbol{W}}\left\|\boldsymbol{W}^{\mathrm{T}} \boldsymbol{P}-\boldsymbol{Y}\right\|_{2, 1}+\alpha\|\boldsymbol{W}\|_{2, 1} $ | (25) |
式(3)考虑内积正则化项的表达式为
| $ \min\limits_{\boldsymbol{W}}\left\|\boldsymbol{W}^{\mathrm{T}} \boldsymbol{P}-\boldsymbol{Y}\right\|_{\mathrm{F}}^2+\alpha\left(\left\|\boldsymbol{W} \boldsymbol{W}^{\mathrm{T}}\right\|_1-\|\boldsymbol{W}\|_{\mathrm{F}}^2\right) $ | (26) |
式(3)考虑依赖分数的表达式为
| $ \min\limits_{\boldsymbol{W}}\left\|\boldsymbol{W}^{\mathrm{T}} \boldsymbol{P}-\boldsymbol{Y}\right\|_{\mathrm{F}}^2+\alpha\|\boldsymbol{W}\|_{2, 1}+\beta \operatorname{Tr}\left(\boldsymbol{W}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{Q} \boldsymbol{W}\right) $ | (27) |
式(3)考虑鲁棒性和式(3)的内积正则化项的表达式为
| $ \min\limits_{\boldsymbol{W}}\left\|\boldsymbol{W}^{\mathrm{T}} \boldsymbol{P}-\boldsymbol{Y}\right\|_{2, 1}+\alpha\left(\left\|\boldsymbol{W} \boldsymbol{W}^{\mathrm{T}}\right\|_1-\|\boldsymbol{W}\|_{\mathrm{F}}^2\right) $ | (28) |
式(3)考虑鲁棒性和式(3)考虑依赖分数的表达式为
| $ \min\limits_{\boldsymbol{W}}\left\|\boldsymbol{W}^{\mathrm{T}} \boldsymbol{P}-\boldsymbol{Y}\right\|_{2.1}+\alpha\|\boldsymbol{W}\|_{2, 1}+\beta \operatorname{Tr}\left(\boldsymbol{W}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{Q} \boldsymbol{W}\right) $ | (29) |
式(3)的内积正则化项和式(3)考虑依赖分数的表达式为
| $ \begin{gathered} \min\limits_{\boldsymbol{W}}\left\|\boldsymbol{W}^{\mathrm{T}} \boldsymbol{P}-\boldsymbol{Y}\right\|_{\mathrm{F}}^2+\alpha\left(\left\|\boldsymbol{W} \boldsymbol{W}^{\mathrm{T}}\right\|_1-\|\boldsymbol{W}\|_{\mathrm{F}}^2\right)+ \\ \beta \operatorname{Tr}\left(\boldsymbol{W}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{Q} \boldsymbol{W}\right) \end{gathered} $ | (30) |
考虑了各个改进点的效果见表 3,打勾表示考虑了对应的改进点,鲁棒性的选择降低了错误预测值对基分类器选择的影响。因此,考虑鲁棒性的改进点取得的效果优于考虑内积正则化项和依赖分数。在鲁棒性选择的基础上,将内积正则化项和依赖分数也进行考虑,即保证了鲁棒性的进行基分类器选择,又迫使基分类器子集数量小且低冗余,从而保证选择优质且低冗余的基分类器。
| 表 3 考虑不同模块的准确率对比 Tab. 3 Comparison of accuracy considering different modules |
将RSLDS在4个数据集上与常见的集成剪枝方法进行了比较,结果见表 4。表中的Baseline表示将所有分类器的预测结果直接用多数投票方法融合得出的结果。获得最佳性能的用粗体表示。从表中可以看出,RSLDS在4个数据上均取得最高的分类准确率,同时,RSLDS选择的基分类器子集数量也更少。这表明,考虑分类器依赖、内积正则化项和鲁棒性的集成剪枝方法不仅仅进一步降低了基分类器池所需的存储容量,而且还提升了模型的分类性能,取得了更好的效果。
| 表 4 将RSLDS与8种集成剪枝方法的准确率比较 Tab. 4 Comparison of accuracy between RSLDS and eight ensemble pruning methods |
本文使用临界距离(critical distance,CD)来分析RSLDS和其他方法之间的相对性能,CD的表达式为
| $ q_\alpha \sqrt{\frac{K(K+1)}{6 N}} $ | (31) |
集成剪枝算法的CD见图 6,横轴代表各种方法在4个数据集上的平均排名,粗红线表明其他对比方法与提出的RSLDS方法在性能上没有明显差异,否则认为其他对比方法与RSLDS有明显差异。观察图 6可以发现,本文提出的RSLDS在所有集成剪枝算法中,取得了最高的平均排序,这说明该方法在集成剪枝领域具有优越性。

|
图 6 集成剪枝算法的临界距离 Fig. 6 Critical distance of ensemble pruning algorithm |
为了选择识别效果更好和冗余度更低的基分类器子集,提高集成剪枝的泛化能力和准确率,提出了一种具有依赖分数的鲁棒性稀疏低冗余集成剪枝方法。首先,该方法使用l2, 1范数作为损失函数提高分类器子集的鲁棒性; 其次,使用互信息来衡量不同基分类器之间的依赖关系并使用熵来评估他们的优先级; 然后,考虑了内积正则化项确保选择的基分类器子集更稀疏; 最后,将基分类器之间的优先级依赖、l2, 1范数和内积正则化项整合到一个基于回归的目标方程中,同时考虑多样性和准确率之间的平衡,实现冗余分类器和弱分类器的修剪。为了验证提出的RSLDS方法的有效性和鲁棒性,在4个公共人脸情感数据集上进行了实验,结果表明,提出的方法不仅有效的提高人脸情感识别的准确率,而且进一步降低了集成模型的运行时间和存储空间。
| [1] |
GUO Yifei, HUANG Jian, XIONG Mingfu, et al. Facial expressions recognition with multi-region divided attention networks for smart education cloud applications[J]. Neurocomputing, 2022, 493: 119. DOI:10.1016/j.neucom.2022.04.052 |
| [2] |
LI Yunkai, MENG Qinghao, WANG Yaxin, et al. MMFN: emotion recognition by fusing touch gesture and facial expression information[J]. Expert Systems with Applications, 2023, 228: 120469. DOI:10.1016/j.eswa.2023.120469 |
| [3] |
LI Danyang, WEN Guihua, LI Xu, et al. Graph-based dynamic ensemble pruning for facial expression recognition[J]. Applied Intelligence, 2019, 49(9): 3188. DOI:10.1007/s10489-019-01435-2 |
| [4] |
HUANG Shisong, LI Danyang, ZHANG Zhuhong, et al. CSLSEP: an ensemble pruning algorithm based on clustering soft label and sorting for facial expression recognition[J]. Multimedia Systems, 2023, 29: 1463. DOI:10.1007/s00530-023-01062-5 |
| [5] |
金志刚, 韩玥, 朱琦. 一种结合深度学习和集成学习的情感分析模型[J]. 哈尔滨工业大学学报, 2018, 50(11): 32. JIN Zhigang, HAN Yue, ZHU Qi. A sentiment analysis model with the combination of deep learning and ensemble learning[J]. Journal of Harbin Institute of Technology, 2018, 50(11): 32. DOI:10.11918/j.issn.0367-6234.201709078 |
| [6] |
ZHANG Chunxia, ZHANG Jiangshe, YIN Qingyan. A ranking-based strategy to prune variable selection ensembles[J]. Knowledge-Based Systems, 2017, 125: 13. DOI:10.1016/j.knosys.2017.03.031 |
| [7] |
WANG Zhenlei, ZHAO Suyun, LI Zheng, et al. Ensemble selection with joint spectral clustering and structural sparsity[J]. Pattern Recognition, 2021, 119(11): 108061. DOI:10.1016/j.patcog.2021.108061 |
| [8] |
DAI Qun, YE Rui, LIU Zhuan. Considering diversity and accuracy simultaneously for ensemble pruning[J]. Applied Soft Computing, 2017, 58(9): 75. DOI:10.1016/j.asoc.2017.04.058 |
| [9] |
MING D, DING C. Robust flexible feature selection via exclusive L21 regularization[C]//Proceedings of the 28th International Joint Conference on Artificial Intelligence. Macao: AAAI Press, 2019: 3158. DOI: 10.24963/ijcai.2019/438
|
| [10] |
DU Shiqiang, MA Yide, LI Shouliang, et al. Robust unsupervised feature selection via matrix factorization[J]. Neurocomputing, 2017, 241: 115. DOI:10.1016/j.neucom.2017.02.034 |
| [11] |
LIM H, KIM D W. Pairwise dependence-based unsupervised feature selection[J]. Pattern Recognition, 2021, 111: 107663. DOI:10.1016/j.patcog.2020.107663 |
| [12] |
LI Yonghao, HU Liang, GAO Wanfu. Robust sparse and low-redundancy multi-label feature selection with dynamic local and global structure preservation[J]. Pattern Recognition, 2023, 134: 109120. DOI:10.1016/j.patcog.2022.109120 |
| [13] |
SUN Zhengya, HAN Jiuqi, HAO Hongwei. Selecting feature subset with sparsity and low redundancy for unsupervised learning[J]. Knowledge-Based Systems, 2015, 86(9): 210. DOI:10.1016/j.knosys.2015.06.008 |
| [14] |
AFONSO M V, BIOUCAS-DIAS J M, FIGUEIREDO M A T. An augmented Lagrangian approach to the constrained optimization formulation of imaging inverse problems[J]. IEEE Transactions on Image Processing, 2011, 20(3): 681. DOI:10.1109/TIP.2010.2076294 |
| [15] |
GOODFELLOW L J, DUMITRU E, CARRIER P L, et al. Challenges in representation learning: a report on three machine learning contests[J]. Neural Networks, 2015, 64: 59. DOI:10.1016/j.neunet.2014.09.005 |
| [16] |
LUCEY P, COHN J F, KANADE T, et al. The extended Cohn-Kanade dataset (ck+): a complete dataset for action unit and emotion-specified expression[C]//2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition-Workshops. San Francisco, IEEE, 2010: 94. DOI: 10.1109/CVPRW.2010.5543262
|
| [17] |
GOELEVEN E, DE R R, LEYMAN L, et al. The Karolinska directed emotional faces: a validation study[J]. Cognition and Emotion, 2008, 22(6): 1094. DOI:10.1080/02699930701626582 |
| [18] |
LI Nan, YU Yang, ZHOU Zhihua. Diversity regularized ensemble pruning[C]//Machine Learning and Knowledge Discovery in Databases. Berlin, Heidelberg: Springer Berlin Heidelberg, 2012: 330. DOI: 10.1007/978-3-642-33460-3_27
|
| [19] |
LI Danyang, WEN Guihua, HOU Zhi, et al. RTCRelief-F: an effective clustering and ordering-based ensemble pruning algorithm for facial expression recognition[J]. Knowledge and Information Systems, 2019, 59(1): 219. DOI:10.1007/s10115-018-1176-z |
| [20] |
DAI Q. A novel ensemble pruning algorithm based on randomized greedy selective strategy and ballot[J]. Neurocomputing, 2013, 122(122): 258. DOI:10.1016/j.neucom.2013.06.026 |
| [21] |
MARTÍNEZ-MUÑOZ G, SUÁREZ A. Pruning in ordered bagging ensembles[C]//Proceedings of the 23rd International Conference on Machine Learning. Pittsburgh: Association for Computing Machinery, 2006: 609. DOI: 10.1145/1143844.1143921
|
 2024, Vol. 56
2024, Vol. 56


