2. 中国建筑科学研究院有限公司,北京 100013;
3. 太原科技大学 应用科学学院,太原 030024
2. China Academy of Building Research, Beijing 100013, China;
3. School of Applied Science, Taiyuan University of Science and Technology, Taiyuan 030024, China
高层建筑是现代城市风灾的主要承灾载体,相对于主体承重结构,高层建筑围护结构(尤其是玻璃幕墙)往往更容易在风灾中发生破坏[1-2]。早在20世纪70年代,研究者们即基于Lubbock风暴的调查结果,指出应重视飞掷物对高层建筑窗户的不利影响[3];在飓风Alicia、Hugo和Andrew的灾后综合研究报告,也明确指出多数幕墙破坏是由飞掷物冲击造成[4-7]。中国东南沿海是台风通过高频区,也是经济发达的城市密集区[8],台风York(1999)、超强台风“莫兰蒂”(2016)、强台风“天鸽”(2017)等均导致登陆城市大量幕墙受飞掷物冲击破坏[9-11]。
飞掷物的冲击破坏问题涉及较多影响因素,比如:流场特征、不同形式的冲击物在风场中的飞行轨迹,以及冲击破坏能力等;而飞掷物飞行轨迹的确定,是开展飞掷物风灾易损性研究的基础[1, 12]。20世纪80年代,研究者们进行了大量富有成效的理论与试验研究,通过系统的碎片基础性试验研究,有针对性地测量了不同形状碎片的气动力系数,建立了考虑马格努斯效应的板状碎片定常气动力模型[13-16],但研究中没有考虑来流湍流及流场三维特性的影响,未分析碎片的三维轨迹等。21世纪初,国外研究者们开始考虑湍流的影响[17],在风洞中进行了不同形式飞掷物的轨迹试验,并设计了低矮房屋周边的飞掷物模拟试验[18-20]。国内在这方面的研究虽起步较晚,但由于近几年风致碎片导致的破坏问题越来越突出,相关理论分析和数值模拟研究工作也陆续开展[21-24]。总体上,目前国内外学者的相关研究主要围绕低矮房屋的飞掷物运动破坏问题,研究对象主要是片状飞掷物;实际上,城市飞掷物类型更具多样性,钢化玻璃碎粒、景观砂砾等粒状物是导致大量幕墙破坏的主要碎片类型[5];此外,在流场影响方面,城市高层建筑群相互干扰效应导致周围流场更为复杂,飞掷物在其中的飞行轨迹与二维流场结果存在显著差异。
针对上述问题,本文基于Fluent软件平台,结合某实际高层建筑群风灾案例,通过大涡模拟方法获取建筑群周围的非定常三维绕流场,采用确定性方法分析颗粒飞掷物的三维运动轨迹。
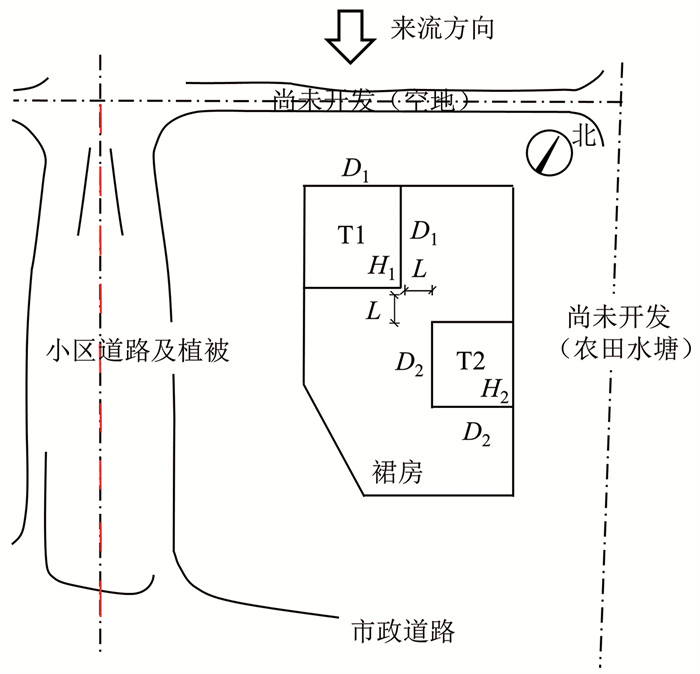
1 研究对象概况某塔楼群由两栋方形截面塔楼和裙房组成,如图 1所示,两塔楼的宽度和高度分别为D1×H1=45.6 m×116.2 m和D2×H2=35.4 m×89.2 m,两塔楼的水平间距L=14.4 m,裙房高度H3=23.5 m。该塔楼群距离台风“莫兰蒂”登陆路径的垂直距离约7 km,登陆期间最大地面观测风速的风向为NNW[10],与该双塔楼立面朝向基本一致,图 1给出了相应的来流方向。
|
图 1 塔楼群布置 Fig. 1 Layout of a high-rise building group |
根据灾害现场统计,本案例在最大地面观测风速NNW风向下(图 1所示来流方向),T2塔楼迎风面玻璃破碎率超过70%,在所有立面中破坏最严重,经初步评估,飞掷物的冲击破坏是导致大面积玻璃损坏的主要原因[10]。由于两楼群周边为空旷场所,其周边高处产生碎片的可能性较低,因此,本研究中主要考虑在台风登陆产生最大风速的NNW风向(图 1所示),处于上游位置的T1塔楼局部钢化玻璃碎粒产生的飞掷物颗粒,对T2塔楼迎风面玻璃幕墙的影响。
2 数值模拟方法及参数设置 2.1 飞掷物风场模拟为研究流场对飞掷物运动轨迹的影响,本文考虑了4类流场类型:1)理想均匀流,即不考虑来流湍流度和平均风剖面;2)绕流场,即以图 1所示塔楼群为对象,进行紊流边界层风场内的三维非定常绕流大涡模拟(large eddy simulation, LES)计算得到;3)三维湍流场,即不考虑建筑影响的三维自由来流湍流场,为确保流场对飞掷物飞行轨迹影响结果的可比性,该工况的风速场来自第2类流场的建筑群三维非定常绕流大涡模拟的计算域入口处记录的脉动风速值;4)三维平均风场,即仅考虑第3类流场的平均风速剖面,不考虑湍流。表 1给出了上述4类流场的主要参数特征。
| 表 1 流场类型 Tab. 1 Flow field types |
非定常绕流大涡模拟中,空气可视为粘性不可压缩流体,对瞬态的Navier-Stokes(N-S)方程进行空间平均,可得大涡模拟方法的控制方程为[25]
| $ \frac{\partial \bar{u}_i}{\partial x_i}=0 $ | (1) |
| $ \frac{\partial \bar{u}_i}{\partial t}+\frac{\partial}{\partial x_j}\left(\bar{u}_i \bar{u}_j\right)=-\frac{1}{\rho} \frac{\partial \bar{p}}{\partial x_i}+\nu \frac{\partial^2 \bar{u}_i}{\partial x_j \partial x_j}-\frac{\partial \tau_{i j}}{\partial x_j} $ | (2) |
式中:ρ为空气密度,ν为空气运动粘性系数,ui、uj表示空间平均滤波后的速度,xi、xj为空间坐标分量,(i,j=1, 2, 3)分别代表水平x、y轴和竖向z轴分量,p为空间平均滤波后的压力,τij为N-S方程空间平均后出现的不封闭项——亚格子应力,需要建立模型来使方程组封闭。
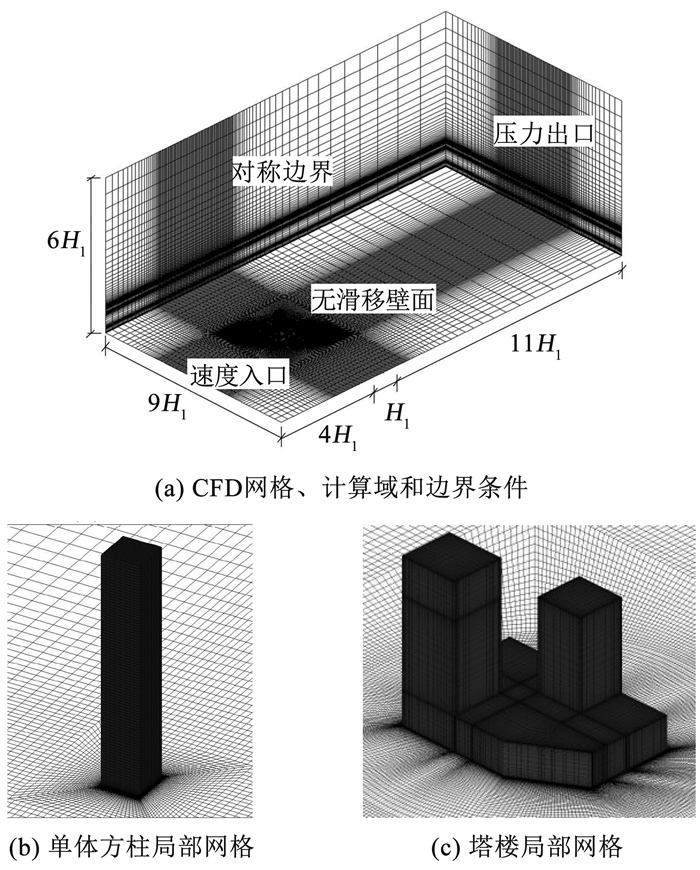
本文首先对宽高比为1∶ 1∶ 6方形截面的单体建筑进行大涡模拟,并将数值模拟结果与风洞试验进行对比,以验证大涡模拟方法及参数设置的准确性。单体建筑数值模拟中,模型缩尺比为1∶ 500,缩尺模型高度H=0.6 m;为保证阻塞率不大于3%,以及绕流后的流场充分发展,计算域大小取为:16H(流向y)×9H(展向x)×6H(竖向z);采用区域分块非均匀结构化网格离散计算域,近壁面处网格加密,远离壁面处采用稀疏网格,边界条件设置及局部网格划分如图 2(a)、(b)所示,采用2种网格划分方案以考察网格分辨率的影响,详细参数见表 2。
|
图 2 CFD网格和计算域示意 Fig. 2 CFD meshes and computational domain |
| 表 2 网格分辨率 Tab. 2 Grid resolution |
塔楼群大涡模拟中计算域大小设置为16H1(流向y)×9H1(展向x)×6H1(竖向z),采用与单体建筑相同缩尺比以及网格划分方案,最小网格尺度与单体建筑Mesh-1网格相同(下文分析中解释),对应近壁面第一层网格无量纲距离y+<5.0;网格总数592万,边界条件设置及网格划分如图 2(a)、(c)所示。
采用速度入口边界条件,大涡模拟入流脉动的合成采用基于大气边界层自保持边界条件的改进的涡合成法[26]。出流面采用压力出口边界条件;两侧面和顶面采用对称边界条件,等价于自由滑移的壁面;计算域底面和研究对象表面采用无滑移壁面。压力速度的耦合采用SIMPLEC算法,动量方程采用Bounded Central Differencing离散格式,时间离散为二阶全隐格式,时间步长0.000 5 s,模拟总时长10.0 s,其中后9.5 s用于记录风速和风压统计计算。亚格子模型采用Dynamic Smagorinsky动态亚格子模型[27-28],该模型可更好地考虑钝体周围的流场的冲撞、分离、自由剪切层、涡脱落等现象。
2.2 飞掷物运动轨迹计算飞掷物在风场中的飞行轨迹,一般将受到升力、阻力、升力矩等气动力的影响,而对于颗粒飞掷物可仅考虑阻力的影响[13-16],即
| $ F_{\mathrm{D}}=\frac{1}{2} \rho\left(\sqrt{\sum\limits_i\left(u_i-v_i\right)^2}\right)^2 C_{\mathrm{D}} A $ | (3) |
式中:ui、vi分别表示飞掷物所在非定常风场的瞬时风速、飞掷物飞行速度; 下标(i=1, 2, 3)表示沿水平向x、y轴和竖向z轴的分量,均为随时间和位置变化的变量,其中非定常风场的瞬时风速ui分别考虑飞掷物风场模拟的4种流场情况;
采用牛顿第二定律,对颗粒飞掷物在3个坐标方向可建立三维非定常风场中的运动方程,整理后如下所示:
| $ \frac{\mathrm{d}^2 x_i}{\mathrm{~d} t^2}=C\left(u_i-v_i\right) \sqrt{\sum\limits_i\left(u_i-v_i\right)^2}-g_i $ | (4) |
式中:t为时间; xi为飞掷物的空间坐标位置; gi为加速度分量,这里仅考虑竖向加速度分量,即水平分量g1=g2=0,竖向分量g3=g(其中g为重力加速度); C表示颗粒的气动力参数与质量参数之比,即:
| $ C=\frac{\rho C_{\mathrm{D}} A}{2 m} $ | (5) |
式中m是飞掷物颗粒质量。飞掷物运动轨迹方程(4)的求解采用五阶Runge-Kutta法。需要说明的是,参数C主要考虑颗粒物固有特性的相对关系,与无量纲化系数Tachikawa数(K数)[13-16]存在对应关系
| $ K=\frac{\rho U^2 A}{2 m g}=\frac{U^2}{g C_{\mathrm{D}}} C $ | (6) |
为说明本文大涡模拟非定常风场的可靠性,首先将宽高比1∶ 6方形截面单体建筑大涡模拟结果与文献风洞试验[29]结果进行了对比。
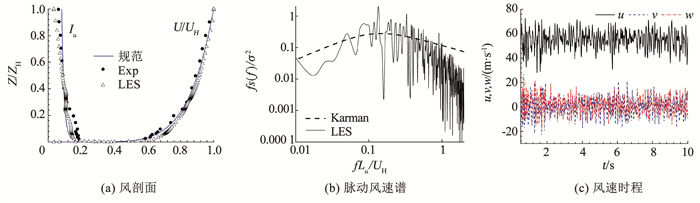
图 3为大涡模拟所得B类风场与风洞试验[29]结果的比较,图中“LES”、“Exp”和“规范”分别表示本文大涡模拟结果、文献风洞试验[29]和《建筑结构荷载规范(GB 50009—2012)》[30]建议风剖面;大涡模拟风场结果来自于空计算域(其网格由图 2中建筑模型位置采用网格填充所得)中拟放置建筑模型位置处,脉动风速谱选取该位置处距离地面H高度处监测点,UH为单体建筑高度H处的来流平均风速。由图 3可见,大涡模拟所得平均风剖面与试验[29]和规范值[30]具有较好的一致性;湍流度剖面与试验[29]剖面也能较好吻合,二者均在近地面处高于规范值;大涡模拟所得脉动风速谱也基本能够反映Karman谱的分布情况,模拟风速谱在无量纲频率超过1.0后的高频处产生了一定衰减,这是由于大涡模拟离散网格的滤波效应所致。
|
图 3 大涡模拟三维自由来流湍流场 Fig. 3 Large eddy simulation of three-dimensional free-stream turbulence |
图 4为单体建筑2/3H高度表面风压系数与试验结果[31]对比,图中风压系数采用模型高度H处来流平均风速UH无量纲化,风压系数均值Cp, mean和根方差值Cp, rms分别表示测点平均与脉动风压系数。

|
图 4 单体建筑风压系数结果对比 Fig. 4 Comparison of wind pressure coefficient of single building |
由图 4可见,Mesh-1和Mesh-2两种网格划分下,大涡模拟结果所得结构表面平均和脉动风压分布与试验结果具有较好一致性;在数值上,两种工况均与试验吻合较好,进一步加密网格Mesh-2工况在模拟精度方面并未明显改善。可见,本文大涡模拟方法及参数设置能够较好地预测结构周围的三维非定常绕流风场。
3.2 塔楼群大涡模拟结果分析综合考虑计算精度和计算效率,塔楼群的大涡模拟计算选取上述单体建筑Mesh-1网格划分方案;来流风向为最大地面观测风速的NNW风向(图 1)。
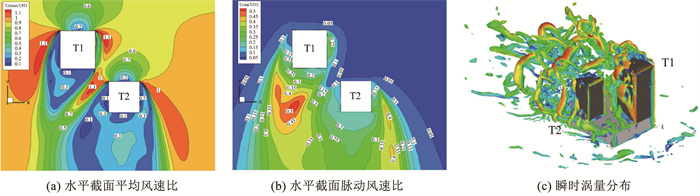
为说明塔楼间三维非定常流动的复杂性,图 5给出了塔楼群周围距地1/2H1高度水平截面的平均和脉动风速云图,以及瞬时涡量分布,图中Umean和Urms分别指平均和根方差风速值。由图 5可见,T1和T2塔楼两侧面流动分离区存在风速加速现象,在两塔楼中间位置也因“狭管效应”而引起了风速加速;两塔楼和底部裙房的顶部、侧面均存在不同尺度的瞬时分离涡,在流动分离后在塔楼群周围及尾流区相互混合掺杂,使得塔楼群周围流动情况分布复杂。可见,塔楼群周围的绕流场具有非常明显的三维特性和非定常特性,预计将对塔楼群周围颗粒飞掷物的运动轨迹产生影响。
|
图 5 塔楼群周围非定常风速场 Fig. 5 Unsteady wind velocity field around tower buildings |
图 6为大涡模拟所得T1塔楼迎风面和侧面的风压系数,并结合瞬时风压时序分析其偏度与峰度分布,图中风压系数均采用塔楼距地10 m高度处来流平均风速无量纲化,偏度(S)与峰度(K)分别为测点风压系数时程的三阶矩和四阶矩[32]。总体来看,塔楼T1迎风面整体均为正压力作用,侧面和顶面为风吸力,其中侧面流动分离现象较为剧烈(图 5),风吸力显著。具体来看,T1塔楼左侧面边角局部区域(黑圈所示位置处)瞬时压力较不利,其风压系数偏度和峰度值分别可达-0.84和4.89(图 6(c)、6(d)),按照文献[32]建议将|S|>0.5且|K|>3.5作为脉动风压非高斯区域的划分标准来判断,则该区域脉动风压具有非高斯特性。

|
图 6 塔楼T1风压系数与偏度和峰度分布 Fig. 6 Wind pressure coefficient and skewness and kurtosis distribution of Tower T1 |
在上述风压非高斯性区域,选择局部区域监测点P0和P1(距离地面高度分别为110 m和100 m),从统计角度分析对于工程设计有意义的极值风压峰值因子和极值风压系数,并以区域监测点结果作为代表值,按照规范方法得到玻璃表面最大应力设计值,结果见表 3。表中Cp, ext为极值风压系数[33-34],q为风荷载组合设计值(此处仅考虑风荷载单工况),σ为截面最大应力设计值,具体计算公式分别如下:
| $ q=\frac{1}{2} \rho U_{\mathrm{r}}^2 C_{p, \mathrm{ext}} \times 1.4 $ | (7) |
| $ \sigma=\frac{6 m_0 q a^2}{t^2} \eta $ | (8) |
| 表 3 监测点参数计算结果 Tab. 3 Parameter calculation results of monitoring points |
式中:Ur为10 m高度来流平均风速,取40 m/s; 可变荷载分项系数取为1.4;η和m0分别为玻璃幕墙折减系数和弯矩系数,按照《玻璃幕墙工程技术规范(JGJ 102—2003)》[35],分别取为0.525 3和0.044 2;a和t分别为幕墙分隔边长和幕墙玻璃厚度,按照工程情况分别为1.5 m和5 mm。
由表 3可见,P0和P1两监测点位置的幕墙表面最大应力设计值σ在90 N/mm2以上。按照规范[35]查阅5 mm厚钢化玻璃幕墙的容许应力设计值fg=84 N/mm2,显然σ>fg,这说明该区域幕墙抗风安全储备不足,是风毁破坏风险点。
3.3 与飞掷物轨迹试验结果对比钢化玻璃破碎后将产生离散碎片,《建筑用安全玻璃第2部分:钢化玻璃》(GB 15763.2—2005)对碎片有严格限定:在任何50 mm×50 mm区域内的最少碎片数在40个以上,允许有少许长条形碎片,但其长度不超过75 mm[36]。从这一规定来看,作为常用的安全破璃,钢化玻璃破碎后不允许产生棱角特别突出的碎片,且要求均匀度较好,基本形状是介于规则正方体与球状之间的颗粒状。
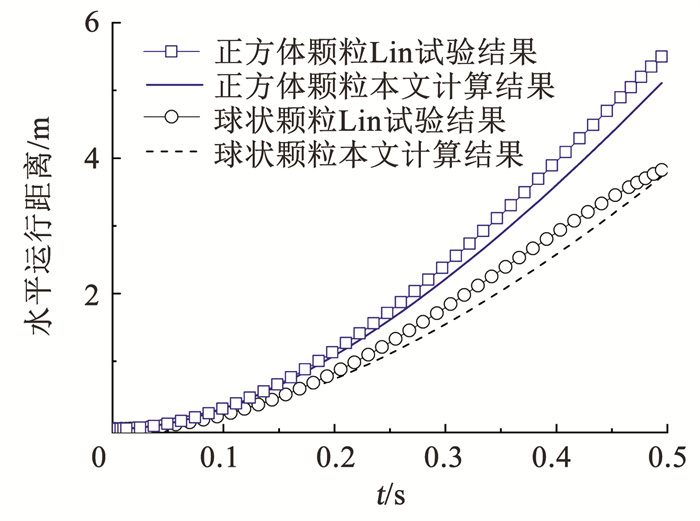
文献[19]在风洞中测量了典型颗粒状飞掷物在均匀流场中的轨迹。为验证本文分析方法的可靠性,现参考其试验基本参数(来流平均风速U=40 m/s,球状和正方体颗粒飞掷物阻力系数分别取CD=0.5和0.8,K数8.0),按照风掷物运动轨迹计算方法模拟飞行轨迹,并与文献[19]试验结果进行对比,比较结果见图 7。
|
图 7 颗粒飞掷物飞行轨迹计算值与试验结果的对比 Fig. 7 Comparison between calculated trajectory of wind-borne debris and experimental results |
由图 7可见,随着时间的增加,两种颗粒的飞行轨迹均呈现非线性增加现象。本文计算结果与试验结果(图 7中“Lin试验”)能够较好地吻合,只是在飞行距离上略低于试验值,其中球状颗粒和正方体颗粒在两种结果下最大误差分别为13.78%、8.9%。本文计算结果与试验结果的一致性在一定程度上说明了本文运动轨迹计算方法的可靠性。
3.4 塔楼群幕墙碎粒飞掷物轨迹研究从塔楼群大涡模拟结果知,气流遇到建筑物后发生冲撞、分离等复杂流动现象(三维非定常绕流场),流场的时空分布与实验室模拟的理想均匀流场或规范研究中采用的特定大气边界层风场(三维自由来流湍流场)等,存在显著的区别。
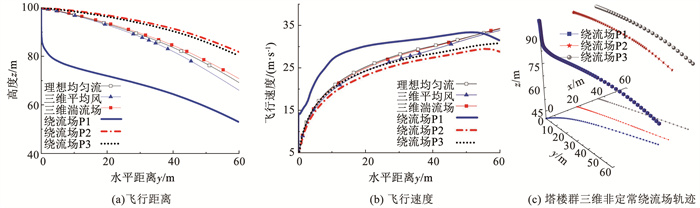
为评估流场差异对颗粒物飞行轨迹的影响,本节固定颗粒飞掷物的K数为8.0,入流10 m高度处平均风速值U10=40 m/s,在T2塔楼迎风面前端水平距离60 m、离地高度100 m范围内释放颗粒物,以接触至塔群墙面或裙房顶面为截止模拟时刻,对比不同流场条件颗粒全过程飞行轨迹及最终飞行速度。图 8和图 9为相应的对比结果,主要考虑了前述4种流场条件:理想均匀流场、基于大涡模拟所得三维自由湍流场(图中“三维湍流场”)、三维自由平均风速场(图中“三维平均风”),以及塔楼群三维非定常绕流场(图中“绕流场”)。具体对比了3个典型释放点(P1、P2和P3)结果,其中P1为前文T1塔楼玻璃幕墙的风致破碎风险点,P2和P3为对比工况,目的在于说明在绕流场中颗粒物初始位置对飞掷物运动轨迹的影响。从图 8和图 9可以看出:

|
图 8 正方体颗粒在不同流场轨迹对比 Fig. 8 Comparison of trajectory of cubic particles in different flow fields |
|
图 9 球状颗粒在不同流场轨迹对比 Fig. 9 Comparison of trajectory of spherical particles in different flow fields |
1) 总体上,在相同的流场条件和释放位置情况下,当接触到T2迎风面时(y=60 m),球状颗粒(图 9)的下降高度略大于正方体颗粒(图 8)。在绕流场中,P1释放的正方体颗粒最终接触到T2迎风面的73 m高度处,比球状体高20.7 m。
2) 对比不同的流场结果来看,理想均匀流场与三维自由湍流场的模拟结果比较接近;对于三维自由来流湍流场,若忽略三维湍流成分时(图中“三维平均风”),颗粒的飞行速度降低,飞行总距离更长。在塔楼群三维非定常绕流场(即前述第2种流场)中,释放位置影响显著,当释放位置靠近上游干扰建筑侧面时(P1位置),颗粒物初始下落,随后向远离壁面方向偏转(图 8(c)、图 9(c)),到达下游建筑立面之前,飞行速度要大于其他2个释放位置结果。
3) P1释放点在三维绕流场中的飞行轨迹模拟结果对于飞掷物所致风灾模拟具有参考意义。从图中可看出,P1释放颗粒物运动表现为2个阶段。a)初始阶段,颗粒物刚脱离建筑近壁面,此时其飞行轨迹主要受重力控制,该阶段轨迹以竖直分量为主,阻力影响较小,飞行速度要大于其他工况(图 8(b)、图 9(b))。b) 第二阶段,颗粒物下降至一定高度后,受回流区水平风速分量的影响进入了T1塔楼的强分离流动区域,开始加速往下游飞行,此时其飞行轨迹主要受流场控制,水平运动分量为主,随后阻力与重力达到相对平衡状态,此时飞行速度变化缓慢,直至接触到T2立面。从这一规律可看出,在塔楼群玻璃幕墙的风致飞掷物破坏评估中,应考虑塔楼群周围三维非定常绕流的影响,理想均匀流或是三维湍流场中的模拟结果可能会错误估计颗粒物在建筑群中的撞击速度,并会误判建筑受飞掷物影响位置。
4 结论对比研究了不同风场中颗粒状飞掷物的运动轨迹,并结合某一实际案例进行了高层建筑群三维非定常绕流场下飞掷物轨迹模拟,主要结论如下:
1) 本文飞掷物运动轨迹计算方法结合大涡模拟获得的流场,能够有效地对飞掷物飞行轨迹进行预测。在保持颗粒释放位置相同的情况下,与三维自由来流场相比,理想均匀流场下颗粒的飞行距离及飞行速度较大;三维自由来流场忽略来流湍流成份时会使颗粒的飞行距离增大,飞行速度降低。
2) 理想均匀流和自由来流场得到的飞行轨迹与三维非定常绕流场结果相差较大;此外,在三维非定常绕流场中,不同初始位置下的颗粒物轨迹相差较大,并可能对于最终的评估结果产生显著影响。因此总体来看,风致飞掷物的飞行轨迹预测,应充分考虑建筑群三维非定常绕流场及可能的初始破坏位置的影响。
| [1] |
LARCHER M, SOLOMOS G, CASADEI F, et al. Experimental and numerical investigations of laminated glass subjected to blast loading[J]. International Journal of Impact Engineering, 2012, 39(1): 42. DOI:10.1016/j.ijimpeng.2011.09.006 |
| [2] |
王洪涛, 万成龙. 国家标准《建筑幕墙和门窗抗风携碎物冲击性能分级及检测方法》解读[J]. 工程质量, 2015, 33(1): 20. WANG Hongtao, WAN Chenglong. Interpretation the national standard of graduations and test method for performance of exterior windows and doors, curtain walls impacted by windborne debris in windstorm[J]. Construction Quality, 2015, 33(1): 20. DOI:10.3969/j.issn.1671-3702.2015.01.006 |
| [3] |
KAREEM A. Performance of cladding in Hurricane Alicia[J]. Journal of Structural Engineering, 1986, 112(12): 2679. DOI:10.1061/(ASCE)0733-9445(1986)112:12(2679) |
| [4] |
MINOR J E. Windborne debris and the building envelope[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1994, 53(1/2): 207. DOI:10.1016/0167-6105(94)90027-2 |
| [5] |
MINOR J E, ASCE F. Lessons learned from failures of the building envelope in windstorms[J]. Journal of Architectural Engineering, 2005, 11(1): 10. DOI: 10.1061(ASCE)1076-0431(2005)11:1(10)
|
| [6] |
POWELL M D, GEORGIOU P N. Response of the Allied Bank Plaza tower during Hurricane Alicia(1983)[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1987, 26(2): 231. DOI:10.1016/0167-6105(87)90046-8 |
| [7] |
SPARKS P R. Wind conditions in Hurricane Hugo and their effect on buildings in coastal South Carolina[J]. Journal of Coastal Research, 1991(8): 13. DOI:10.2307/25735404 |
| [8] |
欧进萍, 段忠东, 常亮. 中国东南沿海重点城市台风危险性分析[J]. 自然灾害学报, 2002(4): 9. OU Jinping, DUAN Zhongdong, CHANG Liang. Typhoon risk analysis for key coastal cities in southeast China[J]. Journal of Natural Disasters, 2002(4): 9. DOI:10.3969/j.issn.1004-4574.2002.04.002 |
| [9] |
LEE B E, WILLS J. Vulnerability of fully glazed high-rise buildings in tropical cyclones[J]. Journal of Architectural Engineering, 2002, 8(2): 42. DOI:10.1061/(ASCE)1076-0431(2002)8:2(42) |
| [10] |
唐意. 莫兰蒂台风城市风灾调查[R]. 北京: 中国建筑科学研究院, 2016 TANG Yi. Investigation of typhoon Moranti's urban wind disaster[R]. Beijing: China Academy of Building Research, 2016 |
| [11] |
杨立国, 唐意. 澳门黑沙环中街和东方明珠街交界街区高层楼宇风洞测压试验报告[R]. 北京: 中国建筑科学研究院, 2017 YANG Liguo, TANG Yi. Wind tunnel pressure test report on high-rise buildings at the junction of central street and oriental pearl street in Heisha, Macau[R]. Beijing: China Academy of Building Research, 2017 |
| [12] |
WILLS J, LEE B E, WYATT T A. A model of wind-borne debris damage[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(4): 555. DOI:10.1016/S0167-6105(01)00197-0 |
| [13] |
TACHIKAWA M. Trajectories and velocities of typhoon-generated missiles: part 1 aerodynamic characteristics of flat plates and equations of motion[J]. Transactions of the Architectural Institute of Japan, 1981, 302: 1. DOI:10.3130/aijsaxx.302.0_1 |
| [14] |
TACHIKAWA M, FUKUYAMA M, HARA H. Trajectories and velocities of typhoon-generated missiles: part 2 two-dimensional motion of flat plates in uniform flow[J]. Transactions of the Architectural Institute of Japan, 1982, 314: 17. DOI:10.3130/aijsaxx.314.0_17 |
| [15] |
TACHIKAWA M, HARA H. Trajectories and velocities of typhoon-generated missiles: part 3 aerodynamic characteristics of various missile shapes[J]. Transactions of the Architectural Institute of Japan, 1982, 319: 23. DOI:10.3130/aijsaxx.319.0_23 |
| [16] |
TACHIKAWA M. Trajectories of flat plates in uniform flow with application to wind-generated missiles[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1983, 14(1/2/3): 443. DOI:10.1016/0167-6105(83)90045-4 |
| [17] |
KORDI B, TRACZUK G, KOPP G A. Effects of wind direction on the flight trajectories of roof sheathing panels under high winds[J]. Wind and Structures, 2010, 13(2): 145. DOI:10.12989/was.2010.13.2.145 |
| [18] |
HOLMES J, LETCHFORD C, LIN N. Investigations of plate-type windborne debris-Part Ⅱ: computed trajectories[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2006, 94: 21. DOI:10.1016/j.jweia.2005.10.002 |
| [19] |
NING L, HOLMES J, LETCHFORD C. Trajectories of wind-borne debris in horizontal winds and applications to impact testing[J]. Journal of Structural Engineering, 2007, 133(2): 274. DOI:10.1061/(ASCE)0733-9445(2007)133:2(274) |
| [20] |
RICHARDS P J. Dispersion of windborne debris[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2012, 104-106: 594. DOI:10.1016/j.jweia.2012.02.026 |
| [21] |
宋芳芳, 欧进萍. 台风致碎片运动及其对围护结构冲击破坏分析[J]. 工程力学, 2010, 27(7): 212. SONG Fangfang, OU Jinping. Typhoon-induced debris movement and impact damage analysis of structural envelopes[J]. Engineering Mechanics, 2010, 27(7): 212. |
| [22] |
FU A M, HUANG P, GU M. Numerical model of three-dimensional motion of plate-type wind-borne debris based on quaternions and its improvement in unsteady flow[J]. Applied Mechanics and Materials, 2013, 405: 2399. DOI:10.4028/www.scientific.net/AMM.405-408.2399 |
| [23] |
FU A M, WANG F, HUANG P. Numerical simulation of 3-D probabilistic trajectory of plate-type wind-borne debris[J]. Wind & Structures, 2016, 22: 17. DOI:10.12989/was.2016.22.1.017 |
| [24] |
HUANG P, LIN H T, GU M. Wind tunnel investigation of autorotation of plate: the effects of geometry, Reynolds number and rotation direction[J]. Journal of Wind Engineering and Industrial Aerodynamics, 196. DOI:10.1016/j.jweia.2019.104012 |
| [25] |
张兆顺, 崔桂香, 许春晓. 湍流理论与模拟[M]. 北京: 清华大学出版社, 2006: 236. ZHANG Zhaoshun, CUI Guixiang, XU Chunxiao. Theory and modeling of turbulence[M]. Beijing: Tsinghua University Press, 2006: 236. |
| [26] |
刘帅永. 倒角和切角措施对方柱表面风荷载影响的大涡模拟研究[D]. 郑州: 河南工业大学, 2020 LIU Shuaiyong. Study of influence of chamfer and corner recession modifications of square cylinder on wind load based on large eddy simulation[D]. Zhengzhou: Henan University of Technology, 2020. DOI: 10.27791/d.cnki.ghegy.2020.000260 |
| [27] |
GERMANO M, PIOMELLI U, MOIN P, et al. A dynamic subgrid-scale eddy viscosity model[J]. Physics of Fluids, 1991, 3(7): 1760. DOI:10.1063/1.857955 |
| [28] |
LILLY D K. A proposed modification of the Germano subgrid-scale closure model[J]. Physics of Fluids, 1992, 4(3): 633. DOI:10.1063/1.858280 |
| [29] |
唐意. 高层建筑弯扭耦合风致振动及静力等效风荷载研究[D]. 上海: 同济大学, 2006 TANG Yi. Research on the wind-excited vibrations and static-equivalent wind loads of torsionally coupled high-rise buildings[D]. Shanghai: Tongji University, 2006 |
| [30] |
住房和城乡建设部. 建筑结构荷载规范: GB 50009—2012[S]. 北京: 中国建筑工业出版社, 2012 Ministry of Housing and Urban-Rural Development of the People's Republic of China. Load code for the design of building structures: GB 50009—2012[S]. Beijing: China Architecture & Building Press, 2012 |
| [31] |
郑德乾, 顾明, 张爱社, 等. 单体1∶ 1∶ 6方形截面建筑绕流的大涡模拟[J]. 振动与冲击, 2011, 30(5): 96. ZHENG Deqian, GU Ming, ZHANG Aishe, et al. Large eddy simulation of flow around a single square building model with 1∶ 1∶ 6 shape[J]. Vibration and Shock, 2011, 30(5): 96. DOI:10.3969/j.issn.1000-3835.2011.05.020 |
| [32] |
GIOFFRE M, GUSELLA V, GRIGORIU M. Non-Gaussian wind pressure on prismatic buildings. I: stochastic field[J]. Journal of Structural Engineering, 2001, 127(9): 981. DOI: 10.1061/(ASCE)0733-9445(2001)127:9(981)
|
| [33] |
KWON D K, KAREEM A. Peak factors for non-Gaussian load effects revisited[J]. Journal of Structural Engineering, 2011, 137(12): 1611. DOI: 10.1061(ASCE)ST.1943-541X.0000412
|
| [34] |
陈凯, 孙海角, 何连华, 等. 建筑结构极值风压估算方法研究[J]. 建筑结构, 2012, 42(7): 123. CHEN Kai, SUN Haijiao, HE Lianhua, et al. Research on the estimation method of extreme wind pressure of building Structure[J]. Building Structure, 2012, 42(7): 123. |
| [35] |
中国建筑科技研究院, 玻璃幕墙工程技术规范: JGJ 102—2003[S]. 北京: 中国建筑工业出版社, 2003 China Academy of Building Research. Technical code for glass curtain wall engineering: JGJ 102—2003[S]. Beijing: China Architecture & Building Press, 2003 |
| [36] |
建筑用安全玻璃第2部分: 钢化玻璃: GB 15763.2—2005[S]. 北京: [s. n. ], 2005 Safety glazing materials in building-Part 2: tempered glass: GB 15763.2—2005[S]. Beijing: [s. n. ], 2005 |
 2024, Vol. 56
2024, Vol. 56


