近年来,类似“水黄”投诉、污染物超标等水质异常事件频发[1-3],对民众健康与社会稳定造成了重大的危害,成为了当前供水企业水质安全运行管理面临的一大问题[4]。当供水管网系统发生水质污染事件时,需要快速、准确地定位污染源,最大限度地控制污染物传播以降低污染事件的不利影响。污染源定位是指根据供水管网基本结构属性和管网反馈的水质相关信息,推算污染物源头的过程[5]。
对于配备了在线水质监测设备的管网系统,学者们提出了一系列定位污染源的方法[6-7],可归纳为:1)粒子回溯法。基于管网模型特征反向追溯污染物在供水管网中的传播路径、浓度及时间信息。Zierolf等[8]首次提出沿反向时间跟踪粒子在管网中传输的I/O模型,在此基础上Shang等[9]提出了粒子反溯算法,提高了反向追踪的效率,但这种方法需要明确污染物质的反应动力学规律。2)模拟-优化法。基于管网水质模拟数据,以最小化模拟值与监测值之差为目标,通过反复调试污染事件水质模拟过程确定污染源的可能位置与侵入时间等信息。Guan等[10]利用EPANET软件进行水力水质计算,结合负梯度法进行污染物溯源,Grbcic等[11]利用随机森林算法进行污染源识别定位,Yan等[12]采用改进的遗传算法作为优化算法研究了动态需水条件下的污染源定位问题,但该方法计算较复杂且耗时量大。3)机器学习相关方法。随着以数据驱动为特点的机器学习方法的不断发展,贝叶斯理论、人工神经网络等也广泛应用于管网的污染源定位。Sun等[13]提出基于卷积神经网络的污染源定位方法,用于解决单污染源的识别问题,Wang等[14]将贝叶斯方法用于供水管网的污染源识别。
机器学习相关方法在污染源识别中得到广泛应用,其中,贝叶斯方法能根据多源观测信息不断更新可疑污染源点的后验概率,具有一定优势。然而,现有基于贝叶斯理论的污染源定位方法要么没有考虑节点需水量的随机波动[15-16],实际应用受到局限;要么没有充分地挖掘传感器的报警信息[14, 17],定位的准确性有待提高。针对现有方法的局限性,提出一种充分挖掘在线水质监测点时序观测信息的贝叶斯方法,实现节点需水量随机波动情况下的供水管网系统污染源定位。首先,基于管网机制模型,利用蒙特卡洛模拟获得不同节点污染情况下传感器观测值的概率分布,然后,根据在线观测信息,实时计算节点作为污染源的后验概率,选择后验概率最高的节点或节点集合作为污染源节点所在区域。结合案例对提出的污染源定位方法进行测试分析,验证了该方法的有效性。对于配备在线水质监测设备的供水管网系统,该方法深度挖掘监测信息,能实现对污染源的快速定位,提高供水管网系统对水质突发事故的应急响应能力。
1 污染源定位方法 1.1 供水管网水力水质模型理论本研究需要大量的水质污染事件样本,由于实际中难以获得,采用供水管网模型进行水质污染事件仿真。
管网水力模型需要满足管网连续性方程和能量守恒方程[18]:
| $ \boldsymbol{A q}+\boldsymbol{Q}=0 $ | (1) |
| $ \boldsymbol{A}^{\mathrm{T}} \boldsymbol{H}-\boldsymbol{h}=\boldsymbol{0} $ | (2) |
式中:A为管网关联矩阵,q为管道流量向量,Q为节点流量向量,H为节点水头向量,h为管段压降向量。
供水管网水质仿真以一维迁移扩散方程模拟污染物质在管网中的传播,不考虑物质在管网中的反应,管网水质模型控制方程[18]如下:
| $ \frac{\partial C_j(t)}{\partial t}=-u_j \frac{\partial C_j(t)}{\partial x} $ | (3) |
式中:Cj(t)为t时刻管段j中的物质浓度,uj为管段j中的流速,x为沿管段j的距离。
研究过程中用于说明和验证所提出方法的数据均来自管网模型仿真模拟,仿真模拟满足以下假设条件:
1) 从发现污染到作出决策采取措施需要一定时间,在这段时间污染物将继续扩散,本研究主要针对未对管网进行任何处置的情景下,污染物在管网中的迁移扩散。
2) 由于污染物质种类众多,反应机制难以完全明确,现有技术条件下准确模拟实际污染物质的衰减和反应过程难度极大。对于污染事件的样本只需要明确是否受到污染,而对污染物浓度精度要求不高,故假定污染物质为惰性物质,仅随水体迁移扩散,在扩散过程中物质本身不衰减且不与水中其他物质发生反应。
3) 污染物能被水质在线监测系统检测并识别出异常。
4) 本研究针对单一污染源事件,污染物可从供水管网的任一节点以等质量浓度持续注入。
1.2 贝叶斯方法计算节点污染概率考虑一个部署了m个水质传感器的供水管网系统,当传感器监测并识别出异常时发出报警信息并传输至调度中心,k表示固定传输频率下的观测次序(反映观测到不同传感器报警信息的时间),接到首次报警为观测的起始时刻,i为直到第k次观测时已经发出报警的传感器数量。Ki为第i个传感器首次发出报警的观测时刻,k时刻i个传感器发出报警的时刻集合表示为
| $ K(i)=\left\{K_1, K_2, \cdots, K_i\right\}, 1 \leqslant i \leqslant I $ | (4) |
式中I为观测到的所有序列中发出报警信息的传感器总数,I≤m。
令S(Ki)为对应Ki时刻的最新发出报警的传感器,则第k次观测时传感器报警序列为
| $ S(i)=\left\{S\left(K_1\right), S\left(K_2\right), \cdots, S\left(K_i\right)\right\}, 1 \leqslant i \leqslant I $ | (5) |
由此,第k次观测时i个传感器报警信息Y(i)表示成包含报警时刻和对应报警的传感器的序列为
| $ Y(i)=\{K(i), S(i)\}, 1 \leqslant i \leqslant I $ | (6) |
更进一步,考虑当前观测时刻与最近一次报警时间的观测次数差X,X反映了在最新的传感器发出报警后没有观测到新报警的时间,即
| $ X=k-K_i $ | (7) |
由于管网中节点具有特定的需水量模式,同一节点的需水量在一天24 h内的不同时段存在变化,不同时段的污染事件会表现出不同的传感器报警信息,故将接到首次报警信息的时刻t0也作为观测信息的一部分。结合以上定义,当管网中发生污染事件后,不同时刻能获取到不同的传感器报警信息,第k次观测序列包含的信息可由Y(i)、X和t0完全表示。
当采用贝叶斯理论进行污染源识别时,若用随机变量Z表示污染源候选节点集合,z表示某个候选点,z∈Z,P0(z)为z的先验概率分布,则污染源识别问题可以表征为给定当前观测到的所有传感器信息计算各候选节点z的后验概率分布P(z|Y(i), X, t0)的问题,认为具有较高后验概率的节点作为潜在污染源节点的可能性较高。采用如下贝叶斯公式计算候选节点后验概率:
| $ P\left(z \mid Y(i), X, t_0\right)=\frac{P\left(Y(i), X, t_0 \mid z\right) \times P_0(z)}{\sum\limits_z P\left(Y(i), X, t_0 \mid z\right) \times P_0(z)} $ | (8) |
式中:P(z|Y(i), X, t0)为节点z作为污染源的后验概率,P(Y(i), X, t0|z)为似然项,P0(z)为节点先验概率,z为污染源节点集合Z中的某个候选节点,t0为首个传感器报警时间,Y(i)为传感器报警信息序列,X为当前观测时刻与最近一次报警时间的观测次数差。
在污染源识别初期无观测信息的情况下,可将先验P0(z)设为均匀分布,分母求和项可看作一个归一化常数,目的是使后验分布总和为1,在进行污染源识别时主要关注的是最有可能的污染源节点而非后验概率的具体数值,因此,只需考虑分子项,式(8)化简如下:
| $ P\left(z \mid Y(i), X, t_0\right) \propto P\left(Y(i), X, t_0 \mid z\right) \times P_0(z) $ | (9) |
由于P0(z)为统一的值,即每个节点具有相同的先验概率,现只考虑P(Y(i), X, t0|z),由条件概率乘法公式得
| $ \begin{gathered} P\left(Y(i), X, t_0 \mid z\right)=P\left(X \mid Y(i), t_0, z\right) \times \\ P\left(Y(i) \mid t_0, z\right) \times P\left(t_0 \mid z\right) \end{gathered} $ | (10) |
当管网中某时刻t0传感器发出首次报警,在给定观测信息{[S(K1), …, S(Ki)], [K1, …, Ki], X, t0}的条件下,可以根据式(10)计算不同节点作为污染节点的后验概率,通过比较后验概率的大小,确定可能的污染源节点,具体地,使用下列决策规则估计污染源节点
| $ z \in\left\{z^1, z^2, \cdots, z^G\right\} $ | (11) |
式中:z1为具有最高后验概率的节点,zi为具有第i个最高后验概率的节点,G为选定的一个较小的整数。
当实际污染源节点属于具有前G个最高后验概率的节点集合时,认为有效地识别到污染源。
为了评估传感器监测信息的价值,引入节点后验概率信息熵这一概念,根据信息学理论,信息熵代表的是随机变量或整个系统的不确定性[19],污染源候选点集合Z的信息熵数学公式表达如下:
| $ H(Z)=-\sum\limits_Z P(z) \log P(z) $ | (12) |
式中P(z)为Z的离散状态的概率,即所有候选污染源点的概率。
H(Z)越大,表示污染源概率分布的不确定性越大,在污染源识别初期无观测信息时,先验概率为均匀分布,H(Z)最大。随着水质传感器观测信息不断更新,H(Z)会随P(z)的变化减小,反映了节点污染概率不确定程度的变化。
1.3 蒙特卡洛模拟求解概率分布函数在根据式(10)计算后验概率的过程中,各项的值通过随机污染事件蒙特卡洛模拟程序进行估计。
蒙特卡洛模拟的基本思想是针对给定的污染节点对供水管网的水力特性进行大量模拟运行,每次运行都会获得模拟的传感器报警观测结果,通过统计特定报警观测的频率,来近似所需的观测信息概率。具体地,根据事先设定的参数,采用python供水管网工具包(water network tool for resilience, WNTR)进行延时水力水质模拟,用户用水呈现24 h变化规律,在各节点24 h用水模式上添加高斯扰动生成节点新用水曲线,在每个时间段分别向每一个污染源候选节点持续注入一定浓度的污染物,模拟其在管网中的扩散,可获得管网各节点不同时刻的水质状况。当水质传感器监测并识别到异常时发出污染报警信息,模拟得到污染发生后各水质监测点的首次被污染时间,生成监测点报警序列及报警时间间隔样本。具体的污染事件模拟步骤如下:
1) 确定影响参数值,如需水量扰动高斯噪声σ、节点模拟次数N、模拟时间;
2) 依次选定候选污染源节点;
3) 设定24 h污染投加模式,对于选定的污染投加时段,通过管网水力水质延时模拟确定各监测点的被污染情况,得到监测点报警序列;
4) 对不同时段重复步骤3)N/24次,为节点生成N/24个样本;
5) 对所有的污染投加模式,重复步骤3)、4),生成单个节点的所有样本;
6) 对于所有的候选污染源节点,重复步骤2)~4),生成所有的随机污染事件报警样本。
针对某一源头的污染事件,通过模拟可以获得污染物在管网中的传播并得到相应的传感器报警信息{[S(K1), …, S(Ki)], [K1, …, Ki], X, t0},包括传感器的首次报警时间、报警的传感器顺序以及时间间隔,式(10)中的各项估计如下:
| $ \hat{P}\left(t_0 \mid z\right)=\frac{N_{t_0}}{N} $ | (13) |
式中:
| $ \hat{P}\left(Y(i) \mid z, t_0\right)=\frac{N_{Y(i), t_0}}{N_{t_0}} $ | (14) |
式中NY(i), t0为首次报警时间为t0且观测到Y(i)的模拟次数。
| $ \hat{P}\left(X \mid Y(i), t_0, z\right)=1-\frac{\sum\limits_{r=1}^X D_{Y(i+1), t_0, r}}{\sum\limits_r D_{Y(i), t_0, r}} $ | (15) |
式中DY(i), t0, r为观测到Y(i)且最近两次传感器报警(即第i-1和第i个报警)时间间隔为r的模拟次数。
对于每个节点作为注入源的模拟事件都可以根据以上方法计算其作为污染源的后验概率,需要注意的是,在一次模拟事件中传感器是否发出警报以及报警传感器的个数是根据模拟结束时观测到的报警信息确定的,这与污染物注入时间和模拟运行的总时间有关,管网中某些点的污染事件可能出现没有任何传感器报警的情况。其他的模拟参数如试验模拟重复次数N、供水管网规模、需水量扰动方差、传感器布设位置和数量都会对识别结果造成影响。
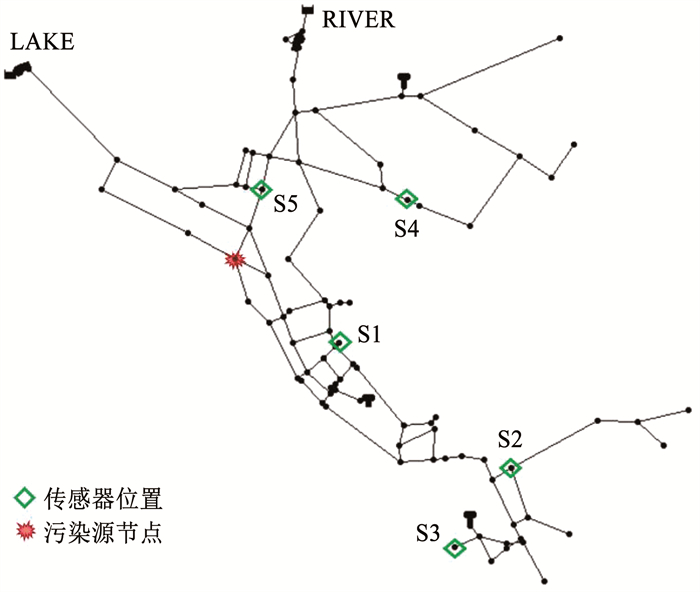
2 案例分析以EPANET软件自带的供水管网案例Net 3[20]为例,对上节中提出的污染源识别方法进行应用分析,该管网模型包含92个节点,117条管段,2个水源,3个水塔和2个泵,管网拓扑结构如图 1所示。节点水力参数和需水量模式等详细参数可以查阅EPANET软件包相关文件[21]。
|
图 1 Net 3管网拓扑结构 Fig. 1 Layout of Network 3 |
假定污染物为惰性物质,以等质量浓度ρ0=25 mg/L持续注入,模拟持续时间为36 h,该值大于管网水流最长流行时间,水力步长为1 h,水质步长为5 min,水质传感器数据采集传输频率为10 min/次,每次模拟运行只考虑一个污染注入点。每个水力周期内各节点的需水量设置为截断正态函数,需水量扰动百分比符合N(0,σ2)的正态分布,σ设为5%,由此为所有节点生成24 h需水量模式。
该管网系统中放置了5个传感器,布置方式与Seth等[22]的研究相同,分别在节点167、213、253、149、117处,对应传感器编号为S1, S2, S3, S4, S5,布置位置如图 1所示。根据Kumar等[23]提出的污染矩阵法,若某点发生的污染事件能被监测点识别到异常,则认为该节点在监测点的覆盖范围内,由此可以得到这5个监测点覆盖的节点范围,对应的候选污染源节点共76个。首先,对每个节点进行N=3 000次重复模拟运行,以获得所需的观测概率分布函数,然后,随机选择一个节点作为污染节点并随机选择注入时间,模拟得到报警观测信息,基于报警观测信息和观测概率分布函数,使用提出的贝叶斯方法识别污染节点并验证结果的可靠性。
2.1 污染源定位结果分析随机选取节点111为污染注入源头,模拟设置如表 1所示,传感器S1在当天第56个观测时刻发出首次报警,随后经过12个观测间隔单位传感器S2发出报警,再经过19个观测间隔传感器S3发出报警,之后再无其他传感器报警信息,1个观测间隔单位即传感器传输数据间隔10 min,根据上述贝叶斯推断方法时序更新各节点的污染源概率。
| 表 1 污染事件模拟参数 Tab. 1 Parameters setting of contamination event simulation |
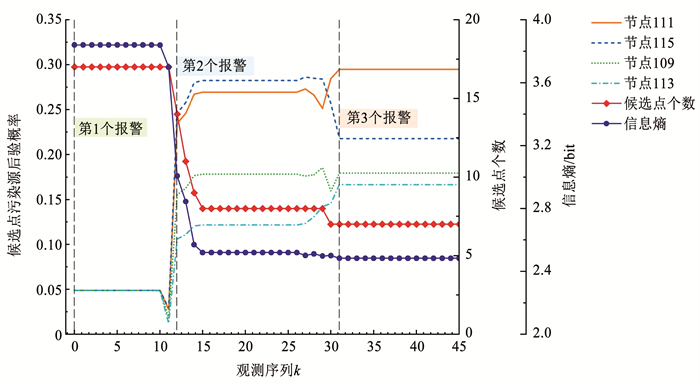
按照1.3中的方法,计算每个节点作为污染源的后验概率,其中,概率最高的4个节点的污染源后验概率随观测时间变化如图 2所示,观测过程中候选点个数和污染概率信息熵的变化也同步显示在图 2中。随着观测时间的推进,传感器信息增加,节点的污染源后验概率不断更新。在收到第3个传感器报警信息后,实际污染源节点111的后验概率显著升高并且明显超过其余节点,成为污染概率最大的节点,这说明使用提出的方法能够有效识别出污染源节点。从候选点个数和信息熵变化曲线也可以看出,随着观测信息的增加,候选污染节点个数大幅减少,收到首个传感器报警后,候选污染源节点个数由最初的76减少至17,并随着传感器信息的更新减少至最终的7,且均位于节点111的邻近区域,这也从一定程度上说明了定位方法的有效性。后验概率信息熵与候选点个数的变化趋势呈现一致性,候选点个数减少的同时信息熵也随之降低,说明在定位过程中污染源概率分布的不确定性也逐渐减小。此外,从图 2还能观察到在第2次和第3次报警之间节点115的污染源概率要高于节点111,且最终定位结果中的节点109、113和115的后验概率接近,这是因为这3个节点都靠近节点111,具有相近的特征和用水模式,其后验概率分布函数具有一定的相似性,同时说明仅依靠前两个传感器的报警信息无法较准确地识别污染源,在这种情况下需要增加观测时间以获得更多的监测信息,用以继续更新节点污染源后验概率。
|
图 2 报警信息累积时可疑污染节点后验概率、候选点个数及信息熵变化 Fig. 2 Posterior probability, number and information entropy of suspicious contamination nodes when sensor information is gathered |
与Cai等[17]提出的方法相比,本文提出的方法在相同节点和注入时间的污染事件识别中表现出显著的优势。当出现第3次传感器报警时,本文方法将真实的污染节点111识别为具有最高污染概率的节点,对应的污染源后验概率约为0.30,相比之下,Cai等方法得到节点111的后验概率仅约为0.10,在所有候选节点中排第3位。从单次污染事件的识别结果来看,本文方法能够更有效地确定污染源的位置,相比现有方法具有一定的优势。
受节点需水量随机波动的影响,同一节点的污染事件可能会导致不同的传感器观测信息,后验概率的计算结果会有一定的随机性。为了评估方法识别真正污染节点的能力,对作为候选污染源的每个节点随机选择污染时间进行了600次模拟。在这45 600个验证案例中,观测到传感器发出报警信息的事件有44 232个,其中,约33.7%的案例中使用决策规则G=1,即将具有最高后验概率的节点看作污染节点,可以正确识别污染节点;如果使用G=3的决策规则,即污染节点在后验概率最高的前3个节点中,在所有验证案例中,约67.3%的情况可以正确识别出污染节点;如果使用G=5的决策规则,约81.4%的情况可以正确识别出污染节点。
考虑到节点的位置会影响污染事件的识别结果,分别计算了不同节点污染事件的识别准确率,结果见图 3。A5为在决策规则G=5时成功定位到真实污染节点事件的比例,未监测节点指的是污染事件无法被已有的水质传感器识别到的节点。可以看出,不同位置候选节点的识别准确率存在较明显的差异,节点的上下游位置和与传感器的距离会影响节点的识别准确率,管网上游节点和靠近水质监测点的节点具有较高的A5,普遍高于90%,管网末端且位于水质传感器下游的节点发生的污染事件无法到达传感器,故无法被传感器识别。

|
图 3 节点污染事件识别准确率(G=5时) Fig. 3 Identification accuracy of each node when G=5 |
现有的基于贝叶斯推断方法通过在线水质监测设备进行污染源定位的研究中,要么仅考虑传感器报警二元信息[15-16],要么仅考虑报警传感器的时间次序,Wang等[14]考虑加入传感器报警的时间间隔进行污染源定位,但上述研究都未考虑当不同时段的节点需水量随机波动时导致的传感器报警信息的差异对定位结果的影响,因此,在已有研究的基础上,综合考虑传感器的报警次序、报警时间间隔以及首个传感器报警的时间段对污染源进行定位,并将不同信息挖掘程度的方法作对比,分析结果如下。
2.2.1 单次污染事件定位结果分析采用表 1的模拟参数,对节点111的同一污染事件进行分析,对比以下3种传感器观测信息挖掘策略进行污染源定位的结果差异。1)策略1。Perelman等[16]提出的方法,仅利用传感器报警的二元信息及相应的报警传感器的次序(以下简称“次序”),即传感器(S1, S2, S3)先后发出报警;2)策略2。Wang等[14]提出的方法,同时考虑传感器报警次序及报警时间间隔(以下简称“次序+间隔”),即传感器S1报警后间隔12个观测单位传感器S2报警,随后间隔19个观测单位传感器S3报警;3)策略3。本文提出的方法同时考虑传感器报警次序、时间间隔以及首个传感器报警的时间(以下简称“次序+间隔+t0”),即传感器S1在当天第56个观测时刻发出首次报警。观测过程中污染源候选点的概率分布如图 4所示,由于第1次传感器报警时还没有时间间隔信息,仅展示第2次(k=12)和第3次(k=31)传感器报警时候选污染节点的后验概率,k为距离接到首次报警时刻的观测次数。

|
图 4 不同信息挖掘策略的候选节点个数与后验概率对比 Fig. 4 Comparison of number and posterior probabilities of candidate nodes in different information utilization strategies |
纵向对比图 4(a)、(c)、(e)和图 4(b)、(d)、(f)可以看出,相同观测时间内,传感器信息挖掘程度越高,候选点个数减少得越多,实际污染源节点111的后验概率也更高,并且在所有候选节点中的排名更靠前,即被识别为污染源的可能性更大,说明深入地挖掘在线传感器观测信息更有助于识别污染源所在位置,提高污染源定位的效率。由图 4(a)和4(b)的概率分布也可以看出,如果仅依靠传感器的报警次序进行定位,较难通过后验概率的大小定位到准确的污染源范围,这是因为固定位置传感器的个数是有限的,且受到经济成本限制,如果仅考虑传感器报警的次序,不同节点处污染事件引发的传感器报警个数及先后次序可能一致,导致该方法得到较多节点的后验概率一致,定位结果准确性较低。
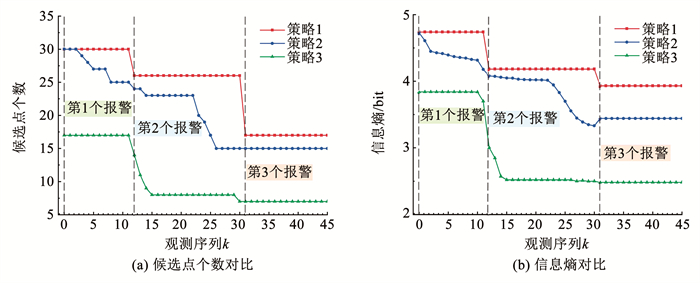
除了计算上述污染源候选点的概率,同时对比了不同传感器信息挖掘策略下定位过程中候选点个数和污染概率信息熵的变化差异,结果如图 5所示。图 5(a)为候选点个数变化曲线,表明利用的信息越多,候选点个数下降的幅度越大,引入首次报警时间t0后,在接到第3个传感器报警信息时,候选点个数减少到7,相比仅利用报警次序和时间间隔方法定位的效率提高。由图 5(b)中污染源概率信息熵的变化曲线可以看出,利用t0可以大幅减小污染概率的信息熵,降低污染源概率分布的不确定性,说明t0这部分信息能为污染源定位提供较高的利用价值。
|
图 5 不同信息挖掘策略的候选点个数和信息熵对比 Fig. 5 Comparison of number and information entropy of candidate nodes in different information utilization strategies |
为了进一步对比不同信息挖掘程度定位方法的准确性,将本文所提方法与文献[14, 16]中的贝叶斯定位方法进行了比较,对2.1节中提到的44 232个验证案例都利用不同的观测信息进行定位分析,计算其不同决策规则G下的识别准确率AG和漏报率RFN(如表 2所示),其中,识别准确率AG为成功定位到真实污染节点事件的比例,漏报率RFN为候选点集合中不包含实际污染源节点事件的比例,下标G表示采取不同的决策规则。
| 表 2 不同方法污染事件识别结果对比 Tab. 2 Identification results of different methods |
表 2中数据反映了不同信息挖掘量用于定位的识别准确率和漏报率的差异,结果显示,随着信息挖掘程度的提高,污染事件定位的准确性也相应提高,但同时会导致定位结果的漏报率提高。然而,与Wang等[14]提出的定位方法相比,加入t0这部分信息后准确率有明显的提高,而RFN仅从0.9%增大到1.4%,漏报事件增加的幅度较小,仍在可接受的范围内。综合考虑,本文提出的采用次序+间隔+t0进行定位的效果要明显优于其他两种方法。对于配备了在线水质传感器的管网系统,当发生水质异常事件后,t0这部分信息是易于获得的,对这部分信息充分挖掘以辅助污染源定位可以提高污染源识别的准确性和效率,便于相关人员和部门尽快定位污染源头,及时采取应对措施,最大程度降低污染事件的不利影响,提升管网的安全性和应对风险的能力。
2.3 需水量波动对定位准确率的影响为了分析实际中需水量波动大小对污染事件识别结果的影响,参考已有研究中σ的取值[24],考虑不同的需水量扰动方差σ=5%、10%和15%,采用本文提出的方法对每个节点的600次污染事件进行识别,不同σ对应的识别准确率和漏报率如图 6所示。可以看出,当σ分别为5%、10%和15%时,A5分别为81.4%、72.7%和65.4%,RFN分别为1.4%、4.7%和8.4%,表明不同的σ会影响污染事件的识别结果,σ越大,需水量不确定程度越高,污染定位的准确率越低,且漏报率亦会增加,这也说明若管网中出现用水量的大幅波动时,定位的效果会受到影响。

|
图 6 不同需水量扰动方差的定位准确率和漏报率 Fig. 6 Identification accuracy and false negative rate of different water demand disturbance variance |
1) 提出一种深度挖掘监测信息的供水管网污染源定位方法,在节点用水需求波动的情况下,将在线水质传感器监测数据作为可用信息,基于贝叶斯推断,并利用传感器报警次序、时间间隔和首次报警时间计算节点作为污染源的后验概率从而实时识别污染源。通过案例研究分析验证了该方法的有效性。
2) 定位结果中节点污染后验概率、候选点个数和污染概率信息熵分析结果表明,所提出的方法可以根据观测到的时序传感器信息实时更新节点污染概率,定位过程中,随着污染相关信息的增加,可疑污染源候选节点个数不断减少,可疑区域范围缩小,污染概率信息熵随之不断降低,污染源不确定性降低。在所分析案例中,当分别采取G=3和G=5的决策规则时,污染源定位的准确性达到67.3%和81.4%,说明该方法可以将污染源有效定位到极少量的节点中,显著提升污染源精准定位效率。
3) 相比现有研究中单纯采用传感器报警次序信息或时间间隔信息的定位方法,引入首次报警时间t0作为辅助定位信息,考虑了不同时段需水量变化规律对污染物传播的影响。不同信息挖掘程度的定位结果对比表明,引入t0用于定位可以提高定位结果的准确性,同时,该方法考虑了节点需水量的随机扰动,具有广泛的工程价值和应用潜力。
| [1] |
李国英. 推动新阶段水利高质量发展为全面建设社会主义现代化国家提供水安全保障[J]. 中国水利, 2021, 922(16): 1. LI Guoying. Promote high-quality water development in the new era, safeguard water security for building a modern socialist country in an all-round way[J]. China Water Resources, 2021, 922(16): 1. |
| [2] |
RODRíGUEZ-MARTíNEZ C, QUIñONES-GRUEIRO M, LLANES-SANTIAGO O. Cyberattack diagnosis in water distribution networks combining data-driven and structural analysis methods[J]. Journal of Water Resources Planning and Management, 2023, 149(5): 04023013. DOI:10.1061/JWRMD5.WRENG-5302 |
| [3] |
JI Yiran, ZHENG Feifei, DU Jiawen, et al. An effective and efficient method for identification of contamination sources in water distribution systems based on manual grab-sampling[J]. Water Resources Research, 2022, 58(11): e2022WR032784. DOI:10.1029/2022WR032784 |
| [4] |
BERGLUND E Z, PESANTEZ J E, RASEKH A, et al. Review of modeling methodologies for managing water distribution security[J]. Journal of Water Resources Planning and Management, 2020, 146(8). DOI:10.1061/(ASCE)WR.1943-5452.0001265 |
| [5] |
GONG Jinyu, GUO Xing, YAN Xuesong, et al. Review of urban drinking water contamination source identification methods[J]. Energies, 2023, 16(2): 705. DOI:10.3390/en16020705 |
| [6] |
SHAHSAVANDI M, YAZDI J, GHAZIZADEH M J, et al. The use of graph theory for search space reduction in contaminant source identification[J]. Journal of Pipeline Systems Engineering and Practice, 2023, 14(2): 04023016. DOI:10.1061/JPSEA2.PSENG-1402 |
| [7] |
LI Zilin, LIU Haixing, ZHANG Chi, et al. Generative adversarial networks for detecting contamination events in water distribution systems using multi-parameter, multi-site water quality monitoring[J]. Environmental Science and Ecotechnology, 2023, 14: 100231. DOI:10.1016/j.ese.2022.100231 |
| [8] |
ZIEROLF M L, POLYCARPOU M M, UBER J G. Development and autocalibration of an input-output model of chlorine transport in drinking water distribution systems[J]. IEEE Transactions on Control Systems Technology, 1998, 6(4): 543. DOI:10.1109/87.701351 |
| [9] |
SHANG F, UBER J G, POLYCARPOU M M. Particle backtracking algorithm for water distribution system analysis[J]. Journal of Environmental Engineering-Asce, 2002, 128(5): 441. DOI:10.1061/(ASCE)0733-9372(2002)128:5(441) |
| [10] |
GUAN Jiabao, ARAL M M, MASLIA M L, et al. Identification of contaminant sources in water distribution systems using simulation-optimization method: case study[J]. Journal of Water Resources Planning and Management, 2006, 132(4): 252. DOI:10.1061/(ASCE)0733-9496(2006)132:4(252) |
| [11] |
GRBCIC L, KRANJCEVIC L, DRUZETA S. Machine learning and simulation-optimization coupling for water distribution network contamination source detection[J]. Sensors, 2021, 21(4): 7. DOI:10.3390/s21041157 |
| [12] |
YAN Xuesong, ZHU Zhixin, LI Tian. Pollution source localization in an urban water supply network based on dynamic water demand[J]. Environmental Science and Pollution Research, 2019, 26(18): 17901. DOI:10.1007/s11356-017-0516-y |
| [13] |
SUN Lian, YAN Hexiang, XIN Kunlun, et al. Contamination source identification in water distribution networks using convolutional neural network[J]. Environmental Science and Pollution Research, 2019, 26(36): 36786. DOI:10.1007/s11356-019-06755-x |
| [14] |
WANG Chao, ZHOU Shiyu. Contamination source identification based on sequential Bayesian approach for water distribution network with stochastic demands[J]. ⅡSE Transactions, 2017, 49(9): 899. DOI:10.1080/24725854.2017.1315782 |
| [15] |
SANKARY N, OSTFELD A. Bayesian localization of water distribution system contamination intrusion events using inline mobile sensor data[J]. Journal of Water Resources Planning and Management, 2019, 145(8). |
| [16] |
PERELMAN L, OSTFELD A. Bayesian networks for source intrusion detection[J]. Journal of Water Resources Planning and Management, 2013, 139(4): 426. DOI:10.1061/(ASCE)WR.1943-5452.0000288 |
| [17] |
CAI Jiaxiang, YE Zhisheng. Contamination source identification: a Bayesian framework integrating physical and statistical models[J]. IEEE Transactions on Industrial Informatics, 2021, 17(12): 8189. DOI:10.1109/TⅡ.2021.3062146 |
| [18] |
严煦世, 刘遂庆. 给水排水管网系统[M]. 2版. 北京: 中国建筑工业出版社, 2008: 81. YAN Xushi, LIU Suiqing. Water supply and drainage pipe network system[M]. 2nd ed. Beijing: China Architecture & Building Press, 2008: 81. |
| [19] |
SHANNON C E. A mathematical theory of communication[J]. The Bell System Technical Journal, 1948, 27(4): 623. DOI:10.1002/j.1538-7305.1948.tb00917.x |
| [20] |
YANG Y J, HAUGHT R C, GOODRICH J A. Real-time contaminant detection and classification in a drinking water pipe using conventional water quality sensors: techniques and experimental results[J]. Journal of Environmental Management, 2009, 90(8): 2494. DOI:10.1016/j.jenvman.2009.01.021 |
| [21] |
ROSSMAN L A. Epanet 2: users manual[M]. [S.l.]: Createspace Independent Publishing Platform, 2000.
|
| [22] |
SETH A, KLISE K A, SⅡROLA J D, et al. Testing contamination source identification methods for water distribution networks[J]. Journal of Water Resources Planning and Management, 2016, 142(4): 04016001. DOI:10.1061/(ASCE)WR.1943-5452.0000619 |
| [23] |
KUMAR A, KANSAL M L, ARORA G. Detecting accidental contaminations in municipal water networks-discussion[J]. Journal of Water Resources Planning and Management-Asce, 1999, 125(5): 308. DOI:10.1061/(ASCE)0733-9496(1999)125:5(308) |
| [24] |
孙炼. 基于卷积神经网络的供水管网污染源定位研究[D]. 上海: 同济大学, 2020: 35 SUN Lian. Research on contamination source identification in water distribution networks using convolutional neural network[D]. Shanghai: Tongji University, 2020: 35 |
 2024, Vol. 56
2024, Vol. 56


