2. 苏州科技大学 土木工程学院,江苏 苏州 215009;
3. 渤海造船厂集团有限公司,辽宁 葫芦岛 125000
2. School of Civil Engineering, Suzhou University of Science and Technology, Suzhou 215009, Jiangsu, China;
3. Bohai Shipyard Co., Ltd., Huludao 125000, Liaoning, China
钢制储罐作为一种薄壳结构,具有容量大、造价低、稳定性好等优点,是储存油气产品的主要设施。油气产品易燃、易挥发,在加工和储运过程中常出现泄漏爆炸事故[1-3]。爆炸事故中不仅产生爆炸荷载,也会产生飞溅物冲击荷载,威胁着钢制储罐和油气罐区的安全。钢制储罐的冲击破坏会导致罐内油气产品泄露,进而引起更大的爆炸事故,因而大钢制储罐的抗冲击防护方法研究对维护油气罐区安全具有重要意义。
近年来,研究者开展了钢制储罐冲击响应特征和影响参数的研究。朱东[4]利用霍普金森压杆进行了缩尺钢制储罐撞击试验,通过数值模拟分析了罐体残余变形与撞击参数的关系。Schneider等[5]使用有限元方法分析了飞机对薄壁钢制储罐的撞击作用,模拟结果显示,单层和双层钢罐结构对飞机高速撞击的抵抗能力极低,且已有的计算临界穿透能量的公式无法精确预测罐体穿透情况。潘旭海等[6]采用LS-DYNA软件对容器爆炸碎片撞击下的储罐结构响应进行了模拟,发现撞击角度为10°时储罐表面产生最大的加速度和位移。陈思宇等[7-9]模拟分析了爆炸碎片撞击下球罐和圆筒形储罐的破坏过程,结果显示,内部压力能起到降低罐体位移的作用,罐壁临界穿透能量与罐壁厚度呈近似指数关系。
对钢制储罐抗冲击防护方法的研究尚未见公开报道。近20年来,喷涂聚脲被证明是有效提高结构抗爆、抗冲击性能的方法[10],聚脲涂层能有效提高钢板、砌体墙、混凝土板、复合板的抗爆和抗冲击性能[11-13]。聚脲弹性体喷涂技术不仅绿色环保,更有施工厚度范围大、粘接强度高、快速固化成型和使用寿命长等优点[14],能满足钢罐表面喷涂的大面积、曲面施工和无焊接的施工要求。因此,聚脲弹性体喷涂技术是一种有应用前景的钢制罐体抗冲击防护方法。
本文通过有限元模拟和理论分析探究聚脲涂覆罐体的冲击响应,研究失效特征和涂层作用机制,分析撞击参数和喷涂参数的影响规律,以明确聚脲涂层的抗冲击防护效果,提出聚脲喷涂技术的应用建议。
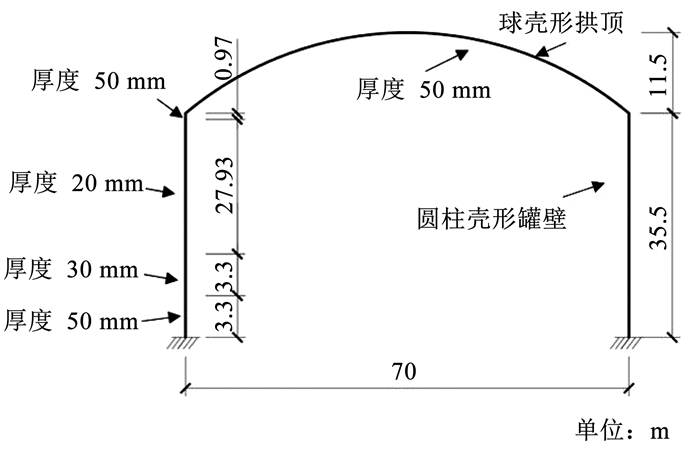
1 罐体设计和冲击荷载根据某10×104 m3容量的大型双钢罐外罐的设计资料建立模型,该钢罐主要几何尺寸如图 1所示,拱顶采用Q345D钢板,罐壁采用镍合金钢板。仅研究单层的钢制储罐结构响应及聚脲涂层作用效果。
|
图 1 钢罐几何尺寸示意 Fig. 1 Geometric size of the steel tank |
多部国内外规范规定了储罐设计时应考虑飞溅物冲击作用[15-18],其中,英国储罐设计规范[17]明确规定了飞溅物为质量50 kg、速度45 m/s的阀门。常用的阀门如图 2所示,外形接近圆柱形,高径比为1.5~2.0。在建模过程中,将阀门简化为圆柱体。当接触面积较小时破坏更严重,因此,高径比设为2。

|
图 2 石油化工产业常用阀门 Fig. 2 Normally used valves in oil industry |
前期工作中,在圆柱体锤头撞击聚脲涂覆钢板的研究中建立了经试验验证的有限元模型[19]。鉴于飞溅物撞击钢罐的几何形式、材料类型和荷载类别与落锤撞击钢板基本相同,在该前续研究的基础上建立飞溅物撞击大型钢制储罐的数值模型。
2.1 大型钢制储罐有限元模型使用薄壳单元对罐体进行网格划分,整体网格尺寸0.2 m。由于壳单元不能模拟沿厚度方向的变形和断裂特征,在撞击区域附近建立实体区域,以*CONSTRAINED_NODAL_RIGID_BODY关键字将实体边缘节点与壳单元节点耦合起来。加密撞击边缘处网格,加密后尺寸为0.007 m。罐底固定约束,通过1/2模型和对称约束模拟冲击响应,以节约计算时间。整体网格划分和加密部位网格划分情况如图 3所示。

|
图 3 罐体有限元模型 Fig. 3 Finite element model of the tanks |
文献[19]证明,Johnson-Cook本构模型能有效模拟钢板在圆柱形撞击物冲击下的变形和断裂。根据相关规范[20],镍合金钢板屈服强度为345 MPa,弹性模量为210 GPa,断裂伸长率为22%。钢材密度设为7 830 kg/m3。采用*MAT_JOHNSON_COOK材料模型模拟钢材,模型参数A、B、n和C分别为345 MPa、400 MPa、0.141 3和0.049 38。采用*MAT_PLASTICITY_POLYMER模拟聚脲,聚脲密度为1 070 kg/m3,弹性模量为150 MPa,泊松比为0.465。使用Cowper-Symonds模型模拟聚脲的应变率效应,参数C和p分别设为98.16 s-1和4.52,与文献[21]的材料参数相同。聚脲与钢罐接触为Tiebreak接触,剥离条件为
| $\left(\frac{\left|\sigma_{\mathrm{n}}\right|}{\sigma_{\mathrm{NFL}}}\right)^2+\left(\frac{\left|\sigma_{\mathrm{s}}\right|}{\sigma_{\mathrm{SFL}}}\right)^2 \geqslant 1$ | (1) |
式中: σn和σs分别为接触面的正应力和剪应力,σNFL和σSFL为接触关键字中定义的容许正应力和容许剪应力,分别等于45 MPa和50 MPa。
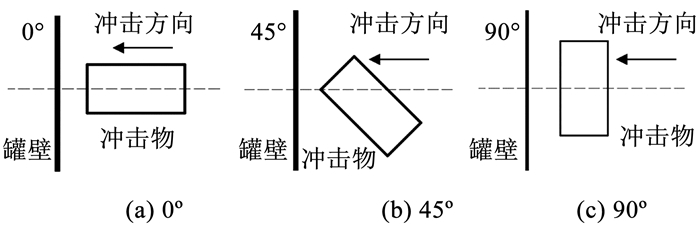
2.2 飞溅物有限元模型钢材密度取为7.83×103 kg/m3,质量为50 kg时飞溅物的体积为6.386×10-3 m3,高径比为2时圆柱体高为0.319 2 m,底面半径为0.079 8 m。在建模过程中,考虑圆柱体与罐壁撞击夹角的影响,撞击夹角定义为圆柱体中心轴线与冲击方向的夹角。撞击夹角以15°为梯度,变化范围为0°~90°。3种典型冲击角度(0°、45°和90°)的相对位置如图 4所示。
|
图 4 圆柱体与罐体夹角示意 Fig. 4 The angle between the tank and the cylinder |
使用实体单元Solid164进行网格划分,网格尺寸为0.01 m。飞溅冲击物视为刚体,使用刚体模型*MAT_RIGID模拟,密度为7.83×103 kg/m3,泊松比为0.3。飞溅物冲击位置为罐体罐壁中间位置,也是罐壁厚度最小的位置,飞溅物与罐体接触为面-面接触。通过*INITIAL_VELOCITY_GENERATION关键字给冲击物赋予45 m/s的初速度。圆柱体飞溅物的有限元模型如图 5所示。

|
图 5 圆柱体冲击物有限元模型 Fig. 5 Finite element model of the cylindrical impactor |
使用LS-PrePost软件进行数值模拟结果的后处理分析,获得罐体位移、应力和应变的分布情况及罐体最大位移时程,对罐体整体和局部的变形程度和变形过程进行分析。
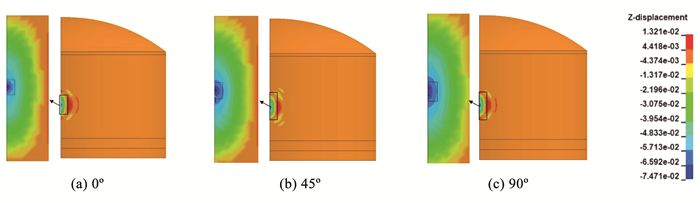
3.1 纯钢罐冲击响应纯钢罐在圆柱体冲击作用下沿冲击方向的位移分布情况如图 6所示。可以看出,罐体整体变形主要为以受冲击位置为中心的凹陷,且出现在受冲击区域的中心位置。圆柱体沿不同方向冲击作用下的罐体变形分布基本相同,最大位移也较为接近,0°、45°和90°冲击角度下的最大位移分别为0.074 6、0.077 0、0.069 7 m。
|
图 6 不同冲击角度下最大位移时刻的位移云图 Fig. 6 Maximum displacement distribution of steel tank subjected to impact loading of different angles |
不同冲击夹角下的罐体局部变形如图 7所示。可以看出,撞击夹角较低或者较高时罐体未出现明显的单元破坏,撞击夹角为30°、45°和60°时产生了穿透破坏,威胁到了罐体安全。夹角为45°时罐体破坏范围最大,说明对罐体威胁最大的撞击夹角在45°附近。

|
图 7 不同冲击夹角的飞溅物撞击下罐体局部变形 Fig. 7 Local deformation process of monolithic tank under impact loading with different angles |
为了更精确地确定破坏最大的冲击夹角,模拟了40°~50°冲击夹角下的罐体响应,如图 8所示,冲击夹角的变化梯度为2.5°。可以看出,冲击夹角为40°时,罐体出现了一定范围的穿透,但是单元破坏范围较小;冲击夹角为50°时,罐体穿透范围较小,单元失效范围较大;冲击夹角为42.5°~47.5°时,罐体同时有较大的穿透和破坏区域,并且,冲击夹角为45°时,罐体的破坏程度略大于冲击夹角为42.5°和47.5°的破坏程度,说明对罐体破坏最严重的冲击夹角为42.5°~47.5°。鉴于45°角度的特殊性,将主要研究45°冲击夹角下的罐体冲击响应和聚脲涂层防护效果。

|
图 8 40°~50°冲击夹角下的飞溅物撞击下罐体局部变形 Fig. 8 Local deformation process of monolithic tank under impact loading with the angles of 40°to 50° |
综上,在规范建议的冲击荷载作用下,罐体响应主要为整体的弹性变形和局部的塑性变形或断裂。罐体最大位移小于0.08 m,仅为罐壁厚度的4倍。在0°~90°冲击作用下,罐体出现局部塑性变形;在30°~60°冲击夹角的冲击荷载作用下出现穿透破坏;冲击夹角接近45°时罐体破坏最为严重,因而45°冲击夹角下的罐体冲击响应和聚脲涂层防护效果是本文的主要研究内容。
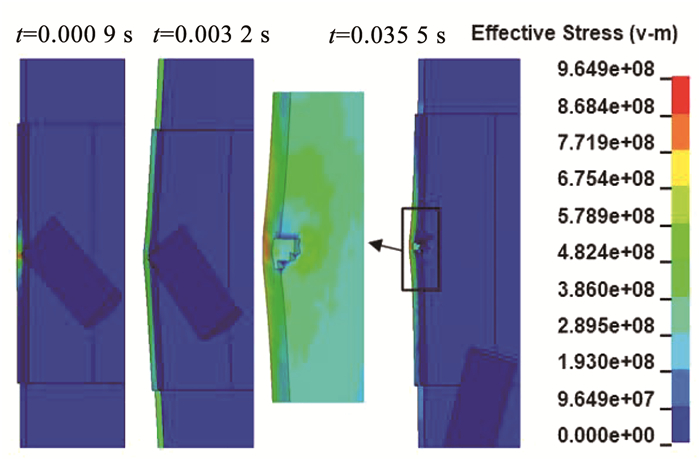
3.2 喷涂聚脲罐冲击响应圆柱体冲击物沿45°方向撞击聚脲厚度为20 mm的外喷涂罐时,其局部变形过程如图 9所示。在圆柱体直角边缘的作用下,罐壁钢壳层和聚脲层均出现了局部单元失效。与纯钢罐相比,聚脲涂覆罐的钢壳层虽然也出现了局部的断裂,但是断裂范围相对较小,且未贯穿罐壁厚度方向,体现了聚脲涂层对罐壁的保护作用。
|
图 9 外喷涂罐体在45°冲击作用下的局部变形过程 Fig. 9 Local deformation process of outer-coated tank under the impact loading of 45° |
根据数值模拟结果,汇总纯钢罐和聚脲涂覆罐的主要响应参数,包括最大位移、局部失效情况和最大塑性应变,如表 1所示。表 1中的响应参数表明,外喷聚脲虽然对罐体最大位移无显著影响,但是有效降低了0°和90°冲击时罐体的局部塑性变形,降低了62.96%和76.23%。在冲击物角度为45°时,外喷聚脲层有效地降低了断裂范围,并且避免了贯穿厚度方向裂孔的出现,保障了罐体和内部液体的安全。
| 表 1 纯钢罐和聚脲涂覆钢罐响应参数 Tab. 1 Response parameters of monolithic steel tanks and polyurea coated tanks |
基于上述有限元模拟方法,进一步研究45°方向冲击荷载作用下外喷罐的响应参数与喷涂参数的关系,以便定量分析涂层作用效果和防护效率,明确涂层应用前景和施工建议。
4.1 罐体最大吸能值以罐壁不产生穿透破坏时能承受的最大冲击物能量(最大吸能值)为抗冲击性能的量化指标。通过控制冲击物速度来控制冲击能量,冲击能量变化梯度为1 kJ。通过数值模拟,发现纯钢罐在冲击物能量为40.625 kJ(40.311 m/s)时未发生穿透破坏,在41.625 kJ(40.804 m/s) 时发生穿透破坏,因此,纯钢罐的最大吸能值近似取为41.125 kJ(40.559 m/s)。通过相同的方法,求得外喷20 mm厚度聚脲层罐体的最大吸能值为61.125 kJ。
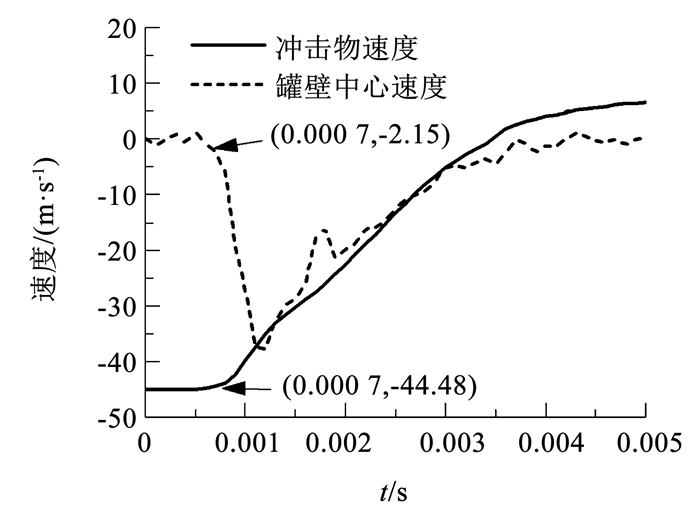
4.2 聚脲涂层作用机制聚脲涂层作为保护层时,能够通过变形降低冲击物速度并提高罐壁局部速度,从而使得冲击物接触罐壁时二者的相对速度减少。喷涂20 mm聚脲层的钢罐在45°冲击作用下的冲击物和罐壁被冲击点的速度时程如图 10所示。模拟结果表明,在模拟时间为0.7 ms时冲击物与罐壁钢壳层接触,此时冲击物速度为44.48 m/s,罐壁中心速度为2.15 m/s,相对速度为42.33 m/s。上述现象说明,聚脲涂层能一定程度上降低罐壁中心和冲击物的相对速度,使得二者接触时冲击力降低,进而避免罐壁破坏。本文将该作用简称为降速作用。
|
图 10 冲击物和罐壁中心速度时程 Fig. 10 Velocity histories of the impactor and the tank′s center |
纯钢罐模拟结果表明,其最大吸能值为41.125 kJ,对应冲击速度为40.559 m/s,而喷涂罐在相对速度为42.33 m/s的冲击作用下未发生穿透破坏,说明在聚脲涂层的保护下,罐体能承受更大速度的冲击作用。这一现象体现了聚脲涂层的另一个作用机制,即喷涂聚脲涂层后,聚脲本身的变形填充了罐壁与冲击物之间的缝隙,间接地提高了罐壁与冲击物的接触面积,从而起到降低罐壁应力集中程度的作用,因此,提升了罐体的最大吸能值,即垫层作用。
4.3 聚脲喷涂厚度在规范建议的冲击荷载作用下,不同喷涂厚度下罐壁局部变形如图 11所示。聚脲厚度为10~50 mm,变化梯度为10 mm。随着聚脲涂层厚度的增加,罐体表面单元失效区域逐渐减小,直至破坏区域完全消失,说明聚脲涂层厚度增加能有效降低或者避免罐体局部破坏。

|
图 11 不同喷涂厚度下罐体局部变形 Fig. 11 Local deformation of the tanks with varying thickness of polyurea coating |
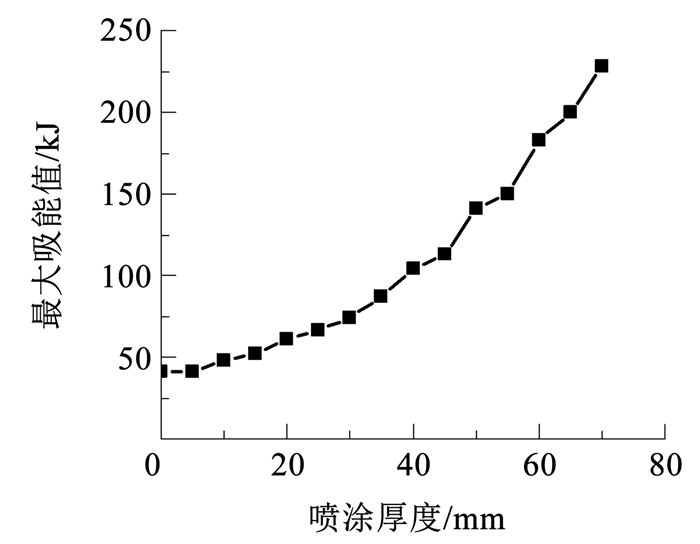
不同喷涂厚度罐体的近似最大吸能值如图 12所示。可以看出,罐体最大吸能值随着聚脲喷涂厚度的增加而增加,二者的关系曲线与幂函数形状相似。规范建议的冲击物能量为50.625 kJ,模拟结果显示涂层厚度为15 mm时,最大吸能值首次超过50.625 kJ,说明需要喷涂15 mm厚的聚脲层才能保证罐体承受规范建议的冲击荷载作用。
|
图 12 最大吸能值与喷涂厚度的关系 Fig. 12 Relationship between maximum energy absorption and coating thickness |
单位面密度吸能值是常用的描述板类构件抗冲击性能的指标[19]。将面密度吸能值用作聚脲涂覆罐吸能效率的量化指标,定义为
| $E_{\mathrm{d}}=\frac{E_{\mathrm{m}}}{A_{\mathrm{d}}}$ | (2) |
其中Ad为试件的面密度,
| $A_{\mathrm{d}}=\rho_{\mathrm{s}} \times d_{\mathrm{s}}+\rho_{\mathrm{p}} \times d_{\mathrm{p}}$ | (3) |
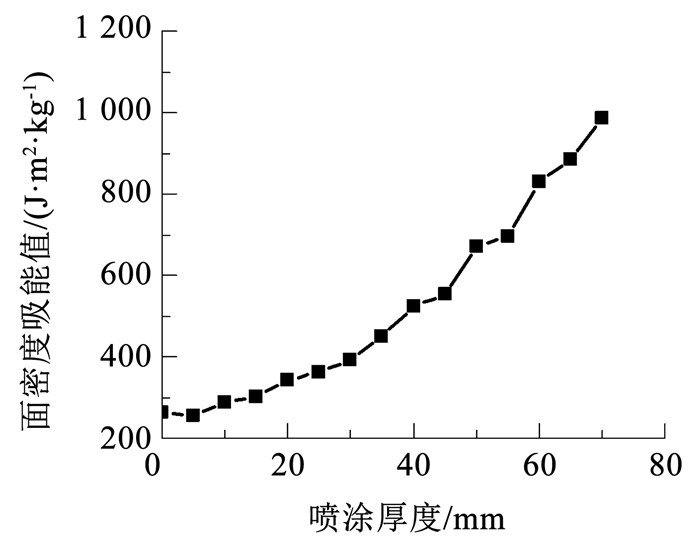
根据罐体最大吸能值与厚度的关系,求得不同喷涂情况下的面密度吸能值,如图 13所示。可以看出,聚脲喷涂罐的吸能效率优于纯钢罐,且随着喷涂厚度增加,吸能效率逐渐增加。说明聚脲涂层对罐体吸能效率有明显的提升作用,且厚度越大,提升效果越明显。
|
图 13 面密度吸能值与喷涂厚度的关系 Fig. 13 Relationship between energy absorption per area density and coating thickness |
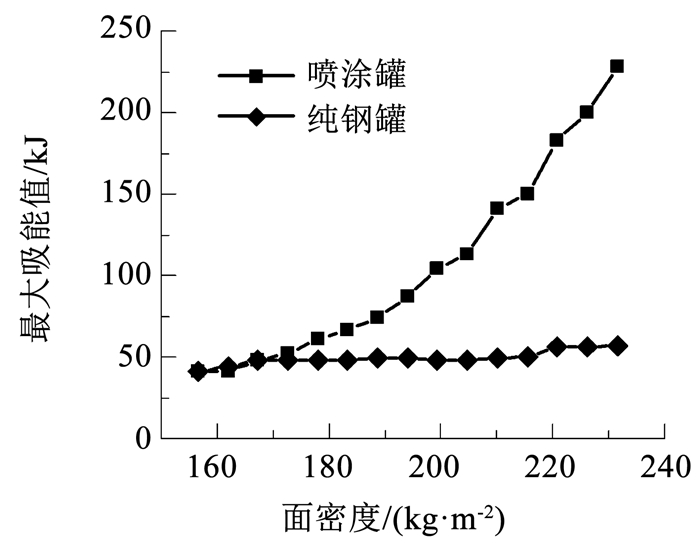
通过数值模拟对比了面密度相同的纯钢罐和喷涂罐的最大吸能值,如图 14所示。可以看出,增加钢壳厚度对罐体最大吸能值的提升效果有限,主要原因是钢壳厚度的提升增加了罐壁的平面外刚度,进而降低罐壁的变形吸能能力,导致冲击物动能更多地转换为罐壁局部断裂的能量,削减了厚度增加对吸能能力的提升效果。
|
图 14 等面密度情况下纯钢罐和喷涂罐抗冲击性能对比 Fig. 14 The impact resistance of uncoated and coated tank with the same area density |
图 14表明,在面密度相同时,聚脲涂层对罐体抗冲击性能的提升作用普遍强于提高钢壳层厚度所起到的效果。主要原因有两点:聚脲的破坏应变远大于钢板材料,且聚脲的密度较低,单位面密度聚脲涂层穿透破坏时的吸能能力大于钢壳材料;钢壳层厚度的增加会提高钢壳的平面外刚度,导致冲击物能量更多地作用于被冲击区域。而聚脲材料对钢壳的平面外刚度影响很小,避免了平面外刚度增加导致罐壁被穿透的情况。
上述内容说明,相比提高罐壁厚度,喷涂聚脲更能起到提高罐体抗冲击性能的作用。因此,聚脲涂层不仅可用于抗冲击加固,也能直接用于新建钢制储罐的抗冲击设计中。
5 罐体穿透能量预测公式参考已有研究[22-24],根据实际情况建立罐壁冲击吸能的预测公式。钢罐罐壁受冲击部位会产生一定的速度,即冲击物的动能一部分转化为罐壁受冲击部位的动能。根据上述现象对应的冲击过程,基于冲击前后的能量守恒可以得
| $\frac{1}{2} m v_0^2=\frac{1}{2} m\left(v_0-\Delta v\right)^2+\frac{1}{2} k \bar{m} v_1^2+E_{\mathrm{s}}+E_{\mathrm{p}}$ | (4) |
式中:v0为冲击物初始速度(m/s);Δv为发生穿透破坏后冲击物速度相对初始值的变化(m/s);v1为发生穿透破坏后,罐壁中心速度(m/s);Es为发生穿透破坏后,钢壳层破坏区域吸收的能量(J);Ep为发生穿透破坏后,聚脲层破坏区域吸收的能量(J);m为冲击过程中罐壁中心区域的等效质量(kg);k为聚脲涂层导致的罐壁面密度放大系数。
当冲击物正好导致罐壁穿透破坏时,穿透后罐壁中心速度与冲击物速度相同,即
| $v_0-\Delta v=v_1$ | (5) |
同时,假设冲击过程中,罐壁其他区域对罐壁中心无显著影响,则根据冲击物与罐壁中心区域的动量守恒,可以得
| $m \Delta v=\bar{m} v_1$ | (6) |
根据式(5)、(6)求得速度之间的关系:
| $\left\{\begin{array}{l}\Delta v=\frac{k \bar{m}}{m+k \bar{m}} v_0 \\ v_1=\frac{m}{m+k \bar{m}} v_0\end{array}\right.$ | (7) |
钢壳层吸能值Es可以根据Mebarki等[24]建立的斜角度下穿透吸能与穿透厚度的关系进行计算:
| $E_{\mathrm{s}}=f_{\mathrm{u}} \varepsilon_{\mathrm{u}} V_{\text {eff }}$ | (8) |
式中:fu为罐壁材料极限抗拉强度,取345 MPa;εu为罐壁材料断裂应变,0.22;Veff为等效塑性变形区域体积(m3), 其计算方法为
| $V_{\mathrm{eff}}=\pi d_{\mathrm{cr}} h_{\mathrm{p}} \sqrt{\pi d_{\mathrm{cr}} h_{\mathrm{p}}}$ | (9) |
式中:dcr为等效塑性变形区域的尺寸(图 15);hp为穿透厚度,冲击物完全穿透钢壳时,hp为钢壳层厚度。

|
图 15 冲击物侵入钢壳层示意 Fig. 15 Perforation of the steel layer |
根据本研究中的冲击物相对角度,可以得dcr=2hp,结合式(8)和(9)可以求得发生穿透破坏时钢壳层吸能值为9.563 kJ。
由于聚脲弹性体材料与钢材的材料性质不同,其断裂伸长率较高,且具有超弹性的应力-应变关系,不能直接用式(8)求Ep。与Mebarki等[24]提出的理论公式相似,假设存在一个等效的聚脲层完全变形区域,由于聚脲材料刚度较低,变形能力较强,可以假设该区域为被冲击物直接压缩的柱状区域,且发生穿透破坏时涂层吸能值等于该部分聚脲涂层完全破坏所吸收的能量,则
| $E_{\mathrm{p}}=e_{\mathrm{pu}} V_{\mathrm{in}}$ | (10) |
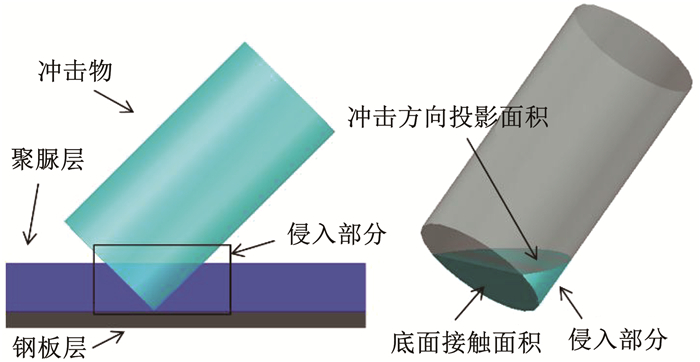
式中:epu为聚脲材料断裂区域应变能密度(J/m3);Vin为冲击物直接压缩的柱状区域的体积(m3)。对聚脲静态应力-应变曲线进行积分,可以求得epu=4×107 J/m3。Vin可以通过投影面积乘以涂层厚度求得。冲击物侵入涂层部分如图 16所示。根据几何关系求得侵入部分体积为
| $V_{\text {in }}=\sqrt{2} \times 0.458\;4 \times H_{\mathrm{p}}^{1.334\;2} \times H_{\mathrm{p}}$ | (11) |
|
图 16 侵入部分及接触面积示意 Fig. 16 Illustration of the contact area and the perforation part |
考虑到聚脲涂层的垫层作用使其在冲击物侵入钢壳层后仍旧起到吸能作用,式(11)中投影面积计算的厚度对应的为钢壳层和聚脲层厚度之和,则
| $V_{\text {in }}=\sqrt{2} \times 0.458\;4 \times\left(0.02+H_{\mathrm{p}}\right)^{1.334\;2} \times H_{\mathrm{p}}$ | (12) |
基于上述结果对式(4)进行简化。代入式(7)、(10)和(12)以及Es后得
| $\begin{aligned} v_0^2= & 2\left[9\;563+2.59 \times 10^7 H_{\mathrm{p}}\left(0.02+H_{\mathrm{p}}\right)^{1.334\;2}\right] \times \\ & \left(\frac{1}{k \bar{m}}+\frac{1}{50}\right)\end{aligned}$ | (13) |
k为聚脲涂层对罐壁的面密度提升比例,即
| $k=\frac{7\;830 \times 0.02+1\;070 \times H_{\mathrm{p}}}{7\;830 \times 0.02}=1+6.83 H_{\mathrm{p}}$ | (14) |
将式(14)代入式(13)并做一定的整理,得
| $\begin{aligned} v_0^2= & {\left[9\;563+2.59 \times 10^7 H_{\mathrm{p}}\left(0.02+H_{\mathrm{p}}\right)^{1.334\;2}\right] \times } \\ & {\left[\frac{1}{\left(1+6.83 H_{\mathrm{p}}\right) \bar{m}}+\frac{1}{50}\right] }\end{aligned}$ | (15) |
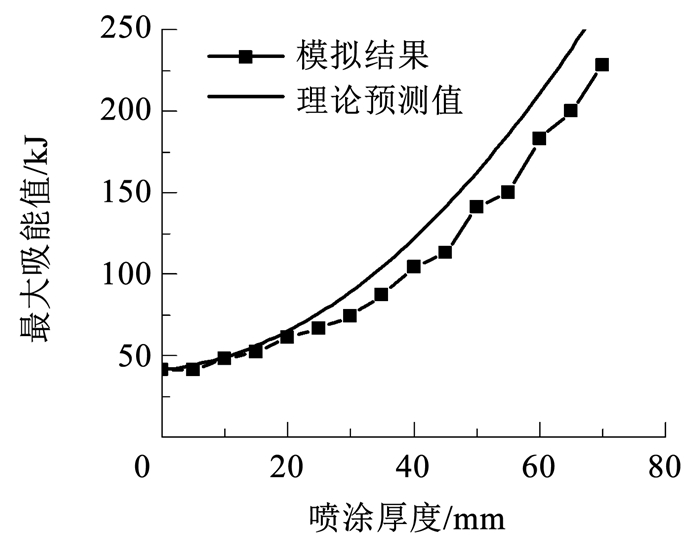
罐壁中心区域等效质量m可以通过纯钢罐穿透情况求得,将Hp=0,v0=40.559 m/s代入式(15),求得 为15.15 kg。将等效质量代入式(15),求得罐壁发生穿透破坏的临界速度,进而得到最大吸能值与喷涂厚度关系的理论预测结果,该结果与数值模拟结果对比如图 17所示。可以看出,理论公式能较为精确地预测喷涂罐最大吸能值与喷涂厚度的关系,误差小于20%,且在变化趋势上与模拟结果完全一致。误差主要来源于数值模拟和预测模型的假设:数值模型中通过删除单元来模拟材料的破坏,因而与理想情况有一定的差距;预测模型中假设接触面投影区域的聚脲层被完全压缩,可能高估了吸能区域的体积,使得预测值略微大于模拟结果。
|
图 17 最大吸能值理论和模拟结果对比 Fig. 17 Comparison between theoretical and simulation results of maximum energy absorption |
为验证本文提出的预测模型的适用性,将模型预测结果与已有模型[24]的预测结果进行对比,如图 18所示。可以看出,已有模型的计算结果与数值模拟结果存在明显的误差,且已有模型预测曲线的变化趋势也与模拟结果不同。主要原因为已有模型适用于金属材料侵彻能量的预测,而聚脲涂层是一种超弹性材料,其材料特性与金属材料有显著差别,因而已有模型在预测喷涂罐最大吸能值时存在较大误差。

|
图 18 最大吸能值的已有模型预测结果与本文结果对比 Fig. 18 Comparison between the predicted results of existing models for maximum energy absorption value and the results of this paper |
1) 根据模拟结果,纯钢罐在规范建议的速度45 m/s、质量50 kg的圆柱体冲击作用下,出现了局部塑性变形,且当冲击物沿45°方向撞击罐体时出现了局部穿孔破坏。说明罐体表面有出现穿孔破坏的可能,无法保持安全。
2) 聚脲喷涂罐体冲击模拟结果显示,外喷涂聚脲有效降低了0°和90°冲击时罐体的局部塑性变形,在冲击物角度为45°时,有效地降低了断裂范围且避免了贯穿厚度方向的裂孔。说明将聚脲涂层作为保护层喷涂于罐体外表面能够起到保护效果。
3) 模拟结果表明:喷涂厚度的增加能持续地增加罐体的最大吸能值和面密度吸能值;当喷涂厚度大于15 mm时,能够避免局部穿孔破坏的产生,使得罐体满足规范要求,体现了罐体外表面喷涂聚脲层的有效性和必要性。模拟结果显示,钢制储罐外表喷聚脲涂层主要起到降速和垫层作用。
4) 考虑冲击作用对罐壁中心速度的影响,根据动量守恒和能量守恒定律,建立了预测罐壁穿孔破坏对应的冲击物动能的理论公式。理论公式预测结果在最大吸能值的大小和变化规律上与模拟结果高度一致,说明该理论公式能有效预测涂层防护钢制储罐的最大吸能值。
| [1] |
张阳, 李勇, 党文义, 等. 典型LNG加气站泄漏事故模拟及探测覆盖率研究[J]. 中国安全科学学报, 2022, 32(增刊1): 108. ZHANG Yang, LI Yong, DANG Wenyi, et al. Leakage accident simulation and detection coverage research of typical LNG filling stations[J]. China Safety Science Journal, 2022, 32(Sup.1): 108. DOI:10.16265/j.cnki.issn1003-3033.2022.S1.0769 |
| [2] |
景国勋, 彭乐, 班涛, 等. 甲烷煤尘耦合爆炸传播特性及伤害研究[J]. 中国安全科学学报, 2022, 32(1): 72. JING Guoxun, PENG Le, BAN Tao, et al. Research on pressure propagation and injury of methane and coal dust coupled explosion[J]. China Safety Science Journal, 2022, 32(1): 72. DOI:10.16265/j.cnki.issn1003-3033.2022.01.010 |
| [3] |
ATKINSON G. Blast damage to storage tanks and steel clad buildings[J]. Process Safety and Environmental Protection, 2011, 89(6): 382. DOI:10.1016/j.psep.2011.06.020 |
| [4] |
朱东. 大型钢储罐在撞击和爆炸荷载作用下的动力响应分析[D]. 杭州: 浙江大学, 2016: 102 ZHU Dong. Dynamic response of large steel storage tank under impact and explosion loads[D]. Hangzhou: Zhejiang University, 2016: 102 |
| [5] |
SCHNEIDER P, BUCHAR F, ZÁPECA F. Structural response to thin steel shell structures due to aircraft impact[J]. Journal of Loss Prevention in the Process Industries, 1999, 12(4): 325. DOI:10.1016/S0950-4230(99)00005-4 |
| [6] |
潘旭海, 徐进, 蒋军成. 爆炸碎片撞击圆柱薄壁储罐的有限元模拟分析[J]. 南京工业大学学报(自然科学版), 2008(3): 15. PAN Xuhai, XU Jin, JIANG Juncheng, et al. Finite element simulation analysis on explosion debris impacting thin-wall cylindrical tanks[J]. Journal of Nanjing University of Technology(Natural Science Edition), 2008(3): 15. DOI:10.3969/j.issn.1671-7627.2008.03.004 |
| [7] |
陈思宇, 陈文江, 胡兆吉, 等. 爆炸碎片撞击球罐的数值模拟及影响因素分析[J]. 南昌大学学报(工科版), 2018, 40(4): 324. CHEN Siyu, CHEN Wenjiang, HU Zhaoji, et al. Numerical simulation of explosion debris impacting spherical tank and analysis of influencing factors[J]. Journal of Nanchang University(Engineering & Technology Edition), 2018, 40(4): 324. DOI:10.3969/j.issn.1006-0456.2018.04.004 |
| [8] |
陈思宇. 爆炸碎片撞击储罐的动力学响应特性数值模拟[D]. 南昌: 南昌大学, 2018: 78 CHEN Siyu. Numerical simulation of explosion debris impacting storage tank[D]. Nanchang: Nanchang University, 2018: 78 |
| [9] |
潘成光, 胡兆吉, 陈文江, 等. 基于LS-DYNA的爆炸碎片撞击圆筒形储罐的数值模拟[J]. 南昌大学学报(工科版), 2019, 41(3): 209. PAN Chengguang, HU Zhaoji, CHEN Wenjiang, et al. Numerical simulation of explosion debris impacting cylindrical tank based on LS-DYNA[J]. Journal of Nanchang University (Engineering & Technology Edition), 2019, 41(3): 209. |
| [10] |
HAMMONS M I, DAVIDSON J S, CONNELL J D, et al. Explosive testing of polymer retrofit masonry walls[J]. Journal of Performance of Constructed Facilities, 2004, 18(2): 100. DOI:10.1061/(ASCE)0887-3828(2004)18:2(100) |
| [11] |
ACKLAND K, ANDERSON C, NGO T D. Deformation of polyurea-coated steel plates under localised blast loading[J]. International Journal of Impact Engineering, 2013, 51: 13. DOI:10.1016/j.ijimpeng.2012.08.005 |
| [12] |
LEBLANC J, SHILLINGS C, GAUCH E, et al. Near field underwater explosion response of polyurea coated composite plates[J]. Experimental Mechanics, 2016, 56(4): 569. DOI:10.1007/s11340-015-0071-8 |
| [13] |
GILBERT J A, CHOI H, TOUTANJI H A, et al. Impact resistance of polyurea-coated high-performance cementitious composites[J]. Journal of Materials in Civil Engineering, 2013, 25(12): 1984. DOI:10.1061/(ASCE)MT.1943-5533.0000714 |
| [14] |
黄微波. 喷涂聚脲弹性体技术[M]. 北京: 化学工业出版社, 2005: 117. HUANG Weibo. Spray polyurea elastomer technology[M]. Beijing: Chemical Industry Press, 2005: 117. |
| [15] |
董鲁生, 张树民. 日本LPG、LNG储罐设计[J]. 油气储运, 1996, 5(15): 51. DONG Lusheng, ZHANG Shumin. LPG and LNG tank design in Japan[J]. Oil & Gas Storage and Transportation, 1996, 5(15): 51. |
| [16] |
Design and manufacture of site built, vertical, cylindrical, flat-bottomed steel tanks for the storage of refrigerated, liquefied gases with operating temperatures between 0 ℃ and-165 ℃, part 1: general: EN 14620-1: 2006[S]. Brussels: European Commite for Standardization Brussels, 2006
|
| [17] |
BSI. Flat-bottomed, vertical, cylindrical storage tanks for low temperature service: BS7777: 1993[S]. London: British Standards Institution, 1993
|
| [18] |
Design and construction of large, welded, low-pressure storage tanks: API620: 2008[S]. Florida: American Petroleum Institute, 2008
|
| [19] |
JIANG Yuexin, ZHANG Boyi, WEI Jianshu, et al. Study on the impact resistance of polyurea-steel composite plates to low velocity impact[J]. International Journal of Impact Engineering, 2019, 133: 103357. DOI:10.1016/j.ijimpeng.2019.103357 |
| [20] |
Flat products made of steel for pressure purposes-part 4: nickel alloy steels with specified low temperature properties: EN 10028-4[S]. Brussels: European Committee For Standardization, 2017
|
| [21] |
JIANG Yuexin, ZHANG Boyi, WEI Jianshu, et al. Study on the dynamic response of polyurea coated steel tank subjected to blast loadings[J]. Journal of Loss Prevention in the Process Industries, 2020, 67: 104234. DOI:10.1016/j.jlp.2020.104234 |
| [22] |
NEILSON A J. Empirical equations for the perforation of mild steel plates[J]. International Journal of Impact Engineering, 1985, 3(2): 137. DOI:10.1016/0734-743X(85)90031-4 |
| [23] |
MEBARKI A, NGUYEN Q B, MERCIER F, et al. A probabilistic model for the vulnerability of metal plates under the impact of cylindrical projectiles[J]. Journal of Loss Prevention in the Process Industries, 2007, 20(2): 128. DOI:10.1016/j.jlp.2006.09.001 |
| [24] |
MEBARKI A, NGUYEN Q B, MERCIER F, et al. Reliability analysis of metallic targets under metallic rods impact: towards a simplified probabilistic approach[J]. Journal of Loss Prevention in the Process Industries, 2008, 21(5): 518. DOI:10.1016/j.jlp.2008.04.002 |
 2024, Vol. 56
2024, Vol. 56


