地下供水管网系统作为城市基础设施的重要组成部分,是保障城市日常生产生活的重要一环。历次地震震害表明,城市供水管网抵御地震的能力较低,特别在地震诱发的断层破裂、滑坡及液化引起的横向扩展和沉降等作用下,接口破坏是管道震损最为常见的破坏形式[1-5]。因此,有效的管线接口抗震措施是优化城市供水管网抗震性能的关键,研究其力学性能对接口管网系统抗震性能的提升具有重要意义。
目前,已有诸多学者对传统球墨铸铁管道柔性接口开展了系列力学性能试验,通过试验研究建立了管道接口抗拉、抗弯和抗扭承载力解析表达式[6],给出了接口受拉变形规律和力-位移关系[7],比较了不同加载形式、管径、加载速率等关键参数对接口力学性能的影响[8-9]。其中,Wham等[10]通过四点弯曲试验推导了关于接口张开量与转角的临界渗漏区间,该失效准则在评估管道在PGD作用下的性能破坏方面取得良好的运用[11]。现有接口力学试验研究多从管线受力和结构破坏角度,缺乏将其使用功能状态与合理的性能水准等级相结合,以量化评定标准。
在管线接口抗震加固方面,主要的措施可分为两类:1)基于在役管线接口的抗震加固和改造;2)研发新型管线材料和新型抗震接口。对于在役管线接口加固改造方面,主要与管线非开挖修复技术相结合[12](包括原位固化法、短管及管片内衬法、螺旋管内衬法,碎管法、不锈钢内衬法等)。试验结果表明,内衬材料特性与黏结强度是影响加固修复效果的关键因素[13-14],其中,部分非开挖修复技术可有效提高管线接口处的变形能力,能够适应高强度的TGD,甚至在接口发生滑脱后依旧保持良好的密封性能[15-16]。在新型管线材料和新型抗震接口方面,日本水道协会(JWWA)指南[17]中给出了12种形式的球墨铸铁管线接口在抗震设计验算中的建议伸缩量及转角。Oda等[18]通过管线断层模拟剪切箱试验和三维有限元模拟,验证了日本Kubota公司研发的球墨铸铁管线可伸缩抗震接口在断层引起的地表大变形作用下可保证管线功能完整。Pariya等[19]测试了两种DN150型球墨铸铁内自锚式接口的轴向拉伸力学性能,分为全约束接口和允许轴向滑移接口,其峰值抗拉承载力分别达到425、370 kN。基于此,Wham等[20-21]比较了该自锚式球墨铸铁管与PVCO两种混合分段管道系统在纵向PGD下的地震响应,结果表明,增加接口允许位移可显著提升管道抗震性能。Kitai等[22]开发了新型耐震钢管接口,经测试DN100型接口可承载400 kN的轴向拉力,达到日本水道协会[23]规定的型式试验标准。现有国外引进的自锚式接口具备更高的抗震性能,但该接口安装附件多,且全管线替换无法实现理想的经济效益,亟待开发一种低成本预制管道卡件且安装便捷的新型抗震接口,实现切实有效且经济环保的目的。
依托机械自锚和自变形补偿的设计思想,在传统球墨铸铁管道承插式接口构造的基础上,研发了一种新型自锚式抗震接口,介绍了该接口的技术设计理念与构造细节。通过轴向拉伸试验比较了两种管道接口的抗拉力学性能与变形特征,探讨了接口张开量与管道功能状态之间的对应关系。最后,结合有限元软件Abaqus对新型抗震接口力学性能试验进行验证与探讨,为进一步深入研究新型自锚式抗震接口对埋地管网抗震性能的影响提供技术支持。
1 新型自锚式抗震接口技术设计 1.1 温度效应供水管网系统在运行过程中,外界环境温度场的变化往往会导致管道应力场和位移场发生改变,对于埋地分段管道,一般通过管土界面摩擦力来调节温度效应引起的管道应力场变化。Jeon等[24]推导了带有圆周裂缝的灰口铸铁管在季节性温度变化下的变形解析式,其假定填料接口具有无限的刚度,因此,管段受温度效应引起的变形均由裂缝断面处代偿。同理,对于具有柔性接口的球墨铸铁管,温差引起的管道膨胀或收缩变形往往会传递至柔性接口处,该变形甚至会导致接口的挤压破坏或插口脱离,图 1给出了管道收缩变形时沿轴线各位置处的管土摩擦力。

|
图 1 温度效应引起的管土摩阻力 Fig. 1 Pipe-soil friction resistance caused by temperature effect |
根据文献[25]中提供的公式,可以计算单位长度管道与土体之间的最大摩擦力为
| $f_{\mathrm{u}}=\left(\frac{1+K_0}{2}\right) \pi D_0 \gamma z \tan \delta_{\mathrm{i}}$ | (1) |
式中:K0为土体静止侧压力系数,D0为管道外径,γ为土的重度,z为管道埋深,δi为管土界面摩擦角。
由土体摩擦而引起的管道轴向应变为
| $F_{\mathrm{f}}(x)=f(x) \mathrm{d} x$ | (2) |
式中f(x)为沿管道方向单位长度上的摩擦力。
则管道由摩擦引起的轴向应变为
| $\delta_{\mathrm{f}}(x)=\frac{F_{\mathrm{f}}(x)}{A E} \mathrm{~d} x$ | (3) |
式中:A为管道横截面积,E为铸铁管道弹性模量。
由温度引起单位长度管道的应变为
| $\delta_{\mathrm{T}}(x)=\frac{\alpha_{\mathrm{T}} \Delta T A E}{A E} \mathrm{~d} x=\alpha_{\mathrm{T}} \Delta T \mathrm{~d} x$ | (4) |
式中:αT为管道的热膨胀系数,ΔT为温差。
则管道接口的变形可由温度引起的位移与摩擦产生的位移差计算,即
| $\delta_{\mathrm{P}}(x)=\alpha_{\mathrm{T}} \Delta T \mathrm{~d} x-\frac{F_{\mathrm{f}}(x)}{A E} \mathrm{~d} x$ | (5) |
单位长度上管道与土体之间的摩擦力f(x)随着管道长度x的增长而增大,到达一定程度后管道与土体之间的摩擦力变为滑动摩擦力,此时两者之间摩擦力的值不再增加,假定此时管道的长度为L0,式(5)化简后得
| $\delta_{\mathrm{u}}\left(L_0\right)=\alpha_{\mathrm{T}} \Delta T L_0-\frac{f_{\mathrm{u}} L_0^2}{6 A E}$ | (6) |
式中δu表示对应临界长度L0处管道在温度与摩擦力作用下的位移。
此时,根据温度引起的管道轴力与摩擦引起的轴力相平衡,即
| $\frac{f_{\mathrm{u}} L_0}{2}=\alpha_{\mathrm{T}} \Delta T A E$ | (7) |
可得
| $L_0=\frac{2 \alpha_{\mathrm{T}} \Delta T A E}{f_{\mathrm{u}}}$ | (8) |
代入式(6)中化简后得
| $\Delta T=\sqrt{\frac{3 \delta_{\mathrm{u}} f_{\mathrm{u}}}{4 \alpha_{\mathrm{T}}^2 A E}}$ | (9) |
通过管道临界长度L0所对应的管道位移δu即可换算临界温差Tc。则对于给定的任意管道长度x,相对于临界长度L0,应分为以下两种情况讨论:
1) 当x≤L0时(温度变化ΔT<Tc)
接口变形为温度效应与管土相互作用引起的变形差值,对管土摩擦引起的变形在[0, x]上积分,即可得接口变形为
| $\delta_{\mathrm{p}}(x)=\alpha_{\mathrm{T}} \Delta T x-\int_0^x \frac{\frac{f_{\mathrm{u}}}{2 L} t^2}{A E} \mathrm{~d} t$ | (10) |
通过式(7)中的轴力平衡可计算具体长度:
| $x_0=\frac{2 \alpha_{\mathrm{T}} \Delta T A E}{f_{\mathrm{u}}}$ | (11) |
将x0代入式(10)中,化简后得到接口变形与温差的关系式为
| $\delta_{\mathrm{p}}=\frac{2 \alpha_{\mathrm{T}}^2 \Delta T^2 A E\left(3 L f_{\mathrm{u}}-2 \alpha_{\mathrm{T}} \Delta T A E\right)}{3 L f_{\mathrm{u}}^2}$ | (12) |
2) 当x>L0时(温度变化ΔT>Tc)
由管土相互作用引起的轴力表达式为
| $F_{\mathrm{f}}(x)=\int_0^L \frac{f_{\mathrm{u}}}{L} x \mathrm{~d} x+f_{\mathrm{u}}(x-L)=\frac{f_{\mathrm{u}} L}{2}+f_{\mathrm{u}}(x-L)$ | (13) |
通过轴力平衡的表达式求解x0,即
| $x_0=\frac{2 \alpha_{\mathrm{T}} \Delta T A E+f_{\mathrm{u}} L}{2 f_{\mathrm{u}}}$ | (14) |
同理,可得接口处变形的积分表达式为
| ${\delta _{\rm{p}}}(x) = {\alpha _{\rm{T}}}\Delta Tx - \int_0^x {\frac{{\frac{{{f_{\rm{u}}}}}{{2L}}{t^2}}}{{AE}}} {\rm{d}}t - \int_L^x {\frac{{{f_{\rm{u}}}(t - L)}}{{AE}}} {\rm{d}}t$ | (15) |
化简并将x0代入式(15)得
| $\delta_{\mathrm{p}}\left(x_0\right)=\frac{\alpha_{\mathrm{T}}^2 \Delta T^2 A E}{2 f_{\mathrm{u}}}-\frac{7 f_{\mathrm{u}} L^2}{24 A E}+\alpha_{\mathrm{T}} \Delta T L$ | (16) |
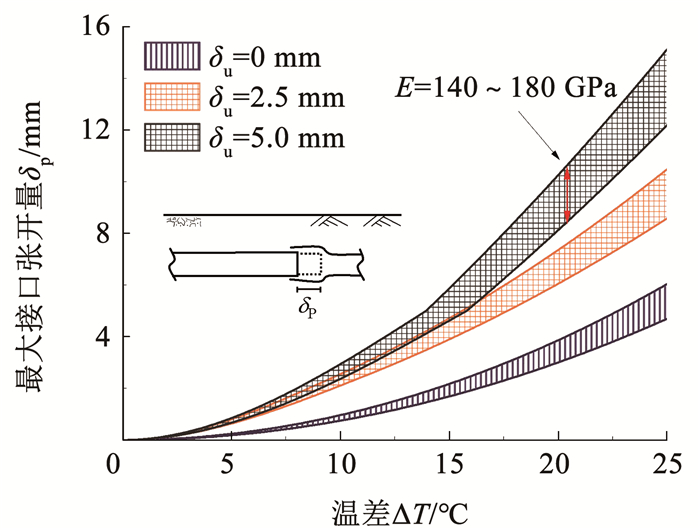
根据上述公式推导,对于给定的物理常量,可计算出不同温差ΔT下的管道接口处张开量δp。以埋深为1 m的DN200型球墨铸铁管为例,假定土体静止侧压力系数K0=1,土体重度γ=19.6 kN/m3,管道外径D0=224 mm,管土界面摩擦角δi=32°,fu=10.8 kN/m,热膨胀系数αT=11.8×10-6/℃,截面积A=7 992 mm2,弹性模量取值范围E=140~180 GPa。对于给定的屈服位移δu,可计算不同温差下的管道接口张开量,详见图 2。
|
图 2 温度效应引起的管道接口变形 Fig. 2 Deformation of pipeline joint caused by temperature effect |
目前城市供水系统所用球墨铸铁管管线普遍采用柔性承插式接口,该接口可承受一定轴向伸缩与径向弯曲,在埋地管线上应用效果较刚性接口更佳。而随着服役年限增长,橡胶密封圈的老化及错位现象往往严重影响接口极限承载能力与密封性,在地震动、震陷、场地液化等作用下,增加了承插式接口滑脱的风险。
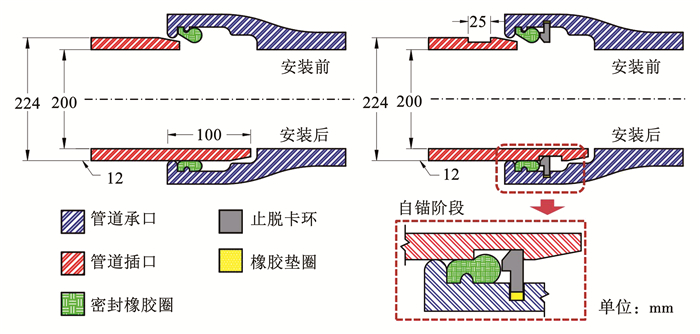
为有效改善普通承插式接口在复杂荷载作用下的防滑脱性能,设计了一种新型自锚式抗震接口。一方面,管节之间既能保持柔性连接的高效密封性和可伸缩性,以吸收温度效应引起的尺寸变化。另一方面,该接口兼具刚性连接的高强抗滑脱特点,尤其在地震荷载引起的断层错位下,所研发接口的抗拉承载力大于单根管道所受的周围土体约束力,进而可有效地将接口处的集中变形传递至相邻管道,以保证管土相对滑移时的接口可靠性。该接口由管道承口、插口、橡胶密封圈和止脱卡环4部分组成,如图 3所示,管道内径为200 mm,其中,密封圈的材质为三元乙丙橡胶,分别由邵氏硬度不同的硬胶和软胶组成,硬胶部分嵌入管道承口预制凹槽中起固定作用,而软胶具有显著高压缩密封性,在管道插口安装到位后发挥止水作用。图 4给出了自锚式抗震接口技术设计流程,具体如下:1)在管道插口外表面环向开槽,宽度为25 mm;2)在承口腔室内侧环向开槽,用以嵌入橡胶垫片和止脱卡环;3)依据承口开槽尺寸,预制3段拼接止脱卡环及相应的垫圈;4)依次将垫片、止脱卡环嵌入承口凹槽,进行承插式接口的安装工作,在管道插口缓慢插入承口过程中,由于卡环与管道插口初次接触面均为梯形斜面,此时橡胶垫片受力压缩,直至止脱卡环完全插入管道凹槽中,安装工作完成;5)在管道接口发生轴向变形时,插口凹槽与止脱卡环接触,进行推力传递,极大提升了管道接口抗拔承载力。
|
图 3 自锚式抗震接口与普通接口构造对比 Fig. 3 Comparison of self anchored seismic joint and ordinary joint construction |

|
图 4 自锚式抗震接口技术设计 Fig. 4 Design of self-anchored seismic joint technology |
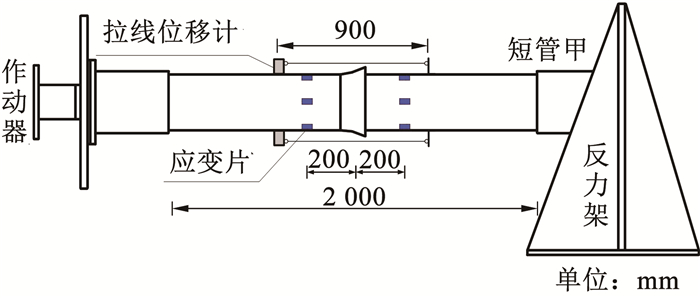
针对供水系统中常见的球墨铸铁管道T型承插式接口和新型自锚式抗震接口开展了轴向拉伸试验研究,图 5为管道接口轴向拉伸试验布置示意,试验装置主要由作动器、滑动支座和反力架组成。首先,按规范要求选取食品级润滑脂进行管道接口安装,安装深度为100 mm,使用吊车将管道试件吊空于滑动支座与反力架之间,分别将入水口短管甲与滑动支座处法兰盘相连接,出水口短管甲与反力架处法兰盘相连接,以确保管道试件在加载过程中受力稳定。管道承口与插口端距200 mm处各环向均布4个应变片,并在接口处环向均匀布置4台拉线位移计(见图 6)。安装完成后,通过注水口控制管内水压强度,加压至试验水压后开始进行接口轴向拉伸试验。
|
图 5 管道接口轴向拉伸试验示意 Fig. 5 Schematic diagram of axial tensile test for pipeline joint |

|
图 6 管道接口轴向拉伸试验 Fig. 6 Axial tensile test of pipeline joints |
本试验针对两类球墨铸铁管道接口开展轴向拉伸加载试验,表 1为管道接口拉伸试验工况,采用位移控制进行轴向加载,单调加载速率为0.1 mm/s,即管道接口承受单方向的拉伸荷载直至发生严重漏水破坏。试验期间通过手压泵控制管道内水压,每组试验加载结束,均更换全新橡胶密封圈再进行下一组试验。
| 表 1 管道接口拉伸试验工况 Tab. 1 Pipeline joints tensile test conditions |
根据管道接口渗漏破坏时水流量大小及管内水压值将损伤状态划分为“初始漏水”状态与“功能失效”状态,“初始漏水”是指管道接口开始出现渗漏或水滴呈间断式下落的状态,“功能失效”是指管内水压卸压至0 MPa时的状态,本试验均在管道接口发生严重漏水后停止加载。
图 7给出了DN200型球墨铸铁管道承插式接口在轴向单调拉伸作用下的轴力-张开量曲线,管道接口轴向抗拉刚度主要来自受压状态下橡胶圈与管道插口外壁间的摩擦力以及橡胶圈自身的抗剪强度。由图 7可知,两种内压下的管道接口承载力曲线发展历程类似,以0.2 MPa工况为例,在加载初期,抗拉承载力处于线性发展阶段,抗拉刚度Kt约为1.0 kN/mm,并在2.8 mm处达到峰值抗拉承载力Fy=1.5 kN。此后承载力出现短暂下降段并开始平稳发展,此时承载力记为Fs,约为1.3 kN。继续加载至37 mm附近时,由于管道插口端管径逐渐减小,橡胶圈产生张力松弛,进而引起管道接口抗拉承载力的下降,直至接口张开量在53.9 mm处发生初始漏水,并在56.6 mm时卸压至0 MPa,接口功能失效,管道接口抗拉性能力学参数见表 2。此外,0~0.2 MPa的水压幅度对承插式管道接口的轴向抗拉强度和抗变形能力的影响较小。

|
图 7 承插式接口轴力-张开量曲线 Fig. 7 Axial force opening curve of socket joint |
| 表 2 管道承插式接口力学性能参数 Tab. 2 Mechanical performance parameters of pipeline socket joint |
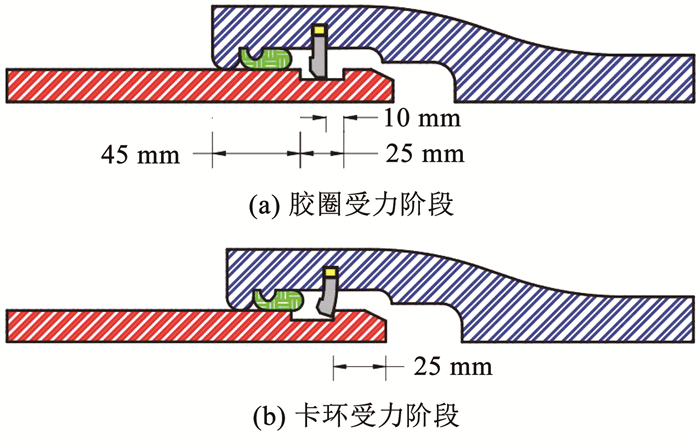
针对DN200型球墨铸铁管道新型抗震接口开展了两组轴向拉伸试验,在插口外表面标注位移刻度线,根据不同的卡环安装位置分别选取10、15 mm两组工况。图 8给出了10 mm安装深度下的接口轴向拉伸过程,其中, 插口外表面开槽宽度为25 mm,深5 mm,卡环宽度为10 mm,该工况在安装过程预留10 mm的可拉伸位移和(25 mm-10 mm-10 mm= 5 mm)的可压缩位移。
|
图 8 抗震接口各受力阶段 Fig. 8 Each stress stage of seismic resistance joint |
图 9给出了安装深度为10 mm时的管道接口轴力-张开量曲线。在加载初期,接口抗拉承载力主要包括橡胶圈与插口间的压应力以及止脱卡环与插口槽间的摩擦力,此时抗震接口首次峰值抗拉承载力达至13.8 kN,略大于上节所述承插式接口,相对应的接口张开量约为1.7 mm,其与普通承插式接口规律类似,均未超过2 mm。随着位移逐步加载,接口承载力同样出现下降阶段,当接口变形量达到10 mm时,卡环初次与插口槽壁接触,在接下来的加载过程中,接口轴向承载力持续上升,并在d=19 mm时达到峰值336 kN。其后承载力并未发生骤降现象,而是出现短暂的稳定波动段,根据接口构造尺寸分析,此时止脱卡环被挤压于承口与插口间,随着加载的继续,直至d=35 mm卡环彻底拔出。在卡环被拔出后,接口承载力便不断骤降,随之胶圈也发生挤压破坏,直到接口承载力降为0 kN时,结束加载。

|
图 9 抗震接口轴力-张开量曲线(卡环深10 mm) Fig. 9 Tensile force-openning curves of anti-seismic joint(snap ring depth 10 mm) |
图 10为安装深度为15 mm时的抗震接口力学性能曲线,在加载初期,与上文分析的工况具有相似的发展规律,在卡环受力前,均由胶圈提供接口抗拉承载力,在张开量为15 mm左右时,开始进入卡环受力阶段,在d=24.3 mm时达到峰值承载力326 kN。但不同于上文结果,该工况在峰值承载力后出现骤降阶段,直至变形量在26.8 mm时出现短暂波动,随后进入第二次承载力骤降段。结合接口构造尺寸及上文分析结果,理论上应在40 mm左右卡环被彻底拔出,接口承载力出现骤降。经分析,由于卡环在承口与插口狭窄间隙中提前发生拉拔滑脱,无法持续提供接口摩阻力,进而承载力提前下降,两组工况下新型抗震接口抗拉性能力学参数见表 3。

|
图 10 抗震接口轴力-张开量曲线(卡环深15 mm) Fig. 10 Tensile force-openning curves of anti-seismic joint(snap ring depth 15 mm) |
| 表 3 抗震接口轴向力学性能参数 Tab. 3 Axial mechanical performance parameters of seismic joint |
总结上述两种工况下DN200型球墨铸铁管道抗震接口试验规律及失效模式,可得:1)抗震接口承载力-张开量曲线大致可分为3个阶段,即密封橡胶圈受力阶段、卡环受力阶段和卡环失效阶段;2)第1阶段中,管道接口屈服位移和峰值承载力与单调加载下的承插式接口力学性能类似;3)第2阶段中,卡环变形量在9 mm左右时,达到峰值承载力(330±4)kN,持续至25 mm时止脱功能完全失效破坏。
4 新型抗震接口力学性能数值模拟 4.1 数值模型基于Abaqus平台建立新型抗震接口数值模型(如图 11所示),考虑到管道接口卡环受力阶段的抗拉承载能力远大于橡胶圈与插口间的摩擦力,本模型未建立密封橡胶圈部分。选用轴对称单元构造等效三维模型,约束管道承口端侧以模拟试验过程中完全固接的法兰连接形式,管道插口端侧建立加载控制点以控制界面区域自由度。根据图 9所示加载过程中止脱卡环的变形规律,将卡环与承口腔室简化为点-面绑定连接。此外,考虑到卡环与插口在加载中发生接触与脱离的过程属于高度非线性问题,采用面-面接触的方式,法向行为采用“硬”接触,切向行为采用“罚”接触,摩擦因数取为0.15。表 4给出了管道接口数值模型材料参数。

|
图 11 抗震接口有限元模型 Fig. 11 Seismic joint finite element model |
| 表 4 数值模型材料参数 Tab. 4 Parameters of numerical model materials |
图 12给出了两种工况下抗震接口数值模拟力学性能与试验实测值对比,由于未考虑橡胶圈的摩擦影响,在初始加载阶段接口承载力为0 kN,当管道插口与卡环接触后,数值模拟与试验结果拟合良好,其中包括明显的抗拉刚度二次上升阶段。

|
图 12 模拟结果与试验结果对比 Fig. 12 Comparison between simulation results and experimental results |
以卡环深15 mm工况为例,在K1=10.8 kN/mm阶段,如图 13(a)中d=16.9 mm时,随着插口的拔出,卡环在腔室间隙中产生轻微偏转,不断下滑,右侧拉应力达到250 MPa。继续加载进入K2=115 kN/mm阶段,此时卡环与腔室紧紧卡住,向下滑移量较小,接口抗拉承载力迅速上升至峰值377.6 kN,高出试验值326 kN约15.8%,此时应力最大值集中于卡环与腔室的接触点,高于卡环的屈服强度,当承载力出现下降段后结束模拟。经分析,在试验过程中,由于插口开槽的尺寸及卡环加工的精度有限,并且卡环与插口凹槽和承口腔室的接触及变形在有限元模型中均比较理想,无法有效反应在轴力过大时,凹槽的塑性大变形和卡环滑脱的试验现象。虽然有限元单元材料的性能误差对接口峰值承载力的影响不可避免,但曲线整体发展规律与试验实测规律基本吻合,体现出较高的真实性,尤其在关键力学特征参数方面,如卡环受力阶段的抗拉刚度分界点以及峰值承载力对应的张开量等。

|
图 13 抗震接口等效应力 Fig. 13 Equivalent stress of seismic joint |
1) 0~0.2 MPa的水压变幅对承插式管道接口的轴向抗拉强度和抗变形能力的影响较小,但对接口屈服位移和极限张开量存在一定影响,呈现出水压越大,屈服位移也逐渐增大的规律,但基本不超过3 mm。此外,接口初始漏水至功能失效状态(卸压至0 MPa)的过渡变形量约为2.5 mm。
2) 新型抗震接口拉伸力学性能曲线分为3个阶段,即胶圈受力阶段、卡环受力阶段和卡环失效破坏,其中,卡环受力阶段变形量在9 mm左右时,达到峰值承载力约为330 kN。
3) 基于Abaqus平台建立的抗震接口数值模型与试验结果有较好的吻合度,有效反应卡环受力阶段抗拉刚度二次上升的过程,其峰值抗拉承载力为377.6 kN,对应张开量为24 mm,与试验实测值误差在2%以内。
| [1] |
孙绍平, 韩阳. 生命线地震工程研究述评[J]. 土木工程学报, 2003, 36(5): 97. SUN Shaoping, HAN Yang. State-of-the-art of the research on lifeline earthquake engineering[J]. China Civil Engineering Journal, 2003, 36(5): 97. DOI:10.15951/j.tmgcxb.2003.05.017 |
| [2] |
O'ROURKE M J, LIU J X. Seismic design of buried and offshore pipelines[M]. New York: Multidisciplinary Center for Earthquake Engineering Research, 2012.
|
| [3] |
李杰. 生命线工程抗震: 基础理论与应用[M]. 北京: 科学出版社, 2005. LI Jie. Structural response network disaster simulation lifeline ground motion reliability[M]. Beijing: Science Press, 2005. |
| [4] |
朱庆杰, 陈艳华, 蒋录珍. 场地和断层对埋地管道破坏的影响分析[J]. 岩土力学, 2008, 29(9): 2392. ZHU Qingjie, CHEN Yanhua, JIANG Luzhen. Influences of site and faults on damage of buried pipelines[J]. Rock and Soil Mechanics, 2008, 29(9): 2392. DOI:10.16285/j.rsm.2008.09.029 |
| [5] |
钟紫蓝, 张亚波, 李锦强, 等. 球墨铸铁管道接口弯曲性能试验[J]. 哈尔滨工业大学学报, 2023, 55(9): 143. ZHONG Zilan, ZHANG Yabo, LI Jinqiang, et al. Bending performance test of push-on joints of ductile iron pipelines[J]. Journal of Harbin Institute of Technology, 2023, 55(9): 143. |
| [6] |
SINGHAL A C. Nonlinear behavior of ductile iron pipeline joints[J]. Journal of Technical Topics in Civil Engineering, 1984, 110(1): 29. DOI:10.1061/JTCEDL.0000018 |
| [7] |
MEIS R D, MARAGAKIS E M, SIDDHARTHAN R. Behavior of underground piping joints due to static and dynamic loading[R]. Technical Report MCEER-03-0006. Buffalo: State University of New York at Buffalo, 2003
|
| [8] |
钟紫蓝, 王书锐, 杜修力, 等. 管道承插式接口轴向力学性能试验研究与数值模拟[J]. 工程力学, 2019, 36(3): 224. ZHONG Zilan, WANG Shurui, DU Xiuli, et al. Experimental and numerical study on axial mechanical properties of pipeline under pseudo-static loading[J]. Engineering Mechanics, 2019, 36(3): 224. DOI:10.6052/j.issn.1000-4750.2017.12.0914 |
| [9] |
李冠潮. 管道柔性接口轴向力学性能及功能性试验研究[D]. 郑州: 河南工业大学, 2020 LI Guanchao. Experimental study on the axial mechanical properties and functional properties of flexible joints in pipelines[D]. Zhengzhou: Henan University of Technology, 2020 |
| [10] |
WHAM B P, O'ROURKE T D. Jointed pipeline response to large ground deformation[J]. Journal of Pipeline System Engineering and Practice, 2016, 7(1): 04015009. DOI:10.1061/(ASCE)PS.1949-1204.0000207 |
| [11] |
QIN X, WANG Y, FU C. Joint kinematics and sealing capacity assessment of ductile iron pipes under abrupt transverse ground movements[J]. Canadian Geotechnical Journal, 2022, 59(3): 342. DOI:10.1139/cgj-2020-0591 |
| [12] |
马保松. 非开挖管道修复更新技术[M]. 北京: 人民交通出版社, 2014. MA Baosong. Trenchless pipeline rehabilitation and renewal tech[M]. Beijing: China Communications Press, 2014. |
| [13] |
ARGYROU C, BOUZIOU D, O'ROURKE T D, et al. Retrofitting pipelines with cured-in-place linings for earthquake-induced ground deformations[J]. Soil Dynamics and Earthquake Engineering, 2018, 115: 156. DOI:10.1016/j.soildyn.2018.07.015 |
| [14] |
钟紫蓝, 王书锐, 甄立斌, 等. 经垫衬法修复后铸铁管道接口力学性能试验[J]. 哈尔滨工业大学学报, 2019, 51(6): 141. ZHONG Zilan, WANG Shurui, ZHEN Libin, et al. Experimental study on mechanical properties of ductile iron pipeline rehabilitated by corrosion protection lining[J]. Journal of Harbin Institute of Technology, 2019, 51(6): 141. DOI:10.11918/j.issn.0367-6234.201812142 |
| [15] |
ZHONG Z, FILIATRAULT A, AREF A. Numerical simulation and seismic performance evaluation of buried pipelines rehabilitated with cured-in-place-pipe liner under seismic wave propagation[J]. Earthquake Engineering & Structural Dynamics, 2017, 46(5): 811. DOI:10.1002/eqe.2832 |
| [16] |
ZHONG Z, BOUZIOU D, WHAM B, et al. Seismic testing of critical lifelines rehabilitated with cured in place pipeline lining technology[J]. Journal of Earthquake Engineering, 2014, 18(6): 964. DOI:10.1080/13632469.2014.916632 |
| [17] |
JWWA. Seismic design specifications for water facilities[S]. [S.l.]: Japan Water Works Association, 1997
|
| [18] |
ODA K, KISHI S, MIYAJIMA M. The pipeline design method against large fault displacement[C]//Pressure Vessels and Piping Conference. [S.l.]: American Society of Mechanical Engineers, 2015, 57034: V008T08A017
|
| [19] |
PARIYA-EKKASUT C. Experimental evaluation of ductile iron pipeline response to earthquake-induced ground deformation[D]. New York: Cornell University, 2018
|
| [20] |
WHAM B P, DAVIS C A. Buried continuous and segmented pipelines subjected to longitudinal permanent ground deformation[J]. Journal of Pipeline Systems Engineering and Practice, 2019, 10(4): 04019036. DOI:10.1061/(ASCE)PS.1949-1204.0000400 |
| [21] |
BANUSHI G, WHAM B P. Deformation capacity of buried hybrid-segmented pipelines under longitudinal permanent ground deformation[J]. Canadian Geotechnical Journal, 2021, 58(8): 1095. DOI:10.1139/cgj-2020-0049 |
| [22] |
KITAI Y, NODA H, KUWATA Y. A development of seismic joint of steel pipe attached on the bridge[J]. Structural Engineering & Earthquake Engineering, 2021, 77(4): 79. DOI:10.2208/jscejseee.77.4_I_79 |
| [23] |
JWWA. GX type ductile iron pipes for watersupply: JWWA G 120[S]. [S.l.]: Japan Water Works Association, 2013
|
| [24] |
JEON S S, O'ROURKE T D, NERAVALI A N. Repetitive loading effects on cast iron pipelines with cast-in-place pipe lining systems[J]. Journal of Transportation Engineering, 2004, 130(6): 692. DOI:10.1061/(ASCE)0733-947X(2004)130:6(692) |
| [25] |
American Lifelines Alliance. Seismic guidelines for water pipelines[M]. [S.l.]: ASCE, 2005.
|
 2024, Vol. 56
2024, Vol. 56


