2. 地震灾害防治应急管理部重点实验室,哈尔滨 150080
2. Key Laboratory of Earthquake Disaster Mitigation, Ministry of Emergency Management, Harbin 150080, China
地震预警是除了加强工程抗震外另一有效的减轻地震灾害的重要手段[1]。地震预警系统利用震中附近台站观测到的P波信号对震源参数以及地震的破坏程度进行估计,并以电子通信的方式在破坏性地震波到达目标场地之前向公众发布地震预警信息,提供几秒甚至几十秒的预警时间去采取防震减灾措施[2-7]。在地震预警中,震级是地震基本参数快速确定中的基本问题之一[8],也是快速判断地震潜在破坏区域的重要参数之一,因此,快速和准确地预测震级对于地震预警系统非常重要[9-10]。随着地震台站记录到的地震数据的增加以及人工智能技术的发展,许多科研工作者将机器学习方法应用到地震学、防震减灾等相关领域的研究中[11-13],包括震源机制的确定[14]、地震动参数的预测[15-17]、地震定位[18]、震相识别[19]等。一些学者尝试将机器学习方法应用到震级估计的研究中[20-23]。基于日本K-NET台网记录的强震动数据,朱景宝等[24]建立了P波到达后不同时间窗下的单台深度卷积神经网络震级估计(deep convolutional neural network for earthquake magnitude estimation, DCNN-M)模型,并根据2021年5月21—22日云南漾濞地震和青海玛多地震中强震仪记录到的强震动数据,分析了该模型在云南漾濞地震和青海玛多地震中震级估计的可行性。
目前,国家预警工程项目采用基准站、基本站、一般站“三网合一”的地震监测方案,其中,烈度仪布设数量超过万台。近年来,中国发生了多次大震,地震发生后,除了强震仪记录到地震数据,烈度仪也记录到大量的地震数据。为了分析地震烈度仪对卷积神经网络模型震级估计的影响,基于朱景宝等[24]建立的预训练的DCNN-M模型,以2022年中国发生的5次破坏性地震(MS≥5.8)为例,其中包括青海门源6.9级地震[25-26]和四川泸定6.8级地震[27],将预训练的DCNN-M模型应用到这5次地震中,讨论了地震发生后,只考虑已触发强震仪情况下的震级估计以及地震发生后引入已触发烈度仪后的震级估计。
1 地震数据为了探索地震烈度仪对朱景宝等[24]建立的预训练DCNN-M模型震级估计的影响,选择2022年发生在中国且烈度仪和强震仪均记录到地震数据的5次破坏性地震事件(MS≥5.8)作为研究对象,目的是可以将同一地震事件中的烈度仪和强震仪的震级估计结果进行比较。5次地震事件信息见表 1,其中包括1 788组烈度仪地震动记录(5 364条三分向加速度记录)和111组强震仪地震动记录(333条三分向加速度记录)。烈度仪和强震仪记录到的地震动数量在不同震中距范围内的分布见图 1(a)。同时,Carranza等[28]将垂直方向P波到达后5 s内的峰值速度与P波到达前5 s内的峰值速度的比值定义为信噪比,并将其用于衡量台站记录到的地震动数据的信号质量。由于Carranza等[28]针对的是宽频带速度记录,而本文采用的是加速度记录,直接采用峰值加速度进行信噪比度量,即
| $R_{\mathrm{SN}}=\frac{P_{\mathrm{a} \text { after }}}{P_{\mathrm{a}, \text { before }}}$ | (1) |
| 表 1 地震事件信息 Tab. 1 Information of earthquake events |

|
图 1 烈度仪和强震仪数据在不同震中距和信噪比范围的分布 Fig. 1 Distribution of data of low-cost sensors and strong motion instrument in different ranges of epicentral distance and signal-to-noise ratio |
式中:RSN为信噪比,Pa,after为P波到达后5 s内的峰值加速度,Pa,before为P波到达前5 s的峰值加速度。烈度仪和强震仪记录到的地震动数据在不同信噪比范围内的分布见图 1(b)。和强震仪记录的地震动数据的信噪比相比,烈度仪记录的地震动数据的信噪比偏低, 且主要分布在0~20。
采用马强等[29]提出的P波捡拾方法对垂直方向未滤波的加速度记录进行P波拾取并进行人工校准。对加速度记录进行积分得到速度记录,再对速度记录进行积分得到位移记录。同时,为了消除积分造成的低频漂移,使用4阶0.075 Hz高通巴特沃斯滤波器对积分后的记录进行滤波。
2 卷积神经网络模型 2.1 模型输入DCNN-M模型输入为单个台站获取的3类12个与震级相关的特征参数[24],分别是3个周期类特征参数、3个幅值类特征参数和6个能量类特征参数。3个周期类特征参数包括[30-32]平均周期参数τc、峰值比参数Tva和构造参数TP;3个幅值类特征参数包括[33-34]峰值加速度参数Pa、峰值速度参数Pv和峰值位移参数Pd;6个能量类特征参数包括[24, 35-37]速度平方积分参数IV2、累积绝对速度参数CAV、累积能量变化率参数PIv、垂直向累积绝对加速度参数cvaa、垂直向累积绝对速度参数cvav和垂直向累积绝对位移参数cvad。根据第1节处理后的烈度仪和强震仪地震数据以及P波到达时间,可以计算P波到达后相应时间窗下的特征参数。根据文献[38-39],将幅值类和能量类特征参数统一校正到参考震源距10 km。此外,由于不同的特征参数之间可能存在不同的数量级,导致作为模型输入的数据之间存在不平衡问题,对每个特征参数做了标准化处理,且统一到[-1, 1],标准化处理的公式为
| $X_{\mathrm{norm}}=\frac{2 X-\left(X_{\max }+X_{\min }\right)}{X_{\max }-X_{\min }}$ | (2) |
式中:X为标准化处理前的特征参数,Xnorm为标准化处理后的特征参数,Xmax为训练集中相应特征参数的最大值,Xmin为训练集中相应特征参数的最小值。在实际运行中,根据已触发的台站可以计算得到特征参数X;将特征参数X代入式(2),可得特征参数X对应的标准化后特征参数Xnorm;将标准化后的每个特征参数Xnorm作为模型的输入。
2.2 模型架构朱景宝等[24]使用日本K-NET台网记录的强震动地震数据建立了P波到达后不同时间窗下的DCNN-M模型,研究表明,与传统的地震预警震级估计τc方法和Pd方法相比,DCNN-M模型有更鲁棒的震级估计结果。
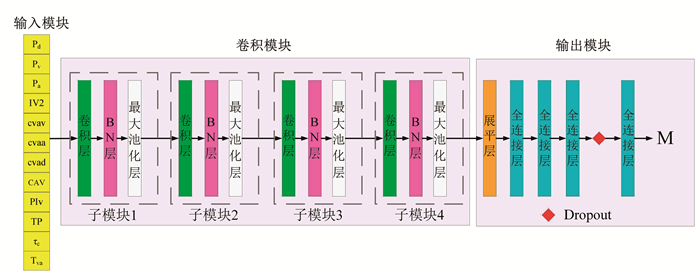
预训练的DCNN-M模型架构(见图 2)主要由3个模块组成[24],即输入模块、卷积模块和输出模块。输入模块主要由2.1节介绍的12个特征参数组成,其输入的尺寸为(12, 1)。卷积模块主要由4个子模块组成,每个子模块主要由卷积层、Batch normalization层(BN层)和最大池化层组成,且对每个最大池化层输出的结果使用了修正线性单元(rectified linear unit, ReLu)激活函数进行非线性的转换。卷积模块的最终输出通过一个展平层传递给全连接层。输出模块主要由4个全连接层组成,前3个全连接层使用ReLu激活函数,最后一个全连接层使用线性函数且输出预测结果。同时,为了防止DCNN-M模型过拟合,在第3个全连接层后接了一个Dropout层。DCNN-M模型详细的超参数设置以及训练过程在朱景宝等[24]的研究中有详细的介绍,不再赘述。
|
图 2 DCNN-M模型的网络架构 Fig. 2 Network architecture of DCNN-M model |
为了探索地震烈度仪对朱景宝等[24]建立的预训练DCNN-M模型震级估计的影响,分析了第1节中地震事件的震级估计结果以及烈度仪和DCNN-M模型在地震预警震级估计中的适用性。
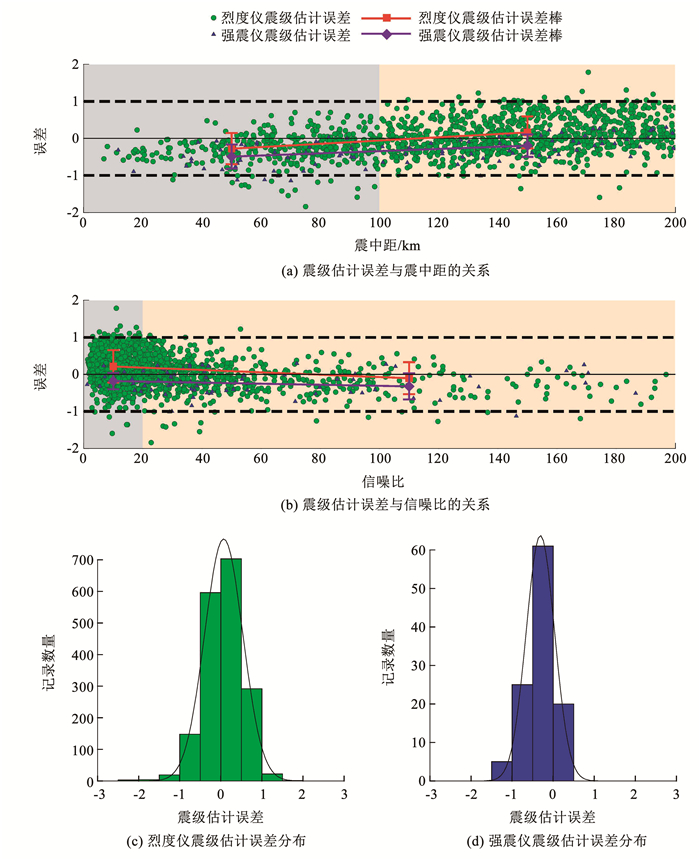
在P波到达后3 s,分析了烈度仪和强震仪地震数据的单台震级估计误差在不同震中距和信噪比的分布,结果见图 3(a)、(b)。可以看出:对于这5次破坏性地震的地震动数据,与强震仪相比,在震中距小于100 km的情况下,烈度仪震级估计误差均值更接近0,且烈度仪和强震仪的震级估计误差的不确定度比较接近;在震中距大于100 km的情况下,与强震仪相比,烈度仪有更大的震级估计误差不确定度;同时,在震中距小于100 km和震中距大于100 km的情况下,烈度仪比强震仪有更大的震级估计误差均值;在信噪比小于20和大于20的情况下,烈度仪震级估计误差均值高于强震仪震级估计误差均值;在信噪比小于20的情况下,与强震仪相比,烈度仪有更大的震级估计误差不确定度,且强震仪震级估计误差均值比烈度仪震级估计误差均值更接近0;在信噪比大于20的情况下,烈度仪和强震仪震级估计误差的不确定度比较接近,且烈度仪震级估计误差均值比强震仪更接近0。同时,对于这5次破坏性地震事件的地震动记录,在P波到达后3 s,图 3(c)、(d)为烈度仪和强震仪的单台震级估计误差分布直方图,可以看出,烈度仪和强震仪的震级估计主要分布在±1震级误差范围内。结合图 4还可以看出:强震仪震级估计误差受信噪比的影响较小;对于烈度仪,低信噪比数据整体上比高信噪比数据有更大的震级估计误差和离散性。
|
图 3 P波到达后3 s单台的震级估计误差 Fig. 3 Magnitude estimation error using single station within 3 s after P-wave arrival |

|
图 4 P波到达后3 s单台的震级估计误差在不同信噪比的分布 Fig. 4 Distribution of magnitude estimation error using single station at different signal-to-noise ratios within 3 s after P-wave arrival |
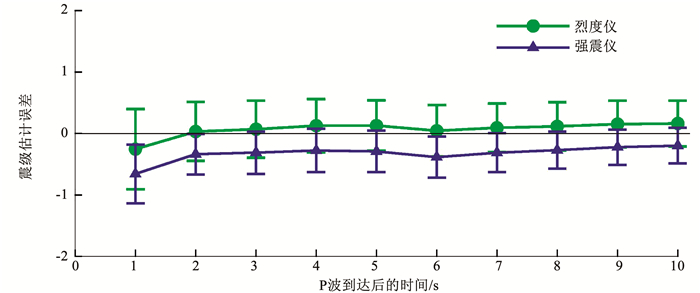
对于5次破坏性地震的地震动记录,图 5为P波到达后1~10 s内,基于烈度仪和强震仪地震数据的单台震级估计误差。单台震级估计误差的计算公式为
| $E_i=M_{\mathrm{pre}, i}-M_{\text {cat }}$ | (3) |
|
图 5 震级估计误差与P波到达后时间的关系 Fig. 5 Relationship between magnitude estimation error and time after P-wave arrival |
式中:Ei为第i条地震记录的震级估计误差,Mpre,i为第i条地震记录的预测震级,Mcat为编目震级。由图 5可以看出:对于这5次破坏性地震的地震动记录,在P波到达后1 s,烈度仪和强震仪的震级估计误差均值都小于0,随着P波到达后时间窗长的增加,烈度仪和强震仪的震级估计误差均值向0靠近;在P波到达后10 s内,与强震仪相比,烈度仪震级估计误差均值更接近0,且烈度仪的震级估计误差均值与强震仪的震级估计误差均值的差值在0.3左右;误差棒一半的长度表示不确定度(即震级估计误差的一倍标准差),且烈度仪和强震仪的不确定度接近。
对于5次破坏性地震的地震动记录,图 6(a)、(b)为不同震中距范围烈度仪和强震仪的震级估计误差与P波到达后时间窗长的关系。可以看出:对于震中距100 km以内的数据,在P波到达后10 s内,与强震仪相比,烈度仪的震级估计误差均值更接近0,且烈度仪和强震仪的震级估计误差的不确定度接近;震中距100 km以内的烈度仪和强震仪震级估计误差均值的差值比震中距100 km以外的烈度仪和强震仪的震级估计误差均值的差值要小。对于5次破坏性地震的地震动记录,图 6(c)、(d)为不同信噪比范围烈度仪和强震仪的震级估计误差与P波到达后时间窗长的关系。可以看出:对于信噪比小于20的数据,在P波到达后10 s内,强震仪震级估计误差均值比烈度仪的震级估计误差均值更接近0,且烈度仪有更大震级估计误差的不确定度;对于信噪比大于20的数据,与强震仪相比,烈度仪震级估计误差均值更接近0,烈度仪和强震仪的震级估计误差的不确定度接近。

|
图 6 不同震中距、不同信噪比情况下震级估计误差与P波时间窗的关系 Fig. 6 Relationship between magnitude estimation error and P-wave time window under different epicentral distance and signal-to-noise ratios |
图 7为5次地震事件DCNN-M模型的震级估计误差随震后时间的演化。由于烈度仪和强震仪的地震触发首台位置不一致,为了在统一的时间标尺上进行比较,从震后时间开始(即发震时刻开始)计算,采用了震后时间,而没有使用首台触发时间。在此基础上,以首台触发后间隔1 s计算对应的震级估计。同时,对于震级估计忽略了数据打包延时、网络传输延时和数据处理时间等的影响,否则,对应的获得震级估计的时间还会再靠后。

|
图 7 5次破坏性地震事件的震级估计误差随震后时间的演化 Fig. 7 Evolution of magnitude estimation errors for five destructive earthquake events with time from origin time |
由于DCNN-M模型输出的是单个台站的震级估计结果,在地震发生后,通过多台平均的方法对已经触发的台站获得震级估计进行多台平均得到最终的震级估计。震后实时多台平均震级计算步骤如下:
1) 地震发生后,对于最先触发的台站,从P波到达后1 s开始计算震级估计;
2) 当再次有新的台站触发后,将P波到达后时间窗满足3 s的台站获得震级求平均值即可得到震后此刻的震级估计结果。多台平均震级计算公式为
| $M=\frac{\sum\limits_{i=1}^N M_i^j}{N}$ | (4) |
式中:N为符合步骤1)和2)的已触发的台站数,Mij为第i个已触发的台站在P波到达后第j秒的震级估计。
对于2022年1月8日门源6.9级地震,由图 7(a)可以看出,仅考虑已触发强震仪的情况下,在震后9.4 s得到震级估计结果,且震级估计误差在±0.5震级单位范围内。由图 7(b)、(c)可以看出:与仅考虑已触发强震仪相比,在引入已触发烈度仪的情况下,更快地(在震后3.1 s)获得震级估计结果;同时,在震后5.1 s时,震级估计误差在±0.5震级单位的范围内。
对于2022年6月1日芦山6.1级地震,由图 7(a)可以看出:仅考虑已触发强震仪的情况下,在震后7.3 s获得震级估计,且震级估计误差大于1;在震后12.3 s时,震级估计误差在±0.5震级单位范围内。由图 7(b)、(c)可以看出:与仅考虑已触发强震仪相比,在引入已触发烈度仪的情况下,更快地(在震后4.1 s)获得震级估计结果;同时,在震后6.1 s时,震级估计误差在±0.5震级单位范围内。
对于2022年6月10日马尔康5.8级地震,由图 7(a)可以看出:仅考虑已触发强震仪的情况下,在震后10.3 s获得震级估计,且震级估计误差大于0.5;在震后11.3 s时,震级估计误差在±0.5震级单位范围内。由图 7(b)、(c)可以看出:与仅考虑已触发强震仪相比,在引入已触发烈度仪的情况下,更快地(在震后4.3 s)获得震级估计结果;且在震后5.3 s时,震级估计误差在±0.5震级单位范围内。
对于2022年6月10日马尔康6.0级地震,由图 7(a)可以看出:仅考虑已触发强震仪的情况下,在震后10.1 s获得震级估计,震级估计误差大于1;在震后11.1 s时,震级估计误差在±0.5震级单位范围内。由图 7(b)、(c)可以看出:与仅考虑已触发强震仪相比,在引入已触发烈度仪的情况下,更快地(在震后4.3 s)获得震级估计结果;在震后5.3 s时,震级估计误差在±0.5震级单位范围内。
对于2022年9月5日泸定6.8级地震,由图 7(a)可以看出:仅考虑已触发强震仪的情况下,在震后4.3 s获得震级估计,且震级估计误差大于0.5;在震后7.3 s时,震级估计误差在±0.5震级单位范围内。由图 7(b)可以看出:仅考虑烈度仪的情况下,在震后6.4 s获得震级估计,且震级估计误差大于1;在震后7.4 s时震级估计误差在±0.5震级单位范围内。此外,由图 7(c)可以看出,同时考虑烈度仪和强震仪的情况下,在震后7.3 s,震级估计误差也在±0.5震级单位范围内。
通过对门源6.9级地震、芦山6.1级地震、马尔康5.8级地震和马尔康6.0级地震的分析可以看出:与仅考虑已触发的强震仪数据相比,引入已触发的烈度仪数据后,可以更快地获得鲁棒的震级估计。对于泸定6.8级地震,最先触发的是强震仪,引入已触发的烈度仪数据后,在震后7.3 s震级估计误差在±0.5震级单位范围内,这也说明在引入烈度仪数据后,进一步提升了震级估计的稳定性和可靠性。
为了减小幅值参数和能量参数因距离增加导致的衰减问题,DCNN-M模型依据前人对幅值参数的通用做法,通过建立点源衰减关系[38-39],将幅值类和能量类特征参数统一校正到参考震源距10 km,即
| $\lg Y=a+b M+c \lg R$ | (5) |
| $\lg Y^{10 \mathrm{~km}}=a+b M+c \lg 10$ | (6) |
| $\frac{Y^{10 \mathrm{~km}}}{Y}=c-c \lg R$ | (7) |
式中:Y为观测的地震动值(幅值类参数或能量类参数),Y10 km为校正到参考震源距10 km后的地震动值,a、b、c为常数,R为震源距,M为震级。通过式(5)和(6)联立可以得到式(7)。然而,对于6~7级地震,地震破裂尺度可达30 km,大陆板内的走滑地震破裂尺度更长[40-41],因此,对于大地震事件的衰减关系,通常应考虑地震的破裂尺度,点源衰减关系得到的地震动预测值要小于考虑破裂尺度的衰减关系;同时,目前文章所作的研究还很难通过简单的方式确定简化断层破裂尺度对地震预警震级估计结果的具体影响大小,这在未来的研究中应重点考虑。
在本文的研究中,由于DCNN-M模型是利用日本K-NET台网数据训练得到的,K-NET台站都布设于地表(土层),记录数据存在一定的场地效应影响,这可能导致DCNN-M模型存在一定程度的震级估计偏差。此外,日本气象厅使用的震级标度为Mj,本文5次地震事件的震级标度为MS,根据Peng等[42]的研究,Mj和MS这两个震级标度可以近似相等,所以,忽略了这两个震级标度的差异。然而这两个震级标度并非完全相同,这种差异可能导致DCNN-M模型直接用于中国烈度仪(或强震仪)观测数据的震级估计存在一定程度的系统偏差。通过本文的研究可以看出:对于本文的地震事件,DCNN-M模型在没有考虑场地特征以及忽略震级标度差异性的情况下,在震后短时间内可以获得鲁棒的震级估计结果。当然,为了提高和改进DCNN-M模型的泛化性能,未来的研究中可以尝试在DCNN-M模型的输入中引入场地特征,扩充DCNN-M模型的训练数据,在训练数据中加入中国的烈度仪(或强震仪)地震数据及对应的震级标度,使DCNN-M进一步学习不同的震级标度。
Mousavi等[43]通过深度学习网络对斯坦福地震数据集中震级在5.7级以下的地震事件进行震级估计,并将地震波形作为输入,虽然预测震级与实际震级存在一定的相关性,但震级估计误差仍存在较大的离散性;胡安东等[22]通过深度学习网络对日本地震数据进行震级估计,并将地震波形的频谱信息作为模型的输入,震级估计结果虽然比传统的τc方法有更高的准确性,但震级估计结果仍存在较大的离散性,并且胡安东等[22]认为多特征组合输入会进一步提高震级估计的准确性。同时,现地地震动预测的研究中,一些学者将特征参数作为机器学习、深度学习模型的输入[44-46]。所以,DCNN-M模型采用了与震级相关的特征作为输入。此外,由于烈度仪的信噪比普遍偏低,在不同信噪比范围下,基于烈度仪数据的DCNN-M模型震级估计性能会受到影响。目前,人工智能方法在低信噪比的条件下对于P波到时拾取也有很高的准确性[47-49],在未来的研究中也会考虑将人工智能P波到时拾取与震级估计相结合。
4 结论1) 本文DCNN-M模型忽略了场地的影响和震级标度的差异性,为了提高DCNN-M模型地震预警震级估计中的性能,可以尝试在DCNN-M模型的输入中加入场地特征,以及在训练集中加入不同震级标度对应的地震数据,使得DCNN-M模型学习场地特征和不同的震级标度。
2) 通过采取人工智能方法提高P波拾取的准确性可能在一定程度上提高DCNN-M模型地震预警震级估计性能。
3) 本文使用的DCNN-M模型展现了鲁棒的震级估计性能。然而,对于7级以上的地震以及震源持续时间更长的地震,DCNN-M模型在应用到地震预警系统之前还有待验证。
4) 在未来的研究中,为了改进DCNN-M模型或将该方法推广应用到全球大震频发地区,可以尝试在DCNN-M模型中引入断层破裂信息、扩大DCNN-M模型的训练数据集(包括不同地区的数据以及最大震级范围)以及结合迁移学习的方法等。
5) 在这5次地震中,由于烈度仪的数量更多、分布更密,引入烈度仪地震数据后,DCNN-M模型更快地获得鲁棒的震级估计。然而,多大的台站密度对于DCNN-M模型地震预警震级估计是最有益的,未来的研究中还需要结合实际的地震预警工程作进一步的研究和分析。
6) 烈度仪的震级估计性能在一定程度上受到低信噪比的影响,在未来的中国地震预警系统建设中,是否可以通过提高台站记录地震信号的信噪比来改进烈度仪在DCNN-M模型地震预警震级估计的性能还有待进一步的研究。
| [1] |
李山有, 金星, 马强, 等. 地震预警系统与智能应急控制系统研究[J]. 世界地震工程, 2004, 20(4): 21. LI Shanyou, JIN Xing, MA Qiang, et al. Study on earthquake early warning system and intelligent emergency controlling system[J]. World Earthquake Engineering, 2004, 20(4): 21. |
| [2] |
ALLEN R M, MELGAR D. Earthquake early warning: advances, scientific challenges, and societal needs[J]. Annual Review of Earth and Planetary Sciences, 2019, 47: 361. DOI:10.1146/annurev-earth-053018-060457 |
| [3] |
PENG Chaoyong, MA Qiang, JIANG Peng, et al. Performance of a hybrid demonstration earthquake early warning system in the Sichuan-Yunnan border region[J]. Seismological Research Letters, 2020, 91(2A): 835. DOI:10.1785/0220190101 |
| [4] |
PENG Hanshu, WU Zhongliang, WU Y M, et al. Developing a prototype earthquake early warning system in the Beijing capital region[J]. Seismological Research Letters, 2011, 82(3): 394. DOI:10.1785/gssrl.82.3.394 |
| [5] |
PENG Chaoyong, JIANG Peng, MA Qiang, et al. Performance evaluation of an earthquake early warning system in the 2019—2020 M6.0 Changning, Sichuan, China, seismic sequence[J]. Frontiers in Earth Science, 2021, 9: 699941. DOI:10.3389/feart.2021.699941 |
| [6] |
PENG Chaoyong, JIANG Peng, MA Qiang, et al. Chinese nationwide earthquake early warning system and its performance in the 2022 Lushan M6.1 earthquake[J]. Remote Sensing, 2022, 14(17): 4269. DOI:10.3390/rs14174269 |
| [7] |
ZHANG Hongcai, JIN Xing, WEI Yongxiang, et al. An earthquake early warning system in Fujian, China[J]. Bulletin of the Seismological Society of America, 2016, 106(2): 755. DOI:10.1785/0120150143 |
| [8] |
马强. 地震预警技术研究及应用[D]. 哈尔滨: 中国地震局工程力学研究所, 2008 MA Qiang. Study and application on earthquake early warning[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2008 |
| [9] |
PENG Chaoyong, YANG Jiansi, CHEN Yang, et al. Application of a threshold-based earthquake early warning method to the Mw6.6 Lushan earthquake, Sichuan, China[J]. Seismological Research Letters, 2015, 86(3): 841. DOI:10.1785/0220140053 |
| [10] |
CHEN Wenkai, WANG Dun, SI Hongjun, et al. Rapid estimation of seismic intensities using a new algorithm that incorporates array technologies and ground-motion prediction equations (GMPEs)[J]. Bulletin of the Seismological Society of America, 2022, 112(3): 1647. DOI:10.1785/0120210207 |
| [11] |
LI Zefeng. A generic model of global earthquake rupture characteristics revealed by machine learning[J]. Geophysical Research Letters, 2022, 49(8): e2021GL096464. DOI:10.1029/2021GL096464 |
| [12] |
ZHAO Ming, XIAO Zhuowei, CHEN Shi, et al. DiTing: a large-scale Chinese seismic benchmark dataset for artificial intelligence in seismology[J]. Earthquake Science, 2022, 35: 1. DOI:10.1016/j.eqs.2022.01.022 |
| [13] |
王墩, 孙琨. 地震大数据和AI如何改进全球大震参数快速测定?[J]. 地球科学, 2022, 47(10): 3915. WANG Dun, SUN Kun. How the big data seismology and AI refine rapid determination of source parameters of large earth-quakes?[J]. Earth Science, 2022, 47(10): 3915. DOI:10.3799/dqkx.2022.863 |
| [14] |
KUANG Wenhuan, YUAN Congcong, ZHANG Jie. Real-time determination of earthquake focal mechanism via deep learning[J]. Nature Communications, 2021, 12(1): 1. DOI:10.1038/s41467-021-21670-x |
| [15] |
宋晋东, 余聪, 李山有. 地震预警现地PGV连续预测的最小二乘支持向量机模型[J]. 地球物理学报, 2021, 64(2): 555. SONG Jindong, YU Cong, LI Shanyou. Continuous prediction of onsite PGV for earthquake early warning based on least squares support vector machine[J]. Chinese Journal of Geophysics, 2021, 64(2): 555. DOI:10.6038/cjg2021O0193 |
| [16] |
陈蒙, 王华. 地震动强度参数估计的可解释性与不确定度机器学习模型[J]. 地球物理学报, 2022, 65(9): 3386. CHEN Meng, WANG Hua. Explainable machine learning model for prediction of ground motion parameters with uncertainty quantification[J]. Chinese Journal of Geophysics, 2022, 65(9): 3386. DOI:10.6038/cjg2022P0428 |
| [17] |
JI Duofa, LIU Jin, WEN Weiping, et al. Prediction of cumulative absolute velocity based on refined second-order deep neural network[J]. Journal of Earthquake Engineering, 2022, 26(15): 8021. DOI:10.1080/13632469.2021.1985017 |
| [18] |
ZHOU Lianqing, ZHAO Cuiping, ZHANG Miao, et al. Machine-learning-based earthquake locations reveal the seismogenesis of the 2020 Mw 5.0 Qiaojia, Yunnan Earthquake[J]. Geophysical Journal International, 2022, 228(3): 1637. DOI:10.1093/gji/ggab420 |
| [19] |
蒋一然, 宁杰远. 基于支持向量机的地震体波震相自动识别及到时自动拾取[J]. 地球物理学报, 2019, 62(1): 361. JIANG Yiran, NING Jieyuan. Automatic detection of seismic body-wave phases and determination of their arrival times based on support vector machine[J]. Chinese Journal of Geophysics, 2019, 62(1): 361. DOI:10.6038/cjg2019M0442 |
| [20] |
ZHANG Xiong, ZHANG Miao, TIAN Xiao. Real-time earthquake early warning with deep learning: application to the 2016 M6.0 central apennines, Italy earthquake[J]. Geophysical Research Letters, 2021, 48(5): 2020GL089394. DOI:10.1029/2020GL089394 |
| [21] |
WANG Yanwei, LI Xiaojun, WANG Zifa, et al. Deep learning for magnitude prediction in earthquake early warning[J]. Gondwana Research, 2022. DOI:10.1016/j.gr.2022.06.009 |
| [22] |
胡安冬, 张海明. 机器学习在地震紧急预警系统震级预估中的应用[J]. 地球物理学报, 2020, 63(7): 2617. HU Andong, ZHANG Haiming. Application of machine learning to magnitude estimation in earthquake emergency prediction system[J]. Chinese Journal of Geophysics, 2020, 63(7): 2617. DOI:10.6038/cjg2020N0070 |
| [23] |
林彬华, 金星, 康兰池, 等. 基于卷积神经网络的地震震级测定研究[J]. 地球物理学报, 2021, 64(10): 3600. LIN Binhua, JIN Xing, KANG Lanchi, et al. The research of earthquake magnitude determination based on convolutional neural networks[J]. Chinese Journal of Geophysics, 2021, 64(10): 3600. DOI:10.6038/cjg2021O0370 |
| [24] |
朱景宝, 宋晋东, 李山有. 基于深度卷积神经网络的2021年5月21—22日云南漾濞地震和青海玛多地震震级估算[J]. 地球物理学报, 2022, 65(2): 594. ZHU Jingbao, SONG Jindong, LI Shanyou. Magnitude estimation of Yunnan Yangbi earthquake and Qinghai Madoi earthquake on May 21—22, 2021 based on deep convolutional neural network[J]. Chinese Journal of Geophysics, 2022, 65(2): 594. DOI:10.6038/cjg2022P0584 |
| [25] |
FAN Liping, LI Boren, LIAO Shirong, et al. High-precision relocation of the aftershock sequence of the January 8, 2022, MS 6.9 Menyuan earthquake[J]. Earthquake Science, 2022, 35(2): 138. DOI:10.1016/j.eqs.2022.01.021 |
| [26] |
潘家伟, 李海兵, CHEVALIERM L, 等. 2022年青海门源MS6.9地震地表破裂带及发震构造研究[J]. 地质学报, 2022, 96(1): 215. PAN Jiawei, LI Haibing, CHEVALIER M L, et al. Coseismic surface rupture and seismogenic structure of the 2022 MS6.9 Menyuan earthquake, Qinghai Province, China[J]. Acta Geologica Sinica, 2022, 96(1): 215. DOI:10.19762/j.cnki.dizhixuebao.2022125 |
| [27] |
YANG Zhigao, DAI Danqing, ZHANG Yong, et al. Rupture process and aftershock mechanisms of the 2022 Luding M6.8 earthquake in Sichuan, China[J]. Earthquake Science, 2022, 35: 1. DOI:10.1016/j.eqs.2022.09.001 |
| [28] |
CARRANZA M, BUFORN E, ZOLLO A. Testing the earthquake early-warning parameter correlations in the southern Iberian Peninsula[J]. Pure & Applied Geophysics, 2015, 172(9): 2435. DOI:10.1007/s00024-015-1061-6 |
| [29] |
马强, 金星, 李山有, 等. 用于地震预警的P波震相到时自动拾取[J]. 地球物理学报, 2013, 56(7): 2313. MA Qiang, JIN Xing, LI Shanyou, et al. Automatic P-arrival detection for earthquake early warning[J]. Chinese Journal of Geophysics, 2013, 56(7): 2313. DOI:10.6038/cjg20130718 |
| [30] |
KANAMORI H. Real-time seismology and earthquake damage mitigation[J]. Annual Review of Earth and Planetary Sciences, 2005, 33(1): 195. DOI:10.1146/annurev.earth.33.092203.122626 |
| [31] |
BÖSE M. Earthquake early warning for Istanbul using artificial neural networks[D]. Karlsruhe: University of Karlsruhe, 2006
|
| [32] |
HUANG Polun, LIN Tingli, WU Y M. Application of τc*Pd in earthquake early warning[J]. Geophysical Research Letters, 2015, 42: 1403. DOI:10.1002/2014gl063020 |
| [33] |
WU Y M, KANAMORI H. Rapid assessment of damage potential of earthquakes in Taiwan from the beginning of P waves[J]. Bulletin of the Seismological Society of America, 2005, 95: 1181. DOI:10.1785/0120040193 |
| [34] |
WU Y M, ZHAO L. Magnitude estimation using the first three seconds P-wave amplitude in earthquake early warning[J]. Geophysical Research Letters, 2006, 33(16): 16312. DOI:10.1029/2006GL026871 |
| [35] |
FESTA G, ZOLLO A, LANCIERI M. Earthquake magnitude estimation from early radiated energy[J]. Geophysical Research Letters, 2008, 35: L22307. DOI:10.1029/2008GL035576 |
| [36] |
REED J W, KASSAWARA R P. A criterion for determining exceedance of the operating basis earthquake[J]. Nuclear Engineering and Design, 1990, 123: 387. DOI:10.1016/0029-5493(90)90259-Z |
| [37] |
NAKAMURA Y. A new concept for the earthquake vulnerability estimation and its application to the early warning system[J]. Early Warning Systems for Natural Disaster Reduction, 2003, 693. DOI:10.1007/978-3-642-55903-7_92 |
| [38] |
ZOLLO A, LANCIERI M, NIELSEN S. Earthquake magnitude estimation from peak amplitudes of very early seismic signals on strong motion records[J]. Geophysical Research Letters, 2006, 33: L23312. DOI:10.1029/2006GL027795 |
| [39] |
彭朝勇, 杨建思, 薛兵, 等. 基于汶川主震及余震的预警参数与震级相关性研究[J]. 地球物理学报, 2013, 56(10): 3404. PENG Chaoyong, YANG Jiansi, XUE Bing, et al. Research on correlation between early-warning parameters and magnitude for the Wenchuan earthquake and its aftershocks[J]. Chinese Journal of Geophysics, 2013, 56(10): 3404. DOI:10.6038/cjg20131016 |
| [40] |
CHEN W, WANG D, ZHANG C, et al. Estimating seismic intensity maps of the 2021 Mw7.3 Madoi, Qinghai and Mw6.1 Yangbi, Yunnan, China earthquakes[J]. Journal of Earth Science, 2022, 33(4): 839. DOI:10.1007/s12583-021-1586-9 |
| [41] |
CHENG C, WANG D, YAO Q, et al. The 2021 Mw7.3 Madoi, China earthquake: transient supershear ruptures on a presumed immature strike-slip fault[J]. Journal of Geophysical Research: Solid Earth, 2023, 128(2): e2022JB024641. DOI:10.1029/2022JB024641 |
| [42] |
PENG C Y, YANG J S, ZHENG Y, et al. New τc regression relationship derived from all P wave time windows for rapid magnitude estimation[J]. Geophysical Research Letters, 2017, 44(4): 1724. DOI:10.1002/2016GL071672 |
| [43] |
MOUSAVI S M, BEROZA G C. A machine-learning approach for earthquake magnitude estimation[J]. Geophysical Research Letters, 2020, 47(1): e2019GL085976. DOI:10.1029/2019GL085976 |
| [44] |
HSU T Y, HUANG S K, CHANG Y W, et al. Rapid on-site peak ground acceleration estimation based on support vector regression and P-wave features in Taiwan[J]. Soil Dynamics and Earthquake Engineering, 2013, 49: 210. DOI:10.1016/j.soildyn.2013.03.001 |
| [45] |
HSU T Y, WU R T, LIANG C W, et al. Peak ground acceleration estimation using P-wave parameters and horizontal-to-vertical spectral ratios[J]. Terrestrial, Atmospheric & Oceanic Sciences, 2020, 31: 1. DOI:10.3319/TAO.2019.07.04.01 |
| [46] |
WANG Ao, LI Shanyou, LU Jianqi, et al. Prediction of PGA in earthquake early warning using a long short-term memory neural network[J]. Geophysical Journal International, 2023, 234(1): 12. DOI:10.1093/gji/ggad067 |
| [47] |
ZHU Weiqiang, BEROZA G C. PhaseNet: a deep-neural-network-based seismic arrival-time picking method[J]. Geophysical Journal International, 2019, 216(1): 261. DOI:10.1093/gji/ggy423 |
| [48] |
MOUSAVI S M, ELLSWORTH W L, ZHU Weiqiang, et al. Earthquake transformer: an attentive deep-learning model for simultaneous earthquake detection and phase picking[J]. Nature Communications, 2020, 11(1): 3952. DOI:10.1038/s41467-020-17591-w |
| [49] |
ZHU Jun, LI Zefeng, FANG Lihua. USTC-pickers: a unified set of seismic phase pickers transfer learned for China[J]. Earthquake Science, 2022, 36(2): 95. DOI:10.1016/j.eqs.2023.03.001 |
 2024, Vol. 56
2024, Vol. 56


