2. 结构工程灾变与控制教育部重点实验室(哈尔滨工业大学),哈尔滨 150090;
3. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨 150090
2. Key Lab of Structures Dynamic Behavior and Control(Harbin Institute of Technology), Ministry of Education, Harbin 150090, China;
3. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters(Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China
随着全球城镇化进程的加快,地震已成为对人类文明最具威胁的自然灾害之一[1-3]。一场毁灭性的地震会导致城市基础设施大面积瘫痪,造成不可估量的人员伤亡和社会经济损失[4-5]。自21世纪以来,城市系统的复杂度不断提高,地震引发的系统功能瘫痪、灾后重建难度大、恢复时间长,以及造成的间接经济损失与社会代价巨大等问题愈发凸显。由此,仅以保障人身安全为主要设防目标的传统防震减灾理论已不再满足人类社会的发展需要,而以城市系统功能为主要关注点并考虑地震灾害综合影响的抗震韧性设防理念逐步得到国际社会的认可。2011年,美国率先发布了《国家抗震韧性》报告[6],并提出了2011—2031年为增强城市韧性设立的18项重要任务;2013年,日本颁布了《国土强韧化基本法》[7],以立法形式规范了韧性城市的建设;2015年,第三次联合国减灾大会上通过的《仙台减轻灾害风险框架》[8]中明确指出,韧性是未来15年联合国的4个优先领域之一;中国也分别在2020年和2021年将城市韧性建设写入《中华人民共和国国民经济和社会发展第十四个五年规划和2035年远景目标纲要》。
现代化韧性城市的建设需要各类工程系统的支撑,作为生产生活中最重要的基础设施系统之一,交通系统韧性的关注度持续攀升,已先后入选中国工程院发布的《全球工程前沿2021》中土木、水利与建筑工程领域的TOP10,和中国科学技术协会发布的《2022重大科学问题》中的10个前沿科学问题。本文将以城市中最重要的道路交通系统为讨论对象,阐明抗震韧性的定义及面临的主要科学问题,并系统性地总结现有研究取得的成果和存在的不足,为今后的研究提供参考。
1 道路交通系统抗震韧性的定义韧性(Resilience)一词源于拉丁语“resilio”,原意为“反弹”,起源于20世纪40年代的心理学和精神学领域[9]。1973年,Holling[10]将“韧性”概念引入生态学,并将生态学韧性定义为“系统持久性及其适应变化和干扰的能力”。2003年,Bruneau[11]首次提出了“城市抗震韧性”的概念,用以描述“城市减轻灾害,在灾害发生时控制灾害的影响,以及恢复活动中尽量减少社会中断和减轻未来地震影响的能力”,并由此开启了城市防震减灾研究的新篇章。
与传统地震工程学相比,城市的抗震韧性研究主要带来以下3个维度的变革。首先是时间维度,由传统只关注地震发生瞬间的损伤分析,转变为对震前预防、震后适应至恢复重建全过程的灾害研究。然后是空间维度,由传统针对单一建筑、桥梁、电塔等设施的抗震性能分析,发展到对建筑群、交通、电力、通信等工程系统的地震灾害评估。最后是科学问题维度,由传统针对各类基础设施力学性能及损伤机制的研究,变革为对复杂工程系统的建模仿真、震后功能评估、间接损失预测、耦联机制以及工程与非工程因素的多元融合研究。
本文探讨的城市交通系统指为居民出行及货物运输提供服务的基础设施系统的总称,包括道路、铁路、地铁、航空、水运等多个子系统。其中,由道路、桥梁、隧道等设施组成的道路交通是城市中最重要的出行方式,地震发生后,保障道路交通系统的功能性是城市应急救援和恢复重建的关键[12-13]。然而,历史震害经验表明,道路交通系统极易遭受地震灾害的影响。例如: 1994年美国北岭地震造成大量交通基础设施损坏,据统计因交通阻塞或中断导致的商业损失超过15亿美元,占当地总体商业损失的27.3%[14];1995年日本阪神地震造成该地区超过50%的桥梁严重损坏或毁坏,致使交通基本瘫痪,严重阻碍了震后应急救援的开展,并造成交通相关经济损失268亿美元[15];2008年中国汶川地震共造成24条高速公路、161条省道、8 618条县道、6 140座桥梁以及156座隧道损坏,直接经济损失超过670亿元人民币[16],地震后道路交通系统的故障迫使大量灾区被孤立,严重迟滞了救援人员和生命线物资的输送,引发了更多的人员伤亡和社会损失。由此可知,维持道路交通系统的震后功能对控制灾害发展和减少灾害的长期影响具有重要的作用,然而,现有防震减灾理论与城市韧性建设的客观需求存在很大差距,迫切需要解决交通系统抗震韧性背后的科学问题。
在已有研究中,学者们给出了多种关于交通系统抗震韧性的描述。Murray-Tuite[17]将交通系统的韧性定义为“系统适应灾害并维持可接受服务水平的能力”,并给出了交通韧性评估的10个维度,分别是冗余、多样性、效率、独立性、强度、协作性、适应性、机动性、安全性和快速恢复;Serulle等[18]定义交通系统的韧性为“适应破坏性事件和在指定时间框架内恢复其灾前服务水平的能力”;D′Lima和Medda[19]将城市地铁系统的韧性考虑为“从破坏性事件或冲击中恢复的速度”;Chan和Schofer[20]将铁路运输系统的韧性描述为“经历负面的、潜在的破坏性事件并在事件发生后的一段合理时间内恢复到健康状态的能力”。
综上,城市道路交通系统的抗震韧性主要包含两方面能力。一方面是系统抵抗和适应地震破坏的能力,需要注意的是,该能力的评估不仅仅是对系统损伤程度的简单叠加,而是关于系统剩余能力对城市交通需求供应关系的功能性表达。一般而言,这种能力可以通过合理的交通规划和震前加固措施来增强。另一方面,系统在功能受损后的快速恢复能力是韧性优于其他防震减灾理念的另一项重要特征[21]。通常情况下,合理的恢复资源投入和施工调度是提升系统恢复能力的有效手段,可以达到减少灾害长期影响的目的。因此,本文将城市道路交通系统的抗震韧性定义概括为“系统在地震时维持和地震后快速恢复其功能的能力”。
2 道路交通系统抗震韧性的研究现状城市道路交通系统抗震韧性研究的目的是了解潜在地震灾害下系统的功能性损失以及重新恢复到供需平衡状态所需的资源与时间,从而为城市的发展建设及投资决策提供指导。为实现该目标,首先应建立道路交通系统的震后功能分析模型,揭示地震损伤对城市应急救援和人们生产生活的影响机制。然后根据系统功能下降到恢复的时变过程,提取关键的特征指标来评定其抗震韧性水平。对于不满足韧性城市建设或决策者需求的道路交通系统,可以通过优化系统的震后恢复策略和维护加固策略的方式来改善系统的抗震韧性。具体而言,在地震发生后,优化修复资源的投入与调度能够使系统更加高效、快速的恢复,从而降低地震导致的间接损失和长期影响;在地震发生前,优化重要基础设施的维护和加固策略能够显著降低系统的地震易损性,从而有效控制道路交通系统的震后功能水平。
城市道路交通系统的韧性研究理论框架如图 1所示,下文将从道路交通系统的震后功能评估方法、抗震韧性评价指标、震后恢复策略、和震前加固策略4个方面逐一进行阐述,系统性地总结已有研究中的主要观点及方法,同时指出当前研究存在的不足之处。

|
图 1 道路交通系统抗震韧性研究框架 Fig. 1 Research framework of seismic resilience for road traffic system |
城市道路交通系统的运行功能需要采用网络化方法建模分析,通常将有人口聚集的交通始末点和道路交叉口简化为节点,将连接各个节点的路段简化为边组成网络架构。合理的功能分析方法是抗震韧性评估的基础,已有研究中常用的功能分析方法可大致归为4类,下面将分别阐述这4种方法的原理及适用范围。
1) 连通性方法。连通性方法基于图论原理[22]描述系统中节点的连接情况,是一种通用的网络结构分析方法。宏观的连通性方法通过比较网络拓扑结构与其对应完全图(所有节点之间都恰有一条边相连的图)来衡量路网的整体连通水平,可用指标包括节点平均度[23-24]、聚类系数[24]、最大连通子图[25-26]等。然而这些指标很难与道路交通系统的复杂出行需求及功能性建立良好的关联,因此, 在近年来已很少单独使用。与之不同的是,微观的连通性方法依托网络拓扑结构及路段长度信息来判断节点之间是否连通以及连通水平如何,常用指标包括最短路径距离[13, 27-28]、连通效率[25, 29-30]、连通可靠度[31-33]、独立路径数量[34-36]等。由于微观连通性方法不需要详细的路况及流量需求数据就可以快速判断道路交通系统的整体运行状态,较适用于评估灾后短时无序环境下的系统功能,缺点是忽略了通行时间、环境因素及用户行为的影响。
2) 交通流方法。交通流方法基于交通工程学原理[37],将城市的流量需求分配到交通网络中的各个路段上,并以交通延误量化系统的功能性变化,常用指标包括通行时间、通行距离和通行速度等[38-42]。相比连通性方法,交通流方法是道路交通系统功能分析的一种独有方法,能够计算得到每个路段的拥堵情况及预估通行时间,缺点是高度依赖于准确的流量需求数据和用户的路径选择假设[43],因此,一般只适用于稳定场景下的系统功能分析或对长期趋势的预测。
3) 网络容量方法。网络容量方法基于最大流原理[44],描述节点之间的最大可行流量。该方法同样是对震后交通延误的描述,且无需详细的流量需求和出行者行为信息, 但使用中存在较大的局限性,通常专用于道路交通系统在紧急情况下的疏散能力研究[45], 不适用于评估系统的整体功能水平。
4) 智能仿真方法。智能仿真方法通过将城市中的交通用户建模为具有特定运行规律的智能体[46],来模拟事故或灾害对道路交通的真实影响。与上述其他方法相比,智能仿真是一种更为精细化的微观分析方法,并且能够在评估地震损坏影响的同时考虑用户行为及心理的变化,缺点是仿真模型的计算成本较高,目前尚不适用于大范围交通网络的地震分析,且存在用户的灾后交通行为难以准确定义等问题。
综上,作为城市中重要的服务性基础设施系统,道路交通系统在地震场景下的功能分析方法并不唯一。历史经验表明,随着地震的发生和发展,城市的交通需求会发生阶段性的改变。地震后的初期主要是对应急救援的需求,此阶段的道路交通通常受到政府部门的统一管控,节点之间的流量需求难以预测,且不满足基于平衡原则的路径选择假设。因此,学者们普遍采用连通性方法来衡量震后短期应急阶段的道路交通功能。例如: Chu和Chen[47]将道路交通系统的灾后短期可靠性定义为能够至少与一个应急中心连通的节点数量期望值; Khademi等[48]提出用隔离指数来衡量震后72 h内道路交通系统的脆弱性,即应急节点对之间的独立路径数量与平均路径长度的乘积; Boakye等[49]使用网络加权效率指标和异质性指标分别量化了灾后道路交通系统的应急连通性和空间不对称性; Liu等[50]提出了基于多节点独立路径算法的道路交通系统应急功能指标,并发展了基于路段惩罚因子模型的震后功能损失评估方法。
在应急阶段过后的长期恢复过程中,城市的道路交通逐渐转向对人们生产生活出行及灾后重建运输的供应。该阶段的持续时间较长,交通流量需求呈现阶段性稳定回升。因而,学者们通常采用交通流方法来评估长期恢复阶段道路交通系统的功能变化,或预测灾害的长期影响。例如: Bocchini和Frangopol[51]采用网络总通行时间和总通行距离的加权倒数作为道路交通系统震后恢复阶段的功能指标;Twumasi-Boakye和Sobanjo[52]基于地震后路段通行时间和通行速度的变化来识别受地震影响最严重的城市区域;Kilanitis等[53]利用地震导致的额外交通成本和行程取消亏损来估算道路交通系统的累计间接经济损失。
此外,在关注特定的交通功能时,也可采用网络容量方法或智能仿真方法作进一步的分析。例如: Chang等[54]使用地震后从受灾区到安全区的总流量作为道路交通系统应急疏散功能的量化指标;Feng等[55]通过将车辆建模为智能体的仿真方法研究了震后混乱环境下医院紧急救助范围的变化规律。
综上,迄今为止学者们已经对道路交通系统的震后功能分析方法进行了广泛探讨,并针对研究时段及关注重点的不同提出了多种功能评价指标。在评估道路交通系统的抗震韧性时,需要综合考量其在震后不同阶段的功能表现,但系统分析方法的多样性显著增加了韧性评价中协调不同功能指标的难度,此问题将在下一节中进一步探讨。
2.2 抗震韧性评价指标在抗震韧性的概念提出之前,常使用脆弱性、鲁棒性、可靠性或风险指标来评估工程结构或系统的抗震能力。其中,脆弱性是结构或系统在地震作用下发生损坏或失效的倾向程度,鲁棒性指结构或系统遭受地震时维持其初始状态的能力, 可靠性是结构或系统在规定条件下确保其设计性能的概率, 风险是对地震事件的发生概率及其造成的损失和影响的评估。
然而,上述概念主要基于物理层面对地震灾害的大小进行评估。韧性的含义不仅局限于物理层面,与地震造成的物理损伤大小相比,韧性更强调地震对系统运行功能的影响。此外,区别于以上所有概念,韧性不仅关注系统抵抗地震破坏的能力,更注重系统从震后失衡状态恢复到供需重新平衡的能力[21],以及地震导致的间接损失情况,这与城市的社会和组织要素密不可分[56-57]。
在城市交通系统的研究中,一些学者基于地震前后系统功能的变化来衡量其抗震韧性水平。例如,Cox等[58]将灾后功能损失率作为交通系统韧性的评价指标,数学表达式为
| $ R_{\Delta}=\frac{\Delta L_{\mathrm{F}_{\max }}-\Delta L_{\mathrm{F}}}{\Delta L_{\mathrm{F}_{\max }}} $ | (1) |
式中:RΔ为基于功能损失率的韧性指标,ΔLF为灾害导致的系统预期功能损失率,ΔLFmax为系统的最大功能损失率。Miller-Hooks等[23, 59]采用系统灾后能够满足灾前需求的期望值作为道路交通系统的韧性指标,数学表达式为
| $ R_{\mathrm{E}}=E\left[\max \sum\limits_{w \in W} d_w / \sum\limits_{w \in W} D_w\right] $ | (2) |
式中:RE为基于供需比的韧性指标,W为系统中所有节点对的集合,Dw为节点对w∈W的初始交通需求,dw为系统灾后能够满足节点对w的交通需求量。类似的指标也被应用于货运系统[60-61]、机场地面运输系统[62]、地铁系统[63-64]、空运系统[65]、应急医疗运输系统[66-67]以及港口集装箱运输系统[68]的韧性评价。
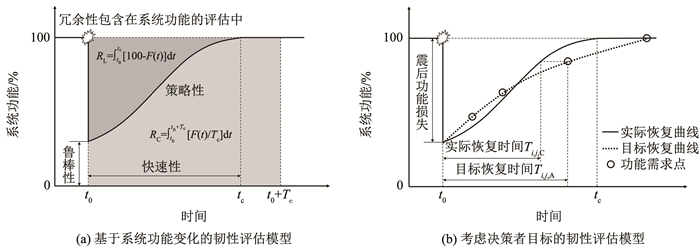
然而,如上文所述,系统的震后功能变化仅反映了其对地震破坏的抵抗和适应能力,而未能考虑系统的恢复能力以及灾害的长期影响。值得注意的是,通常情况下,地震所带来的间接损失要远超过直接损失。因此,目前更广泛接受的理解是,工程系统的抗震韧性是对其在整个灾害管理周期内功能损失及恢复表现的综合评价。图 2(a)展示了工程系统功能随时间变化的韧性评估模型,根据该模型,Bruneau等[11]最早给出了基于功能曲线积分形式的韧性指标,数学表达式为
| $ R_{\mathrm{L}}=\int_{t_0}^{t_{\mathrm{c}}}[100-F(t)] \mathrm{d} t $ | (3) |
|
图 2 工程系统抗震韧性评估模型 Fig. 2 Seismic resilience assessment model for engineering systems |
式中:RL为韧性损失指标,t0为地震发生时刻,tc为恢复完成时刻,F(t)为震后t时刻系统的功能值。
图 2(a)中RL指标的覆盖面积又称为“韧性三角形”,其主要由系统的4项属性(4R)决定,分别为鲁棒性(Robustness)、冗余性(Redundancy)、快速性(Rapidity)和策略性(Resourcefulness)。这里的鲁棒性指系统震后的剩余功能水平;冗余性描述了受损设施可被替代的程度,其决定了系统适应地震损伤的能力;快速性指系统恢复到预定目标功能水平的时间;策略性描述了系统通过合理调配资源来实现功能高效恢复的能力,其结果反映在功能恢复曲线的形状差异。
由于RL并非标准化指标,且数值大小与系统的韧性水平成反比,Cimellaro等[69-70]提出了基于控制时间内系统平均剩余功能的韧性指标,数学表达式为
| $ R_{\mathrm{C}}=\int_{t_0}^{t_0+T_{\mathrm{c}}}\left[F(t) / T_{\mathrm{c}}\right] \mathrm{d} t $ | (4) |
式中:RC为标准化韧性指标,Tc为控制时间的长度。RC是目前应用最广泛的韧性评价指标,已被应用于道路[71-72]、铁路[73-74]、地铁[75-76]等多种交通系统的灾害韧性评价。
此外,同样基于系统功能随时间的变化模型,一些近期研究对韧性的评价方法进行了改进。Liao等[77]提出了一种基于系统震后实际功能与目标功能比值积分的韧性指标,如图 2(b)所示,其数学表达式为
| $ R_{\mathrm{T}}=\int_{t_0}^{t_c}\left[F_{\mathrm{R}}(t) / F_{\mathrm{T}}(t)\right] \mathrm{d} t $ | (5) |
式中FR(t)和FT(t)分别为震后t时刻系统功能的实际值与目标值。RT的重要思想在于韧性评价不仅取决于系统自身的性能,还与决策者的目标有关,如果系统在地震中的功能表现能够满足决策者的需求,则应被视为具备韧性。
然而,在实际应用中决策者的目标值通常是离散的,很难被具象化为目标恢复曲线;另外,上述所有积分指标均为单一的综合性指标,无法反映系统在抵抗地震破坏和震后快速恢复两方面的不同能力。对此,Zhai等[78]提出了一种工程系统通用的双指标抗震韧性评价方法,分别从震后功能损失和恢复时间两个方面来衡量系统的抗震韧性,并考虑了恢复过程中多个离散功能需求点的权重影响,计算方法为
| $ R_{\mathrm{FL}}=\frac{S_{\mathrm{C}}}{S_{\mathrm{A}}} $ | (6) |
| $ R_{\mathrm{RT}}=\sum\limits_{i=1}^n w_i \sum\limits_{j=1}^m \gamma_j \frac{T_{i, j, \mathrm{C}}}{T_{i, j, \mathrm{~A}}} $ | (7) |
式中:RFL为基于功能损失的韧性指标,SC和SA分别为系统震后功能损失的实际值与目标值,RRT为基于恢复时间的韧性指标,Ti, j, C和Ti, j, A分别为第j个用户的第i个功能需求点对应的实际恢复时间和目标恢复时间,wi为第i个功能需求点的权重,γj为第j个用户的权重。
综上,随着近年来研究的深入,城市工程系统抗震韧性的评估理论已经从单纯考虑震后功能损失转变为对灾害管理周期内功能水平的综合分析,并形成了基于时变功能曲线的韧性评估模型,韧性评价方法也由单一量化指标向考虑用户需求及决策权重的分阶段多指标方向发展。在实际应用中,连续型功能曲线模型适用于功能分析方法不随时间变化的工程系统,如以供应用户比例为功能指标的建筑、电力、给水系统等,但该模型对道路交通系统的适用性有限。如2.1节所述,地震后的城市交通需求会随时间的推移而发生根本性的改变,导致需要采用不同的分析方法和指标来评估道路交通系统的功能性。在这种情况下,系统的震后功能变化无法再以连续曲线的形式展现,并且不再满足上述积分指标的计算条件。然而,目前尚缺乏考虑道路交通系统多方面功能特性的综合韧性评价方法,且如何协调多种功能指标在韧性评价中的作用尚不清楚。因此,对于功能需求复杂的城市道路交通系统,仍有必要开发其专用的分阶段、多维度韧性评价指标体系,以衡量系统在不同时段应对多种交通需求的综合表现。
2.3 震后恢复策略根据历史震害经验,地震对一座城市的社会影响是深远的,大地震后的城市重建可能持续数年甚至更长的时间,并消耗大量的人力和物力。作为城市的主动脉,道路交通系统功能的快速恢复对重构城市生态及支持其他工程系统重建具有不可替代的作用。因此,如何合理调配可用资源并优化道路交通系统的震后恢复策略是提升城市抗震韧性的有效手段,也被认为是韧性研究中最具工程应用前景的领域之一[79]。
工程系统的震后功能恢复是一个复杂的问题,早期的研究采用了简化模型来近似功能曲线的恢复轨迹,如线性[80]、指数[81]、三角函数[82]等,或按照资源无限考虑[83],但这些模型的结果与真实情况之间必然存在较大差距。
针对道路交通系统的震后恢复决策问题,在最近的研究中,学者们试探性地提出了多种基于启发式算法的随机规划模型。例如: Bocchini等[84]提出了以系统韧性和修复经费为优化目标的公路网络恢复决策框架,以及基于多目标遗传算法的求解方法; Lertworawanich[85]提出了基于灾后出行损失和交通成本的动态恢复规划模型,并采用粒子群算法对模型进行了求解; EI-Anwar等[86]提出了一种基于混合整数线性规划的交通网络灾后重建决策模型,用于优化项目的修复排序和工程分配; Zhang等[87]提出了基于系统总恢复时间和恢复曲线质心坐标的恢复轨迹优度判别方法,并据此建立了桥梁网络震后恢复策略的优化模型及基于遗传算法的求解方法; Hackl和Adey[88]提出了一种以最小化修复直接成本和系统间接损失之和为目标的恢复优化模型,以及基于模拟退火算法的求解方法。随后,Moghtadernejad等[89-90]对该模型又进行了改进,并对比了模拟退火算法和粒子群算法对模型的求解效率及适用性; Liu等[91]提出了一种基于震后恢复速度与恢复效率的通用双目标恢复优化模型,并采用非支配遗传算法对模型进行了求解; Zhang等[92]建立了考虑施工道路封闭影响的桥梁网络震后恢复规划模型,以及基于混合遗传算法的求解方法。
综上,城市道路交通系统的震后恢复策略优化问题是当前研究的热点之一,目前学术界已经形成了基于随机优化模型和启发式算法的求解方案,但这些方法仍处于理论研究阶段,与工程实践之间尚存在较大差距。因此,下一步的研究应着重解决以下3项核心问题:
1) 现有恢复策略优化模型主要关注于系统的总体韧性水平或恢复阶段的综合表现。然而,实际情况下城市的恢复目标会发生阶段性的改变,在恢复阶段初期,城市对道路交通连通性的关注会高于通行成本[93],而在漫长的恢复过程中,决策者通常会设定多个具有控制作用的功能需求点,如图 2(b)所示。因此,随着道路交通系统抗震韧性评价方法的不断细化,同样需要建立相应的分阶段、多目标优化模型,以满足恢复过程中多个功能需求点的决策需要。
2) 已有研究普遍采用了较多的简化假设条件,例如, 假定恢复阶段的交通需求不发生改变,将资源约束简化为施工队数量,以及忽略或简化考虑施工影响等。这些假设条件能够起到简化数学建模和提高计算速度的作用,但其对恢复决策的影响同样是显著的。因此,如何细化道路交通系统的震后恢复过程,采用更真实的仿真模型替代假设条件,将成为恢复策略优化迈向工程实践的重要研究内容。
3) 随机优化模型的计算成本会随系统复杂度和问题维数的增长而显著提高,从而导致其处理大区域复杂网络问题时过高的计算量。然而,震后恢复策略往往具有很强的时效性,需要根据震后的真实情况快速做出最优判断并实时调整,这对模型的计算效率有较高的要求。因此,在确保优化模型合理性的基础上,如何提升恢复决策的效率或建立科学可靠的替代模型,将成为未来持续探索的方向。
2.4 震前加固策略20世纪80年代是中国大兴土木的开端,距今已有40余年的历史。当下,大量基础设施由于结构老化、维护不当以及规范更迭等原因已经成为城市韧性建设的薄弱环节。因此,如何有效识别城市既有工程系统中的关键设施并予以加固,对提升系统的震后功能表现及抗震韧性具有重要意义[94]。
对于该问题,传统研究中给出了多种基于设施重要性的加固选择方法。早期的重要性排序方法通常只考虑设施的结构性能,如结构指标法[95]和预期损伤法[96]等;另外,一些近期的研究也提出了基于物理、社会等多项属性的主观排序方法[97-99]。但是这些方法仅依据设施自身的属性进行排序,忽略了设施加固对系统层面的影响。
在网络化结构的分析中,组件的中介中心性指标(Betweenness)[100-102]是一种通用的重要性度量,定义为网络中所有节点间最短路径通过某一组件的比率,比率越大,表明该组件的空间重要性越高。然而对于具有明确需求的道路交通系统,中介中心性指标与系统的复杂功能性之间缺乏良好的关联。此外,已有研究中最常用的系统级排序方法是基于组件失效后对系统功能的影响程度来评估其重要性[103-105],影响程度越大,表明组件越重要。尽管该方法可以在一定程度上反映组件对维持系统功能的重要性,但由于忽略了组件之间地震易损性的差异,其结果的参考价值仍然十分有限。
道路交通系统的加固决策本质上是对有限资源的随机分配问题,求解该问题主要面临两方面的挑战。一方面,预测系统的震后功能表现或抗震韧性水平需要考虑来自地震事件和设施易损性的双重不确定性,这使得准确估计给定策略的加固收益面临较大的计算难度;另一方面,可选加固策略的数量随候选设施的增多呈现几何级数增长,这导致城市尺度问题的解集空间巨大。基于以上两点原因,通过枚举法对比所有可行策略的加固收益是不切实际的。在一些研究中,学者们尝试通过蒙特卡洛模拟配合随机优化模型来求解道路交通系统的加固决策问题。例如: Peeta等[106]针对有限预算下高速公路网络的加固选择难题,提出了以最大化灾后网络连通性为目标的两阶段随机规划模型,和基于多线性函数的局部最优解计算方法;Huang等[107]建立了以最小化桥梁总加固成本和预期破坏损失为目标的混合整数规划模型,并通过商用求解器对模型进行了求解;Zhang等[35]提出了以最大化道路系统连通可靠度为目标的震前加固决策框架,并通过多目标遗传算法求解了加固预算与加固收益的非支配最优解集。虽然相比枚举法,以上优化模型的计算成本明显降低,但同样无法避免需要大量重复计算系统的震后功能值,致使应对高维复杂网络问题时计算仍过于耗时。
针对上述缺陷,一些最近的研究提出了多种介于传统重要性排序与随机优化模型之间的有限样本方法[108-109]。这些方法通过分析样本中组件损伤与系统震后功能的相关性来确定其加固优先级,相关性越强,则组件的相对优先级越高。例如: Rokneddin等[110]使用桥梁损伤与系统连通性损失的条件概率来判别其加固重要性;Wang和Jia[111]提出了一种衡量组件损伤不确定性对系统失效影响的概率敏感性指标,并利用该指标确定交通网络的加固优先级排序;Liu等[112]基于特征选择原理,提出了以决策者可接受功能损失为导向的道路交通系统多组件联合重要性判断方法,进一步提升了加固选择的准确性,并将其拓展于资源投入量的决策。上述方法由于可以在有限的计算成本内同时考虑组件易损性和组件损伤对系统功能的影响,所得结果的可靠性较高,具有良好的工程实用前景。
综上,道路交通系统的加固决策是一个由来已久的问题,对此学术界已经提出了多种解决方案。其中,传统重要性排序方法虽然计算效率最高,但准确性差。随机优化模型的适用性和准确性均最佳但计算效率低下,不过随着计算机技术的发展,其必将成为未来研究的主流方法之一。此外,基于有限样本的相关性分析方法能够兼顾效率与准确性,也是值得进一步研究和推广的方法。
尽管近期的研究在计算效率与决策准确性方面取得了进展,但以上所有研究均只考虑了加固对系统抵抗地震的直接影响,忽视了其对系统震后恢复时间和间接损失的积极作用。实际上,震前加固与震后恢复之间存在密切的关联性,但目前缺乏相关的研究,震前加固措施对组件及系统震后修复的影响机制尚不明确。因此,从韧性视角出发,建立震前加固、震时抵抗和震后恢复的关联分析模型,并发展震前加固与功能恢复的耦合优化决策方法,对保障道路交通系统的震后功能水平以及推动韧性城市的建设具有非常重要的意义,这也将成为未来研究的重要方向之一。
3 结论与展望本文详细探讨了城市道路交通系统抗震韧性的重要性、定义及内涵,并全面总结了现有的研究成果及存在的局限性。历经近20 a的探索,道路交通系统的震后功能分析方法已在科学界达成大量共识,韧性评估理论也取得了显著进展,但是,由于道路交通的特殊性,仍有必要进一步开发能够考虑系统震后多种功能贡献的专有韧性评价指标体系。此外,学者们对道路交通系统的震后恢复策略和震前加固策略进行了试探性的研究,为既有城市的抗震韧性提升提供了一定的参考。然而,这些方法与基于韧性理念的工程实践还存在较大差距,震后恢复决策模型在多目标、真实性和计算效率等方面仍有待改进,而现阶段的震前加固决策模型尚未能考虑加固对系统及城市的震后长期影响。
为进一步推进道路交通系统及城市的抗震韧性建设,除上述缺陷外,以下4项关键问题有必要在未来的研究中着重考虑:
1) 精细化的震后交通分析模型。现阶段道路交通系统的抗震韧性研究主要关注于评价方法及优化模型的建立,对震后道路交通条件和运行状况的模拟则较为粗糙。已有研究普遍沿用常态化交通的分析方法,并依据组件的破坏等级假定震后的交通条件及用户行为,但这与实际情况往往存在较大差距,进而影响韧性评价及优化策略的计算结果。因此,有必要建立能够真实反映震后道路交通条件的物理分析模型,并考虑灾害对用户心理及判断力的影响,发展精细化的震后交通仿真和功能分析方法,以提升韧性评估结果的可靠性。
2) 城市系统间的耦联机制。目前城市交通系统的抗震韧性研究主要关注于单一系统,如道路、铁路、地铁等,而忽略了不同交通方式之间的相互依赖和互补性。在发生大规模组件损坏或中断的地震场景下,城市中多种交通方式的联运有助于交通需求的共享,从而增强灾时交通的可用性和冗余性;同时,多种交通方式之间的相互依赖也可能导致以道路交通为主的城市多式联运网络在地震灾害下出现级联失效。此外,道路交通系统与建筑、医疗、电力等其他城市工程系统之间也存在密切的耦联关系,这在已有研究中很少考虑。例如: 地震后建筑系统的大规模破坏会导致城市交通需求的显著变化;震后区域医疗体系的运转必须依赖道路交通系统的可达性;现代化道路交通系统的运行需要电力及通讯系统的支持,而电力和通讯系统的震后恢复则反过来需要道路交通的支持。因此,合理考虑多式联运交通及与其他工程系统间的耦联机制对城市系统抗震韧性评估的意义重大,也将成为后续研究的难点。
3) 工程技术韧性与社会经济要素的有机融合。现有研究聚焦于工程技术角度的抗震韧性评价及提升方法,研究案例中的参数,如震后交通需求、应急设施可用性、指标权重、可用资源等通常为预先设定,而缺乏针对不同地区情况的个性化考虑。事实上,韧性应被视为城市或系统的固有属性,并非依赖于特定情境。除工程技术韧性外,城市的经济组成,人口密度、年龄分布、教育程度等因素同样对城市系统灾后的应对能力和功能恢复具有重要影响。例如,城市的社会经济结构是决定震后资源倾斜的核心要素,良好的灾害应急预案和人员培训同样是保障城市系统灾后高效运转的基础。因此,为全面衡量城市系统的抗震韧性,必须在工程技术韧性的基础上合理融入社会经济要素的影响。
4) 由韧性评价向韧性设计转变。迄今为止的研究均围绕既有城市道路交通系统展开,而缺乏新建、改建、扩建工程可遵循的韧性设计方法。近年来,随着中国经济的快速发展,大城市不断扩张,并涌现出许多新兴城市,在进行大规模基础设施建设之前,基于韧性视角规划城市道路交通的建设,并协调道路交通系统的常态化与灾害设计,以确保系统能够同时满足日常高效运行和抗震韧性的需求,对城市的长久发展具有重要意义。此外,如第3条所述,除在工程技术层面上构建韧性城市的基础之外,在社会管理方面加强灾害监测、预警和应急教育,制定完备的应急预案,并储备充足的灾时资源,也是韧性设计中不可或缺的重要环节。
| [1] |
JACQUES C C, MCINTOSH J, GIOVINAZZI S, et al. Resilience of the Canterbury hospital system to the 2011 Christchurch earthquake[J]. Earthquake Spectra, 2014, 30(1): 533. DOI:10.1193/032013EQS074M |
| [2] |
MERONI F, SQUARCINA T, PESSINA V, et al. A damage scenario for the 2012 Northern Italy earthquakes and estimation of the economic losses to residential buildings[J]. International Journal of Disaster Risk Science, 2017(8): 326. DOI:10.1007/s13753-017-0142-9 |
| [3] |
GODA K, KIYOTA T, POKHREL R M, et al. The 2015 Gorkha Nepal earthquake: insights from earthquake damage survey[J]. Frontiers in Built Environment, 2015(1): 8. DOI:10.3389/fbuil.2015.00008 |
| [4] |
BELLERIVE J M. Haiti earthquake PDNA (post-disaster needs assessment): assessment of damage, losses, general and sectoral needs[R]. 2012
|
| [5] |
YUAN Y. Impact of intensity and loss assessment following the great Wenchuan earthquake[J]. Earthquake Engineering and Engineering Vibration, 2008, 7: 247. DOI:10.1007/s11803-008-0893-9 |
| [6] |
HAMILTON R, ANDREWS R, BAUER R, et al. National earthquake resilience: research, implementation and outreach[R]. Washington DC: The National Academies Press, 2011
|
| [7] |
王江波, 陈涛, 苟爱萍. 亚洲城市韧性发展策略比较[J]. 科技导报, 2022, 40(22): 20. WANG Jiangbo, CHEN Tao, GOU Aiping. Comparative research on resilient development strategies of Asian cities[J]. Science & Technology Review, 2022, 40(22): 20. |
| [8] |
史培军. 仙台框架: 未来15年世界减灾指导性文件[J]. 中国减灾, 2015(4): 30. SHI Peijun. Sendai framework: world disaster reduction guidance document for the next 15 years[J]. Disaster Reduction in China, 2015(4): 30. |
| [9] |
CIMELLARO G, SMITH R. New trends on resiliency research[C]//16th World Conference on Earthquake Engineering. Chile: [s. n. ], 2017
|
| [10] |
HOLLING C S. Resilience and stability of ecological systems[J]. Annual Review of Ecology and Systematics, 1973, 4(1): 1. DOI:10.1146/annurev.es.04.110173.000245 |
| [11] |
BRUNEAU M, CHANG S E, EGUCHI R T, et al. A framework to quantitatively assess and enhance the seismic resilience of communities[J]. Earthquake Spectra, 2003, 19(4): 733. DOI:10.1193/1.1623497 |
| [12] |
DONG Y, FRANGOPOL D M, SAYDAM D. Sustainability of highway bridge networks under seismic hazard[J]. Journal of Earthquake Engineering, 2014, 18(1): 41. DOI:10.1080/13632469.2013.841600 |
| [13] |
GÜNNEÇ D, SALMAN F S. Assessing the reliability and the expected performance of a network under disaster risk[J]. OR Spectrum, 2011, 33(3): 499. DOI:10.1007/s00291-011-0250-7 |
| [14] |
GORDON P, RICHARDSON H W, DAVIS B. Transport-related impacts of the Northridge earthquake[J]. Journal of Transportation and Statistics, 1998, 1(2): 21. |
| [15] |
HORWICH G. Economic lessons of the Kobe earthquake[J]. Economic Development and Cultural Change, 2000, 48(3): 521. DOI:10.1086/452609 |
| [16] |
HAN Qiang, DU Xiuli, LIU Jingbo, et al. Seismic damage of highway bridges during the 2008 Wenchuan earthquake[J]. Earthquake Engineering and Engineering Vibration, 2009, 8(2): 263. DOI:10.1007/s11803-009-8162-0 |
| [17] |
MURRAY-TUITE P M. A comparison of transportation network resilience under simulated system optimum and user equilibrium conditions[C]//Proceedings of the 2006 Winter Simulation Conference. Monterey: IEEE, 2006: 1398
|
| [18] |
SERULLE N U, HEASLIP K, BRADY B, et al. Resiliency of transportation network of Santo Domingo, Dominican Republic: case study[J]. Transportation Research Record, 2011, 2234(1): 22. DOI:10.3141/2234-03 |
| [19] |
D'LIMA M, MEDDA F. A new measure of resilience: an application to the London underground[J]. Transportation Research Part A: Policy and Practice, 2015, 81: 35. DOI:10.1016/j.tra.2015.05.017 |
| [20] |
CHAN R, SCHOFER J L. Measuringroad traffic system resilience: response of rail transit to weather disruptions[J]. Natural Hazards Review, 2016, 17(1): 05015004. DOI:10.1061/(ASCE)NH.1527-6996.0000200 |
| [21] |
ZHOU Yaoming, WANG Junwei, YANG Hai. Resilience of transportation systems: concepts and comprehensive review[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(12): 4262. DOI:10.1109/tits.2018.2883766 |
| [22] |
孙惠泉. 图论及其应用[M]. 北京: 科学出版社, 2004. SUN Huiquan. Graph theory with applications[M]. Beijing: Science Press, 2004. |
| [23] |
ZHANG X, MILLER-HOOKS E, DENNY K. Assessing the role of network topology in transportation network resilience[J]. Journal of Transport Geography, 2015, 46: 35. DOI:10.1016/j.jtrangeo.2015.05.006 |
| [24] |
TESTA A C, FURTADO M N, ALIPOUR A. Resilience of coastal transportation networks faced with extreme climatic events[J]. Transportation Research Record, 2015, 2532(2532): 29. DOI:10.3141/2532-04 |
| [25] |
OSEI-ASAMOAH A, LOWNES N E. Complex network method of evaluating resilience in surface transportation networks[J]. Transportation Research Record, 2014, 2467(2467): 120. DOI:10.3141/2467-13 |
| [26] |
BERCHE B, VON FERBER C, HOLOVATCH T, et al. Resilience of public transport networks against attacks[J]. European Physical Journal B, 2009, 71(1): 125. DOI:10.1140/epjb/e2009-00291-3 |
| [27] |
SOHN J. Evaluating the significance of highway network links under the flood damage: an accessibility approach[J]. Transportation Research Part A: Policy and Practice, 2006, 40(6): 491. DOI:10.1016/j.tra.2005.08.006 |
| [28] |
CHANG S E, NOJIMA N. Measuring post-disaster road traffic system performance: the 1995 Kobe earthquake in comparative perspective[J]. Transportation Research Part A: Policy and Practice, 2001, 35(6): 475. DOI:10.1016/S0965-8564(00)00003-3 |
| [29] |
AYDIN N Y, DUZGUN H S, WENZEL F, et al. Integration of stress testing with graph theory to assess the resilience of urban road networks under seismic hazards[J]. Natural Hazards, Springer Netherlands, 2018, 91(1): 37. DOI:10.1007/s11069-017-3112-z |
| [30] |
GUIDOTTI R, GARDONI P, CHEN Y. Network reliability analysis with link and nodal weights and auxiliary nodes[J]. Structural Safety, 2017, 65: 12. DOI:10.1016/j.strusafe.2016.12.001 |
| [31] |
FRANCHIN P, LUPOI A, PINTO P E. On the role of road networks in reducing human losses after earthquakes[J]. Journal of Earthquake Engineering, 2006, 10(2): 195. DOI:10.1080/13632460609350593 |
| [32] |
KANG W H, SONG J, GARDONI P. Matrix-based system reliability method and applications to bridge networks[J]. Reliability Engineering & System Safety, 2008, 93(11): 1584. DOI:10.1016/j.ress.2008.02.011 |
| [33] |
KONDO R, SHIOMI Y, UNO N. Network evaluation based on connectivity reliability and accessibility[C]//Network Reliability in Practice: Selected Papers from the Fourth International Symposium on Transportation Network Reliability. NewYork: Springer, 2012: 131
|
| [34] |
IP W H, WANG Dingwei. Resilience and friability of transportation networks: evaluation, analysis and optimization[J]. IEEE Systems Journal, 2011, 5(2): 189. DOI:10.1109/jsyst.2010.2096670 |
| [35] |
ZHANG Weili, WANG Naiyu. Resilience-based risk mitigation for road networks[J]. Structural Safety, 2016, 62: 57. DOI:10.1016/j.strusafe.2016.06.003 |
| [36] |
KURAUCHI F, UNO N, SUMALEE A, et al. Network evaluation based on connectivity vulnerability[C]//Transportation and Traffic Theory 2009, Golden Jubilee: Papers Selected for Presentation at ISTTT18, a Peer Reviewed Series Since 1959. Berlin: Springer, 2009: 637
|
| [37] |
王炜, 过秀成. 交通工程学[M]. 南京: 东南大学出版社, 2000. WANG Wei, GUO Xiucheng. Traffic engineering[M]. Nanjing: Southeast University Press, 2000. |
| [38] |
王殿海, 景春光, 曲昭伟. 交通波理论在交叉口交通流分析中的应用[J]. 中国公路学报, 2002, 15(1): 93. WANG Dianhai, JING Chunguang, QU Zhaowei. Application of traffic wave theory in intersections traffic flow analysis[J]. China Journal of Highway and Transport, 2002, 15(1): 93. DOI:10.19721/j.cnki.1001-7372.2002.01.023 |
| [39] |
林瑜, 杨晓光, 马莹莹. 城市道路间断交通流阻塞量化方法研究[J]. 同济大学学报(自然科学版), 2007, 35(3): 336. LIN Yu, YANG Xiaoguang, MA Yingying. Measurement methodology of discrete traffic flow congestion on urban surface streets[J]. Journal of Tongji University(Natural Science), 2007, 35(3): 336. DOI:10.3321/j.issn:0253-374X.2007.03.009 |
| [40] |
GHOSN M, DUEÑAS-OSORIO L, FRANGOPOL D M, et al. Performance indicators for structural systems and infrastructure networks[J]. Journal of Structural Engineering, 2016, 142(9): F4016003. DOI:10.1061/(asce)st.1943-541x.0001542 |
| [41] |
DONOVAN B, WORK D B. Empirically quantifying city-scale transportation system resilience to extreme events[J]. Transportation Research Part C: Emerging Technologies, 2017, 79: 333. DOI:10.1016/j.trc.2017.03.002 |
| [42] |
CHO J, LEE Y J, LEE S M, et al. Analysis of macroscopic traffic network impacted by structural damage to bridges from earthquakes[J]. Applied Sciences, 2021, 11(7): 3226. DOI:10.3390/app11073226 |
| [43] |
WARDROP J G. Road paper some theoretical aspects of road traffic research[J]. Proceedings of the Institution of Civil Engineers, 1952, 1(3): 325. DOI:10.1680/ipeds.1952.11259 |
| [44] |
FENVES S J. Expected flow in a transportation network[C]//Proc 2nd US National Conf on Earthq Eng. [S. l. ]: Transportation, 1979: 673
|
| [45] |
KIM S, SHEKHAR S, MIN M. Contraflow transportation network reconfiguration for evacuation route planning[J]. IEEE Transactions on Knowledge and Data Engineering, 2008, 20(8): 1115. DOI:10.1109/tkde.2007.190722 |
| [46] |
BAZZAN A L C, KLÜGL F. A review on agent-based technology for traffic and transportation[J]. The Knowledge Engineering Review, 2014, 29(3): 375. DOI:10.1017/s0269888913000118 |
| [47] |
CHU J C, CHEN S C. Optimization of transportation-infrastructure-system protection considering weighted connectivity reliability[J]. Journal of Infrastructure Systems, 2016, 22(1): 1. DOI:10.1061/(asce)is.1943-555x.0000264 |
| [48] |
KHADEMI N, BALAEI B, SHAHRI M, et al. Transportation network vulnerability analysis for the case of a catastrophic earthquake[J]. International Journal of Disaster Risk Reduction, 2015, 12: 234. DOI:10.1016/j.ijdrr.2015.01.009 |
| [49] |
BOAKYE J, GUIDOTTI R, GARDONI P, et al. The role of transportation infrastructure on the impact of natural hazards on communities[J]. Reliability Engineering and System Safety, 2022, 219: 108184. DOI:10.1016/j.ress.2021.108184 |
| [50] |
LIU K, ZHAI C, DONG Y, et al. Post-earthquake functionality assessment of urban road network considering emergency response[J]. Journal of Earthquake Engineering, 2023, 27(9): 2406. DOI:10.1080/13632469.2022.2113001 |
| [51] |
BOCCHINI P, FRANGOPOL D M. Optimal resilience-and cost-based postdisaster intervention prioritization for bridges along a highway segment[J]. Journal of Bridge Engineering, 2012, 17(1): 117. DOI:10.1061/(asce)be.1943-5592.0000201 |
| [52] |
TWUMASI-BOAKYE R, SOBANJO J O. Resilience of regional transportation networks subjected to hazard-induced bridge damages[J]. Journal of Transportation Engineering Part A: Systems, 2018, 144(10): 1. DOI:10.1061/jtepbs.0000186 |
| [53] |
KILANITIS I, SEXTOS A. Integrated seismic risk and resilience assessment of roadway networks in earthquake prone areas[J]. Bulletin of Earthquake Engineering, 2019, 17: 181. DOI:10.1007/s10518-018-0457-y |
| [54] |
CHANG Liang, PENG Fan, OUYANG Yanfeng, et al. Bridge seismic retrofit program planning to maximize postearthquake transportation network capacity[J]. Journal of Infrastructure Systems, 2012, 18(2): 75. DOI:10.1061/(asce)is.1943-555x.0000082 |
| [55] |
FENG K, LI Q, ELLINGWOOD B R. Post-earthquake modelling of transportation networks using an agent-based model[J]. Structure and Infrastructure Engineering, 2020, 16(11): 1578. DOI:10.1080/15732479.2020.1713170 |
| [56] |
方东平, 李在上, 李楠, 等. 城市韧性: 基于"三度空间下系统的系统"的思考[J]. 土木工程学报, 2017, 50(7): 1. FANG Dongping, LI Zaishang, LI Nan, et al. Urban resilience: a perspective of system of systems in trio spaces[J]. China Civil Engineering Journal, 2017, 50(7): 1. DOI:10.15951/j.tmgcxb.2017.07.001 |
| [57] |
翟长海, 刘文, 谢礼立. 城市抗震韧性评估研究进展[J]. 建筑结构学报, 2018, 39(9): 1. ZHAI Changhai, LIU Wen, XIE Lili. Progress of research on city seismic resilience evaluation[J]. Journal of Building Structures, 2018, 39(9): 1. DOI:10.14006/j.jzjgxb.2018.09.001 |
| [58] |
COX A, PRAGER F, ROSE A. Transportation security and the role of resilience: a foundation for operational metrics[J]. Transport Policy, 2011, 18(2): 307. DOI:10.1016/j.tranpol.2010.09.004 |
| [59] |
FATURECHI R, MILLER-HOOKS E. Travel time resilience of roadway networks under disaster[J]. Transportation Research Part B: Methodological, 2014, 70: 47. DOI:10.1016/j.trb.2014.08.007 |
| [60] |
MILLER-HOOKS E, ZHANG Xiaodong, FATURECHI R. Measuring and maximizing resilience of freight transportation networks[J]. Computers & Operations Research, 2012, 39(7): 1633. DOI:10.1016/j.cor.2011.09.017 |
| [61] |
CHEN L, MILLER-HOOKS E. Resilience: an indicator of recovery capability in intermodal freight transport[J]. Transportation Science, 2012, 46(1): 109. DOI:10.1287/trsc.1110.0376 |
| [62] |
FATURECHI R, LEVENBERG E, MILLER-HOOKS E. Evaluating and optimizing resilience of airport pavement networks[J]. Computers & Operations Research, 2014, 43: 335. DOI:10.1016/j.cor.2013.10.009 |
| [63] |
JIN Jiangang, TANG L C, SUN Lijun, et al. Enhancing metro network resilience via localized integration with bus services[J]. Transportation Research Part E: Logistics and Transportation Review, 2014, 63: 17. DOI:10.1016/j.tre.2014.01.002 |
| [64] |
WEN W, HU J, ZHAI C, et al. Post-earthquake functionality assessment of subway stations considering the interdependency among sub-systems[J]. Computer-Aided Civil and Infrastructure Engineering, 2023, 1. DOI:10.1111/mice.13008 |
| [65] |
JANIĆ M. Modelling the resilience, friability and costs of an air transport network affected by a large-scale disruptive event[J]. Transportation Research Part A: Policy and Practice, 2015, 81: 77. DOI:10.1016/j.tra.2014.10.023 |
| [66] |
PEI Shunshun, ZHAI Changhai, WANG Zhenqiang, et al. Resilience assessment of the interdependent transportation-healthcare system during emergency response[J]. Structure and Infrastructure Engineering, 2022, 1. DOI:10.1080/15732479.2022.2136719 |
| [67] |
PEI S, ZHAI C, WEN W, et al. A dynamic patients dispatch and treatment model for resilience evaluation of interdependent transportation-healthcare system[J]. Journal of Earthquake Engineering, 2023, 1. DOI:10.1080/13632469.2023.2185863 |
| [68] |
CHEN Hong, CULLINANE K, LIU Nan. Developing a model for measuring the resilience of a port-hinterland container transportation network[J]. Transportation Research Part E: Logistics and Transportation Review, 2017, 97: 282. DOI:10.1016/j.tre.2016.10.008 |
| [69] |
CIMELLARO G P, REINHORN A M, BRUNEAU M. Framework for analytical quantification of disaster resilience[J]. Engineering Structures, 2010, 32(11): 3639. DOI:10.1016/j.engstruct.2010.08.008 |
| [70] |
CIMELLARO G P, ARCIDIACONO V, REINHORN A M. Disaster resilience assessment of building and transportation system[J]. Journal of Earthquake Engineering, 2021, 25(4): 703. DOI:10.1080/13632469.2018.1531090 |
| [71] |
BOCCHINI P, FRANGOPOL D M, UMMENHOFER T, et al. Resilience and sustainability of civil infrastructure: toward a unified approach[J]. Journal of Infrastructure Systems, 2014, 20(2): 04014004. DOI:10.1061/(asce)is.1943-555x.0000177 |
| [72] |
LI Yaohan, DONG You, FRANGOPOL D M, et al. Long-term resilience and loss assessment of highway bridges under multiple natural hazards[J]. Structure and Infrastructure Engineering, 2020, 16(4): 626. DOI:10.1080/15732479.2019.1699936 |
| [73] |
ADJETEY-BAHUN K, BIRREGAH B, CHÂTELET E, et al. A model to quantify the resilience of mass railway transportation systems[J]. Reliability Engineering & System Safety, 2016, 153: 1. DOI:10.1016/j.ress.2016.03.015 |
| [74] |
TANG Y, LI S, ZHAI C. A belief rule-base approach to the assessment and improvement of seismic resilience of high-speed railway station buildings[J]. Soil Dynamics and Earthquake Engineering, 2023, 165: 107680. DOI:10.1016/j.soildyn.2022.107680 |
| [75] |
ZHU Yuan, XIE Kun, OZBAY K, et al. Data-driven spatial modeling for quantifying networkwide resilience in the aftermath of hurricanes Irene and Sandy[J]. Transportation Research Record, 2017, 2604(1): 9. DOI:10.3141/2604-02 |
| [76] |
ZHU Yuan, OZBAY K, XIE Kun, et al. Using big data to study resilience of taxi and subway trips for hurricanes Sandy and Irene[J]. Transportation Research Record, 2016, 2599(1): 70. DOI:10.3141/2599-09 |
| [77] |
LIAO T Y, HU T Y, KO Y N. A resilience optimization model for transportation networks under disasters[J]. Natural Hazards, 2018, 93: 469. DOI:10.1007/s11069-018-3310-3 |
| [78] |
ZHAI C, ZHAO Y, WEN W, et al. A novel urban seismic resilience assessment method considering the weighting of post-earthquake loss and recovery time[J]. International Journal of Disaster Risk Reduction, 2023, 84: 103453. DOI:10.1016/j.ijdrr.2022.103453 |
| [79] |
BOCCHINI P. Computational procedure for the assisted resilience-oriented disaster management of transportation systems[C]//Safety, Reliability, Risk and Life-Cycle Performance of Structures and Infrastructures. Balkema, Leiden: CRC Press, 2013
|
| [80] |
ZHOU Y, BANERJEE S, SHINOZUKA M. Socio-economic effect of seismic retrofit of bridges for highway transportation networks: a pilot study[J]. Structure and Infrastructure Engineering, 2010, 6(1/2): 145. DOI:10.1080/15732470802663862 |
| [81] |
DECÒ A, BOCCHINI P, FRANGOPOL D M. A probabilistic approach for the prediction of seismic resilience of bridges[J]. Earthquake Engineering and Structural Dynamics, 2013, 42(10): 1469. DOI:10.1002/eqe.2282 |
| [82] |
CHANG S E, SHINOZUKA M. Measuring improvements in the disaster resilience of communities[J]. Earthquake Spectra, 2004, 20(3): 739. DOI:10.1193/1.1775796 |
| [83] |
KAMESHWAR S, MISRA S, PADGETT J E. Decision tree based bridge restoration models for extreme event performance assessment of regional road networks[J]. Structure and Infrastructure Engineering, Taylor & Francis, 2020, 16(3): 431. DOI:10.1080/15732479.2019.1668026 |
| [84] |
BOCCHINI P, FRANGOPOL D M. Restoration of bridge networks after an earthquake: multicriteria intervention optimization[J]. Earthquake Spectra, 2012, 28(2): 427. DOI:10.1193/1.4000019 |
| [85] |
LERTWORAWANICH P. Highway network restoration after the great flood in Thailand[J]. Natural Hazards, 2012, 64(1): 873. DOI:10.1007/s11069-012-0278-2 |
| [86] |
EL-ANWAR O, YE J, ORABI W. Efficient optimization of post-disaster reconstruction of transportation networks[J]. Journal of Computing in Civil Engineering, 2016, 30(3): 04015047. DOI:10.1061/(asce)cp.1943-5487.0000503 |
| [87] |
ZHANG Weili, WANG Naiyu, NICHOLSON C. Resilience-based post-disaster recovery strategies for road-bridge networks[J]. Structure and Infrastructure Engineering, 2017, 13(11): 1404. DOI:10.1080/15732479.2016.1271813 |
| [88] |
HACKL J, ADEY B T, LETHANH N. Determination of near-optimal restoration programs for transportation networks following natural hazard events using simulated annealing[J]. Computer-Aided Civil and Infrastructure Engineering, 2018, 33(8): 618. DOI:10.1111/mice.12346 |
| [89] |
MOGHTADERNEJAD S, ADEY B T, HACKL J. Determination of postdisaster restoration programs for road networks using a double-stage optimization approach[J]. Journal of Infrastructure Systems, 2022, 28(3): 04022025. DOI:10.1061/(asce)is.1943-555x.0000700 |
| [90] |
MOGHTADERNEJAD S, ADEY B T, HACKL J. Prioritizing road network restorative interventions using a discrete particle swarm optimization[J]. Journal of Infrastructure Systems, 2022, 28(4): 04022039. DOI:10.1061/(asce)is.1943-555x.0000725 |
| [91] |
LIU K, ZHAI C, DONG Y. Optimal restoration schedules of transportation network considering resilience[J]. Structure and Infrastructure Engineering, 2021, 17(8): 1141. DOI:10.1080/15732479.2020.1801764 |
| [92] |
ZHANG Z, JI T, WEI H. Assessment of post-earthquake resilience of highway-bridge networks by considering downtime due to interaction of parallel restoration actions[J]. Structure and Infrastructure Engineering, 2023, 19(5): 589. DOI:10.1080/15732479.2021.1961826 |
| [93] |
KARAMLOU A, BOCCHINI P. Sequencing algorithm with multiple-input genetic operators: application to disaster resilience[J]. Engineering Structures, 2016, 117: 591. DOI:10.1016/j.engstruct.2016.03.038 |
| [94] |
LIU Chuang, OUYANG Min, WANG Naiyu, et al. A heuristic method to identify optimum seismic retrofit strategies for critical infrastructure systems[J]. Computer-Aided Civil and Infrastructure Engineering, 2021, 36(8): 996. DOI:10.1111/mice.12647 |
| [95] |
Federal Highway Administration. Coding guide for the structure inventory and appraisal of the nation's bridges[R]. Washington DC: Federal Highway Administration, 1995
|
| [96] |
BUCKLE I G, FRIEDLAND I M, COOPER J D. A seismic retrofitting manual for highway bridges[R]. [S. l. ]: Nist Special Publication Sp, 1994
|
| [97] |
CONTRERAS-NIETO C, SHAN Y, LEWIS P, et al. Bridge maintenance prioritization using analytic hierarchy process and fusion tables[J]. Automation in Construction, 2019, 101: 99. DOI:10.1016/j.autcon.2019.01.016 |
| [98] |
YOUSEFI A, AHAMAD M S S, MAJID T A. Application of TOPSIS method in prioritization of highway bridges for seismic retrofitting[J]. Engineering Structures and Technologies, 2014, 6(3): 114. DOI:10.3846/2029882x.2014.980853 |
| [99] |
D'APUZZO M, EVANGELISTI A, NICOLOSI V, et al. A simplified approach for the prioritization of bridge stock seismic retrofitting[C]//Proceedings of the 29th European Safety and Reliability Conference (ESREL). Hannover: [s. n. ], 2019: 3277
|
| [100] |
DUENAS-OSORIO L, VEMURU S M. Cascading failures in complex infrastructure systems[J]. Structural Safety, 2009, 31(2): 157. DOI:10.1016/j.strusafe.2008.06.007 |
| [101] |
SUN Weiman, ZENG An. Target recovery in complex networks[J]. The European Physical Journal B, 2017, 90: 1. DOI:10.1140/epjb/e2016-70618-0 |
| [102] |
ZHAO Taiyi, SUN Li. Seismic resilience assessment of critical infrastructure-community systems considering looped interdependences[J]. International Journal of Disaster Risk Reduction, 2021, 59: 102246. DOI:10.1016/j.ijdrr.2021.102246 |
| [103] |
UKKUSURI S V, YUSHIMITO W F. A methodology to assess the criticality of highway transportation networks[J]. Journal of Transportation Security, 2009, 2: 29. DOI:10.1007/s12198-009-0025-4 |
| [104] |
CUI Hongjun, WANG Fei, LI Xia, et al. Reinforcement and optimization of seismic connectivity of key transportation hubs based on minimum cost[J]. Physica A: Statistical Mechanics and its Applications, 2020, 540: 123231. DOI:10.1016/j.physa.2019.123231 |
| [105] |
CHEN M, MANGALATHU S, JEON J S. Bridge fragilities to network fragilities in seismic scenarios: an integrated approach[J]. Engineering Structures, 2021, 237: 112212. DOI:10.1016/j.engstruct.2021.112212 |
| [106] |
PEETA S, SALMAN F S, GUNNEC D, et al. Computers & operations research pre-disaster investment decisions for strengthening a highway network[J]. Computers and Operation Research, Elsevier, 2010, 37(10): 1708. DOI:10.1016/j.cor.2009.12.006 |
| [107] |
HUANG Yongxi, PARMELEE S, PANG W. Optimal retrofit scheme for highway network under seismic hazards[J]. International Journal of Transportation Science and Technology, Tongji University and Tongji University Press, 2014, 3(2): 109. DOI:10.1260/2046-0430.3.2.109 |
| [108] |
TAK H Y, SUH W, LEE Y J. System-level seismic risk assessment of bridge transportation networks employing probabilistic seismic hazard analysis[J]. Mathematical Problems in Engineering, 2019, 2019: 1. DOI:10.1155/2019/6503616 |
| [109] |
LIU L, FRANGOPOL D M, MONDORO A, et al. Sustainability-informed bridge ranking under scour based on transportation network performance and multiattribute utility[J]. Journal of Bridge Engineering, 2018, 23(10): 04018082. DOI:10.1061/(asce)be.1943-5592.0001296 |
| [110] |
ROKNEDDIN K, GHOSH J, DUEÑAS-OSORIO L, et al. Bridge retrofit prioritisation for ageing transportation networks subject to seismic hazards[J]. Structure and Infrastructure Engineering, 2013, 9(10): 1050. DOI:10.1080/15732479.2011.654230 |
| [111] |
WANG Z, JIA G. Efficient sample-based approach for effective seismic risk mitigation of transportation networks[J]. Sustainable and Resilient Infrastructure, 2020, 5(6): 349. DOI:10.1080/23789689.2019.1598756 |
| [112] |
LIU K, ZHAI C, MENG X. Probabilistic joint importance-based retrofit strategy for seismic risk mitigation of transportation networks[J]. Applied Sciences, 2022, 12(18): 9307. DOI:10.3390/app12189307 |
 2024, Vol. 56
2024, Vol. 56


