热能存储(TES)[1-3]可以解决能源利用的间歇性和不稳定性问题[4-6],以相变材料(PCM)作为蓄热介质的潜热蓄热堆积床(LHTES)[7-9]因其较大的相变潜热、相变温度恒定和化学稳定性而备受关注[10-13]。Mohammadnejad等[14]研究了多层PCM堆积床的放热性能,通过改变每层的高度和孔隙度使性能提高29.2%。Li等[15]研究了储热单元的尺寸对热性能的影响,提供了一个LHTES热性能优化的改进方法。如今,仿生学为新的功能结构材料和系统的研究和开发提供了新的思路[16-18]。自然进化使生物学和环境经历了长期的相互作用,在自然界中出现了许多优秀的功能和完美的结构。以自然材料为基础,结构仿生学和功能仿生学对科学技术的发展和人类的进步有积极和有益的影响[19-20]。Cheng等[21]提出了一种红细胞形状的储热单元并对其传热流动特性进行了实验研究与数值模拟,结果表明,红细胞形胶囊的储放热速率为球形胶囊的2.12倍。Tian等[22]提出了一种人工线粒体储热单元,可以减少53%的熔化时间。王欢等[23-24]将仿生脉络结构应用到太阳热化学与储能领域,结果表明,脉络等级结构的有效组合可以显著提升系统储热效率。
LHTES具有广阔的应用前景,但其存在传热速率不均匀的缺点。本文结合自然界植物体结构,提出了具有仿生葫芦结构的蓄热单元,以探索其在LHTES系统中的潜力。本文分析了传统单元和仿生葫芦单元在LHTES系统中温度、储热效率、储热容量等热性能的影响。研究结果可为LHTES系统的优化设计提供理论指导。
1 模型建立 1.1 堆积床储热单元仿生原理葫芦在生长过程中表现出两大优势,即营养吸收优势和水分扩散优势。葫芦果实的生长过程阶段,在重力影响下,果实从根部吸收营养物质时,营养物质向下沉积使得下部吸收的养分大于上部,产生了上下部的体积差异。葫芦体吸收营养物质时,同时存在水分扩散过程,水分在上下部进一步流动扩散,最终生长成为上下球径不一的几何体。
蓄热单元内部PCM熔化时,固态PCM在导热作用下吸热转变为液态PCM,在重力影响下液态PCM向下沉积,该过程类似于葫芦果实的营养吸收过程。在温差驱动力作用下,液态PCM在单元下部扩散进行自然对流换热,该过程类似于葫芦果实的水分扩散过程。在葫芦果实的营养吸收和水分扩散优势启发下,葫芦体结构可以使储热单元的导热换热量大于对流换热量,有利于储热单元中PCM的熔化相变。因此,所设计的仿生葫芦形储热单元会具有更大的传导和自然对流,葫芦单元独特的喉部结构可增强PCM的熔化过程,提高LHTES的储热效率。
1.2 堆积床储热单元数值模型针对自然界中葫芦的外形进行几何归纳,建立数学几何模型,三维几何描述以及示意如图 1所示[25]。仿生葫芦体可以看作由两个半径不同的球体耦合组成,其中,大球半径为R,小球半径为r,两球中心距为L,两球母线相交点为(x0, y0),相交点和小球圆心连线在水平方向的夹角为θ。定义葫芦体的几何控制参数——复合因子满足式(1)。当n=1时,单元外形为两球相切情况;当n=0时,单元外形为两球重合形成同心球的情况。
| $ n=L /(R+r) $ | (1) |

|
图 1 仿生葫芦体数学模型 Fig. 1 Mathematical model of bionic-calabash capsule |
仿生葫芦体外轮廓线满足
| $ \left\{\begin{array}{l} (x-r)^2+y^2=r^2, 0<x<r \\ {[x-(L+r)]^2+y^2=R^2, x_0<x<L+r+R} \end{array}\right. $ | (2) |
R,r,L满足如下限制条件:
| $r<R \text { 且 } R-r<L<R+r $ | (3) |
其中,相交点坐标(x0, y0)满足如下关系式:
| $ \left\{\begin{array}{l} x_0=r \cos \theta \\ y_0=r \sin \theta+r \end{array}\right. $ | (4) |
由余弦定理与正余弦关系知:
| $\cos \theta=\frac{r^2+L^2-R^2}{2 r L}, \sin \theta=\sqrt{1-\cos ^2 \theta} $ | (5) |
Xia等[26]提出了有效堆积床模型,该模型可以描述不同LHTES系统中储热胶囊的排列情况,对所有的LHTES系统具有普适性。该模型下的堆积床系统等效基于三维系统的孔隙率等于二维系统的孔隙率,即
| $ \left\{\begin{array}{l} \varepsilon_{3 \mathrm{D}}=\frac{V_{\mathrm{PCM}}}{V_{\mathrm{tank}}}=\frac{n_{3 \mathrm{D}}(4 / 3) {\rm{ \mathsf{ π}}}(d / 2)^3}{{\rm{ \mathsf{ π}}}(D / 2)^2 H} \\ \varepsilon_{2 \mathrm{D}}=\frac{S_{\mathrm{PCM}}}{S_{\mathrm{tank}}}=\frac{n_{2 \mathrm{D}} {\rm{ \mathsf{ π}}}(d / 2)^3}{{\rm{ \mathsf{ π}}}(D / 2)^2 H} \end{array}\right. $ | (6) |
式中:ε为孔隙率,V为三维系统下的体积,S为二维系统下的表面积,n为储热单元数量,d为储热单元直径,D为堆积床直径,H为堆积床高度。
图 2为仿生葫芦堆积床系统及球形堆积床的示意。为了与仿生葫芦堆积床系统进行对比,仿生葫芦单元与球形单元均填充于高为1.5 m、半径为0.5 m的圆柱体水箱中,水箱两端设置了换热流体的进出口。仿生葫芦单元的尺寸为r=19.34 mm,L=49.00 mm,R=32.13 mm。在仿生葫芦体单元与球形单元体积相同情况下,仿生葫芦体储热单元的面体比相较球形单元提高了14.5%,意味着内部相变材料与外部流体间的换热更加充分。

|
图 2 潜热蓄热堆积床模型示意 Fig. 2 Schematic diagram of packed-bed LHTES system |
储热过程时,热流体从上方入口流动至下方出口,在温差的作用下,PCM吸收传热流体(HTF)的热量并将其储存至单元中;系统进行放热过程时,冷流体从下方流动至上方,PCM将储存的热量释放给HTF,使HTF温度升高,从而完成释热过程。表 1为PCM与HTF的物性参数,换热流体为水,储热单元内部填充相变材料为石蜡,外壳材料由高聚物组成。
| 表 1 PCM与HTF物性条件 Tab. 1 Thermo-physical properties of PCM and HTF |
模型假设PCM和HTF的物性均匀且具有各向同性,采用Boussinesq假设模拟密度变化;堆积床壁面假设绝热且忽略储热单元壁的换热;换热流体为不可压缩的层流,其热物性不随温度改变;忽略系统内换热流体与相变材料的辐射作用,且系统内无内部热源;堆积床系统内部初始温度为T0=323.15 K;进行储热过程时,入口处的换热流体以恒定温度Tin=343.15 K和速度vin=0.04 m/s流入堆积床与相变材料胶囊进行储热过程,垂直出口方向的热流假设为零;堆积床系统入口流体的温度和速度满足以下边界条件:
| $ T_{\mathrm{f}}=T_{\text {in }}, v=v_{\text {in }}, u=0 $ | (7) |
堆积床系统出口处流体的温度和速度满足以下边界条件:
| $ \frac{\partial T_{\mathrm{f}}}{\partial y}=0, \frac{\partial v}{\partial y}=0, u=0 $ | (8) |
堆积床系统的壁面视作绝热壁面,并满足以下边界条件:
| $ \frac{\partial T_{\mathrm{f}}}{\partial y}=0, \frac{\partial T_{\mathrm{f}}}{\partial x}=0, v=0, u=0 $ | (9) |
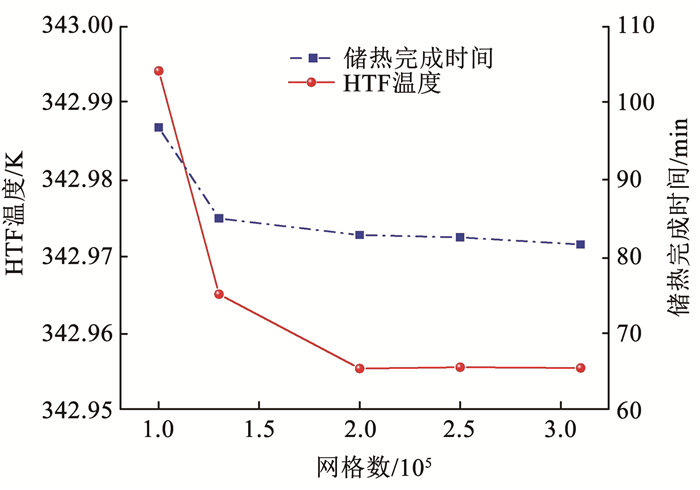
本次数值计算采用5种网格数(1×105,1.3×105,2×105,2.5×105,3.1×105)对仿生葫芦体储热堆积床进行网格独立无关检验。图 3为不同网格数量下的HTF温度变化和堆积床储热完成时间,当网格数达到2×105时,HTF温度与储热完成时间均几乎保持不变。因此,在综合考虑计算时间和计算精度的基础上,选定2×105的网格数以及0.05 s的时间步长组合进行本次堆积床数值模拟的计算。
|
图 3 堆积床数值模型网格独立无关验证 Fig. 3 Grid independence valudation of numerical packed modal |
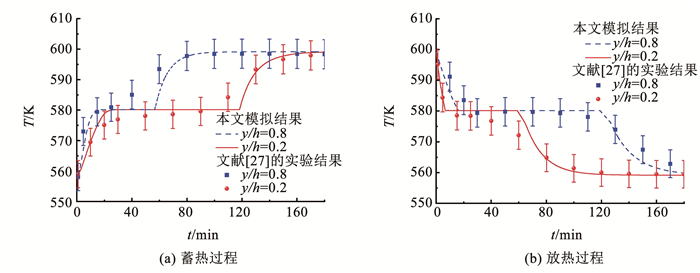
堆积床系统储热过程的数值计算采用Fraction Step算法。梯度方向的离散算法采用Least Square Cell Based格式,压力项的求解采用Standard格式,动量方程与能量方程的求解均选取二阶迎风(second order upwind)格式。松弛因子的压力项、动量方程项以及能量方程项均取1。能量方程的残差绝对值小于10-6,其余项的残差均小于0.001。为了检验所取算法的准确性与可靠性,使用Bellan等[27]的研究进行模型验证,数值结果如图 4所示。可以看出,本文数值模拟结果与文献实验结果的温度变化规律基本一致,误差均在5%以内,故本次数值模拟所用的算法可用于不同堆积床参数下的数值计算。
|
图 4 数值结果与实验结果的温度对比 Fig. 4 Comparison of numerical and experimental results in temperature |
为了确定最优储热特性的仿生葫芦储热单元,对其进行了结构优化研究。仿生葫芦体储热单元的形状由复合因子n中的小球半径r、大球半径R、两球中心距L这3个参数控制,确定下述两个几何优化策略:改变R、L但保持r不变;改变r、L但保持R不变。表 2、3展示了几何优化算例的具体参数尺寸。
| 表 2 优化策略Ⅰ的几何优化参数 Tab. 2 Geometric opimization paramaters of optimization method Ⅰ |
| 表 3 优化策略Ⅱ的几何优化参数 Tab. 3 Geometric opimization paramaters of optimization method Ⅱ |
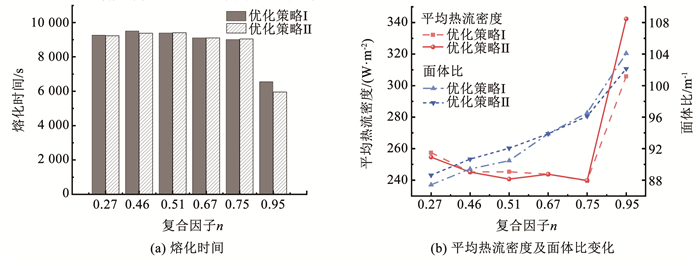
图 5(a)为两种优化策略下的储热单元整体熔化时间。可以看出,随着复合因子n从0.27增大至0.95,在优化策略Ⅰ下,单元整体熔化时间降低至6 546 s,而在优化策略Ⅱ下,单元熔化时间减小至5 961 s。图 5(b)为两种优化策略下的储热单元面体比与单位面积热流密度变化。对于优化策略Ⅰ下的储热单元,随着复合因子的增大,面体比增大至104 m-1,而单位面积热流密度先降低后增大,当复合因子增大时,热流密度由于单元喉部结构剧烈增加。对于优化策略Ⅱ下的储热单元,面体比变化规律与优化策略Ⅰ类似,但是在复合因子n为0.67时,单位面积热流密度短暂上升。这是由于n=0.51的葫芦单元喉部截面积大于n=0.67的葫芦单元,该处平均表面热流局部增大。
|
图 5 不同优化策略下的单元储热特性 Fig. 5 Heat storage performance of PCM capsule of different methods |
与优化策略Ⅰ相比,优化策略Ⅱ中r=19.34 mm,L=49.00 mm,R=32.13 mm的几何组合下的单元熔化时间和热流密度分别缩短了8.93%与提高了10.64%。因此,可以认为结构几何参数r=19.34 mm,L=49.00 mm组合下的葫芦单元是堆积床储热系统中换热熔融的最优结构。
3 系统能量变化及流动特性对比 3.1 换热过程中温度及流动特性对比图 6为不同时刻葫芦堆积床与传统球形堆积床的中心处和近壁面处沿高度方向的温度变化曲线。由于换热流体在单元之间的湍流扰动,监测点温度产生0.05 K以内的周期起伏。由图 6(a)与图 6(b)可以看出,在堆积床中心处,仿生葫芦堆积床的温度变化幅度明显小于球形堆积床,前者温度变化幅度仅0.03 K,而后者温度变化幅度为0.25 K。这说明仿生葫芦堆积床的温度变化更为均匀,更有利于换热流体与相变材料的换热。由图 6(c)与图 6(d)可以看出,仿生葫芦堆积床的温度波动同样小于球形堆积床。对于仿生葫芦堆积床,堆积床中心处的温度变化幅度远小于壁面处。这是由于壁面处的换热流体在黏性作用下使得壁面产生速度边界层,同时由于流动空间的限制,壁面与储热单元之间产生了一定的速度回流,从而使得温度产生剧烈波动。

|
图 6 LHTES系统在不同结构和高度下的温度变化 Fig. 6 Axial temperature variation in LHTES with different structures and heights |
堆积床系统的液相率是衡量堆积床储热速率的重要指标,本节分析了仿生葫芦堆积床与传统球形堆积床的液相率变化以及液相率提升率变化,如图 7所示。可以看出,0~10 min内仿生葫芦堆积床储热慢于传统球形堆积床。从10 min至堆积床完成整个储热的过程内,仿生模型液相率均大于传统模型,即仿生模型的储热速率均快于传统模型。由液相率提升率变化曲线可以看出,液相率提升率呈先上升后下降的趋势,在第50分钟时,液相率提升率达到最大值12.67%。这是由于堆积床中仿生葫芦单元喉部处的截面积较小,此处PCM热流密度高且熔融速度快。当喉部PCM熔融完毕,在单元喉部处液态PCM产生自然对流扰流强化换热。

|
图 7 堆积床系统液相率变化对比 Fig. 7 Comparison of liquid fraction at different times |
堆积床系统的流动特性主要体现在内部储热单元周围流体的流动方式。堆积床内部填充不同形状的储热胶囊会导致储热单元周围换热流体的流动方式产生差异,从而影响堆积床的储热性能。图 8为仿生葫芦堆积床与球形堆积床内部PCM储热单元周围HTF的速度云图及流线图。可以看出,传统球形堆积床中HTF的最大速度为0.2 m/s,而仿生葫芦堆积床中HTF的最大速度为0.167 m/s。尽管球形堆积床中的HTF高于仿生葫芦堆积床系统,但仿生葫芦堆积床系统中HTF在储热单元周围的分布更为均匀,换热流体在仿生葫芦储热单元间流动时,位于单元上半球与下半球的周围流体流速较快,这使得单元尾部的滞留区面积缩小,从而有利于堆积床系统更快地完成储热过程。

|
图 8 堆积床系统速度云图及流线图对比 Fig. 8 Numerical results of (left) flow field and (right) velocity vector of water flowing around PCM capsules |
为了从能量的角度评价堆积床系统的性能,定义了堆积床系统储热完成率ηtotal和相变材料储热完成率ηpcm以评价系统整体储热过程的程度。ηtotal表示某一时刻系统所储存的热量与系统所能保存的总热量的比值。ηpcm表示某一时刻下相变材料所储存的热量与相变材料所能保存的总热量的比值,即
| $ \eta_{\text {total }}=\frac{c_{\mathrm{w}} \rho_{\mathrm{w}} \varepsilon\left(T_{\mathrm{w}, \text { ave }}-T_{\text {ini }}\right) V+c_{\mathrm{p}} \rho_{\mathrm{p}}(1-\varepsilon)\left(T_{\mathrm{p}, \text { ave }}-T_{\text {ini }}\right) V+\beta L \rho_{\mathrm{p}}(1-\varepsilon) V}{\left[c_{\mathrm{w}} \rho_{\mathrm{w}} \varepsilon+c_{\mathrm{p}} \rho_{\mathrm{p}}(1-\varepsilon)\right]\left(T_{\text {ter }}-T_{\text {ini }}\right) V+L \rho_{\mathrm{p}}(1-\varepsilon) V} $ | (10) |
| $ \eta_{\mathrm{pcm}}=\frac{c_{\mathrm{p}} \rho_{\mathrm{p}}(1-\varepsilon)\left(T_{\mathrm{p}, \text { ave }}-T_{\text {ini }}\right) V+\beta L \rho_{\mathrm{p}}(1-\varepsilon) V}{c_{\mathrm{p}} \rho_{\mathrm{p}}(1-\varepsilon)\left(T_{\text {ter }}-T_{\text {ini }}\right) V+L \rho_{\mathrm{p}}(1-\varepsilon) V} $ | (11) |
图 9(a)为仿生葫芦堆积床与传统球形堆积床的系统储热完成率ηtotal及提升率。可以看出,仿生葫芦堆积床在整个储热过程中的储热完成率均高于传统球形堆积床。仿生结构的提升率先上升后下降,在第50分钟时,仿生结构储热完成率的提升率最大为6.2%,说明该时刻下其储热速率最快。图 9(b)为仿生结构与传统结构堆积床的相变材料储热完成率ηtotal及提升率,在0~10 min内仿生结构相变材料储热完成率低于传统结构,而20~100 min内仿生结构的相变材料储热完成率高于传统结构。在整个储热过程内,仿生结构的相变材料储热完成率先增大后降低,在第50分钟时,相变材料储热完成率提升率达到最大值6.35%。储热完成率与相变材料储热完成率的变化表明,仿生葫芦堆积床比传统球形堆积床具有更好的储热性能。

|
图 9 堆积床系统的储热完成率变化 Fig. 9 Changes in heat storage completion rate of LHTES |
为了研究进口流量对仿生葫芦堆积床储热系统的储热影响,对仿生葫芦堆积床分别设置了0.02、0.04、0.06、0.07 m/s 4个进口传热流体速度,分别对应于进口流量为56.5、113.1、169.6、226.2 m3/h,堆积床系统入口流体温度均为343.15 K。图 10为不同进口流量下仿生储热堆积床内储热单元不同高度球部中心位置的温度变化曲线。沿堆积床高度方向,液体PCM温度升高阶段的时间依次减慢。最靠近堆积床入口x/H=0.81高度的储热单元完成储热的时间最快,x/H=0.07高度的储热单元储热完成时间最慢。当堆积床入口流量增大时,换热流体与储热单元间的换热增强,液体PCM温度升高阶段的温升速率逐渐增大,说明堆积床入口流量的增大可以加快内部储热单元的储热过程。

|
图 10 不同流速下仿生堆积床沿高度方向的温度变化 Fig. 10 Temperature changes along the height direction of a bio-structure LHTES at different inlet rates |
随着流量的增加,堆积床储热时间逐渐降低,储热时间从96 min减少为93.7 min。当流量增大为原来的4倍时,堆积床系统的储热时间仅比原来缩短2.4%,说明在56.5~226.2 m3/h流量范围内,流量的增大对提升仿生葫芦堆积床的储热性能十分有限。
4.2 入口温度对堆积床影响为了研究进口温度对仿生葫芦堆积床储热系统的储热影响,对仿生葫芦堆积床设置了343.15、348.15、353.15、358.15 K 4个进口传热流体温度,分别对应高于相变材料熔点10、15、20、25 K,堆积床系统入口流速均为0.04 m/s,即入口流量为113.1 m3/h。图 11为不同进口温度下仿生储热堆积床内沿高度方向储热单元下半球中心位置的温度变化曲线。随着入口温度的提升,PCM潜热储热时间减小。这是由于PCM与HTF间的温差增大使得储热换热强度增大。与上文结论一致,沿堆积床高度方向,液体PCM温度升高阶段的时间依次减慢。

|
图 11 不同进口温度下仿生葫芦堆积床沿高度方向的温度变化 Fig. 11 Temperature changes along the height direction of a bio-structure LHTES at different inlet temperature |
当入口温度增大15 K,堆积床系统的储热时间比原来缩短59.6%,说明入口温度的增大可明显缩短仿生葫芦堆积床系统的储热完成时间,即仿生葫芦堆积床系统的储热性能主要受入口温度影响。
5 结论1) 葫芦体储热单元的优化分析表明,r=19.34 mm,L=49.00 mm,R=32.13 mm的几何组合可以使葫芦体储热单元具有最优的储热特性。
2) 相同体积下,葫芦体储热单元表面积相较球形单元提高了14.5%,意味着其内部相变材料与外部流体间的换热更加充分。
3) 仿生葫芦堆积床比传统球形堆积床具有更好的储热及流动性能,换热过程中温度变化更均匀,液相率最大可提高12.67%。仿生葫芦堆积床储热完成率最大可提升6.2%,相变材料储热完成率最大可提升6.38%。
4) 进口流量由56.5 m3/h升高至226.2 m3/h时,仿生葫芦堆积床系统的储热时间缩短2.4%。进口温度对仿生葫芦堆积床系统的储热性能影响较大,进口温度增大15 K,堆积床系统的储热时间比原来缩短59.6%。
| [1] |
陈海生, 李泓, 徐玉杰, 等. 2022年中国储能技术研究进展[J]. 储能科学与技术, 2023, 12(5): 1516. CHEN Haisheng, LI Hong, XU Yujie, et al. Research progress on energy storage technologies of China in 2022[J]. Energy Storage Science and Technology, 2023, 12(5): 1516. DOI:10.19799/j.cnki.2095-4239.2023.0330.7 |
| [2] |
王秋旺. 节能与储能传递过程原理、技术与应用[J]. 中国科学: 技术科学, 2023(10): 1763. WANG Qiuwang. Principles, technology, and application of transfer processes for energy saving and storage (in Chinese)[J]. Scientia Sinica Technologica, 2023(10): 1763. DOI:10.1360/SST-2022-0386 |
| [3] |
金爱兵, 巨有, 孙浩, 等. 相变储能充填体强度与热学性能[J]. 哈尔滨工业大学学报, 2022, 54(2): 81. JIN Aibing, JU You, SUN Hao, et al. Strength and thermal performance of phase change energy storage backfill[J]. Journal of Harbin Institute of Technology, 2022, 54(2): 81. DOI:10.11918/202101031 |
| [4] |
王富强, 张鑫平, 汤智清, 等. 仿生型辐射制冷膜的可见-近红外双波段光谱辐射特性调控[J]. 中国石油大学学报(自然科学版), 2023, 47(4): 151. WANG Fuqiang, ZHANG Xinping, TANG Zhiqing, et al. Regulation of visible-near infrared dual-band spectral radiative characteristics on biomimetic radiative cooling film[J]. Journal of China University of Petroleum (Edition of Natural Science), 2023, 47(4): 151. DOI:10.3969/j.issn.1673-5005.2023.04.016 |
| [5] |
ZHAO Bin, LIU Jie, HU Mingke, et al. Performance analysis of a broadband selective absorber/emitter for hybrid utilization of solar thermal and radiative cooling[J]. Renewable Energy, 2023, 205: 763. DOI:10.1016/j.renene.2023.01.094 |
| [6] |
DONG Yan, ZOU Yanan, LI Xiang, et al. Introducing masking layer for daytime radiative cooling coating to realize high optical performance, thin thickness, and excellent durability in long-term outdoor application[J]. Applied Energy, 2023, 344: 121273. DOI:10.1016/j.apenergy.2023.121273 |
| [7] |
DONG Yan, HAN Han, WANG Fuqiang, et al. A low-cost sustainable coating: improving passive daytime radiative cooling performance using the spectral band complementarity method[J]. Renewable Energy, 2022, 192: 606. DOI:10.1016/j.renene.2022.04.093 |
| [8] |
MAO Qianjun, ZHANG Yufei. Effect of unsteady heat source condition on thermal performance for cascaded latent heat storage packed bed[J]. Energy, 2023, 284: 129362. DOI:10.1016/j.energy.2023.129362 |
| [9] |
LIANG Huaxu, WANG Fuqiang, ZHANG Dong, et al. Experimental investigation of cost-effective ZnO nanofluid based spectral splitting CPV/T system[J]. Energy, 2020, 194: 116913. DOI:10.1016/j.energy.2019.116575-01 |
| [10] |
ZHANG Yuanting, QIU Yu, LI Qing, et al. Optical-thermal-mechanical characteristics of an ultra-high-temperature graphite receiver designed for concentrating solar power[J]. Applied Energy, 2022, 307: 118228. DOI:10.1016/j.apenergy.2021.118228 |
| [11] |
MA Lingyong, ZHANG Xin, LI Dong, et al. Influence of sunspace on energy consumption of rural residential buildings[J]. Solar Energy, 2020, 211: 336. DOI:10.1016/j.solener.2020.09.043 |
| [12] |
WANG Wei, SHUAI Yong, QIU Jun, et al. Effect of steady-state and unstable-state inlet boundary on the thermal performance of packed-bed latent heat storage system integrated with concentrating solar collectors[J]. Renewable Energy, 2022, 183: 251. DOI:10.1016/j.renene.2021.11.005 |
| [13] |
WANG Fuqiang, ZHANG Guoliang, SHI Xuhang, et al. Biomimetically calabash-inspired phase change material capsule: experimental and numerical analysis on thermal performance and flow characteristics[J]. Journal of Energy Storage, 2022, 52: 104859. DOI:10.1016/j.est.2022.104859 |
| [14] |
MOHAMMADNEJAD F, HOSSAINPOUR S. A CFD modeling and investigation of a packed bed of high temperature phase change materials (PCMs) with different layer configurations[J]. Journal of Energy Storage, 2020, 28: 101209. DOI:10.1016/j.est.2020.101209 |
| [15] |
LI Mingjia, JIN Bo, YAN Junjie, et al. Numerical and experimental study on the performance of a new two-layered high-temperature packed-bed thermal energy storage system with changed-diameter macro-encapsulation capsule[J]. Applied Thermal Engineering, 2018, 142: 830. DOI:10.1016/j.applthermaleng.2018.07.026 |
| [16] |
VINCENT J F V, BOGATYREVA Q A, BOGATYREV N R, et al. Biomimetics: its practice and theory[J]. Journal of the Royal Society Interface, 2007(4): 637. DOI:10.1098/rsif.2006.0127 |
| [17] |
CHENG Ziming, HAN Han, WANG Fuqiang, et al. Efficient radiative cooling coating with biomimetic human skin wrinkle structure[J]. Nano Energy, 2021, 89: 106377. DOI:10.1016/j.nanoen.2021.106377 |
| [18] |
DONG Yan, MENG Weifeng, WANG Fuqiang, et al. "Warm in winter and cool in summer": scalable biochameleon inspired temperature-adaptive coating with easy preparation and construction[J]. Nano Letters, 2023, 23: 9034. DOI:10.1021/acs.nanolett.3c02733 |
| [19] |
DONG Yan, WANG Fuqiang, ZHANG Yaqi, et al. Experimental and numerical study on flow characteristic and thermal performance of macro-capsules phase change material with biomimetic oval structure[J]. Energy, 2022, 238: 121830. DOI:10.1016/j.energy.2021.121830 |
| [20] |
WANG Fuqiang, DONG Yan, LI Yang, et al. Numerical study on the thermal performance of packed-bed latent heat thermal energy storage system with biomimetic alveoli structure capsule[J]. Science China: Technological Sciences, 2021, 64: 1544. DOI:10.1007/s11431-020-1769-9 |
| [21] |
CHENG Xiwen, ZHAI Xiaoqiang. Thermal performance analysis of a novel PCM capsule in red blood cell shape[J]. Applied Thermal Engineering, 2017, 120: 130. DOI:10.1016/j.applthermaleng.2017.03.112 |
| [22] |
TIAN Yang, LIU Xianglei, ZHENG Hangbin, et al. Artificial mitochondrion for fast latent heat storage: experimental study and lattice Boltzmann simulation[J]. Energy, 2021, 245: 123296. DOI:10.1016/j.energy.2022.123296 |
| [23] |
王欢. 仿生多孔陶瓷骨架复合相变材料的制备及其性能研究[D]. 长春: 吉林大学, 2023 WANG Huan. Study on preparation and properties of bionic porous ceramic skeleton composite phase change materials[D]. Changchun: Jilin University, 2023. DOI: 10.27162/d.cnki.gjlin.2023.000392 |
| [24] |
DONG Yan, WANG Fuqiang, YANG Luwei, et al. Thermal performance analysis of PCM capsules packed-bed system with biomimetic leaf hierarchical porous structure[J]. Journal of Thermal Science, 2021, 30: 1559. DOI:10.1007/s11630-021-1462-z |
| [25] |
张国良. 仿生葫芦体储热单元及系统的传热流动性能研究及优化[D]. 哈尔滨: 哈尔滨工业大学, 2022 ZHANG Guoliang. Investigation and optimization of heat transfer and flow performance of biomimetically calabash-insbired heat stoarage capsule and system[D]. Harbin: Harbin Institute of Technology, 2022. DOI: 10.27061/d.cnki.ghgdu.2022.002150 |
| [26] |
XIA Lijun, ZHANG Peng, WANG Ruzhu. Numerical heat transfer analysis of the packed bed latent heat storage system based on an effective packed bed model[J]. Energy, 2010, 35: 2022. DOI:10.1016/j.energy.2010.01.018 |
| [27] |
BELLAN S, ALAM T E, GONZALEZ-AGUILAR J, et al. Numerical and experimental studies on heat transfer characteristics of thermal energy storage system packed with molten salt PCM capsules[J]. Applied Thermal Engineering, 2015, 90: 970. DOI:10.1016/j.applthermaleng.2015.07.056 |
 2024, Vol. 56
2024, Vol. 56


