2. 先进航空发动机协同创新中心,北京 100191;
3. 长寿命高温材料国家重点实验室(东方电气集团东方汽轮机有限公司),四川 德阳 618000
2. Collaborative Innovation Center for Advanced Aero-Engine, Beijing 100191, China;
3. State Key Laboratory of Long-life High Temperature Materials(Dongfang Electric Corporation Dongfang Turbine Co., Ltd., ), Deyang 618000, Sichuan, China
蒸发式透平循环是一种典型的高效率、低污染物排放的先进动力循环,该循环通常集成各种中低位余热用于空气湿化,进而获得更大的比功[1-2]和更低的NOx排放量[3-4]。然而,目前该类循环众多部件的额外投资成本使其在经济性上不具备吸引力,因此,集成度更高、湿化能力更强的应用方案可能更受市场青睐[5]。1976年,M循环问世,该技术作为一种潜力极大的间接蒸发冷却方式,在理想状态下能将来流空气冷却至湿球温度以下甚至达到露点温度[6-7]。近年来,相关研究人员将M循环应用到原本的湿空气透平中,形成了Maisotsenko燃气轮机循环系统(MGTC)[8-9]。
除了利用M循环改进燃气轮机机组进气冷却[10]外,Saghafifar等[5]首次建立了饱和器数学模型,随后Zhu等[11-12]通过仿真模拟获取饱和器的露点效能和湿球效能。Zhu等[13]着重考虑各项损失建立了不可逆Maisotsenko往复布雷顿循环模型。Caliskan等[14]研究了带有压缩机入口冷却系统Maisotsenko燃气轮机循环。施其乐等[15]对比研究了不同类型饱和器对Maisotsenko燃气轮机循环的影响。Saghafifar等[16]开发了新型基于M循环进行加湿的MBC系统,该系统由顶部的简单布雷顿循环以及底部的MGTC系统构成,随后又针对MBC系统分别提出增加太阳能集热器[17]和复合3台饱和器[18]的改进方案。
综上,具备后冷及回热过程的两级MGTC通常是研究的热点, 但给水在热力过程中的重要性目前还缺乏关注。首先,合理地控制给水量可以使得热效率达到最佳值。其次,作到有效地节水可以提升两级MGTC在干旱缺水地区的适用性。再者,核心部件饱和器的设计制造资料极其匮乏。如何在高温、高压下完成大量布水并使其高效蒸发存在诸多难点。为实现上述价值,在原本的两级MGTC中引入中冷过程形成IMGTC系统。该系统既能够将中冷器的冷却水作为饱和器部分给水进行利用,又能够通过中冷器的冷却作用调节饱和器的载水量。本文通过参数分析研究了IMGTC系统的热效率、饱和器载水量、当量二氧化碳排放(EEC)以及平准化电力成本(CLOE)等指标的变化规律,建立多目标优化获取平衡经济效益和环保效益的最佳方案。
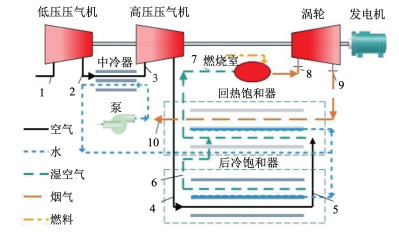
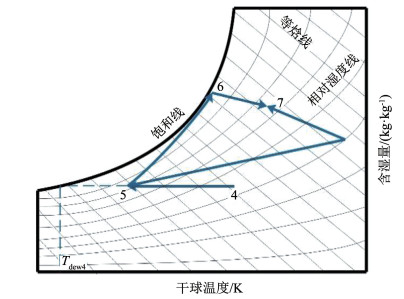
1 IMGTC系统介绍IMGTC运行流程见图 1,各状态点选取位置如图 1中序号所示。给水经给水泵后一部分通过中冷器进行换热后进入后冷饱和器,另外一部分进入回热饱和器中。当冷却水需求量不足时,还可直接由水泵输送第3股给水与冷却水汇合后进入后冷饱和器中。图 2详细表达了饱和器中气流的温度和含湿量随位置的变化,来流空气依次经低压压缩机、中冷器和高压压缩机后,进入后冷饱和器热端进而被冷却(状态4—状态5)。位置5处的部分气流(回流比按1/3进行分配)回流至后冷饱和器冷端与第1股给水进行热质传递(状态5—状态6),在后冷饱和器冷端出口以饱和状态进入回热饱和器冷端,另一部分空气直接进入回热饱和器冷端与第2股给水进行热质传递并与先前的饱和空气进行汇合(状态5—状态7),最终以过热状态进入燃烧室中进行燃烧。高温气流进入涡轮做功,涡轮排气进入回热饱和器热端释放热量,被冷却后排入环境。主要假设如下:1)鉴于压力较低,气流均可视为理想气体。2)输送到饱和器中的给水被充分蒸发。3)饱和器运行过程中完全绝热。4)燃料充分燃烧没有剩余,燃烧产物的生成仅局限于化学方程式[19]。
|
图 1 IMGTC系统布局 Fig. 1 IMGTC system layout |
|
图 2 饱和器温湿图 Fig. 2 Psychrometric chart of saturator |
本节给出了IMGTC系统各部件的详细热力学模型,利用MATLAB进行模拟。根据物性计算程序REFPROPM对气流各组分在各温度和压力状态下焓值等物理量进行求取。
2.1.1 压气机压气机(c)采用两级压气,建立出口空气温度、压缩机功耗的数学模型,计算公式如下[12]:
| $ R_{\mathrm{c} 1}=\frac{P_2}{P_1} $ | (1) |
| $ \frac{T_2}{T_1}=R_{\mathrm{cl} 1}^{\frac{\gamma_{\mathrm{a}}-1}{\eta_{\mathrm{c}, \mathrm{P} \eta_c, \mathrm{M} \gamma_{\mathrm{a}}}}} $ | (2) |
| $ w_{\mathrm{c} 1}=\frac{\left[\left(h_{\mathrm{da}, 2}-h_{\mathrm{da}, 1}\right) \dot{m}_{\mathrm{da}, 1}+\left(h_{\mathrm{w}, 2}-h_{\mathrm{w}, 1}\right) \dot{m}_{\mathrm{w}, 1}\right]}{\dot{m}_{\mathrm{c}} \eta_{\mathrm{c} 1, \mathrm{M}}} $ | (3) |
式中:Tn为空气在序号n状态下的温度(K);T1为入口气温,取288 K;hda, n和ṁda, n分别为空气在序号n状态下的焓值(kJ/kg)和质量流量(kg/s);hw, n和ṁw, n为水蒸气在序号n状态下的焓值(kJ/kg)和质量流量(kg/s);Rc1为低压压比,取4;Rc为总压比;γa为空气比热容比;wc为压缩机输入的比功(kJ/kg);压缩机多变效率(ηc, P)及压缩机机械效率(ηc, M)分别为91%和99%。压缩机入口压降取1.3%。高压压缩机的相关计算同理。
2.1.2 中冷器中冷器(i)中冷却水出口水温、高压压气机入口温度以及冷却水量计算如下:
| $ T_{\text {win }}=T_5-\Delta T_{\mathrm{i}} $ | (4) |
| $ T_3=T_2-R_{\mathrm{i}}\left(T_2-T_{\mathrm{w}}\right) $ | (5) |
| $ \begin{gathered} {\left[\left(h_{\mathrm{da}, 3}-h_{\mathrm{da}, 2}\right) \dot{m}_{\mathrm{da}, 2}+\left(h_{\mathrm{w}, 3}-h_{\mathrm{w}, 2}\right) \dot{m}_{\mathrm{w}, 2}\right] \eta_{\mathrm{i}}=} \\ \left(h_{\mathrm{w}, i}-h_{\mathrm{w}, \mathrm{p}}\right) \dot{m}_{\mathrm{w}, i} \end{gathered} $ | (6) |
式中:Twin为给水经中冷器换热后的出口水温(K);ΔTi为确保后冷饱和器冷却效果的温度端差限制,取10 K;Ri为温降比,表示气流在中冷器中被冷却的程度,当Ri为0时,该系统即为MGTC系统;hw, i、hw, p分别为经历热交换后的水焓值与泵加压之后水的焓值(kJ/kg);ṁw, i为流经中冷器水的流量(kg/s)。中冷器压降为2%[20],入口水温Tw为298 K。
2.1.3 饱和器饱和器(as)的两处出口气温计算过程如下[5]:
| $ T_5=T_4-\eta_{\text {dew }}\left(T_4-T_{\text {dew }, 4}\right) $ | (7) |
| $ T_{10}=T_9-\eta_{\mathrm{wbt}}\left(T_8-T_{\mathrm{wbt}, 5}\right) $ | (8) |
饱和器主体由后冷(a)及回热(r)两部分构成。后冷饱和器的主要任务是对空气进行冷却,同时对回流空气进行加湿。对空气的冷却程度用定义的露点效能ηdew反映,取为0.8。Tdew, 4则为4点位置处空气所对应的露点温度(K),该值为气体在饱和器中的冷却下限。回热器的涡轮排气温度降温下限为状态5时空气的湿球温度,其中,Twbt, 5为在状态5下的空气湿球温度(K),ηwbt为湿球效率,取0.9。对相关参数作如下限定[5]:
| $ T_7=T_9-\Delta T_{\mathrm{as}} $ | (9) |
| $ H_{\text {ASD }}=\frac{\dot{m}_{\text {win }, \mathrm{u}}}{\dot{m}_{\text {win }, \mathrm{m} \text { max }}} $ | (10) |
式中:ΔTas为回热饱和器入口烟气温度与燃烧室入口温度的最小差,取15 K;饱和器出口气流湿化程度(HASD)为回热饱和器实际载水量与最大载水量的比,当回热饱和器载水量达到最大时,气流在出口时会达到饱和状态。后冷饱和器和回热饱和器中的能量平衡可分别表述如下:
| $ \begin{gathered} h_{\mathrm{da}, 4} \dot{m}_{\mathrm{da}, 4}+h_{\mathrm{w}, 4} \dot{m}_{\mathrm{w}, 4}+h_{\mathrm{w}, i} \dot{m}_{\mathrm{win}, \mathrm{a}}=h_{\mathrm{da}, 5} \dot{m}_{\mathrm{da}, 5}+ \\ h_{\mathrm{w}, 5} \dot{m}_{\mathrm{w}, 5}+h_{\mathrm{da}, 6} \dot{m}_{\mathrm{da}, 6}+h_{\mathrm{w}, 6} \dot{m}_{\mathrm{w}, 6} \end{gathered} $ | (11) |
| $ \begin{gathered} h_{\mathrm{g}, 9} \dot{m}_{\mathrm{g}, 9}+h_{\mathrm{w}, 9} \dot{m}_{\mathrm{w}, 9}+h_{\mathrm{da}, 5} \dot{m}_{\mathrm{da}, 5}+h_{\mathrm{w}, 5} \dot{m}_{\mathrm{w}, 5}+ \\ h_{\mathrm{da}, 6} \dot{m}_{\mathrm{da}, 6}+h_{\mathrm{w}, 6} \dot{m}_{\mathrm{w}, 6}+h_{\mathrm{w}, \mathrm{p}} \dot{m}_{\mathrm{win}, \mathrm{u}}=h_{\mathrm{da}, 7} \dot{m}_{\mathrm{da}, 7}+ \\ h_{\mathrm{w}, 7} \dot{m}_{\mathrm{w}, 7}+h_{\mathrm{g}, 10} \dot{m}_{\mathrm{g}, 10}+h_{\mathrm{w}, 10} \dot{m}_{\mathrm{w}, 10} \end{gathered} $ | (12) |
燃烧室(cc)中的能量平衡可表述如下[5]:
| $ \dot{m}_{\mathrm{g}, 8} h_{\mathrm{g}, 8}-\dot{m}_{\mathrm{da}, 7} h_{\mathrm{da}, 7}+\dot{m}_{\mathrm{w}, 8} h_{\mathrm{w}, 8}-\dot{m}_{\mathrm{w}, 7} h_{\mathrm{w}, 7}=\dot{m}_{\mathrm{f}} V_{\mathrm{LH}} \eta_{\mathrm{cc}} $ | (13) |
式中:ṁg和ṁf分别为烟气质量流量(kg/s)和燃料质量流量(kg/s),hg, 8和hw, 8分别为燃烧室出口温度(TCO)所对应的烟气焓值和水蒸气焓值,燃料低热值VLH为50 014 kJ/kg,燃烧室效率ηcc为99%。燃烧室压降为5%。
2.1.5 涡轮涡轮(t)的排气出口温度(K)和输出比功由下式给出[12]:
| $ R_{\mathrm{t}}=\frac{P_8}{P_9} $ | (14) |
| $ \frac{T_9}{T_8}=\left(\frac{1}{R_{\mathrm{t}}}\right)^{\frac{\eta_{\mathrm{t}, \mathrm{P}} \eta_{\mathrm{t}, \mathrm{M}}\left(\gamma_{\mathrm{g}}-1\right)}{\gamma_{\mathrm{g}}}} $ | (15) |
| $ w_{\mathrm{t}}=\frac{\left[\dot{m}_{\mathrm{g}, 8}\left(h_{\mathrm{g}, 8}-h_{\mathrm{g}, 9}\right)+\dot{m}_{\mathrm{w}, 8}\left(h_{\mathrm{w}, 8}-h_{\mathrm{w}, 9}\right)\right] \eta_{\mathrm{t}, \mathrm{m}}}{\dot{m}_{\mathrm{t}}} $ | (16) |
式中:Rt为膨胀比,wt为涡轮输出比功(kJ/kg),ṁt为涡轮气流质量流量(kg/s),涡轮多变效率ηt, P和涡轮机械效率ηt, M分别为90%和99%。
2.1.6 水泵水泵比功输入计算为[5]
| $ w_{\mathrm{p}}=\frac{v_{\mathrm{p}} \Delta P}{\eta_{\mathrm{p}}} $ | (17) |
式中:vp和ΔP分别为供水比体积(m3/kg)和水泵进出口压差(kPa),水泵等熵效率ηp为90%。
2.1.7 热力学指标发电量(kW)、整体效率、当量二氧化碳排放(EEC)(kg/s)的计算分别如下[5, 21]:
| $ \dot{W}_{\text {net }, \mathrm{IMGTC}}=\eta_{\mathrm{G}, \mathrm{ele}}\left[\dot{m}_{\mathrm{t}} w_{\mathrm{t}} \eta_{\mathrm{G}, \mathrm{M}}-\frac{\dot{m}_{\mathrm{c}}\left(w_{\mathrm{c}, 1}+w_{\mathrm{c}, 2}\right)+\dot{m}_{\mathrm{w}} w_{\mathrm{p}}}{\eta_{\mathrm{G}, \mathrm{M}}}\right] $ | (18) |
| $ \eta_{\text {IMGTC }}=\frac{\dot{W}_{\text {net }, \mathrm{IMGTC}}}{V_{\mathrm{LH}} \dot{m}_{\mathrm{f}}} $ | (19) |
| $ E_{\mathrm{EC}}=D_{\mathrm{A}} \times F_{\mathrm{E}}=\dot{m}_{\mathrm{f}} \times V_{\mathrm{LH}} \times C_{\mathrm{C}} \times F_{\mathrm{O}} \times \frac{44}{12} $ | (20) |
式中:发电机电气效率ηG, ele及发电机机械效率ηG, M分别为99%和98%;DA为燃料的活动数据(GJ),与燃料消耗量和热值有关;FE为碳排放因子,与单位热值含碳量CC、碳氧化率FO和相对分子质量之比有关,碳氧化率FO取1。
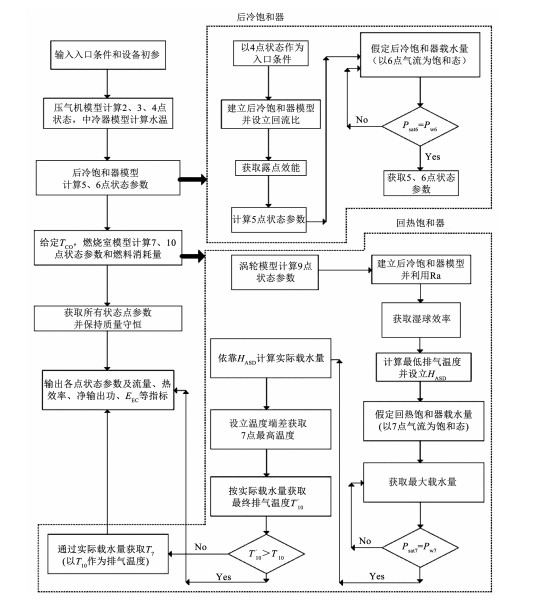
2.1.8 参数验证和仿真流程为证明仿真结果的可靠性,借鉴目前仅有的两级MGTC数据,将无中冷模式下MGTC的仿真数据进行对比[5, 12],结果如表 1、2所示。可以看出,研究结果与先前的研究结果基本一致,这为本文的工作奠定了基础。图 3显示了所用算法的流程图,主要思路为先依据热力学模型求解各状态点物理参数,进而获取所需的热力学指标。在后冷饱和器的计算过程中,通过露点效能获取冷却气流的温度值,假定回流比及回流气流出口状态为饱和态,即可依据能量守恒通过迭代计算获取后冷饱和器载水量。需要关注的是,后冷饱和器的给水首先由中冷器的冷却用水供给,当冷却水量不足时会由常温给水进行补充。在回热饱和器的计算过程中,依据露点效能获取高温排气的最低排放温度值,并对顶部出口温度差值作最大限定,计算出最大载水量后依据能量守恒进一步通过假定HASD获取后冷饱和器的载水量。
|
图 3 计算程序框图 Fig. 3 Calculation program |
开展经济性比较能够促进热力系统的商业化使用,因而进行IMGTC系统的经济性评估。所有的经济模型均来自文献[14, 17-18, 20, 22]。由于使用的数据来源不同,必须考虑通货膨胀对成本分析的影响,采用化学工程装置成本指数(CEPCI)进行修正。在计算平准化电力成本CLOE的过程中,总费用包括投资成本Zinv、退役成本Zdec、运营成本Zopr、维护成本Zmai和人员薪酬Zlab。其中,投资成本包括设备购买费用Zeqp、安装费用Zins及厂地建造费用Zcivil等。退役成本考虑的是在电站寿命结束时拆除电站以使现场恢复到施工之前状态所需的投资。运营成本考虑了3个主要因素,即燃料成本、用水成本和CO2排放罚款。维护成本的主要项目是土木工程、机械部件等。表 3列出各设备采购成本[14, 17-18, 20, 22], 表 4列出各工序所需成本[17-18]。
最后,选择CLOE对拟定配置进行热经济评估,该指标是评估发电成本的一种方法,广泛用于比较不同发电技术的经济性,以便确定长期运行条件下具有最低发电成本的技术,其计算公式如下[17-18]:
| $ C_{\text {LOE }}=\frac{\alpha Z_{\text {inv }}+\beta Z_{\text {dec }}+Z_{\text {opr }}+Z_{\text {mai }}+Z_{\text {lab }}}{W_{\text {net }}} $ | (21) |
| $ \alpha=\left[\frac{(1+i)^{N_{\text {con }}}-1}{N_{\text {con }} i}\right]\left[\frac{i(1+i)^{N_{\text {opr }}}}{(1+i)^{N_{\mathrm{opr}}}-1}\right]+r_{\text {insur }} $ | (22) |
| $ \beta=\left[\frac{(1+i)^{N_{\mathrm{dec}}}-1}{N_{\mathrm{dec}} i(1+i)^{N_{\mathrm{dec}}-1}}\right]\left[\frac{i}{(1+i)^{N_{\mathrm{opr}}}-1}\right] $ | (23) |
式中:α和β分别为折算系数,利率i取7%,保险rinsur为1%,建设期限Ncon为2 a,运营期限Nopr为25 a,退役期限Ndec为2 a。年运营时长为8 100 h,CO2排放处罚成本为40 USD/t,燃料成本为2.53 USD/GJ,无盐水成本为1.83 USD/m3。
3 结果分析首先讨论在不同温降比下压比、燃烧室出口温度以及HASD对于各项输出指标的影响规律。并在此基础上开展多目标优化获取最佳参数组合以平衡经济效益和环境效益。以50 MW作为不同配置下的电厂发电目标[5],采用控制变量法保证研究单一变量时其他相关变量稳定,Rc、HASD和TCO的稳定值分别为16、0.05和1 500 K。
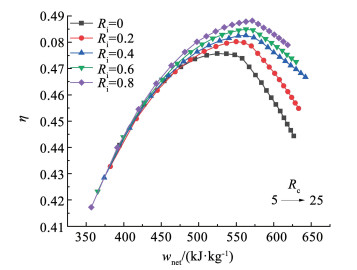
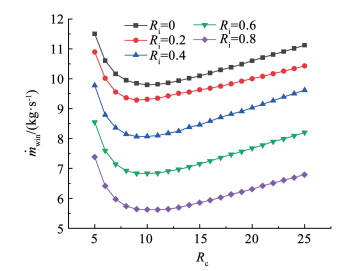
3.1 压比图 4描述了压比变化时,在不同温降比下效率和输出功的变化趋势。效率随压比增长呈现先增加后减小的趋势,在温降比为0.8、压比为18时整体循环取得最大效率48.82%。需要注意的是,净输出功则随效率增长呈现单增趋势,这与常规湿空气透平循环的研究规律并不一致,主要是两者在单位质量空气载水量上的差异所致[15]。另外,在高压比情况下,净输出功还会随着温降比提升表现为先增后减趋势,这是因为温降比增加时一方面会降低压缩机功耗,另一方面却会导致单位质量空气载水量下降,致使涡轮输出比功下降,在这两方面的综合作用下净输出功会在温降比取值偏向中部时获取最大值。图 5说明饱和器载水量在压比变化时存在最低值,这与Saghafifar等[5]发现的现象一致。这主要是考虑到单位质量空气含湿量和空气流量的综合作用。对于单位质量空气,随着压比上升,后冷饱和器的载水量会随着后冷饱和器进口温度上升而不断增大,回热饱和器的载水量变化趋势则恰好与之相反,通常情况下后冷饱和器的水量作为饱和器的主要载水量来源会使得单位质量空气的载水量处于上升趋势。凭借高含湿量气流的做功能力,空气流量反而会持续下降,致使最终饱和器的载水量出现先下降后上升的起伏趋势。另外,饱和器载水量会受到温降比的极大影响,温降比为0.8时的饱和器最低载水量仅为无中冷器时饱和器最低载水量的57.55%。高温降比能够有效减少饱和器载水量,这是因为中冷器的并入以及温降比的调整会改动后冷饱和器的入口气流温度,且此时中冷器冷却水会随温降比的提升起到良好的热回收效果。
|
图 4 压比对效率和净输出比功的影响 Fig. 4 Effect of Rc on η and wnet |
|
图 5 压比对饱和器载水量的影响 Fig. 5 Effect of Rc on ṁwin |
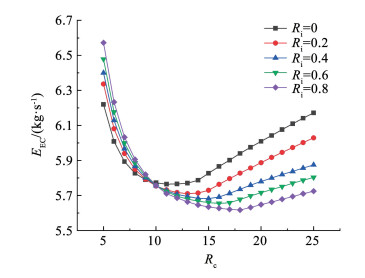
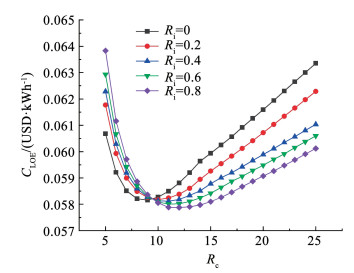
图 6描述了EEC的变化特征,与循环热效率的变化趋势刚好相反。EEC通常在最高效率时获取最低值,这表明对燃料进行充分利用能够同时达到高效率和低排放的效果。图 7表征了CLOE会随着压比变化存在最低值,且温降比越高所对应的最低值越低。这主要是由初始投资和运营成本两方面变化导致。随着压比的提升和换热设备换热量的增加等,初始投资不断上升,运营成本却随热效率的变化表现出相反的趋势,在这两方面的影响下CLOE也会出现起伏趋势。
|
图 6 压比对当量二氧化碳排放的影响 Fig. 6 Effect of Rc on EEC |
|
图 7 压比对平准化电力成本的影响 Fig. 7 Effect of Rc on CLOE |
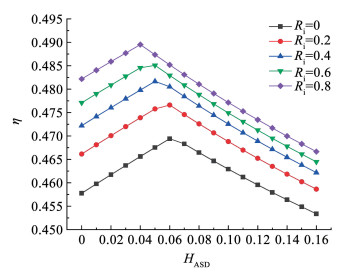
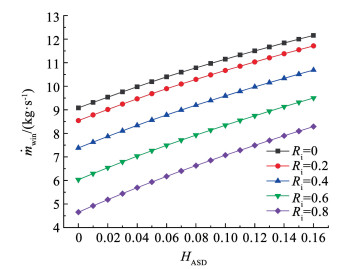
HASD作为描述回热饱和器出口空气被加湿程度的物理量,能够同时影响热回收效果和饱和器载水量。图 8反映了效率在不同温降比下随HASD增加而变化的趋势。热效率随HASD增长出现峰值,对应的最佳HASD通常集中在0~0.1。图 9表明,饱和器总载水量随HASD增加而处于不断上升的趋势。回热饱和器载水量在不同阶段可能会对余热回收效果造成不同影响。在载水量初始上升时,回热饱和器能够充分加强对涡轮排气余热的利用从而提升能效,但在回热饱和器出口气流温度达到最低限度时,过多地增加水量会导致燃烧室入口温度下降,从而效率下降。此外,提升温降比会同时削弱饱和器载水能力,并降低涡轮排气从饱和器离开时的出口温度,造成最佳HASD前移和顶部循环最佳热效率提高。
|
图 8 HASD对效率的影响 Fig. 8 Effect of HASD on η |
|
图 9 HASD对饱和器载水量的影响 Fig. 9 Effect of HASD on ṁwin |
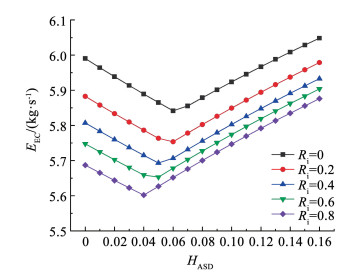
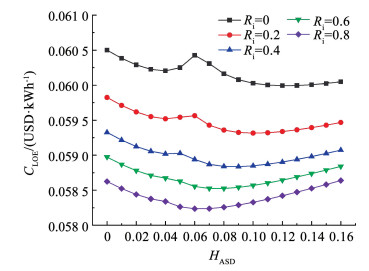
由图 10可知,EEC与循环热效率表现出相反的趋势,同时,EEC的变化在额定碳排放因子的条件下还能有效反映燃料消耗量的变化。温降比为0时的最低EEC相较于温降比为0.8时下降了4.11%。由图 10还可以看出,CLOE随HASD增加整体表现为先下降后上升的趋势,但在中部形成小高峰,并且随着温降比提升小高峰会被逐渐抹平。在没有中冷器或中冷器的温降比较低时,随HASD增加,年度运营成本与热效率表现出相反的变化,呈现先下降后上升的趋势,初始投资成本则呈现与热效率一致的变化,表现为先上升后下降的趋势。为了获取最高效率,年度运营成本的下降已经不足以抵消初始投资成本快速上升的不利影响,从而造成图 11中的小高峰。尽管CLOE随HASD的变化波动幅度并不明显,但中冷器的出现及其效能的提升对于降低初始投资和年度运营成本具有很好的效果。
|
图 10 HASD对当量二氧化碳排放的影响 Fig. 10 Effect of HASD on EEC |
|
图 11 HASD对平准化电力成本的影响 Fig. 11 Effect of HASD on CLOE |
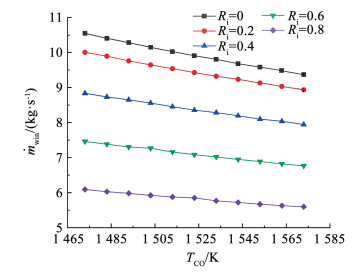
在热力循环上应用较高的TCO通常能够获取更高的收益,但由于材料科学和加工工艺的限制,TCO难以实现更高的突破。随着TCO的上升,整体循环的热效率在额定温降比下均保持持续上升。TCO为1 573 K时,IMGTC系统在温降比为0.8时热效率已经达到最高值50.18%。另外,随TCO增加和温降比增加,饱和器载水量均会进一步下降,图 12展示了这一趋势。尽管TCO增加能够提升回热饱和器中的单位质量载水量,但同时增强了涡轮入口气流的做功能力,使得压缩机入口流量相对下降,因而饱和器总载水量也下降。值得注意的是,增加TCO反而能够缩减水量的消耗。
|
图 12 TCO对饱和器载水量的影响 Fig. 12 Effect of TCO on ṁwin |
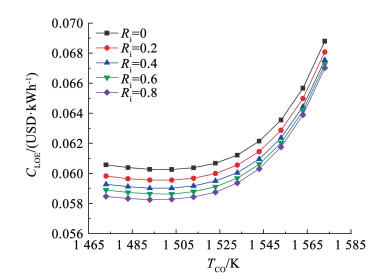
TCO的增加通过提升效率直接降低了EEC,温降比为0.8时,IMGTC系统在所研究的TCO的参数范围内下降幅度达4.03%,这进一步表明,提升TCO不仅对水量上涨起到了抑制作用,还能够减少燃料消耗。但CLOE在不同的TCO范围内表现出不同趋势。如图 13所示,TCO初始增长时,CLOE微弱下降,在温降比为0.8时,最低CLOE已经达0.058 3 USD/kWh,这是能效提升的有益影响。但TCO增长到较高阶段时,CLOE会快速增加。这主要是由于过高提升TCO导致初始投资快速增加,尤其是燃烧室和涡轮等部件的投入增加。这就表明通过提升TCO增加热效率并降低物料消耗的同时,必须兼顾经济性平衡。
|
图 13 TCO对平准化电力成本的影响 Fig. 13 Effect of TCO on CLOE |
在最大化能源转化效率的同时最小化排放和成本,是热力循环多目标优化的基本目标。本文已经通过方案优化直接大幅降低了饱和器载水量,另外,通过参数分析发现EEC和CLOE在随各项参数变化时,其峰谷值并不会出现在同一参数下,在部分区间上甚至存在相反的趋势,这就形成了优化空间。拟采用HASD、Rc、TCO作为决策变量,各自的搜索范围分别为0~0.16、5~25和1 473~1 573 K,借用ISIGHT平台构建Matlab-Optimization组件模型,以EEC和CLOE作为目标函数,并采用NSGA-Ⅱ为多目标优化算法对拟定配置进行整体优化,实现平衡环境效益和经济效益的最佳方案。
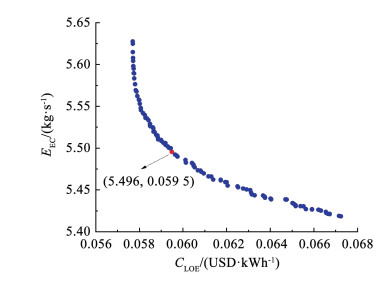
图 14展示了优化过程中形成的帕累托前沿。优化结果表明,当HASD为0.020 2、TCO为1 537.02 K、Rc为12.01时为通过模糊决策筛选出的最佳参数组合,此时可实现EEC为5.496 kg/s,CLOE为0.059 5 USD/kWh,ṁwin仅为4.463 kg/s。这样的优化结果比两级MGTC采用上述最佳参数组合时的年度EEC减少约5 287 t,年燃料消耗量减少约1 922 t,年用水量减少约120 177 t。另外,在采用最佳参数组合时,IMGTC系统可获取的热效率达49.89%,而MGTC系统的热效率仅为48.29%。同时,根据国际能源署发布的数据[23],本研究中计算的最佳CLOE低于中国、欧洲和日本的天然气联合循环发电的中位CLOE (分别约为0.083 8、0.070 4、0.091 0 USD/kWh)。上述分析表明IMGTC具备的一定的环保效益和经济优势。
|
图 14 IMGTC系统多目标优化的帕累托前沿 Fig. 14 Pareto front of multi-objective optimization for IMGTC system |
1) 基于M型饱和器进一步构建出IMGTC系统,该系统实现了同时兼容中冷、后冷、回热3大过程,并对饱和器供水实现了预加热。需要强调的是,IMGTC为提升M型动力循环的能效探索出新的途径,同时平衡好环境效益,并在有效削减载水量的同时降低了饱和器的设计制造难度,扩宽了其适用性。
2) 通过调节压比和饱和器出口气流湿化程度均能实现最大热效率和最低平准化电力成本,增大燃烧室出口温度还会使饱和器载水量下降。另外,中冷器及其能效增进能够有效减少并调节饱和器载水量,可实现IMGTC系统饱和器最低载水量仅为无中冷模式下饱和器载水量的57.55%,而且能提升热效率,降低平准化电力成本和当量二氧化碳排放。
3) 通过多目标优化给出了相应的最优参数组合与优化结果,相比MGTC,IMGTC系统采用最优参数组合时的年当量二氧化碳排放、年燃料消耗量和年用水量都出现一定幅度的减少。
| [1] |
WANG Yuzhang, ZHANG Qing, LI Yixing, et al. Research on the effectiveness of the key components in the HAT cycle[J]. Applied Energy, 2022, 306: S0306261921013544. DOI:10.1016/j.apenergy.2021.118066 |
| [2] |
陈金伟, 梁茂宗, 黄地, 等. 航改燃气轮机的湿空气透平循环改型方案研究[J]. 热能动力工程, 2017, 32(6): 23. CHEN Jinwei, LIANG Maozong, HUANG Di, et al. Study on humid air turbine cycles converted from an aero-derivative gas turbine[J]. Journal of Engineering for Thermal Energy Power, 2017, 32(6): 23. DOI:10.16146/j.cnki.rndlgc.2017.06.005 |
| [3] |
GUILLET R. The humid combustion to protect environment and to save the fuel: the water vapor pump and Maisotsenko cycles examples[J]. International Journal of Energy for a Clean Environment, 2013, 12(2/3/4): 259. DOI:10.1615/InterJEnerCleanEnv.2012006092 |
| [4] |
SERRANO J, JIMENEZ-ESPADAFOR F J, LORA A, et al. Experimental analysis of NOx reduction through water addition and comparison with exhaust gas recycling[J]. Energy, 2019, 168: 737. DOI:10.1016/j.energy.2018.11.136 |
| [5] |
SAGHAFIFAR M, GADALLA M. Analysis of Maisotsenko open gas turbine power cycle with a detailed air saturator model[J]. Applied Energy, 2015, 149: 338. DOI:10.1016/j.apenergy.2015.03.099 |
| [6] |
CUI Yuanlong, ZHU Jie, ZORAS S, et al. Review of the recent advances in dew point evaporative cooling technology: 3E (energy, economic and environmental) assessments[J]. Renewable & Sustainable Energy Reviews, 2021, 148(C). DOI:10.1016/j.rser.2021.111345 |
| [7] |
DENG C, AL-SAMMARRAIE A T, IBRAHIM T K, et al. Review air cooling techniques and corresponding impacts on combined cycle power plant (CCPP) performance: a review[J]. International Journal of Refrigeration, 2020, 120: 161. DOI:10.1016/j.ijrefrig.2020.08.008 |
| [8] |
GILLAN L, MAISOTSENKO V. Maisotsenko open cycle used for gas turbine power generation[C]//Proceedings of ASME Turbo Expo 2003. Atlanta, Georgia, USA: AMSE, 2003: 75. DOI: 10.1115/GT2003-38080
|
| [9] |
WICKER K. Life below the wet bulb: the Maisotsenko cycle[J]. Power, 2003, 147(9): 29. |
| [10] |
SAGHAFIFAR M, GADALLA M. Innovative inlet air cooling technology for gas turbine power plants using integrated solid desiccant and Maisotsenko cooler[J]. Energy, 2015, 87: 663. DOI:10.1016/j.energy.2015.05.035 |
| [11] |
ZHU Guangya, CHOW T T, FONG K F, et al. Investigation on humidified gas turbine cycles with Maisotsenko-cycle-based air saturator[J]. Energy Procedia, 2019, 158: 5195. DOI:10.1016/j.egypro.2019.01.676 |
| [12] |
ZHU Guangya, CHOW T T, FONG K F, et al. Comparative study on humidified gas turbine cycles with different air saturator designs[J]. Applied Energy, 2019, 254(C). DOI:10.1016/j.apenergy.2019.113592 |
| [13] |
ZHU Fuli, CHEN Lingen, WANG Wenhua. Thermodynamic analysis of an irreversible Maisotsenko reciprocating brayton cycle[J]. Entropy, 2018, 20(3): 10. DOI:10.3390/e20030167 |
| [14] |
CALISKAN H, DINCER I, HEPBASLI A, et al. Assessment of Maisotsenko combustion turbine cycle with compressor inlet cooler[C]//Progress in Clean Energy. [S. l. ]: Springer, 2015
|
| [15] |
施其乐, 何纬峰, 韩东, 等. 基于IEC技术的蒸发式布雷顿循环热力学性能研究[J]. 节能技术, 2022, 40(6): 502. SHI Qile, HE Weifeng, HAN Dong, et al. Study on thermodynamic performance of evaporative Brayton cycle based on IEC technology[J]. Energy Conservation Technology, 2022, 40(6): 502. |
| [16] |
SAGHAFIFAR M, POULLIKKASZ A. Comparative analysis of power augmentation in air bottoming cycles[J]. International Journal of Sustainable Energy, 2017, 36(1): 47. DOI:10.1080/14786451.2014.996220 |
| [17] |
SAGHAFIFAR M, GADALLA M. Thermo-economic optimization of hybrid solar Maisotsenko bottoming cycles using heliostat field collector: comparative analysis[J]. Applied Energy, 2017, 190: 686. DOI:10.1016/j.apenergy.2016.12.165 |
| [18] |
SAGHAFIFAR M, OMAR A, ERFANMOGHADDAM S, et al. Thermo-economic analysis of recuperated Maisotsenko bottoming cycle using triplex air saturator: comparative analyses[J]. Applied Thermal Engineering, 2017, 111: 431. DOI:10.1016/j.applthermaleng.2016.09.100 |
| [19] |
ZHU Guangya, CHOW T T, LEE C K. Performance analysis of biogas-fueled Maisotsenko combustion turbine cycle[J]. Applied Thermal Engineering, 2021, 195. DOI:10.1016/j.applthermaleng.2021.117247 |
| [20] |
SAHU M K. Thermoeconomic investigation of power utilities: intercooled recuperated gas turbine cycle featuring cooled turbine blades[J]. Energy, 2017, 138: 490. DOI:10.1016/j.energy.2017.07.083 |
| [21] |
吴艺楠, 李冬, 赵芳, 等. 建设项目环境影响评价中温室气体排放核算方法: 以火电项目为例[J]. 环境工程技术学报, 2022, 12(6): 1890. WU Yinan, LI Dong, ZHAO Fang, et al. Research on greenhouse gas emissions accounting methods in environmental impact assessment of construction projects: a case of thermal power project[J]. Journal of Environmental Engineering, 2022, 12(6): 1890. DOI:10.12153/j.issn.1674-991X.20220560 |
| [22] |
OMAR A, SAGHAFIFAR M, GADALLA M. Thermo-economic analysis of air saturator integration in conventional combined power cycles[J]. Applied Thermal Engineering, 2016, 107: 1104. DOI:10.1016/j.applthermaleng.2016.06.181 |
| [23] |
International Energy Agency (IEA) & Nuclear Energy Agency (NEA). Projected costs of generating electricity[M]. Paris: IEA, 2020: 47.
|
 2024, Vol. 56
2024, Vol. 56


