2. 中国民用航空飞行学院 航空工程学院,四川 广汉 618307;
3. 中国航天科工飞航技术研究院,北京 100074
2. College of Aviation Engineering, Civil Aviation Flight University of China, Guanghan 618307, Sichuan, China;
3. China Aerospace Institute of Science and Technology, Beijing 100074, China
固定翼飞行器面对飞行过程中的各种情况,难以一直保持其气动外形为飞行过程中的最优解。在飞行过程中如果能够实现飞机机翼的面积变化,将会给飞机的气动效益带来显著的提升[1-3]。早期的变体飞行器设计,主要采用伸缩翼、折叠翼、变后掠翼等基于机械结构的变形方式,但是机械驱动机构会占用大量的空间和质量,并且会导致在固定翼段和变形段的连接处出现气动台阶,影响气动性能[4]。因此自上世纪八十年代以来,人们就对光滑无缝隙的柔性变体机翼进行了大量研究。
蜂窝结构作为一种周期性结构,具有优秀的面外承载能力和轻质的特性[5],因此蜂窝结构在变体飞行器上的应用,也成为了研究热点。Vocke等[6]采用零泊松比蜂窝结构作支撑芯子,设计了可变展长机翼,其可在弦长不变的情况下,实现展长方向上的大变形。陈以金[7]对反手性四韧带蜂窝结构的弹性模量、剪切模量和负泊松比等力学性能进行了分析,论证了其作为变体机翼结构蒙皮骨架的可行性。Airoldi等[8-9]提出一种基于六韧带手性蜂窝结构的变弯度机翼, 研究发现具有负泊松比的手性六韧带蜂窝结构对于机翼的弯度变化具有更好的协调效果。黄健[10]对于零泊松比结构进行了拓扑优化,并与气动纤维驱动器相组合,形成了一种新的变弯度机翼结构设计。Dayyani等[11-12]提出了具有双向零泊松比的鱼胞结构,并且对于鱼胞结构的节点位置使用遗传算法进行了优化,设计了变弯度机翼。上述研究将蜂窝结构用作翼肋的支撑结构或者机翼的蒙皮结构,可以解决柔性变体飞行器在变形和承载上的内在矛盾。在蜂窝结构的设计上,大多采用了整体调节单元结构参数的设计方法,对采用局部单元结构参数可调的蜂窝结构实现变形控制的研究较少。
本文提出了一种使用负泊松比蜂窝结构的变面积机翼设计方案。使用负泊松比蜂窝结构作变面积机翼结构的骨架,可以利用负泊松比材料的拉胀特性[13], 实现更大的面积变化。同时提出了一种新型可调负泊松比蜂窝结构,通过对机翼结构各部分单元负泊松比值的调节,实现了对变面积机翼形状的精确控制。
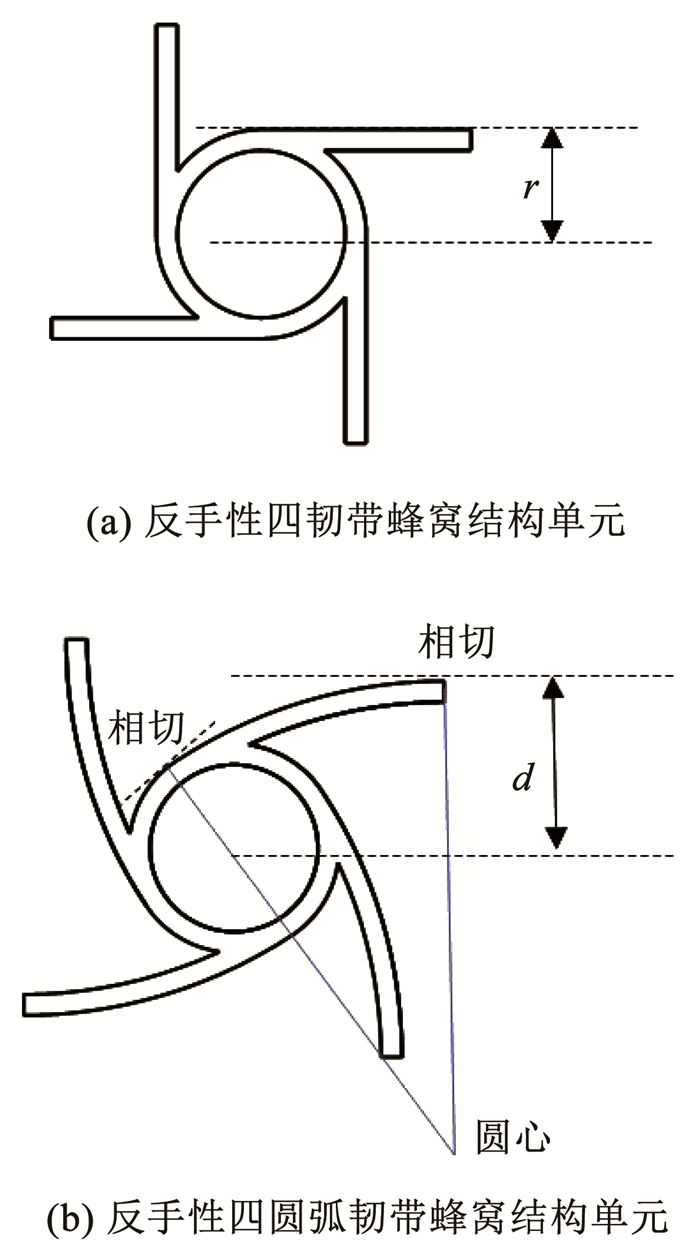
1 可调负泊松比超材料结构单元的设计反手性四韧带(anti-tetrachiral)蜂窝结构,是一种典型的负泊松比结构。当该结构单元在承受拉伸载荷时,会导致与中心圆相切的韧带,绕结构中心发生旋转,在垂直于拉伸方向上结构将会出现膨胀,这是结构负泊松比出现的原因[14-16]。为实现蜂窝结构单元的弹性模量和负泊松比的可调节,本文提出了一种反手性四圆弧韧带蜂窝结构。
图 1(a)为反手性四韧带蜂窝结构单元,反手性四韧带蜂窝结构由一个中心圆环和与之相切的4条直线韧带组成。图 1(b)为反手性四圆弧韧带蜂窝结构单元,该结构将反手性四带蜂窝结构的直线韧带用圆弧韧带取代,圆弧韧带的圆心位于结构的边界线上,并且圆弧韧带和与结构中心距离为d的参考线以及中心圆同时相切。参考线与结构中心的距离d应该大于中心圆的半径r,当距离d与r相等时圆弧韧带将重新退化为直线韧带。
|
图 1 蜂窝单元结构 Fig. 1 Honeycomb unit structure diagram |
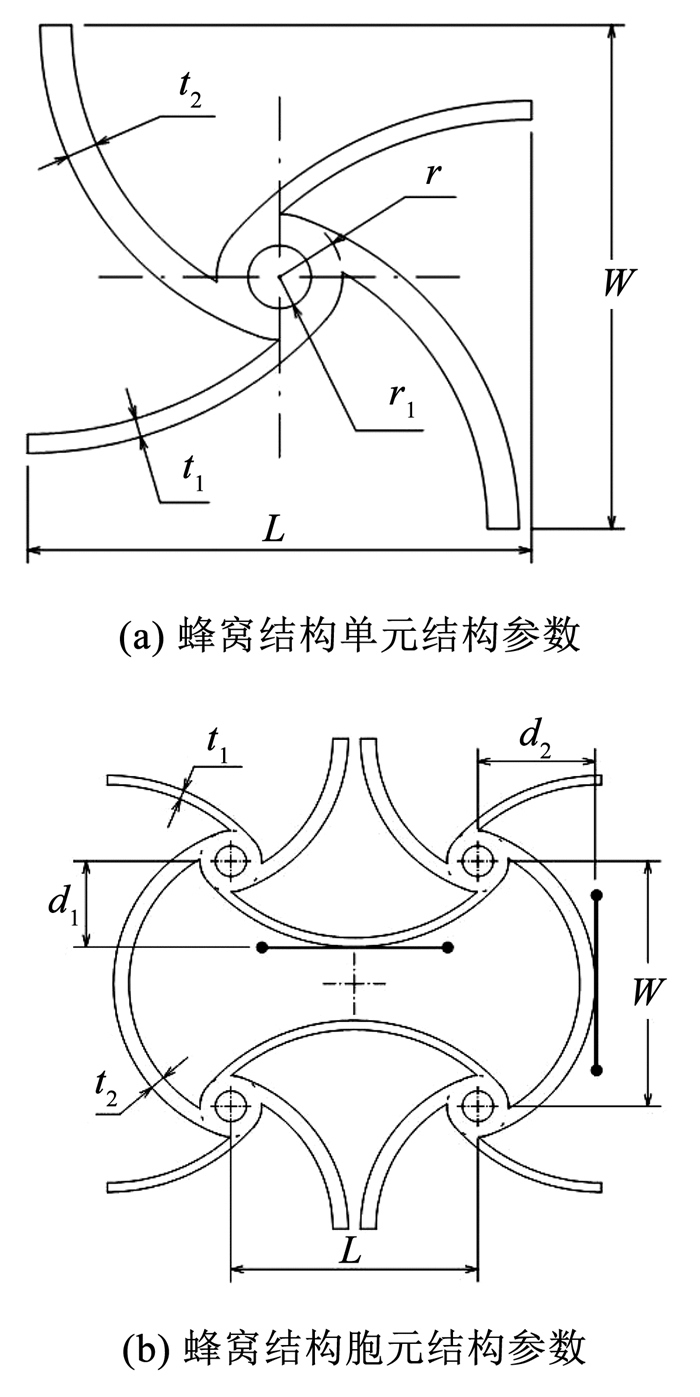
图 2(a)为蜂窝结构单元的结构参数图,图 2(b) 为4个蜂窝结构单元组成的一个蜂窝结构胞元的结构参数图,反手性蜂窝结构的胞元可以进行阵列操作。该蜂窝结构具有8个可调参数,分别为单元长度L、单元宽度W、水平方向韧带切线距离d1、水平方向韧带厚度t1、垂直方向韧带切线距离d2、垂直方向韧带厚度t2,基准圆半径r,基准圆内径r1。在单元尺寸、壁厚确定时,可以通过调整参数d1、d2、r改变结构的弹性模量、泊松比。
|
图 2 新型蜂窝结构单元结构参数 Fig. 2 Structural parameters of new honeycomb structure unit |
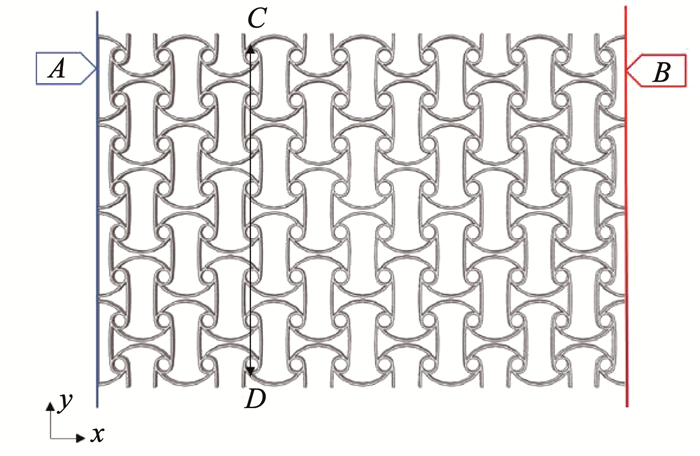
为研究新型蜂窝结构单元的力学性能与结构参数之间的关系,运用ABAQUS软件对其力学性能进行有限元分析。有限元模型选取4×6个反手性蜂窝结构的胞元,组成一个蜂窝结构平板,平板的厚度设置为1 mm,如图 3所示。对于蜂窝结构单元设置如下参数:单元长度L为20 mm、单元宽度W为20 mm、单元壁厚t1、t2为1 mm、基准圆壁厚r-r1为1 mm。有限元仿真中设置蜂窝结构的材料为尼龙材料,弹性模量Es为1 700 MPa, 泊松比υs为0.42,网格大小为0.5 mm,仿真设置的单元类型为C3D8R。
|
图 3 反手性四圆弧韧带蜂窝结构有限元模型 Fig. 3 Finite element model for anti-tetrachiral circular ligament honeycomb structure |
对于A边界,设置x方向位移为0,y方向为自由边界,在B边界施加沿x方向上的位移载荷
| $ \begin{equation*} \bar{\varepsilon}_{x}=\frac{\boldsymbol{u}_{x}}{l} \end{equation*} $ | (1) |
蜂窝结构沿x方向的等效应力
| $ \begin{equation*} \bar{\sigma}_{x}=\bar{\sigma}_{x x}-v_{s}\left(\bar{\sigma}_{y y}+\bar{\sigma}_{z z}\right) \end{equation*} $ | (2) |
式中υs为基体材料的泊松比,运用有限元均匀化方法对蜂窝结构平板进行分析,蜂窝结构沿i(i=x、i=y、i=z)方向的平均应力为
| $ \begin{equation*} \bar{\sigma}_{i i}=\frac{1}{V} \iint \sigma_{\tilde{u}}(x, y, z) \mathrm{d} V \end{equation*} $ | (3) |
等效弹性模量Ex为
| $ \begin{equation*} E_{x}=\frac{\bar{\sigma}_{x}}{\bar{\varepsilon}_{x}} \end{equation*} $ | (4) |
式中: σx为x方向上的等效应变,由施加的位移载荷所确定。
相应的,相对弹性模量为Ex/Es。结构的泊松比为
| $\begin{equation*} v_{x y}=-\frac{\bar{\varepsilon}_{y}}{\bar{\varepsilon}_{x}} \end{equation*} $ | (5) |
其中
| $ \bar{\varepsilon}_{y}=\frac{\Delta y-\Delta y_{0}}{\Delta y_{0}} $ |
式中:
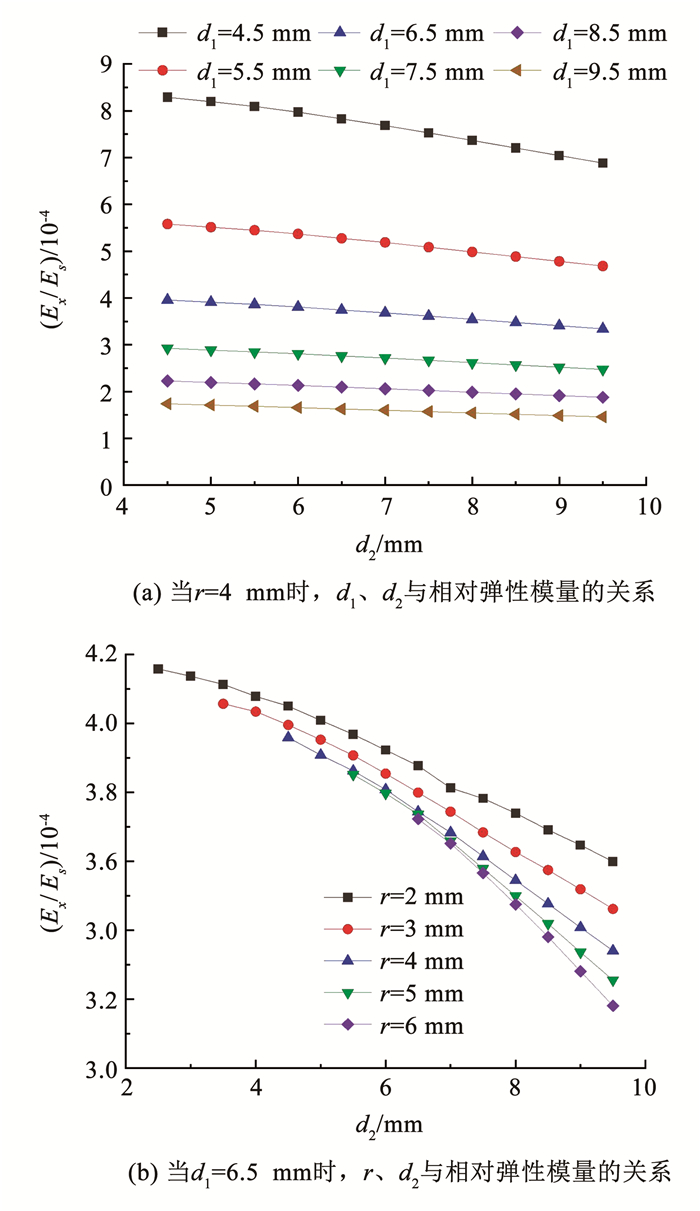
根据上述定义,研究水平方向韧带切线距离d1、垂直方向韧带切线距离d2、基准圆半径r、对于结构泊松比υxy和x方向相对弹性模量Ex/Es的影响。由此可以得到结构x方向弹性模量Ex和蜂窝结构参数d1,d2,r之间的关系,如图 4所示。
|
图 4 结构参数与相对弹性模量关系 Fig. 4 Relationship between structural parameters and relative elastic modulus |
结果表明当r=4 mm时,d1的改变对于结构的相对弹性模量Ex/Es有着较大的影响,Ex/Es会随着d1的增加而减小。例如d2为6.5 mm时,d1从4.5 mm变化到9.5 mm,Ex/Es则由7.82×10-4减小为1.63×10-4,减小了79.1%。d2的改变对于结构的Ex/Es影响较小,Ex/Es会随着d2的增加而减小。例如d1为6.5 mm时,d2从4.5 mm变化到9.5 mm,Ex/Es则由3.95×10-4减小为3.34×10-4,减小了15.4%。r的改变对于结构的Ex改变影响较小,当d1=6.5 mm、d2=6.5 mm时,r从2 mm变化到6 mm,Ex/Es仅仅减少了3.87%。
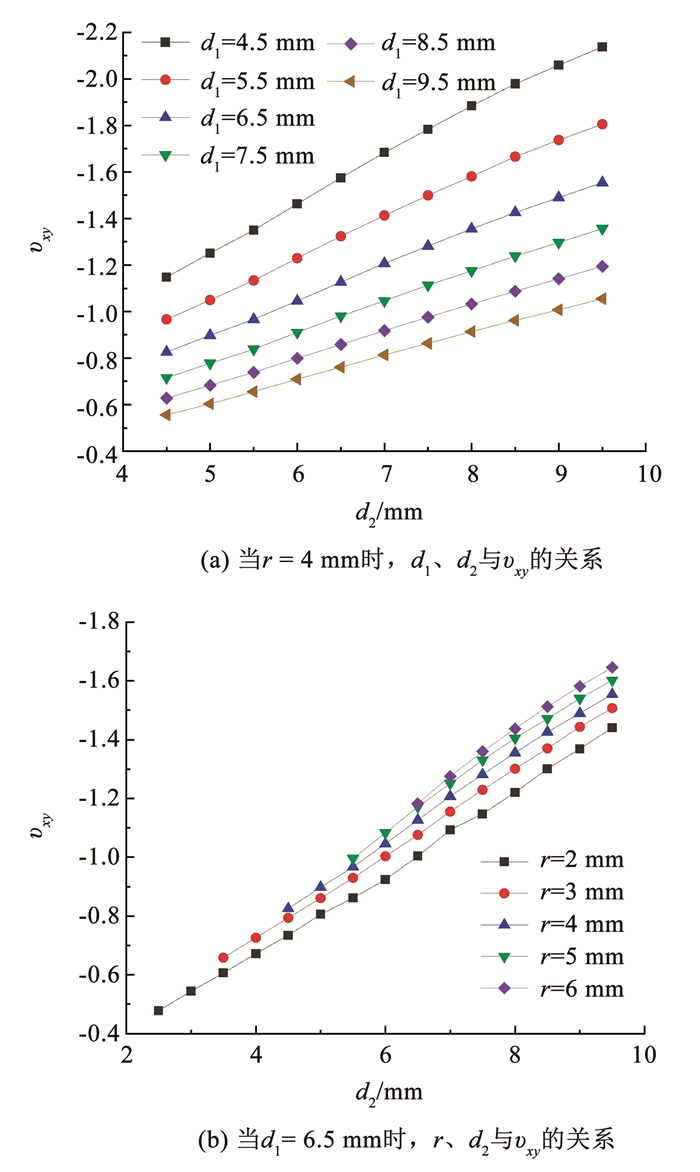
泊松比值υxy和蜂窝结构参数d1,d2,r之间的关系,如图 5所示。
|
图 5 结构参数与泊松比关系 Fig. 5 Relationship between structural parameters and Poisson's ratio |
结果表明当r=4 mm时,d1和d2的改变都会影响对结构的泊松比υxy产生影响。例如d2为6.5 mm时,d1从4.5 mm变化到9.5 mm,υxy则从-1.57变化到-0.76,减少了51.5%。d1为6.5mm时,d2从4.5 mm变化到9.5 mm,υxy则从-0.82变化到-1.55,增加了89.0%。可以发现,d1的增加会减小结构的负泊松比值,d2的增加会增加结构的负泊松比值。结构的基准圆半径r对负泊松比值存在一定影响,当d1=6.5 mm、d2=6.5 mm时,r从2 mm变化到6 mm,υxy从-1.44变化到-1.64,增加了13.8%。
3 变面积机翼的负泊松比分布与形状控制 3.1 变面积机翼的总体设计将负泊松比蜂窝结构单元运用到变面积机翼的设计中,可以在机翼结构发生展向变形时,利用负泊松比效应,让弦向同时发生变形,使机翼结构实现更大的面积变化。同时为了使得机翼结构在弦长方向的变形可控,能与变形的目标轮廓相吻合,需要一种局部参数可调的负泊松比蜂窝结构单元,通过调节局部结构参数的方式实现对机翼结构的变形控制。
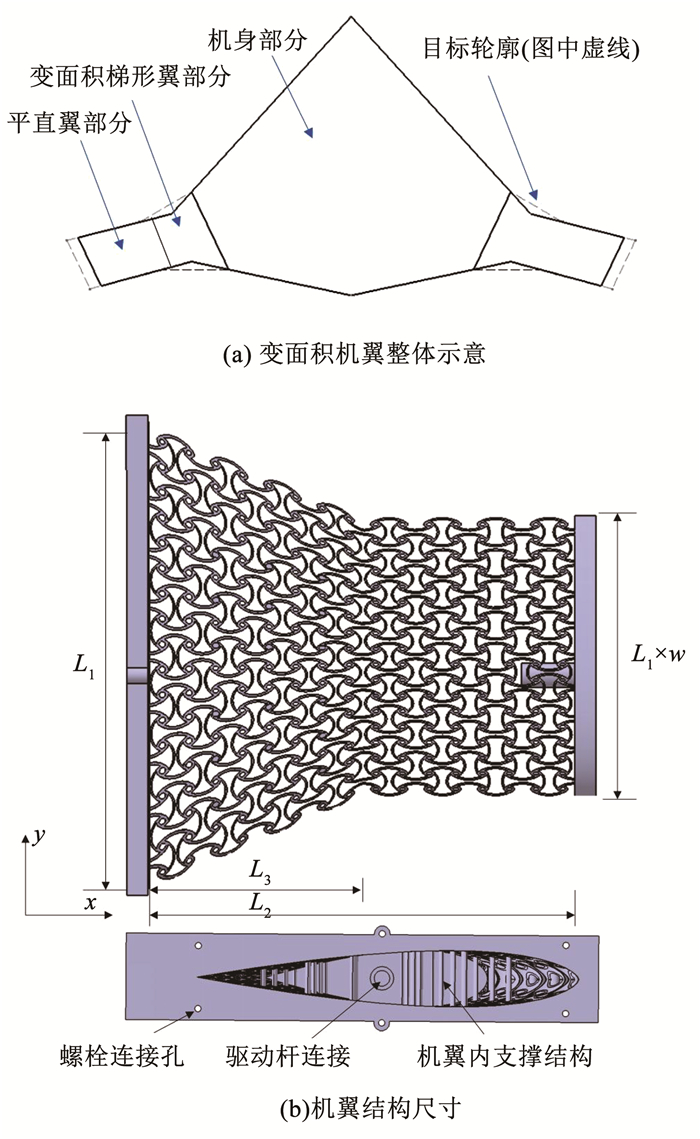
为研究反手性四圆弧韧带蜂窝结构单元在变面积机翼设计中的应用,验证该蜂窝结构通过调节局部结构参数实现变形控制的能力。设计了一种变面积机翼结构,机翼结构变形的初始轮廓和目标轮廓如图 6(a)所示,机翼结构由变面积梯形翼部分和平直翼部分组成。平直翼部分不发生变形,变面积梯形翼部分可以通过变形为一个大梯形翼,实现机翼面积的增加,同时保持整个机翼结构气动外形的光滑柔顺。
|
图 6 机翼结构示意 Fig. 6 Schematic diagram of wing structure |
变面积机翼结构如图 6(b)所示,其中翼根处弦长为L1=350 mm,总体展长为L2=320 mm,梯形部分的展长为L3=160 mm,上、下翼面的蜂窝结构厚度为10 mm,机翼结构梢根比为w。机翼结构梢根比不同,完成目标变形所需要的弦向位移就不同。为充分研究局部参数可调蜂窝结构对变面积机翼变形的控制能力,对梢根比w为0.7、0.6、0.5、0.4的变面积机翼设计都进行研究。为增加机翼结构的承载能力,且不影响机翼结构的变形能力,在若干单元的中心圆环处添加圆柱支撑结构。
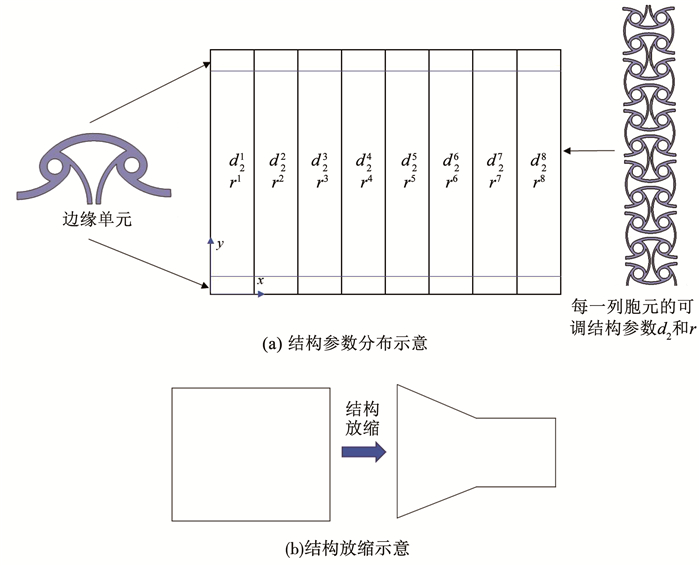
变面积机翼结构骨架由蜂窝结构单元组成。对于组成变面积机翼的蜂窝结构单元,需要通过改变沿展长方向上的负泊松比值分布来实现对变面积机翼的变形控制。考虑蜂窝结构胞元之间的连接关系,对于同一列的蜂窝结构胞元,d2和t2应相同,对于同一行的蜂窝结构胞元,d1和t1应相同。因此可以通过调节沿展长方向分布的每一列胞元的d2和r来实现对局部负泊比值的控制。同时因为蜂窝结构的连接关系,d1和t1,t2等结构参数在整个结构中保持不变。另外为保证整个机翼结构变形前后在边界上的连续性,在上下边界处分别增加一排边缘单元,边缘单元的结构参数r也保持不变。
变面积机翼结构由8×8个蜂窝结构胞元及边缘单元组成,为使蜂窝结构排布与变形前的机翼结构相同,且保证单元排布的连续性,对蜂窝结构单元的y方向坐标进行放缩变换,放缩前后的形状如图 7(b)所示。
|
图 7 结构参数分布示意 Fig. 7 Schematic diagram of structural parameter distribution |
以机翼结构左下方为零点,缩放变换后的y方向坐标
| $ \bar{y}=\left\{\begin{array}{l} \left(y-\frac{L_{1}}{2}\right)\left(1-\frac{x}{L_{3}}+\frac{w x}{L_{3}}\right)+\frac{L_{1}}{2}, x<L_{3} \\ \left(y-\frac{L_{1}}{2}\right) w+\frac{L_{1}}{2}, x \geqslant L_{3} \end{array}\right. $ | (6) |
为研究机翼结构的外形变化,将边缘单元空心圆环最外侧点取为参考点,在机翼边缘共选取32个参考点,通过有限元分析计算参考点变形后的坐标为xi 、yi 。根据xi计算变形目标的y轴坐标值为Yi,根据下式,定义变形后的机翼轮廓与目标轮廓的形状误差K,其中n为参考点个数。
| $ \begin{equation*} K=\sqrt{\frac{\sum\limits_{i=1}^{n}\left(y_{i}-Y_{i}\right)^{2}}{n\left(\frac{L_{1}}{2}\right)^{2}}} \end{equation*} $ | (7) |
同时定义机翼结构的面积变化率为b,表示机翼面积的增加量。
| $ \begin{equation*} b=\frac{A}{A_{0}}-1 \end{equation*} $ | (8) |
式中:A为机翼变形后的面积,A0为机翼变形前的面积。
优化设计的目标是让变形后的机翼轮廓接近目标轮廓,减小形状误差K。变面积机翼,沿展长方向共有8列蜂窝结构单元,因此结构的主要可调参数为{d21, d22, …, d28}和{r1, r2, …, r8}。根据结构单元的仿真分析可知,d2的增加会提高结构的负泊松比值,r的增加也会提高结构的负泊松比值,而负泊松比值的大小将直接影响到结构的y方向位移。因此根据结构y方向位移后坐标yi与目标坐标Yi之间的差值来调整d2和r,是实现机翼结构变形控制的有效方法。
本文优化设计运用CATIA软件对于单元结构进行参数化建模,使用ABAQUS软件划分网格完成后,对网格单元的节点坐标进行修改,完成对模型的放缩。之后进行结构的变形仿真,在后处理中将参考点的位移值与变形前的坐标值相加,得到变形后的坐标值。
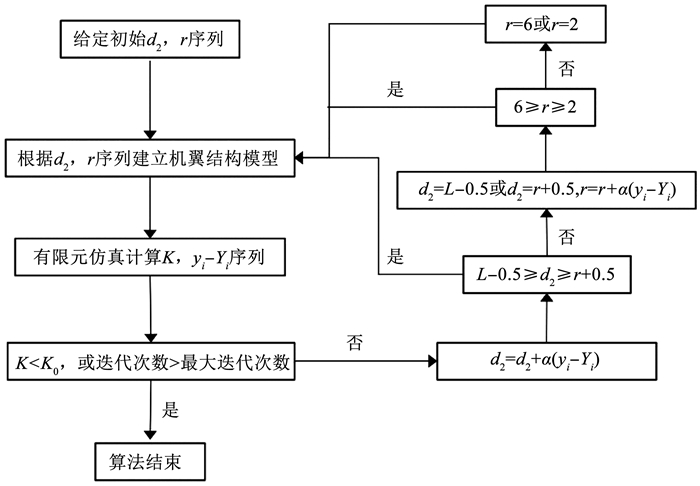
优化算法的步骤如图 8所示。先对初始结构参数建立机翼结构模型,并进行有限元分析,得到形状误差K和yi-Yi序列,判断形状误差K是否小于目标值K0,如果K过大,则对d2进行修正,其中α为修正系数,可以决定参数优化的步长。之后判断d2是否在允许的范围内,当d2超出范围后,会将参数的上限或者下限赋值给d2,之后进行对r的优化。直到K < K0,或迭代次数超出最大迭代次数。
|
图 8 变面积机翼结构参数优化算法流程 Fig. 8 Flow chart of variable area wing structure parameter optimization algorithm |
将机翼结构在展长方向的变形量设置为10.0%,修正系数α设置为0.04,目标值K0为0.5%,最大迭代次数设置为40次,为实现机翼结构的较大变形,令d1=8.5 mm。因为蜂窝结构在放缩后,沿展长方向的韧带壁厚会变薄,为了使放缩后的结构壁厚满足加工工艺的最小壁厚需求,令壁厚t1=2.0 mm、t2=1.2 mm、r-r1=1.2 mm。将结构参数{d21, d22, …, d28}的初始值均设置为6.5 mm,{r1, r2, …, r8}的初始值均设置为4 mm,分别研究梢根比w为0.7,0.6,0.5,0.4时的蜂窝结构变面积机翼的单元结构参数优化。
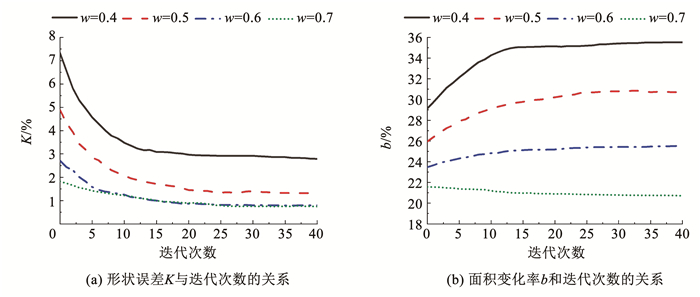
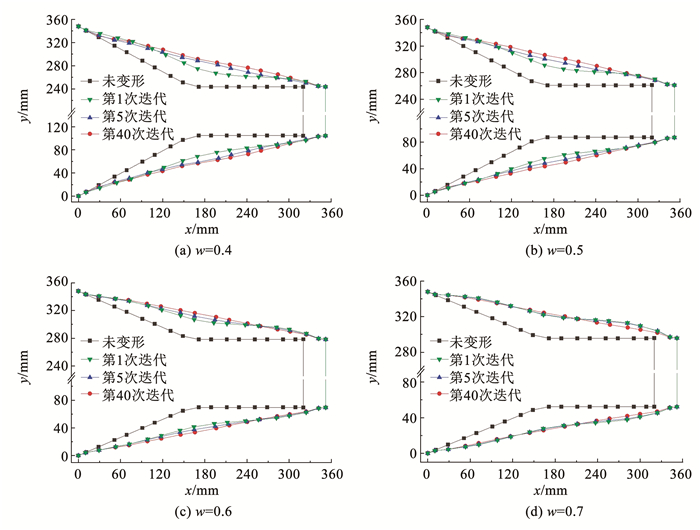
图 9表示结构的形状误差K和面积变化率b与迭代次数的关系,图 10表示不同w下不同迭代次数时参考点位置。当w≤0.5时,机翼结构完成变形所需要的沿弦向变形较大,通过40次参数迭代,变形误差K始终大于1%,说明实现目标变形所需的负泊松比值超过了结构自身的负泊松比上限。对于w=0.7和w=0.6时,对结构参数进行迭代可以有效改善机翼结构变形与目标变形的吻合程度,并且让机翼结构的面积变化率b趋近理论值。
|
图 9 形状误差K和面积变化率b与迭代次数之间的关系 Fig. 9 Relationship between shape error K, area change rate b and iteration times |
|
图 10 不同w下不同迭代次数时参考点位置 Fig. 10 Position of marker points before and after iteration under different w |
优化后的结构参数见表 1,结果表明在中间处蜂窝结构单元的d2和r较大,其原因是在变形过程中该处需要实现较大的弦向变形。从中间处到翼根处和翼尖处的过渡过程中,蜂窝结构单元的d2和r逐渐减小。但是在机翼结构的翼根处和翼尖处,受到边界条件的影响,难以实现弦向的变形,因此又需要蜂窝结构单元具有较大的d2和r。由此可见,蜂窝结构在实现目标变形的过程中,不同位置所需的弦向变形不同,需要的结构参数也不同。如使用整体调节蜂窝结构参数的方法,难以在单向拉伸的过程中实现可控的目标变形。本文所提出的新型蜂窝单元则能够在保持结构连续性的前提下,通过调节局部结构参数,实现对机翼结构变形的控制。
| 表 1 优化后的结构参数序列 Tab. 1 Optimized structural parameter sequence |
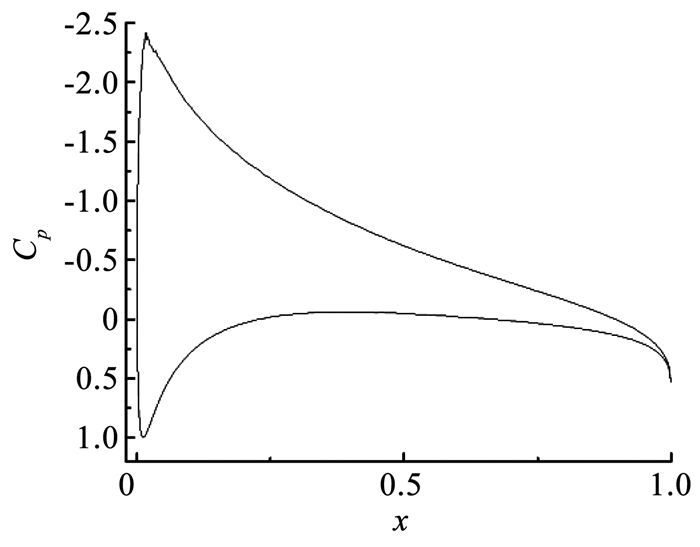
为分析该变面积机翼结构对气动载荷的承载能力,以雷诺数为1×106,机翼攻角为6.75°为例。对NACA 0018翼型进行气动形分析可知,此时机翼表面的压力系数分布如图 11所示,翼型的升力系数为0.873。考虑到目前在飞机结构上实际进行应用的蜂窝结构多为铝材料或复合材料[17],其具有良好的承载性能。因此将变面积机翼结构材料设置为7075铝合金,弹性模量为70 GPa,泊松比为0.33,密度为2.85 g/cm3。此时变面积机翼结构的质量为1.64 kg。
|
图 11 NACA 0018翼型在攻角为6.75°时的压力系数分布图 Fig. 11 Pressure coefficient distribution of NACA 0018 airfoil at an attack angle of 6.75° |
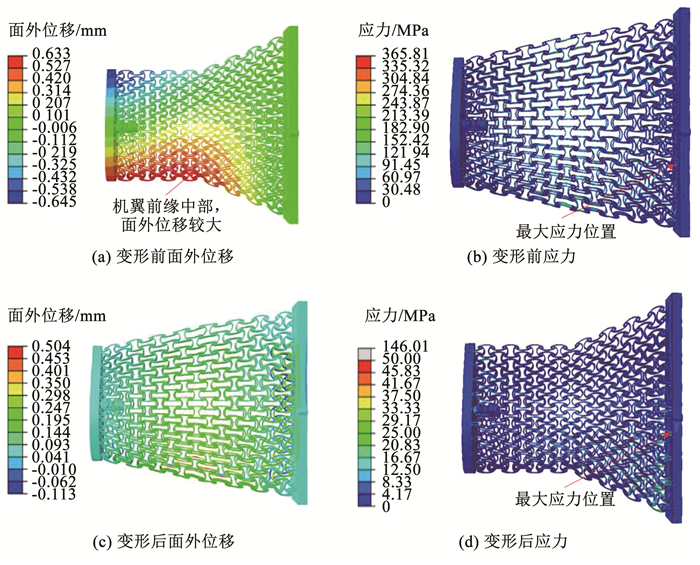
根据不同承载需求,分别向机翼结构施加5,10,15 kPa的气动载荷,对应可以产生的结构升力为63.5,127.0,190.0 N。承受气动载荷的机翼表面与蜂窝结构表面的面积比为3.62,因此对蜂窝结构表面施加的气动载荷应为机翼表面承受气动载荷的3.62倍。在翼根处施加固定约束,在驱动杆与翼尖的连接处设置面外位移为0。施加15 kPa气动载荷后,机翼结构的面外位移和应力云图如图 12所示。
|
图 12 承受气动载荷后的面外位移和应力 Fig. 12 Out-of-plane displacement and stress under aerodynamic load |
根据压力系数分布图可知机翼结构在前缘处承受的气动载荷较大,因此导致在机翼前缘中部出现了较大的面外位移,机翼整体结构出现了一定的扭转变形。承受气动载荷后的最大面外位移和最大应力可见表 2,在承受15 kPa的气动载荷时,结构的最大面外位移为0.645 mm,最大应力为366 MPa,说明应用了反手性蜂窝结构单元的机翼结构具有一定的气动载荷承受能力。
| 表 2 承受气动载荷后的最大面外位移和最大应力 Tab. 2 Maximum out of plane displacement and maximum stress under aerodynamic load |
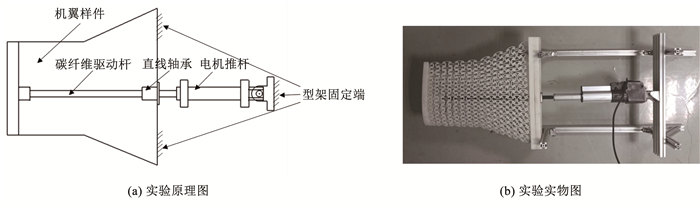
为进行机翼的拉伸变形实验,使用光敏树脂材料,按照优化后的单元结构参数,对w为0.6的机翼模型进行了加工。图 13为变面积机翼结构拉伸变形的实验图,如图 13(a)所示,在翼根固定板上安装直线轴承,通过螺栓将翼根处和翼根固定板连接起来,并将翼根固定板固定到型架上。使用碳纤维驱动杆穿过直线轴承和机翼中的支撑结构,一端与翼尖处相连,另一端与驱动电机相连。
|
图 13 变面积机翼结构实验图 Fig. 13 Experimental diagram of variable area wing structure |
通过电机驱动,进行机翼的变形实验,翼尖处的水平位移为32 mm,通过提取像素点,得到参考点的坐标,计算标记点围成图形的面积,变面积机翼可以实现大约23.9%的面积变化,与仿真中得到的面积变化24.6%相近,形状误差为1.09%,较好的实现了目标变形。机翼结构变形前、后的状态如图 14(a)、14(b)所示,实验中机翼结构上参考点的位置如图 14(c)所示。

|
图 14 变面积机翼实验图 Fig. 14 Experimental diagram of variable area wing |
1) 通过有限元分析研究了该蜂窝结构参数与负泊松比和弹性模量之间的关系。可以在保证蜂窝结构整体连续性的前提下,通过改变局部结参数,可使相对弹性模量减小79.1%,负泊松比从-0.82增加到-1.55。
2) 将负泊松比蜂窝结构单元运用到了变面积机翼的设计上,充分利用蜂窝结构的负泊松比特性,可以在发生10.0%的展向变形时,实现23.9%的面积变化。并初步验证了该蜂窝结构的面外承载能力。
3) 通过优化算法调节蜂窝结构局部参数,实现了对不同梢根比变面积机翼结构的变形控制。变面积机翼结构变形后的形状误差仅为1.09%,保持了整个机翼结构气动外形的光滑柔顺。
| [1] |
冯文正, 于菲, 关玉明, 等. 变形翼面内变形的研究现状及关键技术[J]. 航空工程进展, 2023, 14(3): 1. FENG Wenzheng, YU Fei, GUAN Yuming, et al. Research status and key technologies of in-plane deformation of morphing wing surface[J]. Advances in Aeronautical Science and Engineering, 2023, 14(3): 1. DOI:10.16615/j.cnki.1674-8190.2023.03.01 |
| [2] |
BARBARINO S, BILGEN O, AJAJ R M, et al. A review of morphing aircraft[J]. Journal of Intelligent Material Systems and Structures, 2011, 22(9): 823. DOI:10.1177/1045389X1141408 |
| [3] |
王彬文, 杨宇, 钱战森, 等. 机翼变弯度技术研究进展[J]. 航空学报, 2022, 43(1): 024943. WANG Binwen, YANG Yu, QIAN Zhansen, et al. Technical development of variable camber wing: Review[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(1): 024943. DOI:10.7527/S1000-6893.2020.24943 |
| [4] |
张祖豪. 具有连续机翼表面的伸缩式变形翼研究[D]. 哈尔滨: 哈尔滨工业大学, 2019 ZHANG Zuhao. Study on telescopic morphing wing with continue skin[D] Harbin: Harbin Institute of Technology, 2019. DOI: 10.27061/d.cnki.ghgdu.2019.001236 |
| [5] |
姜松成, 杨慧, 王岩, 等. 变形翼可调泊松比柔性蒙皮力学特性分析[J]. 航空学报, 2023, 44(13): 79. JIANG Songcheng, YANG Hui, WANG Yan, et al. Analysis of mechanical characteristics of flexible skin with tunable Poisson's ratio for morphing wing[J]. Acta Aeronautica et Astronautica Sinica, 2023, 44(13): 79. DOI:10.7527/S1000-6893.2022.27748 |
| [6] |
VOCKE R D Ⅲ, KOTHERA C S, WOODS B K S, et al. Development and testing of a span-extending morphing wing[J]. Journal of Intelligent Material Systems and Structures, 2011, 22(9): 879. DOI:10.1177/1045389x11411121 |
| [7] |
陈以金. 变体飞行器柔性蒙皮及支撑结构性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2014 CHEN Yijin. Study on flexible skin and supporting substructure of morphing aircraft[D]. Harbin: Harbin Institute of Technology, 2014 |
| [8] |
AIROLDI A, CRESPI M, QUARANTI G, et al. Design of a morphing airfoil with composite chiral structure[J]. Journal of Aircraft, 2012, 49(4): 1008. DOI:10.2514/1.c031486 |
| [9] |
AIROLDI A, BETTINI P, PANICHELLI P, et al. Chiral topologies for composite morphing structures-Part I: Development of a chiral rib for deformable airfoils[J]. Physica Status Solidi (b), 2015, 252(7): 1435. |
| [10] |
黄建. 新型零泊松比蜂窝结构力学性能及其变弯度机翼应用研究[D]. 哈尔滨: 哈尔滨工业大学, 2018 HUANG Jian. Mechanical performances of a novel honeycomb design with zero poisson's ratio and its application in camber morphing wings[D] Harbin: Harbin Institute of Technology, 2018 |
| [11] |
JHA A, DAYYANI I. Shape optimisation and buckling analysis of large strain zero Poisson's ratio fish-cells metamaterial for morphing structures[J]. Composite Structures, 2021, 268: 113995. DOI:10.1016/j.compstruct.2021.113995 |
| [12] |
NAGHAVI ZADEH M, DAYYANI I, YASAEE M. Fish Cells, a new zero Poisson's ratio metamaterial-Part I: Design and experiment[J]. Journal of Intelligent Material Systems and Structures, 2020, 31(13): 1617. DOI:10.1177/1045389x20930079 |
| [13] |
REN Xin, DAS R, TRAN P, et al. Auxetic metamaterials and structures: a review[J]. Smart Materials and Structures, 2018, 27(2): 023001. DOI:10.1088/1361-665x/aaa61c |
| [14] |
ALDERSON A, ALDERSON K L, ATTARD D, et al. Elastic constants of 3-, 4-and 6-connected chiral and anti-chiral honeycombs subject to uniaxial in-plane loading[J]. Composites Science and Technology, 2010, 70(7): 1042. DOI:10.1016/j.compscitech.2009.07.009 |
| [15] |
MOUSANEZHAD D, HAGHPANAH B, GHOSH R, et al. Elastic properties of chiral, anti-chiral, and hierarchical honeycombs: a simple energy-based approach[J]. Theoretical and Applied Mechanics Letters, 2016, 6(2): 81. DOI:10.1016/j.taml.2016.02.004 |
| [16] |
GONG Ming, TAO Chongcong, ZHANG Chao, et al. A method for regulating negative Poisson's ratio by a reentrant anti-tetrachiral structure[J]. Mechanics of Advanced Materials and Structures, 2022, 29(28): 7399. DOI:10.1080/15376494.2021.2000076 |
| [17] |
魏贺冉, 闫联生, 孙建涛. 蜂窝夹层结构的制备与应用进展[J]. 航天制造技术, 2022(4): 43. WEI Heran, YAN Liansheng, SUN Jiantao. Progress in preparation and application of honeycomb sandwich structure[J]. Aerospace Manufacturing Technology, 2022(4): 43. DOI:10.3969/j.issn.1674-5108.2022.04.010 |
 2024, Vol. 56
2024, Vol. 56


