2. 航空工业哈尔滨飞机工业集团有限公司 哈尔滨 150066;
3. 哈尔滨工业大学 机电工程学院, 哈尔滨 150001
2. AVIC Harbin Aircraft Industry Group Co., Ltd., Harbin 150066, China;
3. School of Mechanical and Electrical Engineering, Harbin University of Technology, Harbin 150001, China
高端航空装备应用场景的日趋严苛对航空复合材料的综合性能和轻量化设计提出更高的要求。蜂窝夹层复合材料因其特殊的孔穴结构,具有致密固体材料难以比拟的优势:优异的减重特性、低热导系数和高强度牵引比,被广泛应用于新一代大型航空器制备轻量化领域,如飞机雷达罩、主起内舱门、垂直安定面等[1-2]。共固化成型是目前蜂窝夹层结构整体成型普遍采用的方法,将面板固化和蜂窝胶接同时进行,可以有效缩短工艺周期。然而,蜂窝夹层结构的共固化成型是一个涉及材料内部热传导、固化环境热对流和树脂固化收缩的复杂热-化学-结构交替转换过程,存在多物理场协同效应,固化周期内环境温度变化、面板内树脂固化生热收缩以及结构-模具-辅助材料导热性能差异[3-4],导致结构内部产生复杂的温度及应力梯度,造成结构破坏。因此,开展结构固化变形的预测分析从而减轻结构固化变形成为蜂窝夹层件制备优化的重要内容。
制造过程数值模拟是避免传统大量工艺—性能实验从而降低制造成本的重要途径。在数值模拟过程中,通过建立树脂的固化反应动力学模型表征固化过程中反应速率、温度和固化度之间的关系。Bogetti等[5]建立起温度-固化度二维数值模型研究了树脂基复合材料平板件成型的温度分布。Dong[6]考虑了固化环境与预制体的相互作用,通过非线性瞬态热传导分析了T型件温度场分布情况,其模拟结果与实验更加吻合。随着热传导-固化模块有关的各类参数表征方法和树脂力学本构模型趋于成熟,结果的可靠性也得到验证[7]。许多研究人员对树脂基复合材料固化变形的构件几何设计[8]、升温/降温速率[9-10]、模具材料属性[11-12]等内外在影响参数进行仿真研究,为复合材料的传统固化行为提供了有力的理论指导。然而,目前的固化模拟研究多为平板结构,关于蜂窝夹层结构的变形分析相对较少,对夹层结构固化工艺的优化仍然以实验试错为主。少数研究者如Chen等[13]、Hodge等[14]、Franco-Urquiza等[15]通过数值解析模型并提出延长固化降温周期、引入特殊曲率等方法降低结构内部的温度梯度和界面平均应力,但其研究集中于夹层结构温度场及面板-芯层界面性能,忽略了复合材料面板热传导-固化引起内部的温度和固化度梯度的交互,由于蜂窝夹层结构固化过程中物理场分布具有强耦合性,在预测结构固化变形时其精度有待改善。
此外,变厚度铺层夹层结构的固化变形规律和等厚度夹层结构有所不同,除了零件各截面的弯边长度、厚度与芯层位置影响外,结构的变厚度铺层区还会导致周围区域内各截面的变形程度不一致,极大增加了夹层结构固化变形的复杂程度[16]。蜂窝芯层几何结构复杂并具有力学不连续性,直接进行建模求解大量的几何节点非常消耗计算资源因而不易用于工程实际[17],在数值模拟中将芯层等效为均质材料可以降低有限元建模难度并节省大量运算时间。针对无法建立精细几何结构的复杂曲率夹层件,基于等效理论可以通过修改相应参数快速实现构型,进一步提升模型的实用性。
本文的主要研究目标是建立一种便捷准确的蜂窝夹层结构固化变形仿真预测方法,以变厚度铺层AS4/8551碳纤维/环氧树脂复合材料-Nomex蜂窝夹层结构为研究对象,结合复合材料瞬时线弹性本构模型、细观力学理论和Gibson等效理论,通过热-化学-结构多物理场耦合方法建立结构固化循环工艺条件三维仿真模型,重点分析变厚度铺层设计工况下结构固化过程中多物理耦合场量的时空演变过程以及蜂窝等效处理下模拟固化变形的准确性。最后通过解析模型探究了预固化工艺对夹层结构变形的抑制作用和机理。
1 蜂窝夹层结构固化理论模型 1.1 热-化学理论模型在热压罐固化过程中,蜂窝夹层结构的体系热量主要来源于两个方面:一是经模具辅助材料传递给整个结构的外界热量,另一部分是面板内树脂基体固化过程中化学反应产生的非线性内热源。本文采用Fourier热传导[18]和能量平衡关系来建立数学模型,由于蜂窝芯层仅涉及热量传递,对其传热过程采用Fourier热传导微分方程建立模型,如式(1a)所示;对于预浸料面板,其自身温度变化与树脂固化反应存在强耦合关系,故采用含有内热源的Fourier热传导微分方程,如式(1b)所示。
| $ \left\{\begin{array}{l} \rho C \frac{\partial T}{\partial t}=\sum\limits_{i=1, j=1}^3 \frac{\partial}{\partial j}\left(k_{i j} \frac{\partial T}{\partial i}\right) \\ \rho C\left(\frac{\partial T}{\partial t}\right)=\sum\limits_{i=1, j=1}^3 \frac{\partial}{\partial j}\left(k_{i j} \frac{\partial T}{\partial i}\right)+Q \end{array}\right. $ | (1) |
式中:ρ、C、T分别为各材料的密度、热容及实时热力学温度,t为反应时间,k为导热系数,下标i, j(i=1, 2, 3;j=1, 2, 3) 分别为复合材料材料沿x、y、z方向的3个主方向矢量,Q为树脂内部热源,由下式确定:
| $ Q=\frac{\mathrm{d} \alpha}{\mathrm{d} t}\left(1-V_{\mathrm{f}}\right) \rho_{\mathrm{m}} H_{\mathrm{R}} $ | (2) |
式中:α为树脂的固化度,ρm为复合材料树脂的密度,Vf为复合材料纤维的体积分数,HR为固化反应总放热量。
为了描述树脂固化过程中的反应速率、温度和固化度之间的关系,需通过固化反应动力学模型进行建模,对于8552环氧树脂,根据唯象学理论[16]其固化反应动力学方程如下:
| $ \frac{\mathrm{d} \alpha}{\mathrm{d} t}=\frac{K(T) \alpha^m(1-\alpha)^n}{1+\exp \left[\delta\left(\alpha-\alpha_{\mathrm{c} 0}-\alpha_{\mathrm{cT}} T\right)\right]} $ | (3) |
式中:m、n为树脂固化的反应级数,δ、αc0、αcT为模型拟合系数,K(T)为反应速率函数。K(T)计算方法如下:
| $ K(T)=A \exp \left(\frac{-\Delta E_{\mathrm{a}}}{R T}\right) $ | (4) |
式中:A为反应的频率因子,ΔEa为固化反应活化能,R为普适气体常数。上述计算所需的8552环氧树脂的固化动力学参数见表 1。
复合材料的比热容和热导系数与材料状态有关,可根据已知组分材料的性能通过混合律进行计算。其中,材料的比热容根据混合定律计算如下[19]:
| $ c=\frac{C_{\mathrm{f}} \rho_{\mathrm{f}} V_{\mathrm{f}}+C_{\mathrm{m}} \rho_{\mathrm{m}}\left(1-V_{\mathrm{f}}\right)}{\rho_{\mathrm{f}} V_{\mathrm{f}}+\rho_{\mathrm{m}}\left(1-V_{\mathrm{f}}\right)} $ | (5) |
式中:c为复合材料的比热容,ρ为复合材料的密度,下标m、f分别为复合材料树脂和复合材料纤维。
由于复合材料热传导具有各项异性,沿纤维方向的热导系数k1和垂直纤维方向的热导系数k2分别表示为[20]:
| $ k_1=k_{\mathrm{f} 1} V_{\mathrm{f}}+k_{\mathrm{m}}\left(1-V_{\mathrm{f}}\right) $ | (6) |
| $ \begin{aligned} k_2= & k_3=1-2 \sqrt{V_{\mathrm{f}} / \mathtt{π}}+ \\ & \frac{1}{B}\left(\mathtt{π}-\frac{4}{\sqrt{1-B^2 \sqrt{V_{\mathrm{f}} / \mathtt{π}}}} \tan ^{-1} \frac{\sqrt{1-B^2 \sqrt{V_{\mathrm{f}} / \mathtt{π}}}}{1+B \sqrt{V_{\mathrm{f}} / \mathtt{π}}}\right) \end{aligned} $ | (7) |
式中,
上述计算过程所需的树脂和纤维各项热学性能参数见表 2。
1.2 残余应力-应变模型 1.2.1 材料本构模型为进行应力-位移分析,需要获取面板树脂固化过程中的本构模型。在固化过程中,由于树脂材料参数及固化度等性能具有时变特性,以凝胶点为计算起点至玻璃态结束,通过CHILE线弹性本构模型[5]对树脂的弹性模量进行求解:
| $ E_{\mathrm{m}}= \begin{cases}E_{\mathrm{m}}^0, & \alpha<\alpha_{\mathrm{gel}} \\ \left(1-\alpha_{\mathrm{mod}}\right) E_{\mathrm{m}}^0+\alpha_{\mathrm{mod}} E_{\mathrm{m}}^{\infty}, & \alpha_{\mathrm{gel}} \leqslant \alpha<\alpha_{\mathrm{g}} \\ E_{\mathrm{m}}^{\infty}, & \alpha \geqslant \alpha_{\mathrm{g}}\end{cases} $ | (8) |
| $ \alpha_{\mathrm{mod}}=\frac{\alpha-\alpha_{\mathrm{gel}}}{\alpha_{\mathrm{g}}-\alpha_{\mathrm{gel}}} $ | (9) |
式中:Em为树脂的弹性模量;Em0、Em∞分别为树脂凝胶前、后的弹性模量,在数值上满足Em∞=103Em0;αgel、αg分别为树脂凝胶起始和完成时的固化度,具体数值见表 2。假定树脂泊松比υm在固化过程中未发生改变,树脂的剪切模量Gm可根据下式确定:
| $ G_{\mathrm{m}}=\frac{E_{\mathrm{m}}}{2\left(1+v_{\mathrm{m}}\right)} $ | (10) |
以树脂均匀收缩为前提,材料的化学收缩应变Δεsh可通过下式计算[18]:
| $ \Delta \varepsilon^{\mathrm{sh}}=\sqrt[3]{1+\Delta V_{\mathrm{r}}}-1 $ | (11) |
| $ \Delta V_{\mathrm{r}}=\Delta \alpha \zeta_{\mathrm{sh}} $ | (12) |
式中:ΔVr为树脂体积收缩量,ζsh为树脂体积收缩率,Δα为固化度的变化率。
在复合材料固化过程中,由温差引起的材料热应变Δεth可以根据纤维及树脂的热膨胀系数确定:
| $ \Delta \varepsilon^{\text {th }}=\phi_i \Delta T $ | (13) |
式中:ΔT为相对于参考温度的差值,ϕi为复合材料3个主方向的热膨胀系数,计算公式如下[19]:
| $ \phi_1=\frac{\phi_{1 \mathrm{f}} E_{11 \mathrm{f}} V_{\mathrm{f}}+\phi_{\mathrm{m}} E_{11 \mathrm{f}} E_{\mathrm{m}}\left(1-V_{\mathrm{f}}\right)}{E_{11 \mathrm{f}} V_{\mathrm{f}}+E_{\mathrm{m}}\left(1-V_{\mathrm{f}}\right)} $ | (14) |
| $ \begin{aligned} \phi_2= & \phi_3=\left(\phi_{2 \mathrm{f}}+\nu_{12 \mathrm{f}} \phi_{1 \mathrm{f}}\right) V_{\mathrm{f}}+\left(\phi_{\mathrm{m}}+\nu_{\mathrm{m}} \phi_{\mathrm{m}}\right)\left(1-V_{\mathrm{f}}\right)- \\ & {\left[\nu_{12 \mathrm{f}} V_{\mathrm{f}}+\nu_{\mathrm{m}}\left(1-V_{\mathrm{f}}\right)\right] \phi_1 } \end{aligned} $ | (15) |
式中:E为材料的弹性模量,ν为材料的泊松比,下标1、2、3为材料3个主方向。
因此,复合材料3个主方向的总应变可以表示为弹性应变、热应变和化学收缩应变之和:
| $ \Delta \varepsilon_{i j}=\Delta \varepsilon_{i j}^{\mathrm{e}}+\Delta \varepsilon_{i j}^{\mathrm{th}}+\Delta \varepsilon_{i j}^{\mathrm{sh}} $ | (16) |
式中Δεe为材料的弹性应变。
1.2.3 应力-应变求解复合材料的应力-应变关系为:
| $ \sigma_{i j}=\boldsymbol{C}_{i j} \Delta \varepsilon_{i j}^{\mathrm{e}}=\boldsymbol{C}_{i j}\left(\Delta \varepsilon_{i j}-\Delta \varepsilon_{i j}^{\mathrm{th}}-\Delta \varepsilon_{i j}^{\mathrm{sh}}\right) $ | (17) |
| $ \boldsymbol{C}_{i j}=\boldsymbol{S}_{i j}^{-1} $ | (18) |
式中:Cij为复合材料的等效刚度矩阵,Sij为柔度矩阵,可以由材料的工程弹性常数表示。其中
| $ \boldsymbol{S}_{i j}=\left[\begin{array}{llllll} \frac{1}{E_{11}} & \frac{-\nu_{12}}{E_{11}} & \frac{-\nu_{13}}{E_{11}} & 0 & 0 & 0 \\ \frac{-\nu_{12}}{E_{11}} & \frac{1}{E_{22}} & \frac{-\nu_{23}}{E_{22}} & 0 & 0 & 0 \\ \frac{-\nu_{13}}{E_{11}} & \frac{-\nu_{23}}{E_{22}} & \frac{1}{E_{33}} & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{1}{G_{12}} & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{1}{G_{13}} & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{1}{G_{23}} \end{array}\right] $ |
利用复合材料细观力学的自洽场细观力学模型[21],根据纤维与树脂各自的弹性常数及体积分数,确定单向单层板的工程弹性常数。其中,复合材料3个主方向的弹性模量如下:
| $ \begin{aligned} E_{11}= & E_{11 \mathrm{f}} V_{\mathrm{f}}+E_{\mathrm{m}}\left(1-V_{\mathrm{f}}\right)+ \\ & \left[\frac{W_{\mathrm{m}} W_{\mathrm{f}} G_{\mathrm{m}}\left(4 \nu_{\mathrm{m}}-\nu_{12 \mathrm{f}}^2\right)\left[E_{\mathrm{m}}\left(1-V_{\mathrm{f}}\right) V_{\mathrm{f}}\right]}{\left(W_{\mathrm{f}}+G_{\mathrm{m}}\right) W_{\mathrm{m}}+\left(W_{\mathrm{f}}-W_{\mathrm{m}}\right) G_{\mathrm{m}} V_{\mathrm{f}}}\right] \end{aligned} $ | (19) |
| $ E_{22}=E_{33}=\frac{1}{\left(W_{\mathrm{t}}\right)^{-1}+\left(4 G_{23}\right)^{-1}+\left(\nu_{12}^2 / E_{11}\right)} $ | (20) |
各主方向面内的剪切模量和泊松比如下:
| $ G_{12}=G_{13}=\left[\frac{G_{12 \mathrm{f}}+G_{\mathrm{m}}+\left(G_{12 \mathrm{f}}-G_{\mathrm{m}}\right) V_{\mathrm{f}}}{G_{12 \mathrm{f}}+G_{\mathrm{m}}-\left(G_{12 \mathrm{f}}-G_{\mathrm{m}}\right) V_{\mathrm{f}}}\right] $ | (21) |
| $ G_{23}=\frac{G_{\mathrm{m}}\left[\left(G_{23 \mathrm{f}}+G_{\mathrm{m}}\right) W_{\mathrm{m}}+2 G_{23 \mathrm{f}} G_{\mathrm{m}}+\left(G_{23 \mathrm{f}}-G_{\mathrm{m}}\right) W_{\mathrm{m}} V_{\mathrm{f}}\right]}{\left(G_{23 \mathrm{f}}+G_{\mathrm{m}}\right) W_{\mathrm{m}}+2 G_{23 \mathrm{f}} G_{\mathrm{m}}-\left(W_{\mathrm{m}}+2 G_{\mathrm{m}}\right)\left(G_{23\mathrm{f}}-G_{\mathrm{m}}\right) V_{\mathrm{f}}} $ | (22) |
| $ \begin{aligned} & \nu_{12}=\nu_{13}=\nu_{12 \mathrm{f}} V_{\mathrm{f}}+\nu_{\mathrm{m}}\left(1-V_{\mathrm{f}}\right)+ \\ & \quad\left[\frac{W_{\mathrm{m}} W_{\mathrm{f}} G_{\mathrm{m}}\left(4 \nu_{\mathrm{m}}-\nu_{12 \mathrm{f}}\right)\left(W_{\mathrm{f}}-W_{\mathrm{m}}\right) G_{\mathrm{m}} V_{\mathrm{f}}}{\left(W_{\mathrm{f}}+G_{\mathrm{m}}\right) k_{\mathrm{m}}+\left(W_{\mathrm{f}}-W_{\mathrm{m}}\right) G_{\mathrm{m}} V_{\mathrm{f}}}\right] \end{aligned} $ | (23) |
| $ \nu_{23}=\frac{2 E_{11} W_{\mathrm{t}}-E_{11} E_{22}+4 \nu_{12}^2 W_{\mathrm{t}} E_{22}}{2 E_{11} k_{\mathrm{t}}} $ | (24) |
式中, Wt为复合材料的体积弹性模量,可由纤维和基体的体积弹性模量Wf、Wm分别表示为:
| $ W_{\mathrm{t}}=\frac{\left(W_{\mathrm{f}}+G_{\mathrm{m}}\right) W_{\mathrm{m}}+\left(W_{\mathrm{f}}-W_{\mathrm{m}}\right) G_{\mathrm{m}} V_{\mathrm{f}}}{W_{\mathrm{f}}+G_{\mathrm{m}}-\left(W_{\mathrm{f}}-W_{\mathrm{m}}\right) G_{\mathrm{m}}} $ | (25) |
| $ W_{\mathrm{f}}=\frac{E_{1 \mathrm{f}}}{2\left(1-\nu_{12 \mathrm{f}}-2 \nu_{12 \mathrm{f}}^2\right)} $ | (26) |
| $ W_{\mathrm{m}}=\frac{E_{\mathrm{m}}}{2\left(1-\nu_{\mathrm{m}}-2 \nu_{\mathrm{m}}^2\right)} $ | (27) |
上述公式计算所需的8552环氧树脂与AS4纤维的各项性能参数见表 3。
1.3 芯层等效处理Nomex芯层采用正六边形双壁厚蜂窝结构,考虑到芯层复杂的几何结构及其不连续性,直接建立几何模型的计算成本较高,在数值模拟中将芯层等效为均质材料可以降低建模难度并节省运算时间,如图 1(a)所示。

|
图 1 蜂窝芯层等效处理 Fig. 1 Honeycomb core equivalence |
蜂窝芯层等效宏观弹性参数通过改进的Gibson等效梁理论[17]获得,该理论规避了Gibson模型中刚度矩阵的奇异值,具有较高的计算精度与收敛性,具体表达式如下:
| $ \left\{\begin{array}{l} E_{11}=E_{\mathrm{s}} \frac{t^3}{l^3} \frac{\cos \theta}{(1+\sin \theta) \sin ^2 \theta} \times\left(1-\cot ^2 \theta \frac{t^2}{l^2}\right) \\ E_{22}=E_{\mathrm{s}} \frac{t^3(1+\sin \theta)}{l^3 \cos ^3 \theta} \times\left[1-\left(\sec ^2 \theta+\tan ^2 \theta\right) \frac{t^2}{l^2}\right] \\ E_{33}=\frac{E_{\mathrm{s}} t(1+\beta)}{l \cos \theta(\beta+\sin \theta)} \\ \nu_{12}=\frac{\cos ^2 \theta}{(1+\sin \theta) \sin \theta} \times\left(1-\csc ^2 \theta \frac{t^2}{l^2}\right) \\ \nu_{13}=\frac{E_{11}}{E_{33}} \nu_{\mathrm{s}} \\ \nu_{23}=\frac{E_{22}}{E_{33}} \nu_{\mathrm{s}} \\ G_{12}=\frac{E_{\mathrm{s}} t^3(\beta+\sin \theta)}{l^3 \beta^2(2 \beta+1) \cos \theta} \\ G_{13}=\frac{G_{\mathrm{s}} t \cos \theta}{l(\beta+\sin \theta)} \\ \frac{G_{\mathrm{s}} t(\sin \theta+\beta)}{l \cos \theta(1+\beta)} \leqslant G_{23} \leqslant \frac{G_{\mathrm{s}} t\left(\sin ^2 \theta+\beta\right)}{l \cos \theta(\beta \sin \theta)} \end{array}\right. $ | (28) |
式中:t为蜂窝胞壁的单层厚度; h为芯格直壁长度; l为芯格斜壁长度,与芯格直壁长度在数值上相等; β=h/l=1;θ为30°表示胞壁和水平方向夹角; Es、Gs、νs为蜂窝芳纶纸的工程弹性常数。
蜂窝单胞模型的尺寸示意图如图 1(b)所示,Nomex蜂窝芳纶纸的各项材料参数见表 4,其中Hs为芯层高度。
芯层等效模型的热力学参数包括热导率及比热容两部分。由于芯层导热性能受温度影响并具有各向异性[24],采用耐驰LFA467型导热仪测定芯层各方向的导热系数,如图 2所示(图中θ表示瞬时温度)。

|
图 2 不同温度下芯层导热系数 Fig. 2 Thermal conductivity of core layer at different temperatures |
由图 2可知,芯层各方向导热系数随温度线性增长,采用线性拟合函数的形式进行参数输入。芯层等效比热容采用TA仪器DSC250型差示扫描量热仪测得,近似为1 132 J·(kg·℃)-1。
根据表 4中蜂窝芳纶纸的属性参数,通过公式推导及实验拟合得到芯层等效模型的各项参数,见表 5。
| 表 5 蜂窝芯层等效参数 Tab. 5 Honeycomb equivalent model parameters |
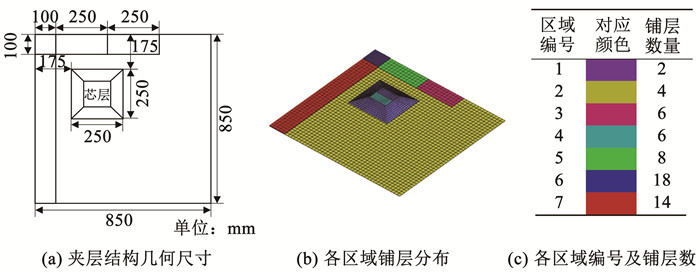
为验证模型的有效性,根据Al-Dhaheri等[23]实验采用的变厚度铺层夹层结构进行建模,具体模型尺寸如图 3(a)所示。用于构建复合材料面板的铺层材料为AS4/8552碳纤维环氧树脂复合材料,单层厚度为0.28 mm;芯层采用Nomex双壁厚正六边形蜂窝,将修剪楔角设置为20°。
|
图 3 夹层结构几何尺寸及各铺层区域分布[23] Fig. 3 Geometric dimensions and layer distribution of sandwich structures[23] |
夹层结构各铺层区域分布如图 3(b)所示,按照面板铺层数量可将夹层结构分为7个区域,各区域对应编号及铺层数量如图 3(c)所示。为通过变厚度铺层设计来控制结构的回弹变形,将各铺层区域沿面板方向依照厚度依次排列,各铺层编号区域的详细铺层顺序见表 6。
| 表 6 各区域铺层顺序 Tab. 6 Layer sequence of each area |
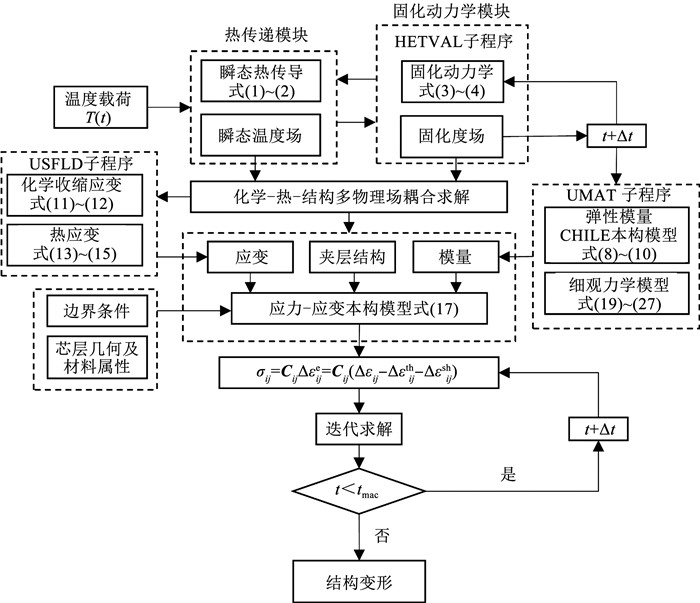
利用商用有限元软件ABAQUS SIMULIA 2021实现夹层结构多物理场的直接强耦合运算。选用瞬态热传递模块、HETVAL子程序、USFLD子程序、UMAT子程序和结构力学模块,分别模拟结构传热、面板固化放热、化学收缩和固化变形。采用顺序耦合的方法,将面板固化度场与结构温度场进行耦合求解,获得结构的温度分布,随后将结构温度场数据导入到热-力耦合的瞬态研究步中最终获得夹层结构的固化变形,如图 4所示。
|
图 4 多场耦合数值模拟方案 Fig. 4 Numerical simulation approach of multi-field coupling |
根据芯层和面板的几何特征,采用扫掠生成实体网格划分芯层和有限元网格,单元类型为三维热传导的C3D8T六面体单元。按照表 6建立各区域面板的铺层顺序,由于面板的每层纤维方向不同,根据面板材料3个主方向建立局部坐标系并赋予材料属性;为保证计算结果的准确性,对芯层内角及面板边缘网格进行局部加密,夹层结构的几何体模型及有限元模型如图 5所示。

|
图 5 夹层结构几何体及有限元模型 Fig. 5 Geometry and finite element model of sandwich structures |
在热-化学模拟过程中,将结构芯层和面板之间的接触方式设置为绑定接触以建立夹层件在固化过程中的内部热量传导。考虑夹层结构与固化环境间的热交换过程,将环境温度设置为固化温度周期,通过对流换热施加到模型上下表面,其控制方程如下:
| $ -\frac{\partial T}{\partial k_{i j}}=H\left(T-T_{\text {env }}\right) $ | (29) |
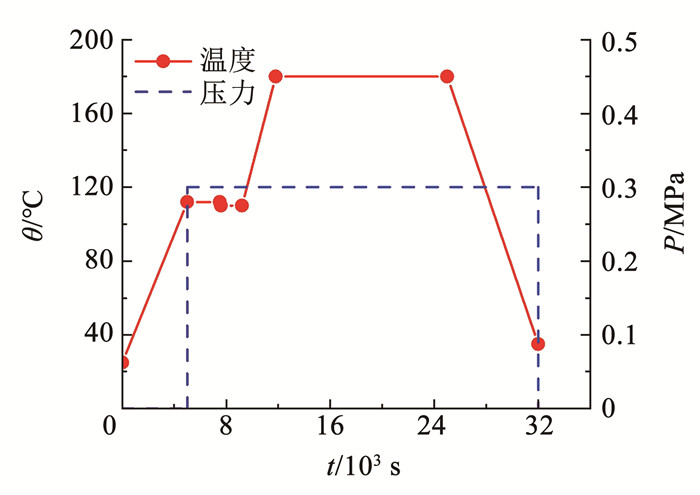
式中:H为夹层件与环境间的对流系数,根据实际工况[23],将其设置为80 W·(m2·℃)-1;Tenv为环境瞬时温度,与固化工艺曲线保持一致,如图 6所示。
|
图 6 固化温度及压力工艺曲线 Fig. 6 Curing temperature and pressure process curves |
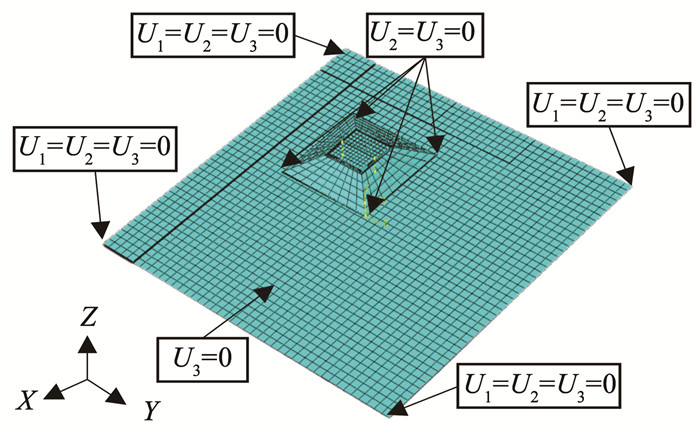
为简化运算同时贴近实际工艺过程,把模具约束设置为边界条件应用到仿真模型中:将整体结构固定于4个边角处(U1=U2=U3=0),同时限制结构下面板的Z方向位移(U3=0)和芯层拐角处铺层面板的Y方向、Z方向位移(U2=U3=0),如图 7所示。
|
图 7 有限元边界条件 Fig. 7 Finite element boundary conditions |
为验证仿真模型的正确性,采用预埋k型热电偶(thermocouple)温度监测的实验结果[23]进行验证,实验装置如图 8(a)所示,夹层结构经控制板固定在模具上,在结构顶部铺设好透气毡等辅助材料并使用密封条在真空袋边缘密封。为精确获取固化过程中温度响应,将热电偶预埋置入铺层内部,实时读取结构件的瞬态温度数据。实验与仿真的材料种类和固化工艺曲线均保持一致,选取反映夹层件各部位固化历程温度变化的4个代表性监测点进行验证对比,各监测点的具体位置以及相应的铺层信息如图 8(b)和表 7所示。

|
图 8 温度监测装置及监测位置 Fig. 8 Temperature monitoring device and location of monitoring |
| 表 7 温度监测点位置铺层信息 Tab. 7 Layer information of temperature monitoring points |
各监测点的有限元仿真和实验的温度对比结果如图 9所示,仿真模型的温度历程与实验结果保持了较高的吻合性,由于热电偶实际位置的微小变化和实际环境的影响,仿真结果的温度响应略微滞后于实验值。对比4个监测点数据可知,位于芯层上方TC2监测点与实验值最接近,说明芯层区域与环境热量交换更加充分。夹层件固化过程中各阶段的温度场分布如图 10所示。
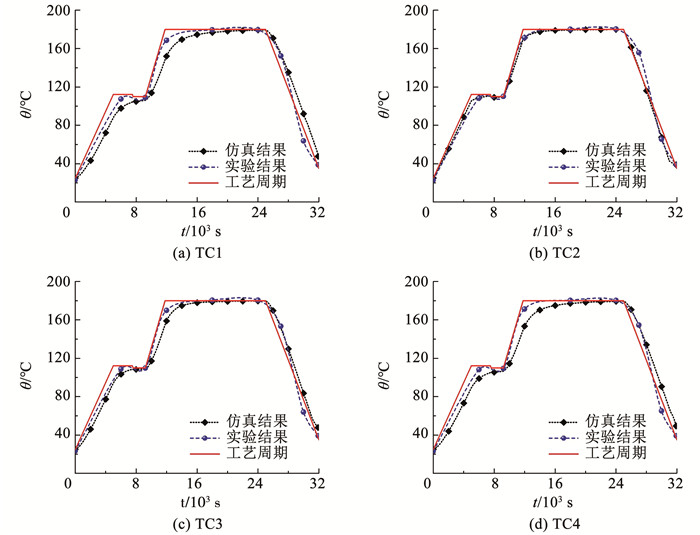
|
图 9 有限元与实验温度历程结果对比 Fig. 9 Comparison of finite element and experimental temperature profiles |
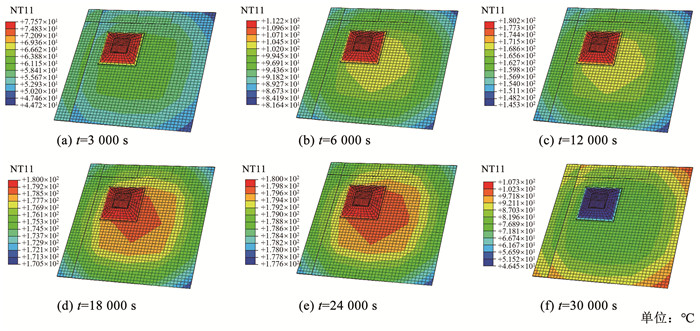
|
图 10 夹层结构温度场云图 Fig. 10 Temperature field distribution cloud map of sandwich structures |
由图 10可以看到,在升温初始期,芯层区域和环境热量交换相对充分,整个制件温度场以芯层附近的最高温度区为中心向外辐射,局部最大温差为32.9 ℃;观察各区域面板的温度分布,底端4层铺层面板的面积很大,其热量传递出现延迟。在随后的第1保温和第2升温阶段,随着面板内树脂迅速固化并放出热量,结构的温度梯度进一步加剧。进入固化保温期,结构温度分布趋于均衡,局部最大温差减小为10.0 ℃,并接近目标固化温度。在冷却阶段,由于结构的芯层冷却更加迅速,结构温度场出现反向,芯层和棱边的最大温差达到54.2 ℃,较低的温度使得芯层区域出现收缩并沿厚度方向上产生向上的剪切应力,导致制件翘曲。
夹层件固化过程中各阶段的固化度分布如图 11所示,图 11中FV1为面板的固化度。可以看到,在第2升温阶段前,夹层件内部树脂的固化度变化不明显,结构固化度梯度处于较小值。随着温度上升至预定固化温度,树脂发生固化凝胶使面板固化度迅速上升,到12 000 s时,位于芯层区域的面板固化度上升到85.7%,而四周棱边区域的固化度值变化不大。经过约6 000 s的保温时间,整体固化程度接近90%,可近似认为完全固化,如图 11(d)所示。
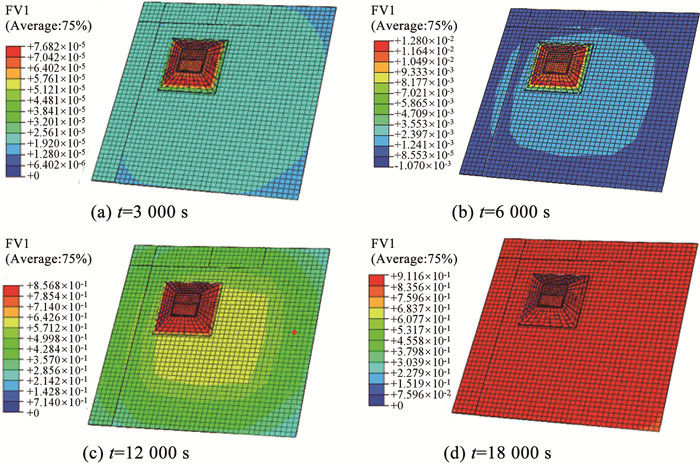
|
图 11 夹层结构固化度云图 Fig. 11 Curing degree field cloud map of sandwich structures |
夹层件固化过程中各阶段的应力场分布如图 12所示,图 12中S为结构的Mises应力。可以知道,在初始升温阶段,夹层件的应力分布受传热顺序影响,固化应力集中在率先升温的芯层区域;在固化保温阶段,面板内树脂迅速固化并发生化学收缩,结构整体应力达到峰值,其平均值上升至65.8 MPa;在冷却阶段,夹层件的平均应力逐渐降低,固化应力开始集中在结构端部。夹层件脱模后的应力场分布如图 13所示,当试件脱模后,夹层件的整体应力降低,结构外端处的高残余应力得到释放并转化为固化变形。上述结果表明,考虑树脂的固化放热和化学缩变的影响后,建立的多物理场模型能够较好地模拟夹层结构的应力变化过程。
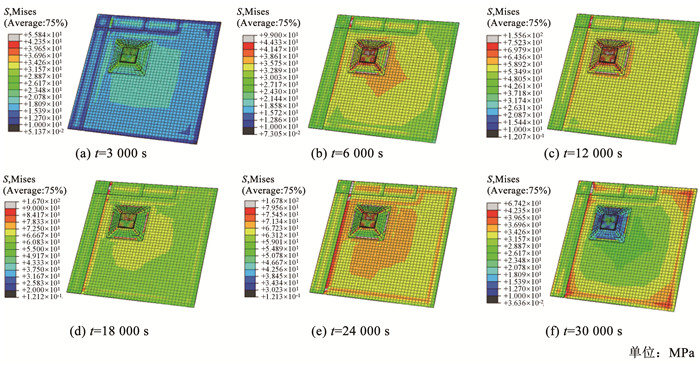
|
图 12 夹层结构应力场分布云图 Fig. 12 Curing stress field cloud map of in sandwich structures |
|
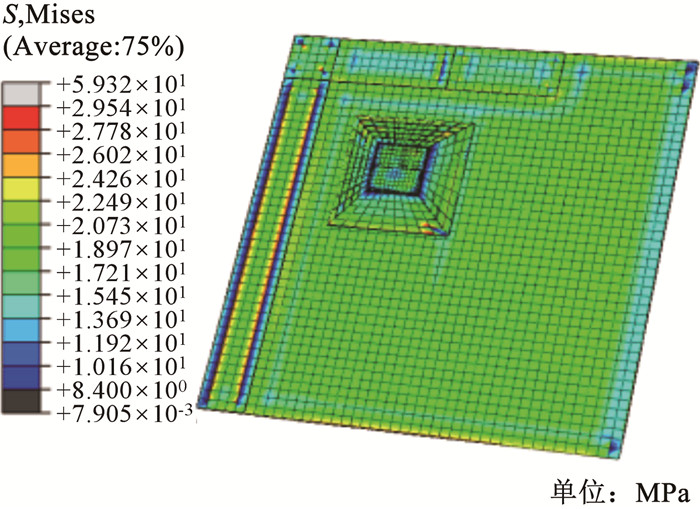
图 13 脱模后应力场分布 Fig. 13 Distribution of stress field after demolding |
图 14为夹层结构脱模后的变形示意图,图 14中U为结构的变形量,观察可知,靠近外端区域脱模前残余应力梯度更高,其变形量相对较大。采用夹层件翘曲变形的回弹位移衡量固化变形值(curing induced deformation,CID),其最大变形出现在底部4层铺层面板的右下端,其值为2.110 mm。
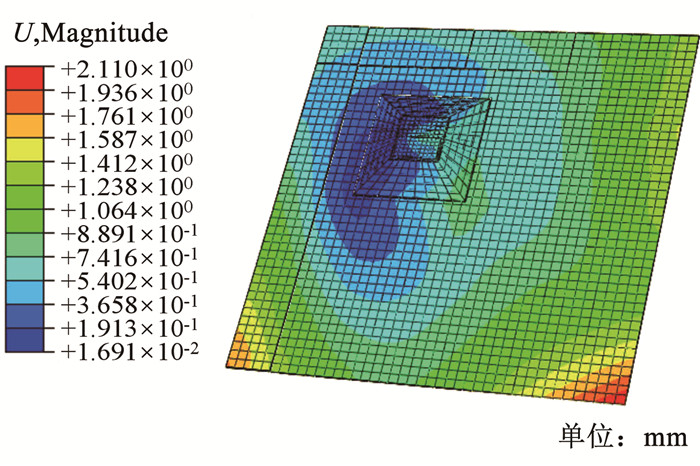
|
图 14 脱模后夹层结构最终变形 Fig. 14 Final deformation of sandwich structures after demolding |
为进一步分析,将脱模后有限元预测的径向积分路径变形分布结果与实验监测结果[23]进行比较,如图 15所示,图 15中CID为夹层件的固化变形,L为截面长度,结果显示有限元模型平均预测误差为4.8%,最大预测误差不超过6.0%,说明应用多物理场耦合方法分析得到的夹层件变形规律比较可靠。
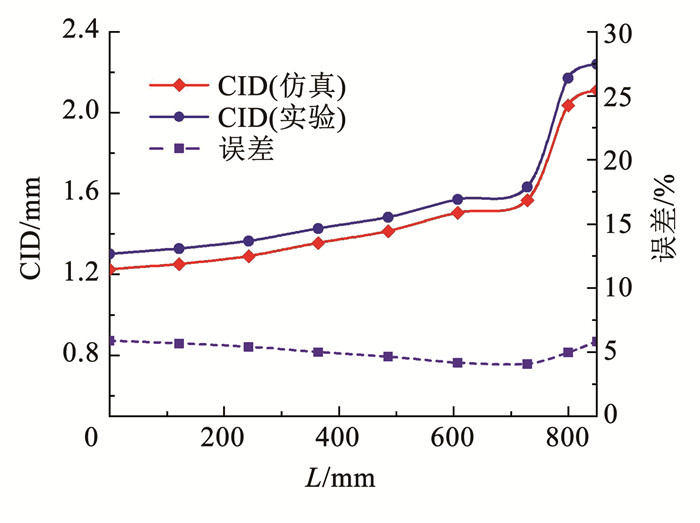
|
图 15 夹层结构固化变形的仿真与实验值对比 Fig. 15 Comparison of simulation and experimental values for curing deformation of sandwich structures |
为降低蜂窝夹层结构的固化变形,目前实际工作从降低结构温度梯度、提升预浸料面板栓系力出发,提出蜂窝分段拼接、铺贴摩擦带、预固化工艺等方法[25-26]。相较于其他几种方法,预固化工艺的流程相对简单、芯层稳定化和构件的挺括性更强。因此,结合该工艺的实际工况,通过建立好的解析模型对结构在不同预固化工艺工况下回弹变形的影响规律进行仿真分析。
面板预固化工艺路线如图 16所示。成型时通过在蜂窝上、下表面铺贴一层织物面板并进行预固化处理,随后对芯层进行机械加工并去除余料,待铺贴另一端面板后进行共固化成型。面板预固化处理的作用主要有:1)经预固化处理的树脂发生部分交联,降低树脂固化反应的放热值,提升结构温度分布的均匀性;2)树脂对纤维的束缚力得到增强,芯层- 面板栓系更加牢固,两方面的作用可以降低结构整体固化变形。
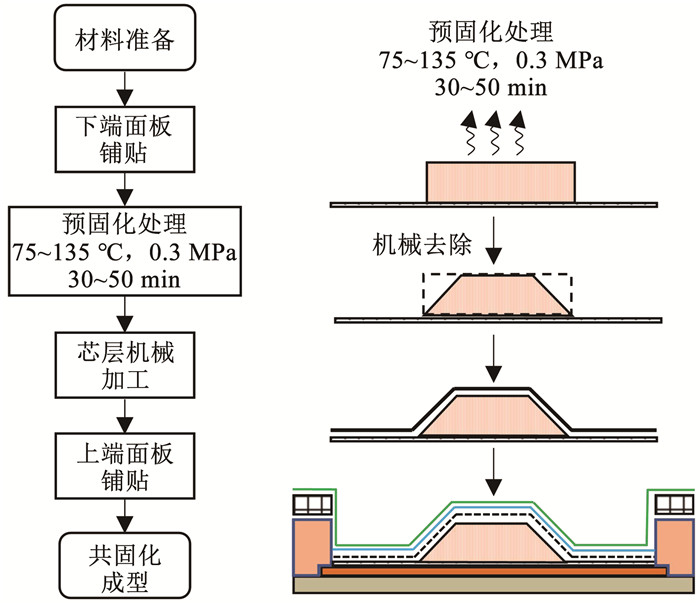
|
图 16 夹层结构预固化工艺 Fig. 16 Pre-curing process of honeycomb sandwich structure |
通过改变面板树脂的预固化程度,可将预浸料的时变参数控制在一个合适的范围。若预固化程度过低,树脂固化放热变化不大,降低效果不显著;若预固化程度过高,树脂黏结力过低不利于错位调整。考虑树脂黏接性能集中下降时的固化度接近或达到凝胶点,将上面板初始固化度分别设置为0.15、0.25、0.35和0.45,模拟不同预固化程度对夹层结构固化变形影响。利用建立好的有限元模型仿真不同预固化程度下夹层结构固化度历程,代入式(3)的固化动力学方程中进行归一化处理,获得不同预固化工艺的详细参数见表 8。
| 表 8 AS4/8552预浸料固化工艺参数 Tab. 8 AS4/8552 prepreg curing process parameters |
夹层结构在上蒙皮不同预固化程度回弹变形如图 17所示,其中α0为预固化度。可以看到,不同预固化度下夹层件沿截面的固化变形趋势保持吻合并随路径距离增大不断上升,结构的主要变形集中在结构外端。随着面板预固化度α0不断增大,固化过程载荷传递效率提高,面板固化变形不断减小。当预固化度α0为0.10(10%)和0.25(25%)时,结构最大CID值为1.898 mm和1.792 mm,相较于未预固化2.110 mm的变形值分别降低了10.04%和14.78%;随着预固化度α0超过0.25,树脂进入固化加速阶段,夹层结构的固化变形趋于稳定。上述结果表明,面板预固化处理削弱了固化放热和材料各向异性对夹层结构固化变形的影响,高于0.25预固化程度可使结构整体变形得到抑制。

|
图 17 不同预固化度下夹层结构固化变形 Fig. 17 Curing deformation of sandwich structures at different pre-curing degrees |
1) 结合多物理场耦合方法的有限元模型和实验监测结果的温度场结果的数值大小及变化趋势均保持一致,模型固化变形平均预测误差为4.8%,最大预测误差不超过6.0%,说明模型对结构变形规律的预报比较可靠。
2) 结构固化变形受到材料属性差异、固化收缩以及模具作用的交互影响。在升温阶段,夹层件的区域比周围区域的固化速率更快,制件温度场以芯层附近的最高温度区域为中心向外辐射,局部温差随树脂固化自加速不断扩大。变厚度铺层设计对较薄区域面板的固化应力影响较大,表现为沿厚度方向的向上剪切应力,在冷却阶段集中于结构的端部并转化为结构回弹变形。
3) 预固化工艺降低树脂的固化放热总值并增强夹层结构的挺括性,模拟预固化度0.25工况下夹层结构的最大CID值为1.792 mm,相较于未预固化处理的变形值降低14.78%,结构整体变形得到抑制。
| [1] |
郑义珠, 顾轶卓, 孙志杰, 等. Nomex蜂窝夹层结构真空袋共固化过程蜂窝变形[J]. 复合材料学报, 2009, 26(4): 29. ZHENG Yizhu, GU Yizhuo, SUN Zhijie, et al. Core crush of Nomex honeycomb sandwich structure during cocuring process with vacuum bag[J]. Acta Materiae Compositae Sinica, 2009, 26(4): 29. DOI:10.13801/j.cnki.fhclxb.2009.04.026 |
| [2] |
赵培晔. 耐高温聚酰亚胺蜂窝芯制备技术研究[D]. 北京: 中国运载火箭技术研究院, 2019 ZHAO Peiye. Study on the preparation of heat-resistant polyimide honeycomb core[D]. Beijing: China Academy of Launch Vehicle Technology, 2019. DOI: 10.27096/d.cnki.ghtdy.2019.000048 |
| [3] |
ANDERS M, ZEBRINE D, CENTEA T, et al. In-Situ observations and pressure measurements for autoclave co-cure of honeycomb core sandwich structures[J]. Journal of Manufacturing Science and Engineering, 2017, 139: 1. DOI:10.1115/msec2017-2887 |
| [4] |
VADAKKE V, CARLSSON L A. Experimental investigation of compression failure of sandwich specimens with face/core debond[J]. Composites Part B: Engineering, 2004, 35(6/7/8): 583. DOI:10.1016/j.compositesb.2003.10.004 |
| [5] |
BOGETTI T A, GILLESPIE J W Jr. Two-dimensional cure simulation of thick thermosetting composites[J]. Journal of Composite Materials, 1991, 25(3): 239. DOI:10.1177/002199839102500302 |
| [6] |
DONG Chensong. Process-induced deformation of composite T-stiffener structures[J]. Composite Structures, 2010, 92(7): 1614. DOI:10.1016/j.compstruct.2009.11.026 |
| [7] |
DING Anxin, WANG Jihui, LI Shuxin. Understanding process-induced spring-in of L-shaped composite parts using analytical solution[J]. Composite Structures, 2020, 250: 112629. DOI:10.1016/j.compstruct.2020.112629 |
| [8] |
BENAVENTE M, MARCIN L, COURTOIS A, et al. Numerical analysis of viscoelastic process-induced residual distortions during manufacturing and post-curing[J]. Composites Part A: Applied Science and Manufacturing, 2018, 107: 205. DOI:10.1016/j.compositesa.2018.01.005 |
| [9] |
DING Anxin, LI Shuxin, SUN Jiuxiao, et al. A thermo-viscoelastic model of process-induced residual stresses in composite structures with considering thermal dependence[J]. Composite Structures, 2016, 136: 34. DOI:10.1016/j.compstruct.2015.09.014 |
| [10] |
BELLINI C, SORRENTINO L. Analysis of cure induced deformation of CFRP U-shaped laminates[J]. Composite Structures, 2018, 197: 1. DOI:10.1016/j.compstruct.2018.05.038 |
| [11] |
刘馨阳, 赵海涛, 袁明清, 等. 模具对复合材料层合板固化成型影响的数值分析[J]. 复合材料学报, 2021, 38(6): 1974. LIU Xinyang, ZHAO Haitao, YUAN Mingqing, et al. Numerical analysis of the effect of mold on the curing of composite laminates[J]. Acta Materiae Compositae Sinica, 2021, 38(6): 1974. DOI:10.13801/j.cnki.fhclxb.20200831.002 |
| [12] |
元振毅, 王永军, 张跃, 等. 基于材料性能时变特性的复合材料固化过程多场耦合数值模拟[J]. 复合材料学报, 2015, 32(1): 167. YUAN Zhenyi, WANG Yongjun, ZHANG Yue, et al. Multi-field coupled numerical simulation for curing process of composites with time-dependent properties of materials[J]. Acta Materiae Compositae Sinica, 2015, 32(1): 167. DOI:10.13801/j.cnki.fhclxb.20140328.001 |
| [13] |
CHEN Yanyang, MALYSHEVA G V. Optimization of the curing modes of three-layer honeycomb panels[J]. Journal of Physics: Conference Series, 2021, 1990(1): 012074. DOI:10.1088/1742-6596/1990/1/012074 |
| [14] |
HODGE A, DAMBAUGH G. Analysis of thermally induced stresses on the core node bonds of a co-cured sandwich panel[J]. Journal of Composite Materials, 2013, 47(4): 467. DOI:10.1177/0021998312441654 |
| [15] |
FRANCO-URQUIZA E A, DOLLINGER A, TORRES-ARELLANO M, et al. Innovation in aircraft cabin interior panels Part Ⅰ: technical assessment on replacing the honeycomb with structural foams and evaluation of optimal curing of prepreg fiberglass[J]. Polymers, 2021, 13(19): 3207. DOI:10.3390/polym13193207 |
| [16] |
BELLINI C, SORRENTINO L, POLINI W, et al. Spring-in analysis of CFRP thin laminates: numerical and experimental results[J]. Composite Structures, 2017, 173: 17. DOI:10.1016/j.compstruct.2017.03.105 |
| [17] |
刘玥. 蜂窝复合材料夹芯结构承载特性及渐进损伤失效研究[D]. 哈尔滨: 哈尔滨工业大学, 2020 LIU Yue. Bearing characteristics and progressive failure behavior of composite honeycomb sandwich structures[D]. Harbin: Harbin Institute of Technology, 2020. DOI: 10.27061/d.cnki.ghgdu.2020.004721 |
| [18] |
丁安心. 热固性树脂基复合材料固化变形数值模拟和理论研究[D]. 武汉: 武汉理工大学, 2016 DING Anxin. Numerical and theoretical study on process-induced distortions in thermoset composites[D]. Wuhan: Wuhan University of Technology, 2016 |
| [19] |
HONG L C, HWANG S J. Study of warpage due to P-V-T-C relation of EMC in IC packaging[J]. IEEE Transactions on Components and Packaging Technologies, 2004, 27(2): 291. DOI:10.1109/TCAPT.2004.828579 |
| [20] |
ABDELAL G F, ROBOTHAM A, CANTWELL W. Autoclave cure simulation of composite structures applying implicit and explicit FE techniques[J]. International Journal of Mechanics and Materials in Design, 2013, 9(1): 55. DOI:10.1007/s10999-012-9205-7 |
| [21] |
孙立帅, 刘闯, 李玉军, 等. 变厚度复合材料U型零件固化变形仿真预测与结构影响因素[J]. 复合材料学报, 2023, 40(1): 553. SUN Lishuai, LIU Chuang, LI Yujun, et al. Prediction and analysis of cure-induced deformation of composite U-shaped parts with variable thickness[J]. Acta Materiae Compositae Sinica, 2023, 40(1): 553. DOI:10.13801/j.cnki.fhclxb.20220126.001 |
| [22] |
ERSOY N, GARSTKA T, POTTER K, et al. Modelling of the spring-in phenomenon in curved parts made of a thermosetting composite[J]. Composites Part A: Applied Science and Manufacturing, 2010, 41(3): 410. DOI:10.1016/j.compositesa.2009.11.008 |
| [23] |
AL-DHAHERI M, KHAN K A, UMER R, et al. Process induced deformations in composite sandwich panels using an in-homogeneous layup design[J]. Composites Part A: Applied Science and M anufacturing, 2020, 137: 106020. DOI:10.1016/j.compositesa.2020.106020 |
| [24] |
张弘弛. 蜂窝夹层结构反射器热变形及型面精度分析[D]. 哈尔滨: 哈尔滨工业大学, 2018 ZHANG Hongchi. Analysis of thermal deformation and profile accuracy of honeycomb sandwich reflectors[D]. Harbin: Harbin Institute of Technology, 2018 |
| [25] |
KHAN L A, MAHMOOD A H, KHAN Z. Post curing effect of poly epoxy on visco-elastic and mechanical properties of different sandwich structures[J]. Polymer Composites, 2013, 34(4): 477. DOI:10.1002/pc.22436 |
| [26] |
郝新超, 胡杰. Nomex蜂窝夹层结构侧向变形机理及蜂窝稳定化[J]. 航空制造技术, 2020, 63(13): 69. HAO Xinchao, HU Jie. Lateral crush mechanism and honeycomb stabilization of nomex honeycomb sandwich structure[J]. Aeronautical Manufacturing Technology, 2020, 63(13): 69. DOI:10.16080/j.issn1671-833x.2020.13.069 |
 2024, Vol. 56
2024, Vol. 56


