离群点被怀疑是由不同机制[1]产生的数据点,因不同于正常数据点而常被视作噪声点、也被认为是具有研究价值的点。目前离群点检测广泛应用于欺诈检测[2-3]、医疗处理[4-5]、环境卫生[6-7]、图像处理[8-9]、视频中异常事件检测[10-11]等。根据数据是否被标记,离群点检测方法分为有监督方法[12]、半监督方法[13]和无监督方法[14]。在难以获取数据标签的情况下,基于无监督的离群点检测成为常用的研究方法。无监督的离群点检测方法大致可分为:基于距离的离群点检测方法、基于密度的离群点检测方法和基于聚类的离群点检测方法[15-16]。
基于距离的方法能够快速地对离群点进行检测。Ramaswamy等[17]提出k近邻(k-nearest neighbor, KNN)离群点检测方法,通过计算数据点与第k个最近邻居之间的距离,将距离大小作为数据点的异常值。对KNN方法的改进,Zhang等[18]提出了一种基于局部距离的离群点检测方法(local distance-based outlier Factor, LDOF)。通过计算数据点的k近邻距离与k近邻数据点间的两两距离的比值来衡量数据点的离群程度。Yang等[19]提出均值偏移的异常值检测方法(mean-shift outlier detector, MOD),通过计算数据点最近邻域的平均值对数据集进行均值偏移处理,然后计算数据点的偏移距离来确定离群程度。上述方法对全局离群点都有着不错的检测性能,但考虑到对局部异常值的检测效果差、难以适应不同密度的数据以及参数k对检测性能的显著影响。Xie等[20]提出基于距离的局部引力离群点检测方法(local-gravitation outlier detection, LGOD),通过计算数据点的局部引力的变化率来得到数据点的异常程度。离群点的局部引力变化率高,而正常数据点的局部引力变化率低。
相比基于距离的离群点检测方法,基于密度的方法在局部异常值检测中表现良好,因为考虑邻域密度可以更好地反映数据的分布特征。Breuning等[21]提出基于密度的局部异常值的离群点检测方法(local outlier Factor, LOF)。通过计算数据点的局部可达密度与其最近邻居密度的比率来计算离群因子,数据点的离群因子越大,表示离群程度越高。对于LOF算法的改进,Tang等[22]提出了基于连通性的离群因子方法(connectivity-based outlier Factor, COF),将LOF的邻域计算方法改为增量计算,利用链距离提高了异常值检测性能。同样,Latecki等[23]提出基于LOF的核密度估计方法(local density Factor, LDF)。对数据点的邻域进行局部核密度估计,然后通过计算数据点的局部密度与邻居的局部密度的比率来确定数据点的异常值。Tang等[24]通过研究数据点的k最近邻、共享最近邻和反向近邻,并结合局部核密度估计方法对离群点进行检测,可以避免对不同密度数据的局部异常值的误判。张忠平等[25]提出了一种基于相对熵权密度离群因子的离群点检测算法。用熵权距离代替欧式距离,结合自然邻居对数据点局部进行高斯核密度估计,最后根据相对距离确定数据点的离群程度。此方法能够提高算法在低密度区域处理局部离群点的能力,但当局部离群点数量增多形成聚类时,离群点检测性能下降。
在基于聚类的离群点检测方法中,He等[26]提出基于聚类的局部离群点检测方法(cluster-based local outlier Factor, CBLOF)。通过聚类方法将数据分成若干个聚类,给出倍数β来判别聚类的规模大小,将规模小的聚类视为离群类,并计算数据点的局部离群因子。利用聚类方法能对离群聚类进行筛除,提高离群点的检测精度。Al-Zoubl等[27]首先使用FCM算法对数据集进行聚类并得到目标函数值。接着,通过剔除数据点后目标函数值变化量来判断数据点的离群程度。当数据形成不同密度的聚类时,该方法对局部离群点的检测性能变弱。对此,周玉等[28]首先利用FCM算法对数据集进行聚类。接着根据目标函数值剔除聚类中心附近的数据点。最后使用LOF算法计算剩余数据点的局部离群因子,提高局部离群点的检测精度。但上述方法受聚类算法限制,对任意形状数据集中的离群点检测性能不高。为此,张忠平等[29]提出了基于快速密度峰值聚类离群因子的离群点检测算法。首先使用DPC算法对数据集聚类,并根据数据点的k近邻平均距离定义了向心相对距离。接着,通过计算数据点的向心相对距离与KNN局部密度的比率得到离群因子。该方法通过聚类来分析每个簇的特征,根据离群因子的大小对离群点进行检测,同时能避免不同密度聚类对离群点检测带来的影响。
基于对全局离群点和局部离群点的考虑,本文提出基于k近邻和核密度估计方法的改进DPC聚类方法的离群点检测与解释方法。首先,通过计算数据点的k近邻距离,将k近邻距离之和作为数据点的全局异常值,并利用核密度估计方法计算数据点的局部密度。其次,根据局部密度得到数据点的相对距离,并对数据集进行聚类。再次,利用簇密度和局部密度的比率获取数据点的局部异常值。最后,将全局异常值与局部异常值相乘获取最终的异常得分,选取异常得分高的Top-n数据点作为离群点。通过构建全局-局部异常值决策图对离群点种类进行解释。
1 预备知识 1.1 DPC聚类算法快速搜索和发现密度峰值聚类算法(clustering by fast search and find of density peaks, DPC)是Rodriguez等[30]在2014年提出的一种聚类算法。构建关于密度与距离的决策图来确定聚类中心,即聚类中心密度最大且被密度小于它的数据点所包围,不同聚类中心间的距离较远。根据数据点归类于密度大且距离最近的簇的原则进行聚类。
DPC算法中定义的两个参数如下。
定义1 (局部密度):
| $ \rho_i=\sum\limits_i \chi\left(d_{i j}-d_{\mathrm{c}}\right) $ | (1) |
式中:当x < 0时,χ(x)=1,否则χ(x)=0。dij为数据点i与j之间的欧式距离,dc为截断距离。dc为超参数,通常被定义为:dc=p%,表示所有数据点的平均邻居数为数据总量的p%。避免数据点局部密度出现相同的情况,采用下式高斯函数来代替式(1), 即
| $ \rho_i=\sum\limits_{i \neq j} \mathrm{e}^{-\left(\frac{d_{i j}}{d_{\mathrm{c}}}\right)^2} $ | (2) |
定义2 (相对距离):
| $ \delta_i=\min\limits_{j: \rho_j>\rho_i} d_{i j} $ | (3) |
计算数据点与密度大于它的最近数据点的距离。当数据点i的密度为数据集中最大时,式(3)不成立。此时,其相对距离为距离i最远点的距离,即
| $ \gamma=\rho \cdot \delta $ | (4) |
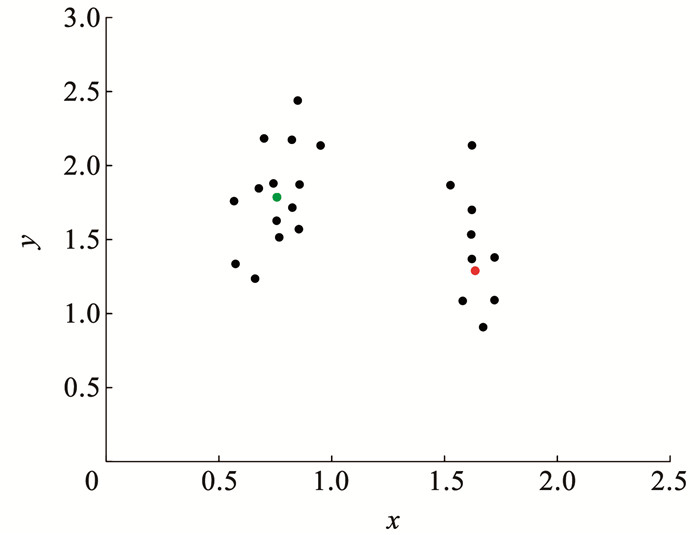
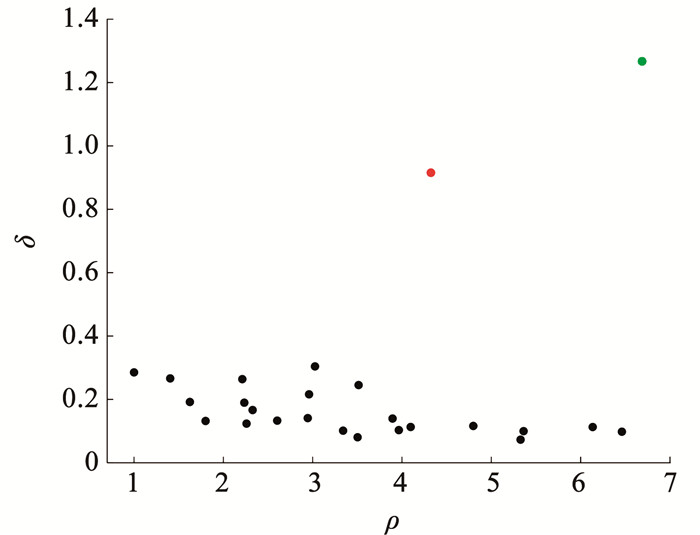
图 1是一组二维数据,图 1中包含两个簇。构建局部密度-相对距离决策图如图 2所示。局部密度大且相对距离大的数据点分布在决策图的右上角,这两个数据点是图 1中两个簇中数据点分布最密集部分,将这两个数据点作为聚类中心。
|
图 1 二维数据 Fig. 1 Two-dimensional data |
|
图 2 决策图 Fig. 2 Decision graph |
确定聚类中心后,根据局部密度和相对距离的值将剩余数据点分配到密度更高且距离最近数据点所属类中。
1.2 k近邻搜索方法k近邻搜索方法是通过计算数据集(N)中数据点间的欧氏距离,将距离值从小到大排列,找到数据点的k个最近邻居。计算公式如下:
| $ d_k\left(x_i, x_j\right)=\sqrt{\sum\limits_{m=1}^d\left(x_{i m}-x_{j m}\right)^2} $ | (5) |
式中:xi, xj∈N, xim为第i个数据点的第m维,xi≠xj, xj为xi的第k近邻数据点,d为维度个数。
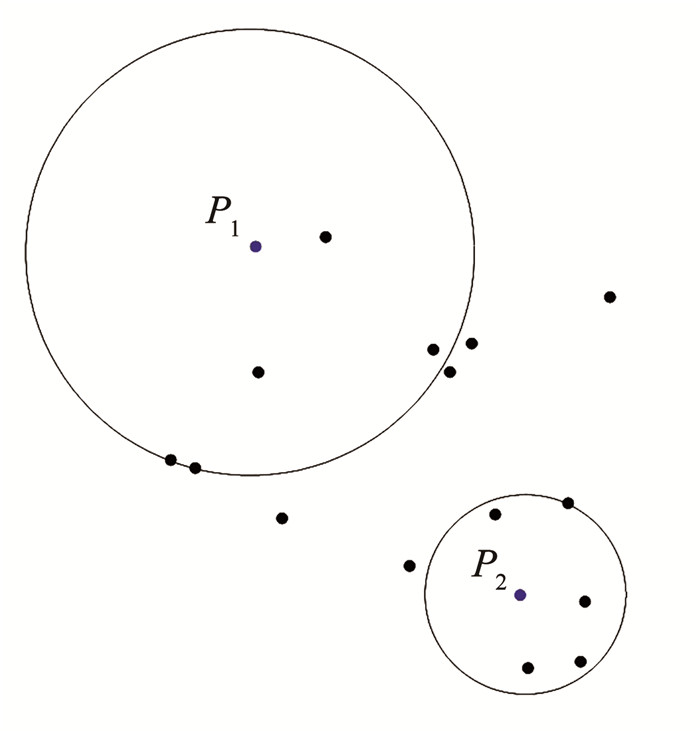
如果两个数据点间的距离越小,那么这两个数据点越靠近。如果数据点的k近邻值很小,则该k+1个数据点分布集中。为直观了解数据点的k近邻值与数据点分布之间的关系,随机生成二维数据如图 3所示。图 3中P1、P2为其中两个数据点,计算得到P1与P2的k近邻数据点,以k=5为例。
|
图 3 KNN邻近分布示意(k=5) Fig. 3 Schematic representation of KNN neighbourhood distribution (k=5) |
从图 3中可知,P1周围的数据点分布相比P2较为分散,使得P1的k近邻数据点与P1间的距离较远,即dk=5(P1)>dk=5(P2)。通过k近邻距离值的大小可以判断数据点的分布情况,也可以对数据点的局部密度进行分析。
2 改进DPC聚类方法当数据点形成不同密度的聚类时,根据传统DPC聚类算法难以确定簇密度小的聚类中心。基于此,利用k近邻和核密度估计方法计算数据点的局部密度,使得不同密度的簇都能有稳定的聚类中心。
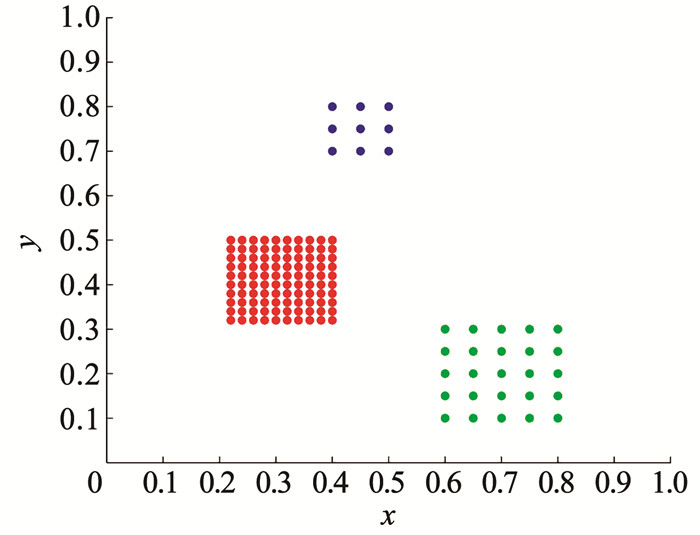
2.1 局部密度DPC聚类方法中截断距离dc的计算方法是:人为设定参数,使数据点的邻居平均数量约为数据集中总数据量的1%~2%。在簇密度大小有明显差异的数据集中,簇密度小的聚类中心很难被选取。图 4为数据点形成密度差异大的3个聚类。
|
图 4 二维数据 Fig. 4 Two-dimensional data |
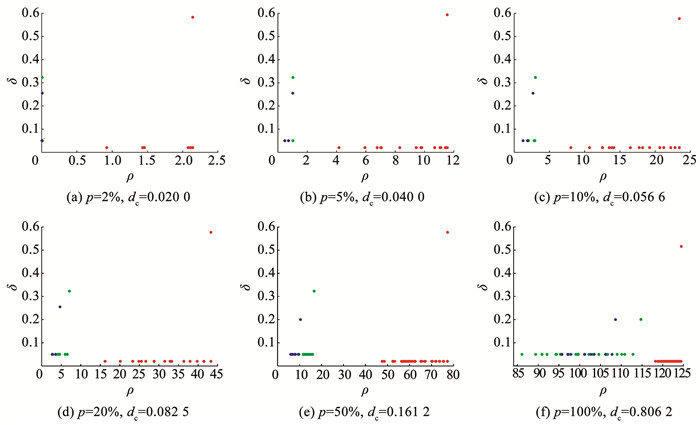
使用DPC方法构建决策图并对图 4的数据集进行聚类。为解释数据点的聚类情况,分别对含有邻居平均数量约为数据集中总数据量的2%、5%、10%、20%、50%、100%,以及对应的dc下的决策图,如图 5所示。
|
图 5 不同dc下的决策图 Fig. 5 Decision diagram for different dc values |
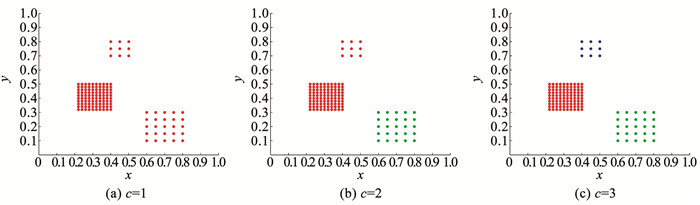
从图 5的结果看出,当数据点形成密度差异大的聚类时,较小的截断距离对应的决策图,无法识别密度小的聚类中心,进而形成错误的聚类。若要实现正确的聚类,需要正确选取3个聚类中心,即每个数据点含有邻居平均数量约为数据集中总数据量的50%以上。图 6为选取不同数量的聚类中心所对应的聚类结果,c为聚类中心个数。
|
图 6 3种不同的聚类结果 Fig. 6 Three different clustering results |
为解决上述问题,计算数据点的k近邻距离并对数据点的局部密度进行核密度估计,让每个数据点都能有较为稳定的局部密度,进而能更加准确的聚类。利用高斯核函数对数据点的局部密度进行估计如式(6)所示。根据式(5)得到数据点的k近邻距离,并将其带入到式(6)并取平均值,得到式(7)。
| $ K_{\text {Gaussian }}(x)=\frac{1}{(2 \mathtt{π})^d} \exp \left(-\frac{\|x\|^2}{2}\right) $ | (6) |
| $ \rho\left(x_i\right)=\frac{1}{k}\sum\limits_{x_j \in \operatorname{KNN}\left(x_i\right)} \frac{1}{(2 \mathtt{π})^d} \exp \left[-\frac{d_k\left(x_i, x_j\right)^2}{2}\right] $ | (7) |
式中:
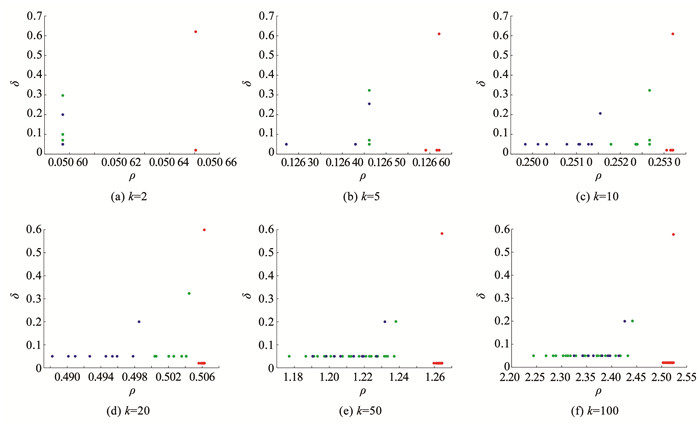
从式(6)、(7)可以看出e-x为单调递减函数,当数据点的k近邻距离越大,局部密度越小,数据点分布越稀疏。为分析不同k下的决策图,如图 7所示。
|
图 7 不同k下的决策图 Fig. 7 Decision graph of different values of k |
从图 7可以看出,当k=5时,可以明显识别出3个不同簇中心在决策图的位置。利用k近邻的核密度估计方法能更加适应不同簇密度下的聚类。
3 基于改进DPC聚类算法的离群点检测方法首先,利用k近邻方法对数据点的全局进行分析,计算数据点的全局异常值。其次,利用高斯核函数计算数据点的局部密度,并计算相对距离。再次,利用局部密度和相对距离值进行聚类,并计算聚类之后的每个簇的平均密度以及数据点的局部异常值。最后,结合全局异常值和局部异常值对离群点进行检测,并构建全局-局部异常值决策图对离群点进行解释。
3.1 全局异常值当数据点分布密集时,数据点间的距离小,k近邻的值小。相反,当数据点分布稀疏时,k近邻的值大。离群点周围的数据分布比正常数据点周围的数据分布稀疏,使得离群点的k近邻数据点离群点较远。通过数据点的k近邻的值的大小能快速准确地检测出全局离群点。数据点的k近邻值的大小如式(8)所示。
| $ S_{\text {Ges }}\left(x_i\right)=\sum\limits_{x_j \in N_k\left(x_i\right)} d_k\left(x_i, x_j\right) $ | (8) |
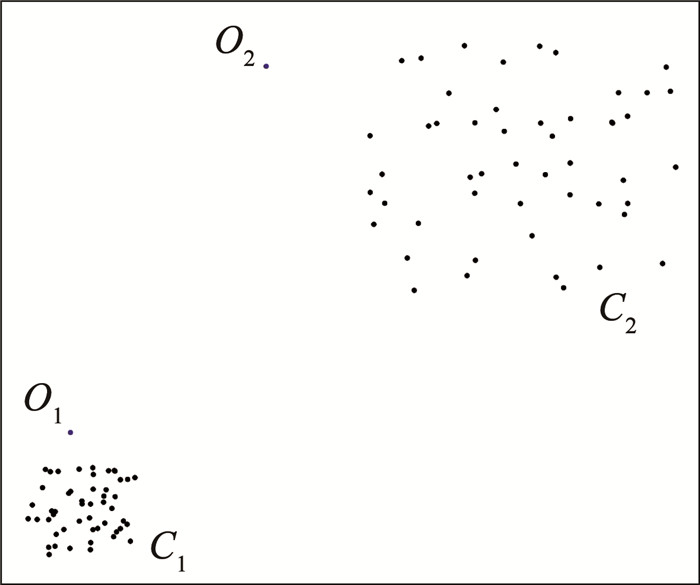
式中: SGes(xi)为数据点xi的全局异常值,dk(xi, xj)为数据点xi的第k近邻距离。SGes越大,说明数据点间的密度越稀疏,则该数据点越有可能是离群点。当数据点形成密度差异大的聚类时,该方法只能检测簇密度小的周围的离群点,对整体数据集中的局部离群点检测性能下降。如图 8所示,C1、C2为两个密度相差较大的两个簇,O1、O2为两个局部离群点。使用KNN方法无法对C1簇中的O1离群点进行检测。
|
图 8 二维数据 Fig. 8 Two-dimensional data |
考虑数据的局部离群信息,进而更加准确的对局部离群点进行检测。通过对数据集进行聚类获取若干个簇,计算簇的平均密度,从而计算数据点的局部异常值。通过聚类方法能快速获取每个数据点的局部异常值,降低计算复杂程度。
首先,根据式(5)得到数据点的k近邻值,利用式(6)、(7)得到数据点的局部密度。
其次,根据式(3)计算数据点的相对距离,使用快速搜索和发现密度峰值方法对数据进行聚类。根据式(9)计算簇的平均密度。
| $ \begin{aligned} \bar{\rho}(l)= & \frac{1}{k \cdot|N(l)|} \sum\limits_{i=1}^{N(l)} \sum\limits_{x_j \in \operatorname{KNN}\left(x_i\right)} \frac{1}{(2 \mathtt{π})^d} . \\ & \exp \left(-\frac{d_k\left(x_i, x_j\right)^2}{2}\right) \end{aligned} $ | (9) |
式中:N(l)为第l簇的数据量,xi为属于第l簇的第i个数据点。
关于数据点xi的局部异常值解释:xi所在簇的平均密度与数据点xi的核密度的比值,即
| $ S_{\text {Les }}\left(x_i\right)=\frac{\bar{\rho}(l)}{\rho\left(x_i\right)} $ | (10) |
式中:SLes(xi)为数据点xi的局部异常值,ρ(l)为第l簇的平均密度。
3.3 数据点异常得分结合数据点的全局和局部的特点,将数据点的全局异常值与局部异常值进行相乘得到最终的异常得分,即
| $ S_{\text {KDPC }}\left(x_i\right)=S_{\text {Les }}\left(x_i\right) \boldsymbol{\cdot} S_{\text {Ges }}\left(x_i\right) $ | (11) |
式中: SKDPC(xi)为数据点xi的异常得分,选取数据点的异常得分最高的Top-n数据点视为离群点。
3.4 理论分析本文将分别对全局异常值和局部异常值进行理论分析,证明离群点检测方法的有效性。
3.4.1 全局异常值离群点是不同于正常特征属性的异常数据。直观来看,离群点远离正常数据点,数量少且分布稀疏。根据定义可以得到,离群点xoutlier的第k近邻值大于正常数据点xnormal的第k近邻值,则
证明 因为
| $ d_k\left(x_{\text {outlier }}\right)>d_k\left(x_{\text {normal}}\right) $ | (12) |
所以
| $ \sum\limits_{x_{\text {outlier }} \in \text { KNN }} d_k\left(x_{\text {outlier }}\right)>\sum\limits_{x_{\text {normal}} \in \text { KNN }} d_k\left(x_{\text {normal}}\right) $ | (13) |
即
| $ \frac{S_{\text {Ges }}\left(x_{\text {outlier }}\right)}{S_{\text {Ges }}\left(x_{\text {normal}}\right)}=\frac{\sum\limits_{x_{\text {outlier }} \in \text { KNN }} d_k\left(x_{\text {outlier }}\right)}{\sum\limits_{x_{\text {normal}} \in \text { KNN }} d_k\left(x_{\text {normal}}\right)}>1 $ | (14) |
从SGes的大小可以得出结论:离群点的全局异常值大于正常数据点的全局异常值,可以通过全局异常值的大小对离群点进行分析。
3.4.2 局部异常值考虑数据点的局部异常值,能更加精确地对离群点进行检测。因为
证明 令
| $ d_k\left(x_{\text {outlier }}\right)=\alpha_k d_k\left(x_{\text {normal}}\right), \alpha_k>1 $ | (15) |
将式(15)带入式(6)可得
| $ \begin{aligned} \frac{K_{\text {Gaussian }}\left(x_{\text {normal}}\right)_k}{K_{\text {Gaussian }}\left(x_{\text {outlier }}\right)_k}= & \frac{\frac{1}{(2 \mathtt{π})^d} \exp \left(-\frac{d_k\left(x_{\text {normal}}\right)^2}{2}\right)}{\frac{1}{(2 \mathtt{π})^d} \exp \left(-\frac{\alpha_k^2 d_k\left(x_{\text {normal}}\right)^2}{2}\right)}= \\ & \exp \left(\frac{d_k\left(x_{\text {normal}}\right)^2}{2}\left(\alpha_k^2-1\right)\right) \end{aligned} $ | (16) |
因为αk>1,且指数函数ex单调递增,那么:
| $ \begin{gathered} \frac{K_{\text {Gaussian }}\left(x_{\text {normal}}\right)_k}{K_{\text {Gaussian }}\left(x_{\text {outlier }}\right)_k}=\exp \left(\frac{d_k\left(x_{\text {normal}}\right)^2}{2}\left(\alpha_k^2-1\right)\right)> \\ \mathrm{e}^0=1 \end{gathered} $ | (17) |
从式(17)可知,正常数据点的第k近邻的核密度估计值是大于离群点的第k近邻的核密度估计值,即
| $ \frac{\rho\left(x_{\text {normal}}\right)}{\rho\left(x_{\text {outlier }}\right)}=\frac{\frac{1}{k} \sum\limits_{x_{\text {normal}} \in \text { KNN }} K_{\text {Gaussian }}\left(x_{\text {normal}}\right)_k}{\frac{1}{k} \sum\limits_{x_{\text {outlier }} \in \text { KNN }} K_{\text {Gaussian }}\left(x_{\text {outlier }}\right)_k}>1 $ | (18) |
从式(18)可以得知,正常数据点的局部密度大于离群点的局部密度。又因为离群点的数量远少于正常数据点的数量。在聚类完成后,第l簇的密度近似等于正常数据点的平均密度,即
| $ \begin{aligned} \bar{\rho}(l)= & \frac{1}{k \boldsymbol\cdot|N(l)|} \sum\limits_{i=1}^{N(l)} \sum\limits_{x_j \in \mathrm{KNN}\left(x_i\right)} \frac{1}{(2 \mathtt{π})^d} \exp \left(-\frac{d_k\left(x_i, x_j\right)^2}{2}\right) \approx \\ & \frac{1}{k \boldsymbol\cdot\left|N\left(x_{\text {normal}}\right)\right|} \sum\limits_{i=1}^{N\left(x_{\text {normal}}\right)} \sum\limits_{x_j \in \mathrm{KNN}\left(x_i\right)} \frac{1}{(2 \mathtt{π})^d} \exp \left(-\frac{d_k\left(x_i, x_j\right)^2}{2}\right) \approx \\ & \frac{1}{\left|N\left(x_{\text {normal}}\right)\right|} \sum\limits_{i=1}^{N\left(x_{\text {normal}}\right)} \rho\left(x_{\text {normal}}\right) \end{aligned} $ | (19) |
结合式(18)、(19)可得:
| $ S_{\text {Les }}\left(x_{\text {normal}}\right)=\frac{\frac{1}{\left|N\left(x_{\text {normal}}\right)\right|} \sum\limits_{i=1}^{N\left(x_{\text {normal}}\right)} \rho\left(x_{\text {normal}}\right)}{\rho\left(x_{\text {normal}}\right)} $ | (20) |
| $ S_{\text {Les }}\left(x_{\text {outlier }}\right)=\frac{\frac{1}{\left|N\left(x_{\text {normal}}\right)\right|} \sum\limits_{i=1}^{N\left(x_{\text {normal}}\right)} \rho\left(x_{\text {normal}}\right)}{\rho\left(x_{\text {outlier }}\right)} $ | (21) |
结合式(18)、(20)、(21)可得
| $ \frac{S_{\text {Les }}\left(x_{\text {outlier }}\right)}{S_{\text {Les }}\left(x_{\text {normal}}\right)}=\frac{\rho\left(x_{\text {normal}}\right)}{\rho\left(x_{\text {outlier }}\right)}>1 $ | (22) |
根据式(22)可知,离群点的局部异常值大于正常数据点的局部异常值。根据局部异常值的大小可以对局部离群点进行分析。
3.4.3 异常得分本文算法中,将全局异常值与局部异常值进行乘积作为最终的异常得分。方法的意义在于能够同时考虑全局与局部信息,且比其中的任意一种单独方法要好。
证明 根据式(14)、(22)可得:
| $ \begin{aligned} \frac{S_{\text {KDPC }}\left(x_{\text {outlier }}\right)}{S_{\text {KDPC }}\left(x_{\text {normal}}\right)}= & \frac{S_{\text {Ges }}\left(x_{\text {outlier }}\right) \boldsymbol\cdot S_{\text {Les }}\left(x_{\text {outlier }}\right)}{S_{\text {Ges }}\left(x_{\text {normal}}\right) \boldsymbol\cdot S_{\text {Les }}\left(x_{\text {normal}}\right)}> \\ & \frac{S_{\text {Ges }}\left(x_{\text {outlier }}\right)}{S_{\text {Ges }}\left(x_{\text {normal}}\right)} \end{aligned} $ | (23) |
| $ \begin{aligned} \frac{S_{\text {KDPC }}\left(x_{\text {outlier }}\right)}{S_{\text {KDPC }}\left(x_{\text {normal}}\right)}= & \frac{S_{\text {Ges }}\left(x_{\text {outlier }}\right) \boldsymbol\cdot S_{\text {Les }}\left(x_{\text {outlier }}\right)}{S_{\text {Ges }}\left(x_{\text {normal}}\right) \boldsymbol\cdot S_{\text {Les }}\left(x_{\text {normal}}\right)}> \\ & \frac{S_{\text {Les }}\left(x_{\text {outlier }}\right)}{S_{\text {Les }}\left(x_{\text {normal}}\right)} \end{aligned} $ | (24) |
下面将简单地给出一个证明,直观看出本文方法与仅考虑全局异常值方法之间的差异。
假设数据集中含有两个簇,两个簇中的数据点分布均匀,簇1的数据点密度高于簇2的数据点密度,即
| $ \begin{aligned} S_{\mathrm{Ges}}\left(x_{\text {normal}_2}\right)= & \sum\limits_{x_{\text {normal}_2} \in \mathrm{KNN}} d_k\left(x_{\text {normal}_2}\right)= \\ & \beta \sum\limits_{x_{\text {normal}_1} \in \text { KNN }} d_k\left(x_{\text {normal}_1}\right)= \\ & \beta \cdot S_{\text {Ges }}\left(x_{\text {normal}_1}\right) \\ \end{aligned} $ | (25) |
同理:
| $ S_{\text {Ges }}\left(x_{\text {outlier }}\right)=\alpha \boldsymbol\cdot S_{\text {Ges }}\left(x_{\text {normal}_1}\right) $ | (26) |
结合式(25)、(26)可得
| $ \frac{S_{\text {Ges }}\left(x_{\text {normal}_2}\right)}{S_{\text {Ges }}\left(x_{\text {outlier }}\right)}=\frac{\beta}{\alpha} $ | (27) |
结果1 根据式(27)可知,若要检测出数据点分布密度更大的簇1中的局部离群点,则
接着计算数据点的局部异常值,由式(22)可知:
| $ S_{\text {Les }}\left(x_{\text {outlier }}\right)=\lambda \boldsymbol\cdot S_{\text {Les }}\left(x_{\text {normal}_1}\right)\approx \lambda \boldsymbol\cdot S_{\mathrm{Les}}\left(x_{\text {normal}_2}\right) $ | (28) |
结合式(27)、(28)可得
| $ \begin{aligned} \frac{S_{\text {KDPC }}\left(x_{\text {normal}_2}\right)}{S_{\text {KDPC }}\left(x_{\text {outlier }}\right)}= & \frac{S_{\text {Ges }}\left(x_{\text {normal}_2}\right) \boldsymbol\cdot S_{\text {Les }}\left(x_{\text {normal}_2}\right)}{S_{\text {Ges }}\left(x_{\text {outlier }}\right) \boldsymbol\cdot S_{\text {Les }}\left(x_{\text {outlier }}\right)}= \\ & \frac{\beta}{\lambda \alpha} \end{aligned} $ | (29) |
结果2 此时需要检测出数据点分布密度更大的簇1中的局部离群点,则
统计这两次的结果见表 1。从表 1中可知,α1> α2。说明在没有乘以局部异常值之前,需要更大的α才能检测出局部离群点。显然离群点的分布是确定的,只有降低检测出局部离群点所需要的α才是提高离群点检测精度的关键。综上所述,KDPC方法能在检测全局离群点的同时,兼顾对局部离群点的考虑。
| 表 1 结果对比 Tab. 1 Comparison of results |
KDPC计算复杂度的分析如下:
1) 使用KD树搜索k个最近邻居的时间是O(Nlog N),其中N为数据集中的样本数量;
2) 计算SGes(xi)和SLes(xi)的复杂度是O(N)。
综上所述,计算KDPC的复杂度为O(Nlog N)+ 2O(N)= O(Nlog N),和KNN、LOF方法拥有着相同的计算复杂度。但本文利用DPC聚类方法,可以得到聚类后的数据点种类以及分布情况。在能够检测全局和局部离群点的情况下,对数据点进行分析解释。
3.6 算法步骤输入 数据集、近邻参数k。
输出 数据点的异常得分。
Step1 根据式(5)计算数据点的k近邻距离,并根据式(8)得到数据点的全局异常值。
Step2 根据式(6)、(7)对数据点进行核密度估计,计算数据点的局部密度ρ。
Step3 根据式(3)计算数据点的相对距离δ。
Step4 依据ρ和δ选择聚类中心。
Step5 将剩余数据分配到密度更高且距离最近数据点所属类中。
Step6 根据式(9)、(10)计算每个簇的平均密度及数据点的局部异常值。
Step7 结合全局异常值和局部异常值,根据式(11)得到数据点最终异常得分。
Step8 构建全局-局部异常值决策图,对数据点离群程度进行解释。
4 离群点种类的解释本文将式(8)与式(10)得到的全局异常值与局部异常值进行归一化,以纵坐标为全局异常值、以横坐标为局部异常值,构建全局-局部离群值决策图,对在不同数量和种类下的离群点进行解释。
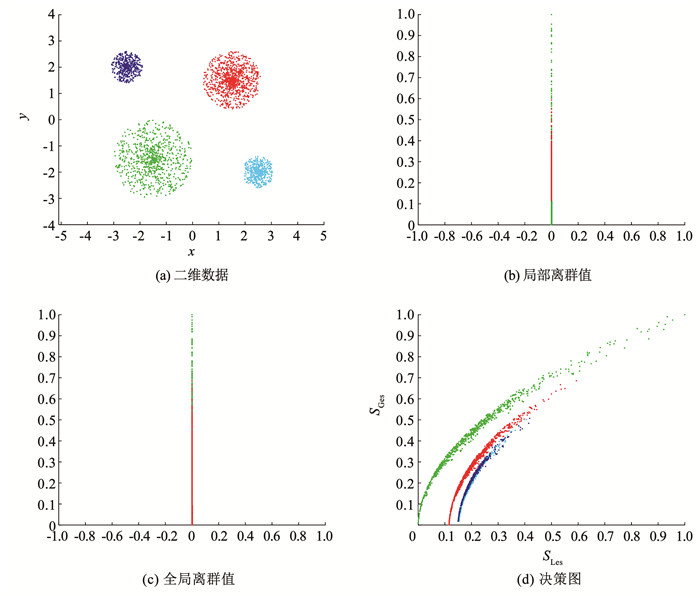
4.1 数据集中无离群点正常数据形成的4个聚类如图 9(a)所示,正常数据点的局部离群值、全局离群值大小接近,在决策图中数据点分布均匀连续如图 9(d)所示。可以通过决策图中的位置了解每个簇数据点的分布情况,例如,分布在决策图左上方的数据点有着更小的局部离群值和更大的全局离群值,这类簇数据点分布会更加稀疏。
|
图 9 数据集中无离群点 Fig. 9 Dataset contains no outliers |
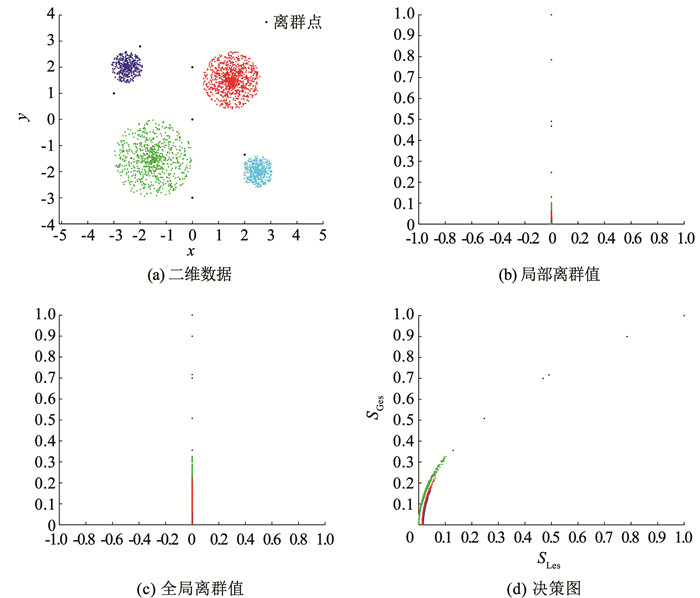
在图 9(a)数据基础上增加部分局部离群点如图 10(a)所示。局部离群点相比正常数据点有较大的局部异常值与全局异常值。在图 10(d)中,离群点会更加远离密集数据点在空间中分布稀疏。
|
图 10 数据集中含少量局部离群点 Fig. 10 Dataset contains few local outliers |
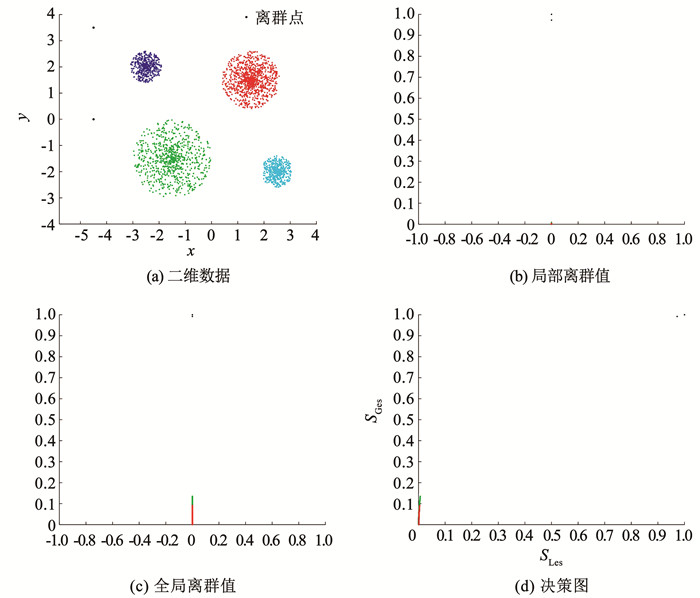
增加少量全局离群点如图 11(a)所示。全局离群点比局部离群点更加远离正常数据。相比局部离群点有更大的全局异常值和局部异常值。与正常数据点相比有着悬殊的异常值差距,在归一化之后,正常数据点在决策图的最左上角,全局离群点位于最右上角如图 11(d)所示。
|
图 11 数据集中含少量全局离群点 Fig. 11 Dataset contains few global outliers |
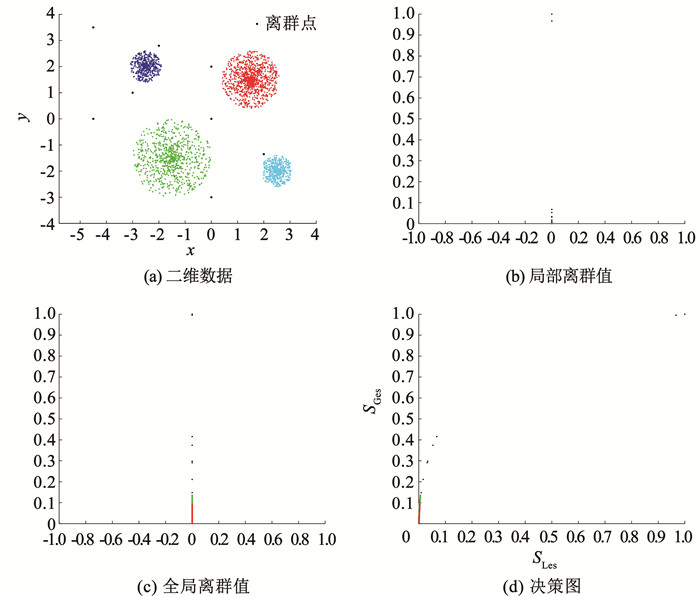
图 12(a)包含全局离群点和局部离群点。决策图中同时含有全局离群点和局部离群点时,由于归一化的原因局部离群点会更加靠近正常数据点,且分布较为稀疏。全局离群点位置不受影响,处于决策图坐标点(1, 1)附近。
|
图 12 数据集中存在局部离群点和全局离群点 Fig. 12 Local and global outliers exist in the dataset |
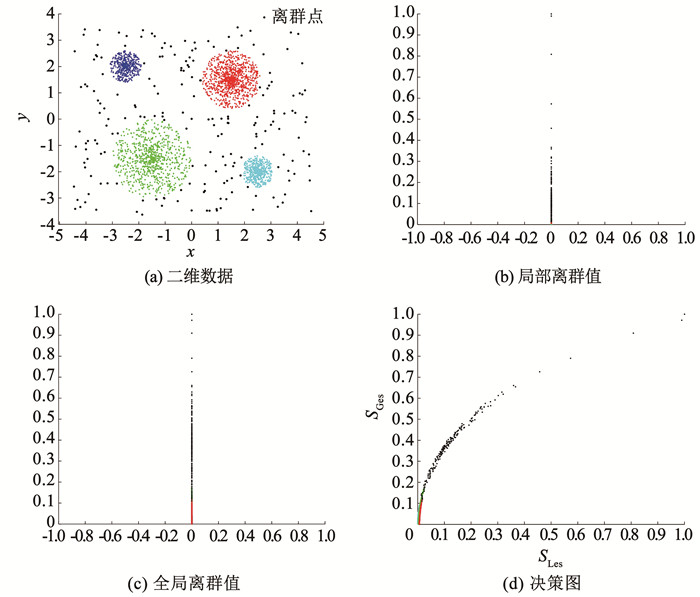
在图 13(a)中,当局部离群点与全局离群点数量增加且不存在明显界限时,决策图如图 13(d)所示。靠近连续数据点的松散数据点视为局部离群点,靠近决策图坐标点(1, 1)的数据点可视为全局离群点。
|
图 13 数据集中存在较多的局部离群点和全局离群点 Fig. 13 A large number of local and global outliers exist in the dataset |
为解释本文方法的离群点检测性能,通过人工数据集对离群点进行检测,人工数据集参数见表 2。
| 表 2 人工数据集 Tab. 2 Artificial datasets |
首先,将数据进行[0, 1]归一化处理,计算数据点的k近邻距离,得到数据点的全局异常值。其次,利用高斯核函数对数据点的局部核密度值进行计算,并计算数据点的高密度最小距离的值,通过决策图确定聚类中心。再次,利用快速搜索和发现密度峰值聚类方法对数据集进行聚类并根据式(10)计算数据点的局部异常值。最后,将全局异常值与局部异常值进行相乘获取数据点的异常得分,选取异常值最高的Top-n个数据点作为离群点,数据形状及离群点分布如图 14所示。

|
图 14 二维人工数据集 Fig. 14 Two-dimensional artificial datasets |
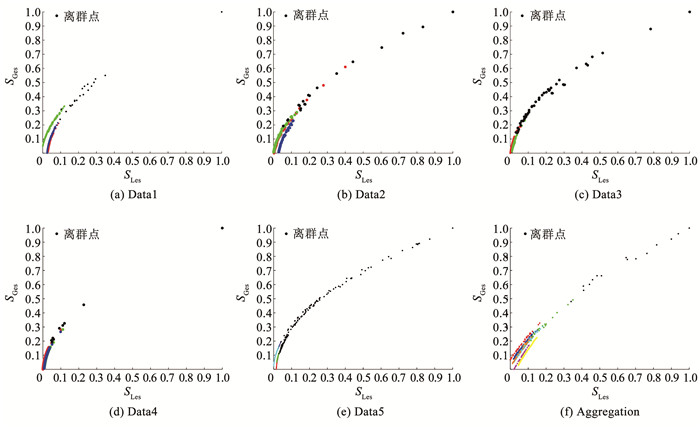
利用全局异常值和局部异常值构建决策图,对数据点的种类进行解释,如图 15所示。位于决策图的左下部分密集的数据点可视为正常数据点;靠中间部分的数据点较为分散,这些数据点可视为局部离群点;在右上角的数据点,全局异常值与局部异常值均为最大,该类型的数据点可视为全局离群点。
|
图 15 决策图 Fig. 15 Decision graph |
关于离群点检测指标,用准确率(Precise)、召回率(Recall)、F1以及AUC值(ROC曲线下降面积)[31-32]来评估该算法的离群点检测性能,即:
| $ P=\frac{T_P}{T_P+F_P} $ | (30) |
| $ R=\frac{T_P}{T_P+F_N} $ | (31) |
| $ F_1=\frac{2 \times P \times R}{P+R} $ | (32) |
式中:TP为算法检测到真实的离群点数量,FP为算法把正常数据错分成离群点的数量,FN为把离群点识别成正常数据点的数量,TN为把正常数据点识别为正常数据点的数量。Precise、Recall、AUC以及F1的取值范围为[0, 1],数值越大离群点检测性能越好。
关于阈值的选择,在人工数据集中选取最终异常值得分最高的Top-n个数据点作为离群点。检测指标见表 3。为了将本文算法与其他离群点检测方法进行对比,表 4中包括10种常见的离群点检测方法。接着,通过计算各个方法的AUC值来对比离群点检测性能,见表 5。
| 表 3 离群点检测的性能指标 Tab. 3 Performance indicators of outlier detection |
| 表 4 比较方法 Tab. 4 Comparison methods |
| 表 5 不同离群点检测方法的AUC值 Tab. 5 AUC values of different outlier detection methods |
通过表 5得到的AUC值,得出以下结论:
1) 通过Data1~Data4可知,离群点检测方法均不错。但由于聚类算法对数据集形状的要求较为苛刻,所以任意形状的数据集(Data3、Data4)会导致CBLOF和FCM的离群点检测性能下降。
2) Data5数据集中存在明显的不平衡情况,且存在离群聚类的情况。在此情况下,KDPC方法优于其他离群点检测方法。
3) Aggregation也存在不平衡的情况,因此FCM的离群点检测性能受到影响,其他离群点检测方法都有较好的检测性能。
5.2 UCI数据集本文将用UCI数据集进行离群点检测方法的对比实验,验证KDPC算法的性能,表 6中含有13种数据集。
| 表 6 UCI数据集 Tab. 6 UCI datasets |
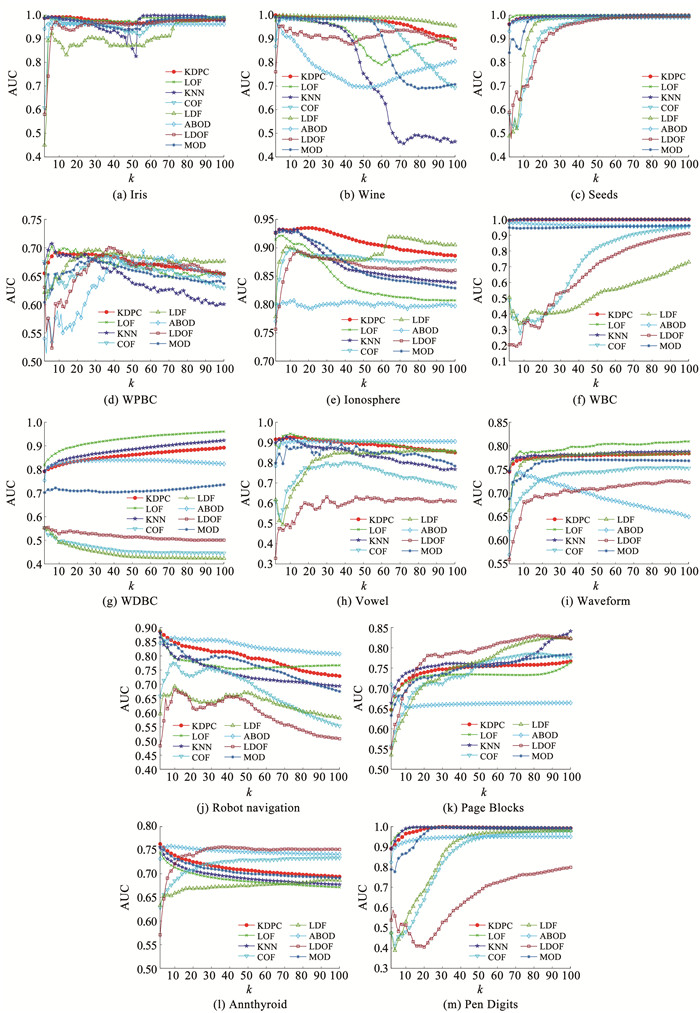
计算各个离群点检测方法的AUC值,结果见表 7。为直观了解不同k下各个离群点检测性能,绘制k= 2~100下各个离群点检测方法的AUC曲线图,如图 16所示。KDPC算法在不同k的离群点检测性能具有稳定性,且在较低的k下,就有较高的离群点检测精度。算法采用MatlabR2020a编写,实验环境为:AMDR7 3.2 GHz CPU, 8.00 GB内存,Windows11操作系统。
| 表 7 UCI数据集的AUC对比 Tab. 7 Comparison of AUC for the UCI dataset |
|
图 16 离群点检测方法在不同k下的AUC值 Fig. 16 AUC values of outlier detection methods at different k values |
从NBA中国官方网站(https://china.nba.cn/statistics/)获取2021―2022年季后赛的50位球员的数据,得到球员的14个方面的信息: 场均得分、场均篮板、场均助攻、出场时间、进攻效率、投篮命中率、三分命中率、罚球命中率、进攻、防守、场均抢断、场均盖帽、失误、犯规。利用这14个方面信息计算球员的全局异常值与局部异常值,并构建决策图,如图 17所示。

|
图 17 NBA球员数据决策图 Fig. 17 NBA player data decision graph |
通过决策图发现,有4个点远离其他大多数球员数据,对这4个数据点进行标号,分别是1号扬尼斯·安特托昆博、3号尼古拉·约基奇、45号约纳斯·瓦兰丘纳斯和37号贾伦·杰克逊,相应的球员及数据见表 8。为方便对比,计算50个球员的平均值。
| 表 8 部分NBA球员数据 Tab. 8 Selected NBA players statistics |
从表 8数据中可以分析:
1) 1号球员最为离群,可视为全局离群点。原因在于他的场均得分、场均篮板、防守、失误都远高于平均值,三分命中率和罚球命中率也低于平均水平。
2) 3号球员可视为全局离群点。他的场均得分、场均篮板、进攻效率、防守、失误都高于平均水平。
3) 45号球员也可视为全局离群点。他离群的主要原因在于有远高于平均水平的场均篮板、进攻和防守,三分命中率也远低于平均水平。
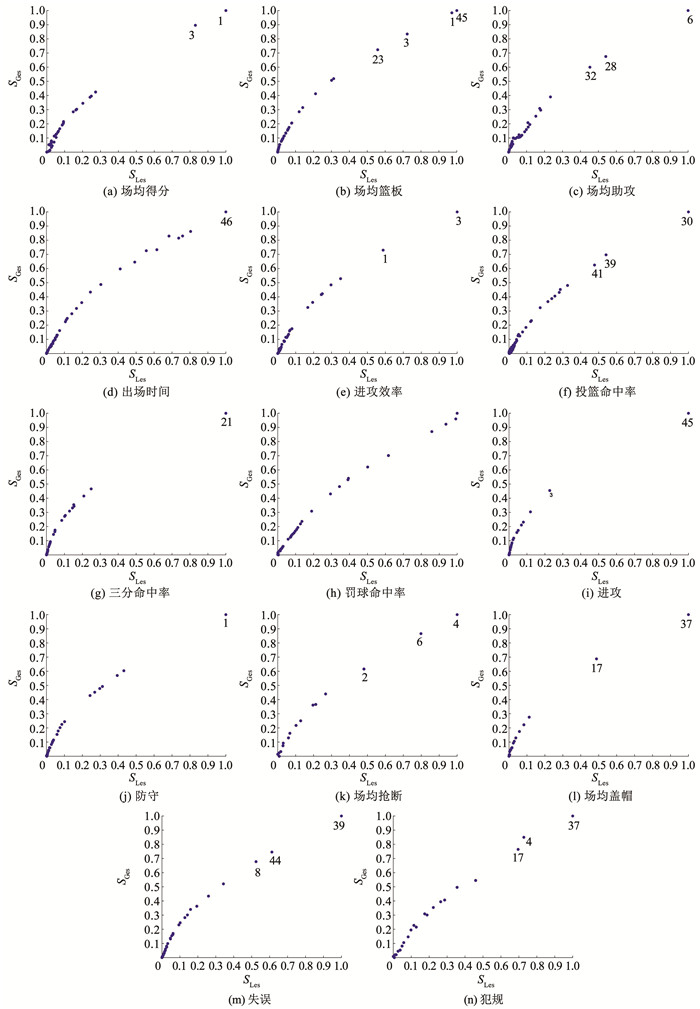
4) 37号球员可视为局部离群点,他能离群的主要原因在于有远低于平均水平的场均助攻,但他的场均盖帽是高于平均水平的。从上述分析可以发现,成为离群点的原因在于有若干方面是明显异于平均值。这些球员有他们的优点,也有他们的短板。然而,NBA球员都是篮球界的精英,从全部属性分析球员,往往不能挖掘全部的信息。接下来本文将从单个属性对每个球员进行分析,找出该方面最具突出的球员,决策图如图 18所示。通过对决策图的观察,分析每个特征属性,找到对应的离群球员见表 9。
|
图 18 单个属性的NBA球员数据决策图 Fig. 18 Decision graph of single attribute in NBA player data |
从表 9数据中可以分析:
| 表 9 每个属性下的离群球员 Tab. 9 Outlier players under each attribute |
1) 场均得分。1号球员扬尼斯·安特托昆博和3号球员尼古拉·约基奇可视为全局离群点,因为他们的场均得分分别为31.7和31.0。
2) 场均篮板。45号球员约纳斯·瓦兰丘纳斯和1号球员扬尼斯·安特托昆博可视为全局离群点,3号球员尼古拉·约基奇和23号球员尼古拉·武切维奇可视为局部离群点。场均篮板分别为:14.3、14.2、13.2和12.4。
3) 场均助攻。6号球员贾·莫兰特可视为全局离群点,28号球员詹姆斯·哈登和32球员克里斯· 保罗可视为局部离群点。场均助攻分别为:9.8、8.6和8.3。
4) 出场时间。46号球员博格丹·博格达诺维奇出场时间为26.7,可视为局部离群点。
5) 进攻效率。3号球员尼古拉·约基奇可视为全局离群点,1号球员扬尼斯·安特托昆博可视为局部离群点,进攻效率分别为:37.8和34.3。
6) 投篮命中率。30号球员德安德烈·艾顿可视为全局离群点,39号球员特雷·杨和41号球员巴姆·阿德巴约可视为局部离群点,投篮命中分别为:64.0%、31.9%和59.4%。
7) 三分命中率。21号球员德马尔·德罗赞视为全局离群点,三分命中率为0%。
8) 罚球命中率。在这一属性中,作为职业球员罚球命中都很出色,没有离群的球员。
9) 进攻。45号球员约纳斯·瓦兰丘纳斯可视为全局离群点,3号球员尼古拉·约基奇可视为局部离群点,进攻分别为:5.5和3.4。
10) 防守。1号球员扬尼斯·安特托昆博视为全局离群点,防守值为12.0。
11) 场均抢断。2号球员卢卡·东契奇、4号球员吉米·巴特勒和6号球员贾·莫兰特可视为局部离群点。场均抢断分别为:1.8、2.1和2.0。
12) 场均盖帽。37号球员贾伦·杰克逊可视为全局离群点,17号球员卡尔·安东尼唐斯可视为局部离群点,场均盖帽为:2.5和2.0。
13) 失误。39号球员特雷·杨可视为全局离群点,8号球员凯文·杜兰特和44号球员克里斯·米德尔顿可视为局部离群点,失误分别为:6.2、5.3和5.5。
14) 犯规。37号球员贾伦·杰克逊可视为全局离群点,4号球员吉米·巴特勒和17号球员卡尔·安东尼唐斯可视为局部离群点,犯规数:4.4、1.5和4.2。
5.4 分析与讨论1) 由于传统DPC聚类算法计算局部密度时没有考虑数据的局部结构,所以当类簇之间具有不同的密度时,DPC无法识别稀疏簇的聚类中心。本文利用k近邻方法和核密度估计方法计算数据点的局部密度,用此代替传统DPC聚类算法中根据截断距离计算的局部密度。该改进方法能提高DPC聚类算法在数据点有不同密度分布中的聚类效果,并提高聚类中心选取的准确度。
2) 基于k近邻和聚类方法得到数据点的全局和局部异常值,并结合全局和局部异常值提高离群点的检测精度。
3) 利用全局和局部异常值构建决策图,通过决策图观察数据点的种类,本文对全局和局部离群点进行解释。
4) 常见的离群点检测方法受k影响较大,本文提出的基于改进DPC聚类算法的离群点检测方法受k影响较小。
6 结论1) 利用k近邻和核密度估计方法计算数据点的局部密度,代替传统DPC聚类算法中根据截断距离计算的局部密度。该改进方法能提高DPC聚类算法在数据点有不同密度分布中的聚类效果,并提高聚类中心选取的准确度。接着,构建局部密度-相对距离决策图选取聚类中心并对数据点进行聚类。
2) 通过k近邻方法计算数据点的全局异常值并计算簇的平均密度与数据点局部密度的比率得到局部异常值。将全局与局部异常值进行乘积得到最终的异常得分,选取异常值得分高的Top-n数据点作为离群点。通过人工数据集和UCI数据集实验发现,通过结合全局和局部异常值的方法能够提高离群点检测精度且受参数k影响较小。
3) 本文提出一种构建全局-局部异常值决策图的离群点解释方法。通过人工数据集和NBA球员数据集的实验发现,全局离群点出现在决策图的右上方,而局部离群点稀疏分布在决策图的中间靠上部分。除此之外,还能观察出每个簇的正常数据点的密度分布情况。在面对未知数据集时,可以通过构建决策图的方式对数据集进行分析。
| [1] |
HAWKINS D M. Identification of outliers[M]. Dordrecht: Springer Netherlands, 1980. DOI:10.1007/978-94-015-3994-4
|
| [2] |
GAO Yongchang, GUAN Haowen, GONG Bin. CODM: an outlier detection method for medical insurance claims fraud[J]. International Journal of Computational Science and Engineering, 2019, 20(3): 404. DOI:10.1504/ijcse.2019.103945 |
| [3] |
HILAL W, GADSDEN S A, YAWNEY J. Financial fraud: a review of anomaly detection techniques and recent advances[J]. Expert Systems with Applications, 2022, 193: 116429. DOI:10.1016/j.eswa.2021.116429 |
| [4] |
ALHARBE N, ALI RAKROUKI M, ALJOHANI A. A healthcare quality assessment model based on outlier detection algorithm[J]. Processes, 2022, 10(6): 1199. DOI:10.3390/pr10061199 |
| [5] |
YANG Yun, FAN Chongjun, CHEN Liang, et al. IPMOD: an efficient outlier detection model for high-dimensional medical data streams[J]. Expert Systems with Applications, 2022, 191: 116212. DOI:10.1016/j.eswa.2021.116212 |
| [6] |
WU Huangjian, TANG Xiao, WANG Zifa, et al. Probabilistic automatic outlier detection for surface air quality measurements from the China national environmental monitoring network[J]. Advances in Atmospheric Sciences, 2018, 35(12): 1522. DOI:10.1007/s00376-018-8067-9 |
| [7] |
KANG S, KYUN KIM S. Outlier behavior detection for indoor environment based on t-SNE clustering[J]. Computers, Materials & Continua, 2021, 68(3): 3725. DOI:10.32604/cmc.2021.016828 |
| [8] |
LLANSÓ L, MOORE U, BOLANO-DIAZ C, et al. Expanding the muscle imaging spectrum in dysferlinopathy: description of an outlier population from the classical MRI pattern[J]. Neuromuscular Disorders, 2023, 33(4): 349. DOI:10.1016/j.nmd.2023.02.007 |
| [9] |
CHEN Zhaomin, YEO C K, LEE B S, et al. Evolutionary multi-objective optimization based ensemble autoencoders for image outlier detection[J]. Neurocomputing, 2018, 309: 192. DOI:10.1016/j.neucom.2018.05.012 |
| [10] |
RIBEIRO M, LAZZARETTI A E, LOPES H S. A study of deep convolutional auto-encoders for anomaly detection in videos[J]. Pattern Recognition Letters, 2018, 105: 13. DOI:10.1016/j.patrec.2017.07.016 |
| [11] |
LI Shifeng, LIU Chunxiao, YANG Yuqiang. Anomaly detection based on maximum a posteriori[J]. Pattern Recognition Letters, 2018, 107: 91. DOI:10.1016/j.patrec.2017.09.001 |
| [12] |
PANG Guansong, SHEN Chunhua, CAO Longbing, et al. Deep learning for anomaly detection: a review[J]. ACM Computing Surveys, 2021, 54(2): 38. DOI:10.1145/3439950 |
| [13] |
VILLA-PÉREZ M E, ÁLVAREZ-CARMONA M Á, LOYOLA-GONZÁLEZ O, et al. Semi-supervised anomaly detection algorithms: a comparative summary and future research directions[J]. Knowledge-based Systems, 2021, 218: 106878. DOI:10.1016/j.knosys.2021.106878 |
| [14] |
ZHANG Ji. Advancements of outlier detection: a survey[J]. ICST Transactions on Scalable Information Systems, 2013, 13(1): e2. DOI:10.4108/trans.sis.2013.01-03.e2 |
| [15] |
周玉, 朱文豪, 房倩, 等. 基于聚类的离群点检测方法研究综述[J]. 计算机工程与应用, 2021, 57(12): 37. ZHOU Yu, ZHU Wenhao, FANG Qian, et al. Survey of outlier detection methods based on clustering[J]. Computer Engineering and Applications, 2021, 57(12): 37. DOI:10.3778/j.issn.1002-8331.2102-0167 |
| [16] |
ZHANG Zhongping, LI Sen, LIU Weixiong, et al. A new outlier detection algorithm based on fast density peak clustering outlier factor[J]. International Journal of Data Warehousing and Mining, 2023, 19(2): 1. DOI:10.4018/ijdwm.316534 |
| [17] |
RAMASWAMY S, RASTOGI R, SHIM K. Efficient algorithms for mining outliers from large data sets[J]. ACM SIGMOD Record, 2000, 29(2): 427. DOI:10.1145/335191.335437 |
| [18] |
ZHANG Ke, HUTTER M, JIN Huidong. A new local distance-based outlier detection approach for scattered real-world data[C]//Pacific-Asia Conference on Knowledge Discovery and Data Mining. Berlin: Springer, 2009: 813. DOI: 10.1007/978-3-642-01307-2_84
|
| [19] |
YANG Jiawei, RAHARDJA S, FRÄNTI P, et al. Mean-shift outlier detection and filtering[J]. Pattern Recognition, 2021, 115: 107874. DOI:10.1016/j.patcog.2021.107874 |
| [20] |
XIE Jiang, XIONG Zhongyang, DAI Qizhu, et al. A local-gravitation-based method for the detection of outliers and boundary points[J]. Knowledge-based Systems, 2020, 192: 105331. DOI:10.1016/j.knosys.2019.105331 |
| [21] |
BREUNIG M M, KRIEGEL H P, NG R T, et al. LOF: identifying density based local outliers[C]//Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data Dallas: ACM, 2000. DOI: 10.1145/342009.335388
|
| [22] |
TANG Jian, CHEN Zhixiang, FU A W C, et al. Enhancing effectiveness of outlier detections for low density patterns[M]//Advances in Knowledge Discovery and Data Mining. Berlin: Springer, 2002: 535. DOI: 10.1007/3-540-47887-6_53
|
| [23] |
LATECKI L J, LAZAREVIC A, POKRAJAC D. Outlier detection with kernel density functions[C]//International Workshop on Machine Learning and Data Mining in Pattern Recognition. Berlin: Springer, 2007: 61. DOI: 10.1007/978-3-540-73499-4_6
|
| [24] |
TANG Bo, HE Haibo. A local density-based approach for outlier detection[J]. Neurocomputing, 2017, 241: 171. DOI:10.1016/j.neucom.2017.02.039 |
| [25] |
张忠平, 刘伟雄, 张玉停, 等. ERDOF: 基于相对熵权密度离群因子的离群点检测算法[J]. 通信学报, 2021, 42(9): 133. ZHANG Zhongping, LIU Weixiong, ZHANG Yuting, et al. ERDOF: outlier detection algorithm based on entropy weight distance and relative density outlier factor[J]. Journal on Communications, 2021, 42(9): 133. DOI:10.11959/j.issn.1000-436x.2021152 |
| [26] |
HE Zengyou, XU Xiaofei, DENG Shengchun. Discovering cluster-based local outliers[J]. Pattern Recognition Letters, 2003, 24(9/10): 1641. DOI:10.1016/S0167-8655(03)00003-5 |
| [27] |
AL-ZOUBI M B, AL-DAHOUD A, YAHYA A A. New outlier detection method based on fuzzy clustering[J]. WSEAS Transactions on Information Science and Applications, 2010, 7(5): 681. |
| [28] |
周玉, 朱文豪, 孙红玉. 一种基于目标函数的局部离群点检测方法[J]. 东北大学学报(自然科学版), 2022, 43(10): 1405. ZHOU Yu, ZHU Wenhao, SUN Hongyu. A local outlier detection method based on objective function[J]. Journal of Northeastern University (Natural Science), 2022, 43(10): 1405. DOI:10.12068/j.issn.1005-3026.2022.10.006 |
| [29] |
张忠平, 李森, 刘伟雄, 等. 基于快速密度峰值聚类离群因子的离群点检测算法[J]. 通信学报, 2022, 43(10): 186. ZHANG Zhongping, LI Sen, LIU Weixiong, et al. Outlier detection algorithm based on fast density peak clustering outlier factor[J]. Journal on Communications, 2022, 43(10): 186. DOI:10.11959/j.issn.1000-436x.2022193 |
| [30] |
RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492. DOI:10.1126/science.1242072 |
| [31] |
DU Xusheng, YU Jiong, CHU Zheng, et al. Graph autoencoder-based unsupervised outlier detection[J]. Information Sciences, 2022, 608: 532. DOI:10.1016/j.ins.2022.06.039 |
| [32] |
LI Kangsheng, GAO Xin, JIA Xin, et al. Detection of local and clustered outliers based on the density-distance decision graph[J]. Engineering Applications of Artificial Intelligence, 2022, 110: 104719. DOI:10.1016/j.engappai.2022.104719 |
| [33] |
KRIEGEL H P, SCHUBERT M, ZIMEK A. Angle-based outlier detection in high-dimensional data[C]//Proceedings of the 14th ACM SIGKDD international conference on Knowledge discovery and data mining. Las Vegas: ACM, 2008: 444. DOI: 10.1145/1401890.1401946
|
| [34] |
LIU F T, TING Kaiming, ZHOU Zhihua. Isolation forest[C]//2008 Eighth IEEE International Conference on Data Mining. Pisa: IEEE, 2008: 413. DOI: 10.1109/ICDM.2008.17
|
 2024, Vol. 56
2024, Vol. 56


