2. 江西省磁悬浮技术重点实验室(江西理工大学),江西 赣州 341000
2. Jiangxi Provincial Key Laboratory of Maglev Technology (Jiangxi University of Science and Technology), Ganzhou 341000, Jiangxi, China
磁悬浮技术由于其独特的悬浮机理,可以大大减少摩擦阻力和机械振动,在交通、航天、工业生产中都有广泛应用[1-4]。绝大部分磁悬浮系统通过恰当的机械与电气解耦可以转换成单点悬浮系统,所以单点悬浮系统的控制问题是磁悬浮系统的关键问题。对此,学者们提出了基于模型控制[5-6]和基于先进算法控制两种思路,但由于模型不准确等因素导致模型控制很难在工程上应用,而先进算法不依赖模型,其适应性更强,如比例积分微分(proportional integral derivative,PID)控制[7-8],滑模控制[9-10],模糊控制[11]等。但目前几种主流算法都存在各自的一些问题,如PID控制结构简单,但抗扰性不足;模糊控制容错能力强,但响应速度不足;滑模控制适应能力强,但稳态始终存在抖震。而自抗扰控制ADRC(active disturbance rejection controller,ADRC)[12]相较于其他算法而言,具有较强的抗扰能力,更适合在悬浮系统中运用。
近年来陆续有学者通过引入自抗扰控制算法提高悬浮控制系统的性能。文献[13]将ADRC应用到磁悬浮系统,实现了列车单点的稳定悬浮。文献[14]针对磁悬浮控制敏感陀螺(magnetically suspended control and sensing gyroscope, MSCSG)转子偏转通道强耦合及航天器姿态测量过程中受扰失稳问题,提出了一种磁悬浮转子偏转解耦抗干扰控制方法。文献[15]提出一种角加速率自适应前馈控制与ADRC相结合的复合控制方法,提高了磁悬浮系统的抗干扰能力。文献[16]提出自抗扰广义预测控制理论,解决悬浮系统轨道不平顺带来的问题。上述文献虽然都是基于ADRC提高悬浮系统的控制性能,但是没有考虑在悬浮系统中,自抗扰的参数整定问题。文献[17]从偏差控制的基本原理出发,提出了一种应用各状态变量与其观测值之间的偏差作为各状态变量的调节依据,提高线性扩张状态观测器的观测精度和收敛速度。文献[18]设计了LMS-ADRC控制器,提出了基于最小均方的控制回路增益估计方法,通过迭代的方式找到LMS(least mean square)滤波器的权重向量,使控制回路增益b0更接近真实值。上述文献虽然对自抗扰结构进行改进以简化关键参数的调节,但扩张状态观测器的观测带宽并没有很好的自调节能力。因此为了适应更加复杂的控制环境,让观测器带宽实现自我调节,本文设计了一种基于观测误差最小化的梯度自适应观测器,能更加及时地获取系统状态信息。仿真和实际测试表明,相较于PID和LADRC,改进后的控制算法具有更强的综合表现和参数适应能力。
1 单点悬浮系统模型单点悬浮控制结构如图 1所示。该系统由固定的F轨道、可上下移动的电磁铁、传感器、信号处理电路、控制器和功率放大器组成。其悬浮原理如下:传感器将悬浮间隙和悬浮电流通过信号处理电路传输给控制器,控制器根据算法产生PWM控制信号,再通过功率放大器驱动电磁铁产生电流,进而产生电磁力,以抵抗物体重力,实现稳定悬浮。

|
图 1 单点悬浮系统控制结构 Fig. 1 Control structure of single-point suspension system |
图 1中c(t)为悬浮间隙、x(t)为悬浮高度、F和mg分别为电磁力和重力、Φ为气隙磁通。为简化建模过程,可进行如下假设[19]:
1) 忽略漏磁的影响,且磁势均匀落在气隙上。
2) 只考虑电磁铁垂直方向的运动。
3) 铁磁截面积A为常值,且等于气隙面积。
为方便理解选择O为参考点,使电磁力增大方向与x增大方向一致。根据虚功原理、基尔霍夫定律和牛顿第二定律可以得到单点悬浮系统的运动模型为:
| $ \left\{\begin{array}{l} m \frac{\mathrm{d}^2 x}{\mathrm{~d} t^2}=F(i, x)-m g+f_{\mathrm{d}} \\ F(i, x)=\frac{\mu_0 N^2 A}{4}\left(\frac{i}{c_{\text {max }}-x}\right)^2 \\ u=R i+\frac{\mu_0 N^2 A}{2\left(c_{\text {max }}-x\right)} \frac{\mathrm{d} i}{\mathrm{~d} t}+\frac{\mu_0 N^2 A i}{2\left(c_{\text {max }}-x\right)^2} \frac{\mathrm{d} x}{\mathrm{~d} t} \end{array}\right. $ | (1) |
模型(1)中的第1个方程描述的是单点悬浮系统的运动过程;第2个方程描述的是电磁力与电流、悬浮间隙的关系;第3个方程描述的是电磁铁运动过程中施加在其上的电压会产生多大的电流。
将模型(1)在平衡点处进行线性化,假设系统的平衡点是(i0, x0),则系统稳定运行时的电流i(t)和高度x(t)是由稳态部分i0、x0和偏离部分Δi、Δx组成,进而可知电磁力满足:
| $ F(i, x)=F\left(i_0, x_0\right)+\Delta F=m g+\Delta F $ | (2) |
对式(2)进行泰勒公式展开,保留一次项忽略高次项可得:
| $ \Delta F=k_i \Delta i+k_x \Delta x $ | (3) |
| $ m \frac{\mathrm{d}^2 \Delta x}{\mathrm{~d} t^2}=k_i \Delta i+k_x \Delta x $ | (4) |
| $ k_i=\frac{\mu_0 N^2 A i_0}{2\left(c_{\text {max }}-x_0\right)^2} $ | (5) |
| $ k_x=\frac{\mu_0 N^2 A i_0^2}{2\left(c_{\max }-x_0\right)^3} $ | (6) |
对等式(4)进行拉氏变换,可得系统的传递函数为
| $ \frac{\Delta x(s)}{\Delta i(s)}=\frac{k_i}{m s^2-k_x} $ | (7) |
本次实验对象物理参数见表 1。
| 表 1 单点悬浮系统参数 Tab. 1 Parameters of single point suspension system |
ADRC是韩京清[12]提出的一种新型实用且不依赖模型的主动抗扰算法,其是基于“利用误差消除误差”进一步发展出来的,展示了一种全新的抗扰范式。Gao[20]通过频率带宽的概念将ADRC线性化得到LADRC。
2.1 线性扩张状态观测器线性扩张观测器可以有效估计系统状态和未知扰动,对于二阶观测器其形式如下:
| $ \left\{\begin{array}{l} e=z_1-y \\ \dot{z}_1=z_2-3 \omega_0 e \\ \dot{z}_2=z_3+b_0 u-3 \omega_0^2 e \\ \dot{z}_3=-\omega_0^3 e \end{array}\right. $ | (8) |
式中:z1、z2分别为系统状态量的估计量,y为系统输出量,u为系统的控制量,ω0为LESO(linear estended state observe)的观测带宽,b0为补偿因子。线性扩张观测器在观测系统状态变量的同时还观测总扰动z3,并且该观测器对系统所需信息已降至最低。
2.2 反馈控制律通过LESO估计出系统状态变量,同时还包括扩张状态变量z3≈f,其中f为系统扰动。
控制器的反馈控制量u0为
| $ u_0=\omega_{\mathrm{c}}^2\left(r-z_1\right)-2 \omega_{\mathrm{c}} z_2 $ | (9) |
式中ωc为控制器带宽。
补偿扰动后的控制量u为
| $ u=u_0-\frac{z_3}{b_0} $ | (10) |
将等式(10)带入原系统,z3与f相消,使整个系统近似为简单的积分串联型系统(11),大大简化了控制难度,尤其是对非线性控制对象。
| $ \left\{\begin{array}{l} \dot{x}_1=x_2 \\ \dot{x}_2=b_0 u_0 \\ y=x_1 \end{array}\right. $ | (11) |
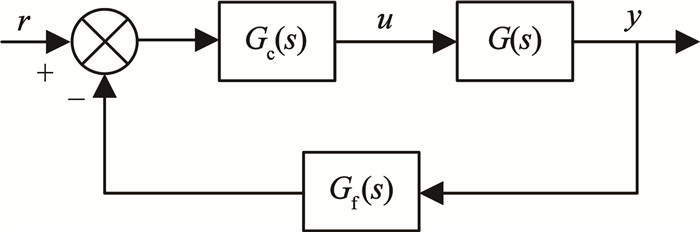
对于LADRC,可以表述为如图 2所示频域结构,图中Gc(s)为直接环路传递函数,Gf(s)为反馈传递函数,G(s)为被控对象传递函数。
|
图 2 LADRC的频域结构 Fig. 2 Frequency domain structure of LADRC |
将式(8)~(10)拉普拉斯变换可得:
| $ \left\{\begin{array}{l} s Z_1=Z_2+3 \omega_0\left(Y-Z_1\right) \\ s Z_2=Z_3+b_0 U+3 \omega_0^2\left(Y-Z_1\right) \\ s Z_3=\omega_0^3\left(Y-Z_1\right) \end{array}\right. $ | (12) |
| $ U=\omega_{\mathrm{c}}^2 R-\omega_{\mathrm{c}}^2 Z_1-2 \omega_{\mathrm{c}} Z_2-Z_3 / b_0 $ | (13) |
式中,Zi为U和Y的函数,可以由U和Y唯一表征:
| $ \left\{\begin{array}{c} Z_1=\frac{b_0 s}{s^3+\beta_1 s^2+\beta_2 s+\beta_3} U+ \\ \frac{\beta_1 s^2+\beta_2 s+\beta_3}{s^3+\beta_1 s^2+\beta_2 s+\beta_3} Y \\ Z_2=\frac{b_0\left(s^2+\beta_1 s\right)}{s^3+\beta_1 s^2+\beta_2 s+\beta_3} U+ \\ \frac{\beta_2 s^2+\beta_3 s}{s^3+\beta_1 s^2+\beta_2 s+\beta_3} Y \\ Z_3=\frac{-b_0 \beta_3}{s^3+\beta_1 s^2+\beta_2 s+\beta_3} U+ \\ \frac{\beta_3 s^2}{s^3+\beta_1 s^2+\beta_2 s+\beta_3} Y \end{array}\right. $ | (14) |
将式(14)带入式(13)可以得出U与R、Y的关系:
| $ \begin{aligned} U= & R \omega_{\mathrm{c}}^2\left(s^3+3 \omega_0 s^2+3 \omega_0^2 s+\omega_0^3\right) / \\ & \left(s^3+\left(3 \omega_0+2 \omega_{\mathrm{c}} b_0\right) s^2+\left(2 \omega_{\mathrm{c}} b_0 3 \omega_0+\right.\right. \\ & \left.\left.3 \omega_0^2+\omega_{\mathrm{c}}^2 b_0\right) s\right)-Y\left(\left(\omega_{\mathrm{c}}^2 3 \omega_0+2 \omega_{\mathrm{c}} 3 \omega_0^2+\right.\right. \\ & \left.\omega_0^3 / b_0\right) s^2+\left(\omega_{\mathrm{c}}^2 3 \omega_0^2+2 \omega_{\mathrm{c}} \omega_0^3\right) s+ \\ & \left.\omega_{\mathrm{c}}^2 \omega_0^3\right) /\left(s^3+\left(3 \omega_0+2 \omega_{\mathrm{c}} b_0\right) s^2+\right. \\ & \left.\left(k_2 b_0 3 \omega_0+3 \omega_0^2+\omega_{\mathrm{c}}^2 b_0\right) s\right) \end{aligned} $ | (15) |
将U改写成图 2的形式:
| $ U=G_{\mathrm{c}}(s) R-G_{\mathrm{c}}(s) G_{\mathrm{f}}(s) Y $ | (16) |
可知Gc(s)直接环路传递函数和Gf(s)反馈传递函数的表达式为:
| $ \begin{aligned} G_{\mathrm{c}}= & \omega_{\mathrm{c}}^2\left(s^3+3 \omega_0 s^2+3 \omega_0^2 s+\omega_0^3\right) / \\ & \left(s^3+\left(3 \omega_0+2 \omega_{\mathrm{c}} b_0\right) s^2+\right. \\ & \left.\left(2 \omega_{\mathrm{c}} b_0 3 \omega_0+3 \omega_0^2+\omega_{\mathrm{c}}^2 b_0\right) s\right) \end{aligned} $ | (17) |
| $ \begin{aligned} G_{\mathrm{f}}= & \left(\left(\omega_{\mathrm{c}}^2 3 \omega_0+2 \omega_{\mathrm{c}} 3 \omega_0^2+\omega_0^3 / b_0\right) s^2+\right. \\ & \left.\left(\omega_{\mathrm{c}}^2 3 \omega_0^2+2 \omega_{\mathrm{c}} \omega_0^3\right) s+\omega_{\mathrm{c}}^2 \omega_0^3\right) / \\ & \omega_{\mathrm{c}}^2\left(s^3+3 \omega_0 s^2+3 \omega_0^2 s+\omega_0^3\right) \end{aligned} $ | (18) |
从式(17)、(18)可以看出,只要b0、ω0和ωc确定,则LADRC的性能就会被唯一确定。
根据式(7)可知,开环系统在右半平面存在一个极点,为二阶不稳定系统,加入二阶LADRC控制环节,并按图 2整理得闭环系统的特征方程为
| $ \begin{aligned} D(s)= & k_i\left(\left(3 \omega_0 \omega_{\mathrm{c}}^2+6 \omega_0^2 \omega_{\mathrm{c}}+\omega_0^3 / b_0\right) s^2+\right. \\ & \left.\left(2 \omega_0^3 \omega_{\mathrm{c}}+3 \omega_0^2 \omega_{\mathrm{c}}^2\right) s+\omega_0^3 \omega_{\mathrm{c}}^2\right)+ \\ & \left(m s^2-k_x\right)\left(s^3+\left(3 \omega_0+2 \omega_{\mathrm{c}} b_0\right) s^2+\right. \\ & \left.\left(6 \omega_0 \omega_{\mathrm{c}} b_0+3 \omega_0^2+\omega_{\mathrm{c}}^2 b_0\right) s\right) \end{aligned} $ | (19) |
根据线性系统稳定理论,D(s)=0的所有根实部小于0时,系统稳定。同时该条件还决定了ω0、ωc、b0满足的约束关系,该约束关系可以看成空间曲面f(ωc, ω0, b0)围成的区域。
| $ \begin{aligned} f\left(\omega_{\mathrm{c}}, \omega_0, b_0\right)= & -\left(( 2 m \omega _ { \mathrm { c } } b _ { 0 } ^ { 2 } + 3 m \omega _ { 0 } b _ { 0 } ) \left(6 k_x b_0^2 \omega_0 \omega_{\mathrm{c}}+k_x b_0^2 \omega_{\mathrm{c}}^2-\right.\right. \\ & \left.\left.2 k_i b_0 \omega_0^3 \omega_{\mathrm{c}}-3 k_i b_0 \omega_0^2 \omega_{\mathrm{c}}^2+3 k_x b_0 \omega_0^2\right)+b_0^2 k_i m \omega_0^3 \omega_{\mathrm{c}}^2\right)^2 \times \\ & \left(2 m \omega_{\mathrm{c}} b_0^2+3 m \omega_0 b_0\right)-\left(\left(2 m \omega_{\mathrm{c}} b_0^2+3 m \omega_0 b_0\right) \times\right. \\ & \left(6 k_x b_0^2 \omega_0 \omega_{\mathrm{c}}+k_x b_0^2 \omega_{\mathrm{c}}^2-2 k_i b_0 \omega_0^3 \omega_{\mathrm{c}}-3 k_i b_0 \omega_0^2 \omega_{\mathrm{c}}^2+\right. \\ & \left.\left.3 k_x b_0 \omega_0^2\right)+b_0^2 k_i m \omega_0^3 \omega_{\mathrm{c}}^2\right) \times\left(\left(2 m \omega_{\mathrm{c}} b_0^2+3 m \omega_0 b_0\right) \times\right. \\ & \left(6 m b_0^2 \omega_0 \omega_{\mathrm{c}}+m b_0^2 \omega_{\mathrm{c}}^2+3 m b_0 \omega_0^2-k_x b_0\right)- \\ & b_0 m\left(-2 k_x b_0^2 \omega_{\mathrm{c}}+6 k_i b_0 \omega_0^2 \omega_{\mathrm{c}}+3 k_i b_0 \omega_0 \omega_{\mathrm{c}}^2-\right. \\ & \left.\left.3 k_x b_0 \omega_0+k_i \omega_0^3\right)\right) \times\left(-2 k_x b_0^2 \omega_{\mathrm{c}}+6 k_i b_0 \omega_0^2 \omega_{\mathrm{c}}+\right. \\ & \left.3 k_i b_0 \omega_0 \omega_{\mathrm{c}}^2-3 k_x b_0 \omega_0+k_i \omega_0^3\right)-b_0 k_i \omega_0^3 \omega_{\mathrm{c}}^2\left(\left(2 m \omega_{\mathrm{c}} b_0^2+\right.\right. \\ & \left.3 m \omega_0 b_0\right) \times\left(6 m b_0^2 \omega_0 \omega_{\mathrm{c}}+m b_0^2 \omega_{\mathrm{c}}^2+3 m b_0 \omega_0^2-k_x b_0\right)- \\ & b_0 m\left(-2 k_x b_0^2 \omega_{\mathrm{c}}+6 k_i b_0 \omega_0^2 \omega_{\mathrm{c}}+3 k_i b_0 \omega_0 \omega_{\mathrm{c}}^2-\right. \\ & \left.\left.3 k_x b_0 \omega_0+k_i \omega_0^3\right)\right)^2 \end{aligned} $ | (20) |
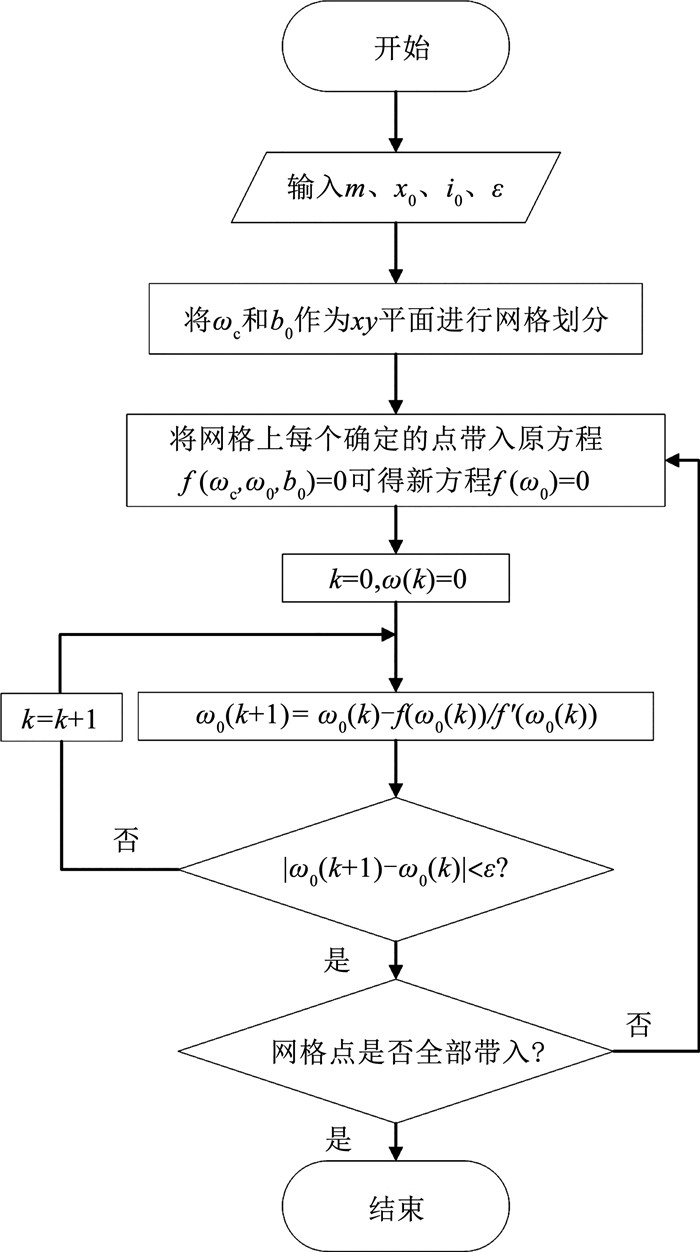
由于该函数难以求其解析解,故采用图 3所示的数值方法求得如图 4阴影曲面围成的稳定域。
|
图 3 稳定域数值解法流程 Fig. 3 Flow chart of numerical solution of stability region |

|
图 4 磁悬浮稳定区域 Fig. 4 Maglev stability region |
扩张观测器的带宽ω0越大,对系统的状态量和未知扰动量估计就越准确,但是大带宽也意味着对系统噪声和动态不确定性也更敏感,而合适的带宽需要花大量时间不断调整,所以有必要让带宽自行整定,以找到当前合适稳定的观测带宽。
定义如下误差:
| $ e=\dot{x}_1-\dot{z}_1=x_2-z_2+3 \omega_0\left(z_1-y\right) $ | (21) |
定义如下目标函数[17]:
| $ J=e^2=\left[x_2-z_2+3 \omega_0\left(z_1-y\right)\right]^2 $ | (22) |
目标函数对ω0求偏导数:
| $ \eta=\frac{\partial J}{\partial \omega_0}=2 e \cdot 3\left(z_1-y\right)=6 e\left(z_1-y\right) $ | (23) |
为了使带宽朝误差减少的方向调整,即J的值越小越好,取负梯度并离散可得ω0的更新规律为
| $ \omega_0(t+1)=\omega_0(t)-\alpha \eta=\omega_0(t)-\alpha e\left(z_1-y\right) $ | (24) |
式中α为学习率。根据稳定域可知,平衡点处的稳定域由f(ωc, ω0, b0)决定,当ωc、b0确定时,f(ωc, ω0, b0)=0的求解问题就变成f(ωc)=0的求根问题,根据图 3的数值方法可求得f(ωc)=0的根ω0*,也即临界稳定带宽,再根据所求ω0*可得临界学习率α的约束公式:
| $ \omega_0-\alpha \sum\limits_{t=0}^{\infty} \eta>\omega_0^* $ | (25) |
进而可得α的取值范围为
| $ \alpha>\frac{\omega_0-\omega_0^*}{\sum\limits_{t=0}^{\infty} \eta} $ | (26) |
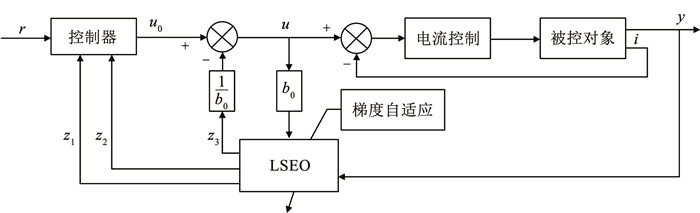
ALADRC算法总结如下:在确定ωc、b0的情况下,求得临界带宽ω0*,初始化LESO带宽ω0和学习率α,并满足式(26),然后根据式(21)计算误差、式(24)更新带宽ω0。实际上为了更快整定α,可以通过临界带宽和系统单位尺度反向推算出α的数量级,加快整定过程。根据表 1的物理参数,ωc=20、b0=10可以算出理想临界带宽ω0*=90.45,又因为该悬浮系统的悬浮高度数量级为10-3,根据式(23)可知η的数量级大致为10-4,为了使带宽能在有限时间内收敛,则α的数量级应该在106。整个单点悬浮系统自适应线性自抗扰控制框图如图 5所示。
|
图 5 ALADRC控制器结构 Fig. 5 ALADRC controller structure |
进行磁悬浮系统仿真,验证ALADRC的有效性,并与LADRC和PID算法作对比。悬浮系统的物理参数见表 1,各算法控制参数见表 2,表 2中h为离散控制周期,Pi、Ii为PI电流内环参数,Kp、Ki和Kd为PID位置外环参数。
| 表 2 仿真控制器参数 Tab. 2 Simulation controller parameter |
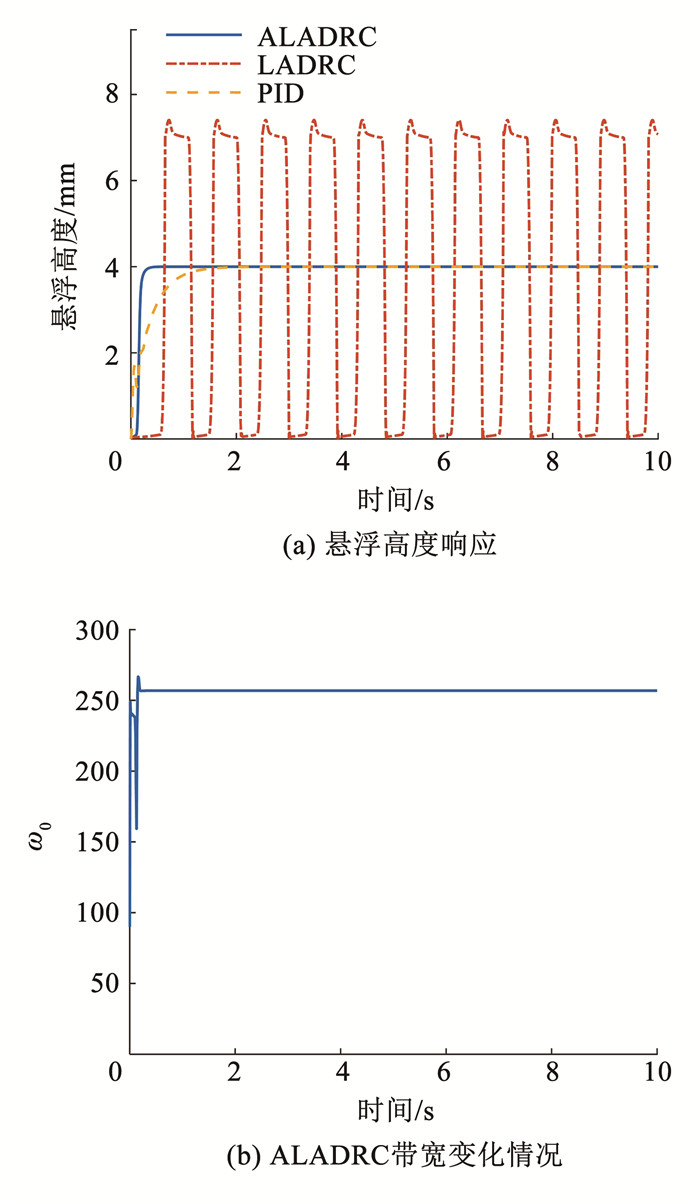
该悬浮系统最高悬浮高度为8 mm,设定悬浮目标值为4 mm,ALADRC的初始观测带宽和LADRC的带宽都是90.00 rad/s,区别在于ALADRC会根据式(24)进行调节,以找到合适的稳定带宽,其他参数不变,仿真结果如图 6所示。
|
图 6 4 mm悬浮实验 Fig. 6 4 mm suspension test |
从图 6(a)中可以看出,当ω0为90.00 rad/s时,小于临界带宽,此时LADRC系统发散,在来回砸击轨道,而ALADRC在初始带宽同样是90.00 rad/s的情况下,可以很好的自我调节到一个稳定带宽如图 6(b)所示,可以保证在参数不理想情况下的系统稳定性,最后在收敛的带宽下系统也表现出了良好控制性能,没有超调,响应速度快,调节时间比PID控制减少76.08%。
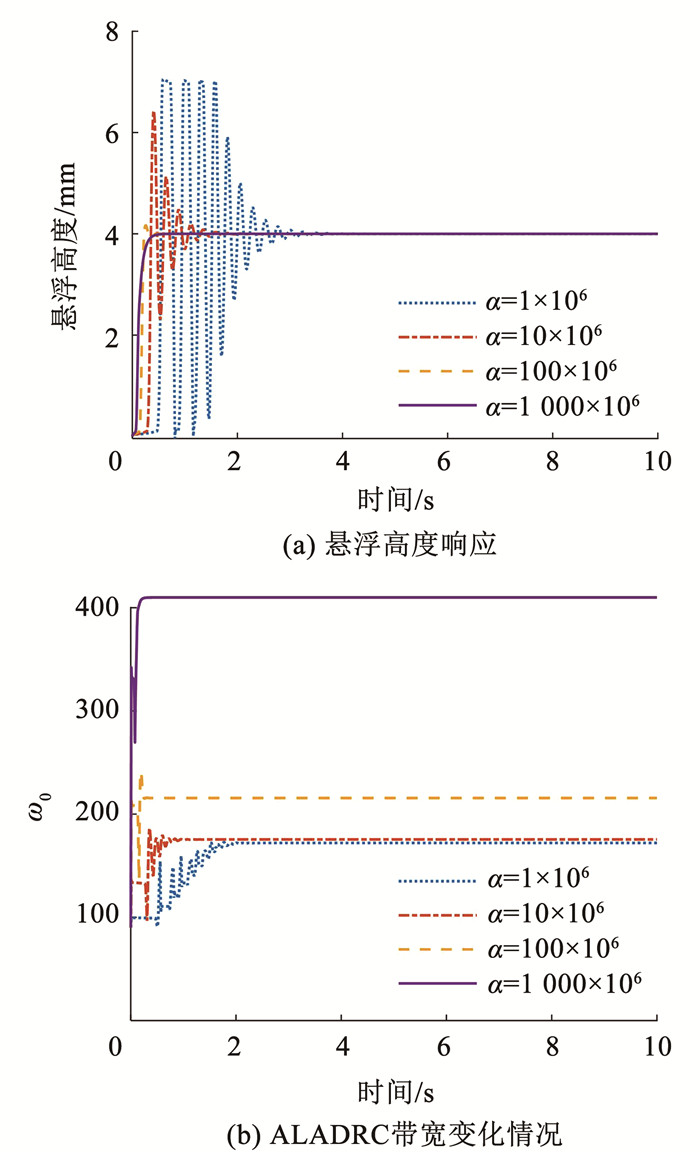
接下来进一步分析不同α对系统影响,根据对自适应扩张观测器的分析可知α的数量级为106,所以进行如下仿真,分别取α=1×106、10×106、100×106和1 000×106,比较不同数量级的学习率对系统带宽收敛和动态性能的影响情况,仿真结果如图 7所示。
|
图 7 不同α下ALADRC的对比情况 Fig. 7 Comparison of ALADRC with different α |
从图 7(a)可以看出,在不稳定初始带宽90.00 rad/s的状态下,所有α都能使系统最终达到稳定状态,且随着α不断增大,系统带宽收敛速度加快,动态响应也变得更好,带宽最终收敛值也变得越大,文献[21]也表明通过分析目标函数J的导数可知,当z1-y收敛至0时,目标函数J有无限多个相对局部最小值,因此不同的学习率会导致ω0最终收敛到不同值,仿真结果表明这些次优解可以使控制器正常工作,因此可以认为ALADRC参数自整定算法是有效的。同时从上述仿真结果也可以看出,α的调节范围非常之广,具有很好调节特性。
4.2 抗扰实验设定悬浮目标值为4 mm,并在5 s时,突加重物1.4 kg,对比PID、LADRC和ALADRC的抗扰效果。PID和ALADRC沿用表 2中的控制参数,而LADRC的带宽选择图 6(b)中ALADRC最终收敛值256.85 rad/s,仿真结果如图 8所示。

|
图 8 抗扰实验 Fig. 8 Immunity experiment |
从图 8(a)可以看出,ALADRC和LADRC的整体表现都要优于PID,且因为LADRC的带宽选择为图 6(b)中ALADRC最终收敛值256.85 rad/s,所以ALADRC和LADRC的初始上升曲线几乎一致,但过度过程ALADRC仍优于LADRC,同时在5 s突加重物时,ALDRC带宽会略微增加,如图 8(b)所示,更大的观测带宽有利于扰动的跟踪,能更加及时补偿掉扰动的影响,所以,ALADRC的抗扰性比LADRC有所增强,综合表现最好。
5 实验分析为了验证仿真结果,搭建了如图 9所示的单点悬浮实验平台。

|
图 9 单点悬浮系统实验平台 Fig. 9 Single point suspension system experiment platform |
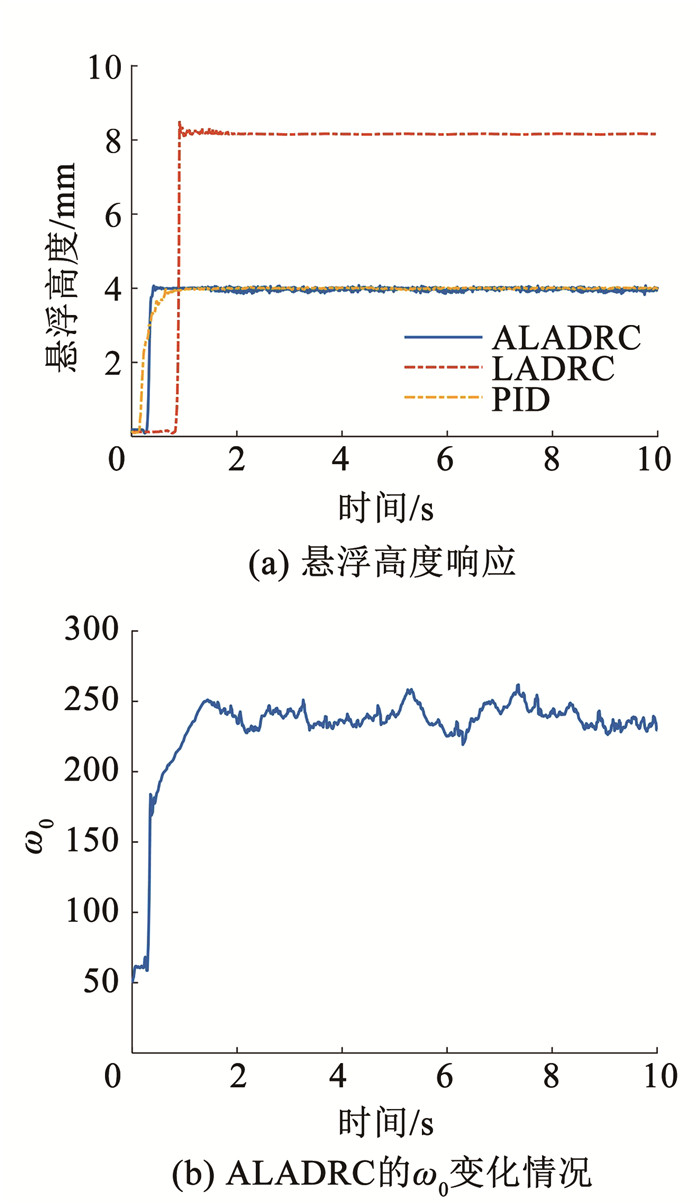
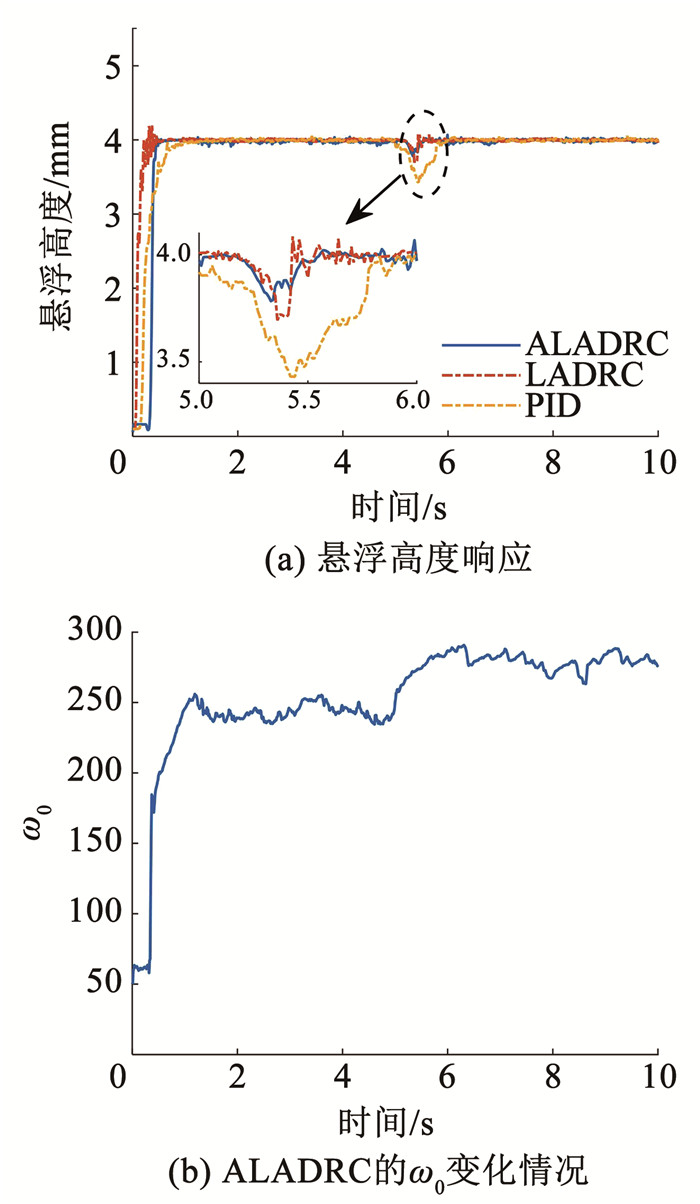
由于实际系统与仿真模型不完全重合,且存在复杂的扰动与噪声干扰,导致实验过程中控制器参数与仿真略有不同,根据实际情况做出了适当调整,新参数见表 3,并在新参数下,分别进行如下两个实验,4 mm稳定悬浮实验和施加1.0 kg扰动实验,其中扰动实验中LADRC的观测带宽为第1个实验中最后ALADRC的收敛带宽值,实验结果如图 10、11所示。
| 表 3 实际控制器参数 Tab. 3 Actual controller parameter |
|
图 10 悬浮实验 Fig. 10 Suspension experiment |
|
图 11 扰动实验 Fig. 11 Disturbance experiment |
实验结果从图 10中可以看出,系统在50.00 rad/s的观测带宽下,LADRC直接吸死在轨道上,而ALADRC可以通过调整带宽将不稳定系统变成稳定系统,带宽值也从50.00 rad/s收敛到平均239.45 rad/s,增强了系统的参数稳定性,使得自抗扰观测带宽的参数自整定变得可行。实验结果从图 11中还可以看出,ALADRC在遇到扰动时也会自动调整带宽,从平均242.76 rad/s的观测带宽变为平均277.86 rad/s,大带宽有利于更快的扰动跟踪,更及时的扰动补偿,ALADRC的扰动超调量比LADRC降低29.33%,比PID降低61.91%。实验结果从图 10、11中可以得出:ALADRC可以将不稳定带宽点自动调节到稳定带宽点,实现快速无超调起浮,使带宽自调节变得可行,而且也进一步增强了系统的抗扰能力。
6 结论1) 通过对LADRC的频域分析,理论推导出单点悬浮系统的自抗扰稳定范围。该方法对其他控制对象的稳定域求解也具有一定参考意义,在后续研究中,还可以考虑更加准确的数学模型和噪声,以确定更加精确的临界带宽。
2) 提出了一种利用梯度信息调整扩张观测器带宽ω0的自适应控制方法,使得自抗扰观测带宽的参数自整定变得可行,加强了系统抗扰能力。
3) 通过实验对比分析可知,ALADRC能快速无超调起浮,在参数整定和抗扰性上比LADRC具有一定优势。在参数整定上,观测带宽ω0不需要刻意调节,系统就能快速收敛到稳定带宽工作点;在抗扰性上,ALADRC在遇到扰动时会自动调节带宽以应对突加的扰动,超调量比LADRC降低了29.33%,比PID降低了61.91%。
| [1] |
TURKER E, ARSLAN-YILDIZ A. Recent advances in magnetic levitation: a biological approach from diagnostics to tissue engineering[J]. ACS Biomaterials Science & Engineering, 2018, 4(3): 787. DOI:10.1021/acsbiomaterials.7b00700 |
| [2] |
SU Xiaojie, YANG Xiaozhan, SHI Peng, et al. Fuzzy control of nonlinear electromagnetic suspension systems[J]. Mechatronics, 2014, 24(4): 328. DOI:10.1016/j.mechatronics.2013.08.002 |
| [3] |
WEI Wei, XUE Wenchao, LI Donghai. On disturbance rejection in magnetic levitation[J]. Control Engineering Practice, 2019, 82: 24. DOI:10.1016/j.conengprac.2018.09.018 |
| [4] |
BOLDEA I, TUTELEA L N, XU Wei, et al. Linear electric machines, drives, and MAGLEVs: an overview[J]. IEEE Transactions on Industrial Electronics, 2018, 65(9): 7504. DOI:10.1109/TIE.2017.2733492 |
| [5] |
吕治国, 龙志强. 磁悬浮球系统的非线性自适应控制方法[J]. 控制工程, 2020, 27(1): 127. LV Zhiguo, LONG Zhiqiang. Method on nonlinear adaptive controller for maglev levitation ball system[J]. Control Engineering of China, 2020, 27(1): 127. DOI:10.14107/j.cnki.kzgc.20180539 |
| [6] |
汤继强, 隗同坤, 宁梦月, 等. 基于反馈线性化的MSCMG转子稳定控制[J]. 北京航空航天大学学报, 2020, 46(6): 1063. TANG Jiqiang, WEI Tongkun, NING Mengyue, et al. Stable control of MSCMG rotor based on feedback linearization[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(6): 1063. DOI:10.13700/j.bh.1001-5965.2019.0401 |
| [7] |
刘丽丽, 左继红. 磁悬浮球系统模糊PID参数自调整控制方法[J]. 控制工程, 2021, 28(2): 354. LIU Lili, ZUO Jihong. Parameter self-adjusting control method of fuzzy PID for magnetic levitation ball system[J]. Control Engineering of China, 2021, 28(2): 354. DOI:10.14107/j.cnki.kzgc.20180583 |
| [8] |
周天豪, 杨智, 祝长生, 等. 电磁轴承高速电机转子系统的内模-PID控制[J]. 电工技术学报, 2020, 35(16): 3414. ZHOU Tianhao, YANG Zhi, ZHU Changsheng, et al. Internal model control-PID control of an active magnetic bearing high-speed motor rotor system[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3414. DOI:10.19595/j.cnki.1000-6753.tces.190852 |
| [9] |
MORAWIEC M, LEWICKI A. Speed observer structure of induction machine based on sliding super-twisting and backstepping techniques[J]. IEEE Transactions on Industrial Informatics, 2021, 17(2): 1122. DOI:10.1109/TⅡ.2020.2974507 |
| [10] |
ZHANG Tianru, XU Zhuang, LI Jing, et al. A third-order super-twisting extended state observer for dynamic performance enhancement of sensorless IPMSM drives[J]. IEEE Transactions on Industrial Electronics, 2020, 67(7): 5948. DOI:10.1109/TIE.2019.2959498 |
| [11] |
董达善, 陈琛, 孙友刚, 等. 非线性磁悬浮系统动力学建模与控制研究[J]. 机械设计与制造, 2019(11): 16. DONG Dashan, CHEN Chen, SUN Yougang, et al. Research on dynamics modeling and control of the nonlinear maglev system[J]. Machinery Design & Manufacture, 2019(11): 16. DOI:10.19356/j.cnki.1001-3997.2019.11.005 |
| [12] |
韩京清. 从PID技术到"自抗扰控制"技术[J]. 控制工程, 2002, 9(3): 13. HAN Jingqing. From PID technique to active disturbances rejection control technique[J]. Control Engineering of China, 2002, 9(3): 13. DOI:10.14107/j.cnki.kzgc.2002.03.003 |
| [13] |
何凌云. 磁悬浮系统的自抗扰控制[D]. 长沙: 国防科学技术大学, 2006 HE Lingyun. Auto-disturbance-rejection control of maglev system[D]. Changsha: National University of Defense Technology, 2006 |
| [14] |
尹增愿, 蔡远文, 任元, 等. 磁悬浮转子状态反馈解耦自抗扰控制方法[J]. 北京航空航天大学学报, 2022, 48(7): 1210. YIN Zengyuan, CAI Yuanwen, REN Yuan, et al. Decoupled active disturbance rejection control method for magnetically suspended rotor based on state feedback[J]. Journal of Beijing University of Aeronautics and Astronautics, 2022, 48(7): 1210. DOI:10.13700/j.bh.1001-5965.2021.0021 |
| [15] |
王舒, 郑世强. 基于复合控制的磁悬浮CMG动框架效应抑制[J]. 北京航空航天大学学报, 2020, 46(12): 2339. WANG Shu, ZHENG Shiqiang. Composite control method for gimbal excitation effect suppression of magnetically suspended CMGs[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(12): 2339. DOI:10.13700/j.bh.1001-5965.2019.0610 |
| [16] |
王金锁, 蒋启龙, 罗雨, 等. 磁悬浮系统自抗扰广义预测控制[J]. 哈尔滨工业大学学报, 2022, 54(9): 141. WANG Jinsuo, JIANG Qilong, LUO Yu, et al. Active disturbance rejection generalized predictive control for magnetic levitation system[J]. Journal of Harbin Institute of Technology, 2022, 54(9): 141. DOI:10.11918/202106088 |
| [17] |
孙佃升, 章跃进. 线性扩张状态观测器的改进及观测精度分析[J]. 国防科技大学学报, 2017, 39(6): 111. SUN Diansheng, ZHANG Yuejin. Improvement and observation accuracy analysis of linear extended state observer[J]. Journal of National University of Defense Technology, 2017, 39(6): 111. DOI:10.11887/j.cn.201706017 |
| [18] |
BAI Changrui, ZHANG Zhou. A least mean square based active disturbance rejection control for an inertially stabilized platform[J]. Optik, 2018, 174: 609. DOI:10.1016/j.ijleo.2018.08.099 |
| [19] |
杨浩. 电磁悬浮系统非线性控制策略的研究[D]. 成都: 西南交通大学, 2021 YANG Hao. Research on nonlinear control strategy of electromagnetic levitation system[D]. Chengdu: Southwest Jiaotong University, 2021 |
| [20] |
GAO Zhiqiang. Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of the 2003 American Control Conference. Denver: IEEE, 2003: 4989. DOI: 10.1109/ACC.2003.1242516
|
| [21] |
JING Anyan, WANG Jiarun, GAO Jian, et al. Self-tuning adaptive active disturbance rejection pitch control of a manta-ray-like underwater glider[J]. Ocean Engineering, 2022, 254: 111364. DOI:10.1016/j.oceaneng.2022.111364 |
 2024, Vol. 56
2024, Vol. 56


