五轴混联机构由串联机构和并联机构组成,同时具备大行程和高刚度的优点[1],然而,其本身结构的复杂性导致了更复杂的运动学映射关系,使其难以应用在对加工精度和效率有高要求的场合[2]。速度规划是提升加工精度与效率的重要手段[3],国内外已开展了大量速度规划方面的研究。
加减速模型法是最常用的速度规划方法,表现为有固定的函数表达式,通过给定关键点(例如间断点、曲率极值点)的运动约束直接计算得到连续的速度曲线,具有计算简单、实时性好的优点,例如梯形、S形、速度前瞻等[4]。该类方法一般用于运动学映射关系为线性的机构,例如Zhao等[5]以平动轴CNC为研究对象,提出考虑加速度连续的梯形速度曲线。Ni等[6]面向XY运动平台,根据路径计算加加速度上、下限并重新排列加减速段,设计了一种改进的S形加减速算法。也有许多学者考虑了多轴机构的非线性因素,例如Luo等[7]从电机运动出发,在传统S形曲线的基础上引入同步比例系数,实现多轴机器人最大速度和加速度的自适应调节。Xiao等[8]提出根据速度变化情况划分区域,利用双向扫描法确定分段点运动情况,生成五轴数控机床的速度前瞻算法。尽管有许多改进的加减速模型方法,但此类方法主要针对末端运动,没有考虑驱动轴的运动约束[9]。
为了将驱动约束加入速度模型,优化模型方法应运而生,该方法需设定一个目标函数,通过不断修改模型参数使目标函数达到极值,但多用于离线规划,难以在线计算,例如时间最优、能量最优等。Zhang等[10]和钟泽杉等[11]考虑驱动轴的运动性能,建立高维度时间最优速度规划模型,最后采用序列二次规划(sequential quadratic programming,SQP)方法求解。Li等[12]以机械臂为研究对象,基于动力学建立了非线性能耗最优模型。Liu等[13]则是基于粒子群算法优化轨迹的时间节点,提出一种同时考虑时间最优与能量最优的速度模型。但高维速度规划模型往往具有非凸性,容易得到局部最优解,特别是面对具有复杂运动学约束的机构时还会导致超出驱动约束[14]。于是有学者考虑模型的降阶方法,例如Zhao等[15]提出从时间最优速度规划模型分离出驱动轴的加加速度约束,再针对拐角处的路径利用加加速度约束再次优化,但此方法在非拐角处忽略了部分约束。杨敏等[16]则是对所有路径采用B样条描述速度函数完成降阶处理,但降阶后的模型是1.5次,依然无法保证模型为凸。针对此问题,Erkorkmaz等[17]提出伪“加加速度”技术进一步将1.5次的模型降为线性模型,该方法仅小幅度牺牲原模型的非线性因素,就可通过线性规划快速稳定地求得全局最优解。然而,优化模型方法需在路径曲线的基础上展开研究,目前较少有学者研究速度模型与路径模型的匹配度,可能导致无法精确在曲率较大点进行速度规划。另外,优化模型方法得到的一般是速度关于路径的函数,为了得到速度关于时间的函数,往往采用泰勒二阶展开进行插补[18],但此方法随着路径的变长会积累截断误差。
本文面向具有复杂运动学约束的五轴混联机构,提出一种准确识别曲率点的时间最优速度规划方法,采用向心法描述路径曲线节点参数,对其作密集化处理生成速度曲线节点参数,配合B样条描述速度与伪加加速度结合的降阶方法[17],将模型变为线性,进而采用线性规划快速收敛到全局最优解。为解决速度-路径函数到速度-时间函数的不准确映射问题,本文提出一种基于速度曲线节点参数的插补方法,通过自适应辛普森积分求解各段路径曲线时间,能够及时消除截断误差并准确得到路程耗时。最后,在一种2P/3-PPR五轴混联机构展开仿真与实验,验证了本文方法的有效性。
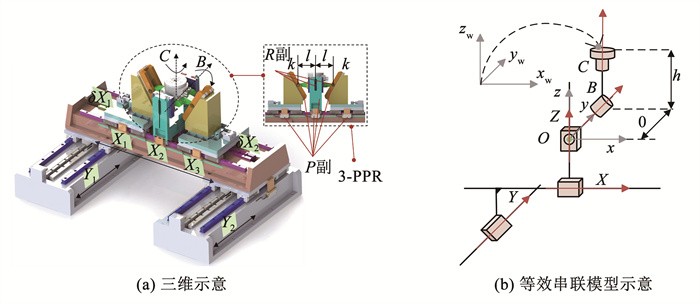
1 运动学及电机运动分析图 1展示了五轴混联机构的三维视图及等效串联机构的运动副示意图。如图 1(a)所示,该混联运动平台包括一个3-PPR并联运动平台,其上方与一个C轴回转平台串联,下方与一个Y轴龙门双驱运动平台串联。该并联机构包括两个具有微驱动器的楔形驱动件、一个U形驱动件、一个X轴导轨与一个末端平台,通过3个驱动件间的配合运动,可实现并联末端动平台X、Z、B三自由度方向的协同运动及微运动。将并联部分的运动等效为X、Z、B运动副后,可视为串联机构,如图 1(b)所示。
|
图 1 2P/3-PPR五轴混联机构示意 Fig. 1 Schematic diagram of 2P/3-PPR five-axis hybrid linked mechanism |
在目前的速度规划工作中,本文将关闭微驱动和双电机驱动,即并联平台只有X1、X2、X3电机驱动,龙门平台只有Y1电机驱动。
1.1 运动学模型分析针对混联机构,应先建立并联部分运动学模型,后将混联整体等效为串联实现运动学建模。此机构的并联部分已由Luo等[19]展开研究,其通过闭环矢量链法建立从X2电机到末端平台中心的3条路,完成并联机构的正逆运动学建模如下:
| $ \left\{\begin{array}{l} X=X_2 \\ B=-\sin ^{-1}\left[\frac{1}{2 l} k\left(2 X_2-X_1-X_3\right)\right] \\ Z=\frac{1}{2} k\left(2 l \cos B-2 l-X_3+X_1\right) \end{array}\right. $ | (1) |
| $ \left\{\begin{array}{l} X_2=X \\ X_1=\frac{Z+l \sin B}{k}+X_2+l-l \cos B \\ X_3=-\frac{Z-l \sin B}{k}+X_2-l+l \cos B \end{array}\right. $ | (2) |
式中:X、B、Z为并联机构中心点在X、B、Z方向上的位移,X1、X2、X3为电机X1、X2、X3的移动量,k为楔形驱动件的斜率,l为楔形驱动件到U形驱动件的杆长。将并联机构的输出当作电机,采用指数积(product of exponentials, POE)方法[20]建立混联整体的运动学模型。POE模型将每一个轴的运动看成是螺旋运动,然后对这些所有轴的螺旋运动相乘,再乘以初始位置即可完成建模。其中,螺旋(又名旋量)用 ξ表示,由两部分组成:ξ=[ω v]T,其中 ω为角速度方向,v为线速度方向。对于移动轴,ω=[0 0 0],v= [vx vy vz],例如图 1(b)中X轴,ξx =[ωx vx]T=[0 0 0 1 0 0]T;对于旋转轴,ω =[ωx ωy ωz],v=-ω×q,q为旋转轴上一点,例如图 1(b)中C轴,ωC=[0 0 1],qC=[0 0 h],ξC=[ωC vC]T=[0 0 1 0 0 0]T。各个轴的螺旋运动见表 1。
| 表 1 五轴等效串联机构的各轴方向及其构成的旋量 Tab. 1 Directions of each axis and motion screw vector in five-axis equivalent serial mechanism |
还需建立末端相对于基坐标系的初始矩阵T(0)∈ R4×4,正运动学可建立如下:
| $ {\boldsymbol{T}} = {{\rm{e}}^{{\xi _y}{\theta _y}}}{{\rm{e}}^{{\xi _x}{\theta _x}}}{{\rm{e}}^{{\xi _z}{\theta _z}}}{{\rm{e}}^{{\xi _B}{\theta _B}}}{{\rm{e}}^{{\xi _C}{\theta _C}}}{\boldsymbol{T}}(0) $ | (3) |
式中:
接着建立逆运动学,需给定末端坐标系下的位置和姿态,反算电机值,可用下式表示:
| $ \boldsymbol{T}(0)\left[\begin{array}{ll} 0 & 0 \\ 0 & 0 \\ 0 & 1 \\ 1 & 0 \end{array}\right]=T\left[\begin{array}{ll} x & v_x \\ y & v_y \\ z & v_z \\ 1 & 0 \end{array}\right] $ | (4) |
式中:[x y z]T为末端坐标系下的位置,[vx vy vz]T为末端坐标系下的法矢。
通过式(4)可得到等效串联模型中各轴的值[X Y Z B C]T,但应注意,法矢[vx vy vz]T到旋转轴[B C]T的映射有两个,应根据轨迹规划的要求选择其中一个,但旋转轴[B C]T到电机值的映射仅有一个。为避免逆运动学模型的多解,首先通过法矢[vx vy vz]T求得旋转轴[B C]T,再通过给定位置和旋转轴 r = [x y z B C]T求得电机值 θ = [X1 X2 X3 Y C]T如下:
| $ \left[\begin{array}{ll} B & C \end{array}\right]=\boldsymbol{F}\left(v_x, v_y, v_z\right) $ | (5) |
| $ \begin{aligned} \boldsymbol{\theta}= & {\left[\begin{array}{lllll} X_1 & X_2 & X_3 & Y & C \end{array}\right]^{\mathrm{T}}=\boldsymbol{G}(\boldsymbol{r})=} \\ & {\left[\begin{array}{lllll} G_1(\boldsymbol{r}) & G_2(\boldsymbol{r}) & G_3(\boldsymbol{r}) & G_4(\boldsymbol{r}) & G_5(\boldsymbol{r}) \end{array}\right]^{\mathrm{T}} } \end{aligned} $ | (6) |
式中:映射关系 F可通过式(4)得到,映射关系 G可通过式(2)与式(4)得到,Gi(r), (i=1, 2, …, 5)为给定末端值 r到各电机的映射关系。
1.2 电机运动状态获取逆运动学是末端位置到电机移动量的映射关系,为进行时间最优速度规划研究,还需获取末端速度、加速度及加加速度到电机速度、加速度、加加速度的映射关系。首先需得到速度雅可比矩阵 J,通过全微分式(6)可获得:
| $ \boldsymbol{J}=\left[\begin{array}{cccc} \frac{\partial G_1}{\partial x} & \frac{\partial G_1}{\partial y} & \cdots & \frac{\partial G_1}{\partial C} \\ \frac{\partial G_2}{\partial x} & \frac{\partial G_2}{\partial y} & \cdots & \frac{\partial G_2}{\partial C} \\ \vdots & \vdots & \cdots & \vdots \\ \frac{\partial G_5}{\partial x} & \frac{\partial G_5}{\partial y} & \cdots & \frac{\partial G_5}{\partial C} \end{array}\right] $ | (7) |
末端速度到电机速度的映射模型可表示为
| $ \boldsymbol{\theta}^{\prime}=\boldsymbol{J} \boldsymbol{r}^{\prime} $ | (8) |
通过对式(8)微分,可进一步获得末端到电机的加速度与加加速度的映射关系为:
| $ \begin{aligned} & \boldsymbol{\theta}^{\prime \prime}=\boldsymbol{J}^{\prime} \boldsymbol{r}^{\prime}+\boldsymbol{J} \boldsymbol{r}^{\prime \prime} \\ & \boldsymbol{\theta}^{\prime \prime \prime}=\boldsymbol{J}^{\prime \prime} \boldsymbol{r}^{\prime}+2 \boldsymbol{J}^{\prime} \boldsymbol{r}^{\prime \prime}+\boldsymbol{J} \boldsymbol{r}^{\prime \prime \prime} \end{aligned} $ | (9) |
式中:
B样条是描述复杂路径的强有力工具,可以光滑连续的对离散点进行插值,其建立路径曲线包括如下步骤[21]:
Step1 根据n+1个路径离散点(即型值点 Q)确定节点参数U;
Step2 确定曲线次数p,由U和p确定节点矢量 U;
Step3 根据U及其对应的B样条基函数 N(u)反算控制点 P。
经过上述步骤后,确定了一个B样条对象的基本参数,可通过下式求出任意节点u对应的B样条函数值C(u)为
| $ \boldsymbol{C}(u)=\sum\limits_{i=0}^n N_{i, p}(u) \boldsymbol{P}_i=\boldsymbol{N}(u) \boldsymbol{P}, 0 \leqslant u \leqslant 1 $ | (10) |
其中:
| $ N_{i, 0}(u)= \begin{cases}1, & u_i \leqslant u \leqslant u_{i+1} \\ 0, & \text { others }\end{cases} $ |
| $ \begin{aligned} N_{i, p}(u)= & \frac{u-u_i}{u_{i+p}-u_i} N_{i, p-1}(u)+ \\ & \frac{u_{i+p+1}-u}{u_{i+p+1}-u_{i+1}} N_{i+1, p-1}(u) \end{aligned} $ |
在B样条对象建立过程的Step1中,主要有均匀法、弦长法以及向心法,其中,向心法能更好识别拐角点以处理曲率频繁变换的曲线,其生成节点参数方法如下:
| $ \left\{\begin{array}{l} \bar{u}_0=0 \\ \bar{u}_n=1 \\ d=\sum\limits_{k=1}^n \sqrt{\left|\boldsymbol{Q}_k-\boldsymbol{Q}_{k-1}\right|} \\ \bar{u}_k=\bar{u}_{k-1}+\frac{\sqrt{\left|\boldsymbol{Q}_k-\boldsymbol{Q}_{k-1}\right|}}{d} \end{array}\right. $ | (11) |
式中,k=1, 2, …, n-1。
由节点参数生成节点矢量方法如下:
| $ \begin{aligned} & u_0=\cdots=u_p=0 \\ & u_{n+1}=\cdots=u_{n+p+1}=1 \\ & u_{j+p}=\frac{1}{p} \sum\limits_{i=1}^{j+p+1} \bar{u}_i \end{aligned} $ | (12) |
式中,j=1, 2, …, n-p。
另外,为便于速度规划模型的建立,应采用弧长参数化方法[22]将路径曲线 C(u)描述为关于弧长s的B样条曲线 C(s),0 ≤ s ≤ L,L为总弧长。相应的,节点参数U与节点向量U应乘以弧长L变为S与S。至此,完成了路径曲线的建立,包括型值点数量n+1、节点参数S、节点矢量S、次数p、弧长L、控制点P。
2.2 时间最优速度规划模型的建立时间最优速度规划以电机约束为条件,时间最小为目标函数,通过数学优化方法求得最优值,可表示为如下数学模型:
| $ \begin{aligned} & \max \int\limits_0^L \dot{s} \mathrm{~d} s \\ & \text { s. t. }: \boldsymbol{v}_{\max } \geqslant|\boldsymbol{v}|, \boldsymbol{a}_{\max } \geqslant|\boldsymbol{a}|, \boldsymbol{j}_{\max } \geqslant|\boldsymbol{j}| \end{aligned} $ | (13) |
式中:
| $ \boldsymbol{\theta}(s)=\left[\begin{array}{lllll} X_1(s) & X_2(s) & X_3(s) & Y(s) & C(s) \end{array}\right]^{\mathrm{T}} $ | (14) |
用f′表示f关于弧长参数s的求导,
| $ \left\{ {\begin{array}{*{20}{l}} {{\boldsymbol{v}} = \frac{{{\rm{d}}{\boldsymbol{\theta}}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}{\boldsymbol{\theta}}}}{{{\rm{d}}s}}\frac{{{\rm{d}}s}}{{{\rm{d}}t}} = {{\boldsymbol{\theta}}^\prime }\mathop s\limits^. }\\ {{\boldsymbol{a}} = \frac{{{{\rm{d}}^2}{\boldsymbol{\theta}}}}{{{\rm{d}}{t^2}}} = \frac{d}{{{\rm{d}}t}}\left( {{{\boldsymbol{\theta}}^\prime }\dot s} \right) = {{\boldsymbol{\theta}}^\prime }^\prime \dot s_{}^2 + {{\boldsymbol{\theta}}^{\prime }}\mathop s\limits^{..} }\\ {{\boldsymbol{j}} = \frac{{{{\rm{d}}^3}{\boldsymbol{\theta}}}}{{{\rm{d}}{t^3}}} = \frac{d}{{{\rm{d}}t}}\left( {{{\boldsymbol{\theta}}^{\prime \prime }}{{\dot s}^2} + {{\boldsymbol{\theta}}^\prime }\mathop s\limits^{..} } \right) = {{\boldsymbol{\theta}}^{\prime \prime \prime }}{{\dot s}^3} + 3{\boldsymbol{\theta}}_{}^{\prime \prime }{\dot s}\mathop s\limits^{..} + {{\boldsymbol{\theta}}^\prime }\mathop s\limits^{...} } \end{array}} \right. $ | (15) |
对式(15)进行降阶处理,令
| $ \left\{\begin{array}{l} \dot{s}=\sqrt{q}, \dot{s}^2=q, \dot{s}^3=q \sqrt{q} \\ \ddot{s}=q^{\prime} / 2, \dddot{s}=q^{\prime \prime} \sqrt{q} / 2, \dot{s}\ddot{s}=q^{\prime} \sqrt{q} / 2 \end{array}\right. $ | (16) |
用含有nv+1个控制点的三次B样条函数描述q,以利用B样条曲线求导后仍是B样条曲线的性质达到降阶目的。建立B样条对象q的节点参数Sv,为了将速度规划模型与路径曲线达到更好的适配性以精准识别拐角点,从而有针对性的建立数学模型,在此不直接采用均匀法设定Sv,而是在路径曲线节点参数S的基础上进一步作密集化处理,取密集化倍数为正整数m,生成Sv的方法如下:
| $ \left\{\begin{array}{l} \bar{s}_{\mathrm{v}, i \times m+j}=\bar{s}_i+\frac{\bar{s}_{i+1}-\bar{s}_i}{m} \times j \\ \bar{s}_{\mathrm{v}, n \times m+0}=\bar{s}_n \end{array}\right. $ | (17) |
式中:i=0, 1, …, n-1, j=0, …, m-1。
按照B样条曲线建立步骤生成 Sv与 Pv,q(s)及其导数可表述如下:
| $ \left\{\begin{array}{l} q(s)=\sum\limits_{i=0}^{n_{\mathrm{v}}} N_{i, 3} P_{\mathrm{v}, i}=\boldsymbol{N}(s) \boldsymbol{P}_{\mathrm{v}} \\ q^{\prime}(s)=\sum\limits_{i=0}^{n_{\mathrm{v}}} N_{i, 3^{\prime}} P_{\mathrm{v}, i}=\boldsymbol{N}^{\prime}(s) \boldsymbol{P}_{\mathrm{v}} \\ q^{\prime \prime}(s)=\sum\limits_{i=0}^{n_{\mathrm{v}}} N_{i, 3^{\prime \prime}} P_{\mathrm{v}, i}=\boldsymbol{N}^{\prime \prime}(s) \boldsymbol{P}_{\mathrm{v}} \end{array}\right. $ | (18) |
因为控制点Pv, i与速度
| $ \begin{aligned} & \max \sum\limits_{i=0}^{n_{\mathrm{v}}} P_{\mathrm{v}, i} \\ & \text { s. t. }: \boldsymbol{v}_{\max } \geqslant|\boldsymbol{v}|, \boldsymbol{a}_{\text {max }} \geqslant|\boldsymbol{a}|, \boldsymbol{j}_{\max } \geqslant|\boldsymbol{j}|, \\ & P_{\mathrm{v}, 0}=0, P_{\mathrm{v}, n_{\mathrm{v}}}=0 \end{aligned} $ | (19) |
式中: Pv, 0= 0,Pv, nv = 0是为了约束首末端点速度为0,将式(16)、(18)依次代入式(15),可得
| $ \left\{\begin{array}{l} \boldsymbol{v}^2=\boldsymbol{\theta}^{\prime 2} \boldsymbol{N}(s) \boldsymbol{P}_{\mathrm{v}} \\ \boldsymbol{a}=\left[\boldsymbol{\theta}^{\prime \prime} \boldsymbol{N}(s)+\frac{1}{2} \boldsymbol{\theta}^{\prime} \boldsymbol{N}^{\prime}(s)\right] \boldsymbol{P}_{\mathrm{v}} \\ \boldsymbol{j}=\sqrt{q^*}\left[\boldsymbol{\theta}^{\prime \prime \prime} \boldsymbol{N}(s)+\frac{3}{2} \boldsymbol{\theta}^{\prime \prime} \boldsymbol{N}^{\prime}(s)+\frac{1}{2} \boldsymbol{\theta}^{\prime} \boldsymbol{N}^{\prime \prime}(s)\right] \boldsymbol{P}_{\mathrm{v}} \end{array}\right. $ | (20) |
式中:θ′、θ ″与 θ″′分别由式(8)、(9)生成; q*为式(20)中,仅由前两行约束优化出的q,作为常量代入加加速度约束中,以此将三阶约束模型转变为关于控制点Pv, i的线性模型;接着,将 Sv中的点逐一代入式(20)表示的约束模型中,使模型离散化;最后采用线性规划方法即可快速得到全局最优解。线性规划描述如下:
| $ \begin{aligned} & \min : \boldsymbol{c}^{\mathrm{T}} \boldsymbol{x} \\ & \text { s. t. }: \boldsymbol{A} \boldsymbol{x} \leqslant \boldsymbol{b} \end{aligned} $ | (21) |
即在 Ax ≤ b的约束下最小化目标函数 cTx。其中,c ∈ R(nv+1)×1为权重向量,在本文中是全为-1的列向量;x ∈ R(nv+1)×1,对应式(20)等式右边的 Pv;A ∈ R5(nv+1)×(nv+1),对应式(20)等式右边除 Pv以外的部分;b ∈ R5(nv+1)×1,对应式(20)等式左边。全部对应后,可调用现有线性规划库求解最优x。
2.3 基于速度曲线节点参数的精准插补方法经过B样条曲线描述及路径曲线建立速度模型求解后,得到的是电机速度、加速度、加加速度关于弧长参数s的曲线,将其转变为关于时间t的曲线,可采用泰勒二阶展开进行插补:
| $ s_{i+1}=s_i+\dot{s}_i T_{\mathrm{s}}+\ddot{s}_i T_{\mathrm{s}}^2 / 2+o\left(T_{\mathrm{s}}^2\right) $ | (22) |
式中: Ts为插补周期,o(Ts2)为Ts2的高阶小量。当路径较长时,高阶小量的叠加会导致较大的累积误差。为能够在插补过程中及时对截断误差进行修正,现以速度规划模型中的节点参数为依据对路径曲线进行分段处理,并在每一小段路径曲线中,构造关于速度的时间积分求解函数,采用自适应辛普森积分法[23]得到最终函数值。其中,所构造积分函数为
| $ F(s)=\int\limits_a^b f(s) \mathrm{d} s=\int\limits_a^b \frac{1}{v} \mathrm{~d} s, v>\varepsilon>0 $ | (23) |
式中: a、b分别为各段路径起始点与终止点;ε为一极小值,用于避免所构造积分函数出现分母为0的情况。辛普森积分法通过二次函数代替原函数,经过推导后得到如下解析式:
| $ S(a, b)=\frac{h}{6}(f(a)+4 f(c)+f(b)) $ | (24) |
式中, c=(a+b)/2。为达到自适应目的,接着将[a, c]和[c, b]作为[a1, b1]和[a2, b2],再次经过式(24)计算, 即
| $ \begin{gathered} S\left(a_1, b_1\right)+S\left(a_2, b_2\right)=\frac{h}{6}\left(f\left(a_1\right)+4 f\left(c_1\right)+\right. \\ \left.f\left(b_1\right)\right)+\frac{h}{6}\left(f\left(a_2\right)+4 f\left(c_2\right)+f\left(b_2\right)\right) \end{gathered} $ | (25) |
如果满足下式:
| $ \frac{1}{15}\left(S\left(a_1, b_1\right)+S\left(a_2, b_2\right)-S(a, b)\right)<\delta $ | (26) |
| $ \left|\int\limits_a^b f(s) \mathrm{d} s-S\left(a_1, b_1\right)-S\left(a_2, b_2\right)\right|<\delta $ | (27) |
此时可认为
| $ \int\limits_a^b f(s) \mathrm{d} s \approx S\left(a_1, b_1\right)+S\left(a_2, b_2\right) $ | (28) |
如果不满足式(26),则需将[a1, b1]和[a2, b2]分别当作新的[a, b]进行一轮计算,直到最后一轮满足式(26)。
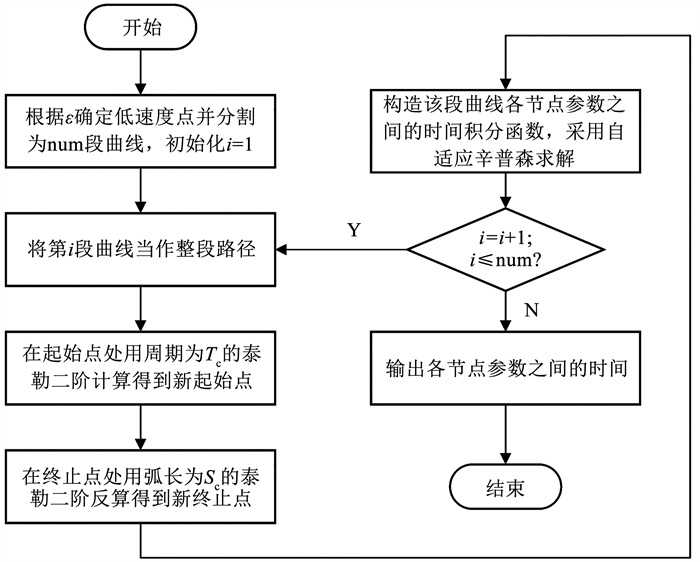
另外,在采用自适应辛普森积分法求解前,首先应根据ε确定低速度点,以此为依据将整段速度曲线分成若干段,在每段起始处根据插补周期用小周期泰勒二阶展开的正运算插补,在终止点处根据弧长用逆运算插补,以避免速度极小值。完整插补流程如图 2所示。
|
图 2 基于速度曲线节点参数的插补流程 Fig. 2 Interpolation procedure based on velocity curve node parameters |
为了验证所提时间最优速度规划方法的有效性,本文采用五维蝴蝶路径用于速度曲线生成。该路径曲率变换频繁且拐角点曲率大,用于非线性和耦合性较强的五轴混联机构时,能够更好地检验速度规划模型的准确性与模型求解的稳定性。
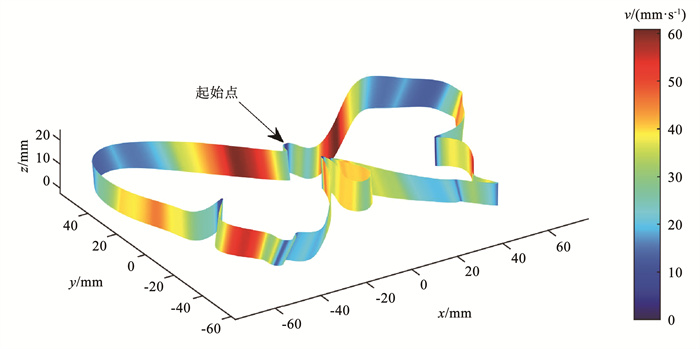
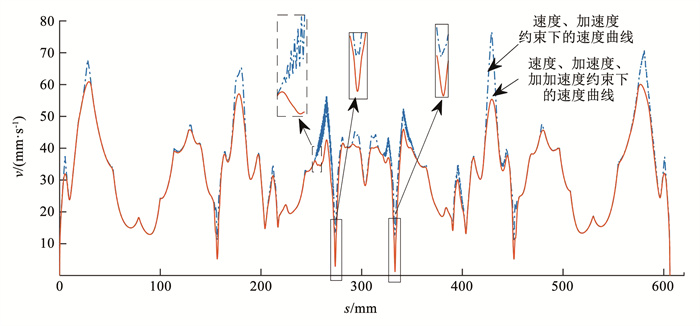
3.1 速度曲线生成设置直线电机的最大运动约束为60, 200, 6 000 mm/s3,旋转电机的最大运动约束为2.2, 8.8, 40.0 rad/s3,取密集化倍数为5,得到速度规划点总数为2 496,取插补参数中的ε、Tc、Sc均为10-4,eps为10-6。按照所提方法先采用向心法对路径曲线进行B样条插值,接着密集化路径曲线节点参数用于速度曲线节点参数,利用B样条描述速度曲线与伪加加速度将高阶速度规划模型降为线性模型,经过线性规划求得全局最优解。在i7 10700F Windows10 Matlab2021a平台计算,整个运行过程耗时3.88 s,得到速度热力图如图 3所示,速度-路径曲线如图 4所示。
|
图 3 速度热力图 Fig. 3 Velocity heatmap |
|
图 4 不同约束条件下的速度-路径曲线图 Fig. 4 Velocity-path curve graph under different constraints |
从图 3可以看出,速度规划模型能够根据路径曲率自适应调整速度,在拐角处速度降低速度值并在曲率较小处提高速度值。其中,在蝴蝶翅膀上半部有较大的角度变化,因此没能将速度提升至最大。在图 4中,由速度、加速度、伪加加速度约束优化出的速度曲线大部分能够贴近由速度、加速度约束优化出的速度曲线,但在曲率变化极大的拐角处,例如蝴蝶尾巴根部,即虚线框处,两种曲线有较大的不一致。这是因为加加速度在大曲率处极易突变,如果没有加加速度约束,将会导致速度曲线急剧震荡。另外,在整段速度-路径曲线中,存在些许速度较低的点,例如实线框处,但其周围点的速度能迅速回升,一定程度上说明了速度规划模型与路径模型的匹配性,能够准确识别曲率较大点并相应地改变速度值。
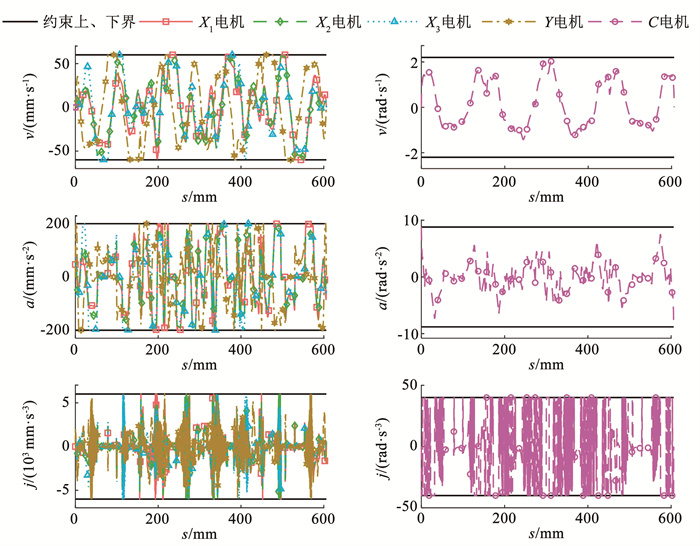
为验证是否超出驱动性能,现给出各个电机速度、加速度、加加速度曲线随路径变化图,如图 5所示,可看出速度规划模型在整段路径曲线中均满足驱动约束。
|
图 5 本文方法下的各电机速度、加速度、加加速度 Fig. 5 Speed, acceleration, and jerk diagrams of each motor under the proposed |
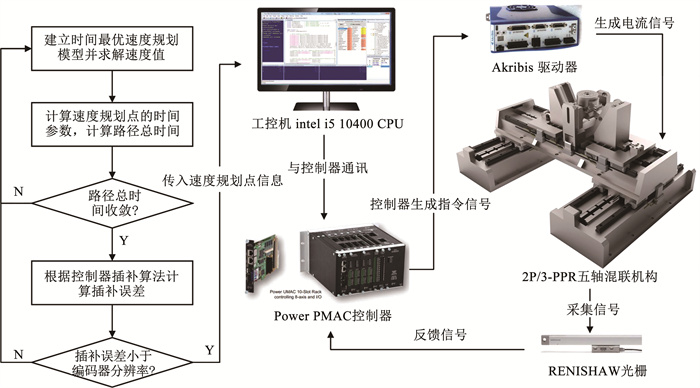
为将速度规划模型结果用于实际物理装置,首先,生成各速度规划点的时间参数并计算路径总时间,当路径总时间收敛到稳定值时,各段时间参数的截断误差得到有效消除,可用于实际加工;然后,检验控制器插补误差是否小于编码器分辨率,小于时, 控制器输出轨迹与期望轨迹等效,否则需增加更多的离散点或重新建立速度规划模型;最后,通过工控机输入轨迹参数,与控制器通讯,由控制器传输信号给驱动器进行电机运动,并根据光栅尺反馈回路及时修正跟踪误差。实验过程及装置如图 6所示。
|
图 6 实验过程的展示与实验装置 Fig. 6 Display of experimental process and experimental device diagram |
实验相关装置的技术参数见表 2。
| 表 2 硬件设备参数 Tab. 2 Hardware device parameter |
经过速度规划模型求解后,已得到速度关于路径的函数,为得到速度关于时间的函数,采用所提构造时间积分函数的方法求解各段路径的时间及总时间。同时,为对比泰勒二阶插补方法,作如下实验:按照总数为1 000对10-12~10-3进行线性插值,作为自适应辛普森积分法中的精度eps(一般取10-6),计算每种eps下对应的计算耗时和路程时间;按照总数为1 000对10-4~10-2进行线性插值,作为泰勒二阶展开的插补周期Ts(一般取10-3),计算每种Ts下对应的计算耗时和路径总时间。得到两种方法结果如图 7所示。
|
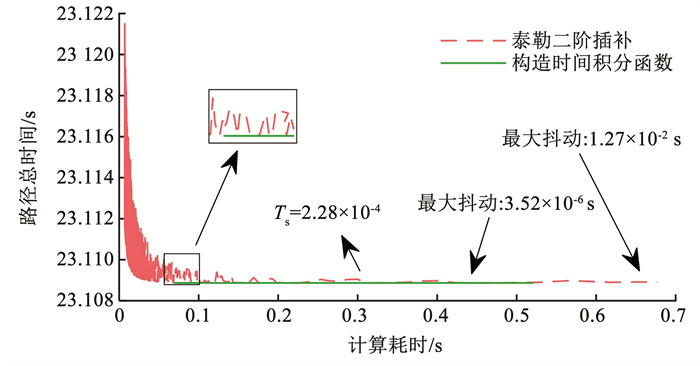
图 7 本文方法与泰勒二阶插补方法计算的路径总时间趋势图 Fig. 7 Trend of total time calculated for proposed method and Taylor's second-order method |
从图 7可看出,泰勒二阶插补方法受插补周期Ts的影响较大,当Ts为2.28×10-4 s后才能达到稳定求解精度,此时计算耗时0.29 s。而构造时间积分函数的方法一直保持稳定求解精度,且计算耗时更小,仅0.10 s内可稳定。为进一步说明此方法的优越性,以低速、中速、高速的运动约束作为不同的工况(见表 3),计算对应的路径总时间,查看波动情况,得到结果见表 4。
| 表 3 不同工况下的电机运动约束 Tab. 3 Motor motion constraints under different working conditions |
| 表 4 本文方法与泰勒二阶方法在不同工况下计算的路径总时间 Tab. 4 Total path time calculated by proposed method and Taylor's second-order method under different working conditions |
从收敛值看,两种算法均能收敛到相同精度,但收敛代价是不一样的:泰勒二阶插补方法在低速、中速、高速的收敛耗时均比本文方法要长,而且受速度影响较大,当速度较小时,插补后的步长也较小,导致步长总量增加,计算耗时更长。相反,自适应辛普森积分法通过二次曲线近似求解,无论速度大小,都不影响其每小段曲线的积分求解函数。另外,从收敛前的最大抖动可以看出,本文方法在不同工况下的表现均优于泰勒二阶插补方法,具备更好的鲁棒性。
综上所述,构造时间积分函数相比泰勒二阶插补方法具备更高的鲁棒性与效率。
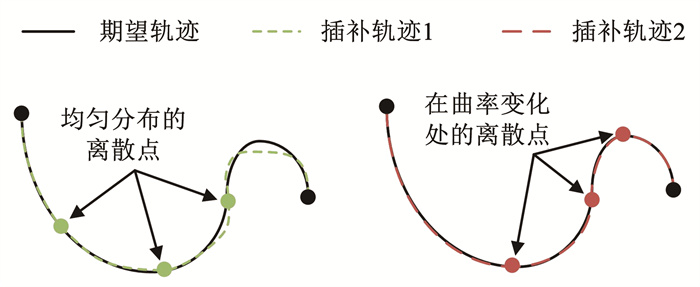
3.2.2 插补误差分析经过生成速度规划点的时间参数及路径总时间求解后,可以得到2 496个离散点的完整信息,还需经过控制器的精插补用于电机连续运动。此时,插补点已脱离速度规划模型的控制,完全由控制器插补算法和给定离散点决定,因此存在插补误差。插补误差即插补轨迹与期望轨迹的偏差,当控制器插补算法确定后,给定的离散点越处于曲率变化处,越具有代表性,插补后的轨迹就越符合期望轨迹。如图 8所示,在一段具有连续拐角的期望轨迹中,由均匀分布离散点插补的轨迹有较大偏差,由曲率变化处离散点插补的轨迹有较小偏差。另外,一般要求插补误差小于编码器分辨率,此时可将插补出的轨迹等效为期望轨迹。
|
图 8 不同离散点的插补误差示意 Fig. 8 Schematic diagram of interpolation errors at different discrete points |
为验证所提速度规划模型识别曲率特征的准确性,以均匀节点参数法为对比,经过速度规划模型求解后,将所得结果与本文所提方法的结果共同输入到控制器的pvt函数(即在这个时间点t以速度v到达位置p)中,其通过三次多项式插补离散点,最后绘制各电机插补误差如图 9所示。
|
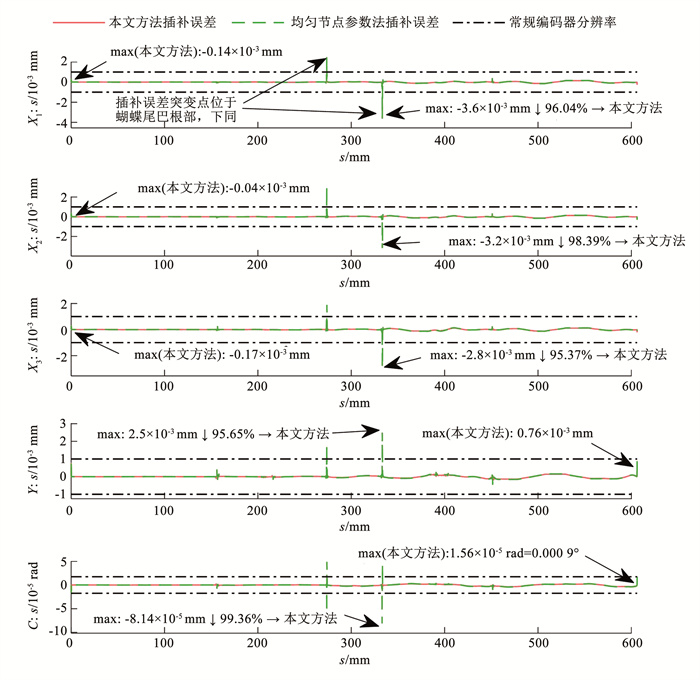
图 9 均匀节点参数法与本文方法的各电机插补误差 Fig. 9 Interpolation errors of each motor between uniform node parameter method and proposed method |
从图 9可看出,本文方法的插补误差一直保持稳定状态,低于常规编码器的分辨率1 μm与0.001°,如果想得到更高的插补精度,可以进一步增加离散点数目或用更高次的插补算法,但需结合计算成本考虑。而均匀节点参数法存在些许跳动,特别是在蝴蝶尾巴根部这种拐角变化接近180°的路径,存在剧烈跳动现象,插补误差明显高于常规编码器的分辨率。这是因为离散点没有精确落在曲率变化点,插补点与期望轨迹偏差较大。
同生成速度规划点的时间参数及路径总时间一致,以不同的电机运动限制作为不同的工况,计算对应的插补误差,由于涉及到高速与高加速,速度曲线更复杂,且变化更频繁,因此采用更高次的pvat函数(即在这个时间点t以速度v和加速度a到达位置p)作为控制器插补算法,其通过五次多项式插补离散点,得到结果见表 5。
| 表 5 本文方法与均匀节点参数法在不同工况下的插补误差 Tab. 5 Interpolation errors between proposed method and uniform node parameter method under different working conditions |
从表 5可知,无论是插补误差最大值还是均方根值,本文方法在不同工况下的插补误差均小于均匀节点参数法,能够更好识别拐角点。因此,在路径曲线基础上生成的速度节点参数更符合路径特征,具备更好的曲率识别性。
3.2.3 平台运动整合离散点路径、速度与时间信息,将其作为输入传入控制卡的pvt运动函数,选择采样周期为4.426 7×10-4 s,记录各电机跟踪情况,绘制跟踪效果如图 10所示。
|
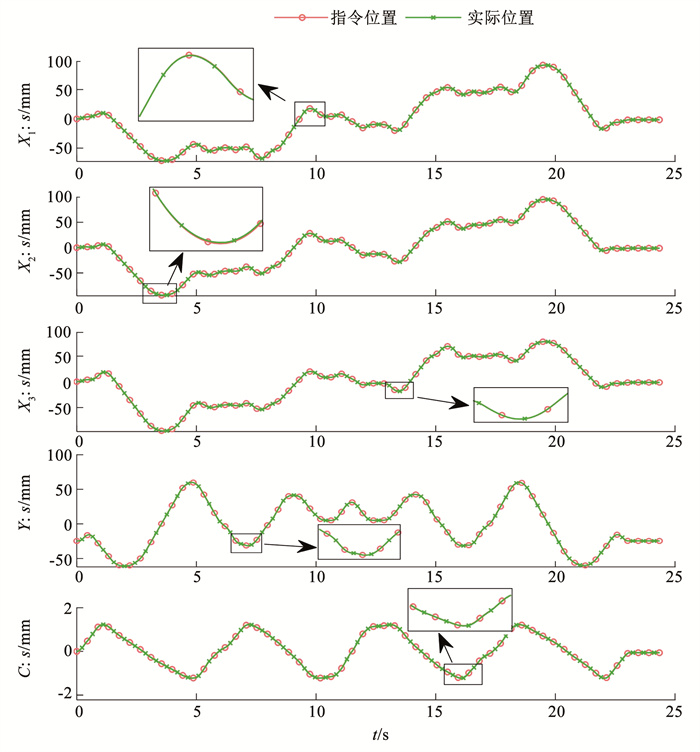
图 10 各电机位置跟踪效果 Fig. 10 Position tracking performance of each motor |
从图 10中指令位置可看出各电机路径曲线光滑、无突变。从实际位置和指令位置的贴合程度可知各电机的跟踪误差较小,电机实际运行情况与理论情况符合,验证了本文方法能在满足驱动约束的条件下生成平滑无波动的运动轨迹。
4 结论1) 建立了一种五轴混联机构末端运动到电机运动的映射模型,通过POE法建立位置映射,在此基础上通过矩阵微分法建立速度、加速度与加加速度映射,使得驱动约束模型具有连续性与可导性,为后续速度规划工作奠定基础。
2) 提出采用向心法描述路径曲线节点参数,将其作密集化处理进一步用于速度模型节点的方法,保证了路径模型与速度模型的匹配性以及速度曲线识别曲率变化点的精确性。
3) 提出一种构造各段路径时间积分函数以求取路径总时间的方法,相比泰勒二阶插补方法具备更高的鲁棒性与精度,保证了速度-路径函数向速度-时间函数的准确映射。
| [1] |
KUMAR S, VON SZADKOWSKI K A, MUELLER A, et al. An analytical and modular software workbench for solving kinematics and dynamics of series-parallel hybrid robots[J]. Journal of Mechanisms and Robotics, 2020, 12(2): 021114. DOI:10.1115/1.4045941 |
| [2] |
ALAMDAR A, SAMANDI P, HANIFEH S, et al. Investigation of a hybrid kinematic calibration method for the "sina" surgical robot[J]. IEEE Robotics and Automation Letters, 2020, 5(4): 5276. DOI:10.1109/LRA.2020.3007466 |
| [3] |
李建刚, 吴响亮, 李泽湘, 等. 连续加工路径的进给速度规划算法研究[J]. 哈尔滨工业大学学报, 2009, 41(3): 29. LI Jiangang, WU Xiangliang, LI Zexiang, et al. A blended feedrate planning algorithm for continuous tool path[J]. Journal of Harbin Institute of Technology, 2009, 41(3): 29. DOI:10.3321/j.issn:0367-6234.2009.03.008 |
| [4] |
马鸿宇, 申立勇, 姜鑫, 等. 数控加工中路径规划与速度插补综述[J]. 图学学报, 2022, 43(6): 967. MA Hongyu, SHEN Liyong, JIANG Xin, et al. A survey of path planning and feedrate interpolation in computer numerical control[J]. Journal of Graphics, 2022, 43(6): 967. DOI:10.11996/JG.j.2095-302X.2022060967 |
| [5] |
ZHAO Guoyong, ZHAO Yugang, WANG Shijun. The acceleration/deceleration control algorithm based on trapezoid-curve jerk in CNC machining[J]. Research Journal of Applied Sciences, Engineering and Technology, 2013, 5: 1639. DOI:10.19026/RJASET.5.4917 |
| [6] |
NI Hepeng, JI Shuai, LIU Yanan, et al. Velocity planning method for position-velocity-time control based on a modified S-shaped acceleration/deceleration algorithm[J]. International Journal of Advanced Robotic Systems, 2022, 19(1): 172988142110724. DOI:10.1177/17298814211072418 |
| [7] |
LUO Zhaojiang, WANG Changkai, LEI Junsong, et al. A new S-curve acceleration/deceleration control considering displacement conditions[C]//2023 26th International Conference on Electrical Machines and Systems (ICEMS). Zhuhai: IEEE, 2023: 4065. DOI: 10.1109/ICEMS59686.2023.10345321
|
| [8] |
Xiao Jianxin, Zhang Hui, Li Bingran. A dual NURBS curve five-axis interpolator with interval division under axial kinematic constraints[J]. IEEE/ASME Transactions on Mechatronics, 2024, 29(2): 1170. DOI:10.1109/TMECH.2023.3295369 |
| [9] |
SUN Yuwen, JIA Jinjie, XU Jinting, et al. Path, feedrate and trajectory planning for free-form surface machining: a state-of-the-art review[J]. Chinese Journal of Aeronautics, 2022, 35(8): 12. DOI:10.1016/j.cja.2021.06.011 |
| [10] |
ZHANG Yunyue, SUN Zhiyi, SUN Qianlai, et al. Time-jerk optimal trajectory planning of hydraulic robotic excavator[J]. Advances in Mechanical Engineering, 2021, 13(7): 168781402110346. DOI:10.1177/16878140211034611 |
| [11] |
钟泽杉, 杨敏, 赵现朝, 等. 轴空间多约束下的五轴B样条路径速度规划[J]. 计算机集成制造系统, 2021, 27(1): 137. ZHONG Zeshan, YANG Min, ZHAO Xianchao, et al. B-spline path velocity planning considering multi-constraints in axis space for five-axis machine tool[J]. Computer Integrated Manufacturing Systems, 2021, 27(1): 137. DOI:10.13196/j.cims.2021.01.012 |
| [12] |
LI Yumeng, WANG Zhengdao, YANG Hui, et al. Energy-optimal planning of robot trajectory based on dynamics[J]. Arabian Journal for Science and Engineering, 2023, 48(3): 3523. DOI:10.1007/s13369-022-07185-7 |
| [13] |
LIU Xuemei, QIU Chengrong, ZENG Qingfei, et al. Time-energy optimal trajectory planning for collaborative welding robot with multiple manipulators[J]. Procedia Manufacturing, 2020, 43: 527. DOI:10.1016/j.promfg.2020.02.174 |
| [14] |
ZHANG Guixin, GAO Jian, ZHANG Lanyu, et al. Generalised NURBS interpolator with nonlinear feedrate scheduling and interpolation error compensation[J]. International Journal of Machine Tools and Manufacture, 2022, 183: 103956. DOI:10.1016/j.ijmachtools.2022.103956 |
| [15] |
ZHAO Kai, LI Shurong, KANG Zhongjian. Smooth minimum time trajectory planning with minimal feed fluctuation[J]. The International Journal of Advanced Manufacturing Technology, 2019, 105(1): 1099. DOI:10.1007/s00170-019-04308-7 |
| [16] |
杨敏, 赵现朝, 钟泽杉, 等. 复杂约束下的五轴数控系统自适应速度规划[J]. 机械工程学报, 2020, 56(11): 161. YANG Min, ZHAO Xianchao, ZHONG Zeshan, et al. Adaptive velocity planning under complex constraints for 5-axis CNC systems[J]. Journal of Mechanical Engineering, 2020, 56(11): 161. DOI:10.3901/JME.2020.11.161 |
| [17] |
ERKORKMAZ K, CHEN Qingge, ZHAO Mingyong, et al. Linear programming and windowing based feedrate optimization for spline toolpaths[J]. CIRP Annals, 2017, 66(1): 393. DOI:10.1016/j.cirp.2017.04.058 |
| [18] |
LI Guangxi, LIU Haitao, YUE Wei, et al. Feedrate scheduling of a five-axis hybrid robot for milling considering drive constraints[J]. The International Journal of Advanced Manufacturing Technology, 2021, 112(11): 3117. DOI:10.1007/s00170-020-06559-1 |
| [19] |
LUO Yuheng, GAO Jian, ZHANG Lanyu, et al. Kinematic calibration of a symmetric parallel kinematic machine using sensitivity-based iterative planning[J]. Precision Engineering, 2022, 77: 164. DOI:10.1016/j.precisioneng.2022.05.007 |
| [20] |
OKAMURA K, PARK F C. Kinematic calibration using the product of exponentials formula[J]. Robotica, 1996, 14(4): 415. DOI:10.1017/s0263574700019810 |
| [21] |
WAN Min, LIU Yang, XING Wanjing, et al. Singularity avoidance for five-axis machine tools through introducing geometrical constraints[J]. International Journal of Machine Tools and Manufacture, 2018, 127: 1. DOI:10.1016/j.ijmachtools.2017.12.006 |
| [22] |
CHEN Zezhong, KHAN M A. A new approach to generating arc length parameterized NURBS tool paths for efficient three-axis machining of smooth, accurate sculptured surfaces[J]. The International Journal of Advanced Manufacturing Technology, 2014, 70(5): 1355. DOI:10.1007/s00170-013-5411-1 |
| [23] |
LEI W T, SUNG M P, LIN L Y, et al. Fast real-time NURBS path interpolation for CNC machine tools[J]. International Journal of Machine Tools and Manufacture, 2007, 47(10): 1530. DOI:10.1016/j.ijmachtools.2006.11.011 |
 2024, Vol. 56
2024, Vol. 56


