引信是弹药的重要组成部分,引信安全系统的状态转换为弹药的安全性和可靠性提供了重要保障。目前,研究主要集中在实现从安全状态到待发状态的转换,而较少研究怎样将待发状态转换回安全状态。随着弹药的毁伤能力增强,对其安全性的要求也越来越高。因此,需要引信安全系统具备恢复能力,以保证弹药的安全性。
2004年涂诗美等[1]较早提出采用一体化设计的安全状态可恢复式电子式安全系统, 该引信的保险具有可逆性。2009年,尚雅玲等[2]利用步进电机带动隔爆件往复运动,从而实现引信安全系统的解除保险和恢复保险。由于步进电机尺寸较大,导致引信安全系统所占用空间较大,因此该设计方案不适用于尺寸较小的弹药中。2017年,付前卫等[3]基于双振子直线超声电机设计了安全状态可恢复的一体化引信隔爆机构。该设计方案采用的电机具有定子、动子以及夹持结构,整个隔爆机构的体积较大,不满足引信微型化的需求。
由于电机抗干扰能力较差,且体积较大,如若用于引信中,无法满足炮弹小型化的要求。压电驱动器[4-5]作为一种微型化的驱动器,其具有体积小、制作简单、响应速度快、运动稳定、抗干扰、运动可逆等优异特性。鉴于压电驱动器在航空、航天等极端环境领域内的成功应用,研究人员将目光投向了武器系统。将压电驱动器应用于引信安全系统中,更容易满足引信安全系统微型化、安全状态可恢复的需求,对于引信的发展具有重要意义。
埃及明尼亚大学[6]报道过将压电驱动器应用在反隐身无人机上。南京航空航天大学的朱鹏飞[7]设计了一种基于纵弯模态的压电驱动器,并将其应用于多通道舵机控件,以实现灵巧的弹道修正。然而文献[7]中只完成了原理样机的装配与加工,对于弹道修正的效果缺乏试验说明。杨明鹏[8]基于宝塔形多自由度压电驱动器设计了一种灵巧弹药构型,利用弹头偏转实现弹道修正。薛成等[9]设计了一种微小型压电驱动器,其单个定子包含4个驱动足。可分别控制4个舵机,该种驱动器为制导导弹的舵机提供了一种新的可能。
2013年,唐玉娟等[10]提出将压电驱动器应用于引信安全系统中,利用压电驱动器运动可逆的特性来实现隔爆滑块的往复运动,进而完成引信安全系统的状态自恢复。该设计方案可实现安全状态和待发状态多次转换,重复利用性好。北京机电工程研究所的研究人员设计了一种基于双振子直线型压电超声驱动器的安全与解除保险装置,该装置可在0.016 s内实现隔爆块的对正。但是该驱动器定子由双振子组成,尺寸大,不利于结构小型化。佟雪梅[11]提出了一种基于压电驱动器的安全与解除保险装置,但加工误差较大,定子楔块的加工精度影响压电陶瓷的预夹紧力。使压电陶瓷的激振效果不佳。
上述基于压电驱动器的安全与解除保险装置具有相同的特征,即动子与定子在预压力的作用下紧密接触,利用动/定子之间的摩擦力将定子的高频微振幅转换成动子的宏观运动,实现传火通道的对正与错位,使得引信安全系统在安全状态与待发状态间实现相互转换。但这对动子与定子之间接触面的加工工艺提出了很高的要求,增加了成本;此外,“动定子并存”的压电驱动器构型,相对于引信内部活动部件可利用的有限工作空间,仍然具有一定的复杂性。为解决上述问题,亟需开展适用于引信安全系统的新型压电驱动器。
同时由于引信的特殊性,会受到诸如高低温、振动、潮湿、冲击以及电磁等环境的影响。在引信所经历的环境中,冲击过载环境对引信的影响最大,很大概率破坏引信的结构,引发失效、炸膛[12]等后果。针对冲击过载对于压电驱动器的影响研究仍旧十分有限。
唐玉娟等[10]对压电驱动器抗过载性能进行了分析,发现在15 kg的过载下压电陶瓷保持完好无断裂,但缺乏冲击前后试验结果的对比分析。任金华等[13]利用有限元方法对旋转型压电驱动器建模,分析了驱动器在10 kg静态过载下的应力分布情况。陈超等[14]分析了压电驱动器在冲击载荷作用下的应力波传递过程,并利用LS-dyna评估了压电驱动器所能承受的极限过载情况,测试了不同冲击过载之后压电驱动器的机械特性,但其建立的是二维模型,不能准确反映出驱动器在冲击环境中的变化过程。Hou等[15]通过仿真的方法得到了一种新型驱动器在冲击载荷下的动态响应过程,但缺乏实验测试验证。
目前针对压电驱动器在冲击环境下的研究主要集中在数值模拟阶段,且建立的模型相对简单。为提升压电驱动器在引信安全系统应用的环境适应性,亟需开展冲击载荷下压电驱动器的相关研究,并验证增强压电驱动器抗高过载的措施的可行性。
1 双工形压电驱动器的结构设计及工作机理采用压电驱动器主要是为了实现引信隔爆块的直线往复运动,其尺寸不能太大且运动需可逆。在现有的压电驱动器种类中,直线型压电驱动器无需机械传动机构直接输出直线位移,实现往复运动所需时间更短,且组成部分更少,所占空间更小,更容易实现结构设计的微小化,因此选用双足式直线型压电驱动器[16],以此设计了一种能够应用于引信安全系统中的新型压电驱动器。
1.1 双工型压电驱动器的工作机理 1.1.1 结构设计依据项目的要求,驱动器的体积不能大于Φ15 mm×10 mm,且引信安全系统状态具有恢复功能,即驱动器运动可恢复,其正向与反向最大运动速度均大于40 mm/s。
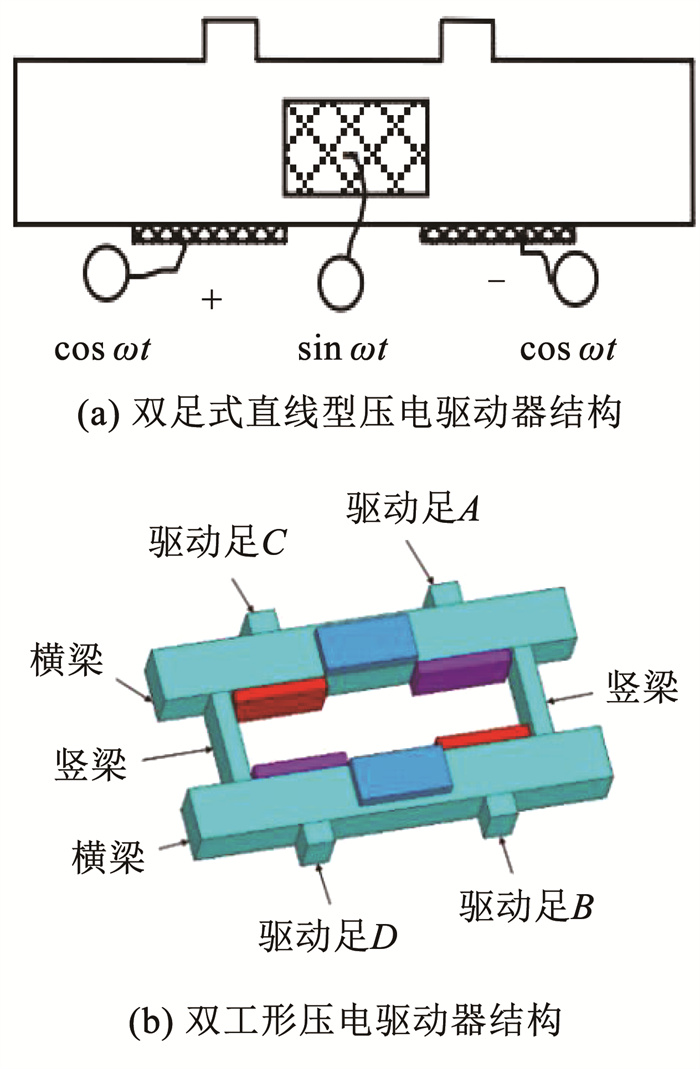
双足式直线型压电驱动器是一种非自行式的压电驱动器,其输出位移依靠定子的两个驱动足带动滑块运动来实现,且由于压电陶瓷片粘贴在定子的下方,因此该驱动器无法做成自行式压电驱动器,其结构图如图 1(a)所示。
|
图 1 结构对比 Fig. 1 Structural comparison |
考虑到对称的设计思想以及双足式压电驱动的构型,得到双工形压电驱动器,如图 1(b)所示。双工形压电驱动器由两根竖梁连接的两个双足结构组成,梁的上表面中间处粘贴一片压电陶瓷片来激发纵向振动模态,梁的内表面靠近外边处各粘贴一片压电陶瓷片来激发横向振动模态,其运动依靠4个驱动足实现。
1.1.2 工作机理当横梁的横向振动模态被激发时,一侧的压电陶瓷片处于缩短状态,而另一侧的压电陶瓷片处于伸长状态,同一根梁上激发横向振动模态的两块压电陶瓷片的极化方向是相反的,结合压电陶瓷片的横向振动模态,可得同一侧的两块压电陶瓷片上所加电压的相位应相差π/2。选用正弦和余弦电压作为压电驱动器横向振动模态的激励电压;对于激发横梁纵向振动的压电陶瓷片,由于纵向振动模态时压电陶瓷片的状态相同,因此该压电陶瓷片对于激励电压类型无要求。为了与激发横向振动模态的激励电压相统一,本文选用正弦电压作为压电驱动器纵向振动的激励电压。
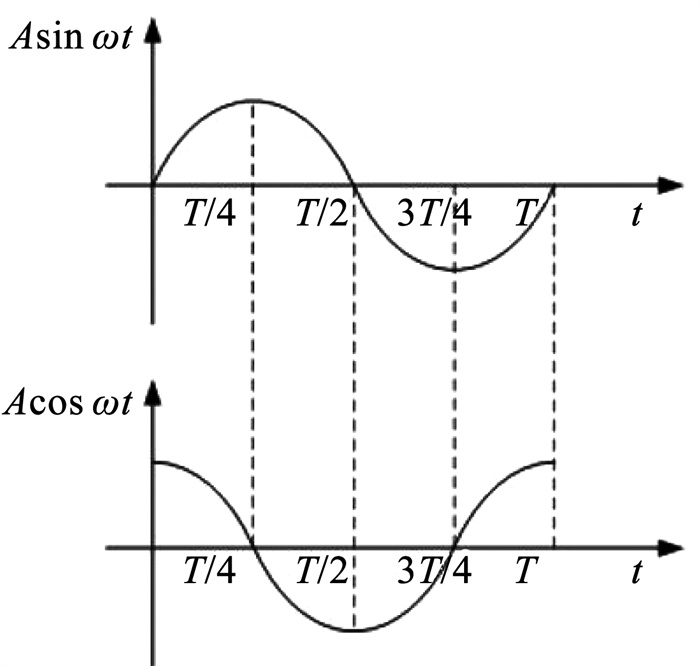
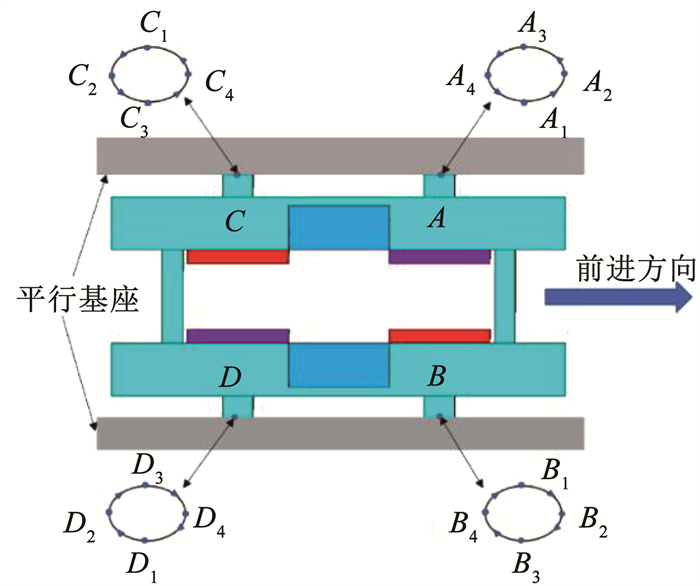
双工形压电驱动器的激励电压如图 2所示。双工形压电驱动器的4个驱动足在激励电压的作用下,各自完成一次椭圆运动,如图 3所示。在平行基座和压电振子的摩擦力作用下,驱动足的椭圆运动轨迹转变为压电驱动器的直线运动。当把激发横向振动模态的激励电压相位差由π/2改为π,压电驱动器驱动足的椭圆运动轨迹转向将改变,导致压电驱动器反向运动。
|
图 2 激励电压 Fig. 2 Excitation voltage |
|
图 3 双工形压电驱动器驱动足的运动轨迹 Fig. 3 Motion trajectory of foot driven by duplex piezoelectric actuator |
为了能够让双工形压电驱动器的驱动足形成类椭圆运动轨迹,压电驱动器的振动模态需满足在横向和纵向均有应变,即在纵振和弯振中各选取一个振动模态进行组合,且为了更好实现工作模态频率的一致化,所选择的模态频率应尽可能接近。
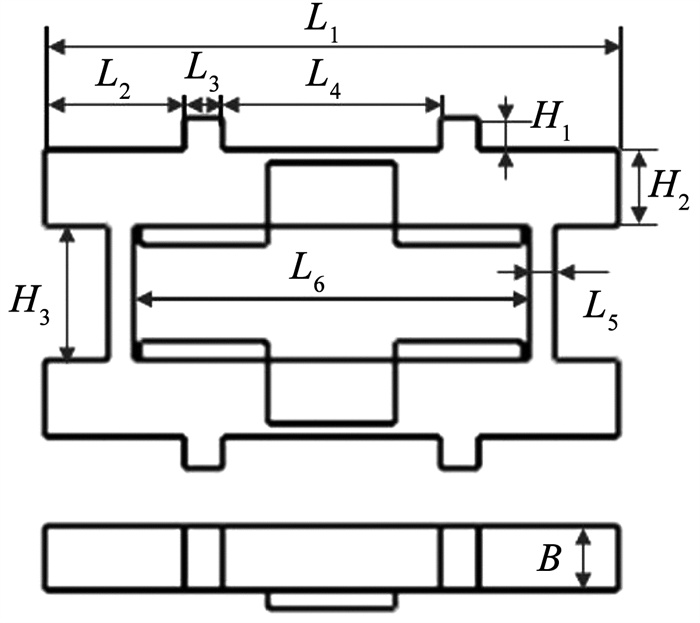
本文选择磷青铜作为双工形压电驱动器的金属弹性体材料,其密度为8 500 kg/m3,弹性为1.02×1011 N/m2,泊松比为0.373;压电陶瓷片选择PZT-4,压电陶瓷片的参数见表 1。初步建立了双工形压电驱动器的尺寸参数,其各尺寸示意图如图 4所示。接下来利用有限元仿真软件建立双工形压电驱动器的有限元模型,并基于灵敏度分析对双工形压电驱动器进行结构优化。
| 表 1 压电陶瓷片的参数 Tab. 1 Parameters of piezoelectric ceramic sheets |
|
图 4 双工形压电驱动器的结构参数 Fig. 4 Structural parameters of duplex piezoelectric actuator |
灵敏度分析是为了找出对两种工作模态频率影响较大的尺寸参数,并为优化分析的设计变量选择作参考。鉴于引信安全系统对双工形压电驱动器有尺寸要求,因此图 4中的L1保持不变, L1的初始值为9 mm。为了使得竖梁不影响横梁的振动模块,竖梁被设置在横梁的二阶弯振节点处,由于横梁的长度不变,因此竖梁的位置也不变,即L6/2+ L5/2的长度不变,而L5是连接两根横梁的关键部分,其长度关系到压电驱动器的强度,为减少连接处竖梁对横梁模态的影响,保持L5不变,则L6也不变;此外,驱动足设置在压电陶瓷片的对应位置,压电陶瓷片粘贴的位置和压电陶瓷片的规格都固定,则L2+L3/2和L4+L3/2是固定的,即知道L3可得到L2和L4,因此,这里将L3设置为变化的。由于双工形压电驱动器的工作模态都是沿着横梁的长度和高度方向振动,因此压电驱动器的厚度B对工作模态影响不大,而高度方向的H1、H2、H3对工作模态有影响,故厚度B保持不变,H1、H2、H3变化。
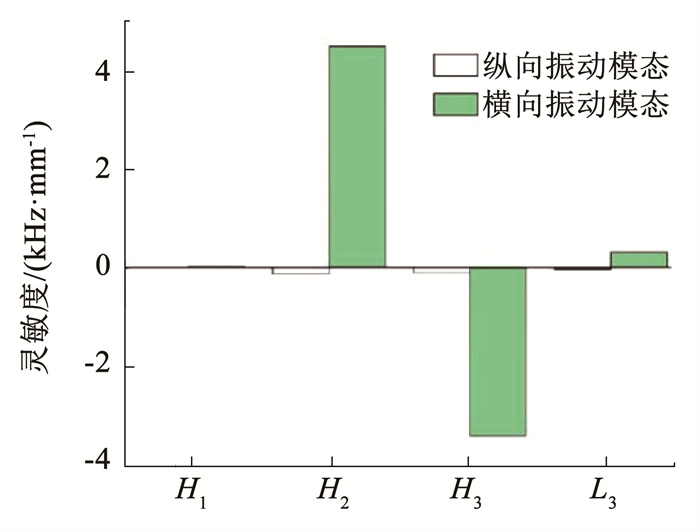
基于尺寸参数关联性分析,选择L3、H1、H2、H3作为灵敏度分析的结构尺寸。将4个结构参数依次用pi(i=1,2,3,4)表示,结构参数的变化量Δpi设置为0.1 mm,利用有限元仿真软件每次更新一个结构尺寸参数对双工形压电驱动器进行模态分析,将每次模态分析得到的纵向振动模态频率、横向振动模态频率及结构尺寸参数带入灵敏度计算式(1)中,可得每个结构尺寸的灵敏度,并绘制出灵敏度参数图,如图 5所示。
| $ \left\{\begin{array}{l} S_{\mathrm{l}i}=\frac{\partial f_1}{\partial p_i}=\frac{f_{\mathrm{l}v}-f_{10}}{\Delta p_i} \\ S_{\mathrm{b} i}=\frac{\partial f_{\mathrm{b}}}{\partial p_i}=\frac{f_{\mathrm{b} v}-f_{\mathrm{b} 0}}{\Delta p_i} \end{array}\right. $ | (1) |
|
图 5 灵敏度参数图 Fig. 5 Sensitivity parameter diagram |
式中:Sli、Sbi分别为第i个参数对纵向振动模态频率和横向振动模态频率的灵敏度值, fl、fb分别为纵向振动模态和横向振动模态的频率, flv、fbv分别为结构尺寸参数更新后的纵向振动模态和横向振动模态频率, fl0、fb0分别为初始结构下的纵向振动模态和横向振动模态频率。
从图 5可得,L3、H1、H2、H3的数值变化对于纵向振动模态频率影响不大;对于横向振动模态,对H2、H3频率的影响更大,其中,频率随着H2的增加而增加,随着H3的增加而减少。因此可以看出H1对纵向和横向的模态影响不大,本文选择H2、H3作为优化分析的设计变量,并将H1的初始值设为0.5 mm。
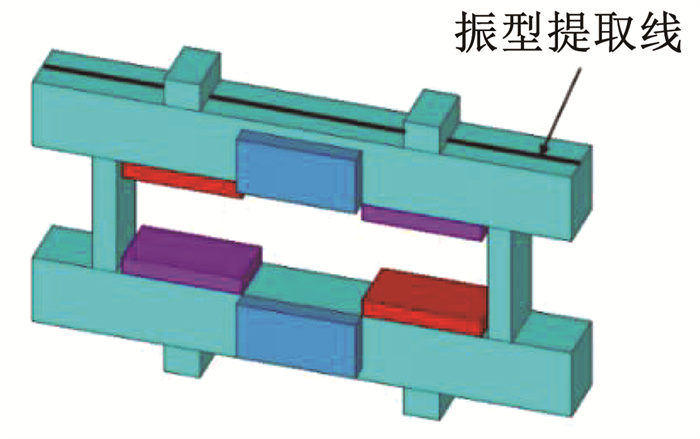
1.2.2 振型提取及模态识别方法在进行优化分析时,需要识别出两个工作模态,选择提取振型后再进行识别的方法,选择驱动器的长度和高度方向作为振型提取的方向,取驱动器横梁的外表面中间处作为振型提取的位置,如图 6所示。
|
图 6 振型提取位置 Fig. 6 Vibration mode extraction position |
对于提取后的振型,利用模态置信准则来识别两相工作模态。模态置信准则(Modal assurance criterion, MAC)[17]是利用MAC计算公式来计算出每个模态的MAC值,并与工作模态的MAC值作比较,MAC值最大的是工作模态。MAC计算公式为
| $ \mathrm{MAC}_j=\frac{\left(\phi_j^{\mathrm{T}} \phi_0\right)^2}{\left(\phi_j^{\mathrm{T}} \phi_j\right)\left(\phi_0^{\mathrm{T}} \phi_0\right)} $ | (2) |
式中:j为待识别振型的序号, ϕj、ϕjT分别为第j个待识别振型及其转置, ϕ0、ϕ0T分别为工作模态振型及其转置。
1.2.3 优化方法及结果优化分析的目标是使压电驱动器的工作模态频率尽可能接近。因此优化的目标函数设置为两相工作模态频率差的绝对值。考虑该驱动器用于引信中,尺寸有限,H2的取值范围为1.0~2.0 mm,H3的取值范围为1.5~3.0 mm。利用有限元仿真软件中提供的零阶优化方法和一阶优化方法[18-19]。先用零阶优化方法进行大范围求解,对得到的结果设定一个小的范围,然后利用一阶优化方法进行小范围精确求解。优化之后的结果见表 2。
| 表 2 优化前、后的结果 Tab. 2 Results before and after optimization |
由表 2可得经过两次优化之后,两相工作模态频率差由1 310 Hz缩小到了155 Hz,考虑到加工精度问题,对优化之后的H2、H3作数值处理,H2为1.2 mm,H3为2.1 mm,根据L1为9 mm,H1为0.5 mm可以判断双工形压电驱动器的尺寸不大于Φ15 mm× 10 mm的设计要求,两相工作模态频率差为173 Hz,满足优化设计的要求。
1.3 双工形压电驱动器的驱动足轨迹分析对双工形压电驱动器进行谐响应分析,将144 250 Hz确定为压电驱动器的工作频率,利用工作频率对压电驱动器进行瞬态动力学分析[20]。施加电压峰值为140 V、频率为工作频率的正弦电压和余弦电压。对于阻尼,通常选择瑞利阻尼,其计算公式如式(3)所示[21],阻尼比设置为5%,通过瑞利阻尼的计算公式可求得阻尼系数α和β。
| $ \left\{\begin{array}{l} \alpha=\frac{2 \xi \omega_{\min } \omega_{\max }}{\omega_{\min }+\omega_{\max }}=\frac{4 \mathsf{π} \xi f_{\min } f_{\max }}{f_{\min }+f_{\max }} \\ \beta=\frac{2 \xi}{\omega_{\min }+\omega_{\max }}=\frac{\xi}{\mathsf{π}\left(f_{\min }+f_{\max }\right)} \end{array}\right. $ | (3) |
式中:α、β分别为瑞利阻尼中的两种阻尼系数, ξ为阻尼比, fmin、fmax分别为两相工作模态频率中较小者和较大者。
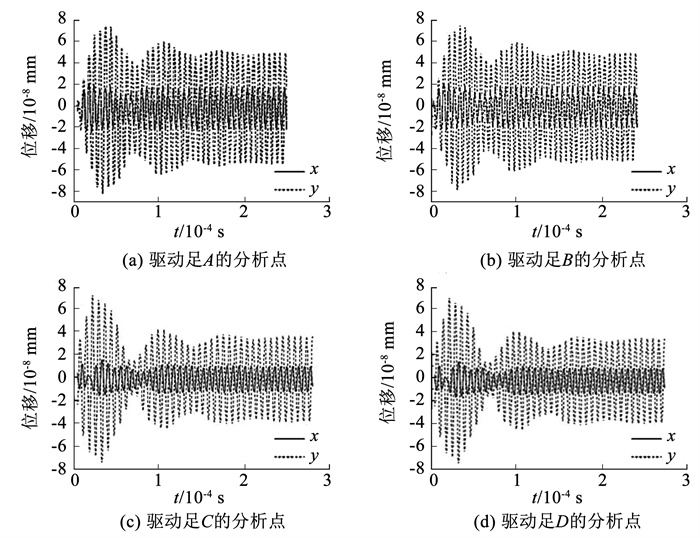
选择4个驱动足最外侧表面的中点作为分析点,通过瞬态动力学分析得到4个分析点的位移-时间曲线如图 7所示。由图 7可知,0.15 ms后分析点的x方向和y方向位移响应进入稳态阶段,此时位移响应最大。
|
图 7 压电驱动器分析点的位移-时间曲线 Fig. 7 Displacement time curve of piezoelectric actuator analysis point |
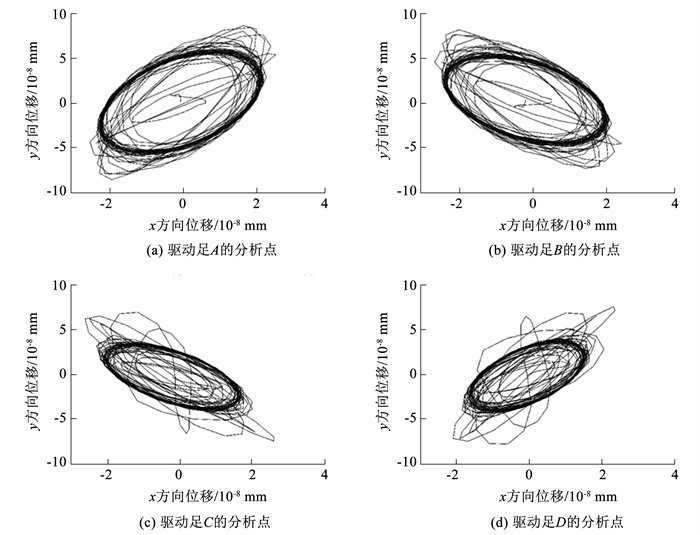
以驱动器前进方向作为x方向,y方向与之面内垂直。将x方向位移响应作为自变量,y方向位移响应作为因变量,可得分析点在x-y平面内的运动轨迹,如图 8所示。
|
图 8 压电驱动器分析点在x-y平面内运动轨迹 Fig. 8 Analysis of motion trajectory of a point in x-y plane using a piezoelectric driver |
由图 8可得,进入稳态运动阶段后,分析点的运动轨迹几乎不再变化,运动轨迹类似椭圆。由上述分析可知,双工形压电驱动器在运动一段时间后,进入稳态阶段,驱动足的运动轨迹类似椭圆。
4个分析点的拟合曲线方程分别为:
| $ \left\{\begin{array}{l} x_A=5.0 \times 10^{-11}+2.3 \times 10^{-8} \sin \left(\frac{\mathsf{π} \times\left(t+4.7 \times 10^{-5}\right)}{3.5 \times 10^{-6}}\right) \\ y_A=5.6 \times 10^{-11}+5.9 \times 10^{-8} \sin \left(\frac{\mathsf{π} \times\left(t+5.3 \times 10^{-5}\right)}{3.5 \times 10^{-6}}\right) \end{array}\right. $ | (4) |
| $ \left\{\begin{array}{l} x_B=4.8 \times 10^{-11}+2.2 \times 10^{-8} \sin \left(\frac{\mathsf{π} \times\left(t+4.7 \times 10^{-5}\right)}{3.4 \times 10^{-6}}\right) \\ y_B=-1.5 \times 10^{-9}+6.1 \times 10^{-8} \sin \left(\frac{\mathsf{π} \times\left(t+4.2 \times 10^{-5}\right)}{3.4 \times 10^{-6}}\right) \end{array}\right. $ | (5) |
| $ \left\{\begin{array}{l} x_C=-3.0 \times 10^{-11}+1.1 \times 10^{-8} \sin \left(\frac{\mathsf{π} \times\left(t+4.6 \times 10^{-5}\right)}{3.5 \times 10^{-6}}\right) \\ y_C=5.2 \times 10^{-11}+3.7 \times 10^{-8} \sin \left(\frac{\mathsf{π} \times\left(t+5.0 \times 10^{-5}\right)}{3.5 \times 10^{-6}}\right) \end{array}\right. $ | (6) |
| $ \left\{\begin{array}{l} x_D=-2.8 \times 10^{-11}+9.0 \times 10^{-9} \sin \left(\frac{\mathsf{π} \times\left(t+5.3 \times 10^{-5}\right)}{3.5 \times 10^{-6}}\right) \\ y_D=-5.4 \times 10^{-11}+3.8 \times 10^{-8} \sin \left(\frac{\mathsf{π} \times\left(t+4.7 \times 10^{-5}\right)}{3.5 \times 10^{-6}}\right) \end{array}\right. $ | (7) |
将其对时间t积分,可得速度方程分别为:
| $ \left\{\begin{array}{l} v_{A x}=6.5 \mathsf{π} \times 10^{-3} \cos \left(\frac{\mathsf{π} \times\left(t+4.7 \times 10^{-5}\right)}{3.5 \times 10^{-6}}\right) \\ v_{A y}=1.7 \mathsf{π} \times 10^{-2} \cos \left(\frac{\mathsf{π} \times\left(t+5.3 \times 10^{-5}\right)}{3.5 \times 10^{-6}}\right) \end{array}\right. $ | (8) |
| $ \left\{\begin{array}{l} v_{B x}=6.5 \mathsf{π} \times 10^{-3} \cos \left(\frac{\mathsf{π} \times\left(t+4.7 \times 10^{-5}\right)}{3.4 \times 10^{-6}}\right) \\ v_{B y}=1.8 \mathsf{π} \times 10^{-2} \cos \left(\frac{\mathsf{π} \times\left(t+4.2 \times 10^{-5}\right)}{3.4 \times 10^{-6}}\right) \end{array}\right. $ | (9) |
| $ \left\{\begin{array}{l} v_{C x}=3.1 \mathsf{π} \times 10^{-3} \cos \left(\frac{\mathsf{π} \times\left(t+4.6 \times 10^{-5}\right)}{3.5 \times 10^{-6}}\right) \\ v_{C y}=1.1 \mathsf{π} \times 10^{-2} \cos \left(\frac{\mathsf{π} \times\left(t+5.0 \times 10^{-5}\right)}{3.5 \times 10^{-6}}\right) \end{array}\right. $ | (10) |
| $ \left\{\begin{array}{l} v_{D x}=2.6 \mathsf{π} \times 10^{-3} \cos \left(\frac{\mathsf{π} \times\left(t+5.3 \times 10^{-5}\right)}{3.5 \times 10^{-6}}\right) \\ v_{D y}=1.1 \mathsf{π} \times 10^{-2} \cos \left(\frac{\mathsf{π} \times\left(t+4.7 \times 10^{-5}\right)}{3.5 \times 10^{-6}}\right) \end{array}\right. $ | (11) |
作为引信安全系统的重要部件之一,双工形压电驱动器的往返运动速度决定引信安全系统的解除保险和恢复保险速度,是引信安全系统设计的一个重要指标。
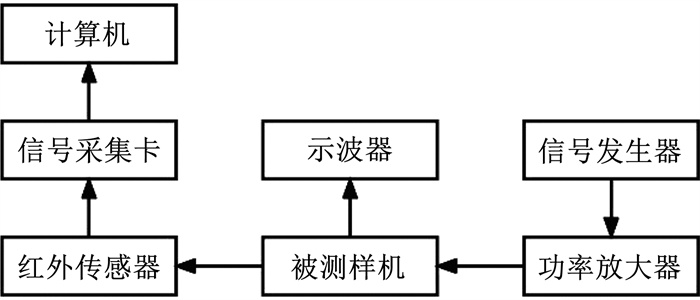
为测试双工形压电驱动器的往返运动速度,本文搭建了驱动特性测试实验平台,各装置连接示意图如图 9所示。其中,预紧力主要通过旋转螺栓的圈数来调整弹簧的压缩力而实现。实际操作过程中,首先同时旋转两侧螺栓直至压电驱动器垂直放置后不会在装置中滑动,然后两侧螺栓每旋进一圈,施加激励电压,测量压电驱动器运动位移随时间变化曲线,通过对位移响应曲线的简单对比,确定出合适的预紧力。最后将实验装置固定,避免其运动影响驱动器速度的测量。信号发生器发出驱动器所需频率的正弦和余弦信号,产生峰峰值为8 Vpp、相位差为90°的正、余弦电压信号,利用功率放大器将电信号的峰峰值放大为140 Vpp,将放大后的电信号作为激励信号输入到驱动器,为了测量放大后电压幅值及验证放大后电信号是否正确,这里采用示波器测量放大之后的正弦和余弦信号,同时将激光位移传感器连接至电脑,获取驱动器的运动速度。
|
图 9 驱动特性实验平台装置连接示意 Fig. 9 Schematic diagram of experimental platform device for connecting the driving characteristics |
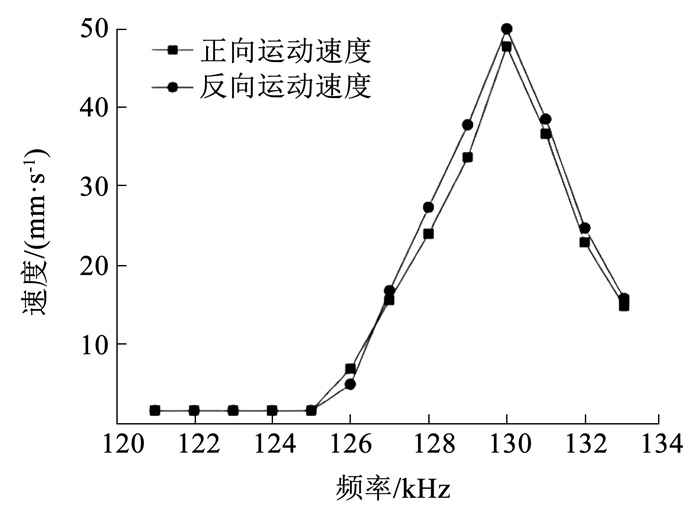
频率范围设置为121~133 kHz,并在测试时,每隔几秒增加1 000 Hz频率,测试不同频率下驱动器的往返运动速度,得到驱动器频率和速度的关系曲线。频率为130 kHz时,压电驱动器往返运动速度达到最大,130 kHz为最佳工作频率,此时正向运动速度约为46.2 mm/s,反向运动速度约为48.4 mm/s,满足正向反向最大速度均大于40 mm/s这一指标(如图 10所示)。
|
图 10 频率和速度曲线图 Fig. 10 Frequency and velocity curves |
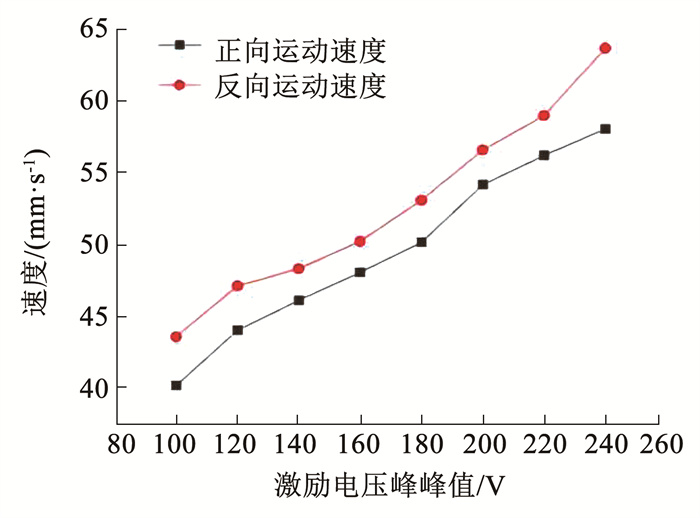
在最佳工作频率确定之后,为进一步增大双工形压电驱动器的运动速度,需增加其驱动电压,探究其激励电压和运动速度的关系。设置激励电压峰峰值的变化范围为100~240 Vpp,每次改变20 V电压,测试压电驱动器的运动速度,得到双工形压电驱动器往返运动速度和激励电压峰峰值的关系曲线,如图 11所示。由图 11可知,双工形压电驱动器的往返运动速度随激励电压峰峰值的增加而增加,且在同一激励电压作用下压电驱动器的正向运动速度始终小于反向运动速度。压电驱动器往返运动速度不同,其主要原因可能是:两个弹簧设置的预压力大小不同;压电陶瓷片粘贴位置不对称,导致椭圆运动轨迹发生变化。
|
图 11 运动速度和激励电压峰峰值关系 Fig. 11 Relationship between motion speed and peek excitation voltage |
引信安全系统在工作的过程中,依据环境信息依次解除相应的保险,实现状态的转变,其可利用的环境信息主要是弹药发射及飞行阶段经历的环境信息。由于作战目标具有不确定性,引信安全系统经历的环境也变得不确定,其可能会经历高冲击、湿热、电磁干扰等恶劣环境,这些环境中对引信安全系统影响最大的是高冲击环境,其会严重干扰引信安全系统的正常工作,甚至导致引信安全系统提前解除保险,引爆弹药。为保障我方作战人员的安全性及保证引信安全系统的正常工作,需提高引信安全系统的抗高过载特性。
3.1 双工形压电驱动器抗高过载措施在高冲击过载作用下双工形压电驱动器的性能会受到影响,可能无法正常工作,甚至被毁坏,而双工形压电驱动器性能被影响是因为驱动器中的部分组件在高冲击载荷作用下失效。双工形压电驱动器由压电陶瓷片、金属弹性体、导线及胶粘剂组成,
可能发生的失效的原因有:1)压电陶瓷片发生拉伸断裂或在制造、运输、粘贴、使用等过程中压电陶瓷片内部产生微小裂纹扩大为宏观上的裂纹;2)金属弹性体发生塑性变形导致工作模态振型发生变化,甚至导致工作模态振型的消失;3)胶粘剂内部产生裂纹甚至直接脱胶,导致压电陶瓷片无法正常粘贴在金属弹性体上,压电陶瓷片无法正常激发金属弹性体的振动模态。
为保证双工形压电驱动器的正常工作,本文提出以下抗高过载措施:1)更改基座材料,选用硬度较低的材料作为基座材料降低碰撞对双工形压电驱动器的损伤;2)更换粘贴强度更大的胶粘剂或增大胶粘剂层厚度,降低由于过载加速度引起胶粘剂层微小变形的影响;3)选用抗弯强度更大的压电陶瓷片,增强双工形压电驱动器的抗高过载能力。
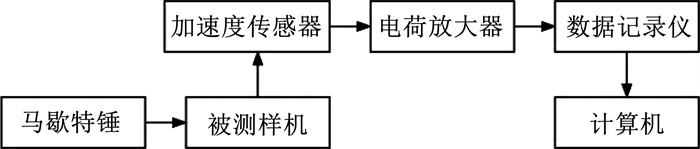
3.2 抗高冲击过载实验为验证双工形压电驱动器的抗高冲击过载的能力,搭建了高冲击过载实验平台,如图 12所示。该实验平台由马歇特锤、电荷放大器、加速度传感器、数据记录仪及夹具等组成,其中加速度传感器的型号为CA-YD-111A,其参考灵敏度为0.044 pC/m · s-2,可测量的最大加速度为3×105 m/s2; 电荷放大器的型号为YE5854A, 其灵敏度设置为4.4 pC/unit,放大增益为1 mV/unit,双工形压电驱动器放在夹具内,在马歇特锤作用下,其受到加速度的作用,加速度传感器实时测量加速度大小,并经过电荷放大器和数据记录仪在计算机上显示。加速度传感器测得其最大值约为2.44 V,通过式(12)计算可得加速度幅值为244 000 m/s2,满足本文20 kg的过载加速度要求。
| $ a=\frac{K_e U}{K K_a} $ | (12) |
|
图 12 高冲击过载实验平台 Fig. 12 High impact overload experimental platform |
式中:a为加速度,m/s2;Ke为电荷放大器灵敏度;U为数据记录仪显示的电压数据,mV;K为电荷放大器的放大增益,Ka为加速度传感器的参考灵敏度。
利用驱动特性测试实验平台对冲击过后的双工形压电驱动器进行速度测试,在激励电压峰峰值140 Vpp、频率130 kHz的作用下,双工形压电驱动器的正向运动速度约为35.1 mm/s,反向运动速度约为40.2 mm/s。与未冲击的双工形压电驱动器相比,冲击过后的压电驱动器往返运动速度明显下降,且运动过程中出现明显的噪声,这表明冲击过载虽然对双工形压电驱动器并没有产生明显的结构损坏,但对其运动性能产生了较大影响。
3.3 抗高过载措施实验验证为验证抗高过载措施的正确性,根据抗高过载措施更改双工形压电驱动器的组件参数之后,先通过驱动特性实验平台测试驱动器是否能运动及往返运动速度,然后通过高冲击过载实验平台对压电驱动器进行冲击实验,再次通过驱动特性实验平台测试冲击过后的压电驱动器的往返运动速度,实验数据见表 3。
| 表 3 根据抗高过载措施更改双工形压电驱动器的往返速度 Tab. 3 Change the round-trip speed of duplex piezoelectric drivers based on anti-high overload measures |
从表 3可得,采用抗高过载措施后的压电驱动器冲击前、后往返运动速度变化较小,压电驱动器运动性能受冲击过载影响较小。
实验结果表明双工形压电驱动器在20 kg冲击过载作用下,结构仍完整,但其运动速度降低。基于抗高过载措施改变压电驱动器的组件参数,通过驱动特性测试实验平台和高冲击过载实验平台先后对其进行实验测试,测试结果表明增加胶粘剂层厚度、选用硬度较低材料制作基座、增强压电陶瓷片的硬度可提高双工形压电驱动器的抗高过载特性。
4 结论1) 本文设计出双工形压电驱动器,并阐述其运动机理。利用有限元仿真软件建立压电驱动器的有限元模型,并经过模态分析、灵敏度分析、优化分析将两相工作模态频率差由1 310 Hz降低至173 Hz,得到压电驱动器的最优尺寸参数。
2) 基于双工形压电驱动器的运动机理,搭建驱动特性测试实验平台,通过扫频测试得到双工形压电驱动器的最佳工作频率为130 kHz,在最佳工作频率下测试压电驱动器的往返运动速度和激励电压峰峰值的关系,结果表明压电驱动器的往返运动速度和激励电压峰峰值呈正相关。
3) 搭建高冲击过载实验平台,对压电驱动器进行幅值20 kg冲击过载实验,冲击之后压电驱动器结构仍完好无损,但运动性能下降。
4) 从双工形压电驱动器的组成部件出发,分析压电陶瓷片、金属弹性体、胶粘剂、导线在高冲击过载作用下可能出现的失效形式,并提出了抗高过载措施。结合抗高过载措施对压电驱动器进行冲击过载实验,结果表明抗高过载措施是可行的。
| [1] |
涂诗美, 商顺昌. 新型鱼雷灵巧引信设计方案[J]. 探测与控制学报, 2004, 26(3): 1. TU Shimei, SHANG Shunchang. The design scheme of smart fuze for the new kind torpedo[J]. Journal of Detection & Control, 2004, 26(3): 1. DOI:10.3969/j.issn.1008-1194.2004.03.001 |
| [2] |
尚雅玲, 张贤彪, 倪保航. 运动可逆式引信安全系统逻辑控制分析[J]. 舰船电子工程, 2009, 9(12): 176. SHANG Yaling, ZHANG Xianbiao, NI Baohang. Analysis of the control of reversing fuze safety system[J]. Ship Electronic Engineering, 2009, 9(12): 176. DOI:10.3969/j.issn.1627-9730.2009.12.048 |
| [3] |
付前卫, 张百亮, 姚志远. 用于引信隔爆机构的双振子直线超声电机设计[J]. 西北工业大学学报, 2017, 35(3): 545. FU Qianwei, ZHANG Bailiang, YAO Zhiyuan. Design of double-vibrator linear ultrasonic motor in fuze isolating explosion mechanism[J]. Journal of Northwestern Polytechnical University, 2017, 35(3): 545. DOI:10.3969/j.issn.1000-2758.2017.03.028 |
| [4] |
RAY A, SINGH A K. Perfectly matched layer and infinite element coupled with finite elements for SH waves in an imperfect piezoelectric viscoelastic structure[J]. European Journal of Mechanics-A/Solids, 2023, 98: 104863. DOI:10.1016/j.euromechsol.2022.104863 |
| [5] |
高强. 新型直驱-超声复合驱动器机理分析与试验研究[D]. 长春: 长春工业大学, 2021 GAO Qiang. Mechanism analysis and experimental study of a new type of DC-ultrasonic compound actuator[D]. Changchun: Changchun University of Technology, 2021. DOI: 10.27805/d.cnki.gccgy.2021.000028 |
| [6] |
EL DIWINY M, EL SAYED A H, HASSANEN E S, et al. Implementation of anti stealth technology for safe operation of unmanned aerial vehicle[C]//2014 IEEE/AIAA 33rd Digital Avionics Systems Conference (DASC). Colorado Springs: IEEE, 2014: 7E2. DOI: 10.1109/DASC.2014.6979527
|
| [7] |
朱鹏飞. 新型微小压电作动器及其在多通道舵机控件中的应用[D]. 南京: 南京航空航天大学, 2016 ZHU Pengfei. Novel micro piezoelectric actuator and its application in multi-channel actuator control system[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2016 |
| [8] |
杨明鹏. 基于多自由度超声电机的灵巧弹药构型及驱动[D]. 南京: 南京航空航天大学, 2014 YANG Mingpeng. Smart munition configuration and drive based on multi degree of freedom ultrasonic motor[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014 |
| [9] |
薛成, 陈超. 新型多通道控制的微小型超声电机[J]. 机械与电子, 2017, 35(4): 44. XUE Cheng, CHEN Chao. A new type of multi-channel servo control of miniature ultrasonic motor[J]. Machinery & Electronics, 2017, 35(4): 44. DOI:10.3969/j.issn.1001-2257.2017.04.010 |
| [10] |
唐玉娟, 王炅. 逆压电驱动的运动可逆式引信隔爆机构[J]. 探测与控制学报, 2013, 35(3): 56. TANG Yujuan, WANG Jiong. A reversible fuze interrupter mechanism based on piezoelectric actuator[J]. Journal of Detection & Control, 2013, 35(3): 56. |
| [11] |
佟雪梅. 引信用压电精密驱动装置的结构优化及其驱动电路设计[D]. 南京: 南京理工大学, 2014 TONG Xuemei. Structure optimization and driving circuit design of piezoelectric precision drive device for pilot credit[D]. Nanjing: Nanjing University of Science and Technology, 2014. DOI: 10.7666/d.Y2520750 |
| [12] |
张合, 李豪杰. 引信机构学[M]. 北京: 北京理工大学出版社, 2014. ZHANG He, LI Haojie. Fuze mechanism[M]. Beijing: Beijing Institute of Technology Press, 2014. |
| [13] |
任金华, 陈超. 高过载环境下旋转型行波超声电机的动力学分析与设计[C]//第五届全国振动利用工程学术会议暨第四次全国超声电机技术研讨会论文集. 南京: 第五届全国振动利用工程学术会议暨第四次全国超声电机技术研讨会, 2012: 451 REN Jinhua, CHEN Chao. Dynamic analysis and design of the travelling wave type rotary ultrasonic motors under overload environment[C]//Proceedings of the Fifth Conference on Vibration Utilization Engineering in China &The Fourth Workshop on Ultrasonic Motor Technology in China (CVUEC & WUMTC 2012). Nanjing: The Fifth Conference on Vibration Utilization Engineering in China &The Fourth Workshop on Ultrasonic Motor Technology in China, 2012: 451 |
| [14] |
陈超, 任金华, 石明友, 等. 旋转行波超声电机的冲击动力学模拟及实验[J]. 振动、测试与诊断, 2014, 34(1): 8. CHEN Chao, REN Jinhua, SHI Mingyou, et al. Impact dynamics simulation and experiment analysis of traveling wave type rotary ultrasonic motor[J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(1): 8. DOI:10.16450/j.cnki.issn.1004-6801.2014.01.030 |
| [15] |
HOU Xiaoyan, LEE H P, ONG C J, et al. Shock analysis of a new ultrasonic motor subjected to half-sine acceleration pulses[J]. Advances in Computational Design, 2016, 1(4): 357. DOI:10.12989/acd.2016.1.4.357 |
| [16] |
时运来. 新型直线超声电机的研究及其在运动平台中的应用[D]. 南京: 南京航空航天大学, 2011 SHI Yunlai. Research on new linear ultrasonic motors and theirapplication in motion stage[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2011 |
| [17] |
张宇航, 倪智宇. 基于MAC法的空间太阳能电站传感器优化配置与参数辨识[J]. 沈阳航空航天大学学报, 2022, 39(2): 28. ZHANG Yuhang, NI Zhiyu. Optimal sensor placement and parameter identification of space solar power station based on MAC method[J]. Journal of Shenyang Aerospace University, 2022, 39(2): 28. DOI:10.3969/j.issn.2095-1248.2022.02.004 |
| [18] |
陈伊军, 黄君, 吴宇, 等. 基于ANSYS软件的联合布置弹簧汽机基础结构抗地震优化设计[J]. 地震工程学报, 2022, 44(1): 119. CHEN Yijun, HUANG Jun, WU Yu, et al. Seismic optimization design of combined layout spring turbine foundations based on ANSYS[J]. China Earthquake Engineering Journal, 2022, 44(1): 119. DOI:10.20000/j.1000-0844.20200714002 |
| [19] |
鲍华. ANSYS一阶优化技术在损伤识别中的应用探讨[J]. 建筑科学, 2020, 36(11): 116. BAO Hua. Application discussion on damage identification with ANSYS based first-order optimization technology[J]. Building Science, 2020, 36(11): 116. DOI:10.13614/j.cnki.11-1962/tu.2020.11.017 |
| [20] |
XUE X J, ZHAO C Y. Transient behavior and thermodynamic analysis of Brayton-like pumped-thermal electricity storage based on packed-bed latent heat/cold stores[J]. Applied Energy, 2023, 329: 120274. DOI:10.1016/j.apenergy.2022.120274 |
| [21] |
HUANG Jiandong, LI Xin, ZHANG Jia, et al. Determining the Rayleigh damping parameters of flexible pavements for finite element modeling[J]. Journal of Vibration and Control, 2022, 28(21/22): 3181. DOI:10.1177/10775463211026763 |
 2024, Vol. 56
2024, Vol. 56


