2. 哈尔滨工业大学 机电工程学院, 哈尔滨 150001;
3. 山东船舶技术研究院, 山东 威海 264209
2. School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150001, China;
3. Shandong Institute of Shipbuilding Technology, Weihai 264209, Shandong, China
近年来,随着中国海洋资源的大力开发,海工平台得到蓬勃发展。波浪引起的海工平台运动严重影响了海上作业的营运性能和安全性能,甚至导致事故发生[1]。因此,开发一种准确的、实时的运动预测方法十分重要。
关于海工平台的运动预测方法主要分为:水动力学方法、统计回归方法、智能学习方法。其中经典的水动力学预测方法有势流方法与黏流方法[2]。虽然水动力学方法具有严谨的数学和物理推导过程,但其求解时长往往难以满足实时响应的需求,且建模和求解过程复杂。统计回归方法的优势在于不需要建立水动力学模型,只需利用运动数据即可完成预测,如:自回归[3-4]、支持向量回归[5]、高斯过程回归已被应用到船舶运动响应的预测上。但是由于统计回归方法是单步预测方法,对于多步预测存在迭代误差,限制了其应用范围。智能学习方法主要指神经网络学习方法,基于其建模原理,该方法具有无限趋近于任何一个非线性函数的能力。相比于水动力学方法与统计回归方法,反向传播(back propagation, BP)神经网络[6]、径向基函数(radial basis function, RBF)神经网络[7]的引入使预测效果更加准确。但以上两种一般的神经网络方法只搭建了简单的输入与输出之间的映射关系,没有考虑不同的输入时间点对于预测结果的影响程度。因此,研究人员[8]进一步将长短期记忆(long short-term memory, LSTM)这一特殊的神经网络模型引入到海上结构物的运动预测中,通过引入3个门控开关与记忆细胞,自适应记忆不同时间点输入数据的时间信息,从而达到更好预测效果。此外卷积神经网络(convolutional neural network, CNN)和Transformer作为一种特殊的神经网络,在图像处理、自然语言处理[9-10]领域也有着很广泛的应用,具有强大的特征提取能力。神经网络方法的预测能力具有优越性,但其学习和预测能力对神经网络超参数的选取较为敏感。在以往的工作中,各种研究把参数优化聚焦在神经网络训练过程中的权值优化[11]上,而对于超参数的选取大都是采用人工调优、网格搜索或随机搜索的方法。其中人工调优方法需要模型的先验知识,而网格搜索和随机搜索效率低下,不属于智能寻优算法,对此本文利用自动机器学习领域中的智能寻优算法即贝叶斯[12](Bayesian)寻优来解决超参数的选取问题。本文设计了一种CNN与LSTM相结合的混合方法,旨在利用CNN的特征提取能力与LSTM的时序建模能力构建预测模型,并将其应用于海工平台的运动预测中。经实验对比,该混合模型比LSTM等模型具有更强预测能力。
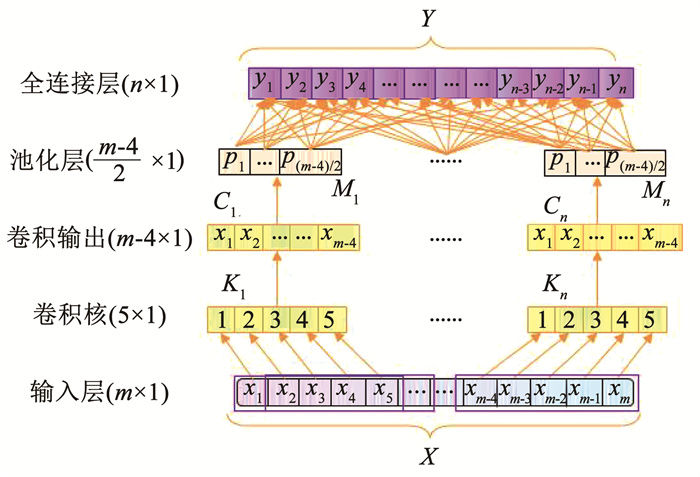
1 模型结构与相关理论 1.1 卷积神经网络(CNN)卷积神经网络已广泛应用于图像识别、图像处理[13]以及大规模的视觉识别等方面。图 1给出了一维卷积神经网络的结构与工作原理。
|
图 1 一维CNN原理图 Fig. 1 One-dimensional CNN schematic diagram |
从图 1中可以看出一维卷积神经网络主要由输入层、卷积层、池化层以及全连接层(输出层)组成。其中输入层有输入向量X∈Rm×1,卷积层有n个卷积核,其中Ki∈R5×1为第i个卷积核。将输入向量X输入卷积层后,对一维向量进行卷积操作,该操作过程使用每一个卷积核对输入向量进行滑动卷积操作,每次滑动一个时间步长,得到卷积输出,图 1中所示Cj∈Rm-4×1即为第j个卷积核的卷积输出,卷积输出的个数为n。在经过卷积操作后将卷积输出输入到池化层,通过最大池化操作,经过最大池化层后得到n个输出,其中Mk即为第k个池化操作的输出。最后,通过全连接层获得整个卷积神经网络的输出Y∈Rn×1。
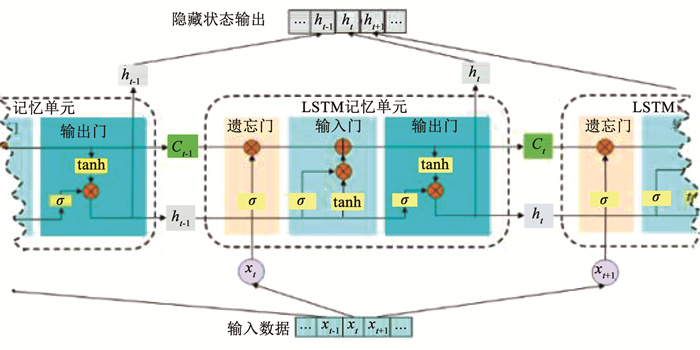
1.2 长短期时间记忆(LSTM)普通的循环神经网络(recurrent neural network, RNN)在遇到长序列输入时会引起梯度消失与梯度爆炸,对此有研究学者提出了改进方法LSTM[14],它通过引入遗忘门、输入门、输出门3个门控开关以及记忆单元有效地解决了RNN中的梯度消失与爆炸问题。LSTM单元的结构如图 2所示。
|
图 2 LSTM结构示意 Fig. 2 LSTM structure diagram |
从图 2中可以看出,整个LSTM模型由输入层、多个LSTM记忆单元以及隐藏状态输出层组成,每一个LSTM记忆单元的结构相同。在图 2中给出了3个LSTM记忆单元,其中左侧和右侧的记忆单元只给出了相应的1/2以表示在左侧或右侧还有多个LSTM记忆单元串联连接。每个记忆单元的输入分为3部分,第1部分是来自于数据的输入即xt,另两部分均为从上一个单元所传递来的细胞状态Ct-1与隐藏状态输出ht-1。在获得3部分的输入之后,将会依次经过遗忘门、输入门以及输出门。其中遗忘门负责决定当前细胞状态中哪些需要遗忘或继续传递;输入门负责决定当前新输入的数据中有多少选择加入到当前的细胞状态中;输出门负责决定多少新的细胞状态可以输出。
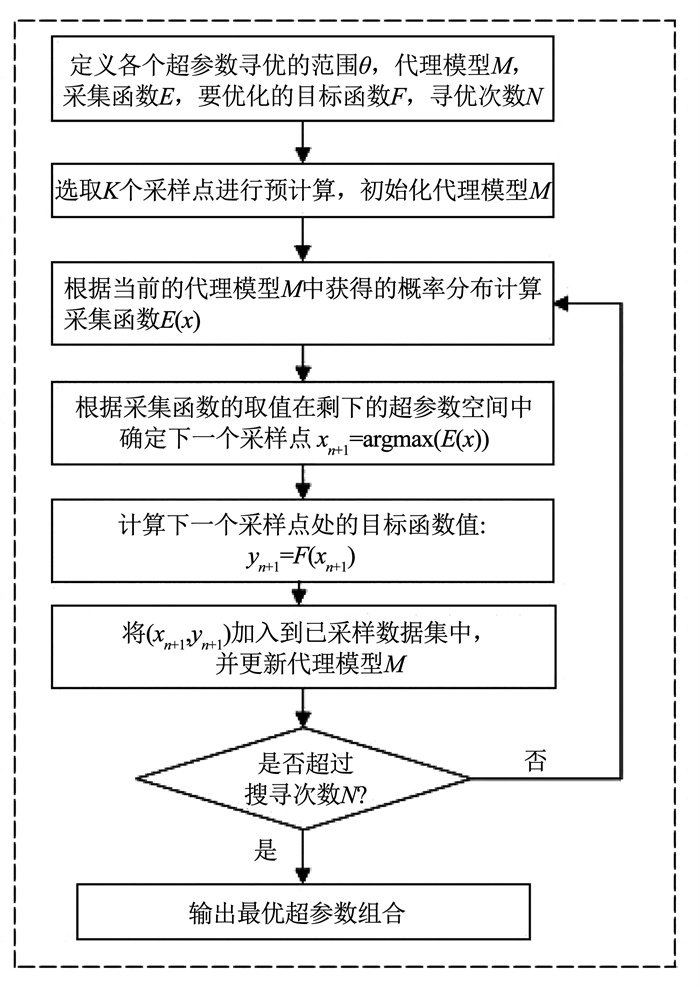
1.3 Bayesian算法贝叶斯(Bayesian)优化算法已广泛应用于自动机器学习领域,它的主要流程如图 3所示。
|
图 3 Bayesian优化算法流程 Fig. 3 Bayesian optimization algorithm flow |
从图 3中可以看出在利用贝叶斯算法寻优之前,需要先定义需要优化选取的参数的范围θ、代理模型M、采集函数E、需要优化的目标函数F以及搜寻的次数N。之后预先选取范围θ内的K个点进行代理模型M的初始化,生成最初的“先验知识”。然后根据采集函数E与代理模型M在搜寻空间θ中寻找下一个有可能是极值的点xn+1,计算出该点在目标函数F处的取值yn+1并更新代理模型M,作为寻找下一个点的新的“先验知识”,重复这一步骤,直至超过定义的搜寻次数N,最后即可得出最优超参数组合。
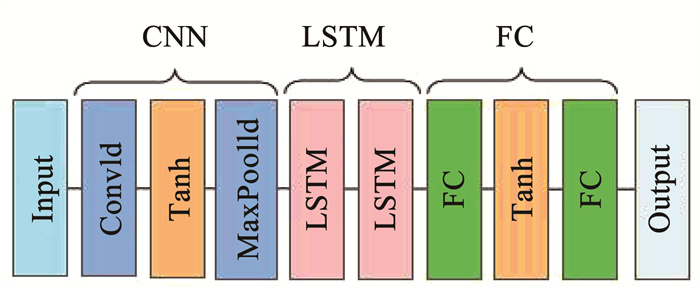
1.4 Bayesian-CNN-LSTM混合模型本文设计一种混合模型,结合了卷积神经网络与循环神经网络的优势,使混合模型能具有处理时间与空间特征的能力。混合模型的结构如图 4所示。
|
图 4 CNN-LSTM结构图 Fig. 4 CNN-LSTM structure diagram |
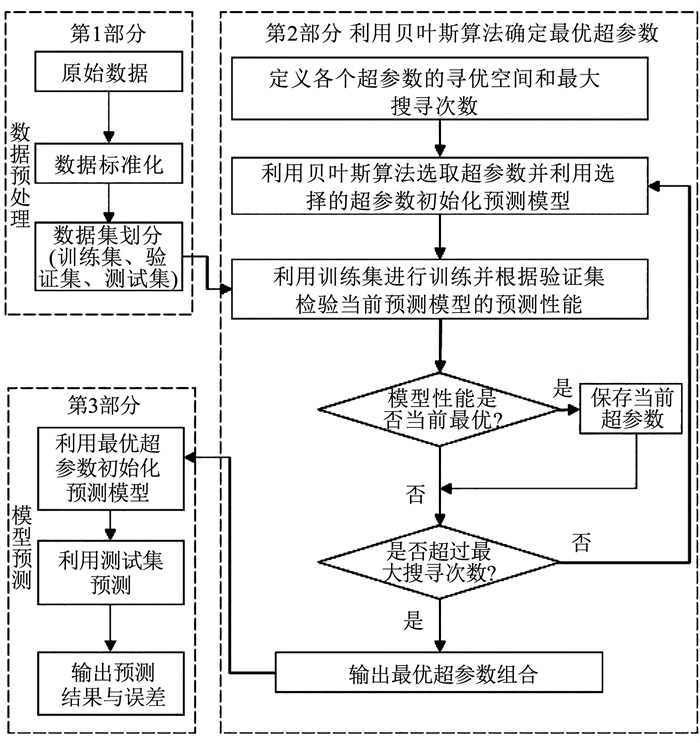
从图 4中可以看出,输入数据先经过卷积神经网络CNN提取空间特征,再通过LSTM的堆叠对提取的特征进行学习,在学习结束后将LSTM层的输出作为全连接层的输入,最后得到的全连接层(fully connected, FC)的输出即为实际预测值。结合Bayesian算法的CNN-LSTM混合模型的预测流程如图 5所示,其中预测的步骤如下:
|
图 5 Bayesian混合CNN-LSTM流程图 Fig. 5 Bayesian hybrid CNN-LSTM flow chart |
Step1 数据预处理。将原始运动数据进行数据标准化,将数据转化为标准正态分布,然后按照6∶ 2∶ 2的比例划分数据集为训练集、验证集与测试集,以供后续使用。
Step2 设置贝叶斯算法的参数。根据CNN-LSTM混合模型的优化需求进行超参数寻优,定义寻优空间以及最大寻优次数。
Step3 初始化模型结构。根据贝叶斯算法选取一组需要优化的超参数的取值,并结合固定的超参数(输出层节点数等)初始化CNN-LSTM模型的结构。
Step4 模型的训练与验证。利用Step1划分的训练集训练Step3中初始化的模型并使用验证集获得验证误差或其他误差衡量指标。最后将当前模型与历史搜寻的超参数建立的模型对比,并保存当前最优的超参数,最后达到迭代次数,获得全局最优超参数。
Step5 最优模型预测。根据Step4中获取的最优超参数与其他固定的超参数初始化最优模型的结构。然后利用训练集与验证集进行模型的训练与验证,从而得到预测模型。最后将测试集的数据作为模型的输入得到相应的运动预测结果。
2 平台建模与计算 2.1 数据准备与处理本文检验的数据取自AQWA软件对海工平台在不规则波中的纵荡运动数据。表 1列出了海工平台模型的主尺度信息,图 6显示了平台的三维建模结果。
| 表 1 海工平台主要参数 Tab. 1 Main parameters of offshore platform |
|
图 6 海工平台三维建模 Fig. 6 Three-dimensional modeling of offshore platform |
本次海工平台在AQWA中的设置工况见表 2。通过对设计工况下海工平台的实例分析,获得了2 000 s纵荡运动数据,其中数据间隔为0.5 s。之后对标准化操作后的原始数据进行数据集划分,其中实际划分比例为(训练集∶验证集∶测试集=6∶ 2∶ 2),即选取0~1 200 s数据用于训练,1 200~1 600 s数据用于验证,1 600~2 000 s数据用于测试。
| 表 2 环境载荷参数 Tab. 2 Environmental load parameters |
其中数据标准化的公式如下:
| $ x_i^*=\frac{x_i-\bar{x}}{s} $ | (1) |
| $ \bar{x}=\frac{1}{N} \sum\limits_{i=1}^N x_i $ | (2) |
| $ s=\sqrt{\frac{1}{N-1} \sum\limits_{i=1}^N\left(x_i-\bar{x}\right)^2} $ | (3) |
式中:xi*即为原始数据xi标准化后的结果,x为原始数据的均值,N为数据集中样本点的个数,s为原始数据的标准差。
2.2 超参数寻优空间由于混合模型输入层和输出层的节点数根据实验人为确定,故不需要对这两个超参数进行优化选取。对于CNN-LSTM混合模型所需要优化选取的超参数为卷积层中卷积核尺寸与个数、LSTM中隐藏层节点个数与隐藏层数、批训练数以及全连接层节点数。超参数寻优空间见表 3。
| 表 3 超参数寻优空间 Tab. 3 Hyperparameter optimization space |
衡量一个模型预测效果的优劣,一般衡量其均方误差ERMS[15],但由于数据大小不一,仅从均方误差的大小上衡量模型预测效果不能全面地表达模型的优劣。本文额外引入平均相对误差EMR与效能系数R2,其中均方误差与平均相对误差越趋于0证明预测效果越好,效能系数R2取值为-∞~1,R2接近1,表示模型可信度高;R2接近0,表示预测结果接近观测值的平均值水平;R2远远小于0,则模型是不可信的。3个衡量指标的公式如下:
| $ R^2=1-\frac{\sum(X-Y)^2}{\sum x^2} $ | (4) |
| $ E_{\mathrm{RMS}}=\sqrt{\frac{\sum\limits_{i=1}^N(X-Y)^2}{N}} $ | (5) |
| $ E_{\mathrm{MR}}=\frac{1}{N} \sum\limits_{i=1}^N \frac{|X-Y|}{X} \times 100 \% $ | (6) |
| $ x=X-\bar{X} $ | (7) |
式中:R2为效能系数,X即为原始数据,Y即为预测数据,N即为预测数据的个数,X即为原始数据的均值,ERMS为均方误差,EMR为平均相对误差。
3 预测模型的实验本文分别选取预测时长为6、12、18 s。本文采取多输入多输出的形式,从而避免因迭代误差导致的模型预测能力下降。9种不同的预测时长与输入时长的对应关系见表 4。
| 表 4 不同预测-输入时长对应关系 Tab. 4 Relationship between different prediction-input durations |
本次实验运行的设备CPU为i5-12400f,运行内存为16 G,显卡为NVIDIA RTX 3060,运行环境为Python 3.8.3和Pytorch 1.8(cuda 12.1)。
3.1 纵荡运动6 s预测模型分别使用海工平台纵荡运动前18、36、54 s的真实数据来预测随后6 s的纵荡运动。使用数据中的前1 600 s用于训练和衡量预测模型的预测能力,使用后400 s进行测试。用于测试的400 s运动数据的预测过程如图 7所示。

|
图 7 测试集的预测过程 Fig. 7 Prediction process of test set |
从图 7中可以看出,假设当前时刻为t0,输入时长为T,预测时长为tpre。模型第1次预测的输入为t0-T~t0,即图 7中的Input1,可以得到t0~ t0+ tpre相应的预测值;在下一次的预测中,模型预测的输入为上一次的输入Input1向右滑动tpre,即图 7中的Input2可以得到t0+ tpre~t0+ 2tpre相应的预测值,直至实现完整预测。在最终的预测示意图中仅展示了400 s的预测时长中能整除预测时长tpre的最大长度。
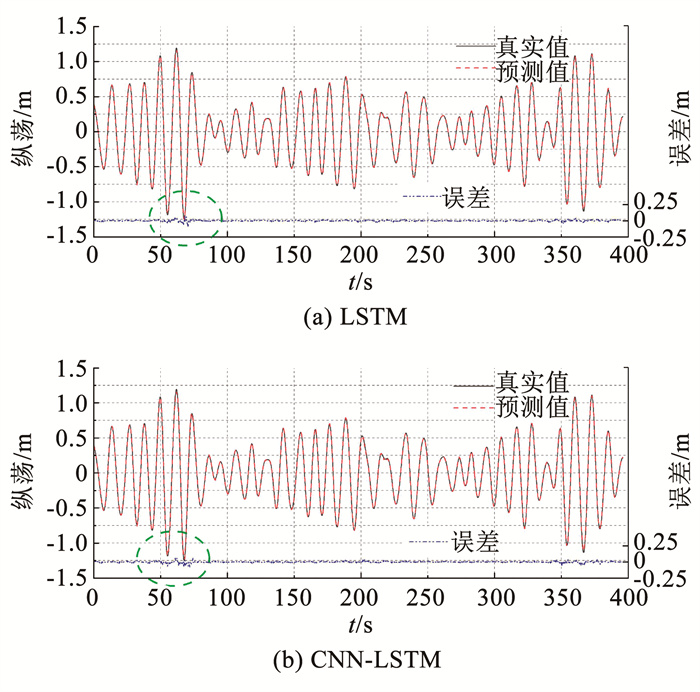
图 8中展示了混合模型与LSTM模型在6 s预测上的对比。从图 8中可以看出,混合模型的预测值与真实值可以做到几乎重合。通过观察预测误差的变化趋势可以看出在绝大多数区域的预测误差可以做到趋于0,足以证明CNN-LSTM模型在6 s预测上具有良好的性能。除此之外,将CNN-LSTM模型与LSTM模型进行对比可以发现,在50~70 s的预测区域内(图中虚线框区域),混合模型比LSTM模型的预测精度更高。由于36、54 s的输入时长的规律与18 s输入时长相同,本文只展示了18 s预测输入的预测效果对比。在以下不同的预测时长上同理。
|
图 8 6 s预测指标对比(输入18 s) Fig. 8 Comparison of 6 s prediction (Input 18 s) |
由于图 8中不能更显著地比较出CNN-LSTM混合模型的预测结果相较于传统LSTM模型的优劣,现将两种模型的对应的预测指标汇总在表 5中。
| 表 5 6 s预测指标对比 Tab. 5 Comparison of 6 s predicted indicators |
从表 5中可以看出输入时长为18、36、54 s时,混合模型的平均相对误差相比于单独LSTM模型减小了15%左右,CNN-LSTM混合模型的预测性能优于单独LSTM模型,表现出混合模型的优越性。在R2方面,所有模型的值均大于0.99,由此表明模型的置信度较高。
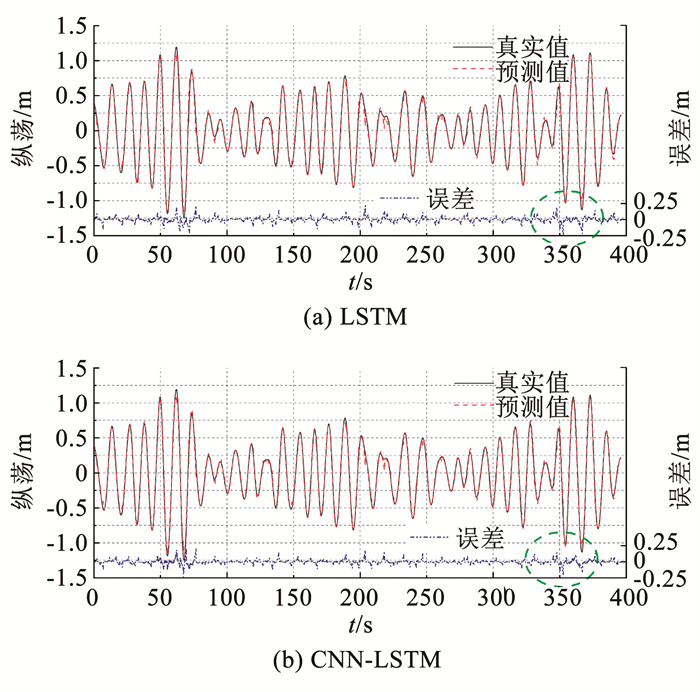
3.2 纵荡运动12 s预测模型分别使用海工平台纵荡运动前18、36、54 s的真实数据来预测随后12 s的纵荡运动如图 9所示。从图 9中可以看出,在运动峰值区域,相较于其他区域,预测效果较差,但CNN-LSTM模型在峰值区域(图中虚线框区域)的预测性能仍比单独LSTM模型的效果好。
|
图 9 12 s预测指标对比(输入18 s) Fig. 9 Comparison of 12 s prediction (Input 18 s) |
表 6为两种模型的12 s预测指标对比,从表 6中可以看出,输入时长为18、36、54 s时,混合模型的平均相对误差相比于单独LSTM模型减小了25%左右,不同输入时长下混合模型的预测性能均优于单独LSTM模型。在R2方面,所有模型的值均大于0.99,由此表明模型的置信度高,但相较于预测时长为6 s时,R2整体有所下降,均方误差有所增大,模型的预测性能有所下降。
| 表 6 12 s预测指标对比 Tab. 6 Comparison of 12 s predicted indicators |
分别使用海工平台纵荡运动前18、36、54 s的真实数据来预测随后18 s的纵荡运动如图 10所示。从图 10中可以看出,相较于6 s预测模型和12 s预测模型,在相同输入长度的条件下,18 s预测模型的预测性能明显低于前两种预测模型,在峰值处容易出现忽高忽低的现象,但总体预测基本符合变化趋势并且有较高的拟合度。在图 10中虚线框区域可以看出,混合模型的误差小于LSTM模型,有更好预测性能。
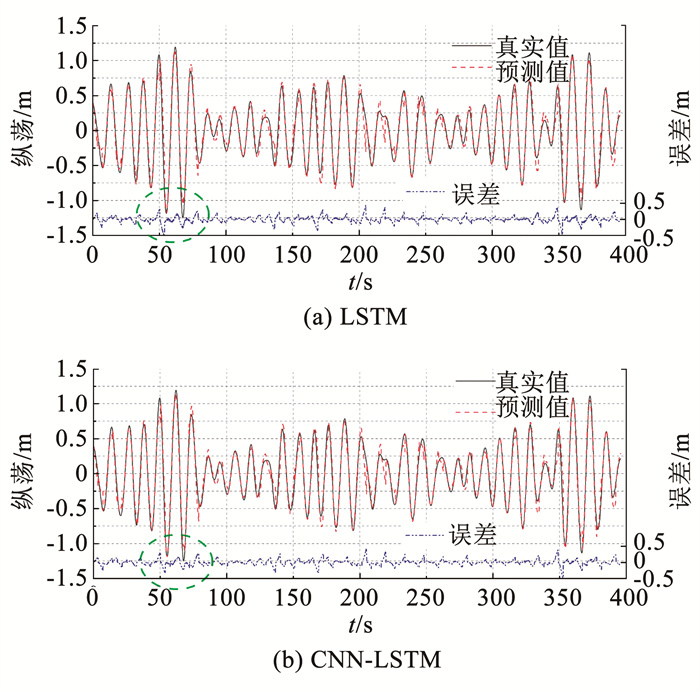
|
图 10 18 s预测对比(输入18 s) Fig. 10 Comparison of 18 s prediction (Input 18 s) |
表 7为两种模型在18 s上的预测指标对比,从表 7中可以看出,在输入时长为18、36、54 s时,混合模型的平均相对误差相比于单独LSTM模型减小了30%左右,混合模型的预测性能均优于单独LSTM模型。在R2方面,所有模型的值均大于0.90,由此时,R2整体再次下降,混合模型的平均相对误差增大至10%左右,相比于6 s预测和12 s预测,整体预测效果较差,但仍在误差允许范围内。表明模型的置信度较高。但相较于预测时长为12 s预测,整体预测效果较差,但仍在误差允许范围内。
| 表 7 18 s预测指标对比 Tab. 7 Comparison of 18 s predicted indicators |
将不同预测时间的所有模型的衡量指标汇总见表 8。由于均方误差在对应不同的数据集时无法根据其值的大小准确反映模型的预测水平,故本文通过平均相对误差来衡量模型的预测能力如图 11所示。
| 表 8 CNN-LSTM混合模型指标汇总表 Tab. 8 Summary table of CNN-LSTM hybrid model indicators |
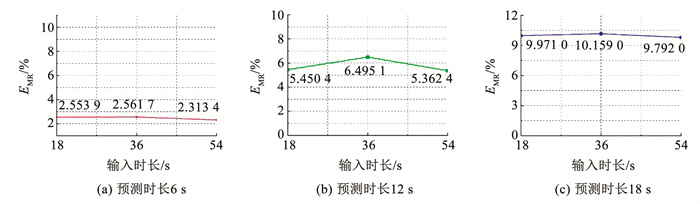
|
图 11 固定预测时长对比 Fig. 11 Comparison chart of fixed prediction duration |
从表 8和图 11中可以看出,当固定预测时长时,平均相对误差会呈现出随输入时长增加而增加的特征,这是由于当模型当前输入时长足以捕获运动数据之间的时空关系时,进一步增加输入时间长度会造成信息冗余,造成模型的“过度学习”,不利于提高模型的鲁棒性。但后续延长输入长度时,平均相对误差会出现减小的情况,这是由于延长的输入中引入了新的“模型知识”,从图 11中可以看出模型具备较强的学习能力。
当通过固定输入时长,改变预测时长时,得到的曲线如图 12所示,从图 12中可以看到模型的平均相对误差近似呈线性上升趋势,即模型的预测能力越来越差,本文可以根据实际预测需求,选取满足误差要求的最大预测时长,使海上作业人员有更多的时间来应对应急情况的发生。LSTM中的规律与CNN-LSTM的规律相似。
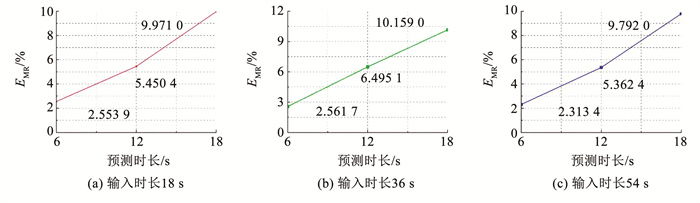
|
图 12 平均相对误差与预测时长关系图 Fig. 12 Relationship between mean relative error and prediction time |
除此之外,模型的训练耗时与预测耗时也是应考虑的条件,表 9给出了在9个不同的输入、输出对应关系上,CNN-LSTM模型与LSTM模型训练以及预测所消耗的时间,其中为了更准确的得到模型训练与预测耗时,分别进行50次实验并取平均,表 9中的训练耗时指模型每训练一代的耗时,预测耗时指模型训练结束后调用测试集完整预测400 s的耗时。
| 表 9 预测模型训练与预测耗时 Tab. 9 Training time and prediction time of prediction models |
通过对比训练耗时可以得出,在9种不同的输入、输出时长的实验上,混合模型在每一个epoch的平均训练耗时约比LSTM模型高出25%,其中多出的耗时是由于CNN的加入,额外添加了特征提取工作,使预测模型的训练参数增加。通过对比预测耗时可以发现,混合模型与LSTM模型在相同的预测任务上计算耗时接近,主要原因在于,在模型预测阶段不需要大量的更新权重等工作,只需利用当前模型的各个权重数据对输入进行矩阵运算等操作,而两种模型参数的数量在数量级上没有明显差异。由于训练耗时均为“秒”级别,在实际的应用过程中差异较小,因此综合预测精度与训练耗时,本文的CNN-LSTM模型更具有优势。
4 结论1) 提出的CNN-LSTM混合模型能够预测海工平台未来一段时间的运动,在6、12、18 s的预测时长上平均相对误差均在10%以内,均具有较高的预测精度,满足应用的要求。
2) 在本文研究的3种不同的预测时长上,证明了混合模型的预测精度均高于LSTM模型,在幅值区域具有更小的预测误差,总体预测精度可提高15%~30%,且随着预测时长的增加优越性越明显。
3) 探究了预测精度与输入时长、预测时长之间的关系,可以看出模型的预测精度随着预测时长的增加呈现线性减小趋势,受输入时长的影响不大,可作为实际预测任务中的参考。
4) 结合预测模型的训练耗时,本文的CNN-LSTM混合模型与LSTM模型的差异较小,综合预测精度与训练耗时,CNN-LSTM模型更具有优越性。
| [1] |
JIANG Yanshu, JIA Mingqi, ZHANG Biao, et al. Ship attitude prediction model based on cross-parallel algorithm optimized neural network[J]. IEEE Access, 2022, 10: 77857. DOI:10.1109/ACCESS.2022.3193573 |
| [2] |
YAO Jianxi, LIU Zuyuan, SONG Xuemin, et al. Ship manoeuvring prediction with hydrodynamic derivatives from RANS: Development and application[J]. Ocean Engineering, 2021, 231: 109036. DOI:10.1016/j.oceaneng.2021.109036 |
| [3] |
FU Huixuan, LIU Sheng, SUN Feng. Ship motion prediction based on AGA-LSSVM[C]//2010 IEEE International Conference on Mechatronics and Automation. Xi'an: IEEE, 2010: 202. DOI: 10.1109/ICMA.2010.5589093
|
| [4] |
CASTRO A, CARBALLO R, IGLESIAS G, et al. Performance of artificial neural networks in nearshore wave power prediction[J]. Applied Soft Computing, 2014, 23: 194. DOI:10.1016/j.asoc.2014.06.031 |
| [5] |
YIN Jianchuan, WANG Ning, PERAKIS A N. A real-time sequential ship roll prediction scheme based on adaptive sliding data window[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2017, 48(12): 2115. DOI:10.1109/TSMC.2017.2735995 |
| [6] |
YAO Yuxin, HAN Liang, WANG Jiangyun. Lstm-pso: long short-term memory ship motion prediction based on particle swarm optimization[C]//2018 IEEE CSAA Guidance, Navigation and Control Conference (CGNCC). Xiamen: IEEE, 2018: 1. DOI: 10.1109/GNCC42960.2018.9018688
|
| [7] |
YIN Wenpeng, SCHVTZE H, XIANG Bing, et al. ABCNN: Attention-based convolutional neural network for modeling sentence pairs[J]. Transactions of the Association for Computational Linguistics, 2016, 4: 259. DOI:10.1162/tacl_a_00097 |
| [8] |
WANG Wenxu, TANG Ruichun, LI Cheng, et al. A BP neural network model optimized by Mind Evolutionary Algorithm for predicting the ocean wave heights[J]. Ocean Engineering, 2018, 162: 98. DOI:10.1016/j.oceaneng.2018.04.039 |
| [9] |
BERGSTRA J, BARDENET R, BENGIO Y, et al. Algorithms for hyper-parameter optimization[C]//Proceedings of the 24th International Conference on Neural Information Processing Systems. Granada, Spain: ACM, 2011: 2546. DOI: 10.5555/2986459.2986743
|
| [10] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6): 84. DOI:10.1145/3065386 |
| [11] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735. DOI:10.1162/neco.1997.9.8.1735 |
| [12] |
LIU Yucheng, DUAN Wenyang, HUANG Limin, et al. The input vector space optimization for LSTM deep learning model in real-time prediction of ship motions[J]. Ocean Engineering, 2020, 213: 107681. DOI:10.1016/j.oceaneng.2020.107681 |
| [13] |
朱鹏程, 杨冰华, 荀顺达, 等. 基于Transformer的船舶运动预测模型研究[J]. 中国造船, 2022, 63(5): 245. ZHU Pengcheng, YANG Binghua, XUN Shunda, et al. Research on ship motion prediction model based on transformer[J]. Shipbuilding of China, 2022, 63(5): 245. DOI:10.3969/j.issn.1000-4882.2022.05.023 |
| [14] |
HUANG Limin, DUAN Wenyang, HAN Yang, et al. Extending the scope of AR model in forecasting non-stationary ship motion by using AR-EMD technique[J]. Journal of Ship Mechanics, 2015, 19(9): 1033. DOI:10.3969/j.issn.1007-7294.2015.09.002 |
| [15] |
JIANG Hua, DUAN Shiliang, HUANG Limin, et al. Scale effects in AR model real-time ship motion prediction[J]. Ocean Engineering, 2020, 203: 107202. DOI:10.1016/j.oceaneng.2020.107202 |
 2024, Vol. 56
2024, Vol. 56


