由于偏远地区的复杂地理环境和通信限制,传统的无线传感器网络(wireless sensor networks,WSN)面临着数据上传实时性差、能源消耗大等问题[1]。近年来,无人机(unmanned aerial vehicle,UAV)技术的迅猛发展为WSN中信息收集问题提供了灵活的解决思路[2],通过相应的轨迹设计和与传感器节点之间的通信协作,可以实时收集和处理WSN中的数据,极大地提高了数据采集的效率和灵活性。
然而,无论是传感器节点还是无人机都需要电池供电,能量消耗问题成为制约无人机辅助信息收集系统寿命的重要因素[3]。近年来,围绕能量消耗优化问题已经取得了一定的研究成果。文献[4]采用K-means聚类算法和增益共享知识算法,在任务时间和无人机内存约束下,设计了多架无人机的轨迹,最小化了系统的能耗;文献[5]针对单架无人机信息收集场景,提出了一种粒子群(particle swarm optimization,PSO)优化算法,在保证传感器节点服务质量(quality of service,QoS)的前提下最小化了传感器节点的能量消耗;文献[6]采用逐次凸逼近和块坐标下降法(block coordinate descent,BCD),在干扰环境和系统能量约束下,最大化了无人机的任务收集数据量;文献[7]考虑了能量异构的传感器节点上行信息传输问题,设计了一种低复杂度的迭代算法,降低了传感器节点的信息传输能耗;文献[8]采用连续凸优化法对传感器节点的唤醒计划和单架无人机的轨迹进行了联合优化,最小化了所有传感器节点的最大能量消耗;文献[9]在传感器节点位置未知的情况下,提出了一种自适应的无人机飞行路径规划,降低了无人机在执行信息收集任务中的能量消耗;文献[10]基于非正交多址(non-orthogonal multiple access, NOMA)系统,通过调整无人机的轨迹和传感器节点的发射功率,优化了地面传感器节点的能量消耗;文献[11]研究了激光充电无人机的实时数据收集问题,并联合优化了信息收集和充电轨迹,延长了无人机的服务时间。
综上所述,现有的无人机辅助信息收集系统能量消耗优化研究中,缺乏对无人机飞行能耗和地面传感器节点传输能耗的联合优化;此外,为了简化问题模型,很少考虑信息传输链路间的干扰,不具现实意义;对干扰与资源约束下的系统能耗优化问题缺乏深入研究。因此,本文在考虑上行信息传输链路间干扰的情况下,联合考虑无人机的飞行能耗和传感器节点传输能耗,同时通过优化无人机轨迹和传感器节点发射功率最小化系统的能量消耗,以期为无人机辅助信息收集系统能量消耗优化研究提供参考。
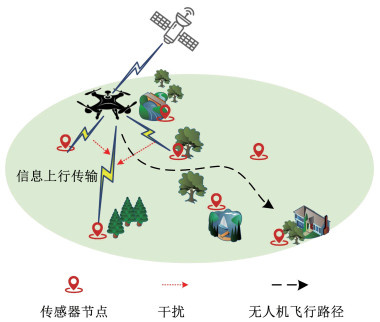
1 无人机辅助信息收集系统模型本文考虑的无人机辅助信息收集系统模型如图 1所示。在一定区域内分布着U个传感器节点,传感器的位置已知,在任务时间T内,无人机从初始位置按照一定的飞行轨迹移动到目的位置,并收集所有传感器节点中的监测信息,通过与近地轨道上的卫星之间的回程链路将数据传输到核心网。为了便于描述无人机的位置,将T划分为N个时隙[12],且无人机在每个时隙内的位置近似不变,多个传感器节点同时对无人机进行数据传输时,采用NOMA技术[13]以提高频谱利用率。
|
图 1 无人机辅助信息收集系统模型 Fig. 1 Model of UAV-assisted data collection system |
当无人机在一定高度与地面传感器节点通信时,大部分时间都存在视距传输路径[14-15]。因此,本文采用自由空间路径损耗模型描述无人机与传感器节点之间的信号衰减情况,无人机与地面传感器节点i之间的信道增益为
| $ g_i=\beta_0 d_i^{-2}[<italic>n</italic>] $ | (1) |
式中:β0为参考距离等于1 m处的信道功率增益; di[n]为在时隙n(n∈N)内无人机与地面传感器节点i之间的距离,可以表示为
| $ d_i[<italic>n</italic>]=\sqrt{\left\|\boldsymbol{q}[<italic>n</italic>]-\boldsymbol{u}_i[<italic>n</italic>]\right\|^2+H^2} $ | (2) |
式中:q[n]和ui[n]分别为在时隙n内无人机和传感器节点i的位置,H为无人机的飞行高度。
为了进行连续时隙过程的无人机轨迹和功率资源优化,当多个传感器节点向无人机传输信息时,本文将无人机与多个传感器之间的信道增益进行排序处理,当有k个传感器节点同时向无人机传输数据时,根据香农定理,在时隙n内传感器节点与无人机之间的可传输数据量可表示为
| $ R_{s_k}[n]=B \log \left(1+\frac{p_{s_k}[n] g_{s_k}[n]}{\sum\limits_{l=1}^{k-1} p_{s_l}[n] g_{s_l}[n]+\sigma^2}\right) \tau $ | (3) |
式中:sk为与无人机之间信道增益第k小的传感器节点序列号,psk[n]为相应传感器节点的发射功率,gsk[n]为相应链路的信道增益, psl[n]为与无人机之间信道增益第l (l∈[1, k-1])小的传感器节点发射功率,gsl[n]为相应链路的信道增益, σ为高斯白噪声, τ=T/N为时隙长度, B为系统带宽。
1.2 能量消耗模型在本文考虑的无人机辅助信息收集系统中,系统能耗主要分为两部分,分别是无人机的飞行能耗和传感器节点的上行信息传输能耗。在整个服务过程中,所有地面传感器节点向无人机进行数据传输的总能耗为
| $ E_{\mathrm{tra}}=\sum\limits_{i=1}^U \sum\limits_{n=1}^N p_i[n] \tau $ | (4) |
式中pi[n]为时隙n内第i个传感器节点的上行传输功率。
随着旋翼无人机速度的增大,其飞行功率呈先减小后上升的趋势,且静止悬停并不是最节能的飞行状态[16],因此本文中无人机在执行任务过程中采用飞行数据收集模式[17-18]。根据文献[19],在执行任务过程中无人机的飞行总能耗为
| $ E_{\operatorname{mov}}=\sum\limits_{n=1}^N \frac{m}{2}(v[n])^2 \tau $ | (5) |
式中m为无人机质量,v[n]为无人机在时隙n中的速度。
综上所述,在整个信息收集任务过程中,系统能量消耗可以表示为
| $ E_{\mathrm{all}}=E_{\mathrm{tra}}+E_{\mathrm{mav}} $ | (6) |
本文的目标是最小化系统能耗,即最小化Eall,无人机在飞行过程中的能量消耗远大于信息传输能耗[20],然而传输能耗却影响着服务质量,因此有必要对飞行能耗和信息传输能耗进行联合优化。为此,本文引入平衡因子γ、传输能耗权重因子α和无人机飞行能耗权重因子β以平衡各个部分的能耗,且有α+β=1,则式(6)中的目标函数可表示为
| $ E_{\text {all }}=\alpha \sum\limits_{i=1}^U \sum\limits_{n=1}^N p_i[n] \tau+\beta\left(\gamma \sum\limits_{n=1}^N \frac{m}{2}(v[n])^2 \tau\right) $ | (7) |
每个传感器节点需上传的数据量为Δ,无人机飞行过程中,在完成传感器节点信息收集任务基础上,重点考虑传感器节点的发射功率约束以及无人机的位置约束,则基于系统能耗最小化的优化问题可建模为
| $ \min _{\boldsymbol{\Phi}, \boldsymbol{q}_{\text {uav }}} E_{\text {all }} $ | (8) |
s.t. C1:0≤pi[n]≤pmax, ∀i∈U, n∈N
C2:
C3:‖quav[n]-quav[n-1]‖≤vmaxτ, n∈N
C4:quav[0]=qinit, quav[N]=qfina, n∈N
式中:Φ和quav分别为传感器节点的发射功率和无人机的空中位置集合;C1规定每个传感器节点的发射功率不超过其最大发射功率pmax;C2规定每个传感器节点在任务周期内完成数据上传任务,Ri[n]为第i个传感器节点在时隙n内的传输数据量;C3和C4约束了无人机的速度和位置,vmax为无人机最大速度,qinit为无人机初始位置,qfina为无人机最终位置。
通过分析可知,由于C2中包含功率和轨迹变量的耦合项,式(8)中的优化问题具有非凸性,直接求解困难。因此,首先基于BCD思想,将优化问题分解为功率分配和轨迹优化两个子问题,再根据各子问题的特性,通过引入中间变量和连续凸近似等方法对各个子问题进行处理,最后通过交替求解两个子问题,逐渐逼近式(8)中问题的近似最优解。
3 轨迹设计与功率分配交替优化算法 3.1 子问题1:确定无人机轨迹下的传感器节点功率分配当无人机的飞行轨迹确定时,Emov为常数, 在数学求解过程中可以忽略不计,式(8)中定义的优化问题可以重新表示为
| $ \min _{\Phi} E_{\text {all }} $ | (9) |
s.t.C1:0≤pi[n]≤pmax, ∀i∈U, n∈N
C2:
由于C2的存在,使得式(9)中的优化问题仍然具有非凸性,难以直接求解。为此, 首先对式(3)进行变换得到
| $ \mathrm{e}^{R_{s_k}[n] \frac{\ln _2}{\tau B}}=1+\frac{p_{s_k}[n] g_{s_k}[n]}{\sum\limits_{l=1}^{k-1} p_{s_l}[n] g_{s_l}[n]+\sigma^2} $ | (10) |
此时引入中间变量
| $ \left\{\begin{array}{l} \Theta=\ln 2 /(\tau B) \\ L_{s_k}[n]=\sum\limits_{l=1}^k p_{s_l}[n] g_{s_l}[n]+\sigma^2 \end{array}\right. $ | (11) |
式中Lsk[n]为k条链路在高斯白噪声下的信号强度,根据式(11)中的递归关系并代入式(10)可得
| $ \left\{\begin{array}{l} p_{s_k}[n]=\frac{L_{s_k}[n]-L_{s_{k-1}}[n]}{g_{s_k}[n]}, k \neq 1 \\ L_{s_k}[n]=\mathrm{e}^{\Theta R_{s_k}[n]} L_{s_{k-1}}[n], k \neq 1 \end{array}\right. $ | (12) |
对式(12)整理,传感器节点的发射功率可以表示为
| $ p_{s_k}[n]=\frac{\left(\mathrm{e}^{\Theta R_{s_k}[n]}-1\right) L_{s_{k-1}}[n]}{g_{s_k}[n]}, k \neq 1 $ | (13) |
为不失一般性,当k=1时, 根据式(3)和式(11)有
| $ \left\{\begin{array}{l} R_{s_1}[n]=B \log \left(1+\frac{p_{s_1}[n] g_{s_1}[n]}{\sigma^2}\right) \tau \\ L_{s_1}[n]=p_{s_1}[n] g_{s_1}[n]+\sigma^2 \end{array}\right. $ | (14) |
综合中间变量对式(14)进行整理, 并对所有传感器节点完备描述,可得
| $ L_{s_k}[n]=\sigma^2 \mathrm{e}^{\Theta \sum\limits_{l=1}^k R_{s_l}[n]} $ | (15) |
此时结合式(13)和式(15),传感器节点的发射功率可以重新表示为
| $ p_{s_k}[n]=\frac{\sigma^2}{g_{s_k}[n]}\left(\mathrm{e}^{\Theta \sum\limits_{l=1}^k R_{s l}[n]}-\mathrm{e}^{\Theta \sum\limits_{l=1}^{k-1} R_{s l}[n]}\right), k \neq 1 $ | (16) |
当规定
| $ p_{s_k}[n]=\frac{\sigma^2}{g_{s_k}[n]}\left(\mathrm{e}^{\Theta Q_k[n]}-\mathrm{e}^{\Theta Q_{k-1}[n]}\right) $ | (17) |
式中Qk[n]为在时隙n内所有传感器节点向无人机传输数据量之和,此时原问题可以重新表示为
| $ \min _{\Phi} E_{\text {all }} $ | (18) |
s.t.C1:
∀k∈U, n∈N
C2:
其中
| $ E_{\text {all }}=\alpha \sum\limits_{k=1}^U \sum\limits_{n=1}^N \frac{\sigma^2}{g_{s_k}[n]}\left(\mathrm{e}^{\Theta Q_k[n]}-\mathrm{e}^{\Theta Q_{k-1}[n]}\right) $ | (19) |
式(18)、(19)的目标函数中,eΘQk[n]-eΘQk-1[n]为指数函数之差,其性质未知,但是对信道增益排序处理使得所有传感器节点的发射功率之和为凸函数,具体证明见附录。在约束条件中,C2为变量的仿射函数,对于C1中的eΘQk[n]-eΘQk-1[n],采用一阶泰勒展开对其进行连续凸逼近处理,定义函数f(Q)=eΘQ,对于给定的任意局部点Q=Q0,均可以对其进行一阶泰勒展开, 得到其全局下界
| $ \begin{aligned} \tilde{f}\left(Q \mid Q_0\right)= & f\left(Q_0\right)+\left(Q-Q_0\right) f^{\prime}\left(Q_0\right)= \\ & \mathrm{e}^{\Theta Q_0}+\Theta\left(Q-Q_0\right) \mathrm{e}^{\Theta Q_0} \end{aligned} $ | (20) |
显然, 式(20)是关于Q的线性函数,基于此方法将式(18)中的C2替换为其一阶泰勒展开式
| $ 0 \leqslant \frac{\sigma^2}{g_{s_k}[n]}\left[\mathrm{e}^{\theta Q_k[n]}-\tilde{f}\left(Q_{k-1} \mid Q_{k-1}^{\prime}\right)\right] \leqslant p_{\max }, \forall s_k \in U, n \in N $ | (21) |
式中:Q′k-1为上次迭代中关于Qk-1[n]的解。式(21)为指数函数与仿射函数的差,其性质为凸函数,此时式(18)中的问题为凸优化问题,可以采用CVX工具求解。
3.2 子问题2:确定传感器发射功率下的无人机轨迹设计当传感器节点的功率分配策略确定时,原问题可以重新定义为
| $ \min _{\boldsymbol{q}_{\text {uav }}} E_{\text {all }} $ | (22) |
s.t.C3:‖quav[n]-quav[n-1]‖≤vmaxτ, ∀n∈N
C4:quav[0]=qinit, quav[N]=qfina, ∀n∈N
无人机的运动不仅改变其在空中的位置,还影响其与地面传感器节点之间的信道增益。信道增益的取值为路径损耗的倒数,此时系统能耗Eall可以表示为
| $ \begin{aligned} E_{\text {all }}= & \alpha \sum\limits_{k=1}^U \sum\limits_{n=1}^N \sigma^2\left(\mathrm{e}^{\Theta Q_k[n]}-\mathrm{e}^{\Theta Q_{k-1}[n]}\right) \Gamma_i+ \\ & \beta \gamma \tau \frac{m}{2} \sum\limits_{n=1}^N\left(\frac{\left\|\boldsymbol{q}_{\mathrm{uav}}[n]-\boldsymbol{q}_{\mathrm{uav}}[n-1]\right\|}{\tau}\right)^2 \end{aligned} $ | (23) |
式中Γi为无人机与传感器节点i之间的自由空间路径损耗。由上文可知,在每个时隙内无人机的位置近似不变,此时eΘQk[n]-eΘQk-1[n]取值为常数且大于零,则式(23)中的优化问题为凸优化问题,同样可以采用CVX工具求解。
3.3 子问题交替优化由于式(8)中定义的原问题是一个联合优化无人机轨迹和传感器节点发射功率的非凸优化问题,直接求解困难。因此,首先通过BCD法将原问题分解为确定无人机轨迹下的传感器功率分配和确定传感器发射功率下的无人机轨迹设计两个子问题,通过对两个子问题的交替求解得到原问题的近似次优解。轨迹设计与功率分配交替优化算法具体步骤如下:
步骤1 已知传感器节点位置坐标u,每个传感器上传数据量Δ,基于初始轨迹quav0,求解凸优化子问题1,得到初始通信资源分配策略Φ1。
步骤2 初始化迭代次数并计算系统的加权能耗Eall。
步骤3 基于初始通信资源分配策略,求解凸优化子问题2,得到无人机轨迹quav1。
步骤4 基于当前无人机轨迹,求解凸优化子问题1,获得新的资源分配策略Φ2。
步骤5 重复步骤3、4直到达到系统预设条件。
步骤6 返回传感器节点的最优发射功率Φ与无人机轨迹quav。
通过优化算法可以看出,本文提出的轨迹设计与功率分配交替优化算法的核心在于步骤3和步骤4,通过对两个凸优化子问题的迭代求解,得到原非凸问题的近似解。在步骤3中的待优化变量个数为2(N-1),步骤4中的待优化变量个数为UN,则采用内点法得到算法1的计算复杂度为O((2(N-1))3)+O(UN)3),其中O表示括号内变量的数学上界。可以看出, 随着传感器节点数量和时隙数量的增加,算法的计算复杂度也随之增加。
4 仿真分析本文采用MATLAB对所提算法进行仿真。8个传感器节点均匀分布在1 000 m×1 000 m区域内,无人机的高度固定并设置为50 m、初始位置为(0, 0, 50),任务执行终点设置为(1 000, 1 000, 50),具体的参数设置见表 1。
| 表 1 仿真参数 Tab. 1 Simulation parameters |
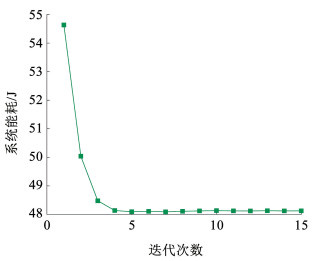
首先,评估本文提出的交替优化算法的收敛性。图 2展示了迭代次数与系统的加权能耗之间的关系。由图 2可知,随着迭代次数的增加,系统能耗逐渐降低,在第5次迭代左右趋于稳定,验证了所提方法的有效性。
|
图 2 加权系统能耗随迭代次数的变化 Fig. 2 Variation of energy consumption of weighted system with iteration times |
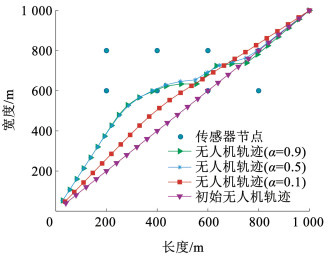
图 3为权重系数对无人机轨迹的影响。由图 3可以看出,随着α的增大,无人机的飞行距离变长,其实质是用更大的飞行能耗换取无人机与传感器节点之间更好的信道状况,从而减小传感器节点的传输能耗。
|
图 3 不同权重系数α下无人机轨迹 Fig. 3 UAV trajectory under different weight of α |
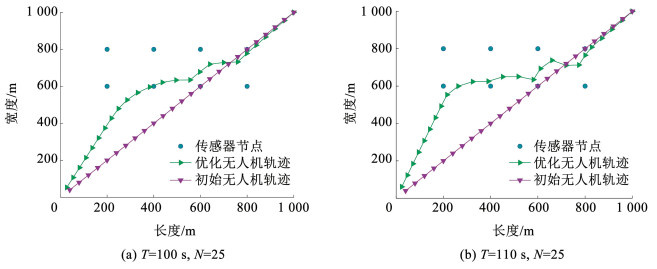
图 4为不同任务时间约束下的无人机轨迹。由图 4可以看出,与初始轨迹相比,无人机在接近传感器节点后,不断调整在每个时隙的位置,通过自身的移动,调整与传感器节点之间的信道状况。同时,随着任务时间的增大,无人机有更充分的时间调整自身的位置,因此图 4(b)中的无人机有着更长的飞行轨迹。
|
图 4 不同T下的无人机轨迹 Fig. 4 UAV trajectory under different T |
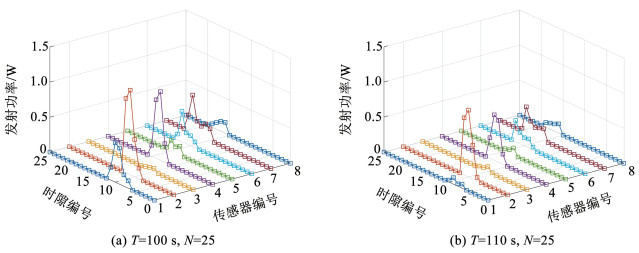
图 5为不同任务时间约束下的每个传感器节点在每个时隙的发射功率。每个传感器在每个时隙的发射功率状态反映了不同的信道状态,无人机距离传感器节点越近,传感器的允许发射功率越低,完成数据上传后,传感器的发射功率置零。
|
图 5 传感器每个时隙的发射功率 Fig. 5 Transmit power of SNs at each slot |
此外,通过对比图 5(a)和图 5(b)可知,当任务执行时间变长时,无人机有更加充分的时间寻找更优的空中位置,改善与传感器节点之间的信道状况,在保证完成数据收集的基础上降低传感器节点的发射功率。
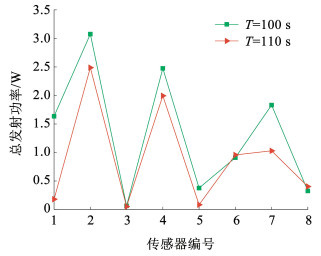
图 6进一步展示了在不同的任务时间下,每个传感器节点在所有时隙的发射总功率情况。在T=110 s下,每个传感器节点的发射功率平均降低了3.2%。
|
图 6 不同T下传感器节点发射总功率 Fig. 6 The total transmit power of SNs under different T |
为了更好地衡量本文所提算法的性能,在传感器节点数量和分布场景相同的情况下,设计了基于正交频分复用(orthogonal frequency division multiplexing,OFDM)系统[5-6]的无人机轨迹和功率分配(trajectory and power allocation,TAPA)算法。在TAPA算法中,虽然传感器节点的带宽为本文NOMA系统的1/U,但却避免了上行链路间的干扰,因此需要仿真对比说明干扰和带宽对信息收集系统性能的影响,并评估本文所提算法是否优化了系统的能量消耗。
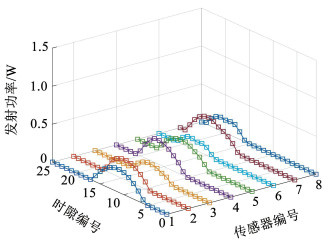
图 7展示了TAPA算法在无人机任务周期T=100 s时每个传感器节点在每个时隙的发射功率情况。与图 5(a)相比,TAPA算法下传感器节点明显受到了带宽的限制,数据上传时间变长;且其功率变化曲线较为平滑,说明为了完成数据上传,每个传感器节点不得不在信道状况不佳时传输数据。在这种情况下,每个传感器节点的总发射功率变大,从而导致传输总能耗增大。
|
图 7 TAPA算法下传感器每个时隙的发射功率 Fig. 7 Transmit power of SNs at each slot with TAPA algorithm |
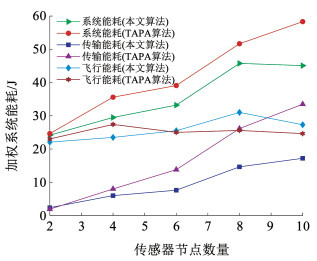
在相同的实验条件下,分别采用TAPA算法和本文提出算法进行100次实验,并统计了系统的平均能耗情况,结果见图 8。由图 8可以看出:当传感器节点数量为2时,带宽和链路间干扰对各自算法的限制相近,导致两种算法下的系统能耗基本相同;随着传感器节点的增多,系统能耗不断上升。然而,在系统带宽一定的情况下,随着传感器节点数量的增加,TAPA算法下每个传感器节点可用带宽变小,依靠调整无人机的位置来改变信道状况逐渐不足以带来性能提升,其飞行能耗曲线趋于平缓;而本文所提算法使得系统性能有更大地提升空间,在严格的任务周期限制下,赋予无人机更大的空间自由度,虽然飞行能耗平均增加了2.9%,但系统能耗平均降低了15.1%,以有限的飞行能耗提升优化了无人机的空中位置,改善了信道状况,从而降低了系统能耗,这也是飞行能耗曲线交叉的原因。
|
图 8 加权系统能耗 Fig. 8 Weighted system energy consumption |
本文在联合考虑无人机辅助信息收集系统中无人机飞行能耗和传感器传输能耗的基础上,以最小化系统能耗为目标,提出了一种考虑链路间干扰的无人机节能轨迹设计和功率分配算法,主要结论如下:
1) 本文建立的考虑链路干扰条件下的无人机轨迹设计和传感器节点功率分配问题具有非凸性,直接求解困难,所提算法通过BCD法将原非凸问题分解为两个可以求解的子问题,通过对两个子问题的交替求解得到了原问题的近似次优解,并具有良好的收敛性。
2) 所提算法联合优化了无人机轨迹和传感器节点的发射功率,在有限增大无人机飞行能耗的同时,有效地降低了系统能量消耗。随着时隙和传感器节点数量的增加,所提算法的复杂度也随之增加。
3) 相较于TAPA算法,随着传感器节点数量的增多,所提算法可以赋予无人机更高的空间自由度。同时,在相同的任务数据量下,传感器节点的发射功率更低,系统能耗优化优势更加明显。
附录由正文可知,经过相应的数学变换,传感器节点的发射功率可表示为
| $ p_{s_k}[n]=\frac{\sigma^2}{g_{s_k}[n]}\left(\mathrm{e}^{\Theta Q_k[n]}-\mathrm{e}^{\Theta Q_{k-1}[n]}\right) $ | (1) |
所有传感器节点的发射功率之和为
| $ \sum\limits_{k=1}^U \frac{\sigma^2}{g_{s_k}[n]}\left(\mathrm{e}^{\Theta Q_k[n]}-\mathrm{e}^{\Theta Q_{k-1}[n]}\right) $ | (2) |
将式(2)展开有
| $ \begin{aligned} \sum\limits_{k=1}^U \frac{\sigma^2}{g_{s_k}[n]}\left(\mathrm{e}^{\Theta Q_k[n]}-\mathrm{e}^{\Theta Q_{k-1}[n]}\right)= & \frac{\sigma^2}{g_{s_1}[n]} \times \mathrm{e}^{\Theta Q_1[n]}-\frac{\sigma^2}{g_{s_1}[n]} \times \mathrm{e}^{\Theta Q_0[n]}+\frac{\sigma^2}{g_{s_2}[n]} \times \mathrm{e}^{\Theta Q_2[n]}- \\ & \frac{\sigma^2}{g_{s_2}[n]} \times \mathrm{e}^{\Theta Q_1[n]}+\frac{\sigma^2}{g_{s_3}[n]} \times \mathrm{e}^{\Theta Q_3[n]}-\frac{\sigma^2}{g_{s_3}[n]} \times \mathrm{e}^{\Theta Q_2[n]}+\cdots+ \\ & \frac{\sigma^2}{g_{s_U}[n]} \times \mathrm{e}^{\Theta Q_U[n]}-\frac{\sigma^2}{g_{s_U}[n]} \times \mathrm{e}^{\Theta Q_{U-1}[n]} \end{aligned} $ | (3) |
对式(3)进行整理可得
| $ \begin{aligned} \sum\limits_{k=1}^U \frac{\sigma^2}{g_{s_k}[n]}\left(\mathrm{e}^{\Theta Q_k[n]}-\mathrm{e}^{\Theta Q_{k-1}[n]}\right)= & \frac{\sigma^2}{g_{s_U}[n]} \times \mathrm{e}^{\Theta Q_U[n]}-\frac{\sigma^2}{g_{s_1}[n]} \times \mathrm{e}^{\Theta Q_0[n]}+\frac{\sigma^2}{g_{s_1}[n]} \times \mathrm{e}^{\Theta Q_1[n]}-\frac{\sigma^2}{g_{s_2}[n]} \times \mathrm{e}^{\Theta Q_1[n]}+ \\ & \underbrace{\frac{\sigma^2}{g_{s_2}[n]} \times \mathrm{e}^{\Theta Q_2[n]}-\frac{\sigma^2}{g_{s_3}[n]} \times \mathrm{e}^{\Theta Q_2[n]}}+\cdots+\underbrace{\frac{\sigma^2}{g_{s_{U-1}}[n]} \times \mathrm{e}^{\Theta Q_{U-1}[n]}-\frac{\sigma^2}{g_{s_U}[n]} \times \mathrm{e}^{\Theta Q_{U-1}[n]}} \end{aligned} $ | (4) |
观察到式(4)的特点,首先定义1/gs0[n]=0和1/gsU+1[n]=0,接着引入1/gs0[n]×σ2eΘQ0[n]和1/gsU+1[n]项,并添加到式(4)中,此时式(4)可重新表示为
| $ \begin{aligned} & \sum\limits_{k=1}^U \frac{\sigma^2}{g_{s_k}[n]}\left(\mathrm{e}^{\Theta Q_k[n]}-\mathrm{e}^{\Theta Q_{k-1}[n]}\right)=\frac{\sigma^2}{g_{s_0}[n]} \times \mathrm{e}^{\Theta Q_0[n]}-\frac{\sigma^2}{g_{s_1}[n]} \times \mathrm{e}^{\Theta Q_0[n]}+\frac{\sigma^2}{g_{s_1}[n]} \times \mathrm{e}^{\Theta Q_1[n]}-\frac{\sigma^2}{g_{s_2}[n]} \times \mathrm{e}^{\Theta Q_1[n]}+\cdots+ \\ & \underbrace{\frac{\sigma^2}{g_{s_{U-1}}[n]} \times \mathrm{e}^{\Theta Q_{U-1}[n]}-\frac{\sigma^2}{g_{s_U}[n]} \times \mathrm{e}^{\Theta Q_{U-1}[n]}}+\underbrace{\frac{\sigma^2}{g_{s_U}[n]} \times \mathrm{e}^{\Theta Q_U[n]}-\frac{\sigma^2}{g_{s_{U+1}}[n]} \times \mathrm{e}^{\Theta Q_U[n]}}= \\ & \sigma^2 \sum\limits_{k=0}^U\left(\frac{1}{g_{s_k}[n]}-\frac{1}{g_{s_{k+1}}[n]}\right) \mathrm{e}^{\Theta Q_k[n]} \end{aligned} $ | (5) |
对信道增益的排序处理使得gsk[n] <gsk+1[n],在式(5)中
| [1] |
AMUTHA J, SHARMA S, NAGAR J. WSN strategies based on sensors, deployment, sensing models, coverage and energy efficiency: review, approaches and open issues[J]. Wireless Personal Communications, 2020, 111(2): 1089. DOI:10.1007/s11277-019-06903-z |
| [2] |
NGUYEN M T, NGUYEN C V, DO H T, et al. UAV-assisted data collection in wireless sensor networks: a comprehensive survey[J]. Electronics, 2021, 10(21): 2603. DOI:10.3390/electronics10212603 |
| [3] |
MESSAOUDI K, OUBBATI O S, RACHEDI A, et al. A survey of UAV-based data collection: challenges, solutions and future perspectives[J]. Journal of Network and Computer Applications, 2023, 216: 103670. DOI:10.1016/j.jnca.2023.103670 |
| [4] |
AMER A A, AHMED R, FAHIM I S, et al. Energy optimization and trajectory planning for constrained multi-UAV data collection in WSNs[J]. IEEE Access, 2024, 12: 9047. DOI:10.1109/ACCESS.2024.3353193 |
| [5] |
BANI-HANI K, HAYAJNEH K F, JARADAT A, et al. Energy-efficient UAV-wireless networks for data collection[J]. Physical Communication, 2023, 60: 102149. DOI:10.1016/j.phycom.2023.102149 |
| [6] |
CAI Qing, TANG Zheng, LIU Chuan. Joint trajectory, transmission time and power optimization for multi-UAV data collecting system[J]. Heliyon, 2024, 10(5): e26627. DOI:10.1016/j.heliyon.2024.e26627 |
| [7] |
CHEN Jie, TANG Jianhua. UAV-assisted data collection for wireless sensor networks with dynamic working modes[J]. Digital Communications and Networks, 2024, 10(3): 805. DOI:10.1016/j.dcan.2022.10.017 |
| [8] |
ZHAN Cheng, ZENG Yong, ZHANG Rui. Energy-efficient data collection in UAV enabled wireless sensor network[J]. IEEE Wireless Communications Letters, 2018, 7(3): 328. DOI:10.1109/LWC.2017.2776922 |
| [9] |
TENG Haojun, DONG Mianxiong, LIU Yuxin. A low-cost physical location discovery scheme for large-scale internet of things in smart city through joint use of vehicles and UAVs[J]. Future Generation Computer Systems, 2021, 118: 310. DOI:10.1016/j.future.2021.01.032 |
| [10] |
TANG Rui, ZHANG Ruizhi, XU Yongjun, et al. Energy-efficient optimization algorithm in NOMA-based UAV-assisted data collection systems[J]. IEEE Wireless Communications Letters, 2023, 12(1): 158. DOI:10.1109/LWC.2022.3219675 |
| [11] |
LUO Chuanwen, ZHANG Jian, QIAN Jin, et al. Data collection of wireless sensor network based on trajectory optimization of laser-charged UAV[J]. High-Confidence Computing, 2024, 4(2): 100181. DOI:10.1016/j.hcc.2023.100181 |
| [12] |
ZENG Yong, ZHANG Rui. Energy-efficient UAV communication with trajectory optimization[J]. IEEE Transactions on Wireless Communications, 2017, 16(6): 3747. DOI:10.1109/TWC.2017.2688328 |
| [13] |
BUDHIRAJA I, KUMAR N, TYAGI S, et al. A systematic review on NOMA variants for 5G and beyond[J]. IEEE Access, 2021, 9: 85573. DOI:10.1109/ACCESS.2021.3081601 |
| [14] |
ZENG Yong, XU Jie, ZHANG Rui. Energy minimization for wireless communication with rotary-wing UAV[J]. IEEE Transactions on Wireless Communications, 2019, 18(4): 2329. DOI:10.1109/TWC.2019.2902559 |
| [15] |
郎磊, 王荆宁, 王一, 等. 无人机辅助通信中基于用户轨迹的无线资源和航迹优化[J]. 通信学报, 2022, 43(3): 225. LANG Lei, WANG Jingning, WANG Yi, et al. Radio resource and trajectory optimization for UAV assisted communication based on user route[J]. Journal on communications, 2022, 43(3): 225. DOI:10.11959/j.issn.1000-436x.2022059 |
| [16] |
TELLI K, KRAA O, HIMEUR Y, et al. A comprehensive review of recent research trends on unmanned aerial vehicles (UAVs)[J]. Systems, 2023, 11(8): 400. DOI:10.3390/SYSTEMS11080400 |
| [17] |
LUO Chuanwen, CHEN Wenping, LI Deying, et al. Optimizing flight trajectory of UAV for efficient data collection in wireless sensor networks[J]. Theoretical Computer Science, 2021, 853: 25. DOI:10.1016/j.tcs.2020.05.019 |
| [18] |
NIE Gaofeng, MA Ting, ZHANG Zhi, et al. Coarse closed-loop trajectory design of multiple UAVs for parallel data collection[J]. IEEE Transactions on Vehicular Technology, 2023, 72(3): 4026. DOI:10.1109/TVT.2022.3222463 |
| [19] |
ENCIU J, HORN J F. Flight performance optimization of a multilift rotorcraft formation[J]. Journal of Aircraft, 2017, 54(4): 1521. DOI:10.2514/1.C034111 |
| [20] |
WANG Haijun, ZHAO Haitao, ZHANG Jiao, et al. Survey on unmanned aerial vehicle networks: a cyber physical system perspective[J]. IEEE Communications Surveys & Tutorials, 2020, 22(2): 1027. DOI:10.1109/COMST.2019.2962207 |
 2024, Vol. 56
2024, Vol. 56


