2. 北京科技大学 自动化学院, 北京 100083
2. School of Automation, University of Science and Technology Beijing, Beijing 100083, China
岩体结构面是指由结构应力所引起的岩体中包括断层、层理、节理和破碎带等地质界面,具有一定的方向,延展较大,厚度较小。经漫长的地质作用的演化,形成了各种各样复杂的岩体结构面。岩体结构面降低了岩体的完整性,使岩体被分割成为不连续的裂隙体。裂隙的存在为流体提供了渗流通道,不利于岩体的稳定性。为了提高岩土工程的效率和项目成果的安全性和稳定性,需要精准且高效的岩土结构面测量方法。
在地质体稳定性研究中结构面起着控制作用[1],文献[2]用结构面的分布与组合解释了杂乱裂隙的规律性,通过数学方法将地质模型转化为力学模型,促进结构面等问题的定量研究。文献[3]基于优势面理论研究了针对区域稳定性的分析方法,将地质研究的理论分析与定量研究相结合。在岩体结构面控制论中,结构面特征是分析岩体力学特性的关键性因素,所以要分析岩体的稳定性需要对结构面进行测量。结构面测量包括接触式测量与非接触式测量两类方法。传统接触式测量主要是人工现场测线统计法,这种方法主要使用地质罗盘和直尺,进行人工现场逐一测量结构面信息。但是这种传统的测量方法不仅工作量大,需要花费大量的人力,而且效率较低、耗费时间长、测量的范围也十分有限、测量人员的现场测量也使得安全系数比较低。无法满足较大规模的断面岩体结构的测量需求。此外,钻探法[4]也只能在有限区域范围里反映局部结构面信息,精度低。随着计算机技术的发展,非接触式测量方法快速发展,逐渐显露出比传统方法更优秀的特性。非接触式测量技术的研究逐渐成为一项前景广阔的重要工作。
非接触式测量主要通过一定的目标处理算法建立三维岩体表面模型(或三维点云),继而开展相关的岩体结构面信息识别和分析工作。这种方法可以一定程度上解决传统方法安全风险高、效率低、工作量大等一系列问题,且可以建立信息数据库,实现信息数据的数字化,为以后的相关工作开展建立基础。非接触式测量技术的核心在于获取岩体表面高精度的三维点云数据,依次开展后续的解析工作。文献[5]提出通过非接触测量的三维激光扫描来获得岩体结构面点云数据,并进一步研究其稳定性。文献[6]提出了一种点云平面拟合方法,利用数学方法对点云数据进行拟合,可以弱化异常值干扰,具有稳健性。文献[7]将利用非接触测量采集的结构面信息得出的数值模型导入GeoSMA-3D系统并利用PFC计算和模拟岩体的局部损伤。文献[8]基于非接触式摄影测量对汶川大溪沟斜坡进行了结构面的采集与几何特征的分析,并进行了三维裂隙网络模拟的研究。目前非接触式测量的测量工具和设备都极大程度上促进了岩体结构面测量的发展,但在另一方面亦存在着缺陷,不能完全顺应岩体测量的需求。全球卫星导航系统(global navigation satellite system, GNSS)[9]测量法是对岩体边坡进行结构监测的一种高效方式,将全球卫星导航系统的传感器安装于所测量的岩体区域范围内,即可实时获取节理裂隙的位移。但是在实际生产中,大部分人工开挖的露天矿岩体边坡与地面所成角度接近垂直,不仅使传感器的安装成为一大难题,而且卫星信号容易被遍挡,导航系统的测量的精度也会受到影响。对于较大范围的岩体表面位移监测,合成孔径雷达(synthetic aperture radar,SAR)[10]近年来已成功应用在很多工程案例,但是对于范围小、形变速度较快的岩体边坡区域,合成孔径雷达的分辨率难以达到实时精确测量的要求[11]。激光雷达(light detection and ranging, LiDAR)[12]也常用于岩体的变形与裂隙发育位移测量,其提供的地形信息具有较高的分辨率,但是其成本较高,且数据体量大,难以满足测量及时性的要求[13]。
非接触测量的摄影测量技术是一种以机器视觉为基础的一种近几年来发展较快且比较成熟的技术,通常机器视觉所用的监测仪器主要有深度相机,它作为一种非接触式的技术能够有效减少人为参与并提升生产效率,相较于一般传感器测量、卫星测量还可以适用于岩体垂直面的测量,相较于三维激光测量成本更加低廉。众多学者利用该技术开展了现场测量与应用研究。文献[14]利用摄影测量技术对积雪的分布进行了测量研究,精度高,误差小;文献[15]探索了多角度图像数据融合的低成本、高效率、易操作的建筑环境信息建模方法;文献[16]对边坡视频数据进行超像素算法的图像处理并裁剪,构建出岩体形变区域的外缘轮廓;文献[17]基于边坡岩体的图像数据利用图像增强方法进行处理,有较高的识别精度;文献[18]通过近地摄影建立了场区数字正射影像模型和三维重建模型;文献[19]引入了微变摄影测量技术,生成了真实、纹理清晰的数字点云模型;文献[20]通过摄影测量开展了对岩体结构面信息的获取,并通过点荷载试验实现了岩体的质量评价;文献[21]使用数码相机对岩体结构进行倾斜摄影测量,在Context Capture中进行了实景建模,获得粗糙度系数来评价各向异性特征;文献[22]建立了ply2parameter和Scanline两种算法,使用主成分分析法算出了三维模型的结构面参数;文献[23]利用统计相似性基于数字近景测量技术测取了岩体结构面迹长、张开度等几何参数,分析了统计模型下的结构面分布类型;文献[24]开展了法向量分析算法开发,基于k近邻值进行法向量的搜索,识别并确定结构面,验证了系统的可行性;文献[25]基于摄影测量进行几何信息处理,纠正了几何畸变,建立了边坡岩体的坐标系,实现了影像镶嵌和产状量计算;文献[26]提出双目重建技术自动化提取结构面间距和岩体粗糙度参数的方法,其优势在于可在环境恶劣的围岩环境中获取稳定高精度的点云模型;文献[27]研究了数字相机在边坡形变位移上的应用,实现了用数字相机测量边坡位移量。以上方法剔除了作业人员与边坡的近距离接触环节,在一定程度上避免了人员受到生命安全威胁,而且相机获取的数据范围更广、维度更高,从而更能反映边坡的整体趋势。此外,文献[28]采用ShapeMetriX3D三维非接触测量系统,在同一位置的两个不同角度对边坡岩体进行了三维模型合成,其中,ShapeMetriX3D是奥地利3GSM公司的系统,是使用通过3G软件和测量来进行标定的数码相机进行数据采集。被标定的相机,需要在同一位置从两个不同的角度来对指定的区域进行成像,然后通过SMX建模软件和JMX分析软件对图像进行3D建模和分析。相关的技术虽然已经比较成熟,但是却具有一定的封闭性,开源性较差,而且数据的分析方面仍需要人工参与,处理结果易受主观因素影响。
本文基于LenaCV双目摄影系统,开展了双目立体成像及三维点云优化参数研究。首先,基于双目相机同一位置一次拍摄获取两张不同角度照片,确定最优棋盘格尺寸和标定距离,并得到相机参数;然后, 选取不同的双目基线距离与物距参数,在相机参数下对左右双目叠加图片进行校正并进行三维点云立体建模;最后,确定了点云建模最佳工况系列试验。本文主要以岩石和立方体为建模对象, 获取不同距离下的数据,并考虑了多种试验因素的影响,研究成果能够为岩体三维结构重建提供方法参考。
1 双目相机标定双目立体成像模拟人的双眼视觉,相比单目捕捉图像,除x、y坐标下的平面二维图像,还建立了z方向的景深,双目成像三维化,使目标更加立体。双目相机的标定即通过提取左右镜头捕捉的图像的三维坐标信息,反算双目相机的内外参数(包括偏移量、旋转角度、焦距等),计算景深,并建立三维模型。
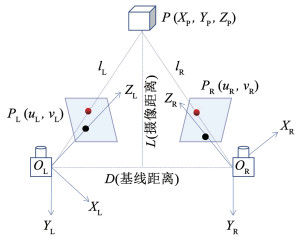
1.1 相机标定原理相机标定原理如图 1所示, 假设在世界坐标系中,目标物体的坐标为P(XP, YP, ZP)。左目镜头所在坐标系为OL(XL, YL, ZL),右目镜头坐所在坐标系为OR(XR, YR, ZR),目标物体P点在单独镜头下有对应的平面坐标,设在左右镜头的坐标系下的平面坐标像点分别为PL(uL, vL)、PR(uR, vR)。分别作投影线OLPL、ORPR,两线交点即为目标物体的坐标P(XP, YP, ZP)。
|
图 1 相机标定原理示意 Fig. 1 Principle for camera calibration |
目前适用范围最广的标定方法有BP神经网络标定法、Tsai两步法以及张正友标定法[29]。张正友标定法是由张正友在1998年提出的,针对相机的标定,给出了一种介于传统定标与自定标之间的方法。张正友标定法只通过以黑白棋盘格作为标定板进行相机标定来计算内外参数的最优解,操作简单,精度高,是目前使用最多的一种标定方法,可有效解决传统的标定方法对标定精度要求较高的问题。标定方法原理如下:
| $ s\left[\begin{array}{l} u \\ v \\ 1 \end{array}\right]=\boldsymbol{C}\left[\begin{array}{llll} r_1 & r_2 & r_3 & t \end{array}\right]\left[\begin{array}{l} X \\ Y \\ 0 \\ 1 \end{array}\right]=\boldsymbol{C}\left[\begin{array}{lll} r_1 & r_2 & t \end{array}\right]\left[\begin{array}{l} X \\ Y \\ 1 \end{array}\right] $ | (1) |
其中:C为相机内参矩阵;[X Y 1]T为z平面点的线性坐标;[u v 1]T为像平面上对应点的线性坐标,此过程将相机坐标转换到了世界坐标;[r1 r2 r3 t] 为相机的相关外参数。
双目系统模拟了人眼,为平行成像系统,则景深、基线距离、焦距和目标到相机光心的距离有如下关系式:
| $ u_{\mathrm{L}}-u_{\mathrm{R}}=D f / l $ | (2) |
式中:uL为目标物体在左镜头坐标系下的坐标值, uR为目标物体在右镜头坐标系下的坐标值, uL-uR为该物体的视差, mm; D为左目和右目镜头光心距离(基线距离), mm;L为物体到双目镜头连线的最短距离(摄像距离), mm;f为镜头焦距(默认左右目焦距相等);l为物体到镜头光心距离, mm。
选用LenaCV双目相机系统为高帧率、可变基线双目相机,输出图像分辨率可达到2 560×960像素,左、右目相机时序同步,拍摄时间误差小于0.01 s。
相机标定过程由MATLAB2021a编程实现。主要步骤如下:1)利用MATLAB APP Visual studio采集双目标定板图像,每组试验标定板固定;2)拍摄时,每组试验的相机基线距离、左右目焦距保持不变,一旦发生改变重新进行试验;3)移动相机位置,使相机在一球面上运动,拍摄不同角度标定板图像,并且标定板均全部位于图像内,背景中无相似色块干扰,拍摄20组;4)输入棋盘格尺寸,启动切割程序,处理出左右双目图像,按照式(1)计算目标物体坐标P(XP, YP, ZP)及相机内参,并按照式(2)计算视差。
1.2 影响标定结果的因素分析 1.2.1 外界干扰影响与标定误差上限相机标定目的是获得相机的内外参数,标定完成后,后续的三维点云建模即在该相机参数下进行,因此自拍摄第一张标定板图像起,需要保证相机基线距离、焦距等固定不变(图 2)。当试验进行过程中,相机发生扰动,相机内部参数即发生改变,产生较大误差(图 3)。当双目相机基线距离固定后,即可基于两个摄像头的距离对目标对象的真实尺寸进行空间标定。

|
图 2 稳定工况下试验误差及建模效果 Fig. 2 Experimental error and modeling effect under stability condition |

|
图 3 扰动下工况试验误差及建模效果 Fig. 3 Experimental error and modeling effect under disturbance condition |
在发生改变的相机参数下校正的目标如图 3(a)~3(f)扰动工况分析结果,校正后图像越靠近边界畸变越明显,且整体图像发生大幅度旋转,在校正后图像基础上建立的三维点云模型无法提取有效图像,点云离散。因此在试验中必须保持相机稳定,避免相机参数发生改变,根据图 2(a)~2(f)所示,相机误差明显减小,校正后图像重合度较为完全,所得三维点云虽边缘尚不完整,但点云图像较为集中,“科技”二字清晰可见。因此误差可一定程度反映试验过程的外界干扰是否足以改变内参并进一步影响立体建模效果。图 3为扰动情况下建模结果,建立的三维点云(图 3(f))非常离散,建模效果较差。基于以上对比明显的试验效果,并根据张正友标定法,将标定误差上限设定为0.5 pixels[27]。即当误差小于0.5 pixels,认为标定合格,相机内参可靠,可以进行进一步探究。下面将基于误差大小进一步讨论影响标定效果的因素,并为三维点云建模确定合适的标定外部参数(棋盘格大小、拍摄距离)。
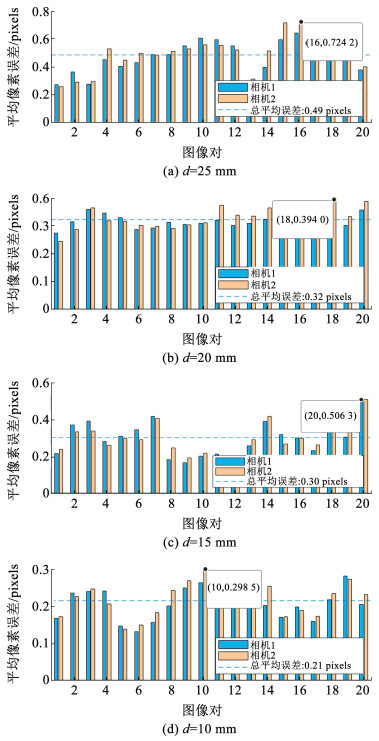
1.2.2 相机标定效果与标定板棋盘格大小的相关性节以7×9标定板棋盘格边长(记为d)作为自变量,研究其与标定误差的相关性。图 4为标定结果, 标定步骤如1.1节所述。棋盘格边长d过大会导致标定板较大而超过视野,边长过小会使镜头无法分辨,导致特征点提取困难,为了使整张7×9的棋盘格完整清晰呈现在该双目相机的视野中,因此棋盘格边长以5 mm为模数分别选取10、15、20、25 mm进行试验。表 1为标定误差分析结果,根据表 1可知,当小格边长为25 mm时,最大误差0.724 2 pixels,平均误差0.49 pixels,小于0.5 pixels;当小格边长为20 mm时,最大误差0.394 0 pixels,平均误差0.32 pixels,此数据低于0.5 pixels,结果理想;当小格边长为15 mm时,最大误差0.506 3 pixels,平均误差0.30 pixels,此误差与20 mm时的相近;当小格边长为10 mm时,最大误差0.298 5 pixels,平均误差0.21 pixels,此误差小于25、20 mm时的误差,明显更加理想。这说明,随着棋盘格边长减小,相机标定的平均误差越小,标定效果越优良。由于相机镜头存在畸变,当棋盘格边长越大,畸变下产生的测量误差越大,观测坐标与3D点投影得到的重投影误差越大。考虑镜头像素质量,为了可以辨别棋盘格,边长亦应适当,不宜过小导致画面模糊导致特征点提取困难,所以可选取10 mm作为标定板棋盘格边长。
|
图 4 不同棋盘格边长标定误差分析 Fig. 4 Calibration error analysis of different checkerboard size |
| 表 1 标定误差分析 Tab. 1 Calibration error analysis |
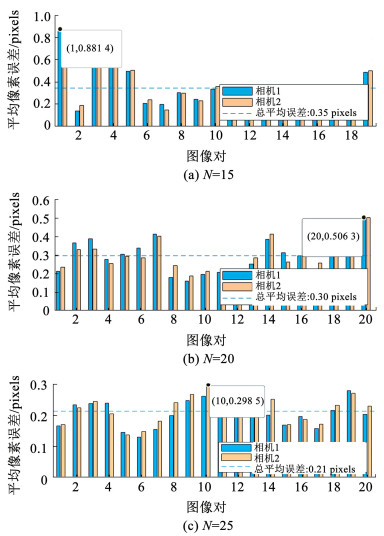
涉及距离的参量有拍摄距离和基线距离,根据图 1,按照“摄像距离=N×基线距离”来确定拍摄距离。为了保证标定板全部呈现在视野中,距离不宜过近,为保证相机像素清晰度,距离不宜过远,因此取N=15、20、25。本试验的基线距离为6 cm,因此拍摄距离分别为90、120、150 cm,试验结果如图 5所示。对比分析试验结果可知,随距离增加,最大误差依次为0.724 2、0.394 0、0.298 5 pixels,平均误差依次为0.49、0.32、0.21 pixels,在保证拍摄完整度和清晰度的距离范围内,随距离增加误差降低。
|
图 5 不同摄像距离/基线距离(N值)与标定误差的关系 Fig. 5 The relationship between different shooting distance/baseline distance and calibration error |
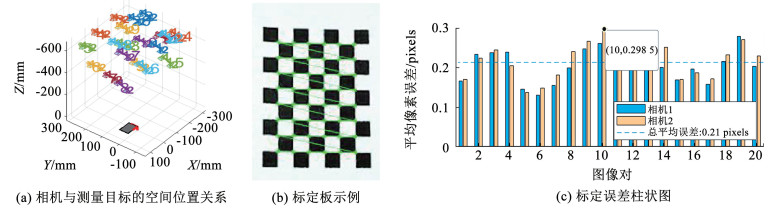
基于以上结果可知,棋盘格边长较小、拍摄距离较远时标定效果好。由于试验误差均已小于0.5 pixels,满足要求,且综合考虑拍摄清晰度与拍摄完整度,棋盘格边长不必再减小,距离不宜再靠近,于是选取10 mm棋盘格,25倍基线距离作为LenaCV相机的最佳标定工况。在该工况下,双目相机拍摄的总体误差如图 6(c)所示,目标图像的像素误差大小应小于0.5 pixels,相机1和相机2分别为左镜头和右镜头的像素误差,浅蓝色虚线为整体平均误差线。最终选取的标定板为7×9,一次性采集20张标定图片,图片为960×1 280像素,右目相机旋转向量和位移向量分别为[1.000 0,-0.007 1,-0.002 5;0.007 1,0.999 9,0.010 6;0.002 4,-0.010 6,0.999 9]和[-1 521.5,-19.837 0,102.341 8],得到的标定平均误差为0.213 9 pixels。
|
图 6 相机标定结果 Fig. 6 Camera calibration result |
本节将对4组不同的建模对象开展研究。利用图 7(a)和图 7(b)所示岩石来对比探究表面粗糙度对建模效果的影响,处理建模后分别对应图 8和图 9。利用图 7(c)所示岩石探究不同主体画面占比对建模效果的影响,对应图 10和图 11。利用图 7(d)所示纸箱模拟岩石立体面,探究不同基线距离在梯度倍数摄距下的景深图与点云建模效果,处理结果如图 12、13所示。

|
图 7 开展三维建模研究对象 Fig. 7 Four research objects for 3D modeling |

|
图 8 难忘石双目建模结果 Fig. 8 Results of binocular modeling of Nanwang stone |

|
图 9 西门石双目建模结果 Fig. 9 Results of binocular modeling of West Gate stone |

|
图 10 图幅占比2/3双目建模结果 Fig. 10 The binocular modeling results when the map proportion is 2/3 |

|
图 11 图幅占比95%双目建模结果 Fig. 11 The binocular modeling results when the map proportion is 95% |
|
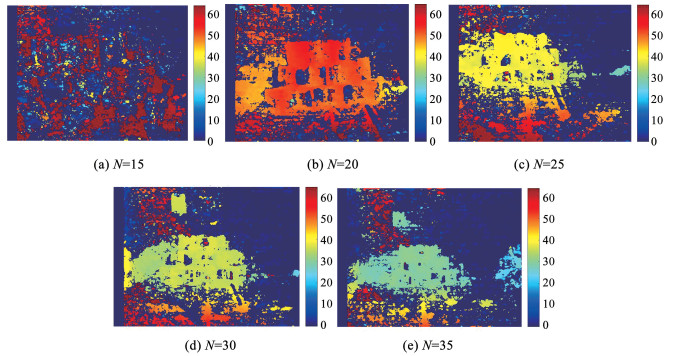
图 12 基线距离12 cm时不同梯度倍数摄距下的景深图(像素) Fig. 12 Depth map modeling of 12 cm baseline distance with multiple spacing(pixels) |

|
图 13 基线距离12 cm时不同梯度倍数摄距下三维点云建模结果 Fig. 13 Point cloud modeling of 12 cm baseline distance with multiple spacing |
试验以粗糙岩石和光滑岩石进行对比。“难忘石”触摸平滑,自然光下无明显明暗区域,为相对较光滑的岩石,“西门石”触摸可感到有明显棱角刮擦,自然光下因表面隆起程度不同有明显的明暗面变化,为相对较粗糙的岩石。通过观察图 8(b)、9(b)两图的点云图中的岩石主体和岩石上的红色字可知,光滑岩石的字迹辨别度低于粗糙岩石,且光滑岩石的完整性也低于粗糙岩石。这是由于光滑岩石表面隆起程度的变化更加连续,节理不明显,平面化程度高,三维立体效果差。因此拍摄对象宜为节理明显,结构面多的物体,这也说明该项研究适于在节理岩体识别、光滑面探伤等领域进行应用。
2.1.2 主体画面占比对试验结果影响图 10(a)、11(a)以近距离的西门石背面岩石及西门石背面的前景为主体,图 10(a)主体约占60%,其余部分为远近不同的树叶、高度不同的条幅,三维点云建模效果显示只有岩石中间小部分区域反映了实物的立体形状,其余均为散点。而对于图 11(a),当主体占据图幅约达95%时,可获得无杂点、纹路清晰的三维重建点云图。因此,当目标对象占据视野越大,远处的杂点越少,对主体建模的干扰越小,主体点云越独立、集中。需要指出的是,尽管占比越高,得到的三维点云越集中,但是会导致摄影测量的目标对象比例偏小。在实际测量中,应综合考虑目标对象的完整程度和非主体因素的影响。
2.2 最佳基线距离及摄像距离分析当主体对象占据图幅越大,图像其他元素在位置和深度上与主体差别越小,主体对象结构面越粗糙,建模效果越理想。于是为了便于试验,采用纸箱堆叠模拟更加复杂的岩体工况,纸箱的棱角模拟岩体的节理,纸箱的面模拟岩体的结构面。与标定不同,由于对象所占图幅比例较大,基线距离的不同会导致双目图像中对象的重合区域大小不同,因此除探究摄像距离与基线距离的最优倍数关系外,还需讨论最佳基线距离。为验证这一猜想,这里选取理论计算的最佳基线距离12 cm作为试验组。考虑纸箱堆叠主体在视野中大小适宜,分别取摄像距离与基线距离比值N为15、20、25、30和35,来讨论最优摄像距离。
选取基线距离12 cm(拍摄距离分别取180、240、300、360、420 cm),根据图 12景深建模结果,当取15倍基距时,景深图特征面识别不清晰,仅能略微辨别部分残缺的面,建模效果不佳,点云非常离散,建模对象边缘基本不成形,且仅有局部纸箱在建模范围内。20倍基距时,景深图呈现出明显的3层纸箱结构,部分纸箱面的深度识别与背景白墙处于同一景深,导致云点图在该处的面和边缘存在空缺,但总体效果较为清晰。取25倍基距时,景深图也可观察出明显的3层纸箱结构,相比20倍基距识别更加有效,空缺明显减少,三维点云中纸箱堆叠情况清晰可见。取30倍基距时,由于摄像距离已经较远,纸箱的深度与整个视野最大深度的比例减小,即纸箱在三维空间中与背景白墙越来越接近,导致纸箱边缘有变模糊的趋势。取35倍基距时,在30倍基距的基础上进一步加大摄像距离,纸箱边缘的糊化程度进一步加深,左侧纸箱的点云变离散,呈现的视觉效果为更加稀疏,出现流纹状的缝隙。因此在12 cm基距下,摄距从15倍基距到35倍基距增加的过程中,视觉三维立体建模效果由差变优再变差。这是因为当距离过近,左右视野的重合程度低,校正效果不佳,进而导致建模不理想;当距离过远,对象与所处背景的深度差异变小,边缘趋于与背景混杂。三维点云结果如图 13所示。堆叠纸箱存在光面和阴暗面,阴暗面往往是建模点云缺损的薄弱区域,因此对阴暗面的建模能力强弱能较直观地反映点云整体的建模效果的好坏。纸箱不同表面之间、纸箱与墙之间是景深发生突变的边缘,边缘的完整性与形状能反映点云建模的效果。因此以下从“面”与“边缘”对建模效果展开评价。根据试验结果可知,基线距离为12 cm时的最优摄像距离为基线距离的25倍。
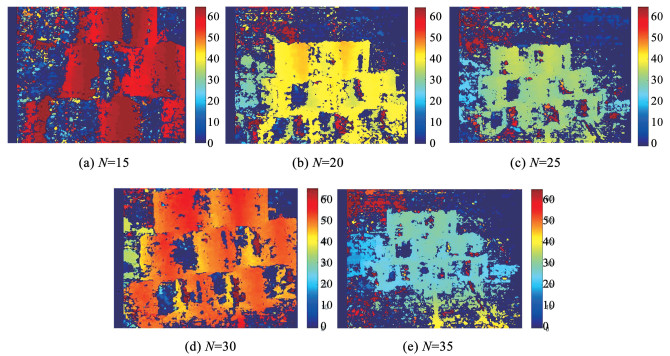
图 14、15分别为选取基线距离为6 cm(拍摄距离分别为90、120、150、180、210 cm)时景深图和三维点云建模结果。在同等倍数梯度下的测试结果与12 cm类似,整体效果欠佳。15倍基距时,同样为大量立体面不完整,35倍基距时边缘向背景畸变严重。30倍基距景深图中的纸箱颜色为橙色,理论上按照距离远近应为绿偏蓝色,可见景深结果不理想。20倍基距和25倍基距则效果近似,且优于其他组别,但是某些面的点云仍存在缺失,建模不完整。通过以上分析,双目立体成像系统是模拟人眼的视觉成像,人眼的距离一般为6 cm左右,对于本试验LenaCV摄像机来说,其摄像头焦距小于人眼,则相同观察情况下,其合适的基线距离理论上应大于人眼,故文中12 cm基距的建模效果明显优于6 cm基距的建模效果,且在12 cm组别的建模试验中最佳的摄像距离为基线距离的25倍。该结果能够为下一步开展双目立体识别优化提供参考。
|
图 14 基线距离6 cm时不同梯度倍数摄距下的景深图(像素) Fig. 14 Depth map modeling of 6 cm baseline distance with multiple spacing(pixels) |

|
图 15 基线距离6 cm时不同梯度倍数摄距下三维点云建模结果 Fig. 15 Point cloud modeling of 6 cm baseline distance with multiple spacing |
本文基于LenaCV双目摄像机立体成像,展开了相机标定、三维点云建模的分析与研究,提出了确定相机内外参数的最优标定工况,并通过试验分析了适于点云建模的目标对象特点以及三维点云建模的最佳拍摄距离与基线距离的关系。得到的主要结论如下:
1) 基于MATLAB平台开展相机标定时,全程不得改变相机内外参数,且当标定误差小于0.5 pixels时结果可靠。标定板棋盘格边长为25、20、15、10 mm时,双目相机标定误差从0.49 pixels降低到0.21 pixels;当拍摄距离按照摄距为基线距离的15、20、25倍时,双目相机标定误差从0.35 pixels减低到0.21 pixels。考虑视野中标定板完整性和清晰度,取棋盘格边长10 mm、标定距离为25倍作为该双目相机的最佳标定工况。
2) 基于对不同目标对象的建模结果分析可知,粗糙、空间面明显的对象建模效果优于光滑平整的对象,且建模效果随目标对象占据双目视野的比例从66.7%到95%的增加而提升。基于以纸箱模拟复杂岩石节理和结构面的试验结果分析可知,在该双目相机参数下,12 cm基线距离优于6 cm基线距离,且随摄像距离依次为基线距离的15、20、25、30、35倍时,建模效果先变优后变差,25倍为最优建模摄影距离。
3) 根据现场试验讨论了最优标定工况、摄影工况和建模对象特点,为岩体三维结构重建提供了可参考的实践经验,验证了基于LenaCV双目摄像机的三维岩体结构面建模的可行性,为进一步研究便携式双目系统在岩体结构面摄影测量的应用提供参考。
| [1] |
谷德振. 岩体工程地质力学基础[M]. 北京: 科学出版社, 1979. GU Dezhen. Engineering geomechanical foundation of rock mass[M]. Beijing: Science Press, 1979. |
| [2] |
孙玉科. 岩体结构力学——岩体工程地质力学的新发展[J]. 工程地质学报, 1997, 5(4): 5. SUN Yuke. Rockmassstructural mechanism——a new advance in rock engineering geological mechanics[J]. Journal of Engineering Geology, 1997, 5(4): 5. |
| [3] |
蒋建平, 章杨松, 罗国煜, 等. 优势结构面理论在岩土工程中的应用[J]. 水利学报, 2001(8): 90. JIANG Jianping, ZHANG Yangsong, LUO Guoyu, et al. The application of preferred plane theory to geotechnical engineering practice[J]. Journal of Hydraulic Engineering, 2001(8): 90. DOI:10.3321/j.issn:0559-9350.2001.08.017 |
| [4] |
王川颖, LAWK T. 钻孔摄像技术的发展与现状[J]. 岩石力学与工程学报, 2005, 24(19): 3440. WANG Chuanving, LAW K T. Review of borehole camera technology[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(19): 3440. DOI:10.3321/j.issn:1000-6915.2005.19.006 |
| [5] |
李杰林, 白德威, 杨承业, 等. 基于三维激光扫描点云数据的地下巷道岩体结构面识别及稳定性分析[J]. 黄金科学技术, 2022, 30(3): 343. LI Jielin, BAI Dewei, YANG Chengye, et al. Recognition and stability analysis of underground tunnel rock mass structural plane based on 3D laser scanning point cloud data[J]. Gold Science and Technology, 2022, 30(3): 343. DOI:10.11872/j.issn.1005-2518.2022.03.070 |
| [6] |
官云兰, 程效军, 施贵刚. 一种稳健的点云数据平面拟合方法[J]. 同济大学学报(自然科学版), 2008, 36(7): 981. GUAN Yunlan, CHENG Xiaojun, SHI Guigang. A robust method for fitting a plane to point clouds[J]. Journal of Tongji University(Natural Science), 2008, 36(7): 981. DOI:10.3321/j.issn:0253-374X.2008.07.023 |
| [7] |
王述红, 昝世明, 王存根, 等. 基于非接触测量技术裂隙岩体隧道开挖局部损伤分析[J]. 现代隧道技术, 2014, 51(3): 110. WANG Shuhong, ZAN Shiming, WANG Cungen, et al. Analysis of local damage induced by tunnelling in a fractured rock mass based on noncontact measurement techniques[J]. Modern Tunnelling Technology, 2014, 51(3): 110. |
| [8] |
张文, 韩博, 孙昊林, 等. 高陡岩质斜坡的结构面非接触式采集技术与三维裂隙网络模拟研究[J]. 工程地质学报, 2020, 28(2): 221. ZHANG Wen, HAN Bo, SUN Haolin, et al. Non-contact collection and 3D fracture network modelling for high steep rock slopes[J]. Journal of Engineering Geology, 2020, 28(2): 221. |
| [9] |
宁津生, 姚宜斌, 张小红. 全球导航卫星系统发展综述[J]. 导航定位学报, 2013, 1(1): 3. NING Jinsheng, YAO Yibin, ZHANG Xiaohong. Review of the development of global satellite navigation system[J]. Journal of Navigation and Positioning, 2013, 1(1): 3. DOI:10.3969/j.issn.2095-4999.2013.01.002 |
| [10] |
朱桐, 周珊珊. SAR成像模式发展综述[J]. 电子科技, 2016, 29(5): 187. ZHU Tong, ZHOU Shanshan. Areview of SAR imaging model development[J]. Electronic Science and Technology, 2016, 29(5): 187. |
| [11] |
王念秦, 申辉辉, 鲁兴生. 边坡变形监测技术发展现状及问题对策[J]. 科学技术与工程, 2021, 21(19): 7845. WANG Nianqin, SHEN Huihui, LU Xingsheng. Developmentstatus and problem countermeasures of slope deformation monitoring technology[J]. Science Technology and Engineering, 2021, 21(19): 7845. DOI:10.3969/j.issn.1671-1815.2021.19.001 |
| [12] |
郝娟, 孙皓月, 唐振禹, 等. 基于大数据分析的激光雷达三维图像重建方法[J]. 激光杂志, 2022, 43(12): 93. HAO Juan, SUN Haoyue, TANG Zhenyu, et al. Lidar 3D image reconstruction method based on big data analysis[J]. Laser Journal, 2022, 43(12): 93. |
| [13] |
廉旭刚, 蔡音飞, 胡海峰. 我国矿山测量领域三维激光扫描技术的应用现状及存在问题[J]. 金属矿山, 2019, 45(3): 35. LIAN Xugang, CAI Yinfei, HU Haifeng. Application status and existing problems of 3D laser scanning technique in mine[J]. Metal Mine, 2019, 45(3): 35. |
| [14] |
张清文, 刘盟盟, 汤文, 等. 积雪深度3D识别与数字摄影测量[J]. 哈尔滨工业大学学报, 2019, 51(12): 194. ZHANG Qingwen, LIU Mengmeng, TANG Wen, et al. 3D identification and digital photogrammetry of snow depths[J]. Journal of Harbin Institute of Technology, 2019, 51(12): 194. DOI:10.11918/j.issn.0367-6234.201903176 |
| [15] |
殷青, 王春兴, 韩昀松. 基于多视角图像的建筑环境信息建模方法[J]. 哈尔滨工业大学学报, 2021, 53(2): 104. YIN Qing, WANG Chunxing, HAN Yunsong. Building environment information modeling based on multi-view image[J]. Journal of Harbin Institute of Technology, 2021, 53(2): 104. DOI:10.11918/202001057 |
| [16] |
YANG Y, SONG S, YUE F, et al. Superpixel-based automatic image recognition for landside deformation areas[J]. Engineering Geology, 2019, 259: 105166. DOI:10.1016/j.enggeo.2019.105166 |
| [17] |
MWANIKI M W, KURIA D N, BOITT M K, et al. Image enhancements of Landsat 8 (OLI) and SAR data for preliminary landslide identification and mapping applied to the central region of Kenyal[J]. Geomorphology, 2017, 282: 162. DOI:10.1016/j.geomorph.2017.01.015 |
| [18] |
许文涛, 李晓昭, 章杨松, 等. 基于摄影测量系统的岩体结构面精细识别表征及应用[J]. 测绘学报, 2022, 51(10): 2093. XU Wentao, LI Xiaozhao, ZHANG Yangsong, et al. Fine identification and characterization of rock mass discontinuities and its application using a digital photogrammetry system[J]. Acta Geodaetica et Cartographica Sinica, 2022, 51(10): 2093. DOI:10.11947/j.AGCS.2022.20220359 |
| [19] |
白奎明, 范庆龙, 杨宝全, 等. 无人机微变摄影测量技术在边坡高位危岩体监测中的应用[J]. 四川水力发电, 2023, 42(1): 89. BAI Kuiming, FAN Qinglong, YANG Baoquan, et al. Application of micro-variation photogrammetry technology based on UAV in the monitoring of high-level and hazardous rock mass of slope[J]. Sichuan Water Power, 2023, 42(1): 89. DOI:10.3969/j.issn.1001-2184.2023.01.022 |
| [20] |
徐东, 范文涛. 基于数字摄影测量的岩体结构面信息获取及岩体质量评价[J]. 黄金, 2022, 43(9): 43. XU Dong, FAN Wentao. Acquisition of rock mass structural plane information and rock mass quality evaluation based on digital photogrammetry[J]. Gold, 2022, 43(9): 43. |
| [21] |
王章琼, 白俊龙, 张明. 数码摄影测量及三维建模在岩体结构面粗糙度教学中的应用[J]. 实验技术与管理, 2020, 37(3): 45. WANG Zhangqiong, BAI Junlong, ZHANG Ming. Application ofdigital photogrammetry and 3D modeling in teaching of rock discontinuity surface roughness[J]. Experimental Technology and Management, 2020, 37(3): 45. |
| [22] |
嵇美伟, 章杨松, 李晓昭. 基于摄影测量技术的岩体结构面参数的获取[J]. 科学技术与工程, 2019, 19(24): 344. JI Meiwei, ZHANG Yangsong, LI Xiaozhao. Extraction of rock mass structural attitudes based on photogrammetry technology[J]. Science Technology and Engineering, 2019, 19(24): 344. DOI:10.3969/j.issn.1671-1815.2019.24.054 |
| [23] |
王明常, 徐则双, 王凤艳, 等. 基于摄影测量获取岩体结构面参数的概率分布拟合检验[J]. 吉林大学学报(地球科学版), 2018, 48(6): 1898. WANG Mingchang, XU Zeshuang, WANG Fengyan. Fitting test on probability distribution of discontinuity parameters in rock mass based on photogrammetry[J]. Journal of Jilin University (Earth Science Edition), 2018, 48(6): 1898. |
| [24] |
王培涛, 覃拓, 黄正均, 等. 基于三维点云的岩体结构面信息快速化识别方法研究[J]. 岩石力学与工程学报, 2021, 40(3): 503. WANG Peitao, QIN Tuo, HUANG Zhengjun, et al. Fast identification of geometric properties of rock discontinuities based on 3D point cloud[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(3): 503. |
| [25] |
李浩, 杜丽丽, 贾晓敏, 等. 基于数码影像的边坡工程地质编录信息系统[J]. 华南理工大学学报(自然科学版), 2008, 36(1): 145. LI Hao, DU Lili, JIA Xiaomin, et al. Fitting test on probability distribution of discontinuity parameters in rock mass based on photogrammetry[J]. Journal of South China University of Technology(Natural Science Edition), 2008, 36(1): 145. DOI:10.3321/j.issn:1000-565X.2008.01.026 |
| [26] |
陈建琴, 李晓军, 朱合华. 基于点云的岩体间距与粗糙度的自动化提取[J]. 地下空间与工程学报, 2017, 13(1): 133. CHEN Jianqin, LI Xiaojun, ZHU Hehua. Automaticextract of rock mass spacing and roughness based on point clouds[J]. Chinese Journal of Underground Space and Engineering, 2017, 13(1): 133. |
| [27] |
OHNISHI Y, NISHIYAMA S, YANO T, et al. Astudy of the application of digital photogrammetry to slope monitoring systems[J]. International journal of Rock Mechanics and Mining Sciences, 2006, 43(5): 756. DOI:10.1016/j.ijrmms.2005.12.002 |
| [28] |
毛权生, 曹纪刚. 高陡边坡岩体结构数字识别及分析[J]. 金属矿山, 2015(8): 147. MAO Quansheng, CAO Jigang. Digital identification and analysis of rock mass structure of high and steep slope[J]. Metal Mine, 2015(8): 147. |
| [29] |
ZHANG Zhengyou. A flexible new technique for camera calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330. DOI:10.1109/34.888718 |
 2024, Vol. 56
2024, Vol. 56


