近年来,随着自动驾驶技术的逐步发展,人机共驾中的驾驶接管安全问题日益突出,如何实时准确地评估驾驶接管过程中的风险水平已成为亟待解决的关键问题。按照美国车辆工程师协会(SAE)的标准,自动驾驶分为6个级别。在L3级自动驾驶阶段,驾驶员不需长时间监控车辆,只需在交通环境复杂或自动驾驶系统失效时接管车辆的控制权。由于驾驶员在自动驾驶过程中从事非驾驶任务,对道路交通环境的感知能力下降,发生风险概率较大[1]。因此,如何准确地评估L3级自动驾驶接管过程中的风险水平,对于提高道路的安全性具有重要意义。
在自动驾驶接管研究方面,文献[2]基于最小车头时距和最小TTC,采用K均值聚类法对驾驶接管时驾驶员的跟车风险接受水平进行度量。文献[3]以接管时间和TTC等指标为因变量,建立了回归模型预测接管绩效。文献[4]研究了非驾驶任务对接管绩效的影响,发现从事非驾驶任务会增加接管时间和降低最小TTC。文献[5]研究了接管前置时间和接管提示方式对接管绩效的影响,发现接管前置时间为5 s时,视觉或视觉+听觉接管提示方式有助于提醒驾驶员尽快接管车辆。文献[6]研究了非驾驶任务对接管绩效的影响,发现驾驶员的上肢操作行为在极大程度上影响接管绩效。文献[7]探究了不同的认知负荷条件下驾驶员的接管绩效规律,结果发现驾驶员认知负荷越高,接管绩效越差。
在风险评估方面,文献[8]利用主观问卷和负二项模型量化驾驶风险。文献[9]提出了一种基于XGBoost监督学习算法和贝叶斯分层模型,用于评估自动驾驶车辆在高速公路合流区的风险水平。文献[10]提出了一种针对遮挡区域内车辆潜在碰撞的概率性风险评估方法。文献[11]使用机器学习方法实时预测了自动驾驶车辆碰撞的风险。文献[12]利用基于回归特性的多项式逻辑模型,预测和划分了驾驶风险等级。此外,文献[13-14]提出了行车风险场理论,对跟驰状态下的人- 车- 路相互作用风险进行评估,为多车交互风险评估提供了新思路。文献[15]为了定量分析变道过程中多车相互作用中速度变化,基于势能场提出了一种多车交互场景下的速度变化模型。文献[16]采用电风险场模型,建立了考虑驾驶员、车辆和环境因素的风险模型。
综上,有关驾驶接管的研究主要集中在接管绩效方面,尚需对接管风险进行评估与量化。在风险评估模型方面,现有研究多集中在传统跟驰换道或非自动驾驶车辆中,难以有效评估多车交互作用下的自动驾驶接管的风险水平。因此,基于以上局限,本文开展了自动驾驶接管仿真实验,引用“行车风险场”思想,构建了基于车辆轨迹数据的接管风险评估模型,为自动驾驶接管安全性的提升提供了理论支撑。
1 自动驾驶接管实验 1.1 实验人员及设备与实车试验相比,自动驾驶模拟技术所需条件简单,具有驾驶接管事件可控、易于获取高精度的多维数据等优势,已成为驾驶接管乃至自动驾驶领域研究的常用手段[17]。因此,本文采用驾驶模拟实验开展研究,科学合理设计模拟实验场景,并通过向被试者讲解自动驾驶系统的相关功能和开展充分预实验的方式使其熟练掌握驾驶接管操作,消除实验过程中学习效应等因素的影响,最后对实验采集的数据进行分析和预处理,确保驾驶模拟实验的有效性。
被试者30人(男性17人,女性13人),均持有效驾照,驾龄为0~3 a,平均驾龄为2.58 a,裸眼力或矫正视力正常。实验设备与软件分析系统如图 1所示,基于SCANeR studio软件构建仿真实验场景,该软件能实时监测自车辆和周边交通参与者,并记录相关车辆运行数据,进而模拟L3级自动驾驶系统。硬件部分由显示器、Logitech G29方向盘、油门踏板、刹车踏板、视频录制设备、音频播放设备组成。实验中车辆设置为自动变速模式。在手动驾驶场景中,被试者仅需要操作方向盘、油门踏板和刹车踏板。在自动驾驶场景中,车辆能够自行实现加速、减速和转向操作。

|
图 1 实验设备与软件分析系统 Fig. 1 Experimental equipments and software analysis system |
实验以双向6车道城市快速路直线段为研究路段,路段长度为7.5 km,环境为晴天且道路状况良好。依据《城市道路工程设计规范》[18]中关于城市快速路设计的相关参数,将实验路段限速设为90 km/h,自车辆的初始车速设定为80 km/h。将交通流设为稳定流(15 pcu/(km · ln)),此时车辆间的相互影响适中,所得数据便于以行车风险场为基础的模型构建与标定。实验开始时,自车辆以自动驾驶模式在中间车道行驶。
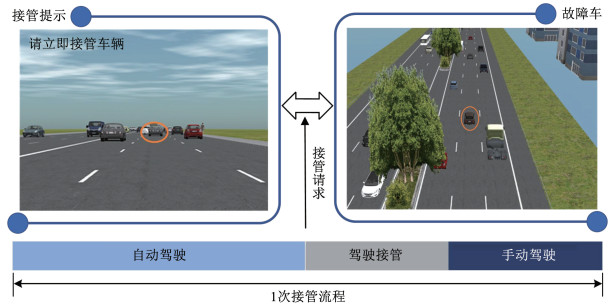
当自车辆以自动驾驶模式行驶时,自车辆所在车道突然出现故障车,因此需要自动驾驶系统发出接管提醒,使驾驶员快速感知周围的道路交通环境。研究表明,当接管前置时间设为5 s时, 视觉+听觉接管提示方式有助于提醒驾驶员尽快接管车辆[5],因此基于自车辆与故障车之间的距离,将接管请求时间统一设置为5 s。每次实验有3次接管,每次接管间隔约2~2.5 km。接管提醒方式为视听结合,当被试者接收到接管提示后,应通过踩下制动踏板或者转动方向盘来迅速接管车辆控制权。被试者事先并不清楚接管事件的位置,因此该实验可以体现驾驶员的真实反应, 实验场景如图 2所示。
|
图 2 实验场景 Fig. 2 Experimental scene |
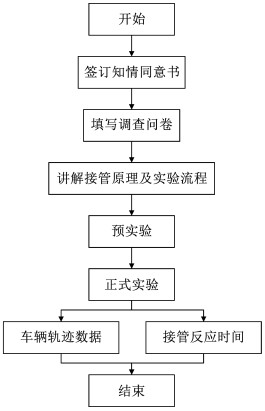
首先,被试者签署知情同意书并填写基本个人信息。实验工作人员向被试者介绍L3级自动驾驶的原理与具体的接管操作流程,被试者开始正式实验前,先进行一次预实验以熟悉驾驶仿真系统的各项操作,被试者熟悉实验操作后方可进行正式实验,以此消除正式实验中可能存在的学习效应。在正式实验中,当自动驾驶系统发出接管提示后,被试者需迅速接管车辆,采取制动或转向操作,以避免发生交通事故。被试者完成接管后,需要将车辆行驶回中间车道,直至系统发出下一次接管请求后, 被试者再次进行接管操作。每名被试驾驶员进行1次正式实验,以此类推重复以上步骤,收集驾驶模拟器采集到的数据信息,同时对实验数据进行备份。接管实验的具体流程如图 3所示。
|
图 3 实验流程 Fig. 3 Flowchart of the experiment |
本次驾驶接管实验获得了30名被试驾驶员共计90个接管片段,每个接管片段的时间包括从接管提示发出时刻至驾驶员接管后9 s的时间窗,实验获得的数据包括驾驶员接管反应时间、自车辆和其他车辆轨迹数据。其中自车辆轨迹数据包括实时位置、线性加速度(x、y、z方向)、实时速度、制动踏板开度和方向盘转角,交互车辆轨迹数据包括交互车辆实时的位置坐标以及车辆的速度。
对车辆轨迹数据类型进行Kolmogorov-Smirnov正态性检验,检验结果表明各数据类型的p值均大于0.05,如表 1所示,服从正态分布。进一步采用箱型图筛选并处理数据中的异常值,当数据值大于箱型图上限或小于箱型图下限时,判断其为异常值。采用等深分箱法和箱边界值平滑的方法,用距离较近的边界值对异常值进行替换,以便能更好地用于后续数据分析。
| 表 1 车辆轨迹数据K-S检验结果 Tab. 1 K-S test results for trajectory data |
根据交通流理论,当跟驰车辆的间距过小时,后车辆驾驶员为避免车辆发生追尾碰撞,会降低车辆速度。
与磁场类似,在不同的时空条件下,不同交通行为的车辆彼此间产生的影响不同。其他车辆距自车辆越远,作用于自车辆的风险就越小。由于磁感应强度是矢量,同理,周围车辆所产生的风险对车辆的影响作用也存在一定的方向性,因此,可以从场论角度来探讨接管风险的问题。
由于车辆的行车风险分布特征和场的特征相似,且会对行车安全造成重要影响,本文引用场论思想,以“行车风险场”[19]的概念和原理为基础,定义“接管安全场场强”为自动驾驶接管过程中量化的行车风险。接管安全场场强越大,接管时的风险就越大。通过计算自车辆接管安全场场强,可有效评估其接管风险。
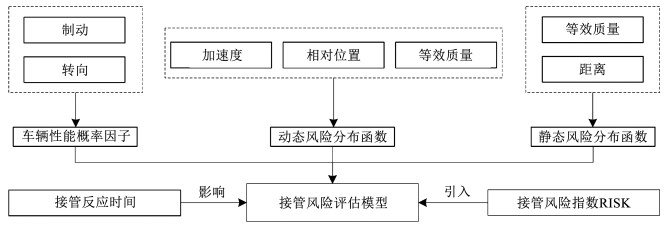
2.2 考虑行车风险场的接管风险评估模型基于行车风险场,采用接管安全场场强量化接管风险,接管风险评估模型由3个部分组成:静态风险分布函数、动态风险分布函数和车辆性能概率因子。模型构成如图 4所示。
|
图 4 模型构成 Fig. 4 Composition of model |
由于驾驶员的感知能力存在上限,接管风险最主要的影响因素是各交通单元间距离及其变化趋势。与行车风险场场源的距离越大,事故发生的概率越小,即场源产生的接管安全场场强越弱。为分析非自动驾驶条件下的静态交通参与者对自车辆造成的风险,文献[14]考虑道路条件、等效质量和距离对静态风险场的空间分布特征进行了刻画,本文以此为基础,构建基于距离的静态风险分布函数:
| $ Q_{j i}^{(s)}=\sum\limits_{j=1}^n \kappa \frac{M_i}{\left|d_{j i}\right|^\gamma} \times \frac{d_{j i}}{\left|d_{j i}\right|} $ | (1) |
式中:Mi为自车辆i的等效质量,kg;κ为常系数,κ>0;dji为其他静态参与者j与自车辆i之间的距离,m;γ为下降速度因子[16],γ≥1,在以自车辆i为圆心的圆形区域闭合边界线上,γ=1。
式(1)中等效质量表示车辆属性对自身所产生的风险,等效质量越大,车辆与其他交通参与者发生碰撞时的严重程度就越大。等效质量不仅与车辆的实际质量有关,还与其类型和速度有关。因此,自车辆i的等效质量Mi的函数表达式[14]可以写为
| $ M_i=M\left(m_i, v_i\right)=m_i\left(\rho v_i^u+\chi\right) $ | (2) |
式中:mi为自车辆i的实际质量,kg;vi为自车辆i的速度,m/s;ρ, u, χ为常系数。
利用交通事故数据表示速度对行车风险的影响,在此基础上确定等效质量的取值,则自车辆i的等效质量Mi表达式[14]为
| $ M_i=m_i \cdot\left(1.566 \times 10^{-14} v_i^{6.687}+0.335\right) $ | (3) |
自车辆的运动速度越大,在其周围处于运动状态的交通单元所产生的场强也越大。自车辆的减速度越小,制动越缓慢,车辆碰撞的概率越大。自车辆指向周围交通参与者的方向向量与x轴正向(规定为道路方向且与自车辆前进的方向一致)的夹角越小,行车风险越大。为评估运动车辆的风险场分布,文献[16]基于风险源速度、风险源运动方向与其他交通参与者的夹角提出了动态风险分布特征函数,在此基础上,本文考虑自车辆减速度指标对其进行修正,构建接管过程中交通单元处于运动状态的动态风险分布函数:
| $ Q_{j i}^{(d)}=\sum\limits_{i=1}^n \frac{M_i\left|\cos \theta_{i j}\right|}{\delta a} $ | (4) |
式中:Mi为自车辆i的等效质量,kg;a为自车辆i的合成减速度,m/s2;δ为合成减速度下降因子,δ>0,本文取δ=0.15;θij为接管过程中自车辆i与行车风险场内其他交通参与者j的连线方向与x轴正方向的夹角,θij∈[0°, 180°]。
式(4)中合成减速度a的计算方法如下:根据车辆轨迹数据中相邻单位时间的自车辆坐标(x0, y0)、(x1, y1),计算自车辆前进方向与世界坐标系x轴之间的角度α, 可表示为
| $ \alpha=\arctan \frac{y_0-y_1}{x_0-x_1} $ | (5) |
取x和y方向上的线性加速度绝对值,标记为ax和ay。则在驾驶过程中,自车辆的纵向加速度与横向加速度表示为
| $ \left\{\begin{array}{l} a_{\mathrm{z}}=a_x \cos \alpha+a_y \sin \alpha \\ a_{\mathrm{h}}=a_y \cos \alpha+a_x \sin \alpha \end{array}\right. $ | (6) |
则自车辆的合成减速度可以表示为
| $ a=\sqrt{a_{\mathrm{z}}^2+a_{\mathrm{h}}^2} $ | (7) |
在自动驾驶系统触发接管提示时,通常驾驶员会采取转向或制动行为,通过踏板的受力和方向盘转角可衡量车辆的风险响应情况。当自车辆与故障车之间的距离一定时,制动踏板下压力越小,驾驶员对车辆的控制程度越低,越容易发生碰撞危险;车辆的方向盘转角越大,驾驶员在接管时成功绕过故障车的可能性越大。因此,引入车辆性能概率因子[16]表示接管过程中车辆轨迹异常而导致潜在交通事故发生的概率,车辆性能概率因子可以表示为
| $ P_c=\left\{\begin{array}{l} \left(\frac{C_{\max }}{C}\right)^{\alpha_1}, \frac{C_{\max }}{C}>\frac{Z_{\max }}{Z} \\ \left(\frac{Z_{\max }}{Z}\right)^{\alpha_2}, \frac{C_{\max }}{C} \leqslant \frac{Z_{\max }}{Z} \end{array}\right. $ | (8) |
式中:C为刹车制动踏板下压力,N;Cmax为制动踏板下压力最大值,N;Z为方向盘转角,(°);Zmax为方向盘转角最大值,(°);α1,α2为常系数,α1>0,α2>0。
在矢量场中,相反方向的同一物理量可以相互抵消,但这一规律在行车风险场中并不适用,因为不同交通因素所产生的风险场在叠加后,自车辆i的接管风险不会降低反而会增加,因此在道路上行驶的自车辆i的接管安全场场强应当按照不同交通因素所引起的场强模之和来进行计算。接管风险评估模型应同时考虑接管反应时间的影响,接管反应时间越长则风险水平越高,故采用指数形式反映接管反应时间对风险的作用,则接管风险评估模型可表示为
| $ S_i=\sum\limits_{j=1}^n\left(\lambda_1 Q_{j i}^{(d)}+\lambda_2 Q_{j i}^{(s)}\right) \mathrm{e}^{\frac{t_i}{\Phi}} \times P_c $ | (9) |
式中:Si为自车辆i的接管安全场场强;Qji(d)为交通单元j在自车辆i处的动态风险分布函数;Qji(s)为交通单元j在自车辆i处的静态风险分布函数;Pc为车辆性能概率因子;ti为自车辆i的接管反应时间,s;λ1为动态风险分布函数所占权重;λ2为静态风险分布函数所占权重;Φ为常系数。
将式(1)、(4)和式(8)代入式(9),则周围车辆j对自车辆i产生的接管安全场场强可以表示为
| $ S_i=\left\{\begin{array}{c} \left(\sum\limits_{j=1}^n \lambda_1 \frac{M_i\left|\cos \theta_{i j}\right|}{\delta a}+\sum\limits_{j=1}^n \lambda_2 \times \kappa \times \frac{M_i}{\left|d_{j i}\right|^\gamma}\right) \times \\ \mathrm{e}^{\frac{i_i}{\Phi}} \times \frac{d_{j i}}{\left|d_{j i}\right|}\left(\frac{C_{\max }}{C}\right)^{\alpha_1}, \frac{C_{\max }}{C}>\frac{Z_{\max }}{Z} \\ \left(\sum\limits_{j=1}^n \lambda_1 \frac{M_i\left|\cos \theta_{i j}\right|}{\delta a}+\sum\limits_{j=1}^n \lambda_2 \times \kappa \times \frac{M_i}{\mid d_{j i}{ }^\gamma}\right) \times \\ \mathrm{e}^{\frac{i_i}{\phi}} \times \frac{d_{j i}}{\left|d_{j i}\right|}\left(\frac{Z}{Z_{\max }}\right)^{\alpha_2}, \frac{C_{\max }}{C} \leqslant \frac{Z_{\max }}{Z} \end{array}\right. $ | (10) |
接管安全场场强是绝对指标,数值范围较大,很难直接对接管风险进行评价。为此对其进行处理,定义其相对指标为“接管风险指数”,以此来对接管过程中的风险大小进行评估。接管风险指数越大,说明此刻车辆在接管过程中越容易产生风险。接管风险指数的表达式为
| $ R_i=\frac{S_i}{\bar{S}} $ | (11) |
式中:Ri为自车辆i的接管风险指数;S为接管安全场场强的平均值。
2.3 模型参数标定采用遗传算法标定接管风险评估模型的待定常系数[8],设定种群规模为200,变异概率为0.2,交叉概率为0.8,迭代600次。每位被试者的数据重复计算10次后选择均方根误差最小的一组参数作为最优解。标定结果如表 2所示。
| 表 2 待定常系数的标定结果 Tab. 2 Calibration results of parameters |
通过对比碰撞时间倒数和接管风险评估模型中的接管风险指数验证模型的有效性。碰撞时间倒数Tdi是评价车辆行车风险的常用指标,Tdi值越大,说明自车辆与前方车辆的碰撞时间越短,车辆更容易发生碰撞事故。其计算式为
| $ T_{\mathrm{d} i}=\left|\frac{v_i-v_j}{d_{i j}}\right| $ | (12) |
式中:Tdi为自车辆i的碰撞时间倒数,s-1;vi为制动过程中,自车辆i的行驶速度,m/s;vj为制动过程中,前车j的行驶速度,m/s,若前方是静止故障车,则vj=0;dij为自车辆i与前车j之间的距离,m。
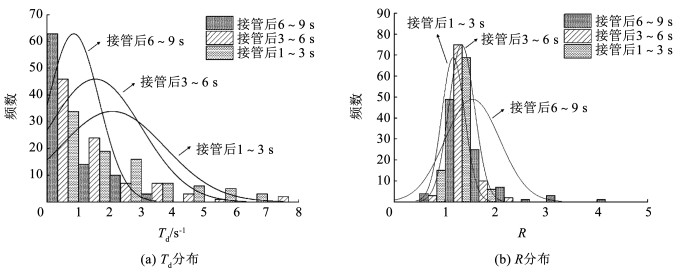
根据本文所建立的接管风险评估模型以及接管风险指数的计算公式,可以得到接管风险指数R值,根据碰撞时间倒数的计算公式,得到碰撞时间倒数Td值。由于接管后9 s内的操作能反映接管的稳定情况,因此研究接管后1~9 s内Td和R的情况,如图 5所示。
|
图 5 接管后1~9 s内Td和R分布图 Fig. 5 Distribution diagram of Td and R values within 1~9 s after takeover |
驾驶员产生接管行为的9 s内Td的频率分布直方图如图 5(a)所示。接管后第1~3秒、3~6秒、6~9秒时的Td均不满足正态分布,因此,采用非参数检验的方法,来检验两者之间的Td分布是否存在显著性差异。Mann-Whitney检验和Kolmogorov-Smirnov检验的结果均为p < 0.05,在此置信水平下,不同时间段的Td分布差异显著。接管后第1~3秒时的Td均值(2.071)明显大于接管后第6~9秒时的Td均值(0.847),这说明驾驶员在Td较大时进行了接管,随着控制权的切换,Td逐渐减小,风险逐渐降低,与实际接管情况一致。因此,Td可以很好地评估自动驾驶车辆在接管过程中的接管风险。
与Td的变化规律相似,驾驶员产生接管行为的9 s内R的频率分布直方图如图 5(b)所示。接管后第1~3秒、第3~6秒、第6~9秒时的R均不满足正态分布,因此,采用非参数检验的方法,来检验两者之间的R分布是否存在显著性差异。Mann-Whitney检验和Kolmogorov-Smirnov检验的结果均为p < 0.05,在此置信水平下,不同时间段的R分布差异显著。接管后第1~3秒时的R均值(1.54)略大于接管后第6~9秒时的R均值(1.16),这说明随着驾驶员对车辆完成接管,车辆的接管风险便逐渐减小,车辆逐渐趋于安全,整体的变化趋势与Td一致,也与事实情况是一致的。作为相对指标,R的变化幅度较小,是可以接受的。因此,R可以有效地表征自动驾驶车辆在接管过程中的接管风险。
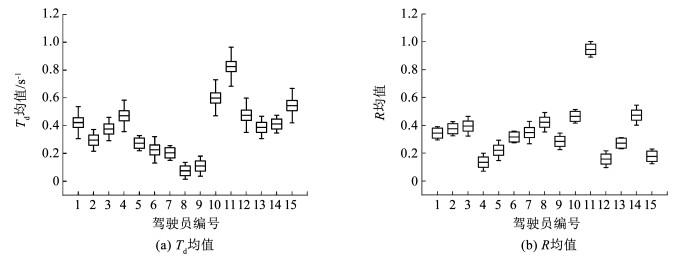
3.2 均方根误差法均方根误差ERMS可以评估模型计算结果准确性。随机选取15组接管数据,对Td和R均值进行归一化处理,并计算均方根误差,如图 6所示。
|
图 6 Td和R均值的误差棒图 Fig. 6 Error bars for the mean values of Td and R |
由图 6可知,接管过程中R均值的误差棒长度均匀且短于Td均值的误差棒。R的均方根误差均值为0.059, 小于Td的均方根误差均值0.093,说明R在表征风险时的误差更小,可信度更高。其原因在于Td多用于评估跟驰或换道场景下前后车辆的风险水平,忽略了周围其他车辆对自车辆运行的影响,而本文所提出的风险评估模型能够综合考量跟驰和换道场景下自车辆周围的多车状态对自车辆接管风险的影响。因此,模型具有较高可靠性,接管安全场场强指标的选取合理有效,能够有效评估驾驶员的在自动驾驶接管过程中的接管风险。
4 结论1) 以行车风险场理论为基础,构建了考虑风险分布函数、车辆性能概率因子和接管反应时间的自动驾驶接管风险评估模型,基于驾驶模拟实验获取车辆轨迹数据和驾驶员接管反应时间数据对模型进行标定并进行了有效性验证。
2) 非参数检验的结果表明:驾驶员接管后第1~3秒、第3~6秒、第6~9秒不同时间段的R分布表现出显著差异。将接管风险指数与碰撞时间倒数进行对比,接管后第1~3秒时的R值大于接管后第6~9秒时的R值,且变化趋势与Td值的变化趋势一致,说明接管风险会随驾驶员执行接管操作逐渐减小。因此,R值能够有效评估驾驶员的接管风险。
3) 均方根误差法的计算结果表明:接管过程中R的均方根误差均值为0.059,Td的均方根误差均值为0.093,且R均值的误差棒长度较短且分布均匀,说明R数据更适合表征风险的准确性,表明接管风险评估模型在风险评估方面具有可靠性。
4) 在模型构建方面,下一步研究可以考虑驾驶员的生理和心理状态对驾驶接管风险的影响,更全面深入地研究驾驶接管风险评估问题;在驾驶模拟实验方面,可进一步考虑不同道路场景和不同接管场景下的接管实验设计。
| [1] |
郭烈, 胥林立, 秦增科, 等. 自动驾驶接管影响因素分析与研究进展[J]. 交通运输系统工程与信息, 2022, 22(2): 72. GUO Lie, XU Linli, QIN Zengke, et al. Analysis and overview of influencing factors on autonomous driving takeover[J]. Journal of Transportation Systems Engineering and Information Technology, 2022, 22(2): 72. |
| [2] |
鲁光泉, 陈发城, 李鹏辉, 等. 驾驶人跟车风险接受水平对其接管绩效的影响[J]. 汽车工程, 2021, 43(6): 808. LU Guangquan, CHEN Facheng, LI Penghui, et al. Effect of drivers' acceptance level of car-following risk on the takeover performance[J]. Automotive Engineering, 2021, 43(6): 808. |
| [3] |
GOLD C, HAPPEE R, BENGLER K. Modeling take-over performance in level 3 conditionally automated vehicles[J]. Accident Analysis & Prevention, 2018, 116: 3. |
| [4] |
林庆峰, 王兆杰, 鲁光泉. 城市道路环境下自动驾驶车辆接管绩效分析[J]. 中国公路学报, 2019, 32(6): 240. LIN Qingfeng, WANG Zhaojie, LU Guangquan. Analysis of take-over performance for automated vehicles in urban road environments[J]. China Journal of Highway and Transport, 2019, 32(6): 240. |
| [5] |
KIM W, JEON E, KIM G, et al. Take-over requests after waking in autonomous vehicles[J]. Applied Sciences, 2022, 12(3): 1438. DOI:10.3390/app12031438 |
| [6] |
WANDTNER B, SCHÖMIG N, SCHMIDT G. Effects of non-driving related task modalities on take-over performance in highly automated driving[J]. Human factors, 2018, 60(6): 870. DOI:10.1177/0018720818768199 |
| [7] |
MELNICUK V, THOMPSON S, JENNINGS P, et al. Effect of cognitive load on drivers' state and task performance during automated driving: introducing a novel method for determining stabilisation time following take-over of control[J]. Accident Analysis and Prevention, 2021, 151: 105967. DOI:10.1016/j.aap.2020.105967 |
| [8] |
BA X, ZHOU F, WANG Y. Predicting personal injury crash risk through working conditions, job strain, and risky driving behaviors among taxi drivers[J]. European Transport Research Review, 2018, 10(2): 1. |
| [9] |
ZHU J Y, MA Y L, LOU Y N. Multi-vehicle interaction safety of connected automated vehicles in merging area: a real-time risk assessment approach[J]. Accident Analysis & Prevention, 2022, 166(9): 106546. |
| [10] |
LEE M, SUNWOO M, JO K. Collision risk assessment of occluded vehicle based on the motion predictions using the precise road map[J]. Robotics and Autonomous Systems, 2018, 106(13): 179. |
| [11] |
KATRAKAZAS C, QUDDUS M, CHEN W H. A new integrated collision risk assessment methodology for autonomous vehicles[J]. Accident Analysis & Prevention, 2019, 127: 61. |
| [12] |
XIONG X, CHEN L, LIANG J, et al. Vehicle driving risk prediction based on markov chain model[J]. Discrete Dynamics in Nature and Society, 2018, 168(8): 1. |
| [13] |
WANG J Q, WU J, LI Y. The driving safety field based on driver-vehicle-road interactions[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(4): 2203. DOI:10.1109/TITS.2015.2401837 |
| [14] |
WANG J, WU J, ZHENG X, et al. Driving safety field theory modeling and its application in pre-collision warning system[J]. Transportation Research Part C: Emerging Technologies, 2016, 72(11): 306. |
| [15] |
MA Y L, YIN B Q, CHEN K, et al. Multi-vehicle interactive lane-changing velocity change model based on potential energy field[J]. Transportation Research Record, 2022, 2676(11): 306. DOI:10.1177/03611981221092383 |
| [16] |
何仁, 赵晓聪, 王建强. 人-车-路交互下的驾驶人风险响应度建模[J]. 中国公路学报, 2020, 33(9): 236. HE Ren, ZHAO Xiaocong, WANG Jianqiang. Modeling of driving risk response under human-vehicle-road interaction[J]. China Journal of Highway and Transport, 2020, 33(9): 236. DOI:10.3969/j.issn.1001-7372.2020.09.023 |
| [17] |
赵晓华, 陈浩林, 李振龙, 等. 不同情景下自动驾驶接管行为的影响特征[J]. 中国公路学报, 2022, 35(9): 195. ZHAO Xiaohua, CHEN Haolin, LI Zhenlong, et al. Influence characteristics of automated driving takerover behavior in different scenarios[J]. China Journal of Highway and Transport, 2022, 35(9): 195. |
| [18] |
中华人民共和国住房和城乡建设部. 城市道路工程设计规范: CJJ 37—2012[S]. 北京: 中国建筑工业出版社, 2012 Ministry of Housing and Urban Rural Development of the People's Republic of China. Code for design of urban road engineering: CJJ 37—2012[S]. Beijing: China Architecture & Building Press, 2012 |
| [19] |
PETERMEIJER S M, CIELER S, WINTER J D. Comparing spatially static and dynamic vibrotactile take-over requests in the driver seat[J]. Accident Analysis &. Prevention, 2017, 99(12): 218. |
 2024, Vol. 56
2024, Vol. 56


