2. 浙江公路水运工程咨询有限责任公司,杭州 310006
2. Zhejiang Highway and Waterage Engineering Consulting Co., Ltd., Hangzhou 310006, China
众所周知,控制方程和定解条件(包含边界条件和初始条件)构成了土体的固结模型。边界条件反映了边界的透水能力,其对土体内孔隙水的排出速率具有直接影响。在Terzaghi给出的经典软土地基一维固结理论中,其假设超静孔隙水压力到达土层顶面就立刻消散(即假定软土顶面为理想的完全透水边界),而在软土底部存在着主要由岩石组成的透水性较差的下卧层,孔隙水基本无法从下卧层流出,故其假定软土底部为理想的完全不透水边界。这两个关于软土排水的边界条件也一直被后续大部分学者沿用。文献[1]通过大量的研究发现不管是软土的顶部还是底部,其排水能力都不是无穷大或无穷小的,而是介于完全透水与完全不透水这两种状态之间,故提出了一种处理此类软土固结问题的全新边界条件(即半透水边界)。然而,在研究的过程中发现半透水边界形式较为复杂,基于此边界条件的固结模型很难获得解析解答。为此,文献[2]提出了一种以指数形式描述孔隙水压力消散规律的软土边界条件(即变边界条件),并且在一定情况下由该边界条件推导出的解析解答可完全退化为由经典Terzaghi一维固结理论中的边界条件所推导出的解答, 使所得解答的形式更为简单明了,更能快速地被应用于实际工程中。
基于该变边界条件,文献[3]得到了单级加载下双层土一维固结广义解析解。文献[4]给出了变边界下竖井地基考虑涂抹和井阻效应的等应变轴对称解析解。文献[5]得到了变边界下考虑土中渗流存在起始水力坡降的一维固结理论解析解。以上基于变边界的固结模型中均认为土体的压缩和渗透特性在固结过程中保持不变。为此,文献[6]基于文献[7]提出了土体的非线性压缩渗透假定,得到了变边界条件下土体一维非线性固结解析解,并通过相关固结试验[8],证明了边界处超静孔压会随时间发生变化,而不是像完全透水边界一样始终为0,验证了变边界条件在实际土体固结中的存在性。
需要说明的是,前述考虑变边界的软土固结理论均是建立在小应变几何假定基础之上。事实上,当软土为高含水量,高孔隙比的高压缩性软土时,在外荷载作用下高压缩性软土容易发生较大应变,此时考虑大应变几何假定在固结计算中尤为重要。文献[9-10]曾假定土体压缩、渗透特性遵循线性变化,推导了在大应变假定下饱和软黏土的一维固结方程并获得了相应的解答,与Terzaghi一维固结理论不同的是,该方程最终是以将软土孔隙比作为变量的形式呈现的。在Gibson一维大应变固结理论基础之上,文献[11-13]建立了特定因素影响下的固结模型及其相应的解答,但高压缩性土体在固结过程中其压缩性和渗透性必然会呈现出明显的非线性特性。目前固结理论中广泛采用半对数压缩、渗透模型考虑土体的非线性压缩、渗透特性, 如:文献[14]基于半对数渗透模型,建立了考虑非达西渗流的土体大应变非线性固结理论;文献[15]假定土体压缩、渗透非线性特性满足半对数关系,在考虑软土非达西渗流问题的情况下建立了双层软土地基的一维大应变固结模型,并用有限差分的方式获得了该模型的数值解答。
现有试验结果[16-18]表明当高压缩性土体发生较大应变时,半对数关系模型在应力较小阶段会出现偏离线性的现象,如果采取双对数压缩、渗透模型描述这种非线性压缩和渗透特性,在双对数坐标系中的线性关系更显著,且纠正了其偏离线性的现象。文献[19]通过对比大量软土固结相关的室内试验数据,验证了在软土发生大应变固结时相较于半对数模型,采用双对数模型能够更加准确地描述软土非线性压缩特性及非线性渗透特性随孔隙比变化的规律,这进一步说明了双对数模型在应用于土体大应变固结问题时的适用性。值得注意的是,前述的软土大应变固结理论均将土体边界视为完全透水或完全不透水状态。文献[20]基于文献[21]进行了土体压缩和渗透特性试验,给出了变边界条件下软土大应变固结解析解, 但仍然不能真实地反映土体固结过程中的非线性压缩和渗透特性。综上所述,在同时考虑软土变边界、非线性压缩特性、非线性渗透特性以及大应变的情况下,现有研究中应用解析理论的方式去处理高压缩性软土的一维固结问题还很少见的。
基于此,本文将采用双对数模型来描述软土压缩性和渗透性与其孔隙之间呈现的非线性关系,建立考虑变边界的软土大变形非线性固结模型并获得固结模型的解析解。开展大量的计算分析,获得界面参数取值以及荷载大小对高压缩性软土大应变非线性固结性状的影响。
1 问题描述厚度为H的饱和软土地基,顶面透水,底面不透水,其上部作用有单调递增的均布荷载q(t)。如图 1所示,以地基顶面为基准面,初始构型下拉格朗日坐标系(a)以向下为正,时间t=0时顶面和底面处的坐标分别为0和H。本文以饱和软弱薄土层为研究对象,土层内部初始有效应力为σ′0,沿深度均匀分布且在固结过程中保持不变,其所对应的土层初始孔隙比为e0。
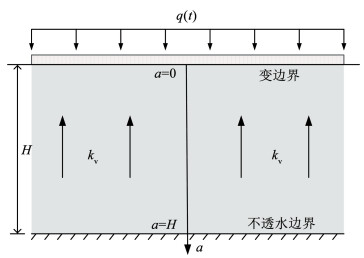
|
图 1 软土层大应变固结模型 Fig. 1 Large strain consolidation model of soft soil layer |
采用更能体现高压缩性软土非线性特性的双对数模型[16-19]描述土体的压缩、渗透特性,其中有效应力σ′与孔隙比e间的非线性关系为[17]
| $ \lg (1+e)-\lg \left(1+e_0\right)=I_{{\mathrm{c}}}\left(\lg \sigma_0^{\prime}-\lg \sigma^{\prime}\right) $ | (1) |
式中:Ic为双对数坐标系中土体的压缩指数,σ′为土体有效应力,e为对应的土体孔隙比。
渗透系数kv与孔隙比e间非线性关系[19]为
| $ \frac{k_{{\mathrm{v}}}}{k_{{\mathrm{v}} 0}}=\left(\frac{1+e}{1+e_0}\right)^\alpha $ | (2) |
即
| $ \lg (1+e)-\lg \left(1+e_0\right)=I_{\mathrm{k}}\left(\lg k_{\mathrm{v}}-\lg k_{{\mathrm{v}} 0}\right) 。$ |
式中:kv为土体渗透系数; kv0为土体初始渗透系数; α为渗透模型参数; Ik为双对数坐标系中土体的渗透指数,二者间的转换关系为Ik=1/α。
2 固结模型及求解条件拉格朗日坐标系下以超静孔隙水压力u为变量的软土大变形固结普遍连续方程[21]为
| $ \frac{1}{\gamma_{{\mathrm{w}}}} \frac{\partial}{\partial a}\left(k_{{\mathrm{v}}} \frac{1+e_0}{1+e} \frac{\partial u}{\partial a}\right)=\frac{1}{1+e_0} \frac{\partial e}{\partial t} $ | (3) |
式中:u为超静孔隙水压力,γw为孔隙水的重度,a为拉格朗日坐标系中某点初始构型的位置坐标,kv和e分别为t时刻软土的渗透系数和孔隙比。
式(1)进一步转化为
| $ \frac{1+e}{1+e_0}=\left(\frac{\sigma_0^{\prime}}{\sigma^{\prime}}\right)^{I_{{\rm{c}}}} $ | (4) |
结合饱和土体的有效应力原理,有
| $ \sigma^{\prime}=\sigma_0^{\prime}+q(t)-u $ | (5) |
将式(2)、(4)、(5)代入式(3)中,可得如下控制方程:
| $ c_{{\mathrm{v}} 0}\left(\frac{\sigma^{\prime}}{\sigma_0^{\prime}}\right)^{I_{{\mathrm{c}}}+1} \frac{\partial}{\partial a}\left[\left(\frac{\sigma^{\prime}}{\sigma_0^{\prime}}\right)^{-I_{{\mathrm{c}}}(\alpha-1)} \frac{\partial u}{\partial a}\right]=\frac{\partial u}{\partial t}-\frac{{\mathrm{d}} q}{{\mathrm{~d}} t} $ | (6) |
式中
控制方程的求解条件:
初始条件为
| $ u(a, 0)=0 $ | (7) |
边界条件为
| $ u(0, t)=q {\mathrm{e}}^{-\beta t} $ | (8) |
| $ \frac{\partial u}{\partial a}(H, t)=0 $ | (9) |
式中:β为反映土层顶面排水性状的界面参数,量纲为d-1,一般β为0.001~1000 d-1。
变边界条件反映土层边界的实际排水能力,通过改变界面参数β的取值可以模拟不同的排水边界,β越大,边界的排水性能越好。其无量纲形式为B=βH2/cv0。为简化式(6)进行如下变量代换:
| $ w=w(a, t)=\left(\frac{\sigma_0^{\prime}+q}{\sigma_0^{\prime}}\right)^{1-I_{{\mathrm{c}}}(\alpha-1)}-\left(\frac{\sigma^{\prime}}{\sigma_0^{\prime}}\right)^{1-I_{{\mathrm{c}}}(\alpha-1)} $ | (10) |
可以得到w为控制变量的固结控制方程:
| $ c_{{\mathrm{v}} 0}\left(\frac{\sigma^{\prime}}{\sigma_0^{\prime}}\right)^{I_{{\mathrm{c}}}(2-\alpha)+1} \frac{\partial^2 w}{\partial a^2}=\frac{\partial w}{\partial t}-R(t) $ | (11) |
式中
变换后的求解条件为
| $ \begin{gathered} w(a, 0)=0 \end{gathered} $ | (12) |
| $ w(0, t)=w_\beta(t) $ | (13) |
| $ \frac{\partial w}{\partial a}(H, t)=0 $ | (14) |
式中
| $ w_\beta(t)=\left(\frac{\sigma_0^{\prime}+q}{\sigma_0^{\prime}}\right)^{1-I_{\mathrm{c}}(\alpha-1)}-\left[1+\frac{q}{\sigma_0^{\prime}}\left(1-\mathrm{e}^{-\beta t}\right)\right]^{1-I_{\mathrm{c}}(\alpha-1)}。$ |
为了将边界条件齐次化,令
| $ v=v(a, t)=w-w_\beta(t) $ | (15) |
则以v为控制变量的固结控制方程为
| $ \frac{\partial v}{\partial t}=c_{{\mathrm{v}} 0}\left(\frac{\sigma^{\prime}}{\sigma_0^{\prime}}\right)^{I_{{\mathrm{c}}}(2-\alpha)+1} \frac{\partial^2 v}{\partial a^2}+f(t) $ | (16) |
式中
控制方程(16)的求解条件为
| $ \begin{gathered} v(a, 0)=0 \end{gathered} $ | (17) |
| $ v(0, t)=0 $ | (18) |
| $ \frac{\partial v}{\partial a}(H, t)=0 $ | (19) |
由文献[9]给出的大应变固结系数定义,可获得双对数压缩、渗透模型下的大应变固结系数表达式
当Ic(α-2)=1时,式(16)变为
| $ \frac{\partial v}{\partial t}=c_{{\mathrm{v}} 0} \frac{\partial^2 v}{\partial a^2}+f(t) $ | (20) |
根据太沙基固结模型解的形式,可设控制方程式(20)在相应求解条件下解的形式为
| $ v=\sum\limits_{m=1}^{\infty}\left\{{\mathrm{e}}^{-b_m t}\left[B_m+C_m T_m(t)\right] \sin \frac{\lambda_m a}{H}\right\} $ | (21) |
将式(21)代入控制方程(20),可得
| $ b_m=c_{{\mathrm{v0}}}\left(\frac{\lambda_m}{H}\right)^2 $ | (22) |
| $ \sum\limits_{m=1}^{\infty}\left(C_m \sin \frac{\lambda_m a}{H}\right)=1 $ | (23) |
| $ T_m(t)=\int_0^t {\mathrm{e}}^{b_m \tau} f(\tau) {\mathrm{d}} \tau $ | (24) |
根据边界条件和初始条件可分别得到
| $ \cos \frac{\lambda_m a}{H}=0 $ | (25) |
| $ B_m=0 $ | (26) |
由式(25)可得
| $ \lambda_m=M=\frac{(2 m-1) \pi}{2} $ | (27) |
其中m=1, 2, 3, …。
由正弦函数的正交关系可知
| $ \int_0^H \sin \frac{\lambda_m a}{H} \sin \frac{\lambda_n a}{H} {\mathrm{~d}} a=\left\{\begin{array}{l} 0, m \neq n \\ \frac{H}{2}, m=n \end{array}\right. $ | (28) |
则式(21)可进一步转化为
| $ v=\sum\limits_{m=1}^{\infty}\left[\frac{2}{M} {\mathrm{e}}^{-b_{m^t}} T_m(t) \sin \frac{M a}{H}\right] $ | (29) |
由此可得,w的表达式为
| $ \begin{aligned} w= & \sum\limits_{m=1}^{\infty}\left[\frac{2}{M} {\mathrm{e}}^{-b_m t} T_m(t) \sin \frac{M a}{H}\right]+\left(\frac{\sigma_0^{\prime}+q}{\sigma_0^{\prime}}\right)^{1-I_{{\rm{c}}}(\alpha-1)}- \\ & {\left[1+\frac{q}{\sigma_0^{\prime}}\left(1-{\mathrm{e}}^{-\beta t}\right)\right]^{1-I_{{\rm{c}}}(\alpha-1)} } \end{aligned} $ | (30) |
进而得到超静孔压u的一般表达式:
| $ \begin{aligned} &\begin{aligned} u= & \sigma_0^{\prime}+\frac{{\mathrm{d}} q}{{\mathrm{~d}} t} t-\sigma_0^{\prime}\left\{\left[1+\frac{q}{\sigma_0^{\prime}}\left(1-{\mathrm{e}}^{-\beta t}\right)\right]^{-I_{{\mathrm{c}}}}-\right. \\ & \left.\sum\limits_{m=1}^{\infty}\left[\frac{2}{M} {\mathrm{e}}^{-b_m t} T_m(t) \sin \frac{M a}{H}\right]\right\}^{2-\alpha} \end{aligned} \end{aligned} $ | (31) |
t时刻土层表面处的沉降值St为
| $ \begin{aligned} S_t= & H\left\{1-\left[1+\frac{q}{\sigma_0^{\prime}}\left(1-{\mathrm{e}}^{-\beta t}\right)\right]^{-I_{{\mathrm{c}}}}+\right. \\ & \left.\sum\limits_{m=1}^{\infty}\left[\frac{2}{M^2} {\mathrm{e}}^{-b_{m} t} \frac{t}{2 N} T_m(t)\right]\right\} \end{aligned} $ | (32) |
土层表面处的最终沉降S∞为
| $ S_{\infty}=H\left[1-\left(1+\frac{q}{\sigma_0^{\prime}}\right)^{-I_{{\mathrm{c}}}}\right] $ | (33) |
t时刻按沉降定义的固结度Ust为
| $ U_{{\mathrm{st}}}=\frac{S_{{\mathrm{t}}}}{S_{\infty}} $ | (34) |
由于孔压表达式复杂,此处按孔压定义的固结度采用数值积分计算,即
| $ \begin{aligned} U_{{\mathrm{pt}}}= & \frac{q}{q_n}-\frac{1}{q_n H} \int_0^H u {\mathrm{~d}} a= \\ & \frac{q}{q_n}-\frac{1}{N q_n} \sum\limits_{r=1}^N \frac{u\left(a_{r-1}, t\right)+u\left(a_r, t\right)}{2} \end{aligned} $ | (35) |
式中:N为数值积分的积分区间数;ar-1、ar分别为第r个区间的起点和终点坐标;u(ar, t)为ar处t时刻的超静孔压;r=1, 2, 3,…,N。
3.1.2 特殊加载条件下的解答常见变荷载形式可大致分为单级等速加载、多级等速加载和多级瞬时加载,如图 2所示。

|
图 2 变荷载形式 Fig. 2 Forms of the time-dependent loading |
1) 单级等速加载工况时,有
| $ q(t)=\left\{\begin{array}{l} \frac{q_{{\mathrm{u}}}}{t_{{\mathrm{c}}}} t, t<t_{{\mathrm{c}}} \\ q_{{\mathrm{u}}}, t \geqslant t_{{\mathrm{c}}} \end{array}\right. $ | (36) |
当t < tc时,对应不同情况下f(t)表达式为
| $ f(t)=\frac{1-I_{{\mathrm{c}}}(\alpha-1)}{\sigma_0^{\prime}}\left[1+\frac{q_{{\mathrm{u}}}}{t_{{\mathrm{c}}} \sigma_0^{\prime}} t\left(1-{\mathrm{e}}^{-\beta t}\right)\right]^{-I_{{\mathrm{c}}}(\alpha-1)} \times\\\left[\frac{q_{{\mathrm{u}}}}{t_{{\mathrm{c}}}}\left(1-{\mathrm{e}}^{-\beta t}\right)+\beta \frac{q_{{\mathrm{u}}}}{t_{{\mathrm{c}}} \sigma_0^{\prime}} t {\mathrm{e}}^{-\beta t}\right] $ | (37) |
当t≥tc时,对应不同情况下f(t)表达式为
| $ f(t)=\frac{1-I_{{\mathrm{c}}}(\alpha-1)}{\sigma_0^{\prime}}\left[N_{{\mathrm{q}}}-\frac{q_{{\mathrm{u}}}}{\sigma_0^{\prime}} {\mathrm{e}}^{-\beta t}\right]^{-I_{{\mathrm{c}}}(\alpha-1)} \beta q_{{\mathrm{u}}} {\mathrm{e}}^{-\beta t} $ | (38) |
式中
由于f(t)表达形式较为复杂,无法获得Tm(t)的显式表达。因此采用数值积分进行计算,令F(t)=ebmtf(t),则
| $ T_m(t)=\left\{\begin{array}{l} \int_0^t {\mathrm{e}}^{b_m \tau} f(\tau) {\mathrm{d}} \tau=\int_0^t F(\tau) {\mathrm{d}} \tau \approx \\ \quad \frac{t}{2 N} \sum\limits_{i=0}^N\left[F\left(\frac{t}{N_{i-1}}\right)+F\left(\frac{t}{N_i}\right)\right], t<t_{{\mathrm{c}}} \\ \int_0^{t_{{\mathrm{c}}}} F(\tau) {\mathrm{d}} \tau+\int_{t_{{\mathrm{c}}}}^t F(\tau) {\mathrm{d}} \tau \approx \\ \frac{t}{2 N} \sum\limits_{i=0}^N\left[F\left(\frac{t}{N_{i-1}}\right)+F\left(\frac{t}{N_i}\right)\right], t \geqslant t_{{\mathrm{c}}} \end{array}\right. $ | (39) |
式中:
2) 多级等速加载工况时,有
| $ q(t)=\left\{\begin{array}{l} q_{j-1}+\frac{q_j-q_{j-1}}{t_{2 j-1}-t_{2 j-2}}\left(t-t_{2 j-2}\right), t_{2 j-2} \leqslant t<t_{2 j-1} \\ q_j, t_{2 j-1} \leqslant t<t_{2 j} \end{array}\right. $ | (40) |
当t2j-2≤t < t2j-1时,不同加载阶段下的f(t)表达式为
| $ \begin{gathered} f(t)=\frac{1-I_{{\mathrm{c}}}(\alpha-1)}{\sigma_0^{\prime}}\left[K_j\left(1-{\mathrm{e}}^{-\beta t}\right)+\beta q {\mathrm{e}}^{-\beta t}\right] \times \\ {\left[1+\frac{q_{j-1}+K_j\left(t-t_{2 j-2}\right)}{\sigma_0^{\prime}}\left(1-{\mathrm{e}}^{-\beta t}\right)\right]^{-I_{{\mathrm{c}}}(\alpha-1)}} \end{gathered} $ | (41) |
式中
当t2i-1≤t<t2i时,不同加载阶段下的f(t)表达式为
| $ f(t)=\frac{1-I_{{\mathrm{c}}}(\alpha-1)}{\sigma_0^{\prime}}\left(N_{{\mathrm{q}}_j}-\frac{q_j}{\sigma_0^{\prime}} {\mathrm{e}}^{-\beta t}\right)^{-I_{{\mathrm{c}}}(\alpha-1)} \beta q_j {\mathrm{e}}^{-\beta t} $ | (42) |
式中
则此时Tm(t)为
| $ T_m(t)=\\ \left\{\begin{array}{c} \sum\limits_{k=1}^{j-1}\left[\int_{t_{2 k-2}}^{t_{2k-1}} F(\tau) {\mathrm{d}} \tau+\int_{t_{2 k-1}}^{t_{2 k}} F(\tau) {\mathrm{d}} \tau\right]+\int_{t_{2 j-2}}^t F(\tau) {\mathrm{d}} \tau \approx \\ \frac{t}{2 N} \sum\limits_{i=0}^N\left[F\left(\frac{t}{N_{i-1}}\right)+F\left(\frac{t}{N_i}\right)\right], t_{2 j-2} \leqslant t<t_{2 j-1} \\ \sum\limits_{k=1}^j \int_{t_{2 k-2}}^{t_{2 k-1}} F(\tau) {\mathrm{d}} \tau+\sum\limits_{k=1}^{j-1} \int_{t_{2 k-1}}^{t_{2 k}} F(\tau) {\mathrm{d}} \tau+\int_{t_{2 j-1}}^t F(\tau) {\mathrm{d}} \tau \approx \\ \frac{t}{2 N} \sum\limits_{i=0}^N\left[F\left(\frac{t}{N_{i-1}}\right)+F\left(\frac{t}{N_i}\right)\right], t_{2 j-1} \leqslant t<t_{2 j} \end{array}\right. $ | (43) |
3) 多级瞬时加载工况时,有
| $ q(t)=q_j, t_{j-1} \leqslant t<t_j $ | (44) |
当tj-1≤t < tj时,有
| $ f(t)=\frac{1-I_{{\mathrm{c}}}(\alpha-1)}{\sigma_0^{\prime}}\left(N_{{\mathrm{q}}_j}-\frac{q_j}{\sigma_0^{\prime}} {\mathrm{e}}^{-\beta t}\right)^{-I_{{\mathrm{c}}}(\alpha-1)} \beta q_j {\mathrm{e}}^{-\beta t} $ | (45) |
则相应的Tm(t)可写为
| $ \begin{gathered} T_m(t)=\sum\limits_{k=1}^j \int_{t_{k-1}}^{t_k} {\mathrm{e}}^{b_m \tau} f(\tau) {\mathrm{d}} \tau \approx \\ \frac{t}{2 N} \sum\limits_{i=0}^N\left[F\left(\frac{t}{N_{i-1}}\right)+F\left(\frac{t}{N_i}\right)\right], t_{j-1} \leqslant t<t_j \end{gathered} $ | (46) |
对于Ic(α-2)≠1这一情况,3.1节中的变量代换依然具有适用性,求解条件不变。与3.1节有所区别的是,当Ic(α-2)≠1时,固结控制方程不再是一个线性方程,很难获得方程的解析解,因此,基于文献[22]取(σ′/σ′0)1-Ic(α-2)近似等于其变化区间的平均值v0={1+[(σ′0+q)/σ′0]1-Ic(α-2)}/2,则式(16)可以转化为
| $ \frac{\partial v}{\partial t}=c_{{\mathrm{v}} 0} v_0 \frac{\partial^2 v}{\partial a^2}+f(t) $ | (47) |
超静孔压u的一般解答为
| $ \begin{aligned} u= & \sigma_0^{\prime}+\frac{{\mathrm{d}} q}{{\mathrm{~d}} t} t-\sigma_0^{\prime}\left\{\left[1+\frac{q}{\sigma_0^{\prime}}\left(1-{\mathrm{e}}^{-\beta t}\right)\right]^{1-I_{{\mathrm{c}}}(\alpha-1)}-\right. \\ & \left.\sum\limits_{m=1}^{\infty}\left[\frac{2}{M} {\mathrm{e}}^{-b_n t} T_m(t) \sin \frac{M a}{H}\right]\right\}^{\frac{1}{1-I_{{\mathrm{c}}}(\alpha-1)}} \end{aligned} $ | (48) |
由于孔压表达式复杂,沉降计算无法获得显式表达,因此采用数值积分计算。t时刻土层表面处的沉降值为
| $ \begin{aligned} S_{{\mathrm{t}}}= & H\left\{1-\frac{1}{2 N} \sum\limits_{r=1}^N\left[\left(\frac{\sigma_0^{\prime}}{\sigma_0^{\prime}+q-u\left(a_{r-1}, t\right)}\right)^{I_{{\mathrm{c}}}}+\right.\right. \\ & \left.\left.\left(\frac{\sigma_0^{\prime}}{\sigma_0^{\prime}+q-u\left(a_r, t\right)}\right)^{I_{{\mathrm{c}}}}\right]\right\} \end{aligned} $ | (49) |
式中:N为数值积分的积分区间数;ar-1、ar分别为第r个积分间距的起点和终点坐标;u(ar, t)为ar处t时刻的超静孔压;r=1, 2, 3,…,N。土层表面处的最终沉降、沉降固结度Ust以及孔压固结度Upt同3.1.1节。
3.2.2 特殊加载条件下的解答不同加载条件下超静孔压的解答区别主要在于Tm(t)的表达式不同。特殊加载条件下的Tm(t)具体表达式如下。
1) 单级等速加载工况时,有
| $ T_m(t)=\left\{\begin{array}{l} \int_0^t {\mathrm{e}}^{b_n \tau} f(\tau) {\mathrm{d}} \tau=\int_0^t G(\tau) {\mathrm{d}} \tau \approx \\ \frac{t}{2 N} \sum\limits_{i=0}^N\left[G\left(\frac{t}{N_{i-1}}\right)+G\left(\frac{t}{N_i}\right)\right], t<t_{{\rm{c}}} \\ \int_0^{t_{{\mathrm{c}}}} G(\tau) {\mathrm{d}} \tau+\int_{t_{{\mathrm{c}}}}^t G(\tau) {\mathrm{d}} \approx \tau \\ \frac{t}{2 N} \sum\limits_{i=0}^N\left[G\left(\frac{t}{N_{i-1}}\right)+G\left(\frac{t}{N_i}\right)\right], t \geqslant t_{{\mathrm{c}}} \end{array}\right. $ | (50) |
式中:bn=cv0v0M2/H2, G(t)=e-bntf(t)。
2) 多级等速加载工况时,有
| $ \begin{aligned} & T_m(t)= \\ & \left\{\begin{array}{l} \sum\limits_{k=1}^{j-1}\left[\int_{t_{2 k-2}}^{t_{2 k-1}} G(\tau) {\mathrm{d}} \tau+\int_{t_{2 k-1}}^{t_{2 k}} G(\tau) {\mathrm{d}} \tau\right]+\int_{t_{2 j-2}}^t G(\tau) {\mathrm{d}} \tau \approx \\ \quad \frac{t}{2 N} \sum\limits_{i=0}^N\left[G\left(\frac{t}{N_{i-1}}\right)+G\left(\frac{t}{N_i}\right)\right], t_{2 j-2} \leqslant t<t_{2 j-1} \\ \sum\limits_{k=1}^{j-1} \int_{t_{2 k-1}}^{t_{2 k}} G(\tau) {\mathrm{d}} \tau+\sum\limits_{k=1}^j \int_{t_{2 k-2}}^{t_{2 k-1}} G(\tau) {\mathrm{d}} \tau+\int_{t_{2 j-1}}^t G(\tau) {\mathrm{d}} \tau \approx \\ \frac{t}{2 N} \sum\limits_{i=0}^N\left[G\left(\frac{t}{N_{i-1}}\right)+G\left(\frac{t}{N_i}\right)\right], t_{2 j-1} \leqslant t<t_{2 j} \end{array}\right. \end{aligned} $ | (51) |
3) 多级瞬时加载工况,有
| $ \begin{gathered} T_m(t)=\sum\limits_{k=1}^j \int_{t_{k-1}}^{t_k} G(\tau) {\mathrm{d}} \tau \approx \\ \frac{t}{2 N} \sum\limits_{i=0}^N\left[G\left(\frac{t}{N_{i-1}}\right)+G\left(\frac{t}{N_i}\right)\right], t_{j-1} \leqslant t<t_j \end{gathered} $ | (52) |
为了验证本文解答的正确性,选取文献[23]室内固结渗透试验沉降曲线与本文理论编制的沉降计算程序进行对比,其中土层厚度H=19.225 mm,初始有效应力σ′0=100 kPa,初始孔隙比e0=1.05,初始渗透系数kv0=3.43×10-8 m/s,B=10。
根据室内土体渗透试验数据,得到了孔隙比与有效应力以及渗透系数之间的关系。通过线性拟合,可以得到双对数压缩模型压缩系数Ic=0.069和双对数渗透模型参数α=6.55。需要说明的是,室内试验采用的是分级加载,并假定每级荷载瞬时施加,加载时间为24 h(Tvi=0.02)。本文选取室内试验100~200 kPa、200~400 kPa加载段的沉降曲线,并在本文程序中设置相应参数,绘制对应沉降曲线,二者对比结果如图 3所示。
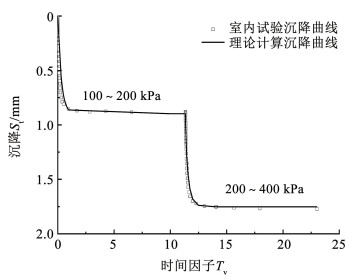
|
图 3 理论计算与时试验实测沉降曲线对比 Fig. 3 Comparison between theoretical calculation and laboratory test |
从图 3可以发现,在100~200 kPa、200~400 kPa加载段,理论计算沉降曲线与实测沉降曲线基本重合。无论是每级荷载下的最终沉降还是沉降曲线的走势,均与实测曲线一致,这一点可说明本文解答的正确性。
5 固结性状分析基于本文所得解析解进行算例分析,选取文献[24]文中的土体参数,其中土层厚度H=10 m,初始有效应力σ′0=50 kPa,初始孔隙比e0=1.571,初始渗透系数kv0=1×10-8 m/s,压缩指数cc=0.637 8,ck=0.8。根据cc、ck以及初始孔隙比e0、初始渗透系数kv0得到相应有效应力与孔隙比及孔隙比与渗透系数间的关系曲线。通过拟合可以得到双对数压缩、渗透模型中的相应参数Ic=0.12,α=6.67。
5.1 界面参数β对固结性状的影响图 4为土层顶部(a/H=0.2),B取不同值时超静孔压随时间变化的关系曲线,其中,B=10 000可看作完全透水边界。此部分荷载分别取0~100 kPa、100~200 kPa加载,加载时间为24 h(Tvi=0.02)。

|
图 4 超静孔压随时间变化关系曲线 Fig. 4 The dissipation of excess pore water pressure with the time factor |
不难看出,同一时刻下,完全透水边界超静孔压消散速率要明显快于变边界超静孔压的消散。基于变边界条件,随着B值的增大,超静孔压消散越快,当B达到一定值时,超静孔压消散曲线逐渐趋近于完全透水边界下的曲线。实际中的土层排水边界并非理想的完全透水边界,如果仍然按理想的完全透水边界开展固结计算会高估超静孔压的消散速率,从而过高估计地基土层的有效应力导致地基发生失稳破坏。如果采用变边界描述土体边界真实的透水性情况,可较为真实地获得地基中有效应力的增长情况,避免设计计算高估地基承载力在固结过程中的增长情况。
5.2 外荷载qn对固结性状的影响外部荷载包括瞬时施加的理想荷载、单级加载以及多级加载等多种形式的荷载。其中,瞬时荷载主要是方便于理论分析研究,在实际工程中荷载形式大多表现为单级加载和逐级加载。为了使本文理论分析结果更贴近于实际,研究外荷载的施加方式对固结性状的影响很有必要。基于此,取如下的荷载作为分析对象,具体见表 1。
| 表 1 荷载分级 Tab. 1 Loading step |
图 5、6分别为参数Ic(α-2)=1时,荷载qn取值对超静孔压u和孔压固结度Upt影响的关系曲线。图 5反映出不同的排水边界下,随着荷载的增大,超静孔压也在逐渐增大,但是超静孔压最终消散的时间几乎相同,说明荷载会影响土层内部超静孔压的大小,但不会对超静孔压消散的最终时间产生影响。当作用相同荷载时,完全透水边界下超静孔压的消散快于变边界条件下的超静孔压的消散,体现在以孔压定义的固结度Upt上(图 6),即完全透水边界下土层的固结速率快于变边界下土层固结速率。

|
图 5 荷载qn与超静孔压u关系曲线 Fig. 5 Influences of loading qn on the dissipation of excess pore water pressure u |
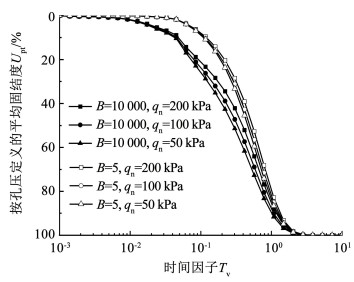
|
图 6 荷载qn与孔压固结度Upt关系曲线 Fig. 6 Influences of loading qn on the average degree of consolidation defined by stress Upt |
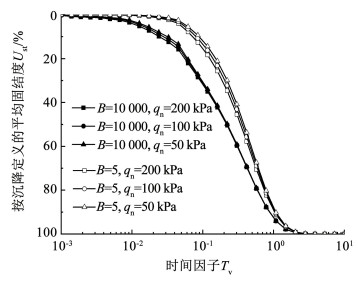
图 7~9为参数Ic(α-2)取不同值时,荷载qn对沉降固结度Ust的影响曲线。从图中可以发现,加载阶段时,不同边界下沉降固结度随着荷载的增大而增大,这一点归结为当荷载增大时,土层中的水流出速度加快,超静孔压消散的速率加快,表现在固结度方面即土层发生相同沉降所需时间缩短。进入持荷阶段后,Ic(α-2)=1时,不同边界下的土体沉降固结度逐渐趋于同一条曲线,完全透水边界下的尤为明显; 当Ic(α-2) < 1时,土体沉降固结度随着荷载的增大逐渐增大;而当Ic(α-2)>1时,土体沉降固结度却随着荷载的增大而减小。在大应变固结中常以大应变固结系数cF表征土体的固结速率。引起上述性状的原因是当参数Ic(α-2)=0时,大应变固结系数为常数,此时土体的固结速率与荷载取值无关; 当Ic(α-2) < 1时,大应变固结系数随着荷载的增大而增大,土体的固结速率加快,相应的沉降固结度增大, 反之,土体固结速率降低,沉降固结度减小。
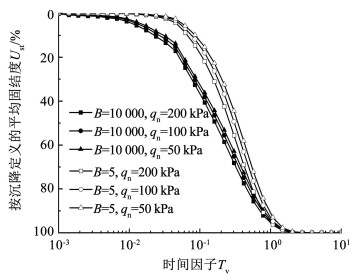
|
图 7 Ic(α-2) < 1时,qn对Ust的影响 Fig. 7 Influences of qn on Ust when Ic(α-2) < 1 |
|
图 8 Ic(α-2)=1,qn对Ust的影响 Fig. 8 Influences of qn on Ust when Ic(α-2)=1 |

|
图 9 Ic(α-2)>1,qn对Ust的影响 Fig. 9 Influences of qn on Ust when Ic(α-2) > 1 |
值得注意的是,随着参数取值的增大,不同荷载下沉降固结度呈现出先增大后减小的固结性状在变边界下显现得较晚,主要原因是变边界下超静孔压消散的比较缓慢,所要表现出的固结性状在固结中、后期才会有所体现。
6 结论本文基于软土大应变几何假定和双对数压缩、渗透模型,得到了变荷载下考虑土层排水边界为变边界的软土一维大应变非线性固结模型解析解。根据所得解析解,对软土土层基于变边界界面参数和外部荷载进行固结性状分析,得到以下结论:
1) 实际工程中假设土体边界为完全透水边界,易造成过高估计超静孔压消散速率的情形,导致地基失稳问题的出现。而变边界可描述土体边界真实透水情况,可通过超静孔压实际消散速率反演获得相应的界面参数,从而有效避免过高估计地基承载力在固结过程中的增长情况。
2) 外荷载的大小会影响超静孔压的消散速率,随着荷载的增大,土体内部超静孔压消散越快,但不会对超静孔压最终消散以及土层最终沉降所需时间产生影响。
3) 在不同的Ic(α-2)取值下,土体沉降固结速率随着荷载的变化规律有所异同。值得强调的是,变边界下荷载对固结性状的影响会比完全透水边界下延迟,主要是由于变边界下超静孔压消散比较缓慢,应显现出的固结性状在固结中、后期才会有所体现。
| [1] |
GRAY H. Simultaneous consolidation of contiguous layers of unlike compressible soils[J]. Transactions, ASCE, 1945, 110: 1327. |
| [2] |
梅国雄, 夏君, 梅岭. 基于不对称连续排水边界的太沙基一维固结方程及其解答[J]. 岩土工程学报, 2011, 33(1): 28. MEI Guoxiong, XIA Jun, MEI Ling. Terzaghi′s one-dimensional consolidation equation and its solution based on asymmetric continuous drainage boundary[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 28. |
| [3] |
WU W B, ZONG M F, EI NAGGAR M H, et al. Analytical solution for one-dimensional consolidation of double-layered soil with time-dependent drainage boundary[J]. International Journal of Distributed Sensor Networks, 2018, 14(10): 1. |
| [4] |
张驿, 吴文兵, 梅国雄, 等. 基于连续排水边界条件的砂井地基固结解析解[J]. 工程技术科学与技术, 2019, 51(2): 1. ZHANG Yi, WU Wenbing, MEI Guoxiong, et al. Analytical solution of sand-drained ground consolidation based on continuous drainage boundary[J]. Advanced Engineering Sciences, 2019, 51(2): 1. |
| [5] |
陈余, 李传勋. 连续排水边界下考虑起始坡降的软黏土固结解[J]. 工程力学, 2021, 38(9): 161. CHEN Yu, LI Chuanxun. Consolidation analysis of soft clay considering the threshold hydraulic gradient and a continuous drainage boundary[J]. Engineering Mechanics, 2021, 38(9): 161. |
| [6] |
宗梦繁, 吴文兵, 梅国雄, 等. 连续排水边界条件下土体一维非线性固结解析解[J]. 岩石力学与工程学报, 2018, 37(12): 2829. ZONG Mengfan, WU Wenbing, MEI Guoxiong, et al. An analytical solution for one-dimensional nonlinear consolidation of soils with continuous drainage boundary[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(12): 2829. |
| [7] |
DAVIS E H, RAYMOND G P. A non-linear theory of consolidation[J]. Geotechnique, 1965, 15(2): 161. |
| [8] |
宗梦繁. 连续排水边界下软土一维非线性固结理论与试验研究[D]. 武汉: 中国地质大学, 2021 ZONG Mengfan. Theoretical and experimental study on one-dimensional nonlinear consolidation of soft soil based on continuous drainage boundary[D]. Wuhan: China University of Geosciences, 2021 |
| [9] |
GIBSON R E, ENGLAND G L, HUSSEY M J L. The theory of one-dimensional consolidation of saturated clays: Ⅰ.finite non-linear consolidation of thin homogeneous layers[J]. Geotechnique, 1967, 17(2): 261. |
| [10] |
GIBSON R E, SCHIFFMAN R L, CARGILL K W. The theory of one-dimensional consolidation of saturated clays: Ⅱ.finite nonlinear consolidation of thick homogeneous layers[J]. Canadian Geotechnical Journal, 1981, 18(2): 280. |
| [11] |
MORRIS P H. Analytical solutions of linear finite-strain one-dimensional consolidation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(4): 319. |
| [12] |
HU Y Y, ZHOU W H, CAI Y Q. Large-strain elastic viscoplastic consolidation analysis of very soft clay layers with vertical drains under preloading[J]. Candian Geotechnical Journal, 2015, 52(1): 127. |
| [13] |
CAO Y P, YANG J, XU G Z, et al. Analysis of large-strain consolidation behavior of soil with high water content in consideration of self-weight[J]. Advances in Civil Engineering, 2018(6): 1. |
| [14] |
李刚, 张金利, 杨庆, 等. 非达西渗流与变渗透系数下的大变形固结分析[J]. 中南大学学报(自然科学版), 2016, 47(3): 977. LI Gang, ZHANG Jinli, YANG Qing, et al. Analysis of large-strain consolidation with non-Darcy and variable permeability coefficient[J]. Journal of Central South University(Science and Technology), 2016, 47(3): 977. |
| [15] |
董兴泉, 李传勋, 陈蒙蒙, 等. 考虑非达西渗流的双层软土地基大变形非线性固结分析[J]. 岩土力学, 2016, 37(8): 2321. DONG Xingquan, LI Chuanxun, CHEN Mengmeng, et al. Analysis of large-strain nonlinear consolidation of double-layer soft clay foundation with considering effect of non-Darcy′s flow[J]. Rock and Soil Mechanics, 2016, 37(8): 2321. |
| [16] |
MESRI G, CHOI Y K. Settlement analysis of embankments on soft clays[J]. Journal of Geotechnical Engineering, 1985, 111(4): 441. |
| [17] |
BUTTERFIELD R. A natural compression law for soils (an advance on e - lg p′)[J]. Geotechnique, 1979, 29(4): 469. |
| [18] |
TAVENAS F, JEAN P, LEBLOND P, et al. The permeability of natural soft clays: PartⅡ. permeability characteristics[J]. Candian Geotechnical Journal, 1983, 20(4): 645. |
| [19] |
李传勋, 仇超. 高压缩性软土一维非线性大应变固结解析解[J]. 岩石力学与工程学报, 2021, 40(11): 2344. LI Chuanxun, QIU Chao. An analytical solution for one-dimensional nonlinear large-strain consolidation of soft clay with high compressibility[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(11): 2344. |
| [20] |
江文豪, 詹良通, 杨策. 连续排水边界条件下饱和软土一维大变形固结解析解[J]. 中南大学学报(自然科学版), 2020, 51(5): 1289. JIANG Wenhao, ZHAN Liangtong, YANG Ce. Analytical solution for one-dimensional large strain consolidation of saturated soft soils with continuous drainage boundary[J]. Journal of Central South University (Science and Technology), 2020, 51(5): 1289. |
| [21] |
谢康和, 郑辉, LEOC J. 软黏土一维非线性大应变固结解析理论[J]. 岩土工程学报, 2002, 24(6): 680. XIE Kanghe, ZHENG Hui, LEO C J. An analytical theory for 1-D nonlinear large strain consolidation of soft clay[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(6): 680. |
| [22] |
LEKHA K R, KRISHNASWAMY N R, BASAK P. Consolidation of clays for variable permeability and compressibility[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(11): 1001. |
| [23] |
齐添. 软土一维非线性固结理论与试验对比研究[D]. 杭州: 浙江大学, 2008 QI Tian. Theoretical and experimental studies on one-dimensional nonlinear consolidation of soft clay[D]. Hangzhou: Zhejiang University, 2008 |
| [24] |
李传勋, 董兴泉, 金丹丹, 等. 考虑起始坡降双层地基的大应变非线性固结[J]. 岩土力学, 2018, 39(5): 1877. LI Chuanxun, DONG Xingquan, JIN Dandan, et al. Large-strain nonlinear consolidation of double-layered soft clay with threshold gradient[J]. Rock and Soil Mechanics, 2018, 39(5): 1877. |
 2024, Vol. 56
2024, Vol. 56


