2. 长安大学 地下结构与工程研究所,西安 710064
2. Institute of Underground Structure and Engineering, Chang′an University, Xi′an, 710064, China
螺纹桩是一种桩身带有螺牙结构的异形截面桩,由Atlas桩和螺旋钢管桩的基础上改进而来,具有一定的挤密和螺牙增效作用[1-2]。国内外研究表明,在相同的地层条件下,螺纹桩与普通圆桩相比,桩身材料利用率提高3倍左右[3],极限承载力高1~4倍[4-5]。由于螺纹桩凭借其造价低、适用性广、单桩承载力高、节约材料等优点,目前已在京沪、大张、郑徐、石济等多条高速铁路和客运专线得到应用[6-7]。尽管螺纹桩的施工工艺已逐渐趋于成熟,但理论研究却远远滞后于工程实践,一方面是由于螺纹桩与桩侧土的相互作用相对于传统的圆形桩较为复杂,另一方面是振动荷载作用下螺纹桩的荷载传递机理、桩土协同工作机制与静载作用下的差别仍不明确。文献[8-9]通过室内模型试验研究了竖向动力荷载下螺纹桩-土荷载传递机制。文献[10]采用振动台试验和动态离心机试验分析螺纹桩在可液化地基的动力特性。针对地震中的反应,文献[11]研究了螺纹单桩在干燥土和饱和土中横向响应,也讨论了群桩的地震响应[12-13]。上述研究表明,螺纹桩具有良好的减振和抗震性能,但结果均建立在缩尺试验之上,无法真实还原螺纹桩在纵向振动下的动力响应机理。
由于试验无法从本质上揭示螺纹桩的动力特征和发展规律,因此需要借助理论分析研究出一套合理评价螺纹桩动力响应的方法。相比之下,桩基振动理论用于圆形等截面桩动力性能研究已经相当广泛而深入。文献[14]通过引入虚土桩模型和Winkler模型,得到了三维轴对称连续介质中浮沉桩纵向振动阻抗的解析解。基于土体三维波动效应模型,文献[15]研究了滞回阻尼土中桩的频域响应解析解,也研究了在黏性阻尼土中桩顶速度导纳解析解[16], 在此基础上,文献[17]建立了桩-土相互作用的摩檫力模型,基于边界条件和连续条件得出圆桩纵向振动闭合形式的解析解。文献[18]在针对圆形等截面桩的解析解研究方面也取得了丰硕的成果。而螺纹桩作为异形截面桩,其螺牙侧摩阻力和螺牙间桩土摩阻力的分布规律并不相同,以上针对圆桩的纵向振动理论对螺纹桩动力响应的适用性仍不清楚,有待进一步研究。
螺纹桩与桩侧土的作用相对复杂,振动荷载作用下螺纹桩受力分析也较为困难。鉴于此,部分学者[19-20]提出在螺纹桩的动力特性研究中将螺纹桩简化为直径不同的变截面桩,且根据螺牙的位置将桩土系统划分为相当数量的薄层,在每一薄层内,螺纹桩微元桩段视为均匀截面段,此时桩侧土对微元段的作用可近似用传统的圆桩理论进行研究。针对螺纹桩而言,它与等截面圆桩的最大区别就在于螺牙的存在增加了与桩侧土的相互作用,因此必须考虑侧摩阻力和桩侧土竖向作用对螺纹桩的影响。
另一方面,针对异形截面桩的纵向振动响应研究均基于桩侧土为均质体假定,然而在实际工程中,由于土体长期自然沉淀,桩侧土往往会分层,应力波在分层界面的反射和折射现象存在复杂性[21-22],该影响对于螺纹桩更加显著,此时仍采用该假定将会引起不可避免的误差。为此,本文考虑桩侧土的竖向作用,基于土体的三维波动效应,建立滞回阻尼土中螺纹桩复阻抗的解析表达式,运用Laplace变换和阻抗函数传递方法对螺纹桩桩顶复刚度进行求解,以期探讨成层土中螺纹桩纵向振动的频域响应。
1 计算模型及基本假定 1.1 计算模型为实现对螺纹桩在成层滞回阻尼土中的振动特性分析,需要对螺纹桩进行一定程度的理论简化。已有的常见理论模型中[23-24]均将螺纹桩简化为变截面桩,在计算螺纹桩承载力时,螺纹桩按多点支撑的浮沉桩考虑,这种考虑是合理的,因为由正视图可以看出,螺纹桩亦是由等截面圆桩和一定厚度的圆盘组成。此观点在规范[25]中也有相同表述,在每一螺距范围内,螺纹桩的螺牙可视为长方形的承载板,承载力由侧摩阻力和若干承载板的承载力组成。对此,本文采用相同方法将螺纹桩模型处理为等间距变截面圆桩形式,截面变化处的面积与螺纹桩叶片纵向投影面积相同,计算简图如图 1所示,螺纹桩外径为D,内径为d,螺牙高度为b,螺距为s,螺牙厚度为c。
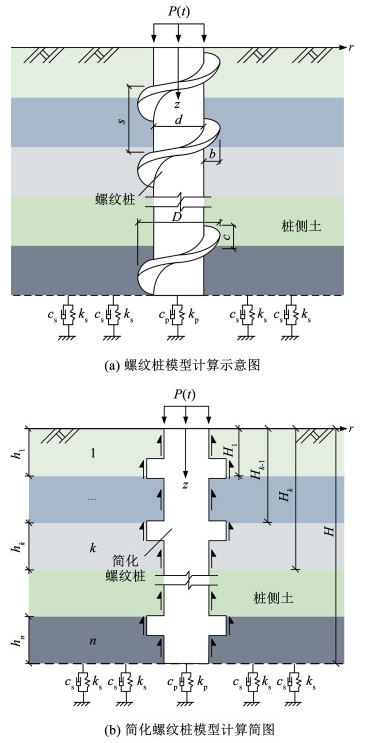
|
图 1 螺纹桩-土相互作用计算简图 Fig. 1 Simplified diagram of screw pile soil interaction calculation |
根据土的成层特性,将桩土系统划分为n段,土层自上而下依次编号为1,2,…,n,同一段土中参数相同,其中第k段土层的密度为ρsk、弹性模量为Esk、厚度为hk,剪切模量和拉梅常数分别为Gk和λk。
桩顶作用竖向动荷载为P(t),桩底土对桩的作用简化为单个线性弹簧和阻尼器并联的开尔文体,弹性系数和阻尼系数分别为kp和cp,可参照文献[26]中的计算公式进行取值。桩侧土底部支承条件简化为沿径向均布的开尔文体,其弹性系数和阻尼系数分别为ks和cs。
1.2 基本假定建立力学模型时,作出以下基本假定:1)忽略土体弹性区与塑性区分界面的相对滑动,土体振动时的能量耗散主要由辐射阻尼和滞回阻尼引起;2)桩侧土纵向成层,每层土体均质、各向同性,土层顶部为自由边界,桩侧土底部支撑条件及土层之间相互作用均简化为开尔文体;3)螺纹桩-土受到谐和激振力作用时,桩侧土既有竖向位移,又有径向位移,其变形均为小变形,忽略桩土交界面上土体径向位移;4)螺纹桩为一维线弹性杆件,应力波在桩身传播满足平截面假定;5)桩与桩侧土之间完全接触,即界面两侧位移协调、受力连续。
2 桩土系统动力方程的建立与求解 2.1 方程的建立 2.1.1 土体动力平衡方程在第k层土中,螺纹桩计算简图如图 2所示。土层上、下截面简化为径向均布的Voigt体,其弹簧和黏壶系数分别为ksk-1、csk-1和ksk+1、csk+1。桩侧土的竖向作用采用单个开尔文体模拟,弹簧和黏壶系数分别为ksk和csk。

|
图 2 第k层土中第j段桩身计算简图 Fig. 2 Calculation diagram of the j-th section pile in the k-th layer of soil |
土层的纵向位移分量和径向位移分量分别为uzk和urk,从弹性动力学理论基础上建立滞回阻尼土的波动方程。
纵向动力平衡方程为
| $ G_{1 k} \frac{\partial^2 u_{z k}}{\partial z^2}+G_{2 k} \frac{\partial^2 u_{r k}}{\partial r \partial z}+G_{2 k} \frac{1}{r} \frac{\partial u_{r k}}{\partial z}+\\G_{3 k} \frac{1}{r} \frac{\partial u_{z k}}{\partial r}+G_{3 k} \frac{\partial^2 u_{z k}}{\partial r^2}=\rho_{s k} \frac{\partial^2 u_{z k}}{\partial t^2} $ | (1) |
径向动力平衡方程为
| $ \begin{gathered} G_{1 k} \frac{\partial^2 u_{r k}}{\partial r^2}+G_{1 k} \frac{1}{r} \frac{\partial u_{r k}}{\partial r}-G_{1 k} \frac{u_{r k}}{r^2}+G_{2 k} \frac{\partial^2 u_{z k}}{\partial r \partial z}+ \\ G_{3 k} \frac{\partial^2 u_{r k}}{\partial z^2}=\rho_{s k} \frac{\partial^2 u_{r k}}{\partial t^2} \end{gathered} $ | (2) |
式中:G1k=[(λk+2Gk)+i(λ′k+2G′k)],G2k=(λk+Gk)+i(λ′k+G′k),G3k=(Gk+iG′k),λ′k、G′k分别为λk和Gk对应的黏性系数。
2.1.2 螺纹桩动力平衡方程在垂直激振力作用下,螺纹桩第j段桩身质点位移为up。其中桩段底部支承等效为弹簧和阻尼器的并联体,下界面的弹性系数和阻尼系数分别为kpk、cpk。
取第j段桩身微元体作动力平衡分析,可得螺纹桩的动力平衡方程为
| $ E_{{\mathrm{p}}} S_{{\mathrm{p}} j} \frac{\partial^2 u_{{\mathrm{p}}}}{\partial z^2}-f_j(z, t)=\rho_{{\mathrm{p}}} S_{{\mathrm{p}} j} \frac{\partial^2 u_{{\mathrm{p}}}}{\partial t^2} $ | (3) |
式中:Ep、Spj、ρp分别为螺纹桩的弹性模量、桩身横截面积和材料密度; fj(z, t)为单位长度内桩侧土对桩身的动摩阻力,可表示为
| $ f_j(z, t)=-R(z)=-2 \pi r_2^{{\mathrm{p}}} \tau_{r z}=-2 \pi r_2^{{\mathrm{p}}}\left(G+{\mathrm{i}} G^{\prime}\right) \gamma_{r z} $ | (4) |
其中: R(z)为单位长度内桩对桩侧土层的反力,r2p为桩段半径。
2.2 边界条件为便于后续公式推导,采用局部坐标形式对螺纹桩微元体进行分析,取第j段顶部坐标为0,底部坐标为hc。
1) 土层的边界条件:
忽略桩土界面上的径向位移边界条件为
| $ \left.u_{r k}\right|_{r=r_2^{{\rm{p}}}}=0 $ | (5) |
土层无穷远处位移为0,即
| $ \left\{\begin{array}{l} \left.u_{r k}\right|_{r \rightarrow \infty}=0 \\ \left.u_{z k}\right|_{r \rightarrow \infty}=0 \end{array}\right. $ | (6) |
土层底部为黏弹性支承边界条件为
| $ \left.\left(k_{{\mathrm{s}}}^{k+1} u_{z k}+c_{{\mathrm{s}}}^{k+1} \frac{\partial u_{z k}}{\partial t}-E_{{\mathrm{s}} k} \frac{\partial u_{z k}}{\partial z}\right)\right|_{z=h_k}=0 $ | (7) |
式中:ksn=ks,csn=cs。
当k=1时,σzk|z=0=0,即
| $ \begin{gathered} {\left[\left(\lambda+2 G_k\right)+{\mathrm{i}}\left(\lambda^{\prime}+2 G_k^{\prime}\right)\right] \frac{\partial u_{z k}}{\partial z}+} \\ \left.\quad\left(\lambda+{\mathrm{i}} \lambda^{\prime}\right) \frac{\partial\left(r u_{r k}\right)}{r \partial r}\right|_{z=0}=0 \end{gathered} $ | (8) |
当k≥2时,可得
| $ \left.\left(k_{{\mathrm{s}}}^{k-1} u_{z k}+c_{{\mathrm{s}}}^{k-1} \frac{\partial u_{z k}}{\partial t}+E_{{\mathrm{s}} k} \frac{\partial u_{z k}}{\partial z}\right)\right|_{z=0}=0 $ | (9) |
2) 桩-土接触面位移连续条件:
| $ \left.u_{z k}\right|_{r=r_j}=u_{{\mathrm{p}}} $ | (10) |
3) 螺纹桩的边界条件:
第j段桩顶边界条件为
| $ P_j(t)+E_{{\mathrm{p}}} S_{{\mathrm{p}} j} \frac{\partial u_{{\mathrm{p}}}}{\partial z}-\left.\left(k_{{\mathrm{s}}}^k u_{{\mathrm{p}}}+c_{{\mathrm{s}}}^k \frac{\partial u_{{\mathrm{p}}}}{\partial t}\right)\right|_{z=0}=0 $ | (11) |
式中Pj(t)为螺纹桩第j-1段桩身对第j段顶部作用的力,P1(t)=P(t)。
第j段桩底边界条件为
| $ \begin{aligned} & {\left[E_{{\mathrm{p}}} S_{{\mathrm{p}} j} \frac{\partial u_{{\mathrm{p}}}}{\partial z}+k_{{\mathrm{p}} k} u_{{\mathrm{p}}}+c_{{\mathrm{p}} k} \frac{\partial u_{{\mathrm{p}}}}{\partial t}+\right.} \\ & \left.\left(k_{{\mathrm{s}}}^k u_{{\mathrm{p}}}+c_{{\mathrm{s}}}^k \frac{\partial u_{{\mathrm{p}}}}{\partial t}\right)\right]\left.\right|_{z=h_{{\mathrm{c}}}}=0 \end{aligned} $ | (12) |
式中:kpn=kp,cpn=cp。
4) 初始条件:
第k层土层初始条件为
| $ \left\{\begin{array}{l} \left.u_{r k}\right|_{t=0}=0,\left.\frac{\partial u_{r k}}{\partial t}\right|_{t=0}=0 \\ \left.u_{z k}\right|_{t=0}=0,\left.\frac{\partial u_{z k}}{\partial t}\right|_{t=0}=0 \end{array}\right. $ | (13) |
螺纹桩第j桩段初始条件为
| $ \left\{\begin{array}{l} \left.u_{{\mathrm{p}}}\right|_{t=0}=0 \\ \left.\frac{\partial u_{{\mathrm{p}}}}{\partial t}\right|_{t=0}=0 \end{array}\right. $ | (14) |
土体的纵向位移uzk和径向位移urk具有关联性,引入势函数对其进行分解,代入式(1)和式(2),可得
| $ \begin{gathered} G_3\left(\frac{\partial^2}{\partial r^2}+\frac{1}{r} \frac{\partial}{\partial r}\right) \nabla^2 \psi-G_1 \frac{\partial}{\partial z} \nabla^2 \phi= \\ \rho_{{{\rm{s}}} k} \frac{\partial^2}{\partial t^2}\left[\frac{\partial \phi}{\partial z}-\frac{1}{r} \frac{\partial \psi}{\partial r}-\frac{\partial^2 \psi}{\partial r^2}\right] \end{gathered} $ | (15) |
| $ G_1 \frac{\partial}{\partial r} \nabla^2 \phi+G_3 \frac{\partial^2}{\partial r \partial z} \nabla^2 \psi=\rho_{{\rm {s }}k} \frac{\partial^2}{\partial t^2}\left(\frac{\partial \phi}{\partial r}+\frac{\partial^2 \psi}{\partial r \partial z}\right) $ | (16) |
式中:
令s=iω,对式(15)、(16)进行关于t的Laplace变换,整理后可得
| $ \left(\frac{\partial^2}{\partial r^2}+\frac{1}{r} \frac{\partial}{\partial r}\right)\left(G_3 \nabla^2+\rho_{{\rm {s }} k} \omega^2\right) \varPsi-\frac{\partial}{\partial z}\left(G_1 \nabla^2+\rho_{{\rm {s }} k} \omega^2\right) \varPhi=0 $ | (17) |
| $ \frac{\partial}{\partial r}\left(G_1 \nabla^2+\rho_{{\rm {s }} k} \omega^2\right) \varPhi+\frac{\partial^2}{\partial r \partial z}\left(G_3 \nabla^2+\rho_{{{\mathrm{s}}}k} \omega^2\right) \varPsi=0 $ | (18) |
式中Φ、Ψ分别为势函数ϕ、ψ的Laplace变换形式。
式(17)、(18)成立,需满足以下方程式:
| $ \begin{aligned} & \nabla^2 \varPsi+\frac{\omega^2}{v_{{\mathrm{s}}}^2} \varPsi=0 \end{aligned} $ | (19) |
| $ \nabla^2 \varPhi+\frac{\omega^2}{v_1^2} \varPhi=0 $ | (20) |
式中:
采用分离变量法对式(19)、(20)进行求解,可得通解:
| $ \begin{aligned} \varPsi= & {\left[A_{2 k} \cos \left(\beta_k z\right)+B_{2 k} \sin \left(\beta_k z\right)\right]\left[C_{2 k} I_0\left(s_k r\right)+\right.} \\ & \left.D_{2 k} K_0\left(s_k r\right)\right] \end{aligned} $ | (21) |
| $ \begin{aligned} \varPhi= & {\left[A_{1 k} \cos \left(\beta_k z\right)+B_{1 k} \sin \left(\beta_k z\right)\right]\left[C_{1 k} I_0\left(\eta_k r\right)+\right.} \\ & \left.D_{1 k} K_0\left(\eta_k r\right)\right] \end{aligned} $ | (22) |
式中I0(·)、K0(·)分别为第1类、第2类修正零阶贝塞尔函数;
由式(21)、(22)可得
| $ \begin{aligned} U_{z k}= & {\left[B_{1 k} \cos \left(\beta_k z\right)-A_{1 k} \sin \left(\beta_k z\right)\right]\left[C_{1 k} I_0\left(\eta_k r\right)+\right.} \\ & \left.D_{1 k} K_0\left(\eta_k r\right)\right] \beta_k-\left[A_{2 k} \cos \left(\beta_k z\right)+B_{2 k} \sin \left(\beta_k z\right)\right] \times \\ & {\left[C_{2 k} I_0\left(s_k r\right)+D_{2 k} K_0\left(s_k r\right)\right] s_k^2 } \end{aligned} $ | (23) |
| $ U_{r k}=\left[A_{1 k} \cos \left(\beta_k z\right)+B_{1 k} \sin \left(\beta_k z\right)\right]\left[C_{1 k} I_1\left(\eta_k r\right)-\right.\\\begin{aligned} & \left.D_{1 k} K_1\left(\eta_k r\right)\right] \eta_k-\left[A_{2 k} \sin \left(\beta_k z\right)-B_{2 k} \cos \left(\beta_k z\right)\right] \cdot \\ & {\left[C_{2 k} I_1\left(s_k r\right)-D_{2 k} K_1\left(s_k r\right)\right] \beta_k s_k} \end{aligned} $ | (24) |
由Bessel函数的自然边界条件性质可知,当r→∞时,I0(·)→∞。
对边界条件(6)进行Laplace变换可得
| $ \left\{\begin{array}{l} \left.U_{r k}\right|_{r \rightarrow \infty}=0 \\ \left.U_{z k}\right|_{r \rightarrow \infty}=0 \end{array}\right. $ | (25) |
则易得到C1k=0、C2k=0,式(23)、(24)可分别简化为
| $ \begin{aligned} U_{z k}= & {\left[b_{1 k} \cos \left(\beta_k z\right)-a_{1 k} \sin \left(\beta_k z\right)\right] K_0\left(\eta_k r\right) \beta_k-} \\ & {\left[a_{2 k} \cos \left(\beta_k z\right)+b_{2 k} \sin \left(\beta_k z\right)\right] K_0\left(s_k r\right) s_k^2 } \end{aligned} $ | (26) |
| $ \begin{aligned} U_{r k}= & {\left[a_{1 k} \cos \left(\beta_k z\right)+b_{1 k} \sin \left(\beta_k z\right)\right] K_1\left(\eta_k r\right) \eta_k+} \\ & {\left[b_{2 k} \cos \left(\beta_k z\right)-a_{2 k} \sin \left(\beta_k z\right)\right] K_1\left(s_k r\right) \beta_k s_k } \end{aligned} $ | (27) |
对式(5)、(7)、(8)、(9)进行Laplace变换后,将式(26)和式(27)代入,可得
| $ \begin{gathered} \cos \left(\beta_k z\right)\left[a_{1 k} K_1\left(\eta_k r_2^{{\mathrm{p}}}\right) \eta_k+b_{2 k} K_1\left(s_k r_2^{{\mathrm{p}}}\right) \beta_k s_k\right]\\+\sin \left(\beta_k z\right)\left[b_{1 k} K_1\left(\eta_k r_2^{{\mathrm{p}}}\right) \eta_k-a_{2 k} K_1\left(s_k r_2^{{\mathrm{p}}}\right) \beta_k s_k\right]=0 \end{gathered} $ | (28) |
| $ K_0\left(\eta_k r\right) \beta_k\left\{\frac{\left(k_{{\mathrm{s}}}^{k+1}+c_{{\mathrm{s}}}^{k+1} s\right) \beta_k}{E_{{\mathrm{s}} k}}\left[b_{1 k} \cos \left(\beta_k h_k\right)-a_{1 k} \sin \left(\beta_k h_k\right)\right]\\+\beta_k^2\left[b_{1 k} \sin \left(\beta_k h_k\right)+a_{1 k} \cos \left(\beta_k h_k\right)\right]\right\}+\\ K_0\left(s_k r\right) s_k^2\left\{\left[b_{2 k} \beta_k \cos \left(\beta_k h_k\right)-a_{2 k} \beta_k \sin \left(\beta_k h_k\right)\right]\\-\frac{k_{{\mathrm{s}}}^{k+1}+c_{{\mathrm{s}}}^{k+1} s}{E_{{\mathrm{s}} k}}\left[a_{2 k} \cos \left(\beta_k h_k\right)+b_{2 k} \sin \left({\boldsymbol{\beta}}_k h_k\right)\right]\right\}=0 $ | (29) |
| $ K_0\left(\eta_1 r\right) a_{11}\left[\left(\lambda+{\mathrm{i}} \lambda^{\prime}\right) \eta_1^2-G_{11}^l \beta_1^2\right]-K_0\left(s_k r\right)\left[G_{11}^l-\left(\lambda+{\mathrm{i}} \lambda^{\prime}\right)\right] \beta_1 b_{21} s_1^2=0 $ | (30) |
| $ K_0\left(\eta_k r\right)\left(\frac{k_{{\mathrm{s}}}^{k-1}+c_{{\mathrm{s}}}^{k-1} s}{E_{{\mathrm{s}} k}} b_{1 k} \beta_k-a_{1 k} \beta_k^2\right)-K_0\left(s_k r\right)\left(\frac{k_{{\mathrm{s}}}^{k-1}+c_{{\mathrm{s}}}^{k-1} s}{E_{{\mathrm{s}} k}} a_{2 k} s_k^2+b_{2 k} \beta_k s_k^2\right)=0 $ | (31) |
由sin(βkz)与cos(βkz)、k0(ηkr)与k0(skr)均线性无关,解出a1k、a2k、b1k、b2k的关系式,即Uzk和Urk分别为
| $ \begin{array}{l} U_{z k}= & \sum\limits_{m=1}^{\infty} a_{k m} \sqrt{1+\frac{\beta_{k m}}{k b_{{\mathrm{s}}}^{k+1}}}\left[\eta_{k m} \frac{s_{k m}}{\beta_{k m}} \frac{K_1\left(\eta_{k m} r_2^{{\mathrm{p}}}\right)}{K_1\left(s_{k m} r_2^{{\mathrm{p}}}\right)} \times\right. \\ & \left.K_0\left(s_{k m} r\right)-\beta_{k m} K_0\left(\eta_{k m} r\right)\right] \times \cos \left(\beta_{k m} z-\theta_{k m}\right) \end{array} $ | (32) |
| $ \begin{array}{l} U_{r k}= & \sum\limits_{m=1}^{\infty} a_{k m}\left[\eta_{k m} K_1\left(\eta_{k m} r\right)-\eta_{k m} \frac{K_1\left(\eta_{k m} r_2^{{\mathrm{p}}}\right)}{K_1\left(s_{k m} r_2^{{\mathrm{p}}}\right)} \times\right. \\ & \left.K_1\left(s_{k m} r\right)\right] \times \sin \left(\beta_{k m} z-\theta_{k m}\right) \sqrt{1+\frac{\beta_{k m}}{k b_{{\mathrm{s}}}^{k+1}}} \end{array} $ | (33) |
式中βkm可由下式确定:
| $ \begin{aligned} & \sin \left(\beta_{k m} h_k\right)\left(-\beta_{k m}^2+k b_{{\mathrm{s}}}^{k+1} \cdot k a_{{\mathrm{s}}}^{k-1}\right)+ \\ & \beta_{k m}\left(k b_{{\mathrm{s}}}^{k+1}+k a_{{\mathrm{s}}}^{k-1}\right) \times \cos \left(\beta_{k m} h_k\right)=0 \end{aligned} $ |
其中:
对式(3)进行Laplace变换,可得
| $ \frac{{\mathrm{d}}^2 U_{{\mathrm{p}}}}{{\mathrm{d}} z^2}+p_k^2 U_{{\mathrm{p}}}=-\frac{R(z)}{E_{{\mathrm{p}}} S_{{\mathrm{p}} j}} $ | (34) |
式中:Up为螺纹桩纵向位移up的Laplace变换形式,
由式(4)可得
| $ R(z)=2 \pi r_2^{{\mathrm{p}}}\left(G+{\mathrm{i}} G^{\prime}\right) \sum\limits_{m=1}^{\infty}\left[a_{k m} M_{k m} K_1\left(\eta_{k m} r_2^{{\mathrm{p}}}\right) \times\right.\\\left.\eta_{k m}\left(\frac{s_{k m}^2}{\beta_{k m}}-\beta_{k m}\right) \times \cos \left(\beta_{k m} z-\theta_{k m}\right)\right] $ | (35) |
式中
利用线性微分方程解的叠加原理可得式(34)的解Up是由通解Uhp和特解Upk组成,分别为
| $ U_{{\mathrm{hp}}}=A \sin \left(p_k z\right)+B \cos \left(p_k z\right) $ | (36) |
| $ U_{{\mathrm{pk}}}=\sum\limits_{m=1}^{\infty} C_{k m} \cos \left(\beta_{k m} z-\theta_{k m}\right) $ | (37) |
式中A、B、Ckm为待定系数。
将式(37)代入式(34)中,可得
| $ \begin{gathered} C_{k m}=C_{k m}^{\prime} a_{k m} \\ C_{k m}^{\prime}=\frac{2 \pi r_2^{{\mathrm{p}}}\left(G+{\mathrm{i}} G^{\prime}\right) M_{k m}\left(s_{k m}^2-\beta_{k m}^2\right) \eta_{k m} K_1\left(\eta_{k m} r_2^{{\mathrm{p}}}\right)}{E_{{\mathrm{p}}} S_{{\mathrm{p}} j}\left(p_k^2-\beta_{k m}^2\right) \beta_{k m}} \end{gathered} $ |
对式(10)进行Laplace变换,可得
| $ \begin{gathered} \sum\limits_{m=1}^{\infty}\left[a_{k m} D_{k m} \cos \left(\beta_{k m} z-\theta_{k m}\right)\right]=A \sin \left(p_k z\right)+ \\ B \cos \left(p_k z\right)+\sum\limits_{m=1}^{\infty}\left[C_{k m} \cos \left(\beta_{k m} z-\theta_{k m}\right)\right] \end{gathered} $ | (38) |
式中
| $ D_{k m}=M_{k m}\left[\eta_{k m} \frac{s_{k m}}{\beta_{k m}} \frac{K_1\left(\eta_{k m} r_2^{{\mathrm{p}}}\right)}{K_1\left(s_{k m} r_2^{{\mathrm{p}}}\right)} K_0\left(s_{k m} r_2^{{\mathrm{p}}}\right)-\beta_{k m} K_0\left(\eta_{k m} r_2^{{\mathrm{p}}}\right)\right] $ |
将式(38)等号两边同时乘以
| $ a_{k m}=\frac{A F_{k 1 m}+B F_{k 2 m}}{\left(D_{k m}-C_{k m}^{\prime}\right) F_{k 3 m}} $ | (39) |
式中:
对边界条件式(11)和式(12)进行Laplace变换后,可解出A和B,即可得到Up:
| $ U_{{\mathrm{p}}}=\frac{h_k p_j(t)}{E_{{\mathrm{p}}} S_{{\mathrm{p}} j}} \frac{\sum\limits_{m=1}^{\infty} \frac{C_{k m}^{\prime} \cos \left(\beta_{k m} z-\theta_{k m}\right)}{\left(D_{k m}-C_{k m}^{\prime}\right) F_{k 3 m}}\left(N_{2 k} F_{k 1 m}-L_{2 k} F_{k 2 m}\right)+\left[N_{2 k} \sin \left(p_k z\right)-L_{2 k} \cos \left(p_k z\right)\right]}{\left(L_{1 k} N_{2 k}-L_{2 k} N_{1 k}\right) h_k} $ | (40) |
式中:
结合阻抗函数定义,
| $ Z_{j 1}=\frac{h_k}{E_{{\mathrm{p}}} S_{{\mathrm{p}} j}} \frac{\sum\limits_{m=1}^{\infty} \frac{C_{k m}^{\prime} \cos \left(\beta_{k m} z-\theta_{k m}\right)}{\left(D_{k m}-C_{k m}^{\prime}\right) F_{k 3 m}}\left(N_{2 k} F_{k 1 m}-L_{2 k} F_{k 2 m}\right)+\left[N_{2 k} \sin \left(p_k z\right)-L_{2 k} \cos \left(p_k z\right)\right]}{\left(L_{1 k} N_{2 k}-L_{2 k} N_{1 k}\right) h_k} $ | (41) |
为考虑相邻微元桩段交界面处环形界面与土的相互作用,采用阻抗函数修正传递公式[27]对交界面进行分析。
第k层土对螺纹桩底部的端阻力Psk为
| $ P_{{\mathrm{s}}}^k=\left(k_{{\mathrm{s}}}^j-k_{{\mathrm{s}}}^{j+1}\right) u_{{\mathrm{p}}}+\left(c_{{\mathrm{s}}}^j-c_{{\mathrm{s}}}^{j+1}\right) \frac{\partial u_{{\mathrm{p}}}}{\partial t} $ | (42) |
式中:ksj和csj分别为第j微元桩段整个(半径为r2p的圆柱)置于第k微元土层上弹性系数和阻尼系数,ksj+1、csj+1分别为半径为r1p的圆柱与第k层土相互作用简化成开尔文体的弹性系数和阻尼系数。
由桩底的应力连续条件可知
| $ P_{j 2}=P_{(j+1) 1}+P_{{\mathrm{s}}}^k $ | (43) |
式中:Pj2为第j微元桩段底部的桩身应力,P(j+1)1为第j+1段桩段顶部的桩身应力。
由阻抗函数的定义可知
| $ Z_{j 2}=Z_{(j+1) 1}+k_{{\mathrm{s}}}^k+c_{{\mathrm{s}}}^k s $ | (44) |
式中ksk、csk分别为第k层土对环形界面相互作用的弹性系数和阻尼系数。其中ksk=ksj-ksj+1,csk=csj-csj+1。ksj、ksj+1和csj、csj+1均由弹性半空间公式计算得到。
桩底的阻抗函数可表示为
| $ Z_{n 2}=k_{{\mathrm{p}}}+c_{{\mathrm{p}}} s $ | (45) |
式中kp和cp可参照文献[26]中的计算公式进行取值。
结合式(41)、(44)、(45)可得到桩顶的阻抗函数,也可用复数表达式表示桩顶阻抗函数:
| $ Z_{11}=K_{11}+{\mathrm{i}} C_{11} $ | (46) |
式中实部K11和虚部C11分别为螺纹桩桩顶复刚度形式的动刚度和阻尼部分。
将s=iω代入Z11,即可得到桩顶阻抗函数在频域的表达式Z11(iω)。螺纹桩桩顶的速度可以表示为
| $ H_{{\mathrm{v}}}(\omega)=\frac{{\mathrm{i}} \omega}{Z_{11}({\mathrm{i}} \omega)}=\frac{1}{\rho_{{\mathrm{p}} n} A_n V_{{\mathrm{p}} n}} \bar{H}_{{\mathrm{v}}}(\omega) $ | (47) |
式中 Hv(ω)为桩顶频域响应的无量纲表达式。
当螺纹桩桩顶受到半正弦脉冲激励力P(t)=Qmaxsin(πt/T)(0≤t≤T)时,其桩顶时域解通过傅里叶逆变换(IFT)可求得
| $ \begin{gathered} v(t)=\operatorname{IFT}\left[H_{{\mathrm{v}}}(\omega) Q_{\max } \frac{T \pi}{\pi^2-T^2 \omega^2}\left(1+{\mathrm{e}}^{-{\mathrm{i}} \omega T}\right)\right]= \\ \frac{Q_{\max }}{\rho_{{\mathrm{p}} n} A_n V_{{\mathrm{p}} n}} \bar{v}(t) \end{gathered} $ | (48) |
式中:Qmax为激振力幅值,T为脉冲宽度,v(t)为螺纹桩桩顶无量纲时域响应。
为便于研究螺纹桩纵向振动响应特性,将时间和角频率转化成无量纲值:
| $ \left\{\begin{array}{l} \bar{t}=t / T_{{\mathrm{c}}} \\ \bar{\omega}=\omega T_{{\mathrm{c}}} \end{array}\right. $ | (49) |
式中:Tc为弹性波在螺纹桩桩体内的传播时间,t、ω分别为无量纲时间和无量纲角频率。
3 验证及参数分析 3.1 合理性验证螺纹桩实际上是一种异形截面桩,由于螺牙结构特殊,桩侧土成层特性影响大,造成其桩身动力特性与其他桩型有较大差异。现对本文中螺纹桩计算模型退化成圆桩模型,与其他已有模型进行对比,以验证本文解的正确性。
为对比方便,引入文献[28]的无量纲参数,桩侧土和桩的物理参数取值如下:桩径比H/r1p为10,桩底无量纲支承刚度kpH/(Eps)为1.5,Vsk与Vlk的比值为0.04,第k层土中桩侧土密度与桩密度比值为0.7,ksH/Es为1。
令r1p=r2p,即将螺纹桩退化为实心圆桩,退化解与文献解对比曲线如图 3所示。从图 3中可以看出,本文退化解与既有文献解吻合较好,验证了本文解的正确性。但值的注意的是,虽然本文土层与文献的土层均为滞回阻尼,但由于引入模拟土层间相互作用的弹簧刚度系数,成层土中退化解与既有解略有差异。
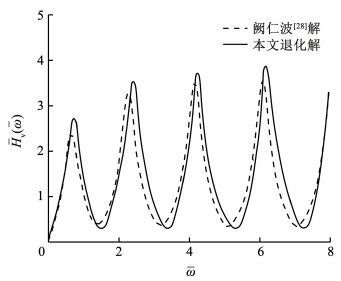
|
图 3 本文退化解与阙仁波[28]解对比曲线 Fig. 3 Comparison of the present reduced solution with the Que Renbo′ solution |
为进一步验证本文提出的成层土中螺纹桩振动响应模型的合理性和实用性,本文选取陕西省高陵市某场地内的螺纹桩进行现场实测。
按照设计要求,工程采用螺纹桩施工,桩长为15 mm,外径D为0.4 m,内径d为0.3 m,螺距s为0.4 m,螺牙高度b为0.05 m,螺牙内侧厚度为0.1 m,螺牙外侧厚度为0.05 m,螺纹桩桩身混凝土为C20,表 1为现场地质参数。
| 表 1 地质参数 Tab. 1 Geologic parameters |
图 4为现场实测曲线与成层土螺纹桩模型结果对比。从曲线整体趋势来看,两条曲线变化规律基本一致,但还存在差异,这是因为测试现场条件比较复杂,岩土勘测和仪器检测可能存在一定的误差,另外低应变检测的理论基础忽略径向位移,只需满足平截面假定即可,而本文中理论模型考虑了桩身中三维波动效应,故模拟桩侧土对螺纹桩的作用是可靠的,即相比基于桩侧土为均质体的假定,考虑土体的成层特性可以充分考虑应力波在分层界面的反射和折射现象,更符合实际情况。总体而言,本文提出的模型能够比较准确地模拟螺纹桩振动特性。

|
图 4 现场实测曲线与理论曲线对比 Fig. 4 Comparison of the on-site measured curves with theoretical curves |
在参数分析中,螺纹桩的桩长、螺牙间距和螺牙外径等尺寸均按照规范[25]中常规螺纹桩构造要求进行选取。
3.2.1 桩长对桩顶响应的影响当螺纹桩外径D为0.4 m,内径d为0.3 m,螺距s为0.4 m,螺牙高度b为0.05 m时,螺纹桩桩长对桩顶复刚度的影响如图 5所示。由图中整个频率范围可知,螺纹桩桩长对桩顶复刚度变化影响显著。随着桩长增加,桩顶动刚度和动阻尼曲线振荡幅值均明显降低,共振频率也有明显减小。这是由于桩长越长,桩侧土对螺纹桩的侧摩阻力越大,阻尼效应越明显。当H=30 m时,随着频率的增加,桩顶复刚度曲线振荡幅值水平趋于稳定,此时频率的增加对复刚度曲线影响较小。这是由于当螺纹桩桩长增加到一定程度后,即当超过有效长度(能够发挥实际承载能力的桩体长度)后,随着频率的增加,桩侧土对螺纹桩的侧摩阻力基本不再变化,侧摩阻力的发挥对螺纹桩的动刚度和动阻尼影响非常有限。结合图 5可以得到一个对螺纹桩设计有重要意义的结论:当设计桩长超过有效桩长时,若螺纹桩全部设计成螺牙结构会增加工程成本,宜采用上部为直杆段,下部为螺纹段构造,使得螺纹桩在兼顾承载力的情况下,降低造价,且便于现场施工。
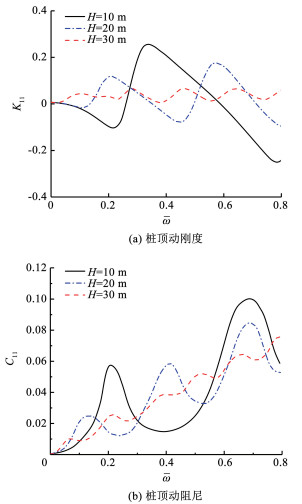
|
图 5 桩长对桩顶复刚度的影响 Fig. 5 Influences of pile length on complex dynamic stiffness |
当螺纹桩外径D为0.4 m,内径d为0.3 m,桩长H为15 m,螺牙高度b为0.05 m时,不同螺牙间距对桩顶复刚复刚度的影响曲线如图 6所示。
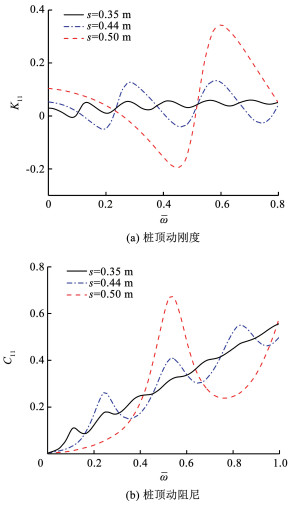
|
图 6 螺牙间距对桩顶复刚度的影响 Fig. 6 The influence of screw tooth spacing on the complex stiffness of pile top |
从图 6中可以看出,螺牙间距对螺纹桩纵向振动响应有显著影响。在其他条件不变的情况下,复刚度曲线振荡幅值随着螺牙间距的增加呈现增大的趋势,这是由于螺牙间距越大,螺牙截面周长越小,螺纹桩中螺牙所受到土的侧摩阻力也会随着减小,动刚度就会降低,阻尼效应就越不明显,因此共振频率处的振动幅值也会随之增加。
3.2.3 螺牙外径对桩顶响应的影响当螺纹桩内径d为0.4m,桩长H为15 m,螺距s为0.4 m,螺牙高度b为0.05 m时,不同螺牙外径对桩顶复刚复刚度的影响曲线如图 7所示。
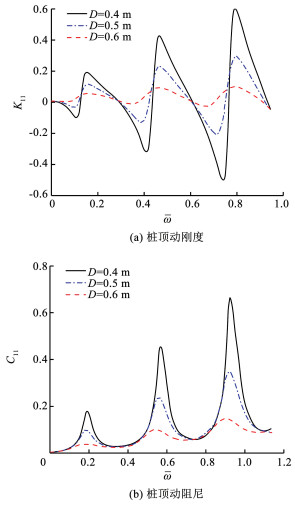
|
图 7 螺牙外径对桩顶响应的影响 Fig. 7 The influence of screw tooth outer diameter on pile top response |
从图 7中可以看出,随着螺纹桩螺牙外径的增加,桩顶复刚度曲线的振幅水平和共振频率均显著减小。当D=0.4 m(即退化为实体圆桩)时,桩顶动力阻抗曲线振幅水平最高,由此可见,螺纹桩螺牙的存在对桩体具有一定的减振效应。因此在软土地区施工时,若圆桩未能达到设计要求,可采用螺纹桩代替圆桩。
4 结论采用三维波动理论和修正阻抗函数传递法对滞回阻尼地基中螺纹桩纵向振动特性进行研究,考虑了土体的成层特性和桩侧土的竖向作用,求得了桩土完全耦合条件下的螺纹桩振动响应解,通过参数分析得到以下结论:
1) 相比基于桩侧土为均质体的假定,考虑土体的成层特性可以充分考虑应力波在分层界面的反射和折射现象,更符合实际情况。
2) 在有效桩长范围内,随着桩长的增加,桩侧土对螺纹桩的侧摩阻力越大,阻尼效应越明显,复刚度曲线振荡趋于平缓。
3) 螺牙间距越大,桩土侧摩阻力越小,共振频率处的振动幅值也会随之增加。
4) 螺纹桩螺牙的存在对桩体具有一定的减振效应,且随着螺牙外径的增加,桩顶复刚度曲线的振幅水平和共振频率均显著减小。
5) 螺纹桩动力响应模型考虑桩侧土的成层特性和桩侧土的竖向作用,适用于与桩身黏结性较强的土体,且土体黏结性越强,螺纹桩的侧摩阻力越大。对于与桩身黏结性较弱的土体来说,螺纹桩的动力响应变化规律还需进一步理论研究。
| [1] |
MA Jiakuan, WANG Rui, HU Zhiping, et al. Limit equilibrium theory in calculating screw pile bearing capacity under compression[J/OL]. Proceedings of the Institution of Civil Engineers-Geotechnical Engineering. (2023-08-24). https://doi.org/10.1680/jgeen.22.00122
|
| [2] |
钱建固, 陈宏伟, 贾鹏, 等. 注浆成型螺纹桩接触面特性试验研究[J]. 岩石力学与工程学报, 2013, 32(9): 1744. QIAN Jiangu, CHEN Hongwei, JIA Peng, et al. Experimental study of mechanical behaviours of grouting-screw pile interface[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(9): 1744. |
| [3] |
周杨, 肖世国, 徐骏, 等. 变截面螺纹桩竖向承载特性试验研究[J]. 岩土力学, 2017, 38(3): 747. ZHOU Yang, XIAO Shiguo, XU Jun, et al. Model test on vertical bearing capacity of variable cross-section thread piles[J]. Rock and Soil Mechanics, 2017, 38(3): 747. |
| [4] |
孟振, 陈锦剑, 王建华, 等. 砂土中螺纹桩承载特性的模型试验研究[J]. 岩土力学, 2012, 33(增刊1): 142. MENG Zhen, CHEN Jinjian, WANG Jianhua, et al. Study of model test on bearing capacity of screw piles in sand[J]. Rock and Soil Mechanics, 2012, 33(Sup.1): 142. |
| [5] |
KARKUSH M O, ALKABY A D. Numerical modeling of pullout capacity of screw piles under seismic loading in layered soil[J]. Transportation Infrastructure Geotechnology, 2023, 10(1): 125. |
| [6] |
蒋鹏程. 粉土地基CFG桩与螺杆桩复合地基承载特性对比分析[J]. 铁道学报, 2019, 41(4): 128. JIANG Pengcheng. Comparative analysis on bearing behaviors of CFG pile and screw pile composite foundation in silt foundation[J]. Journal of the China Railway Society, 2019, 41(4): 128. |
| [7] |
叶阳升, 蔡德钩, 陈晓斌, 等. 高速铁路螺杆桩复合地基桩侧摩阻力原位试验研究[J]. 中国铁道科学, 2020, 41(2): 8. YE Yangsheng, CAI Degou, CHEN Xiaobin, et al. In-situ test study on lateral friction of screw pile composite foundation of high speed railway[J]. China Railway Science, 2020, 41(2): 8. |
| [8] |
关伟, 吴红刚, 余仕江, 等. 列车荷载下螺杆桩复合地基动力特性及承载性状试验研究[J]. 岩石力学与工程学报, 2023, 42(2): 511. GUAN Wei, WU Honggang, YU Shijiang, et al. Experimental study on dynamic and bearing characteristics of part-screw pile[J]. Chinese Journal of Rock Mechanics and Engineering, 2023, 42(2): 511. |
| [9] |
ELKASABGY M, El NAGGAR M H. Dynamic response of vertically loaded helical and driven steel piles[J]. Canadian Geotechnical Journal, 2013, 50(5): 522. |
| [10] |
ORANG M J, BOUSHEHRI R, MOTAMED R, et al. Large-scale shake table experiment on the performance of helical piles in liquefiable soils[R]. Passaic: Deep Foundations Institute, 2021
|
| [11] |
HUSSEIN A F, El NAGGAR M H. Seismic helical pile response in nonliquefiable and liquefiable soil[J]. International Journal of Geomechanics, 2022, 22(7): 04022094. |
| [12] |
HUSSEIN A F, El NAGGAR M H. Effect of model scale on helical piles response established from shake table tests[J]. Soil Dynamics and Earthquake Engineering, 2022, 152: 107013. |
| [13] |
HUSSEIN A F, El NAGGAR M H. Dynamic performance of driven and helical piles in cohesive soil[J]. Acta Geotechnica, 2023, 18(3): 1548. |
| [14] |
孟坤, 崔春义, 许成顺, 等. 考虑桩土非完全粘结及桩底土波动效应的浮承桩纵向振动特性研究[J]. 振动工程学报, 2023, 36(2): 440. MENG Kun, CUI Chunyi, XU Chengshun, et al. Vertical vibration characteristics for floating pile considering the incomplete bonding condition of pile-soil and the wave propagation effect of soil beneath pile[J]. Journal of Vibration Engineering, 2023, 36(2): 440. |
| [15] |
王奎华, 阙仁波, 夏建中. 考虑土体真三维波动效应时桩的振动理论及对近似理论的校核[J]. 岩石力学与工程学报, 2005, 24(8): 1364. WANG Kuihua, QUE Renbo, XIA Jianzhong. Theory of pile vibration considering true three-dimensional wave effect of soil and its check on the approximate theories[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(8): 1364. |
| [16] |
阙仁波, 王奎华. 考虑土体三维波动效应时黏性阻尼土中桩的纵向振动特性及其应用研究[J]. 岩石力学与工程学报, 2007, 26(2): 386. QUE Renbo, WANG Kuihua. Theory on longitudinal vibration of pile in viscous damping soil layer considering three-dimensional wave effect and its applications[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(2): 386. |
| [17] |
ZHENG Changjie, DING Xuanming. Vertical dynamic response of single floating piles in poroelastic soil[J]. Computers and Geotechnics, 2023, 159: 105424. |
| [18] |
XIAO Si, WANG Kuihua, GAO Liu, et al. Dynamic characteristics of a large-diameter pile in saturated soil and its application[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2018, 42(11): 1260. |
| [19] |
ELKASABGY M A. Dynamic and static performance of large-capacity helical piles in cohesive soils[D]. London: The University of Western Ontario, 2011
|
| [20] |
El NAGGAR M H. Recent Advances in helical piles for dynamic and seismic applications: conference on performance-based design in earthquake geotechnical engineering[R]. Beijing: Tsinghua University, 2022
|
| [21] |
崔春义, 孟坤, 梁志孟, 等. 双向非均质黏性阻尼土中管桩纵向振动特性[J]. 哈尔滨工业大学学报, 2020, 52(11): 114. CUI Chunyi, MENG Kun, LIANG Zhimeng, et al. Vertical vibration impedance of pipe pile embedded in radially and vertically inhomogeneous layered soil with viscous damping[J]. Journal of Harbin Institute of Technology, 2020, 52(11): 114. |
| [22] |
崔春义, 孟坤, 武亚军, 等. 径向非均质黏性阻尼土中管桩纵向振动特性[J]. 哈尔滨工业大学学报, 2019, 51(2): 138. CUI Chunyi, MENG Kun, WU Yajun, et al. Dynamic impedance of vertical vibration of pipe pile embedded in radially inhomogeneous viscoelastic soil[J]. Journal of Harbin Institute of Technology, 2019, 51(2): 138. |
| [23] |
董俊利, 陈军浩, 聂如松, 等. 螺纹桩复合地基桩土应力比模型试验与数值模拟[J]. 铁道科学与工程学报, 2022, 19(10): 2970. DONG Junli, CHEN Junhao, NIE Rusong, et al. Model test and numerical simulation study on the pile-soil stress ratio of screw pile composite foundation[J]. Journal of Railway Science and Engineering, 2022, 19(10): 2970. |
| [24] |
叶阳升, 蔡德钩, 陈晓斌, 等. 高速铁路螺杆桩复合地基桩侧摩阻力原位试验研究[J]. 中国铁道科学, 2020, 41(2): 1. YE Yangsheng, CAI Degou, CHEN Xiaobin, et al. In-site test study on lateral friction of screw pile composite foundation of high speed railway[J]. China Railway Science, 2020, 41(2): 1. |
| [25] |
中国人民共和国住房和城乡建设部. 螺纹桩技术规程: JGJ/T 379—2016[S]. 北京: 中国建筑工业出版社, 2016 Ministry of Housing and Urban-Rural Development of the People′s Republic of China. Technical specification for screw concrete pile: JGJ/T 379—2016[S]. Beijing: China Architecture and Building Press, 2016 |
| [26] |
LYSMER J, RICHART F E. Dynamic response of footings to vertical loading[J]. Journal of the Soil Mechanics and Foundations Division, 1966, 92(1): 70. |
| [27] |
GAO Liu, WANG Kuihua, XIAO Si, et al. Dynamic response of a pile considering the interaction of pile variable cross section with the surrounding layered soil[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2017, 41(9): 1211. |
| [28] |
阙仁波, 王奎华. 考虑土体三维波动效应时弹性支承桩的振动理论及其应用[J]. 计算力学学报, 2005, 22(6): 660. QUE Renbo, WANG Kuihua. Theory of vibration of pile on elastic foundation considering 3D wave effect of soil and its applications[J]. Chinese Journal of Computational Mechanics, 2005, 22(6): 660. |
 2024, Vol. 56
2024, Vol. 56


