recent years, there is a growing research on the Automatic Target Recognition (ATR) based on the Inverse Synthetic Aperture Radar (ISAR) images in various fields such as aircraft[1-3], missile and naval ship[4]. By the compensation for the translational motion of a moving target, the ISAR image can be obtained with the corresponding imaging algorithms. In particular, the application of detection and classification for the ship target with real radar system has a good prospect, since it can be used in the target tracking and defending in the military domain. For the high resolution of ISAR image, the target shape is well retained and the features extracted from it can fully represent the target's characters. Using these features, the classification via feature matching[5] and Artificial Neural Networks (ANN) are always applied in the target recognition[6].
In the past decades, many ISAR ATR techniques have been developed in the open literature. However, most of them focused on the recognition of aircrafts. A simple model of aircraft using some geometric features to finish the classification of simulated ISAR images via feature matching was proposed in Ref.[3]. Some rotation and scale invariances of ISAR images have been proposed based on a polar-mapping procedure in Ref. [7]. An approach using Fourier descriptors based on Neural Classifier has been applied to aircrafts in Ref. [8]. However, most of the methods are unable to be applied on the ship target directly due to the shape differences between the ship and aircraft. For example, the ship is always long and narrow while most of the aircrafts have wings which are as long as their bodies' lengths. The features used in the aircraft recognition may not be effective in the ship recognition[9]. Besides, due to the complexity of the ship's motion[10-12], the quality of ISAR images for the ship target are often lower than that of aircrafts.
There are a few literatures focused on the recognition of ship target based on the ISAR images. The technique of extracting features in the image domain and matching them with corresponding models to classify the ship target based on the ISAR images was first proposed in Ref. [13]. Then, an ATR technique using feature matching was proposed in Ref. [14], which needs a library composed of the full knowledge and the model of targets may not be acquired easily. Furthermore, there are less research focusing on the topic of ship recognition based on the real data because of the lack of the real ISAR data of ship target and the low quality of the ship ISAR images. However, the images of simulated ISAR data and real ISAR data are quite different.
Hence, we focus on the ship recognition based on the real ISAR images in this paper. The whole process consists of three steps: ISAR imaging, feature extraction and classification. In this paper, the range-Doppler (RD) technique is used on the real ISAR data to obtain the ISAR images. Then, we propose a comprehensive ATR process as shown in Fig. 1. The first step is image preprocessing. With some traditional techniques of image segmentation and morphological method, this step can eliminate the speckle and streak noises and compensate the deformation of target shape. The next one is feature extraction. Six different features are exploited, including two kinds of moment features, area, ship length, mainmast height. These features' effectiveness is analyzed and then the features are applied in the classical linear classifier-Fisher's linear classifier in the last step. The results of all-feature space with real ship data are obtained. And the robustness of this technique to the real ISAR data will be proved.

|
Figure 1 ATR process scheme |
This paper is organized as follows. The difference between the ISAR images from simulated and real data of ship target is analyzed in Section 2. Then thepreprocessing and feature extraction processes are proposed in Section 3 and Section 4, respectively. The theory of Fisher's linear classifier is briefly introduced in Section 5 and the effectiveness of features and results of classifier with real ship ISAR data are shown and analyzed in Section 6. Finally, the conclusion is depicted in Section 7.
2 ISAR Images on Real DataIn this paper, we use four different targets, two boats and two warships. We create a database composed of more than 200 images, where the numbers of boats and warships are equal. The bandwidth of the transmitted signal is 200 MHz. The pulse repetition frequency is 500 Hz. We set the size of all the images in our database to 400 × 400 and the representative ISAR images of these targets are presented in Fig. 2.

|
Figure 2 ISAR images of ship targets |
As shown in Fig. 2, the images of ships are solid grey-scale images. There are some speckle noises around the targets and some streak noises distributed in both range and azimuth directions (evident in Fig. 2(c)). The streak noise in the azimuth direction is often caused by the superstructure of the ship. As shown in Fig. 2(c), the more complex the superstructure is, the more streak noise exists. Meanwhile, the streak noise in the range direction is caused by the motion of the ship. Sometimes the existing algorithms cannot fully compensate the effects of target's motion for its maneuverability.
In this paper, we use some common methods to clean these noises. Most of these methods have been applied to the simulated ISAR images. However, there are some differences between the simulated ISAR images and real ISAR images:
1) Compared with the real ship target, the distribution of scatters for the simulated image is too sparse. Hence the noise generated by the strong scatters is less. The algorithms to clean the noise applied on simulated ISAR images may be not reliable when applying to the real ISAR image.
2) For the real ISAR image, the scatter migration will overlap other scatter and thus the contour and shape of the target will be destroyed. So the features based on the target contour will be more difficult to be extracted.
3) Compared with the simulated data, the motion of real target is more complex and hard to be estimated. Therefore the noise influence and the deformation of target are severe. Sometimes the target cannot be represented clearly on the ISAR image and it requires the preprocessing procedure before the feature extraction.
Based on these factors, in the following parts of this paper, we will focus on the process of real ISAR images. We combine some classical methods and discuss the problems when applying them to real data. The robustness of the technique will be validated through the recognition results.
3 PreprocessingAs discussed in Section 2, the ISAR images are often affected by the speckle and streak noises. Besides, the complexity of the ship motion generates the deformation and incompletion of the target in the ISAR images. These particularities drastically reduce the image quality and affect the accuracy of the features extraction. Hence, the correct classification rate will be deteriorated. On one hand, the image quality could be improved by the precise estimate of the motion parameters, and this will lead to the higher classification accuracy. However, it is not practical in the consideration of the performance of real-time and considerable computational complexity. On the other hand, the formation and distribution of the noises and flaws of ISAR images always have some characteristics. Therefore, the image preprocessing step is the first and a crucial stage of our procedure. The preprocessing technique in this paper is described in Fig. 3.

|
Figure 3 Flowchart of image preprocessing |
The streak and speckle noise can be eliminated by setting a threshold in each range and Doppler bin, which can be 1/8 or 1/10 of the largest amplitude of the scatterer. Then, the pixel of ISAR image whose amplitude is lower than the threshold can be eliminated, and the weak streak and speckle noise can be cleaned simultaneously.
The median filtering, morphology method and hole filling are commonly used in the field of digital image processing, and thus we can use these methods without difficulty.
Then, the original ISAR image and the image after preprocessing are shown in Fig. 4.
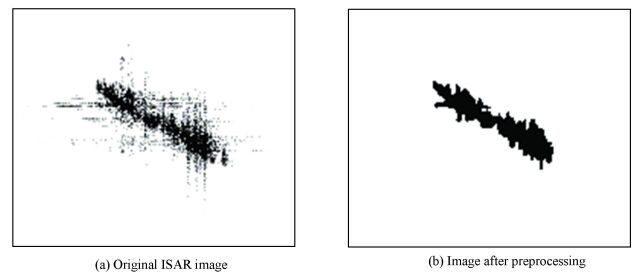
|
Figure 4 Results of the ISAR images |
Fig. 4(a) is the original ISAR image, and the streak and speckle noise is obvious. Fig. 4(b) is the ISAR image after the preprocessing, and it is clear that Fig. 4(b) shows a complete ISAR image of ship target which is suitable for the feature extraction after the whole preprocessing procedure.
4 Feature ExtractionAs the foundation of classification, the precision of target features extraction will influence the accuracy for the recognition. While some classical image features can be applied to ISAR images, selecting the appropriate features based on the characteristics of ship targets is a more effective approach. The features we exploited on each image of our database in this paper include:
4.1 Invariant MomentInvariant moments represent the geometric characters of images and are usually applied in the target recognition. We use the first two invariant moments Φ1 and Φ2 in Ref.[15], just as follows:
| $ \left\{ \begin{array}{l} {\mathit{\Phi }_1}{\rm{ = }}{\eta _{02}} + {\eta _{20}}\\ {\mathit{\Phi }_2}{\rm{ = }}{\left( {{\eta _{02}} - {\eta _{20}}} \right)^2} + 4\eta _{11}^2 \end{array} \right. $ | (1) |
where ηpq corresponds to the (p+q)-order normalized central moment. The two features represent the shape of target and are quite effective to the ship target, which will be discussed in Section 6.
4.2 Ship AreaThe most obvious difference between the boats and warships is the target size. This can be represented by the target image area for the resolution of ISAR image depending just on the aperture and bandwidth. As the image is binary, the area of the target can be estimated as follows:
| $ area = \sum\limits_x {\sum\limits_y {f\left( {x,y} \right)} } $ | (2) |
where f(x, y) is the value of the pixel that has the coordinate of (x, y).
4.3 The Maximum Mean Square Deviation (MSD) of Range BinThe mean square deviation (MSD) of each range bin can illustrate the dispersion of the pixels[15].The superstructure of a ship will influence the dispersion of its ISAR image. Always, the superstructure of warship is far more complex than a boat. Therefore, the MSD of each range bin can be utilized to represent the complexity of a ship target and differentiate the boats and warships. The MSD of each range bin Sj can be calculated as follows:
| $ {S_j} = \frac{1}{{n - 1}}\sqrt {\sum\limits_{i = 1}^n {{{\left( {{x_{ij}} - {{\bar x}_j}} \right)}^2}} } $ | (3) |
where j and n correspond to the indices of range bin and the number of Doppler bin, respectively, xij is the value of the pixel that has the coordinate of (i, j) and xj is the mean value of the pixels in the jth range bin, just as follows:
| $ {{\bar x}_j} = \frac{1}{n}\sum\limits_{i = 1}^n {{x_{ij}}} $ | (4) |
After the sequence of MSD {Sj} is obtained, we can choose the maximum value Smax of {Sj} as the feature, which depends on both the longest mast and the height of the deck. This feature could be useful in the classification for the certain kind of ship with a long mast or high deck. Moreover, if the silhouettes of superstructures of some ships fluctuate severely while others are flat, the mean value of {Sj} could also be an effective feature.
4.4 Ship LengthUsually, the shape of ship is narrow and long. Hence, we can easily distinguish the boats and warships based on their lengths. To estimate the ship length, the preliminary step is to extract the centreline of ship, which is defined as the axis between the bow and stern. We apply the Radon transform-based technique in Ref. [16] to the ISAR image to obtain the centerline. The ship length sL can be estimated by calculating the distance between the bow and stern. This can be defined as the pixels of the target edge intersected with the centerline. The corresponding result is shown in Fig. 5, and the red spots represent the bow and stern.
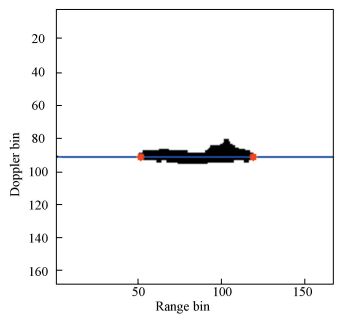
|
Figure 5 Ship centreline and pixels of the bow and stern |
4.5 Mast Length
We use the approach in Ref. [14] to get the silhouette of the ship, where the superstructure portion is the target segment with a larger maximum curve height. There may be a problem that in two cases the infrastructure portion will be judged as superstructure incorrectly. One is that the ship's cabin or mast is not high enough, and the other is that the migration of the scatter or the residual noise will generate a singular peak of the infrastructure curve. In order to solve this problem, we propose another two criteria. First, the deck is often flat while the superstructure curve fluctuates more fiercely, so the superstructure portion should have a bigger curve standard deviation. Second, if the error is caused by the singular peak of the infrastructure curve, the superstructure portion should still have a bigger average value of the curve. Hence, we think that the portion with a bigger weighted mean of the maximum value, mean value and the standard deviation of the curve is the superstructure portion. Noting that because of the smoothing effect in the calculation of the mean value and the standard deviation, the values of them are usually much smaller than the maximum value. To offset this effect, the weights of these two values should be much larger. Fig. 6 shows an example to illustrate the effect of our method where the red portion is the infrastructure portion and the green is the superstructure. It is evident that because of the singular peak of the infrastructure the judgement based on the old criterion is incorrect in Fig. 6(a), but our method performs well as shown in Fig. 6(b). We set the weights of the maximum value, mean value and the standard deviation to 1/15, 7/15 and 7/15 in this example. In practice, weights of the three values can be modified based on different emphasis of the criterion under different conditions.
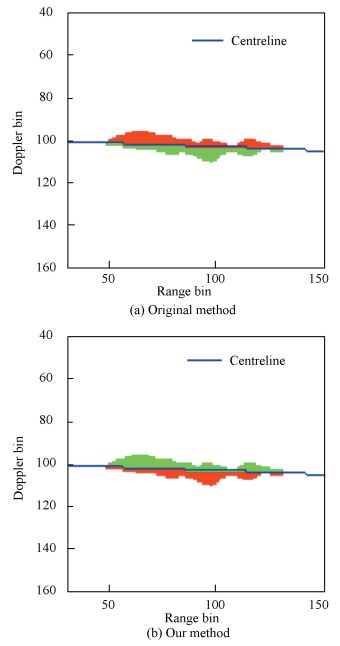
|
Figure 6 Results of new criteria |
After getting the silhouette, we should find the mast of the ship. We consider that the bin corresponding to the largest value of silhouette curve is the bin where the main mast exists. While some boats do not have a mast, it may be the bin where the top of the cabin exists. Therefore, we define the feature of mast length Lmast as the largest value of the silhouette curve exactly. Fig. 7 shows an example for the same target in Fig. 5. The red circle in Fig. 7 shows the position of the mast.
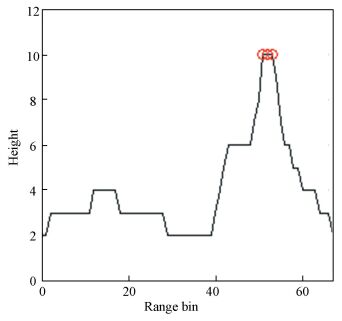
|
Figure 7 Silhouette curve and mast position |
All the features described above are extracted from all the ISAR images in our ISAR database. Some problems of the feature extraction from ISAR images have been overcome. These features are compatible to all kinds of ships and represent the ship's characteristics accurately. The number of features is only six and thus the pressure of data storage and process is considerably small. These features are going to be used to build the library and construct the classifier in the classification step inside the whole process in Fig. 1.
5 Recognition TheoryIn this section, we discuss the theory of commonly used recognition methods. One is the Bayes decision-making theory, which is the foundation of the supervised pattern recognition. Using the minimal error Bayes decision theory, we can transfer the issue of decision making into the estimation of the probability of the feature. Specifically, in the one-dimensional case, if the decision boundary acquired through Bayes decision divides the feature axis x into two regions:
| $ P\left( e \right) = P\left( {{\omega _2}} \right)\int\limits_{{\psi _1}} {p\left( {x\left| {{\omega _2}} \right.} \right){\rm{d}}x} + P\left( {{\omega _1}} \right)\int\limits_{{\psi _2}} {p\left( {x\left| {{\omega _1}} \right.} \right){\rm{d}}x} $ | (5) |
where
| $ P\left( e \right) = \left( {\int\limits_{{\psi _1}} {p\left( {x\left| {{\omega _2}} \right.} \right){\rm{d}}x} + \int\limits_{{\psi _2}} {p\left( {x\left| {{\omega _1}} \right.} \right){\rm{d}}x} } \right)/2 $ | (6) |
Another method of pattern recognition is the linear classifier. Depending on the samples, this method has acceptable classification result. Fisher's linear classifier, which was proposed by R. A. Fisher in 1936 [18], is a classical one and has been widely used. The main idea of this classifier is to find a direction of projection in the sample space, and the samples of the same class will converge while the samples of different classes are as far as possible after the projection. The hyperplane which is perpendicular to the projection direction through this point is the classifier.
For the sample
| $ g\left( {\mathit{\boldsymbol{\vec x}}} \right) = {{\mathit{\boldsymbol{\vec w}}}^{\rm{T}}}\mathit{\boldsymbol{\vec x}} + {\mathit{\boldsymbol{w}}_0} = 0 $ | (7) |
where
| $ {\mathit{\boldsymbol{w}}_0} = - \frac{1}{2}\left( {{{\mathit{\boldsymbol{\tilde m}}}_1} + {{\mathit{\boldsymbol{\tilde m}}}_2}} \right) $ | (8) |
where
The projection vector
| $ {{\mathit{\boldsymbol{\vec w}}}^ * } = \mathit{\boldsymbol{S}}_w^{ - 1}\left( {{{\mathit{\boldsymbol{\vec m}}}_1} - {{\mathit{\boldsymbol{\vec m}}}_2}} \right) $ | (9) |
where
| $ {\mathit{\boldsymbol{S}}_i} = \sum {\left( {{{\mathit{\boldsymbol{\vec x}}}_j} - {{\mathit{\boldsymbol{\vec m}}}_i}} \right){{\left( {{{\mathit{\boldsymbol{\vec x}}}_j} - {{\mathit{\boldsymbol{\vec m}}}_i}} \right)}^{\rm{T}}},i = 1,2} $ | (10) |
The technique described above has been applied to the real ISAR data. As we have shown in Fig. 2, there are two kinds of boat: boat A and boat B and two kinds of warship: warship A and warship B. The aim of our study is to recognize the boat and the warship. Based on the theory in Section 5, there are two different aspects to investigate the effectiveness of our recognition method.
1) The average error probability P(e) obtained by applying the Bayes decision theory.
2) The recognition accuracy obtained by applying the Fisher's linear classifier.
In this section, we will discuss the effectiveness of the extracted features by evaluating the P(e). Then, we present the results obtained by applying the Fisher's linear classifier in different feature spaces.
After analyzing the effectiveness of the extracted features qualitatively, we apply the Fisher's linear classifier to finish the classification procedure in Fig. 1. To improve the classification correct rate of Fisher's linear classifier, we increase the dimension number of the feature space. We combine all the six extracted features to construct a feature space of which the feature vector is [area Lmast sL Smax Φ1 Φ2]T. Before applying the classifier, we scale all the features of samples to make the features' mean value near to 1 so that the distribution of samples in the feature space is more uniform.
The compositions of training samples and test samples are shown in Table 1, where the test samples include all the training samples.
| Table 1 Compositions of training samples and test samples |
The samples' feature mean vector of boat
| $ \begin{array}{l} {{\mathit{\boldsymbol{\vec m}}}_1} = {\left[ {\begin{array}{*{20}{c}} {0.7236}&{0.7800}&{0.8911}&{0.9316}&{0.6312}&{1.2386} \end{array}} \right]^{\rm{T}}}\\ {{\mathit{\boldsymbol{\vec m}}}_2} = {\left[ {\begin{array}{*{20}{c}} {1.9380}&{1.4514}&{1.9407}&{1.1534}&{0.7779}&{1.5516} \end{array}} \right]^{\rm{T}}} \end{array} $ |
The matrices S1 and S2 in Eq.(10) are
| $ {\mathit{\boldsymbol{S}}_1} = \left[ {\begin{array}{*{20}{c}} {2.6425}&{2.0917}&{3.1716}&{0.6542}&{0.7004}&{1.4593}\\ {2.0917}&{4.3745}&{ - 0.7255}&{1.8737}&{ - 0.0893}&{ - 0.3050}\\ {3.1716}&{ - 0.7255}&{11.3804}&{ - 1.8761}&{2.3629}&{5.2387}\\ {0.6542}&{1.8370}&{ - 1.8761}&{1.3067}&{ - 0.3597}&{ - 0.8721}\\ {0.7004}&{ - 0.0890}&{2.3629}&{ - 0.3597}&{0.5003}&{1.1013}\\ {1.4593}&{ - 0.3050}&{5.2387}&{ - 0.8721}&{1.1013}&{2.4620} \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{S}}_2} = \left[ {\begin{array}{*{20}{c}} {99.5265}&{36.3512}&{9.8748}&{9.3991}&{0.5977}&{1.0098}\\ {36.3512}&{65.5107}&{5.4919}&{9.7372}&{0.3050}&{0.2585}\\ {9.8748}&{5.4919}&{6.2389}&{1.4801}&{0.3553}&{0.6980}\\ {9.3991}&{9.7372}&{1.4801}&{5.9360}&{0.0984}&{0.1542}\\ {0.5977}&{0.3050}&{0.3553}&{0.0984}&{0.0302}&{0.0599}\\ {1.0098}&{0.2585}&{0.6980}&{0.1542}&{0.0599}&{0.1211} \end{array}} \right] $ |
The sum of within-class scatter matrix Sw in Eq.(9) is
| $ {\mathit{\boldsymbol{S}}_w} = \left[ {\begin{array}{*{20}{c}} {102.1690}&{38.4429}&{13.0465}&{10.0532}&{1.2981}&{2.4691}\\ {38.4429}&{69.8852}&{4.7664}&{11.6110}&{0.2157}&{ - 0.0464}\\ {13.0465}&{4.7664}&{17.6194}&{ - 0.3960}&{2.7182}&{5.9367}\\ {10.0532}&{11.6110}&{ - 0.3960}&{7.2427}&{ - 0.2613}&{ - 0.7179}\\ {1.2981}&{0.2157}&{2.7182}&{ - 0.2613}&{0.5305}&{1.1612}\\ {2.4691}&{ - 0.0464}&{5.9367}&{ - 0.7179}&{1.1612}&{2.5831} \end{array}} \right] $ |
The best projection direction vector
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\vec w}}}^ * } = {{\left[ {\begin{array}{*{20}{c}} { - 0.0008}&{0.0012}&{ - 0.0722}&{ - 0.0311}&{ - 0.0805}&{0.0732} \end{array}} \right]}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{w}}_0} = {{\left[ {\begin{array}{*{20}{c}} {1.3308}&{1.1157}&{1.4159}&{1.0425}&{0.7045}&{1.3951} \end{array}} \right]}^{\rm{T}}}} \end{array} $ |
We utilize this classification hyperplane to recognize the ship targets, and the classification correct rates of the boat and warship are 0.98 and 0.96, respectively. Detailed results are listed in Table 2.
| Table 2 Results of recognition on all-feature space |
The results show that in the all-feature space, the classification correct rates can exceed 90% by applying the linear classifier. This means all the features we extracted have good recognition ability. This level of correct rate for the real data is acceptable and the recognition method is quite effective. Besides, in consideration of the low image quality, the effectiveness and robustness of our process to the real ISAR data are verified based on these recognition results.
7 ConclusionsA comprehensive ATR process based on ISAR images has been proposed. This method consists of three steps including the preprocessing, feature extraction and classification. Through the imaging with real ISAR data, we obtain a database consisting of four different ship targets. These real ISAR images are quite different from simulated ISAR images and it requires the ATR process to be more robust. After the preprocessing and feature extraction, the Fisher's linear classifier is used in the different feature spaces for the classification. Future work should focus on the study of the recognition inside the boat or warship targets and other features may be extracted. Moreover, in the consideration of the low quality of real ISAR images of ships, the robustness of the algorithm of noise suppression and feature extraction will be another aspect to be investigated in this field.
| [1] |
Saidi M N, Toumi A, Hoeltzener B, et al. Aircraft target recognition: A novel approach for features extraction from ISAR images. Proceedings of the 2009 International Radar Conference "Surveillance for a Safer World" (RADAR 2009). Piscataway: IEEE, 2009. 1-5.
( 0) 0)
|
| [2] |
Wang F, Sheng W X, Ma X F, et al. ISAR image recognition with fusion of gabor magnitude and phase feature. Journal of Electronics & Information Technology, 2013, 8: 1813-1819. DOI:10.3724/SP.J.1146.2012.01500 ( 0) 0)
|
| [3] |
Zeljkovic V, Li Q, Vincelette R. Automatic algorithm for inverse synthetic aperture radar images recognition and classification. IET Radar, Sonar & Navigation, 2010, 4(1): 96-109. DOI:10.1049/iet-rsn.2009.0112 ( 0) 0)
|
| [4] |
Cross P L. Maritime automated targets recognition algorithm test bed for high resolution ISAR imagery. Proceedings of the 2013 IEEE International Conference on Technologies for Homeland Security (HST). Piscataway: IEEE, 2013. 369-374. DOI: 10.1109/THS.2013.6699032.
( 0) 0)
|
| [5] |
Knapskog O. Automatic classification of ships in ISAR images using wire-frame models. Proceedings of the Fifth European Conference on Synthetic Aperture Radar, EUSAR 2004. Ulm, 2004. 953-956.
( 0) 0)
|
| [6] |
Inggs M R, Robinson A D. Ship target recognition using low resolution radar and neural networks. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(2): 386-393. DOI:10.1109/7.766923 ( 0) 0)
|
| [7] |
Kim K T, Seo D-K, Kim H-T. Efficient classification of ISAR images. IEEE Transactions on Antennas and Propagation, 2005, 53(5): 1611-1621. DOI:10.1109/TAP.2005.846780 ( 0) 0)
|
| [8] |
Benedetto F, Fulginei F R, Laudani A. Automatic aircraft target recognition by ISAR image processing based on neural classifier. International Journal of Advanced Computer Science and Applications (IJACSA), 2012, 3(8): 96-103. ( 0) 0)
|
| [9] |
Chen S L. Research of Recognition on Inverse Synthetic Aperture Radar image. Zhejiang: Zhejiang University, 2008. 8-30.
( 0) 0)
|
| [10] |
Hajduch G, Le Caillec J M, Garello R. Airborne high-resolution ISAR imaging of ship targets at sea. IEEE Transactions on Aerospace and Electronic Systems, 2004, 40(1): 378-384. DOI:10.1109/TAES.2004.1292177 ( 0) 0)
|
| [11] |
Zheng J B, Su T, Zhu W T, et al. Radar high-speed target detection based on the scaled inverse Fourier transform. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(3): 1108-1119. DOI:10.1109/JSTARS.2014.2368174 ( 0) 0)
|
| [12] |
Zheng J B, Su T, Zhang L, et al. ISAR imaging of targets with complex motion based on the chirp rate-quadratic chirp rate distribution. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(11): 7276-7289. DOI:10.1109/TGRS.2014.2310474 ( 0) 0)
|
| [13] |
Musman S, Kerr D, Bachmann C. Automatic recognition of ISAR ship images. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(4): 1392-1404. DOI:10.1109/7.543860 ( 0) 0)
|
| [14] |
Pastina D, Spina C. Multi-feature based automatic recognition of ship targets in ISAR. IET Radar, Sonar & Navigation, 2009, 3(4): 406-423. DOI:10.1049/iet-rsn.2008.0172 ( 0) 0)
|
| [15] |
Zhang X G. ISAR Imaging and Target Recognition. Nanjing: Nanjing University of Aeronautics and Astronautics, 2001. 37-48.
( 0) 0)
|
| [16] |
Pastina D, Spina C. Slope-based frame selection and scaling technique for ship ISAR imaging. IET Signal Processing, 2008, 2(3): 265-276. DOI:10.1049/iet-spr:20070122 ( 0) 0)
|
| [17] |
Li J J, Zhao L H, Wang A X. Pattern Recognition. Beijing: Publishing House of Electronics Industry, 2010. 6-37.
( 0) 0)
|
| [18] |
Fisher R A. The use of multiple measurements in taxonomic problems. Annals of Eugenics, 1936, 7(2): 179-188. DOI:10.1111/j.1469-1809.1936.tb02137.x ( 0) 0)
|
| [19] |
Zhang X G. Pattern Recognition. 3rd Ed. Beijing: Tsinghua University Press, 2010, 70-135.
( 0) 0)
|
 2017, Vol. 24
2017, Vol. 24


