The developing trend in VLSI is aggressive scaling in the feature size, in turn, leading to increase the chip size, and then resulting in a growth in chip's interconnect complexity. Meanwhile, the chip's operating frequency is also increasing as well. Thus, an important step in the VLSI design is able to simulate and estimate interconnect line delay, cross-talk noise, and other characteristics in a reasonable time. MOR technique has proved to be a very powerful tool in expanding complexity of nano-scale integrated circuits, since it can dramatically decrease the simulation time of complex interconnect system by constructing small dimension models which save the important properties of the original system. The MOR of interconnect modules has been investigated comprehensively in the last score years[1-12].
A lot of methods that are based on Krylov-subspace projection techniques have been adapted to the model order reduction[5-6, 13-17]. These methods are adopted widely because of their iterative property and small computational cost versus balanced truncation approximation method, which is one of singular-value decomposition (SVD) techniques, and are well fit for reducing the complexity of VLSI interconnect networks. But, the classical single point expansion Krylov sub-space techniques can only match the low frequency response characteristics of interconnect system. Future interconnect system is more and more important in high frequency effects, so frequency selective MOR techniques are also more and more fundamentally important. MOR methods based on frequency selection are either using frequency weighted truncation technique or frequency linearized rational interpolation technique[18]. In addition, adaptive order multi-point MOR is provided by Lee[14]. Afterward, Alam[19] proposed arnoldi projection methods based on multi-shifted technique on account of wavelet transform to select the relevant frequency points. However, this method can not accurately obtain appropriate number of expansion points due to providing the man-made threshold, so it may have a long elapsed time or poor fitting degree. Chu[20] also gave a similar model simplification method of the lumped transformer mechanism, which was restricted to small scale interconnect system due to computing the residual complexity at each expansion point. So, all of these techniques are either computationally complex or not given how to choose the threshold.
In this paper, we show a weighted self-adaptive threshold wavelet interpolation point selection method using in Krylov subspace MOR. The method realizes optimmal matching of the original system response by a low order realization in a large frequency range. Thus, we choose the relevant interpolation point by using weighted threshold Harr wavelet transform to detect the dominant frequencies of system response in complex frequency regions. In order to show the advantage of the proposed method, we apply the method to H-clock tree circuit and power grid net circuit, which are modeled as RC and RLC model in VLSI. The simulation results show that the method in the paper gives higher accuracy than Haar wavelet method of man-made threshold.
2 Interconnect Systems' MOR Principle 2.1 Background of MORIn analyzing interconnect in VLSI, if we assume that a linear subnetwork contains only lumped elements, and then the modified nodal admittance (MNA)[21] formulation of the subnetwork may be used.
| $ \left\{ \begin{align} & \mathit{\boldsymbol{C\dot{x}}}=\rm{-}\mathit{\boldsymbol{Gx}}+\mathit{\boldsymbol{bu}}(\mathit{t}) \\ & \mathit{\boldsymbol{y}}={{\mathit{\boldsymbol{c}}}^{\rm{T}}}\mathit{\boldsymbol{x}} \\ \end{align} \right. $ | (1) |
where, x∈ Rn is a vector of n state variables including node voltage appended by independent voltage source current, and linear inductor current, C∈ Rn×n and G∈ Rn×n are constant matrices giving lumped memory and memoryless circuit elements respectively, b and cT define the linear maps between inputs and outputs, and u, y are input and output vector respectively. As a matter of fact reality simulations of large scale interconnect circuit, all of above matrices are big and sparse. Due to the simulation cost for a large interconnect system, MOR methods have been constructed to reduce the simulation complexity[22].
2.2 Projection-Based Order ReductionConsider a single interconnect system such as single-input single-output (SISO) system A(s) in descriptor form in Eq.(1). In projection-based model order reduction, the primitive state variables x are approximated by a vector xr ∈ Rq of reduced dimension q≪n:
| $ \mathit{\boldsymbol{x}}\approx \mathit{\boldsymbol{V}}{{\mathit{\boldsymbol{x}}}_{\mathit{\boldsymbol{r}}}} $ | (2) |
where V∈ Rn×q is a matrix with full column orthogonal vector. The reduced system Ar(s) approximating the input-output characteristic of the primitive system A(s) is generally obtained by:
| $ \left\{ \begin{align} & {{\mathit{\boldsymbol{C}}}_{\mathit{\boldsymbol{r}}}}{{{\mathit{\boldsymbol{\dot{x}}}}}_{\mathit{\boldsymbol{r}}}}\rm{=-}{{\mathit{\boldsymbol{G}}}_{\mathit{\boldsymbol{r}}}}{{\mathit{\boldsymbol{x}}}_{\mathit{\boldsymbol{r}}}}+{{\mathit{\boldsymbol{b}}}_{\mathit{\boldsymbol{r}}}}\mathit{\boldsymbol{u}}(\mathit{t}) \\ & {{\mathit{\boldsymbol{y}}}_{\mathit{\boldsymbol{r}}}}=\mathit{\boldsymbol{c}}_{\mathit{\boldsymbol{r}}}^{\rm{T}}\mathit{\boldsymbol{ }}\!\!~\!\!\rm{ }{{\mathit{\boldsymbol{x}}}_{\mathit{\boldsymbol{r}}}} \\ \end{align} \right. $ | (3) |
where Cr≈VTCV, Gr≈VTGV, br≈VTb, crT≈crTV.
One possible approach for the computation of V is the Krylov subspace methods, also known as moment matching method. Given an expansion frequency s0∈C, then we can take the Taylor series expansion of the transform function H(s) in s0 like:
| $ \mathit{\boldsymbol{H}}(s)={{\mathit{\boldsymbol{c}}}^{\rm{T}}}{{(s\mathit{\boldsymbol{C}}+\mathit{\boldsymbol{G}}\rm{ })}^{-1}}\mathit{\boldsymbol{b}}=-\sum\limits_{\mathit{i}=0}^{\infty }{\mathit{m}_{\mathit{i}}^{{{s}_{0}}}{{\left( s-{{s}_{0}} \right)}^{i}}} $ | (4) |
where mis0 is the ith order moment at s0. We define:
| $ \mathit{\boldsymbol{A}}={\rm{-}}{{({{s}_{0}}\mathit{\boldsymbol{C}}+\mathit{\boldsymbol{G}})}^{\rm{-}1}}\mathit{\boldsymbol{C}}, \mathit{\boldsymbol{R}}={{({{s}_{0}}\mathit{\boldsymbol{C}}+\mathit{\boldsymbol{G}})}^{\rm{-}1}}\mathit{\boldsymbol{b}} $ | (5) |
The moments are computed using mis0= cTAiR. Thus, the Krylov space is shown as:
| $ {{\mathit{\boldsymbol{\kappa}} }_{\rm{q}}}\left( \mathit{\boldsymbol{A}}, \mathit{\boldsymbol{R}} \right)=[\mathit{\boldsymbol{R}}, \mathit{\boldsymbol{AR}}, \cdots, {{\mathit{\boldsymbol{A}}}^{q\rm{-}1}}\mathit{\boldsymbol{R}}]~ $ | (6) |
The Arnoldi based algorithm can be used to iteratively create an orthonormal basis Vq∈ Rn×q from the successive Krylov sub-space κq(A, R). The underlying moment matching mechanism only guarantees the accuracy in a radius fr around the expansion frequency point f0. As the approximation order q increases, fr increases at the same time; but the relationship between fr and q is not so obvious[23]. And because the Arnoldi iteration firstly approximates the relevent poles in the vicinity of the expansion frequency point, it may make the reduced order models that do not match accurately the primitive system's output response in the interest frequency range. Through multiple point rational Arnoldi iterative method to reduce order of the primitive system at different frequency expansion points, thus the transform function can be approximated accurately based on MOR technique across an interest frequency range. Therefore, the key problem is to reduce the complexity of choosing these interpolation points[24].
3 Self-Adaptive Weighted Threshold Haar Wavelets for Interpolation Point Selection in Rational Arnoldi MethodIn mathematics, the simplest wavelet is Haar wavelet. The weakness of the Haar wavelet is not continuous, but this is also the advantage for the analysis of sudden transition signals. In this paper, we also use this property to detect the variation of system transform characteristic. The calculating Haar wavelet transform process includes first initializing one dimension array with the all sampled values N and then sweeping all samples at each level based on Haar wavelet basis decomposition[25]. After the above two steps, sharp changes in the data stand out, while smooth parts are approach to zero. In order to screen out more unimportant expansion points in the interest frequency range, we should detect the transform coefficients by a threshold. The threshold is a criterion which makes a distinction between the trivial coefficients parts and the important coefficients including significant components. Threshold is very efficiently used in sparse or near-sparse variations signals where only a small number of coefficients subset can be employed for the selection of shift expansion points[25].
It notes that the threshold is very important in interpolation point's selection. The poor choices of threshold will result in a long elapsed time or poor fitting degree in MOR. The procedure for generating threshold is listed in Table 1. Then, the interpolating points selected based Haar wavelet are used to reduce order of the primitive system based on rational Arnoldi method. At each interpolation point, the matching moment order is determined by the required error. In this paper, relative error, which is the difference value of transform functions in continuous reduced order procedure, and absolute error are used. We apply the accurate absolute error proposed by Odabasioglu[23] in our method. For simplicity in this paper, we only give the main results shown in Eq.(7), not detailed derivations. The symbol in Eq.(7) is Ref.[23]. All the vectors in every interpolation point compose the orthogonal matrix V which is used to achieve finally reduced order system.
| $ \begin{array}{l} \mathit{\boldsymbol{\tilde E}}(s) = {\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{X}}{\mathit{\boldsymbol{S}}_\mathit{r}}{\left( {\mathit{\boldsymbol{I}}{\rm{ - }}s\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}} \right)^{{\rm{ - }}1}}\cdot s\left( {\mathit{\boldsymbol{S}}_\mathit{r}^{{\rm{ - }}1}{{\mathit{\boldsymbol{\tilde G}}}^{ - 1}}{\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{G}}_{pr}}{\mathit{\boldsymbol{X}}_l}{\mathit{\boldsymbol{S}}_r}} \right) \cdot \\ \;\;\;\;\;\;\;\;\;{\left( {\mathit{\boldsymbol{I}}{\rm{ - }}s\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}} \right)^{{\rm{ - }}1}}\mathit{\boldsymbol{S}}_\mathit{r}^{{\rm{ - }}1}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{R}} \end{array} $ | (7) |
| Table 1 Self-adaptive weighted threshold for Haar wavelet transform based MOR |
Meanwhile, the weighted self-adaptive threshold Wavelet MOR can also be used multiple-input multiple-output (MIMO) systems based on block Arnoldi technique. The error above mentioned can also extend to MIMO systems.
4 Simulation ResultsA simple mesh power grid circuit and a clock tree circuit shown in Fig. 1 and Fig. 2 are studied to prove the efficiency and accuracy of the method proposed in this paper. The horizontal parameters of Fig. 1: R= 0.05 Ω/mm, L=0.502 5 nH/mm, C=0.155 2 pF/mm and the vertical parameters are: R=0.06 Ω/mm, L=0.548 0 nH/mm, C=0.142 3 pF/mm. Each line is 30 mm long and divided into 20 sections, so the full order n is equal to 719[26]. The clock tree circuit is shown in Fig. 2; the full order n is 33. The driver resistor is 80 Ω, the other distributed resistor is 60 Ω, distributed capacitance is 1 pF, and the all load capacitances are 1.2 pF[27]. From the frequency response of the two circuits, we generate a set of sampled response points in frequency domain that are used by the weighted threshold Haar wavelet MOR method. We compared the accuracy and efficiency of weighted threshold with man-made threshold across a large range of frequency domain (ω=[0, 1012]). All simulations are done by Matlab on Lenovo Yangtian series personal computer. For clock tree circuit, the run time in frequency range 2.5×1011 to 3×1011 and 0 to 1012 including 220 sampling points is 119.526 s and 120.009 s respectively. While the run time in interest frequency range 2.5×1011 to 3×1011 Hz including 64 sampling points is 0.007 98 s. The following simulation results use absolute error; the results from relative error are consistent.
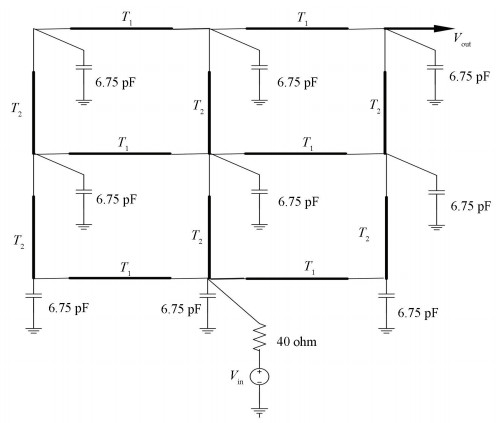
|
Figure 1 The power grid mesh circuit |

|
Figure 2 The clock tree circuit |
4.1 The Comparison of Weighted Threshold and Mean Threshold
To prove the validity of the weighted threshold method, we verified it on clock tree circuit. Fig. 3 shows the fitting degree between weighted and mean threshold reduced order method (uniform interpolation points) compared to original signal in our interested frequency range. From Fig. 3, we can observe the superiority and accuracy of weighted threshold method.
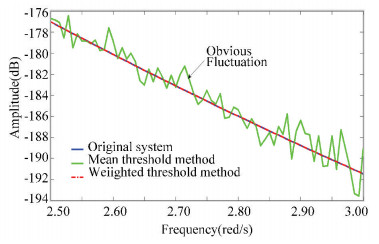
|
Figure 3 The comparison between the two threshold methods on clock tree circuit |
4.2 The Comparison of Self-Adaptive Threshold and Man-Made Threshold
In order to prove the advantage of adaptive threshold method, we analyze the fitting degree between man-made threshold reduced order method and self-adaptive threshold reduced order method compared with original system. The superiority of self-adaptive threshold reduced order method is given in Fig. 4 for the clock circuit of n=33.

|
Figure 4 The fittering degree comparison of clock tree circuit |
While the man-made threshold is oversized in Fig. 4(a), the reduced order method by these interpolation points leads a low fitting degree compared with original system due to choosing little expansion point. In undersized threshold case in Fig. 4(b), although the reduced order method by these interpolation points has the same fitting degree as the one based on the self-adaptive threshold method, the elapsed time is longer. In the clock tree circuit, the running time for man-made threshold reduced order method is 1.750 113 s; one for self-adaptive threshold is 1.449 630 s. This is because too many expansion points are selected. With the increase of the scale of interconnect system, the superiority is bigger and bigger. In order to prove the method to be applicable to large-scale system, we analyze a power grid system of n=719. The Fig. 5 shows the result, which is the same as clock tree circuit.

|
Figure 5 The fitting degree comparison of power grid cricuit |
In summary, the self-adaptive threshold can select optimal expansion points. Besides, using the selected expansion points, the reduced system fits better with the original system.
5 ConclusionIn this paper, we propose a weighted self-adaptive threshold wavelet expansion MOR technique which is based on Krylov sub-space methods to construct reduced order system models that are accurate and efficient over an extensive range of frequency. We can dynamically screen out valuable expansion points by wavelet transform and weighted self-adaptive threshold. This method gives an automated method to construct a low order system which is accurate in interest frequency range. The simulation results prove that the method can provide accurate and efficient reduced order model for complex interconnect structures.
| [1] |
Ferranti F, Nakhla M, Antonini G, et al. Parameterized model order reduction of delayed systems using an interpolation approach with amplitude and frequency scaling coefficients. IEEE Workshop on Signal and Power Integrity. Piscataway: IEEE, 2012, 57-60. DOI:10.1109/SaPIW.2012.6222911 ( 0) 0)
|
| [2] |
Ferranti F, Nakhla M S, ANtonini G, et al. Multipoint full-wave model order reduction for delayed PEEC models with large delays. IEEE Transation Electromagnetic Compatibility, 2011, 53(4): 959-967. DOI:10.1109/TEMC.2011.2154335 ( 0) 0)
|
| [3] |
Alam M, Nieuwoudt A, Massoud Y. Frequency selective model order reduction via spectral zero projection. Proceedings of the IEEE ASP-Design Automation Conference. Piscataway: IEEE, 2007, 379-383. DOI:10.1109/ASPDAC.2007.358015 ( 0) 0)
|
| [4] |
Alam M, Nieuwoudt A, Massoud Y. Wavelet-based passivity preserving model order reduction for wideband interconnect characterization. IEEE Symposium Quality Electronicd Design. Piscataway:IEEE, 2007, 432-437. DOI:10.1109/ISQED.2007.170 ( 0) 0)
|
| [5] |
Alam M, Nieuwoudt A, Massoud Y. Frequency selective model order reduction via spectral zero projection. Proceedings of the IEEE Dallas Circuits and Systems Conference. Piscataway: IEEE, 2006, 379-383. DOI:10.1109/ASPDAC.2007.358015 ( 0) 0)
|
| [6] |
Odabasioglu A, Celik M, Pileggi L T. PRIMA: Passive reduced-order interconnect macromodeling algorithm. IEEE Transaction on Computer-Aided Design of Integrated Circuits System, 1998, 17(8): 645-654. DOI:10.1109/43.712097 ( 0) 0)
|
| [7] |
Pillage L T, Rohrer R A. Asymptotic waveform evaluation for timing analysis. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 1990, 9(4): 352-366. DOI:10.1109/43.45867 ( 0) 0)
|
| [8] |
Feldmann P, Freund R. Efficient linear circuit analysis by Pade approximation via the lanczos process. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 1995, 14(5): 639-649. DOI:10.1109/43.384428 ( 0) 0)
|
| [9] |
Antoulas A C. Approximation of Large-scale Dynamical Systems. New York: SAIM, 2005. 100-115. DOI: 10.1137/1.9780898718713.
( 0) 0)
|
| [10] |
Pinnau R. Model Reduction via Proper Orthogonal Decomposition. Berlin: Springer, 2008, 93-108. ( 0) 0)
|
| [11] |
Tan S X-D, He L. Advanced Model Order Reduction Techniques for VLSI Designs. Cambrede: Cambridge University Press, 2007, 60-100.
( 0) 0)
|
| [12] |
Li Y T, Bai Z, Su Y, et al. Model order reduction of parameterized interconnect networks via a two-directional Arnoldi process. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2008, 27(9): 1571-1582. DOI:10.1109/TCAD.2008.927768 ( 0) 0)
|
| [13] |
Silveira L M, Kamon M, Elfadel I, et al. A coordinate transformed Arnoldi algorithm for generating guaranteed stable reduced order models of RLC circuits. Proceedings of the IEEE/ACM International Conference Computer-Aided Design. Piscataway: IEEE, 1996, 288-294. DOI:10.1109/ICCAD.1996.569710 ( 0) 0)
|
| [14] |
Lee H J, Chu C C, Feng W S. Multi-point model reduction of VLSI interconnects using the rational Arnoldi method with adaptive orders. Proceedings of the IEEE Asia Pacific Conference Circuits and Systems.Piscataway: IEEE, 2004, 1009-1012. DOI:10.1109/APCCAS.2004.1413052 ( 0) 0)
|
| [15] |
Pati A, Kumar A, Chandra D. Suboptimal control using model order reduction. Chinese Journal of Engineering, 2014, 37(5): 1-5. DOI:10.1155/2014/797581 ( 0) 0)
|
| [16] |
Lavania S, Nagaria D. Eigen spectrum based moment matching technique for model order reduction. Proceedings of the 39th National System conference. Piscataway: IEEE, 2015, 1-5. DOI:10.1109/NATSYS.2015.7489100 ( 0) 0)
|
| [17] |
Wittmuess P, Tarin C, Kech A, et al. Parametric model order reduction via balanced truncation with taylor series representation. IEEE Transaction on Automatic Control, 2016, 61(11): 3438-3451. DOI:10.1109/TAC.2016.2521361 ( 0) 0)
|
| [18] |
Elfadel I M, Ling D D. A block rational Arnoldi algorithm for multi-point passive model-order reduction of multiport RLC networks. Proceedings of the IEEE/ACM International Conference Computer-Aided Design. Piscataway: IEEE, 1997, 66-71. DOI:10.1109/ICCAD.1997.643368 ( 0) 0)
|
| [19] |
Alam M, Nieuwoudt A, Massoud Y. Efficient multi-shifted Arnoldi projection using wavelet transform. Journal of Circuits, Systems and Computers, 2007, 16(5): 699-709. DOI:10.1142/S0218126607003927 ( 0) 0)
|
| [20] |
Chu C C, Lee H J. Applications of multi-point Arnoldi algorithms to linear lumped transformer model simplifications. IEEE Power Engineering Society Summer Meeting. Piscataway: IEEE, 2000, 2406-2411. DOI:10.1109/PESS.2000.867367 ( 0) 0)
|
| [21] |
Ho C W, Ruehli A E, Brennan P. The modified nodal approach to network analysis. IEEE Transactions on Circuits and Systems, 1975, 22(6): 504-509. DOI:10.1109/TCS.1975.1084079 ( 0) 0)
|
| [22] |
Wang J M, Chu C C, Yu Q, et al. On projection-based algorithm for model-order reduction of interconnects. IEEE Transactions on Circuits and Systems Ⅰ: Fundamental Theory and Applications, 2002, 49(11): 1563-1585. DOI:10.1109/TCSI.2002.804542 ( 0) 0)
|
| [23] |
Odabasioglu A, Celik M, Pileggi L T. Practical considerations for passive reduction of RLC circuits. Proceedings of the IEEE/ACM International Conference on Computer-Aided Design. Piscataway: IEEE, 1999, 214-219. DOI:10.1109/ICCAD.1999.810652 ( 0) 0)
|
| [24] |
Alam M, Nieuwoudt A, Massoud Y. Model order reduction using spline-based dynamic multi-point rational interpolation for passive circuits. Analog Integrated Circuits and Signal Processing, 2007, 50(3): 273-277. DOI:10.1007/s10470-006-9017-5 ( 0) 0)
|
| [25] |
Massoud Y, Alam M, Nieuwoudt A. On the selection of spectral zeros for generating passive reduced order models. Proceedings of the 6th International Workshop on System-on-Chip for Real-Time Applications. Piscataway: IEEE, 2006, 160-164. DOI:10.1109/IWSOC.2006.348228 ( 0) 0)
|
| [26] |
Chu C C, Lee H J, Feng W S, et al. Interconnect model reductions by using the AORA algorithm with considering the adjoint network. Proceedings of the IEEE International Symposium on Circuits and Systems. Piscataway: IEEE, 2005, 1278-1281. DOI:10.1109/ISCAS.2005.1464828 ( 0) 0)
|
| [27] |
Xu Q, Mazumder P, Ding L. Novel macromodeling for on-chip RC/RLC interconnects. Proceedings of the IEEE International Symposium on Circuits and Systems. Piscataway: IEEE, 2002, 189-192. DOI:10.1109/ISCAS.2002.1010421 ( 0) 0)
|
 2018, Vol. 25
2018, Vol. 25


