For the terminology and notations not defined here, we adopt those in Bondy[1] and Haynes[2] and consider simple graphs only.
Let G=(V, E) be a graph. For any vertex v∈V(G), N(v) denotes the vertex neighborhood of v in G, dG(v)=|N(v)| is called the degree of v in G, Δ=Δ(G) and δ=δ(G) denote the maximum degree and minimum degree of G respectively. Pn, Cn and Kn denote the path, cycle and complete graph of order n, respectively, and Wn=Cn∨K1 denotes the wheel of order n+1. If u, v∈V(G), then dG(u, v) denotes the distance between u and v in G.
Chartrand[3] stated the concept of the locating set and locating number of a graph G as follows:
Definition 1 Let G=(V, E) be a connected graph and W={w1, w2, …, wk} be an ordered subset of V(G). For any vertex v∈V, the locating code of v with respect to W is the k-vector CW(v)={d(v, w1), d(v, w2), …, d(v, wk)}, W is said to be a locating set of G if distinct vertices have the distinct locating code, and the locating number of G is defined as:
| $ Loc\left( G \right) = \min \left\{ {\left| W \right|:W\;{\rm{is}}\;{\rm{a}}\;{\rm{locating}}\;{\rm{set}}\;{\rm{of}}\;G} \right\} $ |
A locating set W of G is said to be a minimum locating set if |W|=Loc(G).
The locating problem of graphs has been applied to various fields, such as network security, fire and burglary prevention, transportation and oil exploration. For example, in a complex network structure (as a graph), the individual nodes may be damaged, thus affecting the entire network of information transmission. Testing all the nodes in the network requires a large amount of engineering. So, it's necessary to select some specific nodes (as few as possible) and to position the positioner. The distances from each node to those specific nodes can be arranged into an order for a locating code (different nodes have different locating codes). The shortest length of the locating code is the locating number of graph G, which is also the number of the fewest locators needed.
Raja[4] discussed the relations between locating number, domination number, clique number and chromatic number of a graph. Chartrand[3] obtained the following two results.
Lemma 1[3] (1) A connected graph G of order n has locating number 1 if and only if G
(2) A connected graph G of order n≥2 has locating number n-1 if and only if G
Lemma 2[3] For any graph G of order n with the diameter d, then
| $ {\log _3}\left( {\Delta + 1} \right) \le Loc\left( G \right) \le n-d\left( G \right) $ |
where Δ is the maximum degree of G.
Similarly, let f be a proper k-coloring of a connected graph G and Π=(V1, V2, …, Vk) be an ordered partition of V(G) into the resulting color classes. For a vertex v of G, the color code of v with respect to Π is defined to be the ordered k-tuple Π(v) =(d(v, V1), (d(v, V2), …, (d(v, Vk)), where (d(v, Vi) = min{(d(v, x): x∈Vi}, 1≤i≤k. If distinct vertices have distinct color codes, then f is called a locating coloring. The minimum number of colors needed in a locating coloring of G is the locating chromatic number of G, denoted by χL(G).
Behtoei and Anbarloei[5] studied the locating chromatic number of the join of graphs, determined the locating chromatic number of the join of paths, cycles and complete multipartite graphs. Behtoei and Omoomi[6] studied the locating chromatic number of Kneser graphs, and showed that χL(KG(n, 2))=n-1 for all n≥5. Chartrand[7] showed that for each integer k with (n+1)/2≤k≤n, there existed such a graph G of order n with χL(G)=k. Asmiati[8] determined the locating-chromatic numbers of non-homogeneous caterpillars and firecracker graphs. Salman and Chaudhry[9] studied the locatic number of paths, cycles and characterize all the connected graphs of order n having locatic number n, n-1 and n-2.
Similar to the locating chromatic number of G, Foucaud and Henning[10-11] studied the locating domination set and locating domination numbers of graphs, obtained some bounds for general graphs, and determined the locating domination numbers for some special graphs. Fazil[12] studied the locating domination set of hypergraphs, and Xing[13] defined the conception of locating total domination in graphs, and determined the locating total domination number of the Cartesian product of cycles and paths.
In this paper, we obtain some bounds for the locating numbers of graphs, and determine the exact value of Loc(G) for some special classes of graphs, we also prove that Loc(T)≥Δ-1 holds for all trees T with maximum degree Δ, and show that this lower bound is the best possible.
2 Main ResultsFirst, we give a sharp lower bound of the locating numbers for all trees with maximum degree Δ≥2.
Theorem 1 For all trees T with maximum degree Δ≥2, then Loc(T)≥Δ-1, and this bound is sharp.
Proof It is obvious for Δ≤2. Next we suppose Δ≥3. Suppose, on the contrary, that there exists a tree T with Loc(T)=t≤Δ-2. Let v∈V(T) is a maximum degree vertex, deg(v)=Δ≥3, and W={w1, w2, …, wt} is a minimum locating set of T, let
| $ T-v = {T_1} \cup {T_2} \cup \cdots \cup {T_\Delta } $ |
Since t≤Δ-2, there exist at least two subtrees Ti and Tj such that V(Ti)∩W=ϕ, and V(Tj)∩W=ϕ. Choose two vertices v1∈V(Ti)∩N(v) and v2∈V(Tj)∩N(v), obviously, this two locating codes of v1 and v2 with respect to W are the same, this is, Cw(v1)=Cw(v2), this contradicts that W={w1, w2, …, wt} is a minimum locating set of T. Thus we have Loc(T)≥Δ-1. Next we may construct a tree T with Loc(T)=Δ-1(Δ≥2).
Obviously, W={1, 2, …, t-1} in Fig. 1 is a locating set of T. We have completed the proof of Theorem 1.
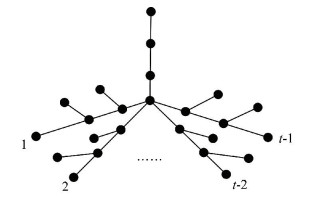
|
Figure 1 A tree T with Loc(T)=t-1 where t=Δ |
Theorem 2 Let G be a connected graph of order n with the diameter d, if Loc(G)=k, then we have dk+k≥n.
Proof Let W={w1, w2, …, wk} be a minimum locating set of G, and V1=V(G)-W. For every vertex v∈V1, CW(v)={(d(v, w1), (d(v, w2), …, (d(v, wk)} is the locating code of v, where 1≤(d(v, wi)≤d(1≤i≤k). Since distinct vertices of V1 have distinct locating code, |V1|≤dk, and thus n=|V(G)|=|V1|+|W|≤dk+k. We have completed the proof of Theorem 2.
Next we consider the locating numbers for several kinds of special graphs.
Theorem 3 (1) For all integers n≥3, then Loc(Cn)=2;(2)Loc(W4)=Loc(W5)=2, and Loc(W3)=Loc(W6)=3;(3)When n≥7, Loc(Wn)=⌈(2n-2)/5⌉.
Proof (1) By Lemma 1 (1), we have Loc(Cn)≥2. On the other hand, we may choose any two adjacent vertices w1 and w2, it is easy to see that W={w1, w2} is a locating set of Cn, and thus Loc(Cn)≤|W|=2, so we have Loc(Cn)=2.
(2) By Lemma 1 (2), Loc(W3)=Loc(K4)=3. When n∈{4, 5, 6}, a minimum locating set W of Wn is shown in Fig. 2. Where W={a, b} or W={a, b, c}.
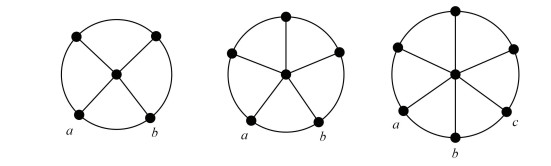
|
Figure 2 A minimum locating set W of Wn when n∈{4, 5, 6} |
(3) When n=7 or 8, a minimum locating set W={a, b, c} of Wn is shown in Fig. 3.
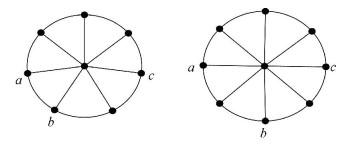
|
Figure 3 A minimum locating set W={a, b, c} of Wn when n∈{7, 8} |
When n≥9, let Wn=Cn∨K1, and W={w1, w2, …, wk} be a minimum locating set of Wn, this is, k=Loc(Wn). Let S=V(Cn)∩W, Cn-S=P1∪P2∪…∪Pt, where t≤|S|≤k, and every Pi is a path of order ni(1≤i≤t).
For any vertex u∈S, there exists at least one vertex v∈S such that dCn(u, v)≤2 (otherwise, let u1 and u2 be the adjacent vertices of u in Cn, then we have CW(u1)=CW(u2), a contradiction). In all paths Pi, every ni≤3(1≤i≤t), and there is at least one path containing three vertices (otherwise, there exist two vertices u1 and u2 in Cn, such CW(u1)=CW(u2), a contradiction). Thus, in all paths Pi, there are at least ⌈t/2⌉ paths containing one vertex, there are at most ⌊t/2」 paths containing two or three vertices, so, we have
| $ \begin{array}{l} n = \left| S \right| = \sum\limits_{i = 1}^t {{n_i} \le } \left| S \right| + \left\lceil {\frac{t}{2}} \right\rceil = 2\left( {\left\lfloor {\frac{t}{2}} \right\rfloor-1} \right) + \\ \;\;\;\;\;3 \le \frac{{5k}}{2} + 1 \end{array} $ |
this is, Loc(Wn)=k≥(2n-2)/5.
Since k is an integer, thus Loc(Wn)=k≥「(2n-2)/5⌉.
On the other hand, we may choose a locating set of Wn=Cn∨K1 as follows:
Let V(Cn)={v1, v2, …, vn}, vivi+1∈E(Cn)(1≤i≤n-1) and v1vn∈E(Cn), V(K1)={v0} and v0vi∈E(Wn)(1≤i≤n). Let
| $ \begin{array}{*{20}{c}} {{M_1}{\rm{ = }}\left\{ {{v_{n-1}}, {v_1}, {v_5}, {v_7}} \right\}}\\ {{M_2} = \left\{ {{v_{5 + 5i}}\left| {1 \le i \le \frac{{n-7}}{5}} \right.} \right\}}\\ {{M_3} = \left\{ {{v_{7 + 5i}}\left| {1 \le i \le \frac{{n-9}}{5}} \right.} \right\}} \end{array} $ |
And let W=M1∪M2∪M3, it is easy to see that W is a locating set of Wn, and
| $ \begin{array}{l} \left| W \right| = 4 + \left\lfloor {\frac{{n-7}}{5}} \right\rfloor + \left\lfloor {\frac{{n-9}}{5}} \right\rfloor = \left\lfloor {\frac{{2n + 2}}{5}} \right\rfloor = \\ \;\;\;\;\;\;\;\;\left\lceil {\frac{{\left( {2n-2} \right)}}{5}} \right\rceil \end{array} $ |
thus we have
Loc(Wn)≤|W|=「2n-2/5⌉, we have completed the proof of Theorem 3.
Theorem 4 For any complete t-partite graph G=K(n1, n2, …, nt) of order n, if n1≥n2≥…≥nt≥2, then Loc(T)=n-t.
Proof Let V(G)=V1∪V2∪…∪Vt be the t-partite vertex set of G, where |Vi|=ni (1≤i≤t), Loc(G)=k and W={w1, w2, …, wk} is a minimum locating set of G. For every i∈{1, 2, …, t}, then |Vi∩W|≥ni-1. Otherwise, there exists integer j(1≤j≤t)such that |Vj∩W|≤nj-2, then for any two vertices u, v∈(Vj-Vj∩W), we have CW(u)=CW(v), a contradiction. Thus |Vi∩W|≥ni-1 hold for every i∈{1, 2, …, t}, so we have
| $ \begin{array}{l} Loc\left( G \right) = k = \left| W \right| = \sum\limits_{i = 1}^t {\left| {{V_i} \cap W} \right| \ge } \sum\limits_{i = 1}^t {\left( {{n_i}-} \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. 1 \right) = n-t \end{array} $ |
On the other hand, for every integer i∈{1, 2, …, t}, let vi∈Vi, and W=V-{v1, v2, …, vt}, obviously, W is a locating set of G, thus Loc(G)=k≤|W|=n-t. We have completed the proof of Theorem 4.
Theorem 5 For any two integers m and n, m≥n≥2, then Loc(Pm×Pn)=2.
Proof By Lemma 1, we have Loc(Pm×Pn)≥2. On the other hand, we may choose two vertices u and v of degree two such that the distance d(u, v)=n-1 in Pm×Pn. Obviously, W={u, v} is a locating set of Pm×Pn, Thus, Loc (Pm×Pn)≤|W|=2. So, we have Loc(Pm×Pn)=2. We have completed the proof of Theorem 5.
| [1] |
Bondy J A, Murty U S R. Graph Theory with Application. Amsterdam: Elsevier, 1976.
( 0) 0)
|
| [2] |
Haynes T W, Hedetniemi S T, Slater P J. Domination in Graph. New York: Marcel Dekker, Inc., 1998.
( 0) 0)
|
| [3] |
Chartrand G, Zhang P. Introduction to Graph Theory. Boston: The McGraw-Hill Companies, Inc., 2006, 341-346.
( 0) 0)
|
| [4] |
Raja R, Pirzada S, Redmond S. On locating numbers and codes of zero divisor graphs associated with commutative rings. Journal of Algebra and Its Applications, 2016, 15(1): 1650-1664. DOI:10.1142/S0219498816500146 ( 0) 0)
|
| [5] |
Behtoei A, Anbarloei M. The locating chromatic number of the join of graphs. Bulletin of the Iranian Mathematical Society, 2014, 40(6): 1491-1501. ( 0) 0)
|
| [6] |
Behtoei A, Omoomi B. On the locating chromatic number of Kneser graphs. Discrete Applied Mathematics, 2011, 159(18): 2214-2221. DOI:10.1016/j.dam.2011.07.015 ( 0) 0)
|
| [7] |
Chartrand G, Erwin D, Henning M A, et al. Graphs of order n with locating-chromatic number n-1. Discrete Mathematics, 2003, 269(1-3): 65-72. DOI:10.1016/S0012-365X(02)00829-4 ( 0) 0)
|
| [8] |
Asmiati A. On the locating chromatic numbers of non-homogeneous caterpillars and firecracker graphs. Far East Journal of Mathematical Sciences, 2016, 100(8): 1305-1316. DOI:10.17654/MS100081305 ( 0) 0)
|
| [9] |
Salman M, Chaudhry M A, Javaid I. On the locatic number of graphs. International Journal of Computer Mathematics, 2013, 90(5): 912-920. DOI:10.1080/00207160.2012.749346 ( 0) 0)
|
| [10] |
Foucaud F, Henning M A. Location-domination and matching in cubic graphs. Discrete Mathematics, 2016, 339(4): 1221-1231. DOI:10.1016/j.disc.2015.11.016 ( 0) 0)
|
| [11] |
Foucaud F, Henning M A, Löwenstein C, et al. Locating-dominating sets in twin-free graphs. Discrete Applied Mathematics, 2016, 200(1): 52-58. DOI:10.1016/j.dam.2015.06.038 ( 0) 0)
|
| [12] |
Fazil M, Javaid I, Salman M, et al. Locating-dominating sets in hypergraphs. Periodica Mathematica Hungarica, 2016, 72(2): 224-234. DOI:10.1007/s10998-016-0121-8 ( 0) 0)
|
| [13] |
Xing H, Sohn M Y. Bounds on locating total domination number of the Cartesian product of cycles and paths. Information Processing Letters, 2015, 115(12): 950-956. DOI:10.1016/j.ipl.2015.07.010 ( 0) 0)
|
 2018, Vol. 25
2018, Vol. 25


