With the increasingly brutal battlefield environment and the unprecedented fierce competition in business, new aerospace vehicles surged all over the world since advanced technology of aircraft design has been attached more significance. Both Fig. 1 and Fig. 2 show some of the most advanced vehicles around the world respectively.

|
Figure 1 American unmanned hypersonic flight "X-43a" |

|
Figure 2 European re-usable spaceplane "Skylon" |
To achieve the idea of fine design, demands for aircraft design have been transformed to keep a comprehensive balance of high performance, high reliability and robustness, low risk and low cost. In order to effectively address these competing objectives, designers would take consideration of various stages throughout the whole vehicle lifecycle from design, manufacturing, operation to final processing. In the practical engineering, uncertainties inherently exist in all these stages, which may cause the actual performance of the aircraft deviates far from the design targets, even leading to failure of some key components. Therefore, it would be significant to take full consideration of uncertainties in aerospace vehicles design optimization process.
Multidisciplinary Design Optimization (MDO) is recognized as an effective way to solve the design problems of large-scale systems like aerospace vehicles. Considering the impacts of uncertainties, designers raise Uncertainty-based Multidisciplinary Design Optimization (UMDO) theory by combining uncertainty-based design and MDO methods. The core idea is to take comprehensive consideration of the propagation of uncertainties among the coupled disciplines to obtain a robust and reliable optimal solution[1]. Since being proposed, UMDO has contributed greatly in aircraft design and promoted the design level of aerospace vehicles. However, there also exist some problems. Compared with uncertainty-based single discipline design optimization, UMDO would face the challenge of computational complexity caused by uncertainties propagating in coupled disciplinaries. Moreover, the organizational complexity of UMDO has been higher than traditional MDO method since taking uncertainty into consideration in the design phase. Therefore, methods to address these problems draw many researchers' attention and numerous theories on this have been proposed[2-4]. The purpose of this context is to give an overview of recent developments in UMDO systematically, introduce the typical processing and approaches, highlight the challenges and opportunities and promote the future research.
2 Basic Introduction of Uncertainties in Aircraft 2.1 Definition and Classification of UncertaintyDefinitions and classifications of uncertainties vary with the disciplinary fields. In system engineering, uncertainties are defined as things not to be understood or be inaccurate understood[5]. Some aerospace engineering documents define uncertainty as the difference in model-based estimates and actual conditions that are represented by specific distribution functions due to incomplete knowledge[6]. The most widely accepted classification of uncertainty is divided into two categories, epistemic uncertainty and aleatory uncertainty. Aleatory uncertainty, also known as random uncertainty, describes the inherent variations in the physical system (or the environment) under consideration, which cannot be reduced or simplified through more information and data. Epistemic uncertainty is defined as the potential or possible deficiency in the process of modeling and simulation due to lack of knowledge and information. Researchers can reduce or eliminate this uncertainty by collecting more data.
2.2 Uncertainties Sources in Aircraft DesignFor a complex system design, the uncertainty classification is specifically studied. In the field of aircraft design, it is usually necessary to use the computer model to achieve the system simulation and design optimization. Therefore, to determine the uncertainties of aircrafts, the main consideration is based on the computer simulation optimization model of aircraft optimization design, which requires the consideration of uncertainties in the entire aircraft lifecycle.
As for actual engineering problems, there are various factors which could bring uncertainties, including loads, mechanical properties of the material, geometric dimensions, initial conditions, boundary conditions and computational models, etc. During the flight of the aircraft, the external flow field is complex and varied, so the aerodynamic load is obviously uncertain[7]. And considering the whole process from take-off to landing, flight posture, speed, and weight of the aircraft constantly change, which brings uncertainties to prediction of flight load. Moreover, manufacture errors are unavoidable, resulting in the uncertainty of shape and geometric parameters such as beam web thickness and skin thickness. For actual problems, dispersion of material properties, especially of composite material properties as well as simplification in modeling process would also lead to uncertainties. In addition, there are also uncertainties in other disciplines. For example, measurement errors can cause some acoustic and thermal parameters uncertain. These uncertainties are usually small but cannot be neglected either.
2.3 Uncertainty ModelingAfter extracting the uncertainty factors, we need to use the corresponding mathematical tools to build models. Uncertainty modeling methods contain two main types based on its mathematical theory, one is the probability method, the other is the non-probability method. Probability methods include Monte-Carlo method and Bayesian method, which develop earlier and more mature. The Monte Carlo method[8] has been widely used in uncertain aircraft design problems, which is the most accurate method for uncertainty description. But it cannot be used when the information or data are not sufficient[9]. As a supplement, the Bayesian statistical method is developed. The Bayesian approach[10-12] can handle epistemic and aleatory uncertainties and is therefore widely used, especially in the field of reliability engineering. Non-probabilistic methods include evidence theory[13-14], possibility theory[13-17], interval analysis[18-21], convex model[22-24] and so on, which can determine uncertainties without numerical probability[25-26]. According to their characteristics, different sources of uncertainties need different modeling methods.
Probabilistic methods have been developed for many years, and non-probabilistic methods have been carried out as a supplement to the probability methods. After non-probabilistic methods were proposed, compatibility study of probabilistic uncertainty and non-probabilistic uncertainty methods have attracted many scholars attention. Sepulveda[27] proposes a method for structural synthesis with reliability constraints under service conditions considering uncertain structural parameters and variables. And then optimization is carried out by generating and solving a sequence of explicit approximate problems with an example problem illustrating the methodology set forth. Guo et al.[28] conducted a comparative study on the non-probabilistic reliability methods and the widely used traditional probabilistic reliability methods in terms of modeling ideas, model structures, and structural optimization based on reliability, further illustrating the validity and practicability of the non-probabilistic reliability method. Yao et al.[29] introduced the development of structural reliability measurement method. The concept of reliability is divided into two categories: the method under the probability system and the method under the non-probability system. The relationship between probabilistic and non-probabilistic reliability analysis is systematically studied, and the compatibility of probabilistic and non-probabilistic reliability analysis is proved. However, in the field of aircraft multidisciplinary optimization, corresponding literature related has not been found yet.
2.4 Uncertainty Propagation and AnalysisFor complex system aircraft, the uncertainty will propagate among the coupling disciplines, and the uncertainty of different disciplines would interrelate through coupling variables. Uncertainty propagation analysis is to analyze the influence of uncertainties of design variables and system parameters, and to characterize and quantify uncertainties of the system state variables and response output. Common methods include Monte Carlo simulation methods (MCS, also known as probability sampling method), Taylor series expansion method and surrogate model based method, the application of which based on probability theory is introduced.
2.4.1 Monte Carlo simulation(MCS)The MCS method is a method of calculating the number of target responses by repeating sampling and computer simulation. As long as the sample size is sufficient, it can obtain statistical results of arbitrary precision and is therefore often used as a criterion for evaluating the performance of a new analytical method. The basic flowchart is shown in Fig. 3.
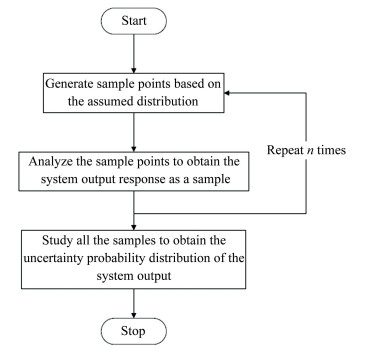
|
Figure 3 The basic flowchart of MSC |
In order to improve the efficiency of the MCS, a variety of sampling techniques have been searched, including the experimental design method, the importance sampling method[30], the importance sampling method based on the Most Probable Point (MPP)[31], the Latin hyper-method[32], etc.
2.4.2 Taylor series expansion methodThe Taylor series expansion method can obtain the mean and variance of the system output under random input uncertainty. Suppose the input parameters is n-dimensional random vector x, the mean value is μx, the standard deviation is σx, then the mean μy and standard deviation σy of the system output can be approximated as follows:
| $ \left\{ \begin{array}{l} {\mu _y} = f({\mu _{{x_1}}}, {\mu _{{x_2}}}, \ldots, {\mu _{{x_n}}}) + \frac{1}{2}\sum\limits_{i = 1}^n {\frac{{{\partial ^2}f}}{{\partial x_i^2}}\sigma _{xi}^2 + } \\ \;\;\;\;\;\;\;\;\sum\limits_{i = 1}^n {\sum\limits_{j = i + 1}^n {\frac{{{\partial ^2}f}}{{\partial {x_i}\partial {x_j}}}{\rho _{ij}}\sigma {x_i}\sigma {x_j}} } \\ {\sigma _y} = \sqrt {\sum\limits_{i = 1}^n {{{\left( {\frac{{\partial f}}{{\partial {x_i}}}} \right)}^2}\sigma _{xi}^2 + 2\sum\limits_{i = 1}^n {\sum\limits_{j = i + 1}^n {\frac{{\partial f}}{{\partial {x_i}}}\frac{{\partial f}}{{\partial {x_j}}}{\rho _{ij}}\sigma {x_i}\sigma {x_j}} } } } \end{array} \right. $ | (1) |
where ρij is a correlation coefficient. If the input variables are independent, the mean value and standard deviation of system output can be approximated as follows:
| $ \left\{ \begin{array}{l} {\mu _y} = f\left( {{\mu _{{x_1}}},{\mu _{{x_2}}}, \ldots ,{\mu _{{x_n}}}} \right)\\ {\sigma _y} = \sqrt {\sum\limits_{i = 1}^n {{{\left( {\frac{{\partial f}}{{\partial {x_i}}}} \right)}^2}\sigma _{{x_i}}^2} } \end{array} \right. $ | (2) |
The Taylor series expanding method has the following drawbacks: an increase of variance coefficient of the input random vectors would lead to the decrease of the evaluation accuracy due to its intrinsic local characteristic; the high order term and the vector X element of the correlation being taken into account, an increase in the order of expansion will lead to the difficulty of assessment increased; for complex simulation model to determine the partial derivative is difficult. However, the Taylor expand approximation method has been widely used by virtue of its relatively easy to understand and operational advantages.
2.4.3 Methods based on surrogate modelA surrogate model is an engineering method used when an outcome of interest cannot be easily directly measured, so a model of the outcome is used insteadly. The uncertainty analysis method based on the surrogate model is used as a replacement of the numerical simulation module in the system uncertainty analysis procedure. This method can effectively reduce the amount of calculation, and can filter the numerical noise produced by the original numerical simulation process. The deficiency lies in the calculation accuracy and computational efficiency being highly dependent on the construction of the surrogate model, and for different problems specific surrogate models are needed.
The surrogate model is commonly constructed by using the Kriging model, polynomial response surface method, radial basis function method, artificial neural network method, etc. The detailed construction ways have been described in Ref.[33]. When the surrogate model is constructed, it can be combined with the Monte Carlo method and the Taylor series expansion method to carry out the uncertainty propagation analysis. Chen et al.[34] combined the surrogate model method with the analytic method to derive the random distribution of the output results directly from the stochastic distribution function of the input parameters by the tensor product basis function.
3 Application of UMDO in Aircraft 3.1 UMDO ProcedureUncertainty-based multidisciplinary optimization process is a systematic approach that needs an overall consideration of UMDO, including organic optimization, multidisciplinary analysis, and uncertainty analysis, etc. The flow chart of UMDO is shown in Fig. 4.
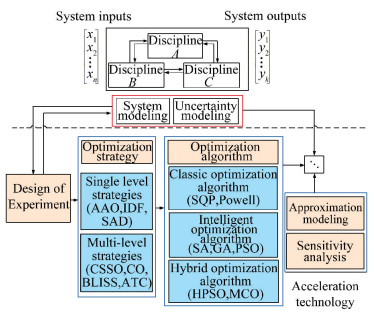
|
Figure 4 UMDO procedure |
UMDO process based on MDO optimization strategy can be divided into two categories, single-stage UMDO process and multi-level UMDO process. The single-level optimization strategy contains simultaneous analysis and design (SAD)[35], All-At-Once method (AAO), Individual Discipline Feasible method (IDF) and Multiple Discipline Feasible method (MDF)[36]. Common multi-level UMDO strategies include Concurrent Subspace Optimization (CSSO)[34, 37], Collaborative Optimization (CO)[38], Bi-Level Integrated System Synthesis (BLISS)[39] process as well as Analytical Target Cascading (ATC)[40], etc. UMDO mainly aims to handle combination of the uncertainty analysis and MDO procedure.
3.2 Uncertainty-Based Aeroelasticity OptimizationAt the beginning of the 20th century, with the development of the aviation field, the flight speed continued to improve, the aerodynamics-structure coupling problems began to emerge, then a new discipline, aeroelasticity, developed. Aeroelasticity is the branch of physics and engineering that studies the interaction between the inertial, elastic, and aerodynamic forces that occur when an elastic body is exposed to a fluid flow, which is divided into static elasticity and dynamic elasticity. Conventional aerodynamic elastic analysis usually treats the model as deterministic, however, there are various uncertainties in design, manufacturing, and other stages in design process that will directly affect the aero-elastic properties of the wing, and even affect the safety of flight. So in the field of aeroelasticity, the robustness and reliability of design are more and more important.
3.2.1 Uncertainty quantification in aeroelasticityAeroelasticity analysis is an important part of aero-structural multidisciplinary optimization of aircraft. In the traditional method, the deterministic mathematical model is used to analyze based on deterministic structural parameters and external loads. However, there are unavoidable uncertainties in the process of aeroelasticity modeling, calculation methods and engineering tests. These uncertainties may have some effects on the aerodynamic-elastic stability, the flight performance and flight safety of the aircraft, especially the accumulation of uncertainties may lead to serious safety hazards.
For different types of uncertainties in aeroelasticity problems, the quantitative analysis methods are mainly as follows: probabilistic analysis method, robust aeroelastic analysis method and evidence theory.
Probabilistic aeroelasticity analysis mainly studies the effect of random parameter uncertainties on the probability distribution. It requires the distribution of random parameters is already known or can be easily obtained. When the distribution of random variables is unknown or difficult to measure, evidence theory can be used to quantify the uncertainty which is commonly treated as epistemic uncertainty.
1) Random uncertainty analysis.
Millwater et al.[41] applied the probabilistic analysis method to the quantitative analysis of the uncertainty of the fighter aircraft wings and compared the results obtained by the traditional deterministic analysis method to illustrate the relative advantages. Pettit[42] used the Monte Carlo method to simulate the uncertainty of the nonlinear supersonic plate boundary conditions and elastic modulus, obtained the probability of fluttering of the plate after quantitative analysis, and studied the distribution of the bifurcation point of the limit ring. Heeg[43] combined the aeroelastic wind tunnel test with the probabilistic analysis method breaking through the traditional method of using the fitting curve and the deterministic calculation method to carry out the experimental data processing, considering the uncertainty of the variable and the experimental data to predict the distribution of the flutter boundary. Choi[44] used polynomial expansion and Latin hypercube sampling method to establish a set of analytical methods that can be used for efficient computing. It can be used for quantitative analysis of uncertainty and can analyze the key influencing factors and is validated to a large finite element wing model. MCS method is one of the probabilistic methods, which has been widely used in quantitative analysis of aerodynamic elasticity uncertainty. Li Yi and Yang Zhichun[45] studied the quantitative analysis of the elasticity uncertainties of the nonlinear binary wing based on the MCS method, discussed the influence of the uncertainty of the sinking and pitch stiffness on the flutter or limit ring oscillation, calculate the probability of system fluttering, and evaluate the risk. From the theoretical point of view, considering the aerodynamic and mass of the large aspect ratio wing to satisfy the uniform perturbation and the probability distribution is known, Dai et al.[46] quantified the flutter uncertainty quantitatively using the MCS method, and obtained the fluttering velocity distribution compared with the results of the robust aeroelastic analysis. Nikbay and Heeg[47] applied a statistic method to quantify the uncertainties of both structural and aerodynamic parameters, and implement reduced order modeling with Ploynomial Chaos Expansion and Proper Orthogonal Decomposition in uncertainty propagation to reduce the computation burden. Finally, Nikbay and Heeg gave the conclusion explaining the influence of the input distribution type on output result. Beran[48] used the First Order Reliability Method (FORM) and MSC method to compute the flutter probability of failure, and also quantified the uncertainty of Limit Cycle Oscillation (LCO) with considering the nonlinear random variables.
2) Epistemic uncertainty analysis.
Furthermore, some investigators have indicated that even small deviations among the distribution parameters may generate results with large deviations when performing a probabilistic reliability analysis. To handle the problem, the study of evidence theory has made a rapid development. After introduced by Zadeh[16], fuzzy set theory which is similar to possibility theory has built the foundation for solving some epistemic uncertainty problems. Wood et al.[49] applied fuzzy parameters to mathematical and theoretical structural design problems. However, it is still difficult to quantify the uncertainty analysis when facing more complex engineering problems. Dampster[50] proposed an uncertainty model method based on the interval theory instead of probability theory, and proposed a new idea for the quantitative analysis of epistemic uncertainty. On this basis, Zadeh[51] proposed evidence theory, also known as Dampster-Shafer theory which can deal with random uncertainties and epistemic uncertainties comprehensively while still possessing some limitations, such as the poor compatibility of different sources of evidence. On the basis of D-S theory, Yager[52] further developes the theory of evidence, proposed a new law of evidence combination, and applied it to quantitative analysis of uncertainty. To a certain extent, Yager law can solve the source of evidence or expert opinion of the conflict, but at the same time reduce the reliability of evidence.
At present, the discussion of using evidence theory to address the cognitive uncertainty quantitative analysis only remain the theoretical level, and its application in practical problem is still relatively small. Gogu et al.[53] discussed the applicability of the reliability and likelihood approximation methods to multidimensional functions and multi-output response problems, and considered their application in aircraft design. Riley[54] analyzed the uncertainties of the model itself. The model and the forecast uncertainty are introduced into the flutter analysis, and the DS theory is used to quantification analysis, the simulation process model selection and design guidance and reference.
Existing literature related to uncertainty-based multidisciplinary design optimization commonly considers only one type of uncertainty source while aircraft design optimization process is often faced with various sources of uncertainty. Only in the field of aeroelasticity, there exists shape uncertainty, load uncertainty, parameter uncertainty, to name a few. These uncertainty sources often cannot be quantified with only one theory, and need both probabilistic and non-probabilistic uncertainty modeling methods.
At present, optimization considering mixed sources of uncertainties has been a tendency. The key to handle mixed uncertainty-based multidisciplinary optimization of aircraft is to solve the problem of mixed uncertainty propagation in multidisciplinary analysis[55-56]. Du et al.[57] proposed a Unified Uncertainty Analysis Method (UUA) based on First Order Reliability Method (FORM), which computed output uncertainties when input uncertainties included stochastic uncertainties described with probability method and epistemic uncertainty described with evidence theory. Yao[58] improved the UUA method, and proposed a hybrid uncertainty analysis method SLO-FORM-UUA based on single-level optimization (SLO), which enhanced the computational efficiency of UUA method. On the basis of previous work, combined with the reliability index method (RIA) and the performance measurement method (PMA), the hybrid uncertainty propagation method of the chromatographic system is proposed. At present, the research on the mixed uncertainty-based multidisciplinary design optimization of aircraft is still at the initial stage. How to get the high-precision results effectively remains a problem.
3.2.2 Reliability aero-elastic design optimizationWith continuous development of reliability theory, researchers gradually realize that the traditional safety factor design optimization which considers the impact of uncertainty by ensuring a certain margin of safety is often conservative, and may damage itself within the period of lifecycle due to randomness of material parameters, load and geometric parameters, etc. Reliability-based design optimization get more attention. In contrast to the safety factor optimization, reliability-based design optimization adds the reliability index of aeroelastic system into constraints or objective functions of the optimization problem, namely under a certain reliability index, adjust the design variables to get optimized results. The mathematical description can be formulated as follows:
| $ \begin{array}{l} {\rm{Find}}\;\mathit{\boldsymbol{X}}\\ \min \;f\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;Pr\left\{ {\mathit{\boldsymbol{g}} \le 0} \right\} \le {\mathit{\boldsymbol{P}}_{f\_{\rm{con}}}} = 1- {\mathit{\boldsymbol{R}}_T}\\ \;\;\;\;\;\;\;\;{\mathit{\boldsymbol{Y}}_i} = C{A_i}({\mathit{\boldsymbol{X}}_i}, \mathit{\boldsymbol{Y}}{._i}, {\mathit{\boldsymbol{P}}_i}), i = 1, 2, \ldots, {N_D}\\ \;\;\;\;\;\;\;\;\mathit{\boldsymbol{X}} = \bigcup\limits_{i = 1, \ldots, {N_D}} {{\mathit{\boldsymbol{X}}_i}}, \mathit{\boldsymbol{P}} = \bigcup\limits_{i = 1, \ldots, {N_D}} {{\mathit{\boldsymbol{P}}_i}} \\ \;\;\;\;\;\;\;\;\mathit{\boldsymbol{Y}} = \bigcup\limits_{i = 1, \ldots, {N_D}} {{\mathit{\boldsymbol{Y}}_i}}, \;\mathit{\boldsymbol{Y}}{._i} \subseteq (\bigcup\limits_{j = 1, \ldots, {N_D}, j \ne i} {{\mathit{\boldsymbol{Y}}_j}} )\\ \;\;\;\;\;\;\;\;\mathit{\boldsymbol{X}} \in \left[{{\mathit{\boldsymbol{X}}^{\rm{L}}}, {\mathit{\boldsymbol{X}}^{\rm{U}}}} \right], f \in \mathit{\boldsymbol{Y}}, \mathit{\boldsymbol{g}} \subseteq \mathit{\boldsymbol{Y}} \end{array} $ | (3) |
where X is a design variable vector whose domain is [XL, XU], Xi is a local design variable vector of discipline i; Y is a system state variable vector, Yi is a local state variable vector of discipline i; Y·i is an input state variable vector of discipline CAi is the analysis model of discipline i; f and g are target function and constraint function of the system respectively.
1) Reliability analysis methods.
The reliability analysis method is a special method in the uncertainty analysis, which is used to calculate the reliability or failure probability whether the system response value would satisfy the constraints under the influence of uncertainty. The failure probability of the system can also be obtained by using the uncertainty modeling method introduced in Section 2.3, and there are also methods directly calculating the reliability, including First Order and Second Moment (FOSM), First Order Reliability Method (FORM), Second Order Reliability Method (SORM), among which FORM and SORM method are more commonly used. These two methods calculate the reliability index of the output by expanding the limit state function in the standard space into the first or second order form at the most probable point MPP (Most Probable Point) via three steps. Firstly, transform the initial non-Gaussian random variable vector of the problem into the Gaussian random variable vector in the standard normal space with zero mean value and unit variance by Rosenblatt transform. The failure probability can be obtained by the following integral formulation.
| $ {p_f} = \int\limits_{{D_u}} {\phi \left( \mathit{\boldsymbol{u}} \right){\rm{d}}\mathit{\boldsymbol{u}}} $ | (4) |
where ϕ(u) is the joint standard normal distribution probability density function, Du is the failure domain in the space U determined by the limit state function. Secondly, obtain the MPP by solving the optimization problem.
| $ \left\{ \begin{array}{l} \mathop {\min }\limits_u \left\| \mathit{\boldsymbol{u}} \right\|\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;G\left( \mathit{\boldsymbol{u}} \right) = 0 \end{array} \right. $ | (5) |
Thirdly, get the first or second order approximation of the limit state function at the MPP point, based on which calculate the approximate failure probability. The reliability of the system can be obtained by the following equation:
| $ R = 1-{p_f} $ | (6) |
The ways of all above methods to build up reliability functions is indirectly using performance parameters through a series of transformation based on the introduction of the concept of MPP. However, this optimization process may increase the computational burden leading to the reduction of computational efficiency and accuracy, especially when dealing with high dimension problems. In view of this, Li et al.[59] searched the aero-structural multidisciplinary design optimization of unmanned aerial vehicles, extended the concept of stress-strength interference theory in structural reliability, gave the description of "stress" and "strain", conducted the multi-variable reliability formulation, built the relationship between performance parameters of unmanned aerial vehicle and reliability function, achieved integrated design and optimization of reliability and performance, avoided the alternate of performance design and reliability design, and enhanced the efficiency. But the relationship between reliability and performance parameters is not versatile and only fits certain cases.
In recent years, researchers proposed a new method combining Bayesian inference and Markov Chain Monte Carlo to construct the post probability distribution[60]. This method can measure the reliability using probabilistic tools with rare uncertainty information. To author's knowledge, this new method has not been used in uncertainty-based aero-elastic design optimization. The research on the improvement and application of this method may attracts more scholars' attention, and further study on probabilistic method handling uncertainty-based design optimization with little prior information may be new research hotspots in the future.
2) Reliability optimization strategy.
The traditional method of solving the reliability of aero-elasticity optimization is the bilevel nested optimization. The reliability analysis is carried out at each search point to calculate the reliability of meeting the constraint, and compare the results with the target value to judge whether the feasibility requirement is satisfied. The advantage of the method is that the model is accurate while the calculation burden is increased also. To reduce the calculation consumption, researchers put forward a variety of acceleration technology which can be divided into two categories, one is to improve the uncertainty analysis method, the other is to improve the reliability of the expression of constraints. Koch et al.[61] proposed a multi-stage parallel optimization strategy based on probabilistic design optimization method improving the computational efficiency of reliability analysis. Zhang Junhong et al.[62] introduced the agent model technique to consider the stochastic uncertainty of material properties and execute the reliability design optimization of the composite plate wing model based on the response surface method. The method can reasonably balance the calculation accuracy and calculation burden and the correctness of the method is finally proved. Meanwhile, the author also discusses the method of aero-elasticity optimization based on interval uncertainty analysis. In the field of multidisciplinary reliability optimization design, some scholars have done this work. Fan et al.[63] proposed a parallel subspace design optimization method based on improved FOSM.
Reliability analysis and optimization procedure are coupled in bilevel nested optimization increasing the computational burden. Especially for aero-elastic problems, which two disciplines couple closely and discipline analysis is complex, computational burden can be hard to afford. Though various methods to improve the optimal efficiency have been studied, the improvement is limited because it's still a double-loop problem.
Later, there have been some new approaches to decompose the original nested optimization into sequential single level problem, in which Du and Chen[64] proposed the SORA (Sequential Optimization and Reliability Assessment) method is emphasized. The main idea of these methods is to decouple the uncertainty analysis from the outer iteration, decompose the UMDO problem into deterministic MDO and uncertainty analysis, and form a single-level problem. This can effectively avoid the cumbersome iterations of reliability analysis procedure and aero-elasticity multidisciplinary optimization, which greatly improves the efficiency to solve the problem. The kth optimization step is as follows. Firstly, the reliability constraint is transformed into the equivalent deterministic constraint according to the information obtained by the aero-elasticity uncertainty analysis in the previous cycle, and the uncertainty-based aero-elastic optimization problem is transformed into the following deterministic problem
| $ \begin{array}{l} \min \;f\left( {\mathit{\boldsymbol{d}}, {\mathit{\boldsymbol{\mu }}_x}, \;{\mathit{\boldsymbol{\mu }}_p}} \right)\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;{g_i}\left( {\mathit{\boldsymbol{d}}, {\mathit{\boldsymbol{\mu }}_x}-\mathit{\boldsymbol{s}}_i^{\left( {k + 1} \right)}, \mathit{\boldsymbol{p}}_{iMPP}^{\left( k \right)}} \right) \ge 0 \end{array} $ | (7) |
where i=1, 2, …, m. Secondly, after finishing deterministic aero-elastic optimization, the uncertainty analysis is employed to optimal program, gaining results to conduct the next deterministic aero-elastic optimization. Padmanabhan et al.[65] firstly adopted parallel subspace strategy to execute reliability-based optimization transforming probabilistic constraints to deterministic constraints by via limit state function. But the method would limit the moving range of design variables since the approximation is only of high accuracy in the place around MPP. Ouyang Qi et al.[66] studies the aero-elastic shear problem of composite wings under uncertain conditions using UMDO method. Firstly, establish the flutter model of the wing by Rayleigh method, and then model the uncertainty considering the material properties of the composite laminate with random uncertainty. The SPATC method is used to optimize the aeroelastic problem under stochastic uncertainties acquiring optimal scheme meeting the reliability requirement. Compared with the traditional nesting optimization, single-level sequential optimization can effectively improve the computational efficiency with maintaining the precision, which is combined with different optimization strategies to develop more optimization methods.
3) Nonprobability reliability-based optimization.
In recent years, with the development of interval mathematics, fuzzy mathematics and other non-probabilistic theories, many scholars have studied the non-probabilistic reliability. Ben-Haim[22] proposed the concept of non-probabilistic reliability based on convex set model, which measured reliability of structure through the max tolerance of uncertainty for structure when uncertainty information was limited.Supposing non-probabilistic reliability belonging to an interval other than being a specific value, Elishakoff[67] also proposed a reliability measure method calculating the boundary of reliability index using interval mathematics based on safety factor. Guo et al.[28] described the uncertain parameters of the structure as interval variables, and proposed a non-probabilistic reliability measure system and analysis method to measure the safety and reliability of the structure via the shortest distance z from the coordinate origin to the failure surface. Tang et al.[69] proposed a new approach for solving design optimization problems of structures involving fuzzy variables.
The finite element model of a vehicle side impact is considered of which details can be found in the Ref.[69]. Thinking about the effect of the fuzzy variables, design optimization for the vehicle side impact can be defined by:
| $ \begin{array}{l} {\rm{Find}}\;\mathit{\boldsymbol{x}}\\ \min \;\mu \left( \mathit{\boldsymbol{x}} \right)\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\mathit{Pr}\left\{ {{g_i}\left( {\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{F}}} \right) \le {c_i}} \right\} \ge {R_{Ti}}\\ \;\;\;\;\;\;{\mathit{\boldsymbol{x}}^l} \le \mathit{\boldsymbol{x}} \le {\mathit{\boldsymbol{x}}^u} \end{array} $ | (8) |
where πfi(x) and πfimax are the possibility safety index and the allowable The result in Table 1 shows that the objective function increases when the allowable PSI πfmax reduces from 0.1 to 0.01. Note that the materials (i.e. x8 and x9) of the critical parts chosen are the high-strength steel. As revealed by table, all the constraints except the seventh one are not violated when the iteration is stopped. Although the seventh constraint is violated a little, it is very close to zero. Thus, the obtained result can be regarded as feasible one.
| Table 1 Design variables and uncertain fuzzy variables for the vehicle side impact |
Zhang Lei, Qiu Zhiping et al.[70] introduced the non-probabilistic reliability index into the aero-structural multidisciplinary optimization design of the aircraft. The uncertainty of output variables influenced by uncertain input variables was determined by the uncertainty analysis employed in the system level, and the coherence of the coupling variables between the disciplines is also coordinated. An aeroelastic multidisciplinary optimization of wing is given to prove the effectiveness of the method. Consider the stochastic uncertainty of the parameters, Zhang Junhong et al.[62] used the Kriging method to establish the agent model. Based on the response surface method, the aero-elastic system of the wing is optimized. The method can effectively solve the problem of wing flutter optimization which is hard to optimize globally due to large calculation.
3.2.3 Robust aero-elastic design optimizationIn the process of optimization, the target function may change greatly leading to optimal results deviating from the design target due to the existence of uncertainty. Meanwhile, the change of the uncertainty parameter will directly result in the change of the hard constraint (such as the strength index, the static aero-elasticity strength index and so on), causing the failure of the structure. In engineering, this situation is very harmful, especially in the aero-elastic design optimization, the violation of rigid constraints such as flutter constraints will lead to catastrophic consequences. One way to avoid this situation is to reduce the number of uncertain design parameters, which may increase the manufacturing costs. The other way is considering the uncertain design parameters at the beginning of the design and seeking the robust optimal result of the structure when the cost is not significant.
1) Robust aeroelastic analysis.
The development of robust control theory has experienced several stages including small gain theorem, μ method, H∞ theory and Kharitonov interval theory, among which the μ method and H ∞ theory have been widely used in the field of aeroelasticity. The μ method can consider the influence of the structural parameter uncertainty on the robust stability of the system, and has become the focus of aeroelasticity analysis with non-random parameters at home and abroad. Initially, the concept of "μ" was proposed by Doyle[71], he transformed the stability analysis, the performance analysis and the control law design in the uncertainty problem into the computational problem of μ establishing the basis of μ method in the robust aeroelastic analysis. Rick Lind[72] introduced the μ method into the field of aeroelasticity, and elaborated on the uncertainty modeling of the frequency, damping perturbation in the elastic structure and the aerodynamic derivative in the frequency domain. The method is applied to the stability margin analysis of F / A18 testing machine. The comparison between the theoretical analysis and the experimental results shows that the method can improve the prediction accuracy of the flutter boundary to a certain extent. Considering various physical parametric and nonparametric perturbations, Wu[73] carried out uncertainty modeling and analyzed the robust stability of system via the LFT form.
2) Robust aeroelastic optimization.
The robust stability design point is insensitive to the uncertainty of the design parameters and can maintain good performance under the uncertain parameter perturbation. Robustness optimization means finding the design point which is not sensitive to the perturbation of the parameter as well as of the highest performance function value satisfying the constraint condition. The definition of a general robust optimization problem is expressed as follows:
| $ \begin{array}{l} {\rm{Given:}}\;{\mathit{\boldsymbol{p}}_d}, {\mathit{\boldsymbol{p}}_p}\\ {\rm{Find:}}\;{\mathit{\boldsymbol{x}}_d}, {\mathit{\boldsymbol{\mu }}_x}_p\\ {\rm{Target:}}\;{\mu _f}, {\sigma _f}\\ {\rm{s}}{\rm{.t}}{\rm{.:}}\;{C_{j1}} + {n_{j1}}{\sigma _{{C_j}}} \le {\mu _{{C_j}}} \le {C_{ju}}-{n_{ju}}{\sigma _{{C_j}}}, j = 1, 2 \ldots, J\\ \;\;\;\;\;\;{\mathit{\boldsymbol{x}}_{{\rm{dl}}}} \le {\mathit{\boldsymbol{x}}_{\rm{d}}} \le {\mathit{\boldsymbol{x}}_{{\rm{du}}}}\\ \;\;\;\;\;\;{\mathit{\boldsymbol{x}}_{{\rm{pl}}}} + n{\sigma _x}_{_{\rm{p}}} \le {\mu _x}_{_{\rm{p}}} \le {\mathit{\boldsymbol{x}}_{{\rm{pu}}}}-n{\sigma _x}_{\rm{p}} \end{array} $ | (9) |
where pd and pp represent the deterministic and uncertain design parameters respectively, xd and xp represent deterministic and uncertain design variables respectively, μf and σf are the mean value and variance of the target. xdl and xdu are the boundary of deterministic design variables while xpl and xpu are the boundary of the random design variables. Cj is the jth constraint function. As we can see, robust optimization is a multi-objective problem which needs a comprehensive consideration on optimization of μf as well as σf.
A robust design optimization of a two-dimensional airfoil with deformable trailing edge is as follows, of which details can be found in Ref. [74].
From Table 2, we can see the mean value of lift to drag ratio of the robust optimization airfoil is higher than which of the deterministic optimization. And the standard deviation of lift to drag ratio of the robust optimization airfoil is lower than which of the deterministic optimization. Meanwhile, the demand for drive energy of robust optimization is lower compared to deterministic optimization. Therefore, the robust optimization result has a comprehensively better performance than the deterministic result. Fig. 5 shows that the lift to drag ratio of robust optimization changes more slowly and the aerodynamic performance is more stable compared to deterministic optimization.
| Table 2 Comparison between deterministic optimization and robust optimization |

|
Figure 5 UMDO procedure |
In Table 2, xm/c represents the starting position of the chord direction of the rear edge deformation, and Δzte represents the deformation distance of the rear edge points, μ(K) and σ(K) are mean and standard deviation of lift to drag ratio respectively, ΔE/J represents the drive energy of the airfoil.
In the Ref.[75], there is a comparison between probabilistic and non-probabilistic methods based on this question. And the result shows that probabilistic and non-probabilistic methods would obtain the same result aiming at this problem. Furthermore, Du Ziliang et al.[76] conducted a robust aeroelastic optimization design on a typical hypersonic low-aspect-ratio wing and used an interval analysis method to handle uncertainties existing in heat flux. Pan et al.[77] adopted interval numbers to describe the uncertain input and develop a robust optimization strategy to deal with the aerodynamic optimization issue, which did not need a large sum of information on the uncertainty of input parameters.
Studies on aero-structural robust design of the aircraft have been carried out early. In 1998, the Multidisciplinary Design Optimization Branch of NASA Langley Research Center began to seriously consider the aerodynamic optimization of the aircraft under various uncertainties, tentatively applying robust optimization to transonic airfoil design. The results show that if the flight velocity is regarded as a random parameter in M0.7-M0.8, the lift-drag ratio of the airfoil obtained by the robust optimization method is much better than the deterministic optimization method throughout the whole speed range. Therefore, robust multi-disciplinary design optimization began to be applied to aircraft design.
3.3 Uncertainty-Based Design Optimization of Other Coupled DisciplinesMultidisciplinary design optimization methods are mainly applied to the aero-structural optimization at the beginning. With the development of modern aircraft, the requirements for performance of aircraft are increasing constantly. The disciplines concerned in multidisciplinary optimization are gradually expanding to heat, sound, stealth, etc. In aerodynamics/structure/thermal multidisciplinary design optimization, there develops an integrated numerical simulation method. Because the present method is difficult to solve, a strategy of partition optimization is proposed. In the study of the impact of uncertainty, researches about the impacts on reheating corridor of uncertainties existing in the surface of the aerodynamic heating and material properties are studied in U.S. using one-dimension heat transfer analysis model.
Allison et al.[78] established a multidisciplinary design optimization framework for supersonic aircraft, in which a number of disciplines such as aerodynamics, structure, stealth, and propulsion were considered. Lee et al.[79] optimized the airfoil to enhance the aerodynamic performance and reduce the radar scattering area using a robust evolutionary algorithm. But only the airfoil rather than the whole wing is concerned in the paper. There are also many researchers who began to consider the stealth discipline in the UAV multi-disciplinary design optimization. Hu et al.[80] performed an aerodynamics/stealth multidiscipline integrated design optimization on a UAV regarding the discipline of structure as another sub-problem, and executed system level optimization to realize the target of the Lift-to-drag ratio largest as well as the weight lightest. For aerodynamics/stealth coupled disciplines, Long et al.[81] used the multi-objective design method to optimize the High-Altitude Long Endurance (HALE) unmanned aerial vehicle. Wang Xiaojun et al.[82] proposed a robust optimization method of structural-acoustic coupled systems with random parameters based on the traditional optimization method.
According to the current literature, the optimization of these disciplines is still in the infancy. Researches considering the discipline of heat, stealth and other disciplines concentrate more on the coupled discipline analysis rather than the multidiscipline optimization, not to mention introducing the uncertainty into the optimization process. In the future, considering the uncertainty of heat, stealth, structure, propulsion to name a few comprehensively in multidisciplinary optimization would be of great value to research.
4 ConclusionsThis paper reviews the uncertainty of aircraft uncertainty-based aero-structural optimization from the aspects of uncertainty definition, source, modeling, and UMDO process and its applications in the field of aero-structural optimization, and emphasis on the comparison of probabilistic and non-probabilistic method dealing with uncertainties. Although UMDO has been developing for many years, there are still some challenges at this stage, and some of the possible future directions for UMDO are given below.
1) Efficient and reasonable multidisciplinary optimization algorithm needs to be developed.
The multidisciplinary optimization of aircraft involves complex disciplines and large calculation requires better optimization algorithms. Traditional optimization algorithms such as gradient method are more mature while also easy to fall into local convergence without gaining the optimal solution. Some of the intelligent algorithms, such as genetic algorithms, can theoretically obtain the global optimal solution with large computational burden and difficulties to converge because the optimization direction is random. The global optimization algorithm with efficiency and precision will continue to be a hotspot in the multidisciplinary design optimization of the aircraft.
2) The multi-disciplinary robust design optimization is an important aspect of applications for uncertainty in aerospace vehicles design optimization.
Compared with the traditional design, the result of robust design usually possesses better stability and anti-interference. To some extent, the stability of the system is more important than the optimization of the results, especially for the design of the aircraft. Therefore, the concept of robust design optimization is introduced into the field of multi-disciplinary optimization of aircraft. How to establish the multi-disciplinary robust design model of aircraft, and differ from the traditional optimization design and reliability optimization design model are also the development direction of aircraft uncertainty design optimization.
3) Uncertainty-based multidisciplinary design optimization of fare events needs to be developed.
In the practical engineering, problems lacking of prior information of uncertainty is common. The traditional probabilistic uncertainty method requires large amount of information samples and is not suitable in this case. Thus, it is necessary to develop an uncertain multidisciplinary optimization method which can conduct uncertainty measurement of rare events. The non-probabilistic uncertainty method can solve this problem to a certain extent, thus has been greatly developed in recent years. Meanwhile, a new probabilistic uncertainty method combing Bayesian inference and Monte Carlo Markov chain is developed. After proposed, the method gradually attracted scholars' attention for its ability to measure uncertainty with little prior information. Combining with probabilistic method, developing methods for uncertainty-based multidisciplinary of fare information may be a research hotspots in the future.
4) Heat, sound, stealth and other kind of coupled-discipline optimization is further developed.
Most of the existing literatures mainly focus on the optimization of aerodynamic/structure multidisciplinary design, whose coupled disciplines are limited. With the continuous development of hypersonic vehicles and improvement of the requirements on stealth performance, the aircraft design needs consideration of the impact of more coupled disciplines. Discussing the uncertainty quantitative analysis among these disciplines and constructing an efficient and reasonable optimization model need further research in the future.
| [1] |
Yao W, Chen X Q, Luo W C, et al. Review of uncertainty-based multidisciplinary design optimization methods for aerospace vehicles. Progress in Aerospace Sciences, 2011, 47(6): 450-479. DOI:10.1016/j.paerosci.2011.05.001 ( 0) 0)
|
| [2] |
Witkowski W R, Allen J. Approximation of parameter uncertainty in nonlinear optimization-based parameter estimation schemes. AIAA Journal, 2015, 31(5): 947-950. DOI:10.2514/3.11709 ( 0) 0)
|
| [3] |
Ng Leo W T, Willcox K E. Monte Carlo information-reuse approach to aircraft conceptual design optimization under uncertainty. Journal of Aircraft, 2015, 1(1): 1-12. DOI:10.2514/1.C033352 ( 0) 0)
|
| [4] |
Cook L W, Jarrett J P. Robust airfoil optimization and the importance of appropriately representing uncertainty. AIAA Journal, 2017, 55(11): 3925-3939. DOI:10.2514/1.J055459 ( 0) 0)
|
| [5] |
Loch C H, Terwiesch C. Communication and uncertainty in concurrent engineering. Management Science, 1998, 44(8): 1032-1048. DOI:10.1287/mnsc.44.8.1032 ( 0) 0)
|
| [6] |
DeLaurentis D A, Mavris D N. Uncertainty modeling and management in multidisciplinary analysis and synthesis. Proceedings of the 38th Aerospace Sciences Meeting and Exhibit, Aerospace Sciences Meetings. AIAA, 2000, 5(21): 2000-2422. DOI: 10.2514/6.2000-422.
( 0) 0)
|
| [7] |
Yang J S, Nikolaidis E, Yang J S, et al. Design of aircraft wings subjected to gust loads-a safety index based approach. AIAA Journal, 1991, 29(5): 804-812. DOI:10.2514/3.10660 ( 0) 0)
|
| [8] |
Jacoboni C, Lugli P. The Monte Carlo Method for Semiconductor Device Simulation. Springer-Verlag, 1989. DOI: 10.1049/ic:19950428.
( 0) 0)
|
| [9] |
Qu X, Haftka R T. Reliability-based design optimization using probabilistic sufficiency factor. Structural & Multidisciplinary Optimization, 2004, 27(5): 314-325. DOI:10.1007/s00158-004-0390-3 ( 0) 0)
|
| [10] |
Kuiken J V, Yu B, Telford D. Managing uncertainty in reliability analysis with Bayesian inference and uncertainty propagation, U. S. Air Force T & E Days 2010, U. S. Air Force T & E Days Conferences. Nashville, 2013. DOI: 10.2514/6.2010-1762.
( 0) 0)
|
| [11] |
Oberkampf W L, Helton J C, Joslyn C A, et al. Challenge problems: uncertainty in system response given uncertain parameters. Reliability Engineering & System Safety, 2004, 85(1-3): 11-19. DOI:10.1016/j.ress.2004.03.002 ( 0) 0)
|
| [12] |
Wang P, Youn B D, Xi Z, et al. Bayesian reliability analysis with evolving, insufficient, and subjective data sets. Journal of Mechanical Design, 2009, 131(11): 259-272. DOI:10.1115/1.4000251 ( 0) 0)
|
| [13] |
Sentz K, Ferson S. Combination of evidence in Dempster-Shafer theory. Contemporary Pacific, 2002, 11: 416-426. DOI:10.2172/800792 ( 0) 0)
|
| [14] |
Tao Y R, Cao L, Cheng G Q, et al. Safety analysis of structures with probability and evidence theory. International Journal of Steel Structures, 2016, 16(2): 289-298. DOI:10.1007/s13296-016-6003-3 ( 0) 0)
|
| [15] |
Braibant V, Oudshoorn A, Boyer C, et al. Non-deterministic 'possibilistic' approaches for structural analysis and optimal design - A comparison of numerical methods for computing structural response uncertainties. 7th AIAA Symposium on Multidisciplinary Analysis and Optimization. AIAA, 2013. DOI: 10.2514/6.1998-4750.
( 0) 0)
|
| [16] |
Zadeh L A. Fuzzy sets. Information and Control, 1965, 8(3): 338-353. DOI:10.1016/S0019-9958(65)90241-X ( 0) 0)
|
| [17] |
Zadeh L A. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets & Systems, 1978, 1(1): 3-28. DOI:10.1016/0165-0114(78)90029-5 ( 0) 0)
|
| [18] |
Hansen E. An overview of global optimization using interval analysis. Reliability in Computing, 1988, 289-307. DOI:10.1016/B978-0-12-505630-4.50021-3 ( 0) 0)
|
| [19] |
Wang Xiaojun, Wang Ruixing, Chen Xianjia, et al. Interval prediction of responses for uncertain multidisciplinary system. Structural & Multidisciplinary Optimization, 2017, 55(6): 1945-1964. DOI:10.1007/s00158-016-1601-4 ( 0) 0)
|
| [20] |
Wang Lei, Xiong Chuang, Wang Ruixing, et al. A novel method of Newton iteration-based interval analysis for multidisciplinary systems. Science China Physics Mechanics & Astronomy, 2017, 60(9): 094611. DOI:10.1007/s11433-017-9068-5 ( 0) 0)
|
| [21] |
Qiu Zhiping, Wang Xiaojun, Li Zhi. Post-buckling analysis of a thin stiffened plate with uncertain initial deflection via interval analysis. International Journal of Non-Linear Mechanics, 2009, 44(10): 1031-1038. DOI:10.1016/j.ijnonlinmec.2009.08.001 ( 0) 0)
|
| [22] |
Ben-Haim Y, Elishakoff I. Convex Models of Uncertainty in Applied Mechanics. Elsevier, 1990. ( 0) 0)
|
| [23] |
Jiang C, Han X, Lu G Y, et al. Correlation analysis of non-probabilistic convex model and corresponding structural reliability technique. Computer Methods in Applied Mechanics & Engineering, 2011, 200(33-36): 2528-2546. DOI:10.1016/j.cma.2011.04.007 ( 0) 0)
|
| [24] |
Qiu Zhiping, Ma Lihong, Wang Xiaojun. Ellipsoidal-bound convex model for the non-linear buckling of a column with uncertain initial imperfection. International Journal of Non-Linear Mechanics, 2006, 41(8): 919-925. DOI:10.1016/j.ijnonlinmec.2006.07.001 ( 0) 0)
|
| [25] |
Ryan R S, Townsend J S. Application of probabilistic analysis and design methods in space programs. Journal of Spacecraft & Rockets, 1994, 31(6): 1038-1043. DOI:10.2514/3.26555 ( 0) 0)
|
| [26] |
Walley P. Towards a unified theory of imprecise probability. International Journal of Approximate Reasoning, 2000, 24(2-3): 125-148. DOI:10.1016/S0888-613X(00)00031-1 ( 0) 0)
|
| [27] |
Sepulveda A E. Structural synthesis with reliability constraints using approximation concepts. AIAA Journal, 2015, 34(8): 1641-1643. DOI:10.2514/3.13283 ( 0) 0)
|
| [28] |
Guo Shuiang, Lu Zhenzhou. Comparision between the non-probabilistic and probabilistic reliability methods for uncertain structure design. Chinese Journal of Applied Mechanics, 2003, 20(3): 107-110. ( 0) 0)
|
| [29] |
Yao Wen, Chen Xiaoqian, Zhao Yong. Research on satellite system design based on uncertainty multidisciplinary design optimization. Journal of Astronautics, 2009, 30(5): 1808-1815. DOI:10.3873/j.issn.1000-1328.2009.05.011 ( 0) 0)
|
| [30] |
Ang G, Ang A H S L, Tang W H. Optimal importance-sampling density function. Journal of Engineering Mechanics, 1992. ( 0) 0)
|
| [31] |
Du X, Chen W. Towards a better understanding of modeling feasibility robustness in engineering design. Journal of Mechanical Design, 2000, 122(4): 385-394. DOI:10.1115/1.1290247 ( 0) 0)
|
| [32] |
Ye K Q, Li W, Sudjianto A. Algorithmic construction of optimal symmetric Latin hypercube designs. Journal of Statistical Planning & Inference, 2000, 90(1): 145-159. DOI:10.1016/S0378-3758(00)00105-1 ( 0) 0)
|
| [33] |
Forrester A I J, Keane A J. Recent advances in surrogate-based optimization. Progress in Aerospace Sciences, 2009, 45(1-3): 50-79. DOI:10.1016/j.paerosci.2008.11.001 ( 0) 0)
|
| [34] |
Chen W, Jin R. Analytical variance-based global sensitivity analysis in simulation-based design under uncertainty. Journal of Mechanical Design, 2016, 127(5): 953-962. DOI:10.1115/1.1904642 ( 0) 0)
|
| [35] |
Haftka R T. Simultaneous analysis and design. AIAA Journal, 1985, 23(7): 1099-1103. DOI:10.2514/3.9043 ( 0) 0)
|
| [36] |
Allison J T. Complex system optimization: A review of analytical target cascading, Collaborative Optimization, and Other Formulations. Michigan: The University of Michigan, 2004.
( 0) 0)
|
| [37] |
Sobieszczanski-sobieski J. Optimization by decomposition: A step from hierarchic to non-hierarchic systems. Proceedings of NASA/air Force Symposium on Recent Advances in Multidisciplinary Analysis & Optimization Nasa Cp, 1988. 89.
( 0) 0)
|
| [38] |
Kroo I, Altus S, Braun R, et al. Multidisciplinary optimization methods for aircraft preliminary design. Proceedings of AIAA Symposium on Multidisciplinary Analysis Ama Fl AIAA. AIAA, 1994. AIAA-94-4325-CP. DOI: 10.2514/6.1994-4325.
( 0) 0)
|
| [39] |
Sobieszczanski J, Agte J S, Sandusky J R R. Bi-Level Integrated System Synthesis. NASA Langley Technical Report Server. Washington: NASA, 1998.
( 0) 0)
|
| [40] |
Kim H M, Rideout G, Papalambros P Y, et al. Analytical target cascading in automotive vehicle design. Journal of Mechanical Design, 2003, 125(5): 481-489. DOI:10.1115/1.1586308 ( 0) 0)
|
| [41] |
Millwater H, Singh G. Development of a localized probabilistic sensitivity method to determine random variable regional importance. Reliability Engineering & System Safety, 2012, 107: 3-15. DOI:10.1016/j.ress.2011.04.003 ( 0) 0)
|
| [42] |
Beran P S, Pettit C L. A direct method for quantifying limit-cycle oscillation response characteristics in the presence of uncertainties. 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, Structures, Structural Dynamics, and Materials and Co-located Conferences. 2004. AIAA 2004-1695. DOI: 10.2514/6.2004-1695.
( 0) 0)
|
| [43] |
Heeg J, Gilbert M G, Pototzky A S. Active control of aerothermoelastic effects for a conceptual hypersonic aircraft. Journal of Aircraft, 1990, 30(4): 453-458. DOI:10.2514/3.56890 ( 0) 0)
|
| [44] |
Choi S-K, Grandhi R V, Canfield R A, et al. Polynomial chaos expansion with Latin hypercube sampling for estimating response variability. AIAA Journal, 2004, 42(6): 1191-1198. DOI:10.2514/1.2220 ( 0) 0)
|
| [45] |
Li Yi, Yang Zhichun. Exploring wing flutter risk assessment with parametric uncertainty. Journal of Northwestern Polytechnical University, 2010, 28(3): 458-463. ( 0) 0)
|
| [46] |
Dai Y, Wu Z, Yang C. Quantification analysis of uncertain flutter risks. Acta Aeronautica et Astronautica Sinica, 2010, 31(9): 1788-1795. ( 0) 0)
|
| [47] |
Nikbay M, Heeg J. Aeroelastic uncertainty quantification studies using the S4T wind tunnel model. 55th AIAA Aerospace Sciences Meeting. Washington: AIAA, 2017. AIAA 2017-1652. DOI: 10.2514/6.2017-1652.
( 0) 0)
|
| [48] |
Beran P, Stanford B, Schrock C. Uncertainty quantification in aeroelasticity. Annual Review of Fluid Mechanics, 2017, 49(1): 361-386. DOI:10.1146/annurev-fluid-122414-034441 ( 0) 0)
|
| [49] |
Wood K L, Otto K N, Antonsson E K. Engineering design calculations with fuzzy parameters. Fuzzy Sets & Systems, 1992, 52(1): 1-20. DOI:10.1016/0165-0114(92)90031-X ( 0) 0)
|
| [50] |
Dempster A P. Upper and lower probabilities induced by a multivalued mapping. Annals of Mathematical Statistics, 2008, 38(2): 325-339. ( 0) 0)
|
| [51] |
Zadeh L A. Review of a mathematical theory of evidence. Ai Magazine, 1984, 5(3): 235-247. ( 0) 0)
|
| [52] |
Yager R R, Kacprzyk J, Fedrizzi M. Advances in the Dempster-Shafer Theory of Evidence. New York, NY: John Wiley & Sons, Inc., 1994.
( 0) 0)
|
| [53] |
Gogu C, Haftka R T, Bapanapalli S K, et al. Dimensionality reduction approach for response surface approximations: Application to thermal design. AIAA Journal, 2009, 47(7): 1700-1708. DOI:10.2514/1.41414 ( 0) 0)
|
| [54] |
Riley M, Grandhi R, Kolonay R. Quantification of modeling uncertainty in aeroelastic design. AIAA Structures, Structural Dynamics, and Materials Conference AIAA Adaptive Structures Conference. Washington: AIAA, 2010. AIAA 2010-2679. DOI: 10.2514/6.2010-2679.
( 0) 0)
|
| [55] |
Shah H R, Hosder S, Leifsson L T, et al. Multi-fidelity robust aerodynamic design optimization under mixed uncertainty. 17th AIAA Non-Deterministic Approaches Conference. Washington: AIAA, 2015. AIAA 2019-0917. DOI: 10.2514/6.2015-0917.
( 0) 0)
|
| [56] |
Liu C W, Li L S, Qian L F. Sequential multidisciplinary reliability design and optimization based on approximate sensitivity method under random and interval uncertainties. Journal of Mechanical Engineering, 2015, 51(21): 174-184. DOI:10.3901/JME.2015.21.174 ( 0) 0)
|
| [57] |
Du X P. Unified uncertainty analysis by the first order reliability method. Journal of Mechanical Design, 2008, 130(9): 1404-1404. DOI:10.1115/1.2943295 ( 0) 0)
|
| [58] |
Yao W, Chen X Q, Huang Y Y, et al. An enhanced unified uncertainty analysis approach based on first order reliability method with single-level optimization. Reliability Engineering & System Safety, 2013, 116: 28-37. DOI:10.1016/j.ress.2013.02.014 ( 0) 0)
|
| [59] |
Li Man, Song Bifeng, Xia Qing. Integrated design reliability and performance of UAV based uncertainty. Journal of Northwestern Polytechnical University, 2017(1): 1-6. DOI:10.3969/j.issn.1000-2758.2017.01.001 ( 0) 0)
|
| [60] |
Hadjidoukas P E, Angelikopoulos P, Papadimitriou C, et al. π4U: A high performance computing framework for Bayesian uncertainty quantification of complex models. Journal of Computational Physics, 2015, 284: 1-21. DOI:10.1016/j.jcp.2014.12.006 ( 0) 0)
|
| [61] |
Koch P, Wujek B, Golovidov O. A multi-stage, parallel implementation of probabilistic design optimization in an MDO framework. 8th Symposium on Multidisciplinary Analysis and Optimization, Multidisciplinary Analysis Optimization Conferences. Washington: AIAA, 2000. AIAA-2000-4805. DOI: 10.2514/6.2000-4805.
( 0) 0)
|
| [62] |
Zhang Junhong, Han Jinglong, Wang Xiaoqing. Flutter optimization of wing structure with random uncertainty. Acta Aeronautica et Astronautica Sinica, 2011, 32(9): 1629-1636. ( 0) 0)
|
| [63] |
Fan Hui, Li Weiji. An efficient method for reliability-based multidisciplinary design optimization. Chinese Journal of Aeronautics, 2008, 21(4): 51-56. ( 0) 0)
|
| [64] |
Du X P, Chen W. Sequential optimization and reliability assessment method for efficient probabilistic design. Journal of Mechanical Design, 2004, 126(2): 871-880. DOI:10.1115/DETC2002/DAC-34127 ( 0) 0)
|
| [65] |
Deb K, Padmanabhan D, Gupta S, et al. Reliability-based multi-objective optimization using evolutionary algorithms. International Conference on Evolutionary Multi-Criterion Optimization, 2007, 2(3): 66-80. DOI:10.1007/978-3-540-70928-2_9 ( 0) 0)
|
| [66] |
Qi Ouyang. Research on the key technologies and applications of uncertainty-based multidisciplinary design optimization for flight vehicles. Changsha: National University of Defense Technology, 2013.
( 0) 0)
|
| [67] |
Elishakoff I. Safety Factors and Reliability: Friends or Foes. Berlin: Springer Netherlands, 2004. DOI:10.1007/978-1-4020-2131-2
( 0) 0)
|
| [68] |
Guo Shuxiang, Lu Zhenzhou, Feng Yuansheng. A non-probabilistic model of structural reliability based on interval analysis. Chinese Journal Of Computational Mechanics, 2001, 18(5): 56-60. ( 0) 0)
|
| [69] |
Tang Z C, Lu Z Z, Hu J X. An efficient approach for design optimization of structures involving fuzzy variables. Fuzzy Sets & Systems, 2014, 255: 52-73. DOI:10.1016/j.fss.2014.05.017 ( 0) 0)
|
| [70] |
Zhang Lei, Qiu Zhiping. Multidisciplinary non-probabilistic reliability optimization based on collaborative optimization method. Journal of Nanjing University of Aeronautics & Astronautics, 2010, 42(3): 267-271. ( 0) 0)
|
| [71] |
Zhou K, Doyle J C. Essentials of Robust Control. Englewood: Prentice Hall, 1998.
( 0) 0)
|
| [72] |
Rick Lind M, Brenner M. Robust Aeroservoelastic Stability Analysis. London: Springer London, 1999.
( 0) 0)
|
| [73] |
Dong K, Wu F. Robust and gain-scheduling control of LFT systems through duality and conjugate Lyapunov functions. International Journal of Control, 2007, 80(4): 555-568. DOI:10.1080/00207170601080213 ( 0) 0)
|
| [74] |
Zheng Yuning, Qiu Zhiping, Huang Ren, et al. Robust design optimization of a two-dimensional airfoil with deformable trailing edge. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(5): 897-903. DOI:10.13700/j.bh.1001-5965.2014.0387 ( 0) 0)
|
| [75] |
Guo Shuxiang, Lv Zhenzhou. Comparison between the non-probabilistic and probabilistic reliability methods for uncertain structure design. Chinese Journal of Applied Mechanics, 2003, 20(3): 107-110. ( 0) 0)
|
| [76] |
Du Ziliang, Wan Z Q, Yang C. Robust aeroelastic design optimization of hypersonic wings considering uncertainty in heat flux. Transactions of the Japan Society for Aeronautical & Space Sciences, 2017, 60(3): 152-163. DOI:10.2322/tjsass.60.152 ( 0) 0)
|
| [77] |
Pan Y L, Huang J, Li F, et al. Aerodynamic robust optimization of flying wing aircraft based on interval method. Aircraft Engineering & Aerospace Technology, 2017, 89(3): 491-497. DOI:10.1108/AEAT-09-2016-0145 ( 0) 0)
|
| [78] |
Allison D, Morris C, Schetz J, et al. A multidisciplinary design optimization framework for design studies of an efficient supersonic air vehicle. AIAA Aviation Technology, Integration, and Operations. Washington: AIAA, 2013. AIAA 2012-5492. DOI: 10.2514/6.2012-5492.
( 0) 0)
|
| [79] |
Lee Sik-Yum, Shi JianQing. Bayesian analysis of structural equation model with fixed covariates. Structural Equation Modeling A Multidisciplinary Journal, 2000, 7(3): 411-430. DOI:10.1207/S15328007SEM0703_3 ( 0) 0)
|
| [80] |
Hu Tianyuan, Yu Xiongqing. Aerodynamic/stealthy/ structural multidisciplinary design optimization of unmanned combat air vehicle. Chinese Journal of Aeronautics, 2009, 22(4): 380-386. DOI:10.1016/S1000-9361(08)60114-4 ( 0) 0)
|
| [81] |
Long Teng, Li Xueliang, Huang Bo, et al. Aerodynamic and stealthy performance optimization of airfoil based on adaptive surrogate model. Journal of Mechanical Engineering, 2016, 52(22): 101-111. DOI:10.3901/JME.2016.22.101 ( 0) 0)
|
| [82] |
Wang Xiaojun, Li Yunlong, Ma Zhiliang, et al. Robust optimization of structural-acoustic coupled system with random parameters. Aerospace Science & Technology, 2016, 60(5): 48-57. DOI:10.1016/j.ast.2016.10.030 ( 0) 0)
|
 2018, Vol. 25
2018, Vol. 25


