Complex network field has made great progress in recent years, in which the nodes denote individuals of network and the part of connection is called as the edges. In general, the dynamical systems are abstracted as nodes, which interacts to constitute a complex network[1]. At present, scientists in different fields have researched on complex networks from physical to biological and social sciences[2-4].
Complex network model can explain some complex phenomena, for example, power grid[5] metabolic networks[6], gene networks[7], and so on. Synchronization is vital in complex networks, and it has raised the concern of many academic researchers since it has a significant impact on many field, such as, in the field of secure communication, information science and biological systems. Many varieties of synchronizations including complex complete synchronization[8-9], cluster synchronization[10-12] and pinning adaptive synchronization[13] etc. have been studied.
Compared with integer order, fractional calculus is its extension, which is used to study the mathematical properties of arbitrary order calculus, and it has been of great importance in the field of engineering and physics because some applications of fractional calculus have obtained great progress in last few years[14-15]. Modeling and simulating some systems by using the concept of fractional order may be closer to reality because the actual phenomenon are generally fractional[16]. So, compared to the integer order method, modeling method of fractional order calculus can make us more accurately describe and simulate the real process. fractional-order complex networks′ synchronization issue has gained the attention of the researchers in recent years [17-20]. Many fractional-order differential systems are certified to be chaotic or hyperchaotic, for example, Rössler system[21]. After these discoveries, owing to great value in the field of control processing and information science, hyper-chaotic differential systems′ synchronization is a central issue.
With regard to synchronization, inner synchronization is happening in a complex network and outer synchronization is appearing in two coupled networks[22]. In general, as the complex network's typical synchronization research, inner synchronization has been broadly studied. Wang et al.[23] and Chen et al.[24] have respectively investigated single complex network's inner synchronization. Outer synchronization has also been studied. Qin et al.[25]and Wang et al.[26] have studied two complex networks′ outer synchronization respectively. However, the above-mentioned inner or outer synchronization was not discussed at the same time. Today, complex dynamical networks′ hybrid synchronization is everywhere[27], for example, infectious disease transmits between different communities and within the group at the same time. Therefore, it is very meaningful that how to reach the two coupled networks′ hybrid synchronization. Recently, the complex networks′ hybrid synchronization gives rise to attention greatly, which was respectively studied in Refs.[28-30] in two complex networks with fractional-order. According to our understanding, the above articles were focused on the hybrid synchronization by different control methods, few researches have been made on the hybrid synchronization via fractional order control.
Due to the flexibility and completeness of fractional-order control, more and more attention has been paid[15, 31-33]. The well-known fractional-order controllers have PIλDμ controller[15], the TID controller[32], and the CRONE controller[33]. Compared to traditional controllers, it has been shown in above articles that the fractional-order controller implements easily.
Under the above discussion, we use a fractional order controller to control two complex networks to reach hybrid synchronization in this article, where hyper-chaotic systems with fractional-order as nodes in complex network give a hybrid synchronization's law via the Lasalle invariance principle and Lyapunov stability theorem. In the practical application, the inner and outer synchronization are discussed at the same time, which is more reasonable. In this article, the given controller is ordinary and can be applied to fractional order complex networks with chaotic (Chen system[26], Lorenz system[26], Liu system[34]) or hyperchaotic type (hyperchaotic Chen system[34]).
Next is the organization of this article. Mathematical preliminaries of fractional derivative and network model are provided in the second part. In the third part, we give hybrid synchronization definitions. Then in the fourth part, according to a controller with fractional-order, the two coupled networks' hybrid synchronization is discussed. Examples are given in the fifth part. This paper concludes with a summary of this work in the sixth part.
Expression of some notations in this paper, such as ‖·‖, AT, I,
| $ \mathit{\boldsymbol{D}}_t^{\rm{q}}x\left( t \right) = \left\{ \begin{array}{l} \frac{1}{{\mathit{\Gamma }\left( {n - q} \right)}}\int_a^t {{{\left( {t - \tau } \right)}^{n - q - 1}}{x^{\left( n \right)}}\left( \tau \right){\rm{d}}\tau } ,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;n - 1 < q < n\\ \frac{{{{\rm{d}}^n}}}{{{\rm{d}}{t^n}}}x\left( t \right),\;\;\;\;\;\;\;\;q = n \end{array} \right. $ | (1) |
in which
A complex network containing N nodes that we introduce[35]:
| $ {\mathit{\boldsymbol{D}}^{\rm{q}}}{\mathit{\boldsymbol{x}}_i}\left( t \right) = \mathit{\boldsymbol{f}}\left( {{\mathit{\boldsymbol{x}}_i}\left( t \right)} \right) + c\sum\limits_{j = 1}^N {{a_{ij}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{x_j}\left( t \right)} $ | (2) |
where the order q∈(0, 1), the ith node's state variable xi belongs to Rn, continuously differentiable vector function f belongs to Rn, the network topology A is equal to (aij)N×N; the inner coupling matrix Γ=diag(ζ1, ζ2, ..., ζn) belongs to Rn×n, c represents the network's coupling strength. aij is the element of matrix A (the ith row and the jth column): if aij satisfies 0 < aij, then there is a connection from node i to node j(i≠j), otherwise, aij is equal to 0.
| $ {a_{ii}} = - \sum\limits_{j = 1,j \ne i}^N {{a_{ij}}} $ | (3) |
The matrix A's diagonal elements satisfy the above equation.
Model (2) is the driving network. System (2) plus a control function φi(ui) equals the controlled response system, which is:
| $ {\mathit{\boldsymbol{D}}^{\rm{q}}}{\mathit{\boldsymbol{y}}_i}\left( t \right) = \mathit{\boldsymbol{f}}\left( {{\mathit{\boldsymbol{y}}_i}\left( t \right)} \right) + c\sum\limits_{j = 1}^N {{a_{ij}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\mathit{\boldsymbol{y}}_j}\left( t \right)} + {\mathit{\boldsymbol{\varphi }}_i}\left( {{\mathit{\boldsymbol{u}}_i}} \right) $ | (4) |
where the ith node's response state vector yi belongs to Rn, the explanation of f, c, Γ as those in Eq.(2), continuous control functions ui and φi:Rn→Rn.
3 Preparation Knowledge of MathematicsDefinition 1[30] We say that the hybrid synchronization in the network (2) and the controlled network (4) is reached when the equations as follows are satisfied:
| $ \left\{ \begin{array}{l} \mathop {\lim }\limits_{t \to \infty } \left\| {{x_i}\left( {t,{X_0}} \right) - {x_j}\left( {t,{X_0}} \right)} \right\| = 0\\ \mathop {\lim }\limits_{t \to \infty } \left\| {{y_i}\left( {t,{Y_0}} \right) - {y_j}\left( {t,{Y_0}} \right)} \right\| = 0\\ \mathop {\lim }\limits_{t \to \infty } \left\| {{y_i}\left( {t,{Y_0}} \right) - {x_i}\left( {t,{X_0}} \right)} \right\| = 0 \end{array} \right. $ | (5) |
Assumption 1[36] According to Function class QUAD(P, Δ): Suppose that Δ is equal to diag(ρ1, ρ2, ..., ρn), matrix P is positive definite and also equal to diag(p1, p2, ..., pn), continuous function f(x) belongs to Rn. When the inequalities as follows are satisfied, then f∈QUAD(P, Δ)
| $ \begin{array}{l} - \alpha {\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{y}}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{y}}} \right) \ge {\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{y}}} \right)^{\rm{T}}}P\left( {\mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{x}} \right) - } \right.\\ \;\;\;\;\;\left. {\mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{y}} \right) - \Delta \left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{y}}} \right)} \right) \end{array} $ | (6) |
supports for all x belongs to Rn, y belongs to Rn, t is positive and some α is positive.
Definition 2[37] Assume that A∈RN×N meets the two conditions as follows:
(ⅰ)
(ⅱ) A is irreducible, and it satisfies:
1) One of the eigenvalues of A is 0 with the multiplicity 1, and other eigenvalues' real part are negative number.
2) Regarding the eigenvalue 0, (1, 1, ...1)T is the A's right eigenvector.
3) Regarding the eigenvalue 0, ξ is equal to (ξ1, ξ2, ..., ξN)T is the A's left eigenvector, and it satisfies
Assume that A is irreducible. According to Definition 2, G and L is defined as diag(ξ1, ξ2, ..., ξN) and G-ξξT respectively, in which the matrix L and ξξT are symmetric, the matrix G is positive definite and also diagonal matrix.
4 The Hybrid Synchronization AnalysisFor the sake of convenience, we describe the specific content of the hybrid synchronization from the following two aspects including the inner synchronization and the outer synchronization.
The Eq.(2) can be rewritten as[28]:
| $ {\mathit{\boldsymbol{D}}^{\rm{q}}}\mathit{\boldsymbol{X}}\left( t \right) = \mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{X}}\left( t \right)} \right) + \left( {c\mathit{\boldsymbol{A}} \otimes \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}} \right)\mathit{\boldsymbol{X}}\left( t \right) $ | (7) |
where
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{X}}\left( t \right) = {{\left( {\mathit{\boldsymbol{x}}_1^{\rm{T}}\left( t \right),\mathit{\boldsymbol{x}}_2^{\rm{T}}\left( t \right), \cdots ,\mathit{\boldsymbol{x}}_N^{\rm{T}}\left( t \right)} \right)}^{\rm{T}}}}\\ {\mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{X}}\left( t \right)} \right) = \left( {{\mathit{\boldsymbol{f}}^{\rm{T}}}\left( {{\mathit{\boldsymbol{x}}_1}\left( t \right)} \right),{\mathit{\boldsymbol{f}}^{\rm{T}}}\left( {{\mathit{\boldsymbol{x}}_2}\left( t \right)} \right), \cdots ,{\mathit{\boldsymbol{f}}^{\rm{T}}}{{\left( {{\mathit{\boldsymbol{x}}_N}\left( t \right)} \right)}^{\rm{T}}}} \right.} \end{array} $ |
When s(t) is equal to
Therefore, ei(t) can be rewritten as:
| $ \begin{array}{l} {\mathit{\boldsymbol{D}}^q}{\mathit{\boldsymbol{e}}_i}\left( t \right) = \mathit{\boldsymbol{f}}\left( {{\mathit{\boldsymbol{y}}_i}\left( t \right)} \right) - \mathit{\boldsymbol{f}}\left( {{\mathit{\boldsymbol{x}}_i}\left( t \right)} \right) + c\sum\limits_{j = 1}^N {{a_{ij}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\mathit{\boldsymbol{e}}_j}} + \\ \;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{\varphi }}_i}\left( {{\mathit{\boldsymbol{u}}_i}} \right) = \mathit{\boldsymbol{B}}\left( {{\mathit{\boldsymbol{y}}_i}\left( t \right),{\mathit{\boldsymbol{x}}_i}\left( t \right)} \right){\mathit{\boldsymbol{e}}_i} + c\sum\limits_{j = 1}^N {{a_{ij}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\mathit{\boldsymbol{e}}_j}} + \\ \;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{\varphi }}_i}\left( {{\mathit{\boldsymbol{u}}_i}} \right) \end{array} $ | (8) |
where
| $ {\mathit{\boldsymbol{\varphi }}_i}\left( {{\mathit{\boldsymbol{u}}_i}} \right) = - {\mathit{\boldsymbol{k}}_i}{\mathit{\boldsymbol{u}}_i} $ | (9) |
where ki is equal to diag(ki1, ki2, ..., kin), where kij is more than or equal to 0, ui is defined by:
| $ {D^{1 - q}}{\mathit{\boldsymbol{u}}_i} = {\mathit{\boldsymbol{\omega }}_i}{\mathit{\boldsymbol{e}}_i} $ | (10) |
with ωi is equal to diag(ωi1, ωi2, ..., ωin), where ωij is more than or equal to 0. Due to Property 1, 2 in Ref.[26] and Eq.(10), we can obtain:
| $ {{\mathit{\boldsymbol{\dot u}}}_i} = {\mathit{\boldsymbol{D}}^1}{\mathit{\boldsymbol{u}}_i} = {\mathit{\boldsymbol{D}}^q}{\mathit{\boldsymbol{D}}^{1 - q}}{\mathit{\boldsymbol{u}}_i} = {\mathit{\boldsymbol{\omega }}_i}{\mathit{\boldsymbol{D}}^q}{\mathit{\boldsymbol{e}}_i} $ | (11) |
And according to Property 3 in Ref.[26], there is a positive number λi>0 for Eq.(10), such that ‖ω(yi-xi)‖≤λi‖ui‖, we can get:
| $ \left\| {{\mathit{\boldsymbol{e}}_i}} \right\| \le {\lambda _i}/\omega _i^ * \left\| {{\mathit{\boldsymbol{u}}_i}} \right\| $ | (12) |
where ωi* is equal to{ωij, j=1, 2, ...n}'s minimum value, and yi is equal to xi if ui=0.
The assumptions as follows are proposed to get some synchronization's sufficient condition.
Assumption 2[26] Assume that Γ meets ‖Γ‖= η, in which η is a positive constant.
Assumption 3[26] Assume that ‖B(yi, xi)‖(i=1, 2, ..., N) is finite, namely, ‖B(yi, xi)‖≤Mi, where Mi is a constant.
Theorem 1 Assume that Assumptions 1, 2 and 3 support, the network (2) and the controlled network (4) will reach the hybrid synchronization when the control parameters ωi and ki meet the inequalities as follows, and the constants ρj and ζj are present, where j=1, 2, ..., n.
| $ \left( {\rm{i}} \right)0 \ge {\rho _j}L + {\left( {c{\zeta _j}GA} \right)^s} $ | (13) |
| $ \left( {{\rm{ii}}} \right)\omega _i^{ * * }{\lambda _i}\left( {{M_i} + c{a_{ii}}\eta } \right) \le k_i^ * \omega _i^{ * 2},1 \le i \le N $ | (14) |
| $ \begin{array}{l} \left( {{\rm{iii}}} \right)\frac{{{{\left( {N - 1} \right)}^2}{c^2}{\eta ^2}{{\left( {{a_{ij}}\omega _i^{ * * }{\lambda _j}\omega _i^ * + {a_{ji}}\omega _j^{ * * }{\lambda _i}\omega _j^ * } \right)}^2}}}{{4\omega _i^ * \omega _j^ * }} \le \\ \;\;\;\;\;\;\left( {k_i^ * \omega _i^{ * 2} - \omega _i^{ * * }{\lambda _i}\left( {{M_i} + c{a_{ii}}\eta } \right)} \right)\left( {k_j^ * \omega _j^{ * 2} - } \right.\\ \;\;\;\;\;\;\left. {\omega _j^{ * * }{\lambda _j}\left( {{M_j} + c{a_{jj}}\eta } \right)} \right),1 \le i \le j \le N \end{array} $ | (15) |
where ωi* and ωi** is equal to {ωim, m=1, 2, ..., n}'s minimum and maximum values respectively, ki* is equal to {kim, m=1, 2, ..., n}'s minimum value.
Based on Lemma 1, Lemma 2 and Lemma 3 in Ref.[28], the following is the Theorem 1's proof.
Proof V1 is a Lyapunov function that we select, in which:
| $ {\mathit{\boldsymbol{V}}_1} = \frac{1}{2}\sum\limits_{i = 1}^N {{\mathit{\boldsymbol{\xi }}_i}{\mathit{\boldsymbol{\delta }}_i}{{\left( t \right)}^{\rm{T}}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{\delta }}_i}\left( t \right)} $ | (16) |
according to Ref.[28], V1 is rewritten by:
| $ {\mathit{\boldsymbol{V}}_1} = \frac{1}{2}\mathit{\boldsymbol{X}}{\left( t \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{P}}} \right)\mathit{\boldsymbol{X}}\left( t \right) $ | (17) |
There is a unitary matrix Q due to the matrix
| $ \mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{P}} = \mathit{\boldsymbol{Q \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{Q}}^{\rm{T}}} $ | (18) |
where Λ=diag(λ1, λ2, ..., λnN), i=1, 2, ..., nN, where λi is positive, and QTQ is equal to I.
We introduce a function Y(t)=QTX(t), so that
| $ {\mathit{\boldsymbol{V}}_1} = \frac{1}{2}\mathit{\boldsymbol{Y}}{\left( t \right)^T}\mathit{\boldsymbol{ \boldsymbol{\varLambda} Y}}\left( t \right) $ | (19) |
There is a (1/2)minλi≥α1>0 and (1/2)maxλi≤α2, that
| $ {\alpha _2}\mathit{\boldsymbol{Y}}{\left( t \right)^2} \ge {\mathit{\boldsymbol{V}}_1} \ge {\alpha _1}\mathit{\boldsymbol{Y}}{\left( t \right)^2} $ |
Based on Lemma 2 in Ref.[28], V1 changes into
| $ \begin{array}{l} {\mathit{\boldsymbol{D}}^{\rm{q}}}{\mathit{\boldsymbol{V}}_1} \le \mathit{\boldsymbol{Y}}{\left( t \right)^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{D}}^{\rm{q}}}\mathit{\boldsymbol{Y}}\left( t \right) = \mathit{\boldsymbol{X}}{\left( t \right)^{\rm{T}}}\mathit{\boldsymbol{Q \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{Q}}^{\rm{T}}}{\mathit{\boldsymbol{D}}^{\rm{q}}}\mathit{\boldsymbol{X}}\left( t \right) = \\ \;\;\;\mathit{\boldsymbol{X}}{\left( t \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{P}}} \right)\left[ {\mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{X}}\left( t \right)} \right) + \left( {c\mathit{\boldsymbol{A}} \otimes \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}} \right)\mathit{\boldsymbol{X}}\left( t \right)} \right] = \\ \;\;\;\mathit{\boldsymbol{X}}{\left( t \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{P}}} \right)\left[ {\mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{X}}\left( t \right)} \right) - \left( {{\mathit{\boldsymbol{I}}_N} \otimes \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}} \right)\mathit{\boldsymbol{X}}\left( t \right)} \right] + \\ \;\;\;\mathit{\boldsymbol{X}}{\left( t \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{P}}} \right)\left[ {\left( {{\mathit{\boldsymbol{I}}_N} \otimes \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}} \right)\mathit{\boldsymbol{X}}\left( t \right) + \left( {c\mathit{\boldsymbol{A}} \otimes } \right.} \right.\\ \;\;\;\left. {\left. \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} \right)\mathit{\boldsymbol{X}}\left( t \right)} \right] = - \sum\limits_{i = 1}^{N - 1} {\sum\limits_{j = i + 1}^N {{L_{ij}}{{\left( {{\mathit{\boldsymbol{x}}_j}\left( t \right) - {\mathit{\boldsymbol{x}}_i}\left( t \right)} \right)}^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{f}}\left( {{\mathit{\boldsymbol{x}}_j}\left( t \right) - } \right.} \right.} } \\ \;\;\;f\left( {{\mathit{\boldsymbol{x}}_i}\left( t \right) - \Delta \left( {{\mathit{\boldsymbol{x}}_j}\left( t \right) - {\mathit{\boldsymbol{x}}_i}\left( t \right)} \right) + \mathit{\boldsymbol{X}}{{\left( t \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{I}}_N} \otimes } \right.} \right.\\ \;\;\;\left. {\mathit{\boldsymbol{P \boldsymbol{\varDelta} }}} \right)\mathit{\boldsymbol{X}}\left( t \right) + \mathit{\boldsymbol{X}}{\left( t \right)^{\rm{T}}}\left( {c\mathit{\boldsymbol{LA}} \otimes \mathit{\boldsymbol{P \boldsymbol{\varGamma} }}} \right)\mathit{\boldsymbol{X}}\left( t \right) \le \\ \;\;\; - \alpha \sum\limits_{j > i}^N {{L_{ij}}{{\left( {{\mathit{\boldsymbol{x}}_j}\left( t \right) - {\mathit{\boldsymbol{x}}_i}\left( t \right)} \right)}^{\rm{T}}}\left( {{\mathit{\boldsymbol{x}}_j}\left( t \right) - {\mathit{\boldsymbol{x}}_i}\left( t \right)} \right)} + \\ \;\;\;\sum\limits_{j = 1}^n {{p_j}{{\mathit{\boldsymbol{\tilde x}}}_j}{{\left( t \right)}^{\rm{T}}}{\rho _j}{L_j}{{\mathit{\boldsymbol{\tilde x}}}_j}\left( t \right)} + \sum\limits_{j = 1}^n {{p_j}{{\mathit{\boldsymbol{\tilde x}}}_j}{{\left( t \right)}^{\rm{T}}}c{\zeta _j}\mathit{\boldsymbol{LA}}{{\mathit{\boldsymbol{\tilde x}}}_j}\left( t \right)} = - \\ \;\;\;\alpha \mathit{\boldsymbol{X}}{\left( t \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{L}} \otimes {\mathit{\boldsymbol{I}}_n}} \right)\mathit{\boldsymbol{X}}\left( t \right) + \sum\limits_{j = 1}^n {{p_j}{{\mathit{\boldsymbol{\tilde x}}}_j}{{\left( t \right)}^{\rm{T}}}\left( {{\rho _j}\mathit{\boldsymbol{L + }}} \right.} \\ \;\;\;\left. {c{\zeta _j}\mathit{\boldsymbol{LA}}} \right){{\mathit{\boldsymbol{\tilde x}}}_j}\left( t \right) \le - \frac{\alpha }{{\max {p_i}}}\mathit{\boldsymbol{X}}{\left( t \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{L}} \otimes \mathit{\boldsymbol{P}}} \right)\mathit{\boldsymbol{X}}\left( t \right) + \\ \;\;\;\sum\limits_{j = 1}^n {{p_j}{{\mathit{\boldsymbol{\tilde x}}}_j}{{\left( t \right)}^{\rm{T}}}\left[ {{\rho _j}\mathit{\boldsymbol{L}} + {{\left( {\mathit{\boldsymbol{c}}{\mathit{\boldsymbol{\zeta }}_\mathit{\boldsymbol{j}}}\mathit{\boldsymbol{LA}}} \right)}^s}} \right]{{\mathit{\boldsymbol{\tilde x}}}_j}\left( t \right)} = \\ \;\;\; - \frac{\alpha }{{\max {p_i}}}\mathit{\boldsymbol{Y}}{\left( t \right)^T}\mathit{\boldsymbol{ \boldsymbol{\varLambda} Y}}\left( t \right) + \sum\limits_{j = 1}^n {{p_j}{{\mathit{\boldsymbol{\tilde x}}}_j}{{\left( t \right)}^{\rm{T}}}\left[ {{\rho _j}\mathit{\boldsymbol{L}} + } \right.} \\ \;\;\;\left. {{{\left( {\mathit{c}{\mathit{\zeta }_\mathit{j}}\mathit{\boldsymbol{LA}}} \right)}^s}} \right]{{\mathit{\boldsymbol{\tilde x}}}_j}\left( t \right) \end{array} $ |
If
| $ {\left( {\mathit{c}{\mathit{\zeta }_\mathit{j}}\mathit{\boldsymbol{LA}}} \right)^s} + {\rho _j}\mathit{\boldsymbol{L}} \le 0 $ | (20) |
we can obtain:
| $ {\mathit{\boldsymbol{D}}^{\rm{q}}}{\mathit{\boldsymbol{V}}_1} \le - \alpha \frac{{\min {\mathit{\boldsymbol{\lambda }}_\mathit{\boldsymbol{i}}}{{\left\| {\mathit{\boldsymbol{Y}}\left( t \right)} \right\|}^2}}}{{\max {p_i}}} $ | (21) |
where
Owing to the controlled network (4) meets Assumptions 2 and 3, we can get ‖Γ‖=η and ‖B(yi, xi)‖≤Mi. V2 is a Lyapunov function that we construct.
| $ \begin{array}{l} {\mathit{\boldsymbol{V}}_2} = \frac{1}{2}\left( {\mathit{\boldsymbol{u}}_1^{\rm{T}},\mathit{\boldsymbol{u}}_2^{\rm{T}}, \cdots ,\mathit{\boldsymbol{u}}_N^{\rm{T}}} \right){\left( {\mathit{\boldsymbol{u}}_1^{\rm{T}},\mathit{\boldsymbol{u}}_2^{\rm{T}}, \cdots ,\mathit{\boldsymbol{u}}_N^{\rm{T}}} \right)^{\rm{T}}} = \\ \;\;\;\;\;\;\;\frac{1}{2}\sum\limits_{i = 1}^N {\mathit{\boldsymbol{u}}_i^{\rm{T}}{u_i}} \end{array} $ | (22) |
Differentiating V2 about t, then we can get:
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot V}}}_2} = \sum\limits_{i = 1}^N {\mathit{\boldsymbol{u}}_i^{\rm{T}}{{\mathit{\boldsymbol{\dot u}}}_i}} = \sum\limits_{i = 1}^N {\mathit{\boldsymbol{u}}_i^{\rm{T}}{\omega _i}{\mathit{\boldsymbol{D}}^{\rm{q}}}{e_i}} = \sum\limits_{i = 1}^N {\mathit{\boldsymbol{u}}_i^{\rm{T}}{\omega _i}B\left( {{y_i}\left( t \right),} \right.} \\ \;\;\;\;\left. {{x_i}\left( t \right)} \right){e_i} + c\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \ne i}^N {{a_{ij}}\mathit{\boldsymbol{u}}_i^{\rm{T}}{\omega _i}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{e_j}} } + c\sum\limits_{i = 1}^N {{a_{ii}}\mathit{\boldsymbol{u}}_i^{\rm{T}}{\omega _i}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{e_i}} - \\ \;\;\;\;\sum\limits_{i = 1}^N {\mathit{\boldsymbol{u}}_i^{\rm{T}}{\omega _i}{k_i}{\mathit{\boldsymbol{u}}_i}} \le \sum\limits_{i = 1}^N {\left\| {\mathit{\boldsymbol{u}}_i^{\rm{T}}} \right\|\left\| {{\omega _i}} \right\|} \\ \;\;\;\;\left\| {B\left( {{y_i}\left( t \right),{x_i}\left( t \right)} \right)} \right\|\left\| {{e_i}} \right\| + c\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \ne i}^N {{a_{ij}}\left\| {\mathit{\boldsymbol{u}}_i^{\rm{T}}} \right\|} } \times \\ \;\;\;\;\left\| {{\omega _i}} \right\|\left\| \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} \right\|\left\| {{e_j}} \right\| + c\sum\limits_{i = 1}^N {{a_{ii}}\left\| {\mathit{\boldsymbol{u}}_i^{\rm{T}}} \right\|\left\| {{\omega _i}} \right\|\left\| \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} \right\|} \\ \;\;\;\;\left\| {{e_i}} \right\| - \sum\limits_{i = 1}^N {\mathit{\boldsymbol{u}}_i^{\rm{T}}{\omega _i}{k_i}{\mathit{\boldsymbol{u}}_i}} \le \sum\limits_{i = 1}^N {\omega _i^{ * * }{M_i}{\lambda _i}} /\\ \;\;\;\;\omega _i^ * \left\| {\mathit{\boldsymbol{u}}_i^{\rm{T}}} \right\|\left\| {{\mathit{\boldsymbol{u}}_i}} \right\| + c\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \ne i}^N {{a_{ij}}\omega _i^{ * * }\eta {\lambda _j}} } /\\ \;\;\;\;\omega _j^ * \left\| {\mathit{\boldsymbol{u}}_i^{\rm{T}}} \right\|\left\| {{\mathit{\boldsymbol{u}}_j}} \right\| + c\sum\limits_{i = 1}^N {{a_{ii}}\omega _i^{ * * }\eta {\lambda _j}} /\omega _i^ * \left\| {\mathit{\boldsymbol{u}}_i^{\rm{T}}} \right\|\left\| {{\mathit{\boldsymbol{u}}_i}} \right\| - \\ \;\;\;\;\sum\limits_{i = 1}^N {\omega _i^ * k_i^ * {M_i}\mathit{\boldsymbol{u}}_i^{\rm{T}}{\mathit{\boldsymbol{u}}_i}} = \sum\limits_{i = 1}^N {\left( {\omega _i^{ * * }{M_i}{\lambda _i}/\omega _i^ * } \right.} + \\ \;\;\;\;\left. {c{a_{ii}}\omega _i^{ * * }\eta {\lambda _i}/\omega _i^ * - \omega _i^ * k_i^ * } \right]\left\| {\mathit{\boldsymbol{u}}_i^{\rm{T}}} \right\|\left\| {{\mathit{\boldsymbol{u}}_i}} \right\| + \\ \;\;\;\;c\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \ne i}^N {{a_{ij}}\omega _i^{ * * }\eta {\lambda _j}} } /\omega _j^ * \left\| {\mathit{\boldsymbol{u}}_i^{\rm{T}}} \right\|\left\| {{\mathit{\boldsymbol{u}}_j}} \right\| = \\ \;\;\;\;\sum\limits_{i = 1}^N {\left( {\omega _i^{ * * }{M_i}{\lambda _i}/\omega _i^ * + c{a_{ii}}\omega _i^{ * * }\eta {\lambda _i}/\omega _i^ * - \omega _i^ * k_i^ * } \right)} \\ \;\;\;\;\left\| {\mathit{\boldsymbol{u}}_i^{\rm{T}}} \right\|\left\| {{\mathit{\boldsymbol{u}}_i}} \right\| + c\sum\limits_{i < j} {\left( {{a_{ij}}\omega _i^{ * * }\eta {\lambda _j}/\omega _j^ * + } \right.} \\ \;\;\;\;\left. {{a_{ji}}\omega _j^{ * * }\eta {\lambda _i}/\omega _i^ * } \right)\left\| {\mathit{\boldsymbol{u}}_i^{\rm{T}}} \right\|\left\| {{\mathit{\boldsymbol{u}}_j}} \right\| \le - \sum\limits_{i < j} {\left[ {\frac{2}{{N - 1}}} \right.} \\ \;\;\;\;\sqrt {\omega _i^ * k_i^ * - \omega _i^{ * * }{M_i}{\lambda _i}/\omega _i^ * - c{a_{ii}}\omega _i^{ * * }\eta {\lambda _i}/\omega _i^ * } \times \\ \;\;\;\;\sqrt {\omega _j^ * k_j^ * - \omega _j^{ * * }{M_j}{\lambda _j}/\omega _j^ * - c{a_{jj}}\omega _j^{ * * }\eta {\lambda _j}/\omega _j^ * } - \\ \;\;\;\;\left. {c\left( {{a_{ij}}\omega _i^{ * * }\eta {\lambda _j}/\omega _j^ * + {a_{ji}}\omega _j^{ * * }\eta {\lambda _i}/\omega _i^ * } \right)} \right]\left\| {\mathit{\boldsymbol{u}}_i^{\rm{T}}} \right\|\\ \;\;\;\;\left\| {{\mathit{\boldsymbol{u}}_j}} \right\| \end{array} $ |
If the control parameters ωi and ki meet the inequalities as follows, the conclusion
| $ \omega _i^{ * * }{\lambda _i}\left( {{M_i} + c{a_{ii}}\eta } \right) \le k_i^ * \omega _i^{ * 2},1 \le i \le N $ | (23) |
| $ \begin{array}{l} \frac{{{{\left( {N - 1} \right)}^2}{c^2}{\eta ^2}\left( {{a_{ij}}\omega _i^{ * * }{\lambda _j}\omega _i^ * + {a_{ji}}\omega _j^{ * * }{\lambda _i}\omega _j^ * } \right)}}{{4\left( {\omega _i^ * \omega _j^ * } \right)}} \le \\ \left( {k_i^ * \omega _i^{ * 2} - \omega _i^{ * * }{\lambda _i}\left( {{M_i} + c{a_{ii}}\eta } \right)} \right)\left( {k_j^ * \omega _j^{ * 2} - } \right.\\ \left. {\omega _j^{ * * }{\lambda _j}\left( {{M_j} + c{a_{jj}}\eta } \right)} \right),1 \le i \le j \le N \end{array} $ | (24) |
Therefore we get
In this part, two complex networks with 5 nodes, where each node is hyper-chaotic Lorenz type with fractional order, are provided as an example to verify above theoretical analysis.
The following is the hyper-chaotic Lorenz's dynamic equation with fractional-order:
| $ \left\{ \begin{array}{l} {D^q}{x_1} = {x_4} + v\left( {{x_2} - {x_1}} \right)\\ {D^q}{x_2} = e{x_1} - {x_2} - {x_1}{x_3}\\ {D^q}{x_3} = {x_1}{x_2} - d{x_3}\\ {D^q}{x_4} = s{x_4} - {x_2}{x_3} \end{array} \right. $ | (25) |
where we set v, d, e and s as 10, 8/3, 28 and -1 respectively. The fractional-order hyper-chaotic Lorenz's system is chaotic with initial value (2, -2, 1, -1) as shown in Fig. 1.
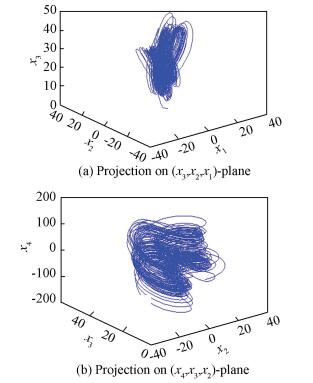
|
Figure 1 Fractional hyperchaotic Lorenz's chaotic attractors when q= 0.98 |
| $ \left\{ \begin{array}{l} {D^q}{x_i}\left( t \right) = f\left( {{x_i}\left( t \right)} \right) + c\sum\limits_{j = 1}^5 {{a_{ij}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{x_j}\left( t \right)} \\ {D^q}{y_i}\left( t \right) = f\left( {{y_i}\left( t \right)} \right) + c\sum\limits_{j = 1}^5 {{a_{ij}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{y_j}\left( t \right)} + {\varphi _i}\left( {{u_i}} \right) \end{array} \right. $ | (26) |
The coupling matrix A is:
| $ \left( {\begin{array}{*{20}{c}} { - 3}&1&1&1&1\\ 1&{ - 3}&1&0&1\\ 1&1&{ - 3}&0&1\\ 1&1&1&{ - 4}&1\\ 1&1&1&1&{ - 4} \end{array}} \right) $ |
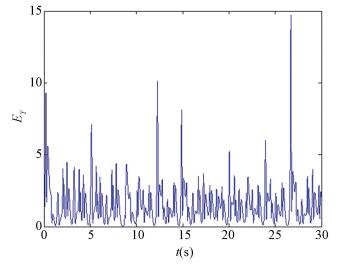
The matrix A's eigenvalues are λ1=-4.236 1, λ2=0.236 1, λ3=-5, λ4=-4, λ5=-4. A does not satisfy Definition 2. We can see that the network (2) and the network (4) cannot achieve the inner synchronization from Figs. 2-3. For the uncontrolled complex network model, we get that the outer synchronization error system does not converges to zero (see Fig. 4).
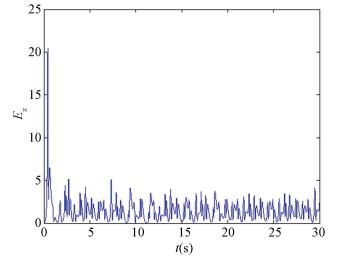
|
Figure 2 Inner synchronization error Ex |
|
Figure 3 Inner synchronization error Ey |

|
Figure 4 Outer synchronization error Eo |
We should satisfy the Assumption 1 to reach the two networks' hybrid synchronization. As in Ref.[30], we can obtain Δ=3I3 and P=diag(1, 1, 1).
Assume that Γ=diag(1, 1, 1), and A is:
| $ \left( {\begin{array}{*{20}{c}} { - 3}&1&1&0&1\\ 1&{ - 3}&1&0&1\\ 1&1&{ - 3}&0&1\\ 1&1&1&{ - 4}&1\\ 1&1&1&1&{ - 4} \end{array}} \right) $ |
The matrix A's eigenvalues are λ1=0, λ2=-4, λ3=-4, λ4=-4, λ5=-5. ξ=[0.25, 0.25, 0.25, 0.05, 0.2]T is the A's left eigenvector regarding the eigenvalue 0. Therefore G and L is equal to diag(0.25, 0.25, 0.25, 0.05, 0.2) and G-ξξT respectively. When c is selected as 1, the eigenvalues of ρjL+(cζGA)s are -0.401 0, -0.25, -0.25, -0.039 0, 0, therefore, the network (2) and the controlled network (4) can reach the inner synchronization respectively. When the control parameters ωi(1≤i≤5) and ki(1≤i≤5) meet the Theorem 1's inequalities, the system (8) can converge to 0, namely, the network (2) and the controlled network (4) can reach the outer synchronization. We choose the parameters ωi=I, ki=50*I, xi(0)=(0.1i+0.2, 0.1i-0.2, 0.1i+0.1, 0.1i-0.1)T, and yi(0)=(0.5i+4, 0.5i, 0.5i+3, 0.5i+1)T so as to calculate easily.
The equations as follows are used to explain the hybrid synchronization[28]:
| $ \left\{ \begin{array}{l} {E_x}\left( t \right) = \frac{1}{{N - 1}}\sum\limits_{i = 1}^N {{{\left\| {{\mathit{\boldsymbol{x}}_{i + 1}}\left( t \right) - {\mathit{\boldsymbol{x}}_i}\left( t \right)} \right\|}^2}} \\ {E_y}\left( t \right) = \frac{1}{{N - 1}}\sum\limits_{i = 1}^N {{{\left\| {{\mathit{\boldsymbol{y}}_{i + 1}}\left( t \right) - {\mathit{\boldsymbol{y}}_i}\left( t \right)} \right\|}^2}} \\ {E_o}\left( t \right) = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left\| {{\mathit{\boldsymbol{y}}_i}\left( t \right) - {\mathit{\boldsymbol{x}}_i}\left( t \right)} \right\|}^2}} \end{array} \right. $ | (27) |
where driving-response networks' outer synchronization error is represented by Eo(t). The each network's inner synchronization errors are represented by Ex(t) and Ey(t) respectively. Clearly, if the above three errors are stabilized to 0 as time tends to infinity at the same time, the hybrid synchronization can be reached.
Based on Figs. 5-7, we can see that the network (2) and the controlled network (4) can reach hybrid synchronization.
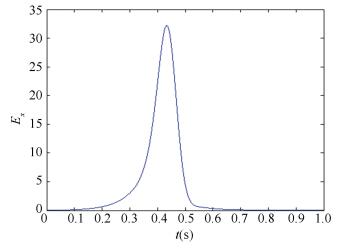
|
Figure 5 Inner synchronization error Ex |
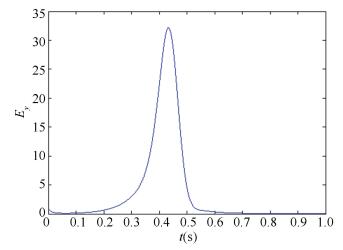
|
Figure 6 Inner synchronization error Ey |
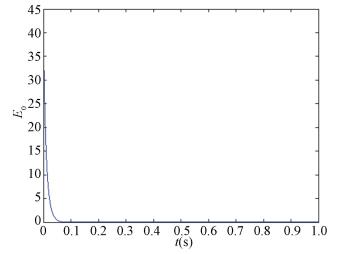
|
Figure 7 Outer synchronization error Eo |
If the control parameters ωi and ki meet Theorem 1, the value of ωi and ki can influence the synchronization speed. Parameter c is set as 1 and inner coupling matrix A=I3, larger control parameters ωi and ki can make outer synchronization faster (see Figs. 8-9).
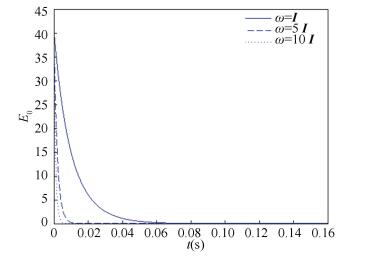
|
Figure 8 Outer synchronization error Eo with different control parameters ωi(ωi=1, 5, 10) |
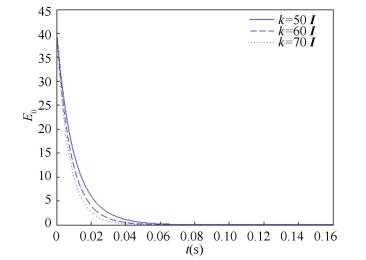
|
Figure 9 Outer synchronization error Eo with different control parameters ki(ki=50, 60, 70) |
6 Conclusions
The hyper-chaotic complex networks' hybrid synchronization law by a controller with fractional order is studied via the LaSalle invariance principle and the Lyapunov stability theorem in this article. When the state of driving-response networks is outer synchronization and each network is in inner synchronization, two coupled dynamics complex networks' hybrid synchronization could be reached. Two fractional-order hyper-chaotic Lorenz complex networks' simulations explain the validity of the theoretical analysis.
| [1] |
Chen Tianping, Liu Xiwei, Lu Wenlian. Pinning complex networks by a single controller. IEEE Transactions on Circuits & Systems I: Regular Papers, 2007, 54(6): 1317-1326. DOI:10.1109/TCSI.2007.895383 (  0) 0) |
| [2] |
Newman M E J. The structure and function of complex networks. SIAM Review, 2003, 45(2): 167-256. DOI:10.1137/S003614450342480 (  0) 0) |
| [3] |
Watts D J. Six Degrees: The Science of a Connected Age. Reflections, 2003, 61(1): 93. (  0) 0) |
| [4] |
Boccaletti S, Latora V, Moreno Y, et al. Complex networks: Structure and dynamics. Physics Reports, 2015, 424(4-5): 175-308. DOI:10.1016/j.physrep.2005.10.009 (  0) 0) |
| [5] |
Strogatz S H. Review article:Exploring complex networks. Nature, 2001, 410(6825): 268-276. DOI:10.1038/35065725 (  0) 0) |
| [6] |
Guimera R, Nunes Amaral L A. Functional cartography of complex metabolic networks. Nature, 2005, 433(7028): 895-900. DOI:10.1038/nature03288 (  0) 0) |
| [7] |
Bergman A, Siegal M L. Evolutionary capacitance as a general feature of complex gene networks. Nature, 2003, 424(6948): 549-552. DOI:10.1038/nature01765 (  0) 0) |
| [8] |
Mahmoud E E. Complex complete synchronization of two nonidentical hyperchaotic complex nonlinear systems. Mathematical Methods in the Applied Sciences, 2014, 37(3): 321-328. DOI:10.1002/mma.2793 (  0) 0) |
| [9] |
Yu T, Cao D, Yang Y, et al. Robust synchronization of impulsively coupled complex dynamical network with delayed nonidentical nodes. Chaos Solitons & Fractals, 2016, 87: 92-101. DOI:10.1016/j.chaos.2016.03.010 (  0) 0) |
| [10] |
Agrawal S K, Das S. Projective synchronization between different fractional-order hyperchaotic systems with uncertain parameters using proposed modified adaptive projective synchronization technique. Mathematical Methods in the Applied Sciences, 2014, 37(14): 2164-2176. DOI:10.1002/mma.2963 (  0) 0) |
| [11] |
He X, Li C, Huang J, et al. Generalized synchronization of arbitrary-dimensional chaotic systems. Optik - International Journal for Light and Electron Optics, 2015, 126(4): 454-459. DOI:10.1016/j.ijleo.2014.09.005 (  0) 0) |
| [12] |
Yang Lixin, Jiang Jun, Liu Xiaojun. Cluster synchronization in community network with hybrid coupling. Chaos Solitons & Fractals, 2016, 86: 82-91. DOI:10.1016/j.chaos.2016.02.022 (  0) 0) |
| [13] |
Li Lixiang, Li Weiwei, Kurths J, et al. Pinning adaptive synchronization of a class of uncertain complex dynamical networks with multi-link against network deterioration. Chaos Solitons & Fractals, 2015, 72: 20-34. DOI:10.1016/j.chaos.2015.01.005 (  0) 0) |
| [14] |
Petras I. fractional-order Systems. fractional-order Nonlinear Systems, 2011, 43-54. DOI:10.1007/978-3-642-18101-6_3 (  0) 0) |
| [15] |
Podlubny I. Fractional Differential Equations. New York: Academic Press, 1998.
(  0) 0) |
| [16] |
Xue Dingyü, Chen Yangquan, Atherton D P. Linear feedback control analysis and design with MATLAB. International Journal of Systems Science, 2007, 19(6): 979-984. (  0) 0) |
| [17] |
Ma Yingdong, Lu Junguo, Chen Weidong. Robust stability and stabilization of fractional order linear systems with positive real uncertainty. ISA Transactions, 2014, 53(2): 199-209. DOI:10.1016/j.isatra.2013.11.013 (  0) 0) |
| [18] |
Lan Yonghong, Gu Haibo, Chen Caixue, et al. An indirect Lyapunov approach to the observer-based robust control for fractional-order complex dynamic networks. Neurocomputing, 2014, 136(8): 235-242. DOI:10.1016/j.neucom.2014.01.009 (  0) 0) |
| [19] |
Wang Junwei, Ma Qinghua, Zeng Li. Observer-based synchronization in fractional-order leader-follower complex networks. Nonlinear Dynamics, 2013, 73(1-2): 921-929. DOI:10.1007/s11071-013-0843-6 (  0) 0) |
| [20] |
Wang Junwei, Zeng Caibin. Synchronization of fractional-order linear complex networks. Isa Transactions, 2015, 55(1): 129-134. DOI:10.1016/j.isatra.2014.11.002 (  0) 0) |
| [21] |
Li Chunguang, Chen Guanrong. Chaos and hyperchaos in the fractional-order Rössler equations. Physica A:Statistical Mechanics & Its Applications, 2004, 341(1-4): 55-61. DOI:10.1016/j.physa.2004.04.113 (  0) 0) |
| [22] |
Li Changpin, Sun Weigang, Kurths J. Synchronization between two coupled complex networks. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2007, 76(4): 70-80. DOI:10.1103/physreve.76.046204 (  0) 0) |
| [23] |
Wang Guansheng, Xiao Jiangwen, Wang Yanwu, et al. Adaptive pinning cluster synchronization of fractional-order complex dynamical networks. Applied Mathematics & Computation, 2014, 231(1): 347-356. DOI:10.1016/j.amc.2014.01.023 (  0) 0) |
| [24] |
Chen Liping, Chai Yi, Wu Ranchao, et al. Cluster synchronization in fractional-order complex dynamical networks. Physics Letters A, 2012, 376(35): 2381-2388. DOI:10.1016/j.physleta.2012.05.060 (  0) 0) |
| [25] |
Qin Jiahu, Zheng Weixing, Gao Huijun. On pinning synchronisability of complex networks with arbitrary topological structure. International Journal of Systems Science, 2011, 42(42): 1559-1571. DOI:10.1080/00207721.2011.555014 (  0) 0) |
| [26] |
Wang Yu, Li Tianzeng. Synchronization of fractional order complex dynamical network. Physica A: Statistical Mechanics & Its Applications, 2015, 428(4): 1-12. DOI:10.1016/j.physa.2015.02.051 (  0) 0) |
| [27] |
Li Baocheng. Pinning adaptive hybrid synchronization of two general complex dynamical networks with mixed coupling. Applied Mathematical Modelling, 2016, 40(4): 2983-2998. DOI:10.1016/j.apm.2015.09.092 (  0) 0) |
| [28] |
Ma Tiedong, Zhang Jun. Hybrid synchronization of coupled fractional-order complex networks. Neurocomputing, 2015, 157: 166-172. DOI:10.1016/j.neucom.2015.01.022 (  0) 0) |
| [29] |
Ma Tiedong, Zhang Jun, Zhou Yongcheng, et al. Adaptive hybrid projective synchronization of two coupled fractional-order complex networks with different sizes. Neurocomputing, 2015, 164: 182-189. DOI:10.1016/j.neucom.2015.02.071 (  0) 0) |
| [30] |
Sun Wen, Chen Zhong, Lü Yibing, et al. An intriguing hybrid synchronization phenomenon of two coupled complex networks. Applied Mathematics & Computation, 2010, 216(8): 2301-2309. DOI:10.1016/j.amc.2010.03.066 (  0) 0) |
| [31] |
Petras I. fractional-order Nonlinear Systems: Modeling, Analysis and Simulation. Berlin: Springer Science & Business Media, 2011.
(  0) 0) |
| [32] |
Lurie B J. Three-parameter tunable tilt-integral-derivative (TID) controller. US: US5371670, 1994.
(  0) 0) |
| [33] |
Oustaloup A, Sabatier J, Lanusse P. From fractal robustness to the CRONE control. Fractional Calculus & Applied Analysis, 1999, 2(1): 1-30. (  0) 0) |
| [34] |
Li Tianzeng, Wang Yu, Luo Maokang. Control of fractional chaotic and hyperchaotic systems based on a fractional order controller. Chinese Physics B, 2014, 23(8): 274-284. DOI:10.1088/1674-1056/23/8/080501 (  0) 0) |
| [35] |
Wu Xiangjun, Lu Hongtao. Outer synchronization between two different fractional-order general complex dynamical networks. Chinese Physics B, 2010, 19(7): 070511-1-070511-12. (  0) 0) |
| [36] |
Lu Wenlian, Chen Tianping. New approach to synchronization analysis of linearly coupled ordinary differential systems. Physica D: Nonlinear Phenomena, 2006, 213(2): 214-230. DOI:10.1016/j.physd.2005.11.009 (  0) 0) |
| [37] |
Wu Xiangjun, Lu Hongtao. Hybrid synchronization of the general delayed and non-delayed complex dynamical networks via pinning control. Neurocomputing, 2012, 89(15): 168-177. DOI:10.1016/j.neucom.2012.02.015 (  0) 0) |
 2018, Vol. 25
2018, Vol. 25


