The finite element method (FEM) has been widely used in the design and analysis of practical structures during recent years. However, the numerical results predicted by a FEM model usually have some deviation with the real mechanical behavior of structures. For example, a 10% difference was noticed between the numerical and measured frequencies for an aircraft wing[1], Ma et al.[2] observed that differences of frequencies is more than 60% between the results predicted by FEM model and measured in an aero-engine casing. Numerous sources of modeling error can be mainly attributed to the following three aspects: the structural errors of the FEM model, results from linearization assumptions of the mechanical behavior of the physical structure and approximation of boundary conditions; the order error of the FEM model, which means that the degree of freedom of the finite element model is limited and cannot simulate the infinite degree of freedom of the real structure; the parameter error of the FEM model, which is mainly due to the imprecise simplification of the initial model and uncertainty of materials and geometry parameters. Therefore, model updating methods are developed to obtain a FEM model with more accuracy that is required in a great number of applications, such as prediction of response, damage identification, optimization design and so on[3].
During the past few years, a variety of model updating methods have been proposed and applied in practical engineering, most of these updating methods utilize modal test data from practical structures. There are two kinds of model updating methods[4], one is one-step methods, which directly reconstruct the stiffness and mass matrix of the model, and therefore the symmetry, correctness and sparsity in the updating matrix cannot be preserved. The other is iterative methods, which repeatedly modify the physical parameters of the FEM model in order to minimize the difference in modal properties between the FEM model and the experimental object, becoming more and more popular. In most iterative model updating methods, optimization techniques are needed to reanalyze the eigensolutions and sensitivity of the analytical model in each iteration[5]. Since the analytical model of the actual structure in the project usually contains a large number of degrees of freedom (DOF), extracting the feature eigensolutions and sensitivity from the large-scale system matrix is very time-consuming, especially when there are many uncertain parameters to be updated.
In order to reduce the computational difficulty, model updating methods based on substructure have been studied. Xia, Weng and Xu et al.[6-8] developed the substructure method in terms of efficiency to extract the eigensolutions and associated eigensensitivities from the large-size system matrices. The substructure method is advantageous mainly in two aspects[9]. One of which is making it easier and faster to analyze the eigensolutions and the sensitivity of small system matrices because the original structure is replaced by smaller substructures. The other is the independent analysis of the separated substructures, which is promising when applied to model updating. When the updating parameters are localized within parts of the structure, only one or more substructures containing the parameters are reanalyzed during model updating, while the other substructures are unchanged[10-11]. The substructure-based model updating method has been successfully applied to a frame structure and a practical bridge[12], a 200-DOF spring-mass model[13], which demonstrated the efficiency and effectiveness of the method. Theoretical and computational developments are demonstrated with model updating and damage identification applications for a highway bridge using a high fidelity model and simulated measurements[14]. However, some limitations of the substructure-based model updating method need to be considered, such as a lot of intricate matrices calculation for the construction of the reduced base, influence of selection of master eigenmodes on the accuracy of the method[12].
For reduction of beam-type structures, Wang and Cheng[15-16] have presented a reduced super beam method, basing on the well-known cross section assumption and displacement interpolation function of beam. By using this model reduction method, the beam-type structure is divided into several parts and each part is reduced to a super beam element, resulting in a free-free reduced super beam, which provides the possibility for further necessary manipulation and can be applicable for the fast approximate frequency analysis and optimization of complicated beam-type structures under different boundary conditions[15-16]. Compared with several other equivalent beam models, the reduced super beam model is easy to construct with high accuracy[17]. Therefore, the reduced super beam method can partially overcome the aforementioned limitations of the substructure method and can be used for model updating.
The beam-type structure such as high-rise building, rockets and missiles, in which the longitudinal dimension is significantly larger than the transverse one, were often simplified as beams prior to the extensive use of computers[18]. The simplified beam model is used for fast rough estimation of structural global dynamic performances and design load distribution among different sections in preliminary design stage. However, the accurate prediction of the dynamic character and load distribution rely on the effective modification of missile dynamic model, which is a great challenge for many young engineers with less experience. For example, all kinds of connection stiffness model updating problems in different parts of the missile frequently concern more and more scholars and engineers.A modification technique of the missile dynamic model based on multi-objective optimization is given[19], the first three order frequencies and modal shapes show good agreement with experimental result.A dynamic missile based model update based on the smallest mode shape area difference is established to meet the requirements of multi-step mode shape areas under the background of missile dynamic model updating[20].Based on the element method, the connection stiffness in different parts of a large-scale rocket were selected as the updating parameters and a dynamic model updating method was presented for the structural response analysis under transient excitation[21].
In this paper, model updating of beam-type structure based on reduced super beam is proposed. The beam-type structures are reduced to a reduced super beam which is utilized for calculation of eigensolutions and eigensensitivities in the model updating process. In particular, Eigensensitivities analyses with respect to updating parameters of the original structure are calculated from the derivative matrices of super beam elements that contain the parameters, while the derivatives of other super beam elements to the parameters are zero, which can save a lot of computational effort for model updating. Optimization techniques are used for the updating of the modal dynamic properties difference. Application to a complicated stiffened cylindrical shell structure and a practical missile structure has shown the effectiveness and efficiency of the proposed method.
2 Introduction of Reduced Super BeamIn this section, a briefly introduction of the reduced super beam method is given. A schematic diagram of a complicated beam-type structure in free-free boundary is shown in Fig. 1, where the x axis is defined along the axis direction of the structure, y axis and z axis are perpendicular to the structural axis.
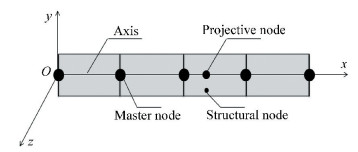
|
Fig.1 Schematic diagram of beam-type structure |
Firstly, the whole structure is divided into several beam parts by imaginary plane perpendicular to the axial direction of the structure. The intersections of the imaginary plane with the structural axis are named as master nodes. Then the displacement field of all the nodes in each beam part is approximated by the generalized displacement (three translational and three rotational degrees of freedom for each master node) of the master nodes at both ends through twice coordinate transformations (i.e., transformation between the structural node and the projective node, transformation between the projective node and the master node respectively). Finally, each beam part is reduced to a super beam element, which can be assembled to form a super beam model. The details of the reduction process will be given in the following section.
In each beam part i, according to the deformation characteristics of beam type structure, the cross-section is assumed to be rigid body based on the well-known plane assumption, then the nodal displacements uj of each structural node j can be approximated by the rigid body motion vector qji of its corresponding projective node on the x axis, which can be expressed as
| $ {\mathit{\boldsymbol{u}}_j} = {\mathit{\boldsymbol{R}}_j}{\mathit{\boldsymbol{q}}_{ji}} $ | (1) |
The expand form of Eq. (1) is
| $ \left\{ {\begin{array}{*{20}{c}} {{u_{jx}}}\\ {{u_{jy}}}\\ {{u_{jz}}}\\ {{u_{j\theta x}}}\\ {{u_{j\theta y}}}\\ {{u_{j\theta z}}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&{{z_{cj}}}&{ - {y_{cj}}}\\ 0&1&0&{ - {z_{cj}}}&0&0\\ 0&0&1&{{y_{cj}}}&0&0\\ 0&0&0&1&0&0\\ 0&0&0&0&1&0\\ 0&0&0&0&0&1 \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{q_{jix}}}\\ {{q_{jiy}}}\\ {{q_{jiz}}}\\ {{q_{ji\theta x}}}\\ {{q_{ji\theta y}}}\\ {{q_{ji\theta z}}} \end{array}} \right\} $ | (2) |
where ycj, zcj are the local coordinates of the structural node j relative to its projective node in the y, z directions. ujx, ujy, ujz, ujθx, ujθy, ujθz are the translational displacements and rotations of the node j along the x, y, z directions, respectively. qjix, qjiy, qjiz, qjiθx, qjiθy, qjiθz are the translational displacements and rotations of projective node along the x, y, z directions, respectively. The six columns of Rj is denoted by Rj1, Rj2, Rj3, Rj4, Rj5, Rj6.
According to the finite element theory, the displacement qji of the projective node can be calculated through displacement interpolation of beam. Here the displacement vectors of the two master nodes are marked as uL=(u1, v1, w1, θx1, θy1, θz1)T (left) and uR=(u2, v2, w2, θx2, θy2, θz2)T (right) respectively, as shown in Fig. 2. The displacement qji can be defined as
| $ {\mathit{\boldsymbol{q}}_{ji}} = \mathit{\boldsymbol{N}}{\left\{ {{\mathit{\boldsymbol{u}}_{\rm{L}}},{\mathit{\boldsymbol{u}}_{\rm{R}}}} \right\}^{\rm{T}}} $ | (3) |
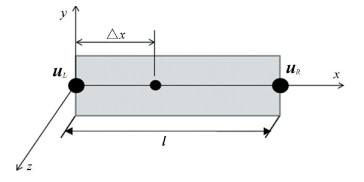
|
Fig.2 sketch of main nodes and projective node for part i |
The expand form of interpolation functions N is
| $ {\mathit{\boldsymbol{N}}^{\rm{T}}} = \left[ {\begin{array}{*{20}{c}} {1 - \xi }&0&0&0&0&0\\ 0&{2{\xi ^3} - 3{\xi ^2} + 1}&0&0&0&0\\ 0&0&{2{\xi ^3} - 3{\xi ^2} + 1}&0&0&0\\ 0&0&0&{1 - \xi }&0&0\\ 0&0&{ - \left( {{\xi ^3} - 2{\xi ^2} + \xi } \right)l}&0&{1 - \xi }&0\\ 0&{\left( {{\xi ^3} - 2{\xi ^2} + \xi } \right)l}&0&0&0&{1 - \xi }\\ \xi &0&0&0&0&0\\ 0&{ - 2{\xi ^3} + 3{\xi ^2}}&0&0&0&0\\ 0&0&{ - 2{\xi ^3} + 3{\xi ^2}}&0&0&0\\ 0&0&0&\xi &0&0\\ 0&0&{ - \left( {{\xi ^3} - {\xi ^2}} \right)l}&0&\xi &0\\ 0&{\left( {{\xi ^3} - {\xi ^2}} \right)l}&0&0&0&\xi \end{array}} \right] $ | (4) |
where ξ=Δx/l, l is the length of part i along x direction. The deflection qjiy, qjiz are assumed to be cubic interpolations of the axis coordinate x, the displacement qjix, qjiθx, qjiθy, qjiθz are assumed to be linear interpolations of the axis coordinate x. Substituting Eq. (3) into Eq.(1), the displacement transformation relationship between the structural node j and the two master nodes in each part i can be obtained
| $ {\mathit{\boldsymbol{\bar R}}_j} = {\mathit{\boldsymbol{R}}_j}{\rm{N}} $ | (5) |
Then the displacement transformation equation of the beam part i with
| $ {\mathit{\boldsymbol{U}}_i} = {\mathit{\boldsymbol{\bar T}}_i}{\left\{ {{\mathit{\boldsymbol{u}}_{\rm{L}}},{\mathit{\boldsymbol{u}}_{\rm{R}}}} \right\}^{\rm{T}}} $ | (6) |
where
| $ {\mathit{\boldsymbol{m}}_{si}} = \mathit{\boldsymbol{\bar T}}_i^{\rm{T}}{\mathit{\boldsymbol{m}}_i}{\mathit{\boldsymbol{\bar T}}_i},{\mathit{\boldsymbol{k}}_{si}} = \mathit{\boldsymbol{\bar T}}_i^{\rm{T}}{\mathit{\boldsymbol{k}}_i}{\mathit{\boldsymbol{\bar T}}_i} $ | (7) |
where msi and ksi are the reduced mass and stiffness matrices with dimension of 12×12 obviously, which have same size with beam element. So msi and ksi are marked as the reduced mass and stiffness matrices of a reduced super beam element in our study, which means the beam part is reduced to a reduced super beam element.
Finally, a free-free reduced super beam model can be obtained by assembling the super beam elements, the mass matrix MR and stiffness matrix KR of the reduced super beam model can be written as
| $ {\mathit{\boldsymbol{M}}_{\rm{R}}} = \sum\limits_{i = 1}^p {{\mathit{\boldsymbol{m}}_{si}}} ,{\mathit{\boldsymbol{K}}_{\rm{R}}} = \sum\limits_{i = 1}^p {{\mathit{\boldsymbol{k}}_{si}}} $ | (8) |
where p is the number of beam part, which is much less than the structural node number s. In Section 4 and Section 5, a uniform stiffened cylindrical shell model and a non-uniform practical missile structure will be employed to show the construction of the reduced super beam model.
The advantages of the proposed reduction method can be summarized as follows. The reduced models obviously possess their original physical characteristics, which provide the possibility for further necessary manipulation. The construction of the reduced base avoids a large amount of matrix calculation. Wang and Cheng[16-17] also give a rational way to improve the accuracy of the reduced super beam model, considering the effect of shear deformation.
By using the displacement assumptions, the structural deformation mode is restricted by the applied transformation. Therefore, the results of frequency and mode shape only reflect the overall vibration mode of the original model which is more important in engineering design.
3 Model Updating Using Modal PropertyThe purpose of most model updating methods is to minimize the difference between numerical modal properties and experimental results, including the frequencies and modal shapes. Classical eigenequation of the original structure is defined as
| $ \mathit{\boldsymbol{K \phi}}{ _l} = {\lambda _l}\mathit{\boldsymbol{M \phi}}{ _l} $ | (9) |
where M and K are the mass and stiffness matrices of the original structure, λl and ϕl are the lth eigenvalue and eigenvector respectively.
The iterative model updating method, especially the optimization updating method, often involves many iterative runs of eigensolutions and eigensensitivities analysis, which means that a large amount of computational effort is required based on large-scale models. In this paper, a reduced super beam model based model updating method is presented, aiming at reducing matrix sizes and the workload requirements of the model updating process.
3.1 Eigensolutions of Reduced Super BeamSuppose a beam-type structure was divided into p beam parts, and there are Ni structural model parameters Xi=(xi1, xi2, …, xiNi)T to be updated for each part i. The mass matrix mi and stiffness matrix ki are supposed to depend linearly on the model parameters, which is often encountered in practical model updating applications. So the mass and stiffness matrices of each part i are defined as
| $ {\mathit{\boldsymbol{m}}_i}\left( {{\mathit{\boldsymbol{X}}_i}} \right) = \sum\limits_{j = 1}^{{N_i}} {{\mathit{\boldsymbol{m}}_j}{\mathit{\boldsymbol{x}}_{ij}}} ,{\mathit{\boldsymbol{k}}_i}\left( {{\mathit{\boldsymbol{X}}_i}} \right) = \sum\limits_{j = 1}^{{N_i}} {{\mathit{\boldsymbol{k}}_j}{\mathit{\boldsymbol{x}}_{ij}}} $ | (10) |
where kj and mj are constant matrices, independent of parameter xij. As mentioned before, the transformation matrix
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{k}}_{si}}\left( {{\mathit{\boldsymbol{X}}_i}} \right) = \mathit{\boldsymbol{\bar T}}_i^{\rm{T}}\sum\limits_{j = 1}^{{N_i}} {{\mathit{\boldsymbol{k}}_j}{\mathit{\boldsymbol{x}}_{ij}}{{\mathit{\boldsymbol{\bar T}}}_i}} = \sum\limits_{j = 1}^{{N_i}} {\mathit{\boldsymbol{\bar T}}_i^{\rm{T}}{\mathit{\boldsymbol{k}}_j}{{\mathit{\boldsymbol{\bar T}}}_i}{\mathit{\boldsymbol{x}}_{ij}}} = \sum\limits_{j = 1}^{{N_i}} {{\mathit{\boldsymbol{k}}_{sj}}{\mathit{\boldsymbol{x}}_{ij}}} \\ {\mathit{\boldsymbol{m}}_{si}}\left( {{\mathit{\boldsymbol{X}}_i}} \right) = \mathit{\boldsymbol{\bar T}}_i^{\rm{T}}\sum\limits_{j = 1}^{{N_i}} {{\mathit{\boldsymbol{m}}_j}{\mathit{\boldsymbol{x}}_{ij}}{{\mathit{\boldsymbol{\bar T}}}_i}} = \sum\limits_{j = 1}^{{N_i}} {\mathit{\boldsymbol{\bar T}}_i^{\rm{T}}{\mathit{\boldsymbol{m}}_j}{{\mathit{\boldsymbol{\bar T}}}_i}{\mathit{\boldsymbol{x}}_{ij}}} = \sum\limits_{j = 1}^{{N_i}} {{\mathit{\boldsymbol{m}}_{sj}}{\mathit{\boldsymbol{x}}_{ij}}} \end{array} \right. $ | (11) |
Then the matrices of the reduced super beam model can be defined as
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{K}}_{\rm{R}}} = \sum\limits_{i = 1}^p {{\mathit{\boldsymbol{k}}_{si}}\left( {{\mathit{\boldsymbol{X}}_i}} \right)} = \sum\limits_{i = 1}^p {\sum\limits_{j = 1}^{{N_i}} {{\mathit{\boldsymbol{k}}_{sj}}{\mathit{\boldsymbol{x}}_{ij}}} } \\ {\mathit{\boldsymbol{M}}_{\rm{R}}} = \sum\limits_{i = 1}^p {{\mathit{\boldsymbol{m}}_{si}}\left( {{\mathit{\boldsymbol{X}}_i}} \right)} = \sum\limits_{i = 1}^p {\sum\limits_{j = 1}^{{N_i}} {{\mathit{\boldsymbol{m}}_{sj}}{\mathit{\boldsymbol{x}}_{ij}}} } \end{array} \right. $ | (12) |
Then the eigensolution analysis can be performed on the reduced super beam model as
| $ {\mathit{\boldsymbol{K}}_R}{\boldsymbol{\phi} _{Rl}} = {\lambda _{Rl}}{\mathit{\boldsymbol{M}}_R}{\boldsymbol{\phi} _{Rl}} $ | (13) |
where λRl and ϕRl can be solved from the reduced eigenequation using common eigensolvers, such as Subspace Iteration or Lanczos method[22]. As mentioned before, the accuracy of the reduced super beam model can be further improved by considering the effect of shear deformation[16-17], the error between λRl and corresponding λl is slight, and the eigenvectors of the global structure are recovered by
| $ {\boldsymbol{\phi} _l} = \sum\limits_{i = 1}^p {{{\mathit{\boldsymbol{\bar T}}}_i}{\boldsymbol{\phi} _{Rl}}} $ | (14) |
It is only necessary to deal with the design variables dependent part in the model updating process.
3.2 Sensitivity Analysis of Reduced Super BeamThe aim of sensitivity analysis is to find an optimal searching direction, which can be obtained by computing the change rate of a particular structural response quantity with respect to the updating parameters.
Based on the reduced super beam method, a beam-type structure is divided into a few independent super beam elements. The eigensensitivities of the global structure can be calculated from the derivative matrices of one super beam element that contains the parameter, and the derivatives of other super beam element to the parameter are zero. The sensitivity matrices of the eigenvalues Sλ and eigenvectors Sϕ with respect to a updating parameter xij in beam part i can be expressed as[23]
| $ {S_\lambda }\left( {{x_{ij}}} \right) = \frac{{\partial {\lambda _{Rl}}\left( {{x_{ij}}} \right)}}{{\partial {x_{ij}}}} = \boldsymbol{\phi} _{Rl}^T\left[ { - {\lambda _{Rl}}\frac{{\partial {M_R}}}{{\partial {x_{ij}}}} + \frac{{\partial {K_R}}}{{\partial {x_{ij}}}}} \right]{\boldsymbol{\phi} _{Rl}} $ | (15) |
| $ {S_\phi }\left( {{x_{ij}}} \right) = \frac{{\partial {\boldsymbol{\phi} _l}\left( {{x_{ij}}} \right)}}{{\partial {x_{ij}}}} = \sum\limits_{h = 1}^H {{\alpha _{lh}}{\boldsymbol{\phi} _h}} $ | (16) |
| $ {\alpha _{lh}} = \left\{ \begin{array}{l} \frac{{\boldsymbol{\phi} _h^{\rm{T}}\left( { - {\lambda _l}\frac{{\partial {\mathit{\boldsymbol{M}}_R}}}{{\partial {x_{ij}}}} + \frac{{\partial {\mathit{\boldsymbol{K}}_R}}}{{\partial {x_{ij}}}}} \right){\boldsymbol{\phi} _l}}}{{\left( {{\lambda _l} - {\lambda _h}} \right)}},h \ne l\\ - \frac{1}{2}\boldsymbol{\phi} _h^{\rm{T}}\left( {\frac{{\partial {\mathit{\boldsymbol{M}}_R}}}{{\partial {x_{ij}}}}} \right){\boldsymbol{\phi} _l},\;\;\;\;\;\;\;\;\;h = l \end{array} \right. $ | (17) |
Substituting Eq.(12) into Eqs.(15)-(17), the sensitivity matrices can be simplified as
| $ {S_\lambda }\left( {{x_{ij}}} \right) = \frac{{\partial {\lambda _{Rl}}\left( {{x_{ij}}} \right)}}{{\partial {x_{ij}}}} = \boldsymbol{\phi} _{Rl}^{\rm{T}}\left[ { - {\lambda _{Rl}}{\mathit{\boldsymbol{m}}_{sj}} + {\mathit{\boldsymbol{k}}_{sj}}} \right]{\boldsymbol{\phi} _{Rl}} $ | (18) |
| $ {S_\phi }\left( {{x_{ij}}} \right) = \frac{{\partial {\boldsymbol{\phi} _l}\left( {{x_{ij}}} \right)}}{{\partial {x_{ij}}}} = \sum\limits_{h = 1}^H {{\alpha _{lh}}{\boldsymbol{\phi} _h}} $ | (19) |
| $ {\alpha _{lh}} = \left\{ \begin{array}{l} \frac{{\boldsymbol{\phi} _h^{\rm{T}}\left( {\mathit{\boldsymbol{ - }}{\lambda _l}{\mathit{\boldsymbol{m}}_{sj}} + {\mathit{\boldsymbol{k}}_{sj}}} \right){\boldsymbol{\phi} _l}}}{{\left( {{\lambda _l} + {\lambda _h}} \right)}},h \ne l\\ - \frac{1}{2}\boldsymbol{\phi} _h^{\rm{T}}\left( {{\mathit{\boldsymbol{m}}_{sj}}} \right){\boldsymbol{\phi} _l},\;\;\;\;h = l \end{array} \right. $ | (20) |
Since size of the reduced eigenequation (Eq.(13)) is much smaller than the original structure (Eq.(9)), calculation of sensitivity matrices Sλ(xij) and Sϕ(xij) can be processed much faster than that based on the global structure. As calculation of the eigensolutions and eigensensitivities dominates the whole model updating process, the reduced super beam based model updating method will improve the computational efficiency significantly, which will be demonstrated in the following two examples.
4 Model Updating of a Stiffened Cylindrical Shell StructureA stiffened cylindrical shell structure with uniform longitudinal and transverse size is employed to demonstrate the feasibility and efficiency of the proposed updating method in this section. The structural drawings of the structure are shown in Fig. 3 and the FEM model is given in Fig. 4. There are 4 530 shell elements and 3 060 nodes of the free-free FEM model, including 18 360 DOFs in total. The structure is made of aluminum material, with Young's modulus E=7.0×104 MPa, Poisson's ratio ν=0.3, and mass density ρ=2.7×10-3g/mm3.

|
Fig.3 Structural drawings of the stiffened cylindrical shell |
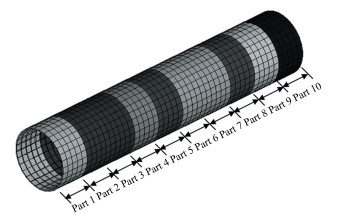
|
Fig.4 FEM model of the structure |
Based on the reduced super beam method, the original model was divided into 50 beam parts. For the uniformity, only one super beam element need to be constructed, which can be assembled to obtain a reduced super beam model with 50 elements and 306 DOFs (as shown in Fig. 5).
|
Fig.5 Reduced super beam model |
To show the efficiency of the reduced super beam method, the first six orders of overall vibration frequencies and their corresponding modal shapes are calculated as shown in Table 1. When comparing with the FEM model, we can find some minor differences both for frequencies and modal shapes. The results show that the relative differences of almost all frequencies are less than 3%, and the MAC (Modal assurance criterion)[15, 24]values are all above 0.88, which indicate that the reduced super beam model has similar modal characteristics as the original model.
| Table 1 Comparison of modal characteristics data |
In model updating process, experimental data used for model updating are usually obtained by intentionally introducing some defects to the FEM model, and then updating the analytical model to confirm identify these defects[25]. In this paper, the structural rigidity of the stiffened cylindrical shell is intentionally reduced in some parts as given in Table 2, which is denoted in Fig. 4. Then the experimental modal characteristics are calculated from the damaged FEM model for model updating.
| Table 2 Structural rigidity reduction cases |
Based on the reduced super beam model as shown in Fig. 5, model updating of the experimental data is processed using optimization method. Considering model updating of both frequencies and modal shapes, the optimization objective function is defined as[6]
| $ \begin{array}{l} J\left( X \right) = \sum\limits_l {w_{\lambda l}^2{{\left[ {{\lambda _l}{{\left( X \right)}^A} - \lambda _l^E} \right]}^2}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_l {w_{\phi l}^2} \sum\limits_k {{{\left[ {{\boldsymbol{\phi} _{kl}}{{\left( X \right)}^A} - \boldsymbol{\phi} _{kl}^E} \right]}^2}} \end{array} $ | (21) |
where λlE is the lth experimental eigenvalue, the corresponding frequency flE can be obtained by
Based on the reduced super beam model, the stiffness of each reduced super beam element is chosen as an updating parameter, so there are a total of 50 updating parameters. The objective function in Eq. (21) is minimized through optimization process using Method of Moving Asymptotes (MMA)[26], which stops upon a specified tolerance 0.05%, resulting in optimal parameters.
For the Case 1, the 'experimental' frequencies and modal shapes are obtained based on an assumed damaged structure, which has 30% rigidity reduction in part2, part3, part8 and 20% reduction in part6. Then the initially established reduced super beam model is updated to obtain analytical results, which are needed to be close with the 'experimental' data. Result comparisons are given in Table 3, which show that the analytical modal data are in good agreement with the simulated 'experimental' results after the updating. The frequency differences are all less than 4.5% for the first six global vibrations, and the MAC values indicate the high consistency of the stiffness distribution.
| Table 3 The frequencies and modal shapes of the cylinder structure before and after updating (Case 1) |
In order to be more persuasive, stiffness reduction of different parts was chosen in case2, specifically, part1 and part9 with a 30% reduction and a 20% reduction in part4, part5. The results of comparison between the frequencies and modal shapes before and after modification are given in Table 4, which also demonstrate the effectiveness of the proposed model updating method.
| Table 4 The frequencies and modal shapes of the cylinder structure before and after updating (Case 2) |
Fig. 6 gives the changes of the 50 updating parameters after optimization. The rigidity parameters of part2, part3 and part8 are reduced by about 30%, as well as about a 20% reduction of part6 in case1 (Fig. 6(a)). For case2, obvious negative values are observed in part 1, part4, part5 and part9 (Fig. 6(b)). In particular, the rigidity of part1 and part9 are reduced by about 0.3 and those of part4 and part5 are reduced by about 0.2. It can be seen from Fig. 6 that the updated analytical model confirms the assumed defects in Table 2. Due to small calculation errors between the reduced super beam model and the FEM model, some small changes are also observed in the rest parts, however, the influence of these changes on the model updating results are negligible.
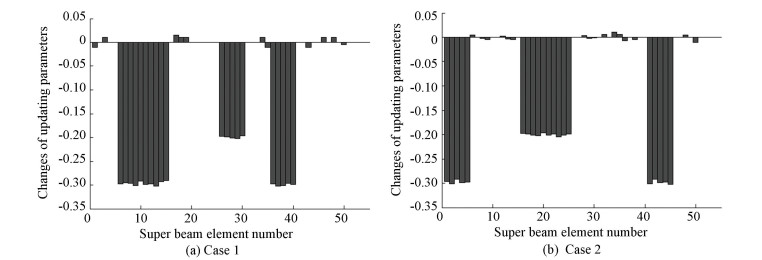
|
Fig.6 Changes of updating parameters after optimization |
The original model-based model updating process is not given in this paper, however, computational efficiency is another area that needs attention. Since the model updating process is based on a matrix, which is far less than the original model with size of 18 360×18 360. For each eigenvalue analysis processed on an ordinary personal computer using the Lanczos method[27-28], the small model only takes 0.25 s, while the original model requires more than 5 000 s, which shows that the proposed reduced super beam-based model updating method in this paper has a high computational efficiency.
5 Practical Example: A Missile StructureTo illustrate the feasibility and computational efficiency of the proposed reduced super beam based model updating method in real structures, a practical missile structure is employed here. The geometric model of this missile structure is shown in Fig. 7, which is designed and analyzed in different departments (including 44 parts). A FEM model with more than tens of thousands of DOFs is routinely constructed and used for static analysis of the missile structures. However, due to the huge computational time and storage requirement of dynamic analysis and optimization, it is impossible to optimize and update the structural dynamic performances based on such a model. Based on the FEM model used in different departments, each part is condensed to a super beam element, i.e. the whole missile structure is simplified to a reduced super beam model with 44 elements and 45 nodes (as shown in Fig. 8, size of 270×270), considering the shear deformation and lumped mass[16-17].

|
Fig.7 Geometric model of the missile structure |

|
Fig.8 Reduced super beam model of the missile structure |
Comparisons of bending frequencies and modal shapes are given in Table 5. The relative differences in frequencies are less than 5% and MAC values of all modal shapes are above 0.90, which indicate that the reduced super beam model of the missile structure can be applied in model updating process. In this paper, the first three overall bending frequencies and modal shapes of the missile are updated using optimization process. The objective function based on modal normalization and dimensionless parameter is formulated as follows.
| Table 5 Comparison of frequencies and modal shapes of the missile structure |
As shown in Fig. 9(a), the first bending mode curve has an extreme value point P1, so the vibration mode curve of CC′ is divided into two parts:CP1 and P1C′. Setting projection of CP1 on the x axis is L1 and on the y axis is A1, similarly, projection of P1C′ on the x axis is L2 and on the y axis is A2 respectively. Therefore, the dimensionless parameters for the first mode are defined as
| $ \left\{ \begin{array}{l} {\eta _{11}} = {A_1}/{L_1}\\ {\eta _{12}} = {A_2}/{L_2}\\ {\eta _{13}} = {A_1}/{A_2} \end{array} \right. $ | (22) |
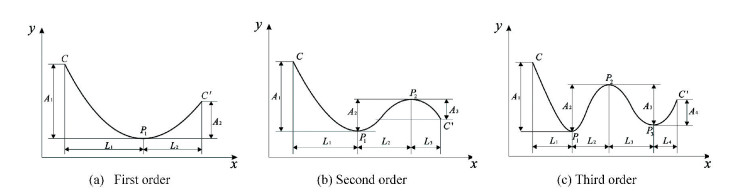
|
Fig.9 Schematic of dimensionless parameter for vibration mode |
In the same way, the dimensionless parameters for the second mode (Fig. 9(b)) are
| $ \left\{ \begin{array}{l} {\eta _{21}} = {A_1}/{L_1}\\ {\eta _{22}} = {A_2}/{L_2}\\ {\eta _{23}} = {A_3}/{L_3}\\ {\eta _{24}} = {A_1}/{A_2}\\ {\eta _{25}} = {A_1}/{A_3} \end{array} \right. $ | (23) |
And the dimensionless parameters for the third mode (Fig. 9(c)) are
| $ \left\{ \begin{array}{l} {\eta _{31}} = {A_1}/{L_1}\\ {\eta _{32}} = {A_2}/{L_2}\\ {\eta _{33}} = {A_3}/{L_3}\\ {\eta _{34}} = {A_4}/{L_4}\\ {\eta _{35}} = {A_1}/{A_2}\\ {\eta _{36}} = {A_1}/{A_3}\\ {\eta _{37}} = {A_1}/{A_4} \end{array} \right. $ | (24) |
Then the objective function is described as
| $ F\left( X \right) = \sum\limits_k^t {{{\left( {{w_k}{f_k}\left( X \right)} \right)}^2}} $ | (25) |
| $ {f_k}\left( X \right) = \left\{ \begin{array}{l} {f_1}\left( X \right) = \left( {{\omega _1} - {\omega _{1e}}} \right)/{\omega _{1e}}\\ {f_2}\left( X \right) = \left( {{\omega _2} - {\omega _{2e}}} \right)/{\omega _{2e}}\\ {f_3}\left( X \right) = \left( {{\omega _3} - {\omega _{3e}}} \right)/{\omega _{3e}}\\ {f_4}\left( X \right) = \left( {{\eta _{11}} - {\eta _{11e}}} \right)/{\eta _{11e}}\\ {f_5}\left( X \right) = \left( {{\eta _{12}} - {\eta _{12e}}} \right)/{\eta _{12e}}\\ \;\;\;\;\;\;\;\;\;\;\;\; \cdots \\ {f_{18}}\left( X \right) = \left( {{\eta _{37}} - {\eta _{37e}}} \right)/{\eta _{37e}} \end{array} \right. $ | (26) |
where wk is the weight factor for each objective function fk(X), ω is the natural frequencies obtained from reduced super beam, ωe is the natural frequencies obtained from experiment. η is the dimensionless parameters obtained from reduced super beam, ηe is the dimensionless parameters obtained from experiment data. As the missile structure remains essentially unchanged after design, the Young's modulus and material density of each super beam element are selected as updating parameters X, therefore, there are 80 physical parameters to be updated, minimizing the objective function(Eq. (25)).
The optimization solver MMA[26] is applied to update the parameters X. The sensitivity of ω is solved using Eq.(18) and the sensitivity of η is obtained by using difference method[29]. The model updating process stops when the pre-defined tolerance of the objective function or the maximum number of the iterations is reached.
The corresponding frequencies and modal shapes of the updated missile structure are compared with those values before updating as listed in Table 6. It is observed that the difference of frequencies between the analytical model before updating and the experimental measurement is about 30%, and the MAC values are all less than 0.85, especially worse for the third bending vibration. After model updating, both the frequencies and modal shapes results are improved, in particular, the relative differences of frequencies are less than 5% and MAC values of all the three modal shapes are 0.95, 0.92, 0.91 respectively. Comparison of the three updated modal shapes with experiment test results is given in Fig. 10. This reduced super beam based model updating method achieves the precision needed.
| Table 6 Comparisons of bending frequencies and modal shapes of the missile structure |
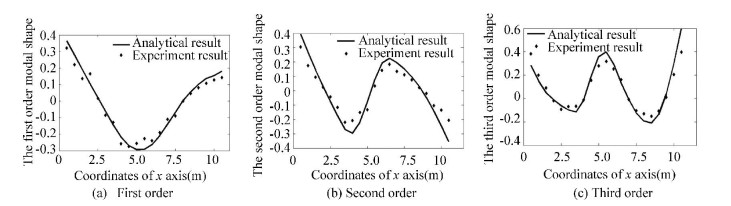
|
Fig.10 Modal shape comparison of the updated model and experiment result |
Using the proposed method, the eigensolutions and eigensensitivities are calculated in reduced super beam manner in each iteration. The calculation of the eigensensitivity only requires the derivative matrices of one super beam element that contains the updating parameter, while those in other elements are set to zero. With this scheme, the reduced super beam based model updating process is completed within 56 iterations. The computation time is about 840 s and totals about 6 300 s adding the model reduction time, the presented model updating method achieves higher efficiency.
6 ConclusionsIt is unavoidable to have deviation between the numerical results and the real mechanical behavior of structures, which sometimes go beyond our level of acceptance. Due to these deficiencies, much work has been conducted to improve the numerical accuracy and efficiency using model updating method. In this paper, a new model updating method for large scale beam-type structures is proposed based on reduced super beam model. The analysis of eigensolutions and eigensensitivities based on the reduced super beam model are firstly derived. Advantages of the proposed model updating methods can be summarized as:calculation of the eigensolutions and eigensensitivities are from greatly reduced matrix, and sensitivity analysis is carried out at super beam element level, resulting in high computational efficiency. Model updating of a typical stiffened cylindrical shell structure and a practical missile structure are served as the demonstration examples, the results have shown the effectiveness and efficiency, which means the proposed model updating method is efficient for model updating of large scale beam-type structures.
| [1] |
He E M, Chen Y, Li Y R, et al. Dynamic modification and application of wing double-beam model. Chinese Journal of Applied Mechanics, 2013, 30(3): 367-372. (in Chinese) DOI:10.11776/cjam.30.03.B066.(inChinese) (  0) 0) |
| [2] |
Ma S C, Zang CP, Lan H B. Dynamic model updating of an aero-engine casing. Journal of Aaerospace Power, 2013, 28(4): 878-884. (in Chinese) DOI:10.13224/j.cnki.jasp.2013.04.024.(inChinese) (  0) 0) |
| [3] |
Mottershead J, Friswell M I. Model updating in structural dynamics: A survey. Journal of Sound and Vibration, 1993, 167(2): 347-375. DOI:10.1006/jsvi.1993.1340 (  0) 0) |
| [4] |
Brownjohn J M W, Xia P Q, Hao H, et al. Civil structure condition assessment by FE model updating: Methodology and case studies. Finite Elements in Analysis and Design, 2001, 37(10): 761-775. DOI:10.1016/S0168-874X(00)00071-8 (  0) 0) |
| [5] |
Bakira P G, Reynders E, Roeck G D. Sensitivity-based finite element model updating using constrained optimization with a trust region algorithm. Journal of Sound and Vibration, 2007, 305(1-2): 211-225. DOI:10.1016/j.jsv.2007.03.044 (  0) 0) |
| [6] |
Xia Y, Lin R M. Improvement on the iterated IRS method for structural eigensolutions. Journal of Sound and Vibration, 2004, 270(4-5): 713-727. DOI:10.1016/S0022-460X(03)00188-3 (  0) 0) |
| [7] |
Weng S, Xia Y, Xu Y L, et al. Improved substructuring method for eigensolutions of large-scale structures. Journal of Sound and Vibration, 2009, 323(3-5): 718-36. DOI:10.1016/j.jsv.2009.01.015 (  0) 0) |
| [8] |
Xia Y, Weng S, Xu Y L. A substructuring method for calculation of eigenvalue derivatives and eigenvector derivatives. The 4th International Conference on Structural Health Monitoring of Intelligent Infrastructure. Zurich, 2009.
(  0) 0) |
| [9] |
de Klerk D, Rixen D J, Voormeeren S N. General framework for dynamic substructuring: History, review, and classification of techniques. AIAA Journal, 2008, 46(5): 1169-1181. DOI:10.2514/1.33274 (  0) 0) |
| [10] |
Perera R, Ruiz A. A multistage FE updating procedure for damage identification in large-scale structures based on multi-objective evolutionary optimization. Mechanical Systems and Signal Processing, 2008, 22(4): 970-991. DOI:10.1016/j.ymssp.2007.10.004 (  0) 0) |
| [11] |
Ko J M, Sun Z G, Ni Y Q. Multi-stage identification scheme for detecting damage in cable-stayed Kap Shui Mun Bridge. Engineering Structures, 2002, 24(7): 857-68. DOI:10.1016/S0141-0296(02)00024-X (  0) 0) |
| [12] |
Weng S, Xia Y, Xu Y L, et al. Substructure based approach to finite element model updating. Computers and Structures, 2011, 89(9-10): 772-782. DOI:10.1016/j.compstruc.2011.02.004 (  0) 0) |
| [13] |
Zhu D P, Dong X J, Wang Y. Substructure model updating through modal dynamic residual approach. Proceedings of the 9th International Workshop on Structural Health Monitoring. Stanford, CA. 2013.1047-1054
(  0) 0) |
| [14] |
Papadimitriou C, Papadioti D C. Component mode synthesis techniques for finite element model updating. Computers and Structures, 2013, 126(15): 15-28. DOI:10.1016/j.compstruc.2012.10.018 (  0) 0) |
| [15] |
Wang W S, Cheng G D, Li Q H. Fast dynamic performance optimization of complicated beam-type structures based on two new reduced physical models. Engineering Optimization, 2013, 45(7): 835-850. DOI:10.1080/0305215X.2012.709513 (  0) 0) |
| [16] |
Cheng G D, Wang W S. Fast dynamic analysis of complicated beam-type structure based on reduced super beam model. AIAA Journal, 2014, 52(5): 952-963. DOI:10.2514/1.J052312 (  0) 0) |
| [17] |
Wang W S, Cheng G D, Hao P. Frequency analysis of stiffened cylindrical shell based on reduced super beam model. Journal of Solid Rocket Technology, 2015, 38(3): 401-406. (in Chinese) (  0) 0) |
| [18] |
Zipfel P H. Modeling and Simulation of Aerospace Vehicle Dynamics. 2nd ed. Reston, VA : American Institute of Aeronautics and Astronautics, Inc. 2007.
(  0) 0) |
| [19] |
Li Bingwei, Dai Xianjin, Wang Liang. A modification technique of missile dynamic model based on multi-objective optimization algorithm. Structure and Environment Engineering, 2012, 39(6): 30-35. (in Chinese) (  0) 0) |
| [20] |
Zhao Ling, Liu Changchang, Liu Ziqiang. Dynamic model updating of missile based on the smallest mode shape area difference. Missile and Space Vehicles, 2013, 328(5): 59-62. (in Chinese) (  0) 0) |
| [21] |
Lyu Haibo, Li Ming, Guo Baisen, et al. An updating method for structural dynamic model applicable for transient rocket response computation. Noise and Vibration Control, 2013, 33(6): 11-14. (in Chinese) DOI:10.3969/j.issn.1006-1335.2013.06.003.(inChinese) (  0) 0) |
| [22] |
Bathe K J. Finite element procedures in engineering analysis. Englewood Chiffs: Prentice-Hall, Inc., 1982.
(  0) 0) |
| [23] |
Mottershead J E, Link M, Friswell M I. The sensitivity method in finite element model updating: A tutorial. Mechanical Systems and Signal Processing, 2011, 25(7): 2275-2296. DOI:10.1016/j.ymssp.2010.10.012 (  0) 0) |
| [24] |
Allemang R J, Brown D L. A correlation coefficient for modal vector analysis. Proceeding of the 1st International Modal Analysis Conference. Berlin: Springer, 1982. 110-116.
(  0) 0) |
| [25] |
Modak S V, Kundra T K, Nakra B C. Comparative study of model updating methods using simulated experimental data. Computers and Structures, 2002, 80(5-6): 437-447. DOI:10.1016/S0045-7949(02)00017-2 (  0) 0) |
| [26] |
Svanber K. The method of moving asymptotes—a new method for structural optimization. International Journal for Numerical Methods in Engineering, 1987, 24(2): 359-373. DOI:10.1002/nme.1620240207 (  0) 0) |
| [27] |
Louis K. The Lanczos Method: Evolution and Application. Society for Industrial and Applied Mathematics, 1987.
(  0) 0) |
| [28] |
Wu K S, Simon H. Thick-restart Lanczos method for large symmetric eigenvalue problems. SIAM Journal on Matrix Analysis and Applications (SIAM), 2000, 22(2): 602-616. DOI:10.1137/S0895479898334605 (  0) 0) |
| [29] |
Choi K K, Kim N H. Structural Sensitivity Analysis and Optimization 1: Linear Systems. New York: Springer Science and Business Media, Inc., 2005.
(  0) 0) |
 2019, Vol. 26
2019, Vol. 26


