2. Changzhou Vocational Institute of Light Industry Technology, Changzhou 213000, Jiangsu, China
Descriptor systems, which can be defined as the singular systems or differential-algebraic equation systems as well, were proposed by the famous scholar Rosenbrock in 1970s[1]. For some practical systems, descriptor system theory has a better characterization than the space description method, such as in electrical networks[2], constrained mechanical systems[3], aircraft modeling[4]. Based on this reason, the descriptor system has received more and more attention in recent years. Especially in the domain of state estimation for the descriptor systems, prominent methods such as the design of the descriptor observer has been proposed by the former studies[5-9]. Howwever for most practical systems, there exists noises in both the dynamic model and measurement which makes the state estimation problem more complex. It is well known that the Kamlan filter method can solve this problem efficiently. So this work is based on this background to study the Kalman filter design for a precise state estimation of descriptor systems with noises and guarantee the convergence of the estimate.
Some preliminary work has been done by former studies[10-14] to guarantee the feasibility of the Kalman filtering method for descriptor systems[15]. This model of the descriptor type which has a natural starting point for modeling when deriving relations among the quantities of dynamic evolution has been discussed. For a general class of descriptor model with time-varying, the optimal filter and its corresponding Riccati equation with "3 block" form have been deduced through a"dual approach"[16]. A further estimate method which is depending on recursive restructuring algorithm has been proposed for general discrete-time linear descriptor systems[17]. By transforming the problem of state estimation into a new one which the future dynamics having no influence on the present states[18]. An Extend Kalman filter (EKF) algorithm has been proposed for non-linear descriptor systems using a time-varying linearising semi-explicit index differential-algebraic equation. However, little existing work focuses on the state estimation problem of sampled-data nonlinear descriptor systems, and the optimal filter parameters of the descriptor systems in practical works may be singular ones which make the following work inconvenient [16-17]. So there is great incentive for us to develop a novel Kalman filter for the state estimation of non-linear sampled-data descriptor systems.
Recently, a novel Kalman filtering method has been proposed[19] for the state estimation of the non-linear systems with the existence of the stochastic uncertainties in the dynamic model. For this class of systems, an EKF algorithm is firstly proposed for estimating the non-linear parts in the dynamic model. However the error covariance matrix for state estimation is impossible to calculate as the parameters are unknown because of the stochastic uncertainties. So an upper-bounded method has been proposed for the error covariance matrix and then to confirm the filtering gain by the proposed upper-bound. The method for choosing the upper-bounds[19] has already been researched[20].
In this paper, a new approach of state estimation for norm-bounded non-linear sampled-data descriptor systems is proposed based on such results[19]. The non-linear sampled-data descriptor system is firstly discretized to obtain a discrete-time non-singular model by the Euler discretization method. By the introduced parameters, a discrete-time EKF is proposed for the state estimation of the transformed non-singular system. Due to the introduced parameters, uncertainties exist in the estimation error covariance. To solve this problem, we optimize the corresponding upper-bound with a matrix inequality. Then the filter gain is obtained by minimizing the corresponding upper-bound. Finally, a theorem is proposed and proofed to show the robustness of the designed REKF which is against the systems uncertainties.
This paper is organized as follows. A norm-bounded non-linear sampled-data descriptor model is proposed in Section 2, and then the system is discretized into a discrete-time non-singular one by an efficient way, assumption is given to guarantee the Kalman filtering process of the sampled-data descriptor system. In Section 3, A REKF algorithm is proposed for state estimation and implemented in the transformed non-singular system based on an upper-bound, and its robustness is proofed. In Section 4, a simulating example is proposed to demonstrate the validity of our results. In the Section 5, conclusions are drawn at the end.
2 Problem Statement and AssumptionConsider a non-linear sampled-data descriptor model as the following equation:
| $ \left\{ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{E\dot x}}(t) = \mathit{\boldsymbol{\varphi }}(\mathit{\boldsymbol{x}}(t)) + \mathit{\boldsymbol{w}}(t)}\\ {\mathit{\boldsymbol{y}}\left( {{t_k}} \right) = \mathit{\boldsymbol{Cx}}\left( {{t_k}} \right) + \mathit{\boldsymbol{v}}\left( {{t_k}} \right)} \end{array}} \right. $ | (1) |
where x∈Rn denotes the state vector, y(tk) ∈Rm denotes the sampled output at time tk with the sampling interval τ=tk+1-tk. In system (1), E satisfies that rank(E)= r≤n, which means that E may be singular. Additionally, the matrix [E C]T satisfies that rank[E C] T = n.
In the system (1), the state vector x should satisfy that
| $ \mathit{\boldsymbol{M}} - \mathit{\boldsymbol{E}}\left( {\mathit{\boldsymbol{x}}{\mathit{\boldsymbol{x}}^{\rm{T}}}} \right) > 0 $ | (2) |
where M∈Rn×n is a known matrix.
The following assumption is proposed for Kalman filter of the sampled-data nonlinear descriptor system.
Assumption 1 [C R] has full row rank[16].
For the system (1), because of the singular matrix E exists in the dynamic model, it is very hard to calculate the covariance matrix in the process of the Kalman filtering. In this paper, our purpose is to find parameters to transform the descriptor system (1) into a non-singular one.
Lemma 1[21] If there exist matrix R1∈Ra1×b1, matrix R2∈Rb1×c1 and matrix R3∈Ra1×c1, where R2 satisfies that rank R2=c1, then
| $ {\mathit{\boldsymbol{R}}_1}{\mathit{\boldsymbol{R}}_2} = {\mathit{\boldsymbol{R}}_3} $ | (3) |
has a general solution as the following equation:
| $ {\mathit{\boldsymbol{R}}_1} = {\mathit{\boldsymbol{R}}_3}\mathit{\boldsymbol{R}}_2^\dagger + \mathit{\boldsymbol{\xi }}\left[ {{\mathit{\boldsymbol{I}}_{{\mathit{\boldsymbol{b}}_1}}} - {\mathit{\boldsymbol{R}}_2}\mathit{\boldsymbol{R}}_2^\dagger } \right] $ | (4) |
where ξ is an arbitrary matrix and R2† denotes the pseudo-inverse of R2.
Since
| $ \mathit{\boldsymbol{TE}} + \mathit{\boldsymbol{NC}} = {\mathit{\boldsymbol{I}}_\mathit{\boldsymbol{n}}} $ | (5) |
where the general solution matrix of T and N are defined as [T N] which is calculated by
| $ \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{T}}&\mathit{\boldsymbol{N}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{E}}\\ \mathit{\boldsymbol{C}} \end{array}} \right]^\dagger } + \mathit{\boldsymbol{S}}\left( {{\mathit{\boldsymbol{I}}_{n + m}} - \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{E}}\\ \mathit{\boldsymbol{C}} \end{array}} \right]{{\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{E}}\\ \mathit{\boldsymbol{C}} \end{array}} \right]}^\dagger }} \right) $ | (6) |
where S∈Rn×(n+m) is an arbitrary matrix which denotes the design freedom.
Nonetheless, it is easy to see that the dynamic model of Eq.(1) is continuous-time one, and the measurement is the discrete-time one. So we firstly discretize the system (1) to be a discrete non-singular model.
For any of x(t), the following equation exists based on Eq.(6):
| $ \begin{array}{l} \mathit{\boldsymbol{\dot x}}(t) = \left( {\mathit{\boldsymbol{TE}} + \mathit{\boldsymbol{NC}}} \right)\mathit{\boldsymbol{\dot x}}(t) = \\ \;\;\;\;\;\;\;\mathit{\boldsymbol{TE\dot x}}(t) + \mathit{\boldsymbol{NC\dot x}}(t) = \\ \;\;\;\;\;\;\;\mathit{\boldsymbol{T}}\left[ {\varphi \left( {\mathit{\boldsymbol{x}}\left( t \right)} \right) + \mathit{\boldsymbol{w}}\left( t \right)} \right] + \mathit{\boldsymbol{NC\dot x}}(t) = \\ \;\;\;\;\;\;\;\mathit{\boldsymbol{T}}\varphi \left( {\mathit{\boldsymbol{x}}\left( t \right)} \right) + \mathit{\boldsymbol{Tw}}\left( t \right) + \mathit{\boldsymbol{NC\dot x}}(t) \end{array} $ | (7) |
Then using the Euler discretization method, Eq.(7) can be discretized as
| $ {\mathit{\boldsymbol{x}}_k} = {\mathit{\boldsymbol{x}}_{k - 1}} + \mathit{\boldsymbol{T\tau }}\varphi \left( {{\mathit{\boldsymbol{x}}_{k - 1}}} \right) + \mathit{\boldsymbol{T\tau }}{\mathit{\boldsymbol{w}}_{k - 1}} + \mathit{\boldsymbol{NC}}{\mathit{\boldsymbol{x}}_k} + O\left( {{\mathit{\boldsymbol{\tau }}^2}} \right) $ | (8) |
where
| $ \begin{array}{l} O\left( {{\mathit{\boldsymbol{\tau }}^2}} \right) = \mathit{\boldsymbol{T}}\left[ {\frac{{{\tau ^2}}}{{2!}}\dot \varphi (\mathit{\boldsymbol{x}}(t)) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\frac{{{\tau ^3}}}{{3!}}{\varphi ^{(2)}}(\mathit{\boldsymbol{x}}(t)) + \cdots + \frac{{{\tau ^k}}}{{k!}}{\varphi ^{\left( {k - 1} \right)}}(\mathit{\boldsymbol{x}}(t))} \right] \end{array} $ |
In this paper, the sampling interval τ is choosing to be sufficiently small so that the terms in O(τ2) can be omitted.
The measurement is represented as
| $ {\mathit{\boldsymbol{y}}_k} = \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{x}}_k} + {\mathit{\boldsymbol{v}}_k} $ | (9) |
So the system (1) is discretized and represented as the following equation
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{x}}_k} = {\mathit{\boldsymbol{x}}_{k - 1}} + \mathit{\boldsymbol{T}}\tau \varphi \left( {{\mathit{\boldsymbol{x}}_{k - 1}}} \right) + \mathit{\boldsymbol{T}}\tau {\mathit{\boldsymbol{w}}_{k - 1}} + \mathit{\boldsymbol{NC}}{\mathit{\boldsymbol{x}}_k}}\\ {{\mathit{\boldsymbol{y}}_k} = \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{x}}_k} + {\mathit{\boldsymbol{v}}_k}} \end{array}} \right. $ | (10) |
The Eq.(9) can be rewritten as the following equation:
| $ \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{x}}_k} = {\mathit{\boldsymbol{y}}_k} - {\mathit{\boldsymbol{v}}_k} $ | (11) |
So the Eq.(10) is rewritten as the following equation:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{x}}_k} = {\mathit{\boldsymbol{x}}_{k - 1}} + \mathit{\boldsymbol{T}}\tau \varphi \left( {{\mathit{\boldsymbol{x}}_{k - 1}}} \right) + \mathit{\boldsymbol{T\tau }}{\mathit{\boldsymbol{w}}_{k - 1}} + \mathit{\boldsymbol{N}}{\mathit{\boldsymbol{y}}_k} - \mathit{\boldsymbol{N}}{\mathit{\boldsymbol{v}}_k}}\\ {{\mathit{\boldsymbol{y}}_k} = \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{x}}_k} + {\mathit{\boldsymbol{v}}_k}} \end{array}} \right. $ | (12) |
In Eq.(12), wk-1, vk are defined as
| $ {\mathit{\boldsymbol{Q}}_{k - 1}} = \mathit{\boldsymbol{E}}\left[ {{\mathit{\boldsymbol{w}}_{k - 1}}\mathit{\boldsymbol{w}}_{k - 1}^{\rm{T}}} \right] $ |
| $ {\mathit{\boldsymbol{R}}_k} = \mathit{\boldsymbol{E}}\left[ {{\mathit{\boldsymbol{v}}_k}\mathit{\boldsymbol{v}}_k^{\rm{T}}} \right] $ |
| $ \mathit{\boldsymbol{E}}\left[ {{\mathit{\boldsymbol{w}}_k}\mathit{\boldsymbol{v}}_k^{\rm{T}}} \right] = 0 $ |
Define
| $ f\left( {{\mathit{\boldsymbol{x}}_{k - 1}}} \right) = {\mathit{\boldsymbol{x}}_{k - 1}} + \mathit{\boldsymbol{T\tau }}\varphi \left( {{\mathit{\boldsymbol{x}}_{k - 1}}} \right) $ | (13) |
| $ \Delta {\mathit{\boldsymbol{E}}_k} = \mathit{\boldsymbol{N}}{\mathit{\boldsymbol{y}}_k} - \mathit{\boldsymbol{N}}{\mathit{\boldsymbol{v}}_k} $ | (14) |
Substitute the Eqs. (13) and (14) into the system (12), then Eq.(12) can be written as the following equation:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{x}}_k} = f\left( {{\mathit{\boldsymbol{x}}_{k - 1}}} \right) + \Delta {\mathit{\boldsymbol{E}}_{k - 1}} + \mathit{\boldsymbol{T\tau }}{\mathit{\boldsymbol{w}}_{k - 1}}}\\ {{\mathit{\boldsymbol{y}}_k} = \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{x}}_k} + {\mathit{\boldsymbol{v}}_k}} \end{array}} \right. $ | (15) |
In this section, a REKF is proposed for the transformed non-singular system (15).
The structure of EKF is also suitable for the proposed REKF, define
| $ {{\mathit{\boldsymbol{\hat x}}}_{k/k - 1}} = f\left( {{{\mathit{\boldsymbol{\hat x}}}_{k - 1}}} \right) $ | (16) |
| $ {{\mathit{\boldsymbol{\hat x}}}_k} = {{\mathit{\boldsymbol{\hat x}}}_{k/k - 1}} + {\mathit{\boldsymbol{K}}_k}\left( {{\mathit{\boldsymbol{y}}_k} - {\mathit{\boldsymbol{C}}_k}{{\mathit{\boldsymbol{\hat x}}}_{k/k - 1}}} \right) $ | (17) |
where
| $ {{\mathit{\boldsymbol{\tilde x}}}_k} = {\mathit{\boldsymbol{x}}_k} - {{\mathit{\boldsymbol{\hat x}}}_k} $ | (18) |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_k} = \mathit{\boldsymbol{E}}\left( {{{\mathit{\boldsymbol{\tilde x}}}_k}\mathit{\boldsymbol{\tilde x}}_k^{\rm{T}}} \right) $ | (19) |
Our purpose is to find a bound Pk which satisfies
| $ {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_k} \le {\mathit{\boldsymbol{P}}_k} $ | (20) |
The predicted error and its corresponding covariance matrix can be defined as follows
| $ {{\mathit{\boldsymbol{\tilde x}}}_{\mathit{\boldsymbol{k}}/\mathit{\boldsymbol{k}} - 1}} = {\mathit{\boldsymbol{x}}_k} - {{\mathit{\boldsymbol{\hat x}}}_{k/k - 1}},{{\mathit{\boldsymbol{\tilde x}}}_{k/k - 1}} = {\mathit{\boldsymbol{x}}_k} - {{\mathit{\boldsymbol{\hat x}}}_{k/k - 1}} $ | (21) |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{k/k - 1}} = \mathit{\boldsymbol{E}}\left( {{{\mathit{\boldsymbol{\tilde x}}}_{k/k - 1}}\mathit{\boldsymbol{\tilde x}}_{k/k - 1}^{\rm{T}}} \right) $ | (22) |
Substitute the dynamic model of the Eqs. (15) and (16) into Eq.(21) it is obtained that
| $ {{\mathit{\boldsymbol{\tilde x}}}_{k/k - 1}} = f\left( {{\mathit{\boldsymbol{x}}_{k - 1}}} \right) - f\left( {{{\mathit{\boldsymbol{\hat x}}}_{k - 1}}} \right) + \Delta {\mathit{\boldsymbol{E}}_\mathit{\boldsymbol{k}}} + \mathit{\boldsymbol{T\tau }}{\mathit{\boldsymbol{w}}_{k - 1}} $ | (23) |
Using a Taylor series expansion about
| $ f\left( {{\mathit{\boldsymbol{x}}_{k - 1}}} \right) = f\left( {{{\mathit{\boldsymbol{\hat x}}}_{k - 1}}} \right) + {\mathit{\boldsymbol{F}}_k}{{\mathit{\boldsymbol{\tilde x}}}_{k - 1}} + {\Delta _f}\left( {\mathit{\boldsymbol{\tilde x}}_{k - 1}^2} \right) $ | (24) |
where
| $ {\Delta _f}\left( {\mathit{\boldsymbol{\tilde x}}_{k - 1}^2} \right) = {\mathit{\boldsymbol{A}}_k}{\mathit{\boldsymbol{\beta }}_k}\mathit{\boldsymbol{G}}{{\mathit{\boldsymbol{\tilde x}}}_{k - 1}} $ | (25) |
where Ak∈Rn×n, βk∈Rn×n are unknown matrix to consider the linearising error of the dynamic model, and βk is assumed to be bounded. i.e.
| $ {\mathit{\boldsymbol{\beta }}_k}\mathit{\boldsymbol{\beta }}_k^{\rm{T}} \le \mathit{\boldsymbol{I}} $ | (26) |
G∈Rn×n is introduced to tune the filter.
Combine the Eqs. (24) and (25), then the Eq. (23) is rewritten as
| $ {{\mathit{\boldsymbol{\tilde x}}}_{k/k - 1}} = \left( {{\mathit{\boldsymbol{F}}_k} + {\mathit{\boldsymbol{A}}_k}{\mathit{\boldsymbol{\beta }}_k}\mathit{\boldsymbol{G}}} \right){{\mathit{\boldsymbol{\hat x}}}_{k - 1}} + \Delta {\mathit{\boldsymbol{E}}_k} + \mathit{\boldsymbol{T\tau }}{\mathit{\boldsymbol{w}}_{k - 1}} $ | (27) |
ΔEk can be processed as
| $ \Delta {\mathit{\boldsymbol{E}}_k} = \Delta \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{w}}_{k - 1}} = \left( {{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{\alpha }}_k}{\mathit{\boldsymbol{L}}_k}} \right){\mathit{\boldsymbol{w}}_{k - 1}} $ | (28) |
where αk is assumed to be bounded which is similar as βk.
| $ {\mathit{\boldsymbol{\alpha }}_k}\mathit{\boldsymbol{\alpha }}_k^{\rm{T}} \le \mathit{\boldsymbol{I}} $ | (29) |
Substitute the Eq. (28) into Eq.(27), it is obtained that
| $ {{\mathit{\boldsymbol{\tilde x}}}_{k/k - 1}} = \left( {{\mathit{\boldsymbol{F}}_k} + {\mathit{\boldsymbol{A}}_k}{\mathit{\boldsymbol{\beta }}_k}\mathit{\boldsymbol{G}}} \right){{\mathit{\boldsymbol{\hat x}}}_{k - 1}} + \left( {{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{\alpha }}_k}{\mathit{\boldsymbol{L}}_k} + \mathit{\boldsymbol{T\tau }}} \right){\mathit{\boldsymbol{w}}_{k - 1}} $ | (30) |
Substitute the Eq. (30) into Eq.(22), it is obtained that
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{k/k - 1}} = \left( {{\mathit{\boldsymbol{F}}_k} + {\mathit{\boldsymbol{A}}_k}{\mathit{\boldsymbol{\beta }}_k}\mathit{\boldsymbol{G}}} \right){\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{k - 1}}{{\left( {{\mathit{\boldsymbol{F}}_k} + {\mathit{\boldsymbol{A}}_k}{\mathit{\boldsymbol{\beta }}_k}\mathit{\boldsymbol{G}}} \right)}^{\rm{T}}} + }\\ {\left( {{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{\alpha }}_k}{\mathit{\boldsymbol{L}}_k} + \mathit{\boldsymbol{T\tau }}} \right){\mathit{\boldsymbol{Q}}_{k - 1}}{{\left( {{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{\alpha }}_k}{\mathit{\boldsymbol{L}}_k} + \mathit{\boldsymbol{T\tau }}} \right)}^{\rm{T}}}} \end{array} $ | (31) |
Substitute the Eq. (17) into Eq.(18), it is obtained that
| $ {{\mathit{\boldsymbol{\tilde x}}}_k} = {\mathit{\boldsymbol{x}}_k} - {{\mathit{\boldsymbol{\hat x}}}_k} = \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}\mathit{\boldsymbol{C}}} \right){{\mathit{\boldsymbol{\tilde x}}}_{k/k - 1}} - {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{v}}_k} $ | (32) |
Substitute the Eq. (32) into Eq.(19), it is obtained that
| $ {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_k} = \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}\mathit{\boldsymbol{C}}} \right){\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{k/k - 1}}{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}\mathit{\boldsymbol{C}}} \right)^{\rm{T}}} + {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{R}}_k}\mathit{\boldsymbol{K}}_k^{\rm{T}} $ | (33) |
Our purposed is to find the optimal filter parameters T(Fk+AkβkG) and Kk which minimize Σk, so the following equation is obtained as
| $ \frac{{\partial {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_k}}}{{\partial {\mathit{\boldsymbol{K}}_k}}} = 0 $ | (34) |
From Eq.(32) and Eq.(33), it is obtained that
| $ {\mathit{\boldsymbol{K}}_k} = \frac{{{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{k/k - 1}}\mathit{\boldsymbol{C}}}}{{\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{k/k - 1}}{\mathit{\boldsymbol{C}}^{\bf{T}}} + {\mathit{\boldsymbol{R}}_k}}} $ | (35) |
Although the error covariance is obtained by the showing deducing, since βk and αk are unknown, it is impossible to calculate Σk to solve this problem, the following lemma is needed.
Lemma 2[21] If there exist matrix A, B, C, D as follows, where DTD≤I, X is a positive definite matrix and there exist arbitrary α>0 that satisfy α-1I-CXCT>0 then the following inequality holds
| $ \begin{array}{l} \left( {\mathit{\boldsymbol{\bar A}} + \mathit{\boldsymbol{\bar B\bar D\bar C}}} \right)\mathit{\boldsymbol{X}}{\left( {\mathit{\boldsymbol{\bar A}} + \mathit{\boldsymbol{\bar B\bar D\bar C}}} \right)^{\bf{T}}} \le \\ \mathit{\boldsymbol{\bar A}}{\left( {{\mathit{\boldsymbol{X}}^{ - 1}} - \mathit{\boldsymbol{\alpha }}{{\mathit{\boldsymbol{\bar C}}}^{\bf{T}}}\mathit{\boldsymbol{\bar C}}} \right)^{ - 1}}{{\mathit{\boldsymbol{\bar A}}}^{\rm{T}}} + {\mathit{\boldsymbol{\alpha }}^{ - 1}}\mathit{\boldsymbol{\bar B}}{{\mathit{\boldsymbol{\bar B}}}^{\bf{T}}} \end{array} $ |
Based on Lemma 2, the Eq.(31) can be rewritten as
| $ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{k/k - 1}} \le {\mathit{\boldsymbol{F}}_k}{\left( {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{k - 1}^{ - 1} - {\gamma ^{ - 2}}{\mathit{\boldsymbol{G}}^{\bf{T}}}\mathit{\boldsymbol{G}}} \right)^{ - 1}}\mathit{\boldsymbol{F}}_k^{\rm{T}} + \\ \;\;\;\;\;\;\;\;\;{\gamma ^2}{\mathit{\boldsymbol{A}}_k}\mathit{\boldsymbol{A}}_k^{\rm{T}} + \mathit{\boldsymbol{T\tau }}{\left( {\mathit{\boldsymbol{Q}}_{k - 1}^{ - 1} - {\lambda ^{ - 1}}\mathit{\boldsymbol{L}}_k^{\rm{T}}{\mathit{\boldsymbol{L}}_k}} \right)^{ - 1}}{\mathit{\boldsymbol{\tau }}^{\bf{T}}}{\mathit{\boldsymbol{T}}^{\bf{T}}} + \\ \;\;\;\;\;\;\;\;\;\lambda {\mathit{\boldsymbol{H}}_k}\mathit{\boldsymbol{H}}_k^{\rm{T}} \le {\left( {\mathit{\boldsymbol{P}}_{k - 1}^{ - 1} - {\gamma ^2}{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{G}}} \right)^{ - 1}}\mathit{\boldsymbol{F}}_k^{\rm{T}} + \\ \;\;\;\;\;\;\;\;\;{\gamma ^2}{\mathit{\boldsymbol{A}}_k}\mathit{\boldsymbol{A}}_k^{\rm{T}} + \mathit{\boldsymbol{T\tau }}{\left( {\mathit{\boldsymbol{Q}}_{k - 1}^{ - 1} - {\lambda ^{ - 1}}\mathit{\boldsymbol{L}}_k^{\rm{T}}{\mathit{\boldsymbol{L}}_k}} \right)^{ - 1}}{\mathit{\boldsymbol{\tau }}^{\bf{T}}}{\mathit{\boldsymbol{T}}^{\bf{T}}} + \\ \;\;\;\;\;\;\;\;\;\lambda {\mathit{\boldsymbol{H}}_k}\mathit{\boldsymbol{H}}_k^{\rm{T}} = {\mathit{\boldsymbol{P}}_{k/k - 1}} \end{array} $ | (36) |
Substitute Σk/k-1 into Eq.(35) by Pk/k-1, it is obtained that
| $ {\mathit{\boldsymbol{K}}_k} = \frac{{{\mathit{\boldsymbol{P}}_{k/k - 1}}{\mathit{\boldsymbol{C}}^{\rm{T}}}}}{{\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{P}}_{k/k - 1}}{\mathit{\boldsymbol{C}}^{\rm{T}}} + {\mathit{\boldsymbol{R}}_k}}} $ | (37) |
By the aforementioned deduction, we get the gain Kk by using the upper-bound method based on Lemma 1.
Remark 1 Now we review the filtering process. It can be seen that for the transformed system (15), the one-step prediction and the corresponding error covariance matrix are calculated by Eqs.(16) and (31), the state estimation and its corresponding error covariance matrix are obtained by Eqs.(17) and (32). By the upper-bound Eq.(36), we get the filter gain Eq.(37).
The following discussion is about the robustness of the proposed filter. Consider the non-singular system as follows:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{x}}_k} = {\mathit{\boldsymbol{F}}_k}{\mathit{\boldsymbol{x}}_{k - 1}} + {{\mathit{\boldsymbol{\bar w}}}_{k - 1}}}\\ {{\mathit{\boldsymbol{y}}_k} = \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{x}}_k} + {\mathit{\boldsymbol{v}}_k}} \end{array}} \right. $ | (38) |
where Fk∈Rn×n is a known matrix, wk-1=ΔEk +Tτwk-1.
It is obtained that
| $ {\mathit{\boldsymbol{P}}_{k/k - 1}} \le {{\mathit{\boldsymbol{\bar P}}}_{k/k - 1}} $ | (39) |
where
| $ {{\mathit{\boldsymbol{\bar P}}}_{k/k - 1}} = {\mathit{\boldsymbol{F}}_k}{\left( {\mathit{\boldsymbol{P}}_{k - 1}^{ - 1} - {\gamma ^{ - 2}}{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{G}}} \right)^{ - 1}}\mathit{\boldsymbol{F}}_k^{\rm{T}} + {{\mathit{\boldsymbol{\bar Q}}}_{k - 1}} $ | (40) |
| $ \begin{array}{l} {{\mathit{\boldsymbol{\bar Q}}}_{k - 1}} = \mathit{\boldsymbol{NC}}{\mathit{\boldsymbol{M}}_k}{\mathit{\boldsymbol{C}}^{\rm{T}}}{\mathit{\boldsymbol{N}}^{\rm{T}}} + \mathit{\boldsymbol{N}}{\mathit{\boldsymbol{R}}_k}{\mathit{\boldsymbol{N}}^{\rm{T}}} + \mathit{\boldsymbol{T\tau }}{\mathit{\boldsymbol{Q}}_k}{\mathit{\boldsymbol{\tau }}^{\rm{T}}}{\mathit{\boldsymbol{T}}^{\rm{T}}}\\ {\rm{Define }}\\ {{\mathit{\boldsymbol{\bar P}}}_k} = \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{C}}_k}} \right){{\mathit{\boldsymbol{\bar P}}}_{k/k - 1}}{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{C}}_k}} \right)^{\rm{T}}} + {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{R}}_k}\mathit{\boldsymbol{K}}_k^{\rm{T}} \end{array} $ | (41) |
where Qk-1 and Pk satisfy
| $ \lambda \mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{L}}_k}{\mathit{\boldsymbol{Q}}_{k - 1}}\mathit{\boldsymbol{L}}_k^{\rm{T}} > 0,{\gamma ^2}\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{G}}{{\mathit{\boldsymbol{\bar P}}}_k}{\mathit{\boldsymbol{G}}^{\rm{T}}} > 0 $ | (42) |
The robustness of the proposed REKF algorithm is guaranteed by the following theorem.
Theorem 1 For every 0≤k≤n, if the following assumption is established:
| $ \det \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{C}}_k}} \right) \ne 0,\det \left( \mathit{\boldsymbol{F}} \right) \ne 0,\det \left( \mathit{\boldsymbol{L}} \right) \ne 0 $ | (43) |
Then the proposed REKF algorithm for system (38) can guarantee the robustness against uncertainties in system by the following inequality:
| $ \frac{{\sum\limits_{k = 0}^n {\left\| {{{\mathit{\boldsymbol{\tilde x}}}_k}} \right\|_{{\mathit{\boldsymbol{G}}^{\bf{T}}}\mathit{\boldsymbol{G}}}^2} }}{{\left\| {{{\mathit{\boldsymbol{\tilde x}}}_0}} \right\|_{\mathit{\boldsymbol{P}}_0^{ - 1}}^2 + \sum\limits_{k = 0}^n {\left( {\left\| {{{\mathit{\boldsymbol{\bar w}}}_{k - 1}}} \right\|_{\mathit{\boldsymbol{\bar Q}}_{k - 1}^{ - 1}}^2 + \left\| {{\mathit{\boldsymbol{v}}_k}} \right\|_{\mathit{\boldsymbol{R}}_k^{ - 1}}^2} \right)} }} \le {\gamma ^2} $ | (44) |
where
Theorem 1 is proofed in the appendix.
Remark 2 1) For the non-singular system (38), E(wk-1wk-1T)=E(ΔEkΔEkT)+TτQk-1τTT. It is known that ΔEk satisfies ΔEk=Nyk-Nvk, so E(ΔEkΔEkT)=NCE(xkxkT)CTNT+NRkNT, from the Eq.(2) it is known that E(xkxkT)≤Mk, so E(wk-1wk-1T)≤NCMkCTNT+NRkNT+TτQk-1τTT=Qk-1, then the Eq. (40) is obtained.
2) The Eq.(44) shows that the proposed REKF has a robustness against the uncertainties taken by T and N, the process and measurement noises, and is arising from the H∞ design. In Ref.[19], the author has argued that, γ should be sufficiently large so that Eq.(44) is satisfied.
4 SimulationsA simulating example of a sampled-data descriptor system with a non-linear structure in the dynamic model is shown in this section to illustrate the effectiveness of our method.
Consider a model of norm-bounded non-linear sampled-data descriptor system as follows:
| $ \left\{ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{E\dot x}}\left( t \right) = \left[ {\begin{array}{*{20}{c}} {\cos \left( {{x_1}\left( t \right)} \right)}\\ {\cos \left( {sin\left( {{x_2}\left( t \right)} \right)} \right.} \end{array}} \right] + \mathit{\boldsymbol{w}}\left( t \right)}\\ {\mathit{\boldsymbol{y}}\left( {{t_k}} \right) = \left[ {\begin{array}{*{20}{c}} {0.5}&0\\ 0&{0.5} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_1}\left( {{t_k}} \right)}\\ {{x_2}\left( {{t_k}} \right)} \end{array}} \right] + \mathit{\boldsymbol{v}}\left( {{t_k}} \right)} \end{array}} \right. $ |
where
The initial condition is choosing as
| $ {x_1}\left( 0 \right) = 0.2,{x_2}\left( 0 \right) = 0.3,{{\hat x}_1}\left( 0 \right) = 0.1,{{\hat x}_2}\left( 0 \right) = 0.1 $ |
Using the Eq.(6), choosing
| $ \mathit{\boldsymbol{S}} = \left[ {\begin{array}{*{20}{c}} 1&0&1&0\\ 0&1&0&1 \end{array}} \right] $ |
Then T and N is obtained as
| $ \mathit{\boldsymbol{T = }}\left[ {\begin{array}{*{20}{c}} {0.6}&0\\ 0&1 \end{array}} \right],\mathit{\boldsymbol{N}} = \left[ {\begin{array}{*{20}{c}} {0.8}&0\\ 0&2 \end{array}} \right] $ |
Obviously, T is non-singular matrix.
To ensure the robustness of the proposed REKF algorithm, γ is chosen as γ=102.231 2;
To ensure the convergence of ΔEk, λ H, L are choosing as
| $ \lambda = 0.4116,\mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} 1\\ 1 \end{array}} \right],\mathit{\boldsymbol{L}} = 0.1 $ |
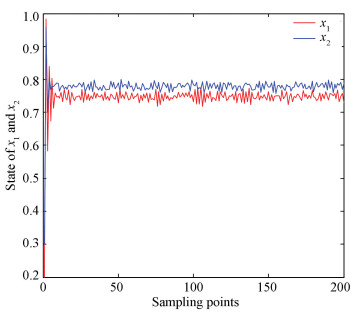
Fig. 1 shows the state of x1and x2.
|
Fig.1 The state of x1 and x2 |
As the aforementioned, for the state estimation of the proposed non-linear sampled-data descriptor system, the superiority of the REKF algorithm is that the convergence of the error covariance matrix of the Kalman Filtering can be guaranteed. Based on this reason, we choose to compare the state estimation error obtained by REKF algorithm with the one obtained by the EKF algorithm to show the effectiveness of the REKF algorithm.
The previous simulations were carried out with MATLAB programs on a Intel(R) Core(TM) i5-3210M CPU@ 2.50 GHz and 8 GB memory PC. The state estimation error obtained by REKF algorithm and EKF algorithm is shown in Fig. 2 and Fig. 3.
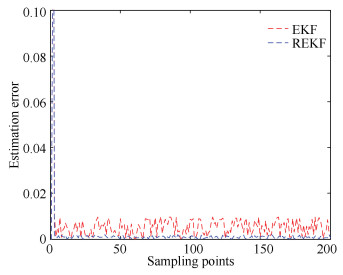
|
Fig.2 State estimation error of x1 by EKF and REKF |
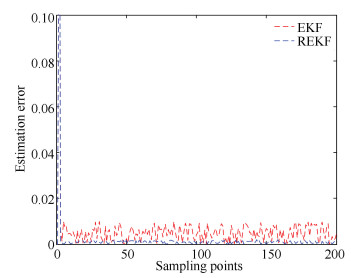
|
Fig.3 State estimation error of x2 by EKF and REKF |
The Root Mean Square Error (RMSE) of the estimation for the two state vectors of the proposed non-linear sampled-data descriptor system separately by using the conventional EKF algorithm and the REKF algorithm is shown in Table 1.
| Table 1 RMSE of the estimation in EKF and REKF |
Now we analyze the simulation figures and the tables.
From Fig. 2 and Fig. 3, it can be seen that for the proposed sampled-data descriptor system, REKF algorithm has a better state estimation than the conventional EKF algorithm. The estimation error in the both two figures obtained by the REKF algorithm is smaller the one obtained by the EKF algorithm.
Table 1 further proofed that the proposed REKF algorithm is more accurate in the state estimation of the proposed descriptor systems when comparing with the conventional EKF algorithm.
By analyzing the figures and the tables, As the proposed REKF algorithm provided an upper-bound for the new uncertainties caused by the introduced parameters in the dynamic model of the transformed non-singular system, the convergence of the estimating error can be guaranteed, and the state of the proposed norm-bounded non-linear sampled-data descriptor systems can be accurately estimated by our method.
5 ConclusionIn this paper, a REKF algorithm is proposed for the state estimation of norm-bounded non-linear sampled-data descriptor system with noises. First, using the Euler discretization method and the introduced parameters, the proposed sampled-data descriptor model is discretized to be a non-singular discrete time one. Then, the EKF algorithm is proposed for solving the non-linear problem for the transformed non-singular system. As the introduced parameters and the transforming way, an uncertainty exists in the dynamic model of the transformed system. Then an upper-bound is introduced for depressing the influence of the uncertainties on the estimation results so that the convergence of the error covariance matrix in the process of the Kalman filtering is guaranteed. At last, the given simulating example shows that, the proposed REKF algorithm has a better estimating effect comparing with the conventional EKF one for this class of sampled-data descriptor systems.
AppendixIn this section, Theorem 1 is proofed.
Proof
Substitute Eq.(27) into Eq. (32), and for the system (38), Ak=0 it is obtained that
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\tilde x}}}_k} = {\mathit{\boldsymbol{x}}_k} - {{\mathit{\boldsymbol{\dot x}}}_k} = \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}\mathit{\boldsymbol{C}}} \right){\mathit{\boldsymbol{F}}_k}{{\mathit{\boldsymbol{\hat x}}}_{k - 1}} + }\\ {\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}\mathit{\boldsymbol{C}}} \right){{\mathit{\boldsymbol{\bar w}}}_{k - 1}} - {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{v}}_k}} \end{array} $ | (AP1) |
From the Eq.(AP1) it is obtained that
| $ \begin{array}{l} \left\| {{{\mathit{\boldsymbol{\tilde x}}}_k}} \right\|_{\bar P_k^{ - 1}}^2 = \mathit{\boldsymbol{E}}\left( {\mathit{\boldsymbol{\tilde x}}_k^{\rm{T}}\mathit{\boldsymbol{\bar P}}_\mathit{\boldsymbol{k}}^{ - 1}{{\mathit{\boldsymbol{\tilde x}}}_\mathit{\boldsymbol{k}}}} \right) = \\ \;\;\;\;\;\;\;\;\;\left\{ {\mathit{\boldsymbol{\tilde x}}_{k - 1}^T\mathit{\boldsymbol{F}}_k^{\rm{T}}{{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}\mathit{\boldsymbol{C}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\bar P}}_k^{ - 1}\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}\mathit{\boldsymbol{C}}} \right){\mathit{\boldsymbol{F}}_k}{{\mathit{\boldsymbol{\tilde x}}}_{k - 1}} + } \right.\\ \;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{\bar w}}_{k - 1}^{\rm{T}}{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}\mathit{\boldsymbol{C}}} \right)^{\rm{T}}}\mathit{\boldsymbol{\bar P}}_k^{ - 1}\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}\mathit{\boldsymbol{C}}} \right){{\mathit{\boldsymbol{\bar w}}}_{k - 1}} + \\ \;\;\;\;\;\;\;\;\;\left. {\mathit{\boldsymbol{v}}_k^{\rm{T}}\mathit{\boldsymbol{K}}_k^{\rm{T}}\mathit{\boldsymbol{\bar P}}_\mathit{\boldsymbol{k}}^{ - 1}{\mathit{\boldsymbol{K}}_v}{\mathit{\boldsymbol{v}}_k}} \right\} \end{array} $ | (AP2) |
From the Eq. (41) it is obtained that
| $ {{\mathit{\boldsymbol{\bar P}}}_k} \ge \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}\mathit{\boldsymbol{C}}} \right){{\mathit{\boldsymbol{\bar P}}}_{k/k - 1}}{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}\mathit{\boldsymbol{C}}} \right)^{\rm{T}}} $ | (AP3) |
From the Eq.(AP3), the second term of Eq.(AP2) can be rewritten as the following inequality
| $ \begin{array}{l} \mathit{\boldsymbol{\bar w}}_{k - 1}^{\rm{T}}{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}\mathit{\boldsymbol{C}}} \right)^{\rm{T}}}\mathit{\boldsymbol{\bar P}}_\mathit{\boldsymbol{k}}^{ - 1}\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}\mathit{\boldsymbol{C}}} \right){{\mathit{\boldsymbol{\bar w}}}_{k - 1}} \le \\ \;\;\;\;\;\mathit{\boldsymbol{\bar w}}_{k - 1}^{\rm{T}}\mathit{\boldsymbol{\bar P}}_{k/k - 1}^{ - 1}{{\mathit{\boldsymbol{\bar w}}}_{k - 1}} \end{array} $ | (AP4) |
Substitute the Eq.(40) into Eq.(AP4), it is obtained that
| $ \begin{array}{l} \mathit{\boldsymbol{\bar w}}_{k - 1}^{\rm{T}}{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}\mathit{\boldsymbol{C}}} \right)^{\rm{T}}}\mathit{\boldsymbol{\bar P}}_\mathit{\boldsymbol{k}}^{ - 1}\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}\mathit{\boldsymbol{C}}} \right){{\mathit{\boldsymbol{\bar w}}}_{k - 1}} \le \\ \;\;\;\;\;\mathit{\boldsymbol{\bar w}}_{k - 1}^{\rm{T}}\mathit{\boldsymbol{\bar Q}}_{k - 1}^{ - 1}\mathit{\boldsymbol{\bar w}}_{k - 1}^{\rm{T}} \end{array} $ | (AP5) |
It is easy to verify that
| $ {\mathit{\boldsymbol{K}}_k} = {{\mathit{\boldsymbol{\bar P}}}_k}{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{R}}_k^{ - 1} $ | (AP6) |
Using the Eq.(AP6), the third term of Eq.(AP2) can be rewritten as
| $ \mathit{\boldsymbol{v}}_k^{\rm{T}}\mathit{\boldsymbol{K}}_k^{\rm{T}}\mathit{\boldsymbol{\bar P}}_k^{ - 1}{\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{v}}_k} = \mathit{\boldsymbol{v}}_k^{\rm{T}}\mathit{\boldsymbol{R}}_k^{ - 1}\mathit{\boldsymbol{C}}{{\mathit{\boldsymbol{\bar P}}}_k}{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{R}}_k^{ - 1}{\mathit{\boldsymbol{v}}_k} $ | (AP7) |
It is also verified that
| $ \mathit{\boldsymbol{R}}_k^{ - 1} - \mathit{\boldsymbol{R}}_k^{ - 1}\mathit{\boldsymbol{C}}{{\mathit{\boldsymbol{\bar P}}}_k}{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{R}}_k^{ - 1} = {\left( {\mathit{\boldsymbol{C}}{{\mathit{\boldsymbol{\bar P}}}_{k/k - 1}}{\mathit{\boldsymbol{C}}^{\rm{T}}} + {\mathit{\boldsymbol{R}}_k}} \right)^{ - 1}} \ge 0 $ | (AP8) |
From the Eq.(AP8), the following inequality is obtained as
| $ \mathit{\boldsymbol{v}}_k^{\rm{T}}\mathit{\boldsymbol{K}}_k^{\rm{T}}\mathit{\boldsymbol{\bar P}}_k^{ - 1}{\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{v}}_k} \le \mathit{\boldsymbol{v}}_k^{\rm{T}}\mathit{\boldsymbol{R}}_k^{ - 1}{\mathit{\boldsymbol{v}}_k} $ | (AP9) |
From the Eq.(AP3), the first term of Eq.(AP2) can be rewritten as
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\tilde x}}_{k - 1}^{\rm{T}}\mathit{\boldsymbol{F}}_k^{\rm{T}}{{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}\mathit{\boldsymbol{C}}} \right)}^{\rm{T}}}{{\mathit{\boldsymbol{\bar P}}}^{ - 1}}\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}\mathit{\boldsymbol{C}}} \right){\mathit{\boldsymbol{F}}_k}{{\mathit{\boldsymbol{\tilde x}}}_{k - 1}} \le }\\ {\mathit{\boldsymbol{\tilde x}}_{k - 1}^{\rm{T}}{\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{\bar P}}_{k/k - 1}^{ - 1}{\mathit{\boldsymbol{F}}_k}{{\mathit{\boldsymbol{\tilde x}}}_{k - 1}}} \end{array} $ | (AP10) |
From the Eq.(40) we can see that
| $ {{\mathit{\boldsymbol{\bar P}}}_{k/k - 1}} \ge {\mathit{\boldsymbol{F}}_k}{\left( {\mathit{\boldsymbol{\bar P}}_{k - 1}^{ - 1} - {\gamma ^{ - 2}}{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{G}}} \right)^{ - 1}}\mathit{\boldsymbol{F}}_k^\Gamma $ | (AP11) |
From the Eqs.(AP3) and (AP11), (AP10) can be rewritten as
| $ \begin{array}{l} \mathit{\boldsymbol{\tilde x}}_{k - 1}^{\rm{T}}\mathit{\boldsymbol{F}}_k^{\rm{T}}{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}\mathit{\boldsymbol{C}}} \right)^{\rm{T}}}\mathit{\boldsymbol{P}}_k^{ - 1}\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}\mathit{\boldsymbol{C}}} \right){\mathit{\boldsymbol{F}}_k}{{\mathit{\boldsymbol{\tilde x}}}_{k - 1}} \le \\ \;\;\;\;\;\;\;\;\mathit{\boldsymbol{\tilde x}}_{k - 1}^{\rm{T}}\mathit{\boldsymbol{F}}_k^{\rm{T}}\mathit{\boldsymbol{\bar P}}_{\mathit{\boldsymbol{k}}/\mathit{\boldsymbol{k}} - 1}^{ - 1}{\mathit{\boldsymbol{F}}_k}{{\mathit{\boldsymbol{\tilde x}}}_{k - 1}} \le \mathit{\boldsymbol{\tilde x}}_{k - 1}^{\rm{T}}\mathit{\boldsymbol{P}}_{k - 1}^{{\rm{ - 1}}}{{\mathit{\boldsymbol{\tilde x}}}_{k - 1}} - \\ \;\;\;\;\;\;\;\;{\gamma ^{ - 2}}\mathit{\boldsymbol{\tilde x}}_{k - 1}^{\rm{T}}{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{G}}{{\mathit{\boldsymbol{\tilde x}}}_{k - 1}} \end{array} $ | (AP12) |
From the Eqs.(AP5), (AP9) and (AP12), (AP12) can be rewritten as the following inequality
| $ \begin{array}{*{20}{c}} {\left\| {{{\mathit{\boldsymbol{\tilde x}}}_k}} \right\|_{\bar P_k^{ - 1}}^2 \le \left\| {{{\mathit{\boldsymbol{\tilde x}}}_{k - 1}}} \right\|_{\bar P_{k - 1}^{ - 1}}^2 - {\gamma ^{ - 2}}\left\| {{{\mathit{\boldsymbol{\tilde x}}}_k}} \right\|_{{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{G}}}^2 + }\\ {\left\| {{{\mathit{\boldsymbol{\bar w}}}_{k - 1}}} \right\|_{\bar Q_{k - 1}^{ - 1}}^2 + \left\| {{\mathit{\boldsymbol{v}}_k}} \right\|_{R_k^{ - 1}}^2} \end{array} $ | (AP13) |
Further, adding the both sides of the Eq. (AP13), it is obtained that
| $ \begin{array}{*{20}{c}} {\left\| {{{\mathit{\boldsymbol{\tilde x}}}_n}} \right\|_{\bar P_n^{ - 1}}^2 \le \left\| {{{\mathit{\boldsymbol{\tilde x}}}_0}} \right\|_{\bar P_0^{ - 1}}^2 - {\gamma ^{ - 2}}\sum\limits_{k = 0}^{n - 1} {\left\| {{{\mathit{\boldsymbol{\tilde x}}}_k}} \right\|_{{G^{\rm{T}}}G}^2} + }\\ {\sum\limits_{k = 1}^n {\left( {\left\| {{{\mathit{\boldsymbol{\bar w}}}_{k - 1}}} \right\|_{\mathit{\boldsymbol{\bar Q}}_{k - 1}^{ - 1}}^2 + \left\| {{\mathit{\boldsymbol{v}}_k}} \right\|_{\mathit{\boldsymbol{R}}_k^{ - 1}}^2} \right)} } \end{array} $ | (AP14) |
where
From the Eq.(40) it is obtained that
| $ \mathit{\boldsymbol{\bar P}}_n^{ - 1} > {\gamma ^{ - 2}}{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{G}} $ | (AP15) |
By the Eqs.(AP14) and (AP15) it is obtained that
| $ \begin{array}{l} \sum\limits_{k = 0}^n {\left\| {{{\mathit{\boldsymbol{\tilde x}}}_k}} \right\|_{{\mathit{\boldsymbol{G}}^{\bf{T}}}\mathit{\boldsymbol{G}}}^2} \le {\gamma ^2}\left[ {\left\| {{{\tilde x}_0}} \right\|_{\mathit{\boldsymbol{\bar P}}_0^{ - 1}}^2 + } \right.\\ \;\;\;\;\;\;\left. {\sum\limits_{k = 1}^n {\left( {\left\| {{{\mathit{\boldsymbol{\bar w}}}_{k - 1}}} \right\|_{\mathit{\boldsymbol{\bar Q}}_{k - 1}^{ - 1}}^2 + \left\| {{\mathit{\boldsymbol{v}}_k}} \right\|_{\mathit{\boldsymbol{R}}_k^{ - 1}}^2} \right)} } \right] \end{array} $ | (AP16) |
So Theorem 1 is proofed.
| [1] |
Zhou Zhenhua. Robust Control and Filtering for Singular Piecewise-Affine Systems with Norm-Bounded Uncertainties. Harbin: Harbin Institute of Technology, 2016.
(  0) 0) |
| [2] |
Duan G R. Analysis and Design of Descriptor Linear Systems. New York: Springer New York, 2010.
(  0) 0) |
| [3] |
Liu P, Zhang Q, Yang X, et al. Passivity and optimal control of descriptor biological complex systems. IEEE Transactions on Automatic Control, 2008, 53(Special Issue): 122-125. DOI:10.1109/TAC.2007.911341 (  0) 0) |
| [4] |
Stevens B L, Lewis F L. Aircraft Modeling, Dynamics and Control. New York: Wiley, 1991.
(  0) 0) |
| [5] |
Zhang B. Parametric eigenstructure assignment by state feedback in descriptor systems. IET Control Theory & Applications, 2008, 2(4): 303-309. DOI:10.1049/iet-cta:20070337 (  0) 0) |
| [6] |
Gao Z, Ding S X. Actuator fault robust estimation and fault-tolerant control for a class of nonlinear descriptor systems. Automatica, 2007, 43(5): 912-920. DOI:10.1016/j.automatica.2006.11.018 (  0) 0) |
| [7] |
Darouach M, Boutayeb M. Design of observers for descriptor systems. IEEE Transactions on Automatic Control, 1995, 40(7): 1323-1327. DOI:10.1109/9.400467 (  0) 0) |
| [8] |
Koenig D, Mammar S. Design of proportional-integral observer for unknown input descriptor systems. IEEE Transactions on Automatic Control, 2002, 47(2): 2057-2062. DOI:10.1109/TAC.2002.805675 (  0) 0) |
| [9] |
Koenig D. Observer design for unknown input nonlinear descriptor systems via convex optimization. IEEE Transactions on Automatic Control, 2006, AC-51(6): 1047-1052. (  0) 0) |
| [10] |
Nikoukhah R. A Deterministic and Stochastic Theory for Two-point Boundary-value Descriptor Systems. Cambridge, MA: Massachusetts Institute of Technology, 1988.
(  0) 0) |
| [11] |
Nikoukhah R, Levy B C, Willsky A S. Generalized Riccati equations for two-point boundary-value descriptor systems. In hoc. 26th ZEEE Conf. Decision Contr., Los Angeles, CA, 1987. 1040-1141.
(  0) 0) |
| [12] |
Wang X M, Bernhard P. Filtrage et lissage des systèmes implicites discrets. Tech. Rep. 1083, Institut National de Recherche en Informatique et Automatique, Rocquencourt, France, 1989.
(  0) 0) |
| [13] |
Mehrmann V. Existence, uniqueness, and stability of solutions to singular linear quadratic optimal control problems. Linear Algebra, 1989, 121: 291-331. DOI:10.1016/0024-3795(89)90707-6 (  0) 0) |
| [14] |
Darouach M, Zasadzinski M, Mehdi D. State estimation of stochastic singular linear systems. Int. J. Syst. Sci., 1993, 2(2): 345-354. (  0) 0) |
| [15] |
Darouach M, Zasadzinski M, Onana A B, et al. Kalman filtering with unknown inputs via optimal state estimation of singular systems. Int. J. Syst. Sci., 1995, 26(10): 2015-2028. DOI:10.1080/00207729508929152 (  0) 0) |
| [16] |
Nikoukhah R, Willsky A S, Levy B C. Kalman filtering and Riccati equations for descriptor systems. IEEE Transactions on Automatic Control, 1992, 37(9): 1325-1342. DOI:10.1109/9.159570 (  0) 0) |
| [17] |
Nikoukhah R, Campbell S L, Delebecque F. Kalman filtering for general discrete-time linear systems. IEEE Transactions on Automatic Control, 1999, 44(10): 1548-1552. (  0) 0) |
| [18] |
Becerra V M, Roberts P D, Griffiths G W. Applying the extended Kalman filter to systems described by nonlinear differential-algebraic equations. Control Engineering Practice, 2001, 9(3): 267-281. DOI:10.1016/S0967-0661(00)00110-6 (  0) 0) |
| [19] |
Kai Xiong, Wei Chunling, Liu Liangdong. Robust extended Kalman filtering for nonlinear systems with stochastic uncertainties. IEEE Transactions on systems, Man, and Cybernetics-Part A: Systems and Humans, 2010, 40(2): 399-405. DOI:10.1109/TSMCA.2009.2034836 (  0) 0) |
| [20] |
Adi B-I, Greville T N E. Generalized Inverses Theory and Applications. New York: Springer, Science & Business Media, 2003.
(  0) 0) |
| [21] |
Theodor Y, Shaked U. Robust discrete-time minimum-variance filtering. IEEE Transactions on Signal Processing, 1996, 44(2): 181-189. DOI:10.1109/78.485915 (  0) 0) |
 2019, Vol. 26
2019, Vol. 26


