2. School of Mathematics and Computer Science, Hezhou University, Hezhou 542899, Guangxi, China
In recent years, a focus of active research has been developed in the first-order methods of convex optimization, e.g., Refs.[1-4]. Their improved convergence rates and low complexity of each iteration have made them a feasible alternative in large-scale problems. The popularity of first-order methods has been further increased the rapid development of convex optimization and has been applied in machine learning and signal processing.
Nesterov pioneers the class of first-order methods[5] which are called accelerated gradient methods. Compared with the classical gradient method, these first-order methods enjoy a better convergence rate. Several variants of accelerated gradient methods have been developed in Refs. [6-10]. These first-order methods have become particularly popular. In particular, we notice the fast iterative shrinkage-thresholding Algorithm (FISTA) in Ref.[6]. FISTA and Nesterov's optimal gradient method[2] enjoy a better convergence rate for convex composite functions.
Both FISTA and Nesterov's optimal gradient method[2] have an ε-optimal solution in
Unlike the Nesterov's optimal gradient method[2], FISTA is required to calculate one gradient at each iteration. The Nesterov's optimal gradient method[2] uses a more general framework, compared to the FISTA. The convergence rate of FISTA has not been analyzed in Ref. [2]. FISTA and analysis of FISTA are especially intuitive and simple, which has made it being used in many applications. The principal drawback of FISTA is that it needs to estimate the Lipschitz constant in each iteration, compared to the Nesterov's optimal gradient method [2]. What's more, the estimated Lipschitz constant must remain non-decreasing during the iterative process. Therefore, when the estimated Lipschitz constant is too large, it substantially limits the performance of FISTA and causes that the sizes of the steps to be very small in the early iteration.
One characteristic of FISTA is that the iterates are not monotone. This is sometimes an unpopular behavior which has been described in Refs. [9, 12]. A monotonic version of FISTA has been proposed in Ref. [12]. In these methods, the non-monotonicity is determined by comparing the current iteration function value with the function value of the previous iteration, and the monotonicity is guaranteed by taking appropriate measures. To achieve a faster convergence rate, an algorithm is proposed by exploiting the non-monotonicity in Ref. [13]. In the numerical results, the algorithm in Ref. [13] performs much better than FISTA, at in least medium to high precision.
In this paper, we first present an accelerated first-order method that preserves the computational simplicity of FISTA. A difference of the first proposed algorithm and FISTA is that the first proposed algorithm chooses the step size 1/Lk to be 1/L0 at the beginning of each iteration. The first proposed algorithm is a non-monotone algorithm. To avoid this behavior, we also present an accelerated monotone first-order method. The proposed two accelerated first-order methods have a better convergence rate when solving composite convex programming.
The contents of this article are as follows. The model problem and preliminary results are described in Section 2. We present two accelerated first-order methods and prove that the two algorithms exhibit a better convergence rate in Section 3. Numerical experiments are introduced in Section 4.
2 Model Problem and Preliminary ResultsIn this paper, we consider useful composite unconstrained convex programming:
| $ \min \left\{ {F\left( x \right) = f\left( x \right) + g\left( x \right):x \in {R^n}} \right\} $ | (1) |
An important assumption is described as following and satisfies throughout the paper.
Assumption 1:
1) g:Rn→(-∞, +∞] is a proper, closed, and convex function.
2) f:Rn→R is continuously differentiable function with Lipschitz continuous gradient Lf:
‖∇f(x)-∇f(y)‖≤Lf‖x-y‖ for ∀x, y∈Rn where ‖·‖ denotes the standard Euclidean norm and Lf is the Lipschitz constant of ∇f(x).
3) Problem (1) is solvable, i.e., X*=argminF≠ϕ, and for x*∈X* we set F*=F(x*).
In Ref. [6], FISTA is presented for solving composite unconstrained convex programming (1). We introduce an approximation model and some preliminary results which are described in Ref. [6].
For ∀L>0, consider a quadratic approximation of F(x)=f(x)+g(x) at a given point y:
| $ \begin{array}{*{20}{c}} {{Q_L}\left( {x,y} \right) = f\left( y \right) + \left\langle {x - y,\nabla f\left( y \right)} \right\rangle + }\\ {\frac{L}{2}{{\left\| {x - y} \right\|}^2} + g\left( x \right)} \end{array} $ |
which has a unique minimum point
| $ {p_L}\left( y \right) = {\rm argmin}\left\{ {{Q_L}\left( {x,y} \right):x \in {R^n}} \right\} $ |
Obviously, the pL(y) can be written by
| $ {p_L}\left( y \right) = \mathop {{\rm argmin}}\limits_x \left\{ {g\left( x \right) + \frac{L}{2}{{\left\| {x - \left( {y - \frac{1}{L}\nabla f\left( y \right)} \right)} \right\|}^2}} \right\} $ |
Clearly, the general step of FISTA is to be
| $ {x^k} = {p_{{L_k}}}\left( {{y^k}} \right) $ |
where 1/Lk is a step size.
The following two lemmas play a key role in the analysis. The first lemma is well-known and has the basic properties of the smooth function, e.g., Ref.[14].
Lemma 2.1 Let f:Rn→R is a continuously differentiable function with Lipschitz continuous gradient Lf. Then, ∀L≥Lf,
| $ f\left( x \right) \le f\left( y \right) + \left\langle {x - y,\nabla f\left( y \right)} \right\rangle + \frac{L}{2}{\left\| {x - y} \right\|^2} $ | (2) |
for ∀x, y∈Rn.
Lemma 2.2 (Lemma 2.3 in Ref. [6]) Let y∈Rn, L>0 be such that
| $ F\left( {{p_L}\left( y \right)} \right) \le {Q_L}\left( {{p_L}\left( y \right),y} \right) $ | (3) |
Then
| $ \begin{array}{l} F\left( x \right) - F\left( {{p_L}\left( y \right)} \right) \ge \frac{L}{2}{\left\| {{p_L}\left( y \right),y} \right\|^2} + \\ \;\;\;\;\;\;\;\;\;\;L\left\langle {x - y,y - {p_L}\left( y \right)} \right\rangle = \\ \;\;\;\;\;\;\;\;\;\;\frac{L}{2}\left( {{{\left\| {{p_L}\left( y \right) - x} \right\|}^2} - {{\left\| {y - x} \right\|}^2}} \right) \end{array} $ | (4) |
for ∀x∈Rn.
3 Two Accelerated First-Order MethodsThe principal drawback of FISTA is that it needs to estimate the Lipschitz constant in each iteration. What's more, the estimated Lipschitz constant must remain nondecreasing during the iterative process. Consequently, when the estimated Lipschitz constant is too large, it substantially limits the performance of FISTA and causes the sizes of the steps to be very small in the early iteration. To overcome this drawback, consider the following modified FISTA.
| Algorithm 1 |
| Let L0>0, η>1, and x0∈Rn. Take y1=x0, t1=1; For k=1, 2, … do Lk=L0 Finding the smallest non-negative integers ik such Lk=ηikLk and F(pLk(yk))≤QLk(pLk(yk), yk) xk=pLk(yk) |
Remark 1 Algorithm 1 is similar to the FISTA. One common characteristic of Algorithm 1 and FISTA is that the current iterative information uses the two previous iterative information sets in an extraordinary way. A difference of the Algorithm 1 and FISTA is that Algorithm 1 chooses the step size 1/Lkto be 1/L0 at the beginning of each iteration.
Remark 2 For Lk≥Lf, inequality (3) is satisfied. For ∀k≥1, there is inequality Lk≤ηLf by algorithm 1. Therefore,
| $ \beta {L_f} \le {L_k} \le \alpha {L_f} $ | (5) |
where α=η, β=L0/Lf in the backtracking case.
In Ref. [6], the proof of the convergence rate of FISTA depends on a fact which the selected Lk satisfies inequality Lk≤Lk-1, for ∀k≥1. In other words, the step size 1/Lk is monotonically decreasing. We make use of an analysis which is similar to the analysis in Ref. [6]. The analysis increases the step sizes of Algorithm 1 and preserves the complexity
The proof of complexity result of Algorithm 1 make use of the following two lemmas.
Lemma 3.1 The sequences {xk}, {yk} generated by Algorithm 1.Then, for uk=tkxk-(tk-1)xk-1-x* and vk=F(xk)-F(x*),
| $ \left( {2/{L_f}} \right)t_k^2{v^k} + \left\| {{u^k}} \right\| \ge \left\| {{u^{k + 1}}} \right\| + \left( {2/{L_f}} \right)t_{k + 1}^2{v^{k + 1}} $ | (6) |
for ∀k≥1.
Proof In Lemma 2.2, let y=yk+1, L=Lk+1, and pLk+1(yk+1)=xk+1. Then, for x=xk, we obtain
| $ \begin{array}{l} {v^k} - {v^{k + 1}} \ge \left( {{L_{k + 1}}/2} \right){\left\| {{y^{k + 1}} - {x^{k + 1}}} \right\|^2} + \\ \;\;\;\;{L_{k + 1}}\left\langle {{x^{k + 1}} - {y^{k + 1}},{y^{k + 1}} - {x^k}} \right\rangle \end{array} $ | (7) |
and for x=x* we have
| $ \begin{array}{*{20}{c}} { - {v^{k + 1}} \ge \left( {{L_{k + 1}}/2} \right){{\left\| {{y^{k + 1}} - {x^{k + 1}}} \right\|}^2} + }\\ {{L_{k + 1}}\left\langle {{x^{k + 1}} - {y^{k + 1}},{y^{k + 1}} - {x^ * }} \right\rangle } \end{array} $ | (8) |
Multiplying Eq.(7) by (tk+1-1) and adding it to Eq.(8), we obtain
| $ \begin{array}{*{20}{c}} {\left( {{t_{k + 1}} - 1} \right){v^k} - {t_{k + 1}}{v^{k + 1}} \ge \left( {{L_{k + 1}}/2} \right){t_{k + 1}}{{\left\| {{y^{k + 1}} - {x^{k + 1}}} \right\|}^2} + }\\ {{L_{k + 1}}\left\langle {{x^{k + 1}} - {y^{k + 1}},{t_{k + 1}}{y^{k + 1}} - \left( {{t_{k + 1}} - 1} \right){x^k} - {x^ * }} \right\rangle } \end{array} $ | (9) |
Multiplying Eq.(9) by tk+1, and using equality tk2=tk+12-tk+1, we obtain
| $ \begin{array}{*{20}{c}} {\frac{2}{{{L_{k + 1}}}}\left( {t_k^2{v^k} - t_{k + 1}^2{v^{k + 1}}} \right) \ge {{\left\| {{t_{k + 1}}\left( {{y^{k + 1}} - {x^{k + 1}}} \right)} \right\|}^2} + }\\ {2{t_{k + 1}}\left\langle {{x^{k + 1}} - {y^{k + 1}},{t_{k + 1}}{y^{k + 1}} - \left( {{t_{k + 1}} - 1} \right){x^k} - {x^*}} \right\rangle } \end{array} $ | (10) |
Then, applying Eq.(4) to right-hand side of the Eq.(10), thus we get
| $ \begin{array}{l} \frac{2}{{{L_{k + 1}}}}\left( {t_k^2{v^k} - t_{k + 1}^2{v^{k + 1}}} \right) \ge {\left\| {{t_{k + 1}}{x^{k + 1}} - \left( {{t_{k + 1}} - 1} \right){x^k} - {x^*}} \right\|^2} - \\ \;\;\;\;\;\;{\left\| {{t_{k + 1}}{y^{k + 1}} - \left( {{t_{k + 1}} - 1} \right){x^k} - {x^*}} \right\|^2} \end{array} $ | (11) |
Obviously, yk+1 and uk are written by
| $ {t_{k + 1}}{y^{k + 1}} = {t_{k + 1}}{x^k} - \left( {{t_k} - 1} \right)\left( {{x^k} - {x^{k - 1}}} \right) $ |
and
| $ {u^k} = {t_k}{x^k} - \left( {{t_k} - 1} \right){x^{k - 1}} - {x^ * } $ |
From Eq. (11), it follows that
| $ \frac{2}{{{L_{k + 1}}}}\left( {t_k^2{v^k} - t_{k + 1}^2{v^{k + 1}}} \right) \ge {\left\| {{u^{k + 1}}} \right\|^2} - {\left\| {{u^k}} \right\|^2} $ | (12) |
Finally, combined with the inequality Lk+1≥Lf, we then obtain
| $ \frac{2}{{{L_f}}}t_k^2{v^k} - \frac{2}{{{L_f}}}t_{k + 1}^2{v^{k + 1}} \ge {\left\| {{u^{k + 1}}} \right\|^2} - {\left\| {{u^k}} \right\|^2} $ |
which is equivalent to Eq. (6).
Lemma 3.2 (Lemma 4.3 in Ref.[6]) The sequence {tk} generated by Algorithm 1 and satisfies t1=1. Then, for ∀k≥1,
| $ {t_k} \ge \left( {k + 1} \right)/2 $ |
The following theorem indicates the convergence rate O(1/k2) of Algorithm 1. We are now ready to prove the complexity result for Algorithm 1.
Theorem 3.1 Let {xk}, {yk} be generated by Algorithm 1. Then, for ∀k≥1
| $ F\left( {{x^k}} \right) - F\left( {{x^*}} \right) \le \frac{{2\eta {L_f}{{\left\| {{x^0} - {x^*}} \right\|}^2}}}{{{{\left( {k + 1} \right)}^2}}} $ | (13) |
Proof Obviously ‖uk‖2≥0, u1=x1-x*, and t1=1. From Lemma 3.1, it follows that
| $ \begin{array}{l} \left( {2/{L_f}} \right)t_k^2{v^k} \le \left( {2/{L_f}} \right)t_k^2{v^k} + {\left\| {{u^k}} \right\|^2} \le \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {2/{L_f}} \right){v^1} + {\left\| {{x^1} - {x^*}} \right\|^2} \end{array} $ | (14) |
From Lemma 3.1, let x=x*, y=y1=x0, t1=1 and L=L1, we obtain
| $ - \left( {2/{L_1}} \right){v^1} \ge {\left\| {{x^1} - {x^*}} \right\|^2} - {\left\| {{x^0} - {x^*}} \right\|^2} $ |
which combined with the inequality L1≤ηLf, we then have
| $ \left( {2/\eta {L_f}} \right){v^1} \le {\left\| {{x^0} - {x^*}} \right\|^2} - {\left\| {{x^1} - {x^*}} \right\|^2} $ | (15) |
Therefore, combining Eq. (14) and Eq. (15), we obtain
| $ \left( {2/{L_f}} \right)t_k^2{v^k} \le \eta {\left\| {{x^0} - {x^*}} \right\|^2} $ |
which combined with tk≥(k+1)/2, we then have
| $ F\left( {{x^k}} \right) - F\left( {{x^*}} \right) \le \frac{{2\eta {L_f}{{\left\| {{x^0} - {x^*}} \right\|}^2}}}{{{{\left( {k + 1} \right)}^2}}} $ |
Nesterov's first-order methods[5]indicates that Algorithm 1 can not guarantee monotonous decreasing of {F(xk)}. Therefore, many authors try to guarantee monotonicity via restart techniques[13, 15]. We present the following an algorithm with restart: set yk=xk whenever F(xk)>F(xk-1).
| Algorithm 2 |
| Let L0>0, η>1, and x0∈Rn. Take y1=x0, t1=1; For k=1, 2, … do Lk=L0 Finding the smallest non-negative integers ik such Lk=ηikLk and F(pLk(yk))≤QLk(pLk(yk), yk) xk=pLk(yk) If F(xk)>F(xk-1) then yk+1=xk |
For Lk≥Lf, inequality (3) is satisfied. For ∀k≥1, there is inequality Lk≤ηLf by algorithm 1. Therefore,
| $ \beta {L_f} \le {L_k} \le \alpha {L_f} $ |
where α=η, β=L0/Lf in the backtracking case.
In the analysis of complexity result for Algorithm 2, we suppose that for a limited number of iterations, the restart is satisfied. To prove complexity result of Algorithm 2, we first give the following function
| $ \varphi \left( {y,x} \right) = f\left( x \right) + \left\langle {\nabla f\left( y \right),x - y} \right\rangle + g\left( x \right) $ |
Clearly, the xk-update can be changed
| $ {x^k} = \mathop {{\rm argmin}}\limits_x \left\{ {\varphi \left( {{y^k},x} \right) + \frac{{{L_k}}}{2}{{\left\| {x - {y^k}} \right\|}^2}} \right\} $ | (16) |
To prove complexity result of Algorithm 2, the following a lemma is also required.
Lemma 3.3 (Lemma 1 in Ref.[15]) Suppose that ϕ:Rn→ (-∞, +∞] is a proper, closed, and convex function. For L>0, and
| $ {x^ + } = \mathop {{\rm argmin}}\limits_x \left\{ {\phi \left( x \right) + \frac{L}{2}{{\left\| {x - y} \right\|}^2}} \right\} $ |
Then for ∀x∈ dom ϕ
| $ \begin{array}{l} \phi \left( x \right) + \frac{L}{2}{\left\| {x - y} \right\|^2} \ge \phi \left( {{x^ + }} \right) + \frac{L}{2}{\left\| {{x^ + } - y} \right\|^2} + \\ \;\;\;\;\;\frac{L}{2}{\left\| {{x^ + } - x} \right\|^2} \end{array} $ | (17) |
Now, we prove complexity result of Algorithm 2.
Theorem 2 Let {xk}, {yk} be generated by Algorithm 2. For iterations k=k1, …, kq, restart is satisfied. Then for ∀k≥1
| $ \begin{array}{l} F\left( {{x^{k + 1}}} \right) - F\left( {{x^*}} \right) \le \frac{{2\eta {L_f}}}{{{{\left( {k + 2} \right)}^2}}}\left\{ {{{\left\| {{x^*} - {x^0}} \right\|}^2} + } \right.\\ \left. {\sum\limits_{k \ge {k_i}} {\left\{ {{{\left\| {{x^{{k_i}}} - {x^*}} \right\|}^2} - {{\left\| {{z^{{k_i}}} - {x^*}} \right\|}^2}} \right\}} } \right\} \end{array} $ | (18) |
where zk=xk-1+tk(xk-xk-1).
Proof Let
| $ \begin{array}{l} F\left( {{x^{k + 1}}} \right) \le \varphi \left( {{y^{k + 1}},{x^{k + 1}}} \right) + \frac{{{L_{k + 1}}}}{2}{\left\| {{y^{k + 1}} - {x^{k + 1}}} \right\|^2} \le \\ \;\;\;\;\varphi \left( {{y^{k + 1}},y} \right) + \frac{{{L_{k + 1}}}}{2}\left\{ {{{\left\| {{y^{k + 1}} - y} \right\|}^2} - {{\left\| {{x^{k + 1}} - y} \right\|}^2}} \right\} = \\ \;\;\;\;\varphi \left( {{y^{k + 1}},y} \right) + \frac{{{L_{k + 1}}}}{{2t_{k + 1}^2}}\left\{ {{{\left\| {x + {t_{k + 1}}\left( {{x^k} - {y^{k + 1}}} \right) - {x^k}} \right\|}^2} - } \right.\\ \;\;\;\;\left. {{{\left\| {x + {t_{k + 1}}\left( {{x^k} - {x^{k + 1}}} \right) - {x^k}} \right\|}^2}} \right\} = \varphi \left( {{y^{k + 1}},y} \right) + \\ \;\;\;\;\frac{{{L_{k + 1}}}}{{2t_{k + 1}^2}}\left\{ {{{\left\| {x - {z^k}} \right\|}^2} - {{\left\| {x - {z^{k + 1}}} \right\|}^2}} \right\} = \\ \;\;\;\;\varphi \left( {{y^{k + 1}},\left( {1 - \frac{1}{{{t_{k + 1}}}}} \right){x^k} + \frac{1}{{{t_{k + 1}}}}x} \right) + \\ \;\;\;\;\frac{{{L_{k + 1}}}}{{2t_{k + 1}^2}}\left\{ {{{\left\| {x - {z^k}} \right\|}^2} - {{\left\| {x - {z^{k + 1}}} \right\|}^2}} \right\} \le \\ \;\;\;\;\;\left( {1 - \frac{1}{{{t_{k + 1}}}}} \right)\varphi \left( {{y^{k + 1}},{x^k}} \right) + \frac{1}{{{t_{k + 1}}}}\varphi \left( {{y^{k + 1}},x} \right) + \\ \;\;\;\;\;\;\frac{{{L_{k + 1}}}}{{2t_{k + 1}^2}}\left\{ {{{\left\| {x - {z^k}} \right\|}^2} - {{\left\| {x - {z^{k + 1}}} \right\|}^2}} \right\} \le \\ \;\;\;\;\;\;\left( {1 - \frac{1}{{{t_{k + 1}}}}} \right)F\left( {{x^k}} \right) + \frac{1}{{{t_{k + 1}}}}F\left( x \right) + \\ \;\;\;\;\;\;\;\frac{{{L_{k + 1}}}}{{2t_{k + 1}^2}}\left\{ {{{\left\| {x - {z^k}} \right\|}^2} - {{\left\| {x - {z^{k + 1}}} \right\|}^2}} \right\} \end{array} $ | (19) |
where the first inequality holds from Eq.(2) in Lemma 2.1, the second inequality is due to Eq. (16) and Eq. (17) from Lemma 3.3, the first equality holds by using y, the second equality holds by using yk+1 and identifies zk, the third equality insert y, the third inequality uses convexity of φ(·, x) and tk+1-1∈(0, 1], the last inequality holds by using convexity of f.
For k=ki, we have yk+1=xk, which indicates that in Eq. (19), we obtain
| $ {\left\| {x + {t_{k + 1}}\left( {{x^k} - {y^{k + 1}}} \right) - {x^k}} \right\|^2} = {\left\| {x - {x^k}} \right\|^2} $ | (20) |
where take the place of ‖x-zk‖2.
Therefore, using Eq. (20) in the Eq. (19), we obtain
| $ \begin{array}{*{20}{c}} {F\left( {{x^{k + 1}}} \right) \le \left( {1 - \frac{1}{{{t_{k + 1}}}}} \right)F\left( {{x^k}} \right) + \frac{1}{{{t_{k + 1}}}}F\left( x \right) + }\\ {\frac{{{L_{k + 1}}}}{{2t_{k + 1}^2}}\left\{ {{{\left\| {x - {x^k}} \right\|}^2} - {{\left\| {x - {z^{k + 1}}} \right\|}^2}} \right\}} \end{array} $ | (21) |
for k=ki.
Letting x=x*, multiplying Eq. (19) by tk+12, using the relation tk2=tk+1(tk+1-1), and using the inequality Lk+1≤ηLf, we obtain
| $ \begin{array}{*{20}{c}} {t_{k + 1}^2\left( {F\left( {{x^{k + 1}}} \right) - F\left( {{x^*}} \right)} \right) \le t_k^2\left( {F\left( {{x^k}} \right) - F\left( {{x^*}} \right)} \right) + }\\ {\frac{{\eta {L_f}}}{2}\left\{ {{{\left\| {{z^k} - {x^*}} \right\|}^2} - {{\left\| {{z^{k + 1}} - {x^*}} \right\|}^2}} \right\}} \end{array} $ |
for k≠ki.
Similarly, letting x=x*, multiplying Eq. (21) by tk+12, using the relation tk2=tk+1(tk+1-1), and using the inequality Lk+1≤ηLf, we obtain
| $ \begin{array}{*{20}{c}} {t_{k + 1}^2\left( {F\left( {{x^{k + 1}}} \right) - F\left( {{x^*}} \right)} \right) \le t_k^2\left( {F\left( {{x^k}} \right) - F\left( {{x^*}} \right)} \right) + }\\ {\frac{{\eta {L_f}}}{2}\left\{ {{{\left\| {{x^k} - {x^*}} \right\|}^2} - {{\left\| {{z^{k + 1}} - {x^*}} \right\|}^2}} \right\}} \end{array} $ |
for k=ki.
For k=ki to ki+1≤k≤ki+1-1, where i=0, 1, …, q (define k0=1, kp=∞), we obtain
| $ \begin{array}{l} t_{k + 1}^2\left( {F\left( {{x^{k + 1}}} \right) - F\left( {{x^*}} \right)} \right) \le t_{{k_i}}^2\left( {F\left( {{x^{{k_i}}}} \right) - F\left( {{x^*}} \right)} \right) + \\ \;\;\;\;\;\frac{{\eta {L_f}}}{2}\left\{ {{{\left\| {{x^{{k_i}}} - {x^*}} \right\|}^2} - {{\left\| {{z_{k + 1}} - {x^*}} \right\|}^2}} \right\} \end{array} $ | (22) |
and especially, if summing from ki to ki+1-1, we get
| $ \begin{array}{l} t_{{k_{i + 1}} - 1}^2\left( {F\left( {{x^{{k_{i + 1}}}}} \right) - F\left( {{x^*}} \right)} \right) \le t_{{k_i}}^2\left( {F\left( {{x^{{k_i}}}} \right) - F\left( {{x^*}} \right)} \right) + \\ \;\;\;\;\frac{{\eta {L_f}}}{2}\left\{ {{{\left\| {{x^{{k_i}}} - {x^*}} \right\|}^2} - {{\left\| {{z^{{k_{i + 1}}}} - {x^*}} \right\|}^2}} \right\} \end{array} $ | (23) |
Summing by Eq. (22) and Eq. (23), for ∀k≥1, we obtain
| $ \begin{array}{l} F\left( {{x^{k + 1}}} \right) - F\left( {{x^*}} \right) \le \frac{{\eta {L_f}}}{{2t_{k + 1}^2}}\left\{ {{{\left\| {{x^*} - {x^0}} \right\|}^2} + } \right.\\ \;\;\;\;\;\;\;\;\left. {\sum\limits_{k \ge {k_i}} {\left\{ {{{\left\| {{x^{{k_i}}} - {x^*}} \right\|}^2} - {{\left\| {{z^{{k_i}}} - {x^*}} \right\|}^2}} \right\}} } \right\} \le \\ \;\;\;\;\;\;\;\;\frac{{2\eta {L_f}}}{{{{\left( {k + 2} \right)}^2}}}\left\{ {{{\left\| {{x^0} - {x^*}} \right\|}^2} + } \right.\\ \left. {\;\;\;\;\;\;\;\;\sum\limits_{k \ge {k_i}} {\left\{ {{{\left\| {{x^{{k_i}}} - {x^*}} \right\|}^2} - {{\left\| {{z^{{k_i}}} - {x^*}} \right\|}^2}} \right\}} } \right\} \end{array} $ |
since t1=1, using the inequality (15) and inequality tk≥(k+1)/2. This concludes the proof.
Remark 3 The sum in Eq. (18) is zero and the theoretical convergence rate of Algorithm 2 is the same as that for Algorithm 1 when the Algorithm 2 does not restart.
Remark 4 As described above, Algorithm 2 is similar to FISTA with adaptive restart[13]. The main difference between the proposed algorithm and the FISTA with adaptive restart[13] lies in the choice of tk after the restart. In Ref.[13], tk=1 after the restart, but the tk is unaffected in Algorithm 2. When algorithm 2 is applied to solve convex programming, the above difference makes the convergence rate of Algorithm 2 able to be proved. The FISTA with adaptive restart[13] does not have such results. In addition, numerical results demonstrate that Algorithm 2 has good practical performance compared with the FISTA with adaptive restart[13].
4 Numerical ExperimentsWe now test Algorithm 1 and Algorithm 2 by randomly generated lasso problems:
| $ \min \left\{ {F\left( \mathit{\boldsymbol{x}} \right) \equiv \frac{1}{2}{{\left\| {\mathit{\boldsymbol{Ax}} - \mathit{\boldsymbol{c}}} \right\|}^2} + \lambda {{\left\| x \right\|}_1}:\mathit{\boldsymbol{x}} \in {{\bf{R}}^n}} \right\} $ | (24) |
where A=(a1, a2, …, an)∈Rm×n is sparse m×n(m < n) matrix, c∈Rn is n dimensional vector. Clearly, letting
The following we randomly generate the data of the numerical cases. First of all, the entries of A are sampled from a standard normal distribution. Secondly, we randomly generated a sparse vector y∈Rn, only m* of which are non-zero. We then set c=Ay+s, where the entries in s are IID sampled from N(0, 0.1). The x* is approximate optimal solution.
The proposed two algorithms are compared to FISTA and FISTA with adaptive restart[13].
In all methods, we use the following values of the parameters:
| $ \eta = 2,{L_0} = \left( {1/5} \right)\mathop {\max }\limits_{1 < i < n} {\left\| {{a_i}} \right\|^2} \le {L_f},\lambda = 1 $ |
Problem 1 Function value progress of four algorithms when n=2 000, m=500, m*=100 (as shown in Fig. 1).
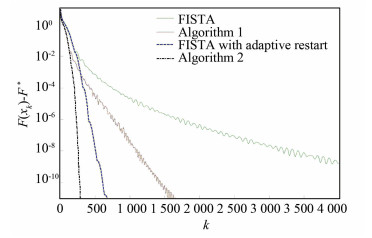
|
Fig.1 Function value progress of four algorithms |
Problem 2 Function value progress of four algorithms when n=4 000, m=1 000, m*=100 (as shown in Fig. 2).
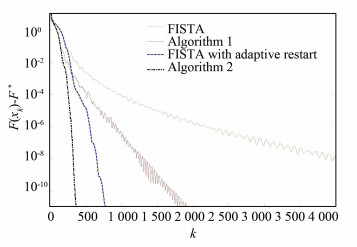
|
Fig.2 Function value progress of four algorithms |
In Fig. 2, the proposed two algorithms are compared to FISTA and FISTA with adaptive restart. Fig. 1 reveals that Algorithm 1 performs better than FISTA and shows a non-monotone behavior. Compared with the Algorithm 1 and FISTA, Algorithm 2 performs better. In addition, Fig. 1 also reveals that Algorithm 2 performs much better than FISTA with adaptive restart[13].
In Fig. 2, the proposed two algorithms are compared to FISTA and FISTA with adaptive restart. Numerical results of Fig. 2 are similar to Fig. 1.
Two numerical cases show that the proposed two algorithms are more efficient than FISTA and FISTA with adaptive restart for composite unconstrained convex programming.
5 ConclusionsWe have developed two new versions of accelerated first-order methods and proved convergence rate O(1/k2) for composite unconstrained convex programming. Algorithm 1 is similar to the FISTA, but the main difference is that Algorithm 1 chooses the step size 1/Lk to be 1/L0 at the beginning of each iteration. Algorithm 1 is a non-monotone algorithm. We have also proposed Algorithm 2 which is Algorithm 1 with restart. Numerical results demonstrate the efficiency of Algorithm 1 and Algorithm 2 when the solution of middle to high accuracy is desired.
| [1] |
Auslender A, Teboulle M. Interior gradient and proximal methods for convex and conic optimization. SIAM Journal on Optimization, 2006, 16(3): 697-725. DOI:10.1137/S1052623403427823 (  0) 0) |
| [2] |
Nesterov Y. Gradient methods for minimizing composite objective function. Mathematical Programming, 2013, 140(1): 125-161. DOI:10.1007/s10107-012-0629-5 (  0) 0) |
| [3] |
Becker S R, Candès E J, Grant M C. Templates for convex cone problems with applications to sparse signal recovery. Mathematical Programming Computation, 2011, 3(3): 165-218. DOI:10.1007/s12532-011-0029-5 (  0) 0) |
| [4] |
Lan G, Lu Z, Monteiro R D C. Primal-dual first-order methods with O(1/ε) iteration complexity for cone programming. Mathematical Programming, 2011, 126(1): 1-29. DOI:10.1007/s10107-008-0261-6 (  0) 0) |
| [5] |
Nesterov Y. A method of solving a convex programming problem with convergence rate O(1/k2). Soviet Mathematics Doklady, 1983, 27(2): 372-376. (  0) 0) |
| [6] |
Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM Journal on Imaging Sciences, 2009, 2(1): 183-202. DOI:10.1137/080716542 (  0) 0) |
| [7] |
Parikh N, Boyd S. Proximal algorithms. Foundations & Trends in Optimization, 2014, 1(3): 127-239. (  0) 0) |
| [8] |
Nesterov Y. Introductory lectures on convex optimization: A basic course. Applied Optimization, 2004, 87(5): ⅹⅷ, 236. DOI:10.1007/978-1-4419-8853-9 (  0) 0) |
| [9] |
Nesterov Y. Smooth minimization of non-smooth functions. Mathematical Programming, Ser. A, 2005, 103(1): 127-152. DOI:10.1007/s10107-004-0552-5 (  0) 0) |
| [10] |
Scheinberg K, Goldfarb D, Bai X. Fast first-order methods for composite convex optimization with backtracking. Foundations of Computational Mathematics, 2014, 14(3): 389-417. DOI:10.1007/S10208-014-9189-9 (  0) 0) |
| [11] |
Nesterov Y. Lexicographic differentiation of nonsmooth functions. Mathematical Programming, 2005, 104(2-3): 669-700. DOI:10.1007/s10107-005-0633-0 (  0) 0) |
| [12] |
Beck A, Teboulle M. Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Transactions on Image Processing, 2009, 18(11): 2419-2434. DOI:10.1109/TIP.2009.2028250 (  0) 0) |
| [13] |
O'Donoghue B, Candès E. Adaptive restart for accelerated gradient schemes. Foundations of Computational Mathematics, 2015, 15(3): 715-732. DOI:10.1007/s10208-013-9150-3 (  0) 0) |
| [14] |
Ortega J M, Rheinboldt W C. Iterative solution of nonlinear equations in several variables. Mathematics of Computation, 1971, 25(114): 398-399. DOI:10.2307/2004942 (  0) 0) |
| [15] |
Giselsson P, Boyd S. Monotonicity and restart in fast gradient methods. 53rd IEEE Conference on Decision and Control. Piscataway: IEEE, 2014, 2015: 5058-5063. DOI: 10.1109/CDC.2014.7040179.
(  0) 0) |
 2019, Vol. 26
2019, Vol. 26


