| Author Name | Affiliation | | Qipeng Li | Department of Mathematics, Xidian University, Xi’an 710126, China | | Hongwei Liu | Department of Mathematics, Xidian University, Xi’an 710126, China | | Zexian Liu | Department of Mathematics, Xidian University, Xi’an 710126, China
School of Mathematics and Computer Science, Hezhou University, Hezhou 542899, Guangxi, China |
|
| Abstract: |
| Two new versions of accelerated first-order methods for minimizing convex composite functions are proposed. In this paper, we first present an accelerated first-order method which chooses the step size 1/Lk to be 1/L0 at the beginning of each iteration and preserves the computational simplicity of the fast iterative shrinkage-thresholding algorithm. The first proposed algorithm is a non-monotone algorithm. To avoid this behavior, we present another accelerated monotone first-order method. The proposed two accelerated first-order methods are proved to have a better convergence rate for minimizing convex composite functions. Numerical results demonstrate the efficiency of the proposed two accelerated first-order methods. |
| Key words: first-order method iterative shrinkage-thresholding algorithm convex programming adaptive restart composite functions. |
| DOI:10.11916/j.issn.1005-9113.18033 |
| Clc Number:O221.2 |
| Fund: |
|
| Descriptions in Chinese: |
| 最小化凸合成函数的快速一阶方法 李启朋1,刘红卫1,刘泽显1,2 (1. 西安电子科技大学 数学与统计学院,西安 710126; 2. 贺州学院 数学与计算机学院,广西 贺州 542899) 摘要:针对最小化凸合成函数,给出了两种加速一阶方法。首先提出在每次迭代开始时选择步长 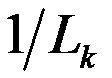 为 为 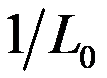 的加速一阶方法,该方法不仅保持了快速迭代收缩阈值算法的计算简单性,而且也是一种非单调算法。另外,为避免非单调性,又提出一种加速单调一阶方法。本文从理论上证明了所提出的两种加速一阶方法具有较好的收敛速度,数值实验结果也表明两种算法的有效性。 的加速一阶方法,该方法不仅保持了快速迭代收缩阈值算法的计算简单性,而且也是一种非单调算法。另外,为避免非单调性,又提出一种加速单调一阶方法。本文从理论上证明了所提出的两种加速一阶方法具有较好的收敛速度,数值实验结果也表明两种算法的有效性。 关键词:一阶方法,快速迭代收缩阈值算法,凸规划,自适应重启,合成函数 |




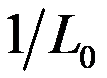 的加速一阶方法,该方法不仅保持了快速迭代收缩阈值算法的计算简单性,而且也是一种非单调算法。另外,为避免非单调性,又提出一种加速单调一阶方法。本文从理论上证明了所提出的两种加速一阶方法具有较好的收敛速度,数值实验结果也表明两种算法的有效性。
的加速一阶方法,该方法不仅保持了快速迭代收缩阈值算法的计算简单性,而且也是一种非单调算法。另外,为避免非单调性,又提出一种加速单调一阶方法。本文从理论上证明了所提出的两种加速一阶方法具有较好的收敛速度,数值实验结果也表明两种算法的有效性。