2. Science and Technology on Space Intelligent Control Laboratory, Beijing 100190, China
Thruster is commonly used as satellite actuator, which provides force and torque required by satellite. Thruster configuration is related to the completion of the satellite mission, the layout of the payloads and the components, and the propellant consumption, thus thruster configuration is critical to satellite design[1].
Thruster configuration mainly involves two aspects: one for type selection and the other for thruster installation location and installation angle. At present, thrusters are divided into two types: chemical thruster and electric thruster[2-4]. Chemical thruster can provide greater force and smaller specific impulse and its propellant consumption is relatively high. So far it has been applied in SS/L-1300 satellite platform[5], LS3000 satellite platform[6], DFH-4 satellite platform, and so on. Electric thruster can provide smaller force and bigger specific impulse. Its propellant consumption is relatively low. So far it has been applied in HS-702[7]. Therefore, in selecting thruster type, the benefits and risks of the thruster should be considered[8-9]. As for installation position and installation angle, the structural design of the satellite should be considered, as well as the effects of the plume, heat radiation, and combustion on the satellite. In addition, antenna, solar wings, and other components installation area restrictions also need to be considered. Take Japan's DRTS satellite[10] as an example. In order not to affect the installation of the payloads and components, eight thrusters are installed on the front and back panel of the satellite. Another example is US Intelsat Ⅶ/Ⅶ A satellite[6]. All of its twelve thrusters are installed on the front and back panel of the satellite to avoid their influence on the antenna and solar wings. When the restriction condition is satisfied, the installation position and installation angle of the thruster are limited to a certain area, and optimization is required for installation position and installation angle of the thruster. At present, there is very little literature on the optimization of thruster configuration. The way to optimize thruster configuration needs to be studied. In general, the objective function of the thruster configuration optimization can be selected as the minimum propellant consumption, the minimum torque coupling, and the maximum thrust. Specific ways of optimization depends on actual engineering needs.
This paper presents a thruster configuration and optimization method for GEO satellite. Due to the design of the satellite subdivision structure, the thruster cannot be installed on the angular position of the satellite; due to the installation room requirements of the payloads and the components, the layout of the thruster cannot take up too much room of satellite panels, so all thrusters were installed on the back panel of the satellite. Chemical thruster and electric thruster have different advantages and therefore were selected to be used in different phases, which can effectively reduce the propellant consumption. Meanwhile, in order to minimize propellant consumption, the installation angle of the chemical thruster and the installation position of the electric thruster were optimized. Lastly, based on an engineering example, a GEO satellite thruster was configured and optimized using this method.
2 Mathematical ModelsThe mechanical coordinate system of the satellite are defined as follows: origin is located in the mechanical separation surface of satellite and launch vehicle, and it is fixed on the satellite; the z-axis is perpendicular to the connecting surface, and its positive direction is from the origin to the panel of the satellite facing the earth; the positive direction of the x-axis is from the origin to the east panel of the satellite; the positive direction of the y-axis is from the origin to the south panel of the satellite. The body coordinate system of the satellite are defined as follows: origin is in the satellite center-of-mass; xb, yb, zb are parallel to 3 axes of the mechanical coordinate system. Assume a single thruster nominal thrust is F; the azimuth and pitch angles of the thrust vector F in the satellite body coordinate system are φ and θ, respectively; φ is the angle between the thrust vector and the xb-axis in the ob-xb-yb plane, φ∈ [0, 360o]; θ is the angle between the thrust vector and the ob-xb-yb plane, θ∈ [-90o, 90o]; Rc is the position vector of the satellite center-of-mass in the mechanical coordinate system, Rc = [xc, yc, zc]; R is the position vector of the thruster in the mechanical coordinate system, R =[x, y, z]; D is the position vector of the thruster in the satellite body coordinate system, D = R - Rc, as shown in Fig. 1.
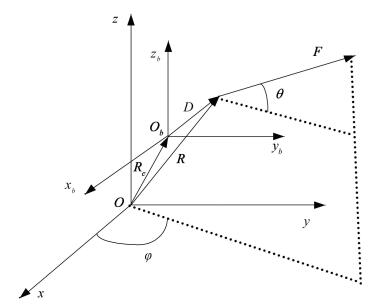
|
Fig.1 Thruster vector orientation |
Define Mx, My, Mz as the three-axis torque generated by the thruster; Fx, Fy, Fz as the three-axis force generated by the thruster; α, β, γ as the angles of the thruster vector F and xb-axis, yb-axis, zb-axis, respectively, then
| $ \alpha = \arccos (\cos \theta \cos \varphi ) $ | (1) |
| $ \beta = \arccos (\cos \theta \sin \varphi ) $ | (2) |
| $ \gamma = \arccos (\sin \theta ) $ | (3) |
| $ {M_x} = F\left[ {\left( {z - {z_c}} \right)\cos (\beta ) - \left( {y - {y_c}} \right)\cos (\gamma )} \right] $ | (4) |
| $ {M_y} = F\left[ { - \left( {z - {z_c}} \right)\cos (\alpha ) + \left( {x - {x_c}} \right)\cos (\gamma )} \right] $ | (5) |
| $ {M_z} = F\left[ {\left( {y - {y_c}} \right)\cos (\alpha ) - \left( {x - {x_c}} \right)\cos (\beta )} \right] $ | (6) |
| $ {F_x} = \mathit{\boldsymbol{F}}\cos (\alpha ) $ | (7) |
| $ {F_y} = \mathit{\boldsymbol{F}}\cos (\beta ) $ | (8) |
| $ {F_z} = \mathit{\boldsymbol{F}}\cos (y) $ | (9) |
The installation angle satisfies the constraint equation:
| $ {\cos ^2}(\alpha ) + {\cos ^2}(\beta ) + {\cos ^2}(\gamma ) = 1 $ | (10) |
Installation position and torque satisfies the constraint equation:
| $ \left( {x - {x_c}} \right){M_x} + \left( {y - {y_c}} \right){M_y} + \left( {z - {z_c}} \right){M_z} = 0 $ | (11) |
From the above equation, the installation position and installation angle of the thruster can be uniquely determined by the position vector R and the two azimuths, φ and θ.
3 Thruster Configurations 3.1 Thruster Configuration and Working ModeThruster layout is shown in Fig. 2. All thrusters are installed on the -z-plane of the satellite, where 1A-4A and 1B-4B are chemical thrusters; A and B are two branches[11]; NW, NE, SW, and SE are electric thrusters. The force of the electric thrusters points to the center of mass. The center of mass is on the z-axis in the mechanical coordinate system. The thrusters are symmetrical to each other, which can effectively suppress the interference torque.
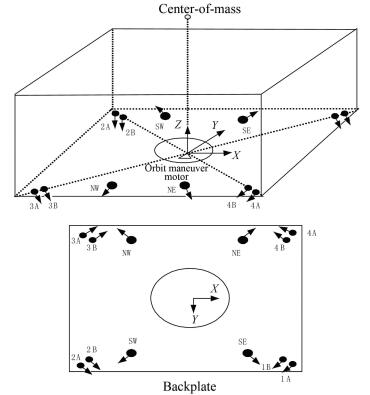
|
Fig.2 Thruster layout |
Thruster working mode is shown in Table 1.
| Table 1 Thruster working mode |
This thruster configuration has the following advantages:①under the premise of completion of tasks, the number of the thrusters used is smaller, which effectively reduces the weight and cost of the satellite; ②the configuration is relatively simple and all thrusters are installed on the -z-plane of the satellite, which provides a large room for the installation of the payloads and components of satellites; ③chemical thruster and electric thruster are selected for use, which can effectively reduce the propellant consumption; ④ each working mode has a backup, which can effectively enhance the reliability of the task.
Admittedly, this thruster configuration has the disadvantage that the force and the torque provided by thruster are coupled to each other, which increase the difficulty of thruster configuration, but this does not affect the completion of satellite missions.
For GEO satellites, the primary responsibilities of the thruster are propellant sinking, satellite attitude control, station keeping, and angular momentum unloading. From the separation of the satellite from the rocket to the end of the satellite life, thruster task is divided into two phases: ①In the orbital transition phase, thruster is used for propellant sinking because the propellant may contain gas; meanwhile, thruster is also used for attitude control due to the change of satellite center-of-mass, deviations from the orbit maneuver motor, and tanking shaking. Chemical thruster works at this phase. ②In the geostationary orbit phase, thruster is used for station keeping because the earth's non-sphere causes orbit east-west perturbation and the gravity of the moon and sun causes orbit north-south perturbation; meanwhile, satellite attitude is typically adjusted by the flywheel, and thruster is used to unload the flywheel angular momentum when the flywheel reaches saturation. Electric thruster works at this phase.
In addition, orbital transfer is typically performed by the orbit maneuver motor, which provides speed increment for the satellite, thereby changing the orbit. In this thruster configuration, chemical thruster or electric thruster can provide force for orbital transfer, or they can be used in combination to improve the orbital transfer speed. When force is provided by the electric thruster, two electric thrusters on the diagonal can work in high power mode.
3.2 Analysis of Thruster Working Task 3.2.1 Propellant sinkingIn the microgravity environment, the propellant and the pressurized gas in the tank no longer maintain a stable interface, and they may be gas-liquid inclusions. So before the orbit maneuver motor works, propellant needs to sink to the bottom. As for the propellant sinking, the amount of force the thruster provides should be considered, so that the inertia force of the liquid propellant can overcome the surface tension and a certain amount of tension from the interference, ensuring that the propellant is always maintained at the bottom of the tank. The force required for the propellant sinking is given as follows:
| $ {F_s} \ge \left( {{\sigma _{1g}}M{N_B}} \right)/\left( {{L^2}\rho } \right) $ | (12) |
where Fs is the force required for the propellant sinking; L is the feature size of tank; ρ is the propellant density; σ1g is the liquid-gas surface tension; NB is the bond number; M is the quality of the satellite.
The force required for the propellant sinking is provided by four chemical thrusters:
| $ {F_s} = F\cos {\gamma _1} + F\cos {\gamma _2} + F\cos {\gamma _3} + F\cos {\gamma _4} $ | (13) |
where γ1, γ2, γ3, γ4 are the angle between the four thrusters and the zb-axis, respectively.
To ensure that the force generated by the four chemical thrusters is able to cause propellant to sink, the installation angle of the thruster needs to be limited.
According to Ref. [12], the force duration time t for the propellant sinking is proportional to the characteristic time tc (the time taken for the propellant to move as a rigid body). In general, the force duration time t is 10 times that of the characteristic time tc:
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{1}{2}\frac{{{F_s}}}{M}t_c^2 = s}\\ {t = 10{t_c}} \end{array}} \right. $ | (14) |
where s is the propellant movement distance, generally taken as the height of the tank.
3.2.2 Attitude controlWhen the satellite is disturbed during the transitional orbit phase, the control torque can be provided by the thruster for attitude control. In general, the control torque provided by the thruster is linear with the interference torque:
| $ \left\{ {\begin{array}{*{20}{l}} {{M_{dx}}{t_{dx}} = {M_x}{t_x}}\\ {{M_{dy}}{t_{dy}} = {M_y}{t_y}}\\ {{M_{dz}}{t_{dz}} = {M_z}{t_z}} \end{array}} \right. $ | (15) |
where Mdx, Mdy, Mdz are the satellite three-axis interference torque; tdx, tdy, tdz are the three-axis interference torque duration time; Mx, My, Mz are the three-axis torque generated by the thruster; tx, ty, tz are the three-axis thruster working time.
In general, satellite attitude control is performed after each orbital transition.
3.2.3 Station-keepingFig. 2 shows that electric thruster NW and NE provide the normal force pointing to the south; SW and SE provide the normal force pointing to the north; NW and SW provide the tangential force pointing to the east; NE and SE provide the tangential force pointing to the west; the forces of the four thrusters in the radial direction all point to the center of mass.
The station-keeping strategy is taken every day. When the north-south station-keeping strategy is executed, electric thrusters NW and NE are ignited at the ascending node attachment and electric thruster SW and SE are ignited at the descending node attachment, so that each ignition can produce radial speed increments and tangential speed increments that can control the inclination, eccentricity, and east-west drift[13]. The relationship of incremental speed provided by four electric thrusters is given as follows:
| $ \left\{ \begin{array}{l} {V_s}\mathit{\Delta} i = {k_N}\left( {\mathit{\Delta} {V_{{\rm{NW}}}} + \mathit{\Delta} {V_{{\rm{NE}}}} + \mathit{\Delta} {V_{{\rm{SW}}}} + \mathit{\Delta} {V_{{\rm{SE}}}}} \right)\\ {V_s}\mathit{\Delta} {e_x} = - {k_R}\left( {\mathit{\Delta} {V_{{\rm{NW}}}} + \mathit{\Delta} {V_{{\rm{NE}}}} - \mathit{\Delta} {V_{{\rm{SW}}}} - \mathit{\Delta} {V_{{\rm{SE}}}}} \right)\sin {l_0} + \\ \;\;\;\;\;\;\;\;\;2{k_T}\left( {\mathit{\Delta} {V_{{\rm{NW}}}} - \mathit{\Delta} {V_{{\rm{NE}}}} - \mathit{\Delta} {V_{{\rm{SW}}}} + \mathit{\Delta} {V_{{\rm{SE}}}}} \right)\cos {l_0}\\ {V_s}\mathit{\Delta} {e_y} = {k_R}\left( {\mathit{\Delta} {V_{{\rm{NW}}}} + \mathit{\Delta} {V_{{\rm{NE}}}} - \mathit{\Delta} {V_{{\rm{SW}}}} - \mathit{\Delta} {V_{{\rm{SE}}}}} \right)\cos {l_0} + \\ \;\;\;\;\;\;\;\;\;2{k_T}\left( {\mathit{\Delta} {V_{{\rm{NW}}}} - \mathit{\Delta} {V_{{\rm{NE}}}} - \mathit{\Delta} {V_{{\rm{SW}}}} + \mathit{\Delta} {V_{{\rm{SE}}}}} \right)\sin {l_0}\\ - \frac{{{V_s}\mathit{\Delta} \lambda }}{{3 \times 360.9856}} = {k_T}\left( {\mathit{\Delta} {V_{{\rm{NW}}}} - \mathit{\Delta} {V_{{\rm{NE}}}} + \mathit{\Delta} {V_{{\rm{SW}}}} - \mathit{\Delta} {V_{{\rm{SE}}}}} \right) \end{array} \right. $ | (16) |
where Δi is the orbital inclination drift amount; Δex, Δey are the components of the eccentricity change in the x and y directions; Δλ is the longitude drift amount; ΔVNW, ΔVNE, ΔVSW, ΔVSE are the speed increment of the four electric thruster; KR, KT, KN are the electric thruster force along the radial, tangential, and normal projection coefficient; l0 is the latitude of the ignition position.
According to the speed increment of the electric thruster, the working time of each electric thruster can be calculated according to Eq.(17):
| $ {T_j} = \frac{2}{{{\mathit{\boldsymbol{\omega }}_e}}}{\sin ^{ - 1}}\left[ {\frac{{{\mathit{\boldsymbol{\omega }}_e}}}{2}\left( {\frac{{M \mathit{\mathit{\Delta}} {V_j}}}{F}} \right)} \right] $ | (17) |
where j is the label of the electric thruster, ωe is the angular velocity of the stationary orbital.
Due to space factor, electric thruster failure mode is not discussed here.
3.2.4 Angular momentum unloadingAngular momentum unloading and station keeping are performed simultaneously. Using the vector adjustment mechanism to adjust the angle of the electric thruster, the angle momentum unloading can be completed. Analysis of the layout of the electric thruster indicates at least two of the electric thrusters on the diagonal perform unloading task, so that angular momentum in all directions can be unloaded. In general, the ignition duration, the ignition position, and the unloading deflection angle need to be solved in combination and repeated iterations before they can be finalized. Since the amount of displacement on the xb-yb plane is small due to the angular deflection of the electric thruster, and the station-keeping is not affected by the angular momentum unloading, it is possible to take a method, which determines the ignition duration and the ignition position of the electric thruster first, and then determines the deflection angle of the electric thruster[14].
Take angular momentum unloading with electric thruster SW and NE as an example. Assume that the installation position of the electric thruster in the body coordinate system is given as follows:
| $ {\mathit{\boldsymbol{r}}_{{\rm{SW}}}} = \left[ {\begin{array}{*{20}{c}} { - {x_0}}\\ {{y_0}}\\ { - {z_0}} \end{array}} \right],{\mathit{\boldsymbol{r}}_{{\rm{NE}}}} = \left[ {\begin{array}{*{20}{c}} {{x_0}}\\ { - {y_0}}\\ { - {z_0}} \end{array}} \right] $ | (18) |
Due to the deflection angle of the electric thruster, the displacement of the electric thruster in the xb-yb plane is dxSW, dySW, dxNE, dyNE. The angular momentum unloading formula is simplified as follows:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{F}}_{{\rm{SW}}}} = - \left( {{\mathit{\boldsymbol{r}}_{{\rm{SW}}}} + \left[ {\begin{array}{*{20}{l}} {d{x_{{\rm{SW}}}}}\\ {d{y_{{\rm{SW}}}}}\\ 0 \end{array}} \right]} \right) \cdot \frac{\mathit{\boldsymbol{F}}}{r}\\ {\mathit{\boldsymbol{F}}_{{\rm{NE}}}} = - \left( {{\mathit{\boldsymbol{r}}_{{\rm{NE}}}} + \left[ {\begin{array}{*{20}{l}} {d{x_{{\rm{NE}}}}}\\ {d{y_{{\rm{NE}}}}}\\ 0 \end{array}} \right]} \right) \cdot \frac{\mathit{\boldsymbol{F}}}{r} \end{array} \right. $ | (19) |
where r is the distance from the installation position of the thruster to the center of mass.
The electric thruster ignition time is relatively long, so the ignition time can be regarded as an arc in the orbit. The angular momentum of the electric thruster is given as follows:
| $ \left\{ {\begin{array}{*{20}{l}} {{H_{{\rm{SW}}}} = \int_0^{{t_{{\rm{SW}}}}} {{R_{{\rm{SW}}}}} \cdot \left( {{r_{{\rm{SW}}}} \times {F_{{\rm{SW}}}}} \right){\rm{d}}t}\\ {{H_{{\rm{NE}}}} = \int_0^{{t_{{\rm{NE}}}}} {{R_{{\rm{NE}}}}} \cdot \left( {{r_{{\rm{NE}}}} \times {F_{{\rm{NE}}}}} \right){\rm{d}}t} \end{array}} \right. $ | (20) |
where tSW, tNE are the working time of the thruster calculated by station keeping; RSW, RNE are the transformation matrix of the orbital coordinate system to the inertial coordinate system:
| $ {\mathit{\boldsymbol{R}}_{{\rm{SW}}}} = \left[ {\begin{array}{*{20}{c}} {\cos k}&0&{ - \sin k}\\ { - \sin k}&0&{\cos k}\\ 0&{ - 1}&0 \end{array}} \right] $ | (21) |
| $ {\mathit{\boldsymbol{R}}_{{\rm{NE}}}} = \left[ {\begin{array}{*{20}{c}} { - \cos k}&0&{\sin k}\\ { - \sin k}&0&{ - \cos k}\\ 0&{ - 1}&0 \end{array}} \right] $ | (22) |
where k is the ignition position offset caused by north-south station keeping, which is related to the season and year.
When the arc loss is not taken into account, the angular momentum provided by the electric thruster is given as follows:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{H}}_{{\rm{SW}}}} = {\mathit{\boldsymbol{R}}_{{\rm{SW}}}} \cdot \left( {{\mathit{\boldsymbol{r}}_{{\rm{SW}}}} \times {\mathit{\boldsymbol{F}}_{{\rm{SW}}}}} \right) \cdot {t_{{\rm{SW}}}}}\\ {{\mathit{\boldsymbol{H}}_{{\rm{NE}}}} = {\mathit{\boldsymbol{R}}_{{\rm{NE}}}} \cdot \left( {{\mathit{\boldsymbol{r}}_{{\rm{NE}}}} \times {\mathit{\boldsymbol{F}}_{{\rm{NE}}}}} \right) \cdot {t_{{\rm{NE}}}}} \end{array}} \right. $ | (23) |
The angular momentum provided by the electric thruster and the target unloading angular momentum satisfies:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\left( {{\mathit{\boldsymbol{H}}_{{\rm{SW}}}} + {\mathit{\boldsymbol{H}}_{{\rm{NE}}}}} \right)}_x} = {\mathit{\boldsymbol{H}}_x}}\\ {{{\left( {{\mathit{\boldsymbol{H}}_{{\rm{SW}}}} + {\mathit{\boldsymbol{H}}_{{\rm{NE}}}}} \right)}_y} = {\mathit{\boldsymbol{H}}_y}}\\ {{{\left( {{\mathit{\boldsymbol{H}}_{{\rm{SW}}}} + {\mathit{\boldsymbol{H}}_{{\rm{NE}}}}} \right)}_z} = {\mathit{\boldsymbol{H}}_z}} \end{array}} \right. $ | (24) |
where Hx, Hy, Hz are the target unloading angular momentum in three directions in the inertial coordinate system.
4 Optimization of the Thruster ConfigurationIn order to reduce the weight of the satellites, the thruster configuration is optimized for minimum propellant consumption during the whole life of the satellite. From the configuration of the thruster, it is known that the installation angle of the chemical thruster and the installation position of the electric thruster need to be optimized. Analysis of the working tasks of the thruster shows that the installation angle of the chemical thruster and the installation position of the electric thruster can be optimized separately.
4.1 Optimization of Installation Angle of Chemical ThrusterThe chemical thruster mainly works in the orbital transition phase, and the propellant at this phase is mainly used by the orbit maneuver motor to carry out the orbital transfer and the chemical thruster to carry out the propellant sinking and attitude control. Propellant consumption can be calculated by Eqs. (25), (26):
| $ \mathit{\Delta} m = (F\mathit{\Delta} t)/\left( {{I_{sp}}g} \right) $ | (25) |
| $ \mathit{\Delta} m = M\left[ {1 - {{\rm{e}}^{ - \mathit{\Delta} V/\left( {{I_{sp}}\eta g} \right)}}} \right] $ | (26) |
where Δm is the propellant consumption, Δt is the duration time of the thruster work, ΔV is the speed increment, g is the gravitational acceleration, Isp is the thruster specific impulse, and η is the efficiency of the thruster.
According to Eqs. (4)-(6), the force and the torque provided by the chemical thruster are coupled with each other, and the torque provided by the chemical thruster is related to the satellite center of mass. Satellite center of mass in the mechanical coordinate system is given as follows:
| $ {Z_0} = \frac{{{Z_{{\rm{payload }}}}{m_{{\rm{payload }}}} + {Z_{{\rm{bus }}}}{m_{{\rm{bus }}}} + Z_{{\rm{fuel}}}^{(t)}m_{{\rm{fuel}}}^{(t)}}}{{{m_{{\rm{payload }}}} + {m_{{\rm{bus }}}} + m_{{\rm{fuel}}}^{(t)}}} $ | (27) |
Due to the constant consumption of the propellant, the remaining propellant center of mass is constantly changing. As a result, the satellite center of mass is constantly changing as well. The remaining propellant center of mass is not only related to the mass of the remaining propellant, but also to the shape and the number of the tanks. Assume there are four side-by-side tanks, the upper and lower ends of a single tank are a hemisphere, the middle section is a cylinder, the tank height is H, the radius is R, and the four tanks are placed on the buttocks[15], as shown in Fig. 3.
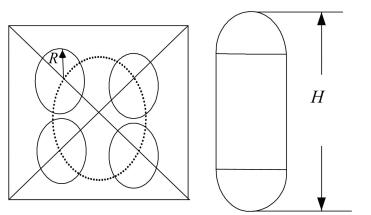
|
Fig.3 Tank installation location and size |
In the orbital transition phase, the propellant has acceleration on the -z-axis and the propellant liquid surface is the same as the free liquid, and the propellant center of mass is on the z-axis[16].
When the remaining amount of the propellant is mfuel, the volume of the propellant in a single tank is given as follows:
| $ {V_0} = {m_{{\rm{fuel }}}}/(4\rho ) $ | (28) |
For a single tank, there are three possibilities for the remaining propellant in the tank: ① the remaining propellant is in the lower hemisphere of the tank; ② the propellant is consumed into the cylindrical section of the tank; ③ the upper hemisphere of the tank also has propellant. Thus, the center of mass of the remaining propellant is given as follows:
when V0≤(2πR3)/3,
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{ \mathsf{ π} }}\left( {{R^2}h - \frac{{{h^3}}}{3}} \right) = {V_0}}\\ {{Z_{{\rm{fuel }}}} = \frac{{{\rm{ \mathsf{ π} }}\left( {2{R^2}{h^2} - {h^4}} \right)}}{{4{V_0}}}} \end{array}} \right. $ | (29) |
when (2/3)πR3 < V0 < πR2H-(4/3)πR3,
| $ \left\{ {\begin{array}{*{20}{l}} {{Z_{{\rm{fuel }}}} = \frac{{{\rm{ \mathsf{ π} }}{R^2}\left( {2{h^2} - {R^2}} \right)}}{{4{V_0}}}}\\ {{\rm{ \mathsf{ π} }}\left( {{R^2}h - \frac{1}{3}{R^3}} \right) = {V_0}} \end{array}} \right. $ | (30) |
when V0>πR2H-(4/3)πR3,
| $ \left\{ \begin{array}{l} {Z_{{\rm{fuel}}}} = \frac{{3\left( {{h^4} + 2{R^2}{h^2} - {R^4}} \right)}}{{12{V_0}}} + \\ \;\;\;\;\;\;\;\;\frac{{{{(H - R)}^2}\left[ {(H - R)(3H + 5R - 8h) - 6{{(R - h)}^2}} \right]}}{{12{V_0}}}\\ \left( {{\rm{ \mathsf{ π} }}{R^2}(h - R/3) - ({\rm{ \mathsf{ π} }}/3){{(h + R - H)}^3} = {V_0}} \right. \end{array} \right. $ | (31) |
For a chemical thruster configuration with an installation angle of (φ0, θ0), the propellant consumption in the orbital transition phase is given as follows:
1) According to the mass of the current satellite and Eqs. (12) and (14), the time required for the propellant sinking can be calculated. Then by Eq.(25), the propellant used for the propellant sinking can be calculated.
2) According to the speed increment required for orbital transfer and the current satellite mass, the propellant used for the orbital transfer can be calculated by Eq.(26).
3) The center of mass of the current propellant is calculated according to Eqs. (28)-(31), and then the center of mass of the current satellite can be calculated by Eq. (27).
4) According to the center of mass of the current satellite, the torque of the thruster can be updated by Eqs. (4)-(6).
5) According to the propellant used for the orbital transfer, the time of orbital transfer can be calculated by Eq. (25).
6) According to the time of orbital transfer, the time required for the attitude control of the thruster can be calculated by Eq. (15).
7) According to the time for the attitude control, the propellant consumed for the attitude control can be calculated by Eq. (25).
8) Update the current satellite mass.
Repeat steps to calculate the propellant consumed mp during the orbital transition phase.
Therefore, the optimization model of chemical thruster can be expressed as:
| $ \begin{array}{l} {\rm{find}}\;\;\;\left( {{\varphi _i},{\theta _i}} \right),\;i = 1,2, \cdots n\\ \min \;\;\;{m_p}\\ {\rm{s}}.{\rm{t}}.\;\;\;\;\;\varphi _i^l \le {\varphi _i} \le \varphi _i^u,\theta _i^i \le {\theta _i} \le \theta _i^u \end{array} $ | (32) |
This model can be optimized using genetic algorithms, particle swarm optimization, and so on, which will not be discussed here.
4.2 Optimization of Installation Position of Electric ThrusterThe propellant consumption of the electric thruster is equal to the propellant used for north-south station-keeping. In order to reduce the propellant consumption, it is necessary to increase the normal projection coefficient KN of the electric thruster. In the body coordinate system, the installation positions of four electric thrusters are [-x0, -y0, -z0], [x0, -y0, -z0], [-x0, y0, -z0], and [x0, y0, -z0]. Since the force of the electric thruster points to the center of mass, the following can be obtained:
| $ \left\{ \begin{array}{l} {K_R} = \cos (\alpha ) = \frac{{{z_0}}}{{\sqrt {x_0^2 + y_0^2 + z_0^2} }}\\ {K_T} = \cos (\beta ) = \frac{{{x_0}}}{{\sqrt {x_0^2 + y_0^2 + z_0^2} }}\\ {K_N} = \cos (\gamma ) = \frac{{{y_0}}}{{\sqrt {x_0^2 + y_0^2 + z_0^2} }} \end{array} \right. $ | (33) |
From Eq. (33), it is known that if KN is increased, it is necessary to increase y0 and decrease x0 and z0. Analysis of the configuration of the thruster shows that y0 is determined by installation area of the electric thruster and z0 by the center of mass of the satellite. Therefore, the increase of KN can only be achieved by optimizing x0.
Therefore, the optimization model of electric thruster is expressed as:
| $ \begin{array}{l} {\rm{find}}\;\;\;{x_0}\\ \min \;\;\;{m_p}\\ {\rm{s}}.{\rm{t}}.\;\;\;\;\;F \le 0 \end{array} $ | (34) |
F≤0 is set to meet all functional requirements.
The main effect of the electric thruster is station-keeping and angular momentum unloading, which will be directly affected by the change of x0. Therefore, it is necessary to determine the minimum x0 that satisfies both station-keeping and angular momentum unloading.
4.2.1 Station-keepingGenerally, the electric thruster cannot work more than two hours. Therefore, the maximum speed increment provided by the electric thruster is given as follows:
| $ \mathit{\Delta} {V_{\max }} = \frac{{2F}}{{{\mathit{\boldsymbol{\omega }}_e}M}}\sin \left( {\frac{{{T_0}{\mathit{\boldsymbol{\omega }}_e}}}{2}} \right) $ | (35) |
where T0 is two hours.
ΔVNW, ΔVNE, ΔVSW, ΔVSE are the speed increments of the four electric thrusters which are determined by Eq. (16), then:
| $ \left. {\begin{array}{*{20}{l}} {\mathit{\Delta} {V_{{\rm{NW}}}} \le \mathit{\Delta} {V_{{\rm{max}}}}}\\ {\mathit{\Delta} {V_{{\rm{NE}}}} \le \mathit{\Delta} {V_{\max }}}\\ {\mathit{\Delta} {V_{{\rm{SW}}}} \le \mathit{\Delta} {V_{\max }}}\\ {\mathit{\Delta} {V_{{\rm{SE}}}} \le \mathit{\Delta} {V_{\max }}} \end{array}} \right\} \Rightarrow {x_0} \ge {x_1} $ | (36) |
where x1 is the minimum that meets station keeping requirements.
4.2.2 Angular momentum unloadingAs can be known from Eq. (24), when unloading the target angular momentum [Hx, Hy, Hz] without considering the loss of the arc, the angle deflects and the displacement in the xb-yb plane is given as follows:
| $ \left\{ \begin{array}{l} d{x_{{\rm{SW}}}} = - \frac{{{t_{{\rm{SW}}}} \cdot {H_z} \cdot r}}{{{z_0} \cdot \left( {t_{{\rm{SW}}}^2 + t_{{\rm{NE}}}^2} \right) \cdot F}}\\ d{y_{{\rm{SW}}}} = \frac{{r\left( {{y_0} \cdot {H_z} - \cos k \cdot {H_x} \cdot {x_0} + \cos k \cdot {H_y} \cdot {z_0}} \right)}}{{2{z_0} \cdot {x_0} \cdot {t_{{\rm{SW}}}} \cdot F}} - \\ \;\;\;\;\;\;\;\frac{{r\left( {\sin k \cdot {H_x} \cdot {z_0} + \sin k \cdot {H_y} \cdot {x_0}} \right)}}{{2{z_0} \cdot {x_0} \cdot {t_{{\rm{SW}}}} \cdot F}}\\ d{x_{{\rm{NE}}}} = - \frac{{{t_{{\rm{NE}}}} \cdot {H_z} \cdot r}}{{{z_0} \cdot \left( {t_{{\rm{SW}}}^2 + t_{{\rm{NE}}}^2} \right) \cdot F}}\\ d{y_{{\rm{NE}}}} = \frac{{r\left( {{y_0} \cdot {H_z} + \cos k \cdot {H_x} \cdot {x_0} + \cos k \cdot {H_y} \cdot {z_0}} \right)}}{{2{z_0} \cdot {x_0} \cdot {t_{{\rm{NE}}}} \cdot F}} - \\ \;\;\;\;\;\;\frac{{r\left( {\sin k \cdot {H_x} \cdot {z_0} - \sin k \cdot {H_y} \cdot {x_0}} \right)}}{{2{z_0} \cdot {x_0} \cdot {t_{{\rm{NE}}}} \cdot F}} \end{array} \right. $ | (37) |
Considering the limitation of the deflection angle of the electric thruster and the effect on station-keeping, the displacement in the xb-yb plane should be less than d, thus:
| $ \left. \begin{array}{l} \left| {d{x_{{\rm{SW}}}}} \right| \le d\\ \left| {d{y_{{\rm{SW}}}}} \right| \le d\\ \left| {d{x_{{\rm{NE}}}}} \right| \le d\\ \left| {d{y_{{\rm{NE}}}}} \right| \le d \end{array} \right\} \Rightarrow {x_0} \ge {x_2} $ | (38) |
where x2 is the minimum that meets angular momentum unloading requirements.
By Eqs. (36) and (38), it can be obtained that
| $ {x_0} = \max \left( {{x_1},{x_2}} \right) $ | (39) |
At this time, the optimization of the installation position of the electric thruster is completed.
5 Example DemonstrationTable 2 shows the basic technical indicators of a GEO satellite. The number of satellite orbit transitions is five; the speed increment for each orbital transition is [451, 110, 211, 150, 49] (m/s); the interference torque of the three axes after each orbital transition are [-4, 5, 0.5], [3, 4, -0.1], [3, -1, 0.2], [-2, 5, 0.4], [4, 3, 0.05] (N· m); daily target unloading angular momentum is Hx= Hy=Hz=5 (N·m·s).
| Table 2 GEO satellite technology index |
(1) The chemical thrusters are configured and optimized.
The chemical thrusters are divided into A and B branches, which are backed up by each other, so A-branch can be configured firstly. By the analysis of the installation angle, four chemical thrusters installation angle constraint range is shown in Table 3.
| Table 3 Angle constraint range |
Optimize Eq. (32) using PSO algorithm[17]. The optimized installation angle is as shown in Table 4. Notably, the thruster installation structure proposed in this paper has symmetry, while the thruster must have the same value in order to provide torque or force in one direction, and to cancel the torque or force in other directions. Because the coupling of the thruster installation structure is relatively serious, the optimal values obtained by using the PSO algorithm are basically the same, which can be verified.
| Table 4 Optimized installation angle |
The optimized chemical thrusters are used for orbital transfer, and the consumption of propellant is mp=996.23 kg.
(2) The electric thrusters are configured and optimized.
It should be noted that, the target orbit inclination of the GEO satellite is 0.01°, and the fixed location longitude is 100E.
After the orbital transfer, the satellite mass is M=2 666.8 kg, and the center of mass in the mechanical coordinate system is Z0=2 179 mm. In order to reduce the impact of the plume on the solar array, the maximum installation position of the electrical thruster in the north-south direction is y0=1 080 mm; constrained by the electrical thruster deflection angle and the effect on station-keeping, the maximum displacement is d=100 mm. Thus, by Eqs. (36), (38), and (39), it can be calculated that x0=550 mm.
Finally, the optimized thruster installation position and installation angle are shown in Table 5. It should be noted that the detailed optimization process is not given for some reasons.
| Table 5 Optimized thruster installation position and installation angle |
As can be seen from the values in the table, the values in the table are symmetrical, which is consistent with the characteristics of the thruster configuration. After analysis, the optimized values are feasible and effective, meeting the practical application of the project.
6 ConclusionsThruster configuration and optimization is a complex project and many factors should be taken into account. It requires repeated iterations to find the optimal design scheme. Mainly based on the actual project needs, this paper proposed a thruster configuration method and optimized the thruster configuration aiming to minimize propellant consumption. Regarding optimization method, this paper focused on the establishment of optimization models and the determination of optimization problems. The thruster configuration and optimization method proposed in this paper were mainly considered from aspects of the completion of satellite task and the limitation of installation area. However, there are many factors that are not considered or involved, which will be the focus of subsequent research.
Thruster configuration and optimization is a complex project and many factors should be taken into account. It requires repeated iterations to find the optimal design scheme. Mainly based on the actual project needs, this paper proposed a thruster configuration method and optimized the thruster configuration aiming to minimize propellant consumption. Regarding optimization method, this paper focused on the establishment of optimization models and the determination of optimization problems. The thruster configuration and optimization method proposed in this paper were mainly considered from aspects of the completion of satellite task and the limitation of installation area. However, there are many factors that are not considered or involved, which will be the focus of subsequent research.
| [1] |
Claudio Bruno. The International Handbook of Space Technology. Berlin: Springer, 2014: 279-321.
(  0) 0) |
| [2] |
Feuerborn S A, Perkins J, Neary D A. Finding a way: Boeing's All Electric Propulsion Satellite. Proceedings of the 49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference. San Jose, CA, 2013.
(  0) 0) |
| [3] |
Martynov M B, Petukhov V G. Applications of electric Propulsion in Scientific Space Projects: Benefits, Features, and Implementation Examples. Solar System Research, 2012, 46(7): 523-530. DOI:10.1134/S0038094612070180 (  0) 0) |
| [4] |
Leonardo Mazzini. Flexible Spacecraft Dynamics, Control and Guidance. Berlin: Springer, 2016: 261-287.
(  0) 0) |
| [5] |
David K, Jonathan W. SS/L-1300 satellite optimized for land launch. Proceedings of the 24th AIAA International Communications Satellite Systems Conference. California, 2006. http://arc.aiaa.org/doi/abs/10.2514/6.2006-5302
(  0) 0) |
| [6] |
John H, Peter G. Earth re-acquisition and attitude recovery for Intelsat Ⅶ/ⅦA satellites. Proceedings of the 20th AIAA International Communication Satellite Systems Conference and Exhibit. Quebec, 2002. http://gateway.proquest.com/openurl?res_dat=xri:pqm&ctx_ver=Z39.88-2004&rfr_id=info:xri/sid:baidu&rft_val_fmt=info:ofi/fmt:kev:mtx:article&genre=article&jtitle=Aiaa%20Journal&atitle=Earth%20Re-Acquisition%20and%20Attitude%20Recovery%20for%20Intelsat%20VII/VIIA%20Satellites
(  0) 0) |
| [7] |
Ocampo C A. Geostationary orbit transfer using electric for the Hughes HS-702 satellite. Proceedings of the 49th International Astronautical Congress. Melbourne, 1998.
(  0) 0) |
| [8] |
Herman J F C, Zimmer A K, Reijneveld J P J, et al. Human exploration of near earth asteroids: Mission analysis for chemical and electric propulsion. Acta Astronautica, 2014, 104(1): 313-323. DOI:10.1016/j.actaastro.2014.07.034 (  0) 0) |
| [9] |
Freeh J E, Burke L M. Comparison of solar electric and chemical propulsion missions. Proceedings of the 66th International Astronautical Congress. Jerusalem, 2015.
(  0) 0) |
| [10] |
Hitoshi K. Activities on electric propulsion in Japan space flight from basic research. Proceedings of the 38th AIAA Joint Propulsion Conference and Exhibit. Indianapolis, 2002.
(  0) 0) |
| [11] |
David Bates, Allen Lee. Fault protection design and testing for the Cassini spacecraft in a "mixed" thruster configuration. AIAA Guidance, Navigation, and Control Conference. Boston, MA, 2013.
(  0) 0) |
| [12] |
Huang H D. Missile and Aerospace Series-Vibration Engineering. Beijing: Aerospace Press, 1989: 81-82.
(  0) 0) |
| [13] |
Anzel B.Station keeping the Hughes HS 702 satellite with a xenon ion propulsion system. Proceedings of the 49th International Astronautical Congress. Melbourne, 1998,
(  0) 0) |
| [14] |
Ma X, Han D, Tang L. Study on moment dumpling of electric propulsion satellite. Chinese Space Science and Technology, 2016, 36(1): 70-76. DOI:10.3780/j.issn.1000-758X.2016.0013 (  0) 0) |
| [15] |
Peng L, Liu L, Long T, et al. Satellite thruster configuration design based on propellant consumption optimization. Journal of Astronautics, 2015, 36(3): 268-277. DOI:10.3873/j.issn.1000-1328.2015.03.004 (  0) 0) |
| [16] |
Pan H L. Liquid quality characteristics analysis for propellant. Control Engineering, 2002, 5: 12-18. (  0) 0) |
| [17] |
Sun Z Q, Deng Z D, Zhang Z X. Intelligent Control Theory and Technology. Beijing: Tsinghua University Press, 2011: 380-386.
(  0) 0) |
 2020, Vol. 27
2020, Vol. 27


