Before 1971, it was generally believed that basic circuit elements comprised three well-known components: resistance, inductance, and capacitance. However, after the publication of the missing circuit element by Chua[1], the discovery of memristor changed people's traditional perception of electronic circuits. Memristive systems with integer-order have been well discussed, but fractional-order memristive systems have rarely been studied.
Fractional calculus plays a very important role in various fields of science and engineering. In 1974, Oldham & Spanier [2] gave it a complete mathematical presentation. A large number of studies show that the fractional-order model can depict the characteristics of the actual system more accurately. One year later[3], described a fractional-order memristor-based classical Chua's oscillator, in which the memristor is a flux-controlled memristor. Since then, a lot of research has been focused on fractional-order memristor models and fractional-order memristor-based systems [4-8].
The nonlinear dynamic of the fractional-order delayed chaotic system has been analyzed [9-14]. In Ref.[13], the researcher analyzed the bifurcation oscillators with delay. In addition, the crucial focus chaos behaviors in the fractional time-delay chaotic system were also investigated[15-16]. However, most of the current researches are limited to mathematical models. No circuit experiments have been conducted[17-18]. In this paper, we propose a nonlinear time-delay chaotic circuit based on fractional-order memristive system. Results of the system circuit simulation accomplished by Multisim are consistent with theoretical analysis and numerical simulation. The structure of this article is as follows: In Section 2, we propose a fractional-order memristor and analyze the electrical characteristics of the fractional-order memristor. In Section 3, we propose a fractional-order memristive delayed chaotic circuit and present the phase portraits of the proposed fractional-order memristive delayed chaotic circuit. Section 4 provides a detailed analysis on the dynamic behaviors of the memristive circuit mentioned. Remarkably, the results of the system circuit simulation accomplished by Multisim are perfectly consistent with theoretical analyses and numerical simulation in Section 5. Finally, the conclusions are given in Section 6.
2 Modeling and Analysis of Fractional-Order Memristor 2.1 Fractional CalculusSeveral existing concept of fractional calculus were proposed in Ref.[2]. The fundamental operator aDtq is defined as follows:
| $_aD_t^q = \left\{ {\begin{array}{*{20}{l}} {\frac{{{{\rm{d}}^q}}}{{{\rm{d}}{t^q}}}, }&{q > 0}\\ {1, }&{q = 0}\\ {\int_a^t {{{({\rm{d}}\tau )}^{ - q}}, } }&{q < 0} \end{array}} \right. $ | (1) |
where a, t are the upper and lower limits of the operation, respectively; q is the order of the calculus operator, whose value can be any complex number. If q > 0, aDtq means fractional derivative; if q < 0, aDtq is expressed as fractional integral [2].
In the development of fractional calculus theory, the initial conditions corresponding to the Riemann-Liouville derivatives have no physical meaning, while the initial conditions of the systems described by the Caputo derivatives have clear physical meanings and the forms are similar to the integer-order differential equations. The fractional derivative of f(t) is as follows:
| $ _aD_t^q\cdot f\left( t \right) = \frac{1}{{\Gamma \left( {n - q} \right)}}\int_a^t {\frac{{{f^n}\left( \tau \right)}}{{{{\left( {t - \tau } \right)}^{q - n + 1}}}}{\rm{d}}\tau } $ | (2) |
where 0≤n-1≤q≤n, n=[q]+1, [q] is the largest integer not exceeding q, Γ(n) is the Euler Gamma function, x(n)(t) is the n-order derivative of x(t), Γ(·) is the Gamma function, which is a function of a variable x defined via a convergent improper integral
| $ \Gamma \left( x \right) = \int_0^\infty {{t^{x - 1}}{e^{ - t}}{\rm{d}}t} $ | (3) |
n∈N is the first integer which is not less than α. It is a fractional derivative of a continuous function of time, namely f(t), which is given in terms of a time integral. Under natural conditions on the function f(t), the Laplace transform satisfies
| $ \begin{array}{l} L\left\{ {_aD_t^q\cdot f\left( t \right)} \right\} = {s^q}F\left( s \right) - \sum\limits_{k = 0}^{n - 1} {{s^{q - k - 1}}{f^{(k)}}\left( 0 \right)} , \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {n - 1 < q \le n} \right) \end{array} $ | (4) |
Muthuswamy et al.[19] studied the flux-controlled memristor model equivalent realization circuit shown in Fig. 1. It consists of three remote arithmetic amplifiers, five resistors, two multipliers, and one capacitor. The first stage op amp U1 circuit can avoid the load effect. The second stage op amp U2 circuit connected to resistor R0 and capacitor C0 is an integrator.
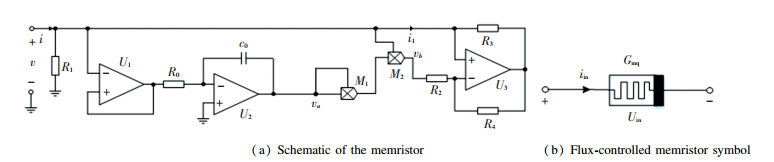
|
Fig.1 Flux-controlled memristor and the corresponding circuit realization |
The mathematical model describing the memristive behavior is established as follows:
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}{x_2}}}{{{\rm{d}}t}} = \frac{1}{{{R_0}{C_0}}}{x_1}\left( t \right)\\ i\left( t \right) = f\left( {{x_1}, {x_2}} \right) = \left( {\frac{1}{{{R_1}}} - \frac{1}{{{R_2}}} + \frac{{{g_1}{g_2}}}{{{R_2}}}{{\left[ {{x_2}\left( t \right)} \right]}^2}} \right){x_1}\left( t \right) \end{array} \right. $ | (5) |
where x1 is the input of the memristor, x2 is internal state of the memristor, f(x1, x2) is the output of the memristor. g1 is the variable scale factor in multiplier M1, g2 is the variable scaling factor in multiplier M2. Assume α=R1-1-R2-1, β=g1g2/R2 in the active magnetron memristive equivalent circuit described by the quadratic nonlinear characteristic curve in Fig. 1. Thus, we set R0=8.2 k Ω, C0=47 nF, R1=750 Ω, R2=1.5 k Ω, R3=R4=8.2 k Ω, g1=0.1, g2=1.3. The equivalent parameters for the proposed active magnetron memristor can be calculated as α=0.666 7 ms and β=0.008 7 S/Wb.
In practical calculations, there are a variety of methods to solve fractional calculus. By obtaining the complex frequency domain transfer function 1/sq, the expanded form of the complex frequency domain is obtained and the complex frequency domain form is converted into the time domain form for numerical solution. Ref.[20] introduced a Bode graph approximation method. We determined the expansion of F=1/sq. Ref.[21] derived the 1/sq expansion of q from 0.1 to 0.9. In order to implement the equivalent circuit of fractional-order memristor shown in Eq. (8), we first considered applying the approximation technique proposed by Oustaloup to get the approximate transfer function of the fractional-order integrator operator [22].
We designed a unit circuit that implements a 1/sq expansion of q from 0.1 to 0.9 based on the 1/sq expansion of the approximate error of 2 dB, as shown in Fig. 3. The complex frequency domain expression of the equivalent circuit is as follows:
| $ H\left( s \right) = {C^{ - 1}}{s^{ - q}} = \sum\limits_{k - 1}^n {\frac{{C_k^{ - 1}}}{{\left( {s + {{({R_k}{C_k})}^{ - 1}}} \right)}}} $ | (6) |
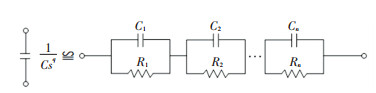
|
Fig.3 Unit circuit for implementing the fractional-order integrator '1/Csq' |
where C is the unit parameter. Let C=1 μF, H(s)=1/sq.
Table 1 gives the approximate transfer functions of fractional integrator F(s) when fractional order q is selected as 0.6, 0.7, 0.8, 0.9. The corresponding resistance and capacitance values are shown in Table 2.
| Table 1 Boolean approximation of 1/sq |
| Table 2 Calculated values of resistances and capacitances |
Then, we used electronic circuits to achieve the fractional-order flux-controlled memristor in the complex frequency domain as shown in Fig. 2, with a unit circuit (Fig. 3) for implementing the approximate transfer functions of fractional-order integrator operator depicted in Table 2.

|
Fig.2 Fractional-order flux-controlled memristor |
According to the concept of fractional calculus, the real capacitor can be extended to fractional-order to describe the real electricity characteristics [23]. In this paper, the integer-order capacitor C in the memristor is actually fractional-order capacitor in reality. The fractional-order unified model of memristor is derived as follows:
| $\begin{array}{l} \frac{{{\rm{d}}x_2^q}}{{{\rm{d}}t}} = \frac{1}{{{R_0}C_0^q}}{x_1}\\ f({x_{1, }}{x_2}) = \left( {\frac{1}{{{R_1}}} - \frac{1}{{{R_2}}} + \frac{{{g_1}{g_2}}}{{{R_2}}}{{[{x_2}]}^2}} \right){x_1} \end{array} $ | (7) |
where q is the order of the fractional-order.
To prove the validity of the theory mentioned above, circuit simulations were carried out to realize the memristor. The driven voltage was chosen as x1(t)=X1sin(2πft)V. When X1=4 V, the current-voltage curve is described in Fig. 4.
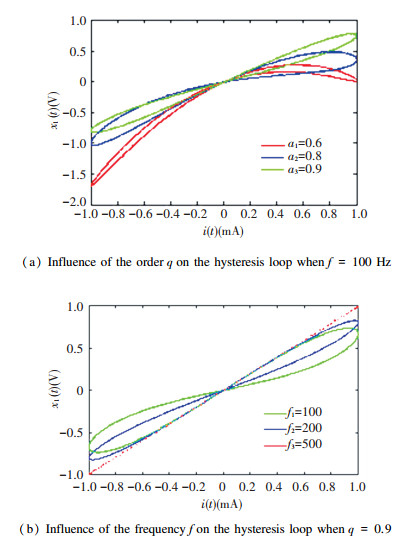
|
Fig.4 Pinched hysteresis loop of the fractional-order memristor |
Fig. 4(a) exhibits the pinched hysteresis loop when f=100 Hz and the fractional q is 0.6, 0.8, and 0.9, respectively. Fig. 4(b) exhibits the pinched hysteresis loop when q=0.9 and f equals to 100, 200, and 500 Hz, respectively. Through simulation experiments, we concluded that in the same frequency, as the order q increases, the area of the pinched hysteresis loop increases monotonically; in the same order, as the frequency f increases, the area of the pinched hysteresis loop decreases monotonically.
2.3 Delay CircuitRef.[24] compared the APF with the LCL, Bessel delay circuit. Other delay circuits have their own shortcomings. APF is the most efficient compared with other delay blocks. Therefore, APF experimental system was chosen in this paper.
This delay unit is included by a series of All Pass Filter (APF) as shown in Fig. 5 [25]. The same delay unit is used in Refs.[26-27]. Variable delay was studied as delay blocks. The transfer function of the APF is as follows:
| $ T(s) = - {a_1}\frac{{s - {w_0}}}{{s + {w_0}}} $ | (8) |
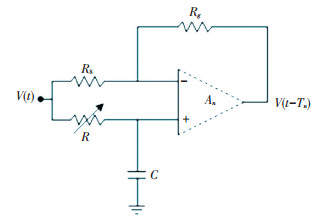
|
Fig.5 Active first-order all pass filter (APF) |
The flat gain q1=1 is determined by R8 and Rg. TD≈RC is the time delay provided by each APF block. Thus this delay unit needs i sections to realize a delay TD≈iRC, (i=1, 2, 3).
Because TD changes with the resistance change of the sliding rheostat, in order to avoid emergency, we used two time-delay modules in series as shown in Fig. 5.
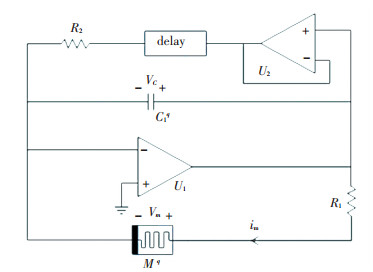
3 Fractional-Order Memristive Time-Delay Chaotic CircuitIn this module, we present a circuital realization of the fractional-order memristive delayed Chaotic system (9) to prove the feasibility and correctness of the theoretical model. The designed circuit is shown in Fig. 6. Fractional-order memristive device and delayed unit was analyzed in Ref.[28]. The equation of the circuit in Fig. 6 is derived as follows:
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}x_2^q}}{{{\rm{d}}{t^q}}} = l{x_1}\\ \frac{{{{\rm{d}}^q}{x_1}}}{{{\rm{d}}{t^q}}} = a{x_1} + b{x_{1\tau }} + c{x_1}{\left( {{x_2}} \right)^2} \end{array} \right. $ | (9) |
|
Fig.6 Delayed chaos circuit based on fractional-order memristor |
where a=-α/C1q, b=-(RC1q)-1, c=-β/C1q, l=(R0C0q)-1, α=0.666 7 ms, β=0.008 7 S/Wb, and τ is the time-delay.
The fractional-order q is set to be 0.9, and initial values are set to be x1=0.1 V, x2=0.1 V. In this paper, we studied delayed memristive chaotic system in Fig. 6 [29].
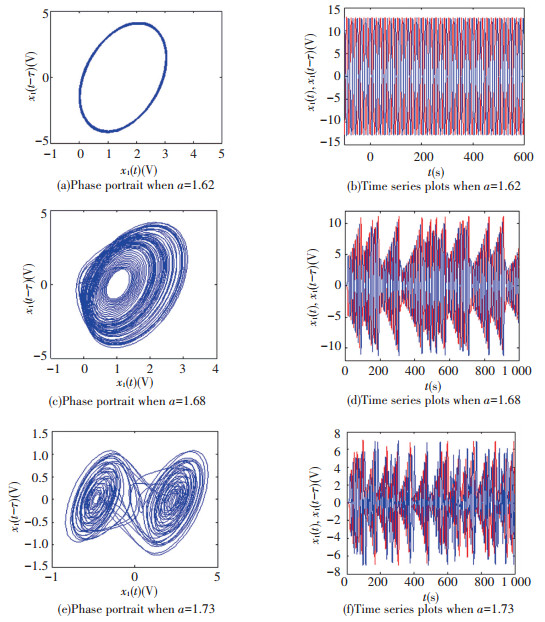
Subsequently, we performed numerical simulation on the decomposed fractional mathematical model. The simulation was carried out by MATLAB, via utilizing the predictor-corrector method to simulate the fractional differential Eq. (9).Other parameters include fractional order q=0.9, l=2.5, b=-2, τ=1 and initial values (0.1, 0.1). In order to easily see the influence of the parameter a on the time-delayed chaotic circuit of the fractional memristor, we drew the two-dimensional phase diagrams and time-series plots of different parameter a, as is shown in Fig. 7. The phase portrait is a stable limit cycle with parameter a=1.62 as shown in Fig. 7(a). The corresponding time-series plots is shown in Fig. 7(b). When parameter a > 1.64, the system goes into a chaotic state. When parameter a > 1.64, the real time and phase plane plots are shown in Fig. 7(c) and Fig. 7(d), respectively. When parameter a≥1.7, the system enters double-scroll chaotic attractor in Fig. 7(e)-(f).
|
Fig.7 Phase plane and time-series plots for variable a |
4 Analysis of Dynamical Behaviors 4.1 Stability of Equilibrium Points
We presume that the system (9) has an equilibrium point X*=(x1*+x2*). Then, the linearized system near the equilibrium point X* is as follows:
| $ D_t^q\mathit{\boldsymbol{X}} = \mathit{\boldsymbol{JX}} + {\mathit{\boldsymbol{J}}_\tau }{\mathit{\boldsymbol{X}}_\tau } $ | (10) |
where X and Xτ are the column vectors (x1, x2) at t and t-τ,
| $ \mathit{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} {a + c{{(x_2^*)}^2}}&{2cx_1^*x_2^*}\\ l&0 \end{array}} \right] $ | (11) |
and
| $ {\mathit{\boldsymbol{J}}_\tau } = \left[ {\begin{array}{*{20}{c}} b&0\\ 0&0 \end{array}} \right] $ | (12) |
Theorem 1 We can get all the roots of the characteristic equation[30]
| $ {\rm{det}}\left( {{s^q}\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{J}} - {\rm{exp}}\left( { - s\tau } \right){\mathit{\boldsymbol{J}}_\tau }} \right) = 0 $ | (13) |
where I is the identity matrix.
The necessary factor for the system (9) to generate chaos is that Eq.(13) has the root of the real part.
Thus we have the following equation:
| $ {\rm{det}}\left( {\begin{array}{*{20}{c}} {{s^q} - \left( {a + c{{\left( {x_2^*} \right)}^2} + b{e^{ - s\tau }}} \right)}&{2cx_1^*x_2^*}\\ { - l}&{{s^q}} \end{array}} \right) = 0 $ | (14) |
Based on Eq.(14), the characteristic equation is as below:
| $ {s^{2q}} + {A_1}{s^q} + {A_2}{s^q}{e^{ - s\tau }} + {A_3} = 0 $ | (15) |
where
| $ \left\{ \begin{array}{l} {A_1} = - \left( {a + c{{\left( {x_2^*} \right)}^2}} \right)\\ {A_2} = - b\\ {A_3} = - 2lcx_1^*x_2^* \end{array} \right. $ | (16) |
Assuming that a root of Eq.(15) is s=iw= |w|(cos(π/2)+isin(±(π/2))), and w is a real number, when w > 0, we obtain isin(π/2); when w < 0, we obtain -isin(π/2). Real and imaginary parts are separated, then we get
| $ \left\{ \begin{array}{l} {\omega ^{2q}}{\rm{cos}}\;q{\rm{ \mathsf{ π} }} + {A_1}{\omega ^q}{\rm{cos}}\frac{{q{\rm{ \mathsf{ π} }}}}{2} + {A_3} + \\ \;\;\;\;\;\;{A_2}{\omega ^q}{\rm{cos}}\frac{{q{\rm{ \mathsf{ π} }}}}{2}{\rm{cos}}\;\omega \tau + {A_2}{\omega ^q}{\rm{sin}}\frac{{q{\rm{ \mathsf{ π} }}}}{2}{\rm{sin}}\;\omega \tau = 0\\ {\omega ^{2q}}{\rm{sin}}\;q{\rm{ \mathsf{ π} }} + {A_1}{\omega ^q}{\rm{sin}}\frac{{q{\rm{ \mathsf{ π} }}}}{2} - \\ \;\;\;\;\;\;\;{A_2}{\omega ^q}{\rm{cos}}\;\frac{{q{\rm{ \mathsf{ π} }}}}{2}{\rm{sin}}\;\omega \tau + {A_2}{\omega ^q}{\rm{sin}}\frac{{q{\rm{ \mathsf{ π} }}}}{2}{\rm{cos}}\;\omega \tau = 0 \end{array} \right. $ | (17) |
We assume
| $ \left\{ \begin{array}{l} {B_1} + C{\rm{cos}}\;\omega \tau + D{\rm{sin}}\;\omega \tau = 0\\ {B_2} + C{\rm{sin}}\;\omega \tau + D{\rm{sin}}\;\omega \tau = 0 \end{array} \right. $ | (18) |
and
| $ \left\{ \begin{array}{l} {B_1} = {\omega ^{2q}}{\rm{cos}}\;q{\rm{ \mathsf{ π} }} + {A_1}{\omega ^q}{\rm{cos}}\frac{{q{\rm{ \mathsf{ π} }}}}{2} + {A_3}\\ {B_2} = {\omega ^{2q}}{\rm{sin}}\;q{\rm{ \mathsf{ π} }} + {A_1}{\omega ^q}{\rm{sin}}\frac{{q{\rm{ \mathsf{ π} }}}}{2}\\ C = {A_2}{\omega ^q}{\rm{cos}}\frac{{q{\rm{ \mathsf{ π} }}}}{2}\\ D = {A_2}{\omega ^q}{\rm{sin}}\frac{{q{\rm{ \mathsf{ π} }}}}{2} \end{array} \right. $ | (19) |
We set
| $ B_1^2 + B_2^2 = {C^2} + {D^2} $ | (20) |
Then, we get
| $ {\left| \omega \right|^{4q}} + {\psi _1}{\left| \omega \right|^{3q}} + {\psi _2}{\left| \omega \right|^{2q}} + {\psi _3}{\left| \omega \right|^q} + {\psi _4} = 0 $ | (21) |
where
| $ \left\{ \begin{array}{l} {\psi _1} = 2{A_1}\left( {{\rm{cos}}\;\frac{{q{\rm{ \mathsf{ π} }}}}{2}{\rm{cos}}\;q{\rm{ \mathsf{ π} }} + {\rm{sin}}\;q{\rm{ \mathsf{ π} }}\;{\rm{sin}}\;\frac{{q{\rm{ \mathsf{ π} }}}}{2}} \right)\\ {\psi _2} = 2\left( {{A_3}{\rm{cos}}\;q{\rm{ \mathsf{ π} }} + A_1^2 - A_2^2} \right)\\ {\psi _3} = 2{\rm{cos}}\frac{{q{\rm{ \mathsf{ π} }}}}{2}{A_1}{A_3}\\ {\psi _4} = A_3^2 \end{array} \right. $ | (22) |
We can calculate the root of Eq.(21).
We set
| $ y\left( \omega \right) = {\left| \omega \right|^{4q}} + {\psi _1}{\left| \omega \right|^{3q}} + {\psi _2}{\left| \omega \right|^{2q}} + {\psi _3}{\left| \omega \right|^q} + {\psi _4} $ | (23) |
Lemma 1 For Eq.(15), the following results hold:
(a) If Ψk > 0(k=1, 2, 3, 4) and A3+A4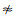
(b) If Ψk > 0(k=1, 2, 3, 4) and Ψk < 0, Eq.(15) has a pair of purely imaginary roots ±w when τ=τj, j=0, 1, 2, …, where
| $ \tau _j^{(k)} = \frac{1}{{{\omega _k}}}\left[ {{\rm{arccos}}\left( { - \frac{{{B_1}C + {B_2}D}}{{{C^2} + {D^2}}}} \right) + 2j{\rm{ \mathsf{ π} }}} \right] $ | (24) |
where j=0, 1, 2, …; k=1, 2, 3, …, and w0 is the unique positive zero of the function y(w).
Proof
(a) From ΨK > 0(k=1, 2, 3, 4), we obtain y=(0)=Ψ4 > 0,
| $ \begin{array}{l} {y^\prime }\left( \omega \right) = 4q{\left| \omega \right|^{4q - 1}} + 3{\psi _1}q{\left| \omega \right|^{3q - 1}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;2{\psi _2}q{\left| \omega \right|^{2q - 1}} + {\psi _3}q{\left| \omega \right|^{q - 1}} \end{array} $ | (25) |
Combine q > 0 and Ψk > 0(k=1, 2, 3, 4) we get that Eq.(15) has no real root. Hence, Eq.(15) has no purely imaginary root, provided that A3+A4≠0, Ψ4 < 0 is not a root of Eq.(15).
(b) If Ψ4 < 0, it is simple to get y(0)=Ψ4 < 0. Then, by
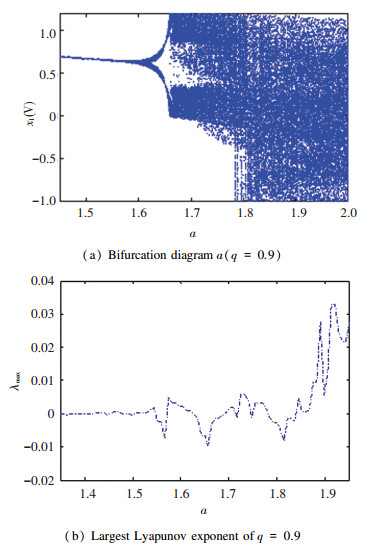
As the system parameter a changes, balance point of the fractional-order delayed chaotic system, stability of the system, and state of the system will alter. The largest Lyapunov exponent and bifurcation diagram of the fractional-order delayed chaotic system are considered in order to demonstrate the chaos. Under the initial condition (0.1, 0.1), when a changes in the range [1.35, 2], the maximum Lyapunov exponent and bifurcation diagram of the fractional-order delayed chaotic system is shown in Fig. 8. For better observation, the maximum Lyapunov exponent of the fractional-order delayed chaotic system is basically consistent with the bifurcation diagram.
|
Fig.8 Dynamical behaviors with different a (q=0.9, l=2.5, b=-2, τ=1) |
It is obvious that the orbits of the memristive circuit start from the periodic state, then when a passes through the threshold, Hopf bifurcation appears, and finally turn into chaotic state with the increase of a. When parameter a increases to 1.62, the phase portrait of the system (9) turns to be a limit cycle. Besides, with decrease of parameter a, the orbit degenerates into a single-scroll attractor as shown in Fig. 7(c).
4.3 Coexistence Attractors and Coexisting Bifurcation ModeWhen we set q=0.9, l=2.5, b=02, τ=1, parameter a changes in the range [1.35, 2], and the state initial values are (0.1, 0.1) and (-0.1, -0.1) by blue and red, respectively, it is clear from Fig. 9 that there is a coexistence bifurcation mode phenomenon. In the case of different initial values, the system's bifurcation diagram is inconsistent.
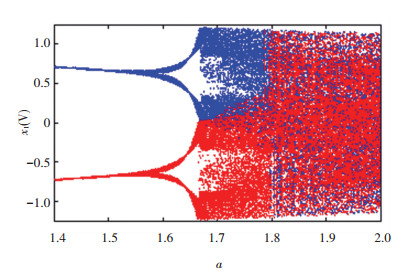
|
Fig.9 Bifurcation diagram of initial values (0.1, 0.1) and (-0.1, -0.1) with a as a varying parameter (q=0.9, l=2.5, b=-2, τ=1) |
According to dynamics given in Fig. 10, when parameter a > 1.64, the system (9) manifests coexisting attractors. When parameter a=1.68, the state initial values are (0.1, 0.1) and (-0.1, 0.1) by blue and red, respectively. The coexistence of single-scroll chaotic attractors are shown in Fig. 10(a), and the state initial values are (0.1, 0.1) and (-0.1, -0.1) by blue and red, respectively, as is shown in Fig. 10(b). When parameter a=1.73, the state initial values are (0.1, 0.1) and (-0.1, -0.1). The coexistence of double-scroll chaotic attractors are expressed in Fig. 10(c). From this phenomenon, we know that the fractional-order memristive time-delay chaotic system has wealth dynamic characteristics.
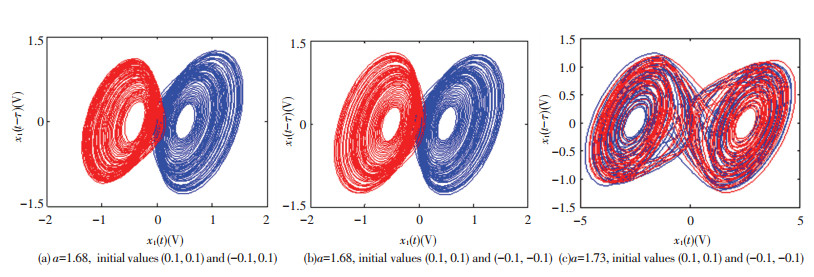
|
Fig.10 Coexisting attractors with different parameter a and initial values |
5 Experimental Research on Circuit
To confirm the theoretical investigations, circuit simulations are carried out by Multisim. The structure of the circuit was designed as Fig. 11 when q is 0.9. The proposed circuit was designed on Multisim software using op-amp AD711KN and multiplier AD633JN with ±15 volts and R=11.24 k Ω. The phase plane and time-series plots for variable a is as shown in Fig. 12. The phase portrait is a stable limit cycle when a=1.62, a single-scroll chaotic attractor when a=1.68, and a double-scroll attractor when a=1.73. Simulation results demonstrate the influence of parameter a on chaotic behaviors.

|
Fig.11 Schematic of the circuit structure |

|
Fig.12 Phase plane and time-series plots for variable a |
6 Conclusions
In this paper, we presented a fractional-order memristive delayed chaotic system. Some dynamical properties, including equilibrium points, stability, bifurcation, and Lyapunov exponent of the oscillator, were investigated in detail by theoretical analyses and simulations. Moreover, we also found the nonlinear phenomena of coexisting bifurcation and coexisting attractor. The phenomenon shows that the state of this oscilator was highly sensitive to its initial value, which is called coexistent oscillation in this paper. Besides, the results of the circuit simulation accomplished by Multisim were perfectly consistent with theoretical analyses.
| [1] |
Chua L. Memristor-The missing circuit element. IEEE Transactions on Circuit Theory, 1971, 18(5): 507-519. DOI:10.1109/TCT.1971.1083337 (  0) 0) |
| [2] |
Oldham K B, Spanier J. The Fractional Calculus. New York: Academic Press, 1974: 396-400.
(  0) 0) |
| [3] |
Petráš I. Fractional-order memristor-based Chua's circuit. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2010, 57(12): 975-979. DOI:10.1109/TCSⅡ.2010.2083150 (  0) 0) |
| [4] |
Fouda M E, Radwan A G. On the fractional-order memristor model. Journal of Fractional Calculus and Applications, 2013, 4(1): 1-7. (  0) 0) |
| [5] |
Chen L, He Y, Lv X, et al. Dynamic behaviours and control of fractional-order memristor-based system. Pramana-Journal of Physics, 2015, 85(1): 91-104. DOI:10.1007/s12043-014-0880-9 (  0) 0) |
| [6] |
Huang W, Ge Y, Min F, et al. Circuit implementations and bifurcations of a novel fractional-order chaotic system. Proceedings of the 2015 Sixth International Conference on Intelligent Control and Information Processing. Piscataway: IEEE, 2015.98-104. DOI: 10.1109/ICICIP.2015.7388151.
(  0) 0) |
| [7] |
Semary M S, Abdel Malek H L, Hassan H N, et al. An optimal linear system approximation of nonlinear fractional-order memristor-capacitor charging circuit. Microelectronics Journal, 2016, 51: 58-66. DOI:10.1016/j.mejo.2016.02.005 (  0) 0) |
| [8] |
Si G, Diao L, Zhu J. Fractional-order charge-controlled memristor: Theoretical analysis and simulation. Nonlinear Dynamics, 2017, 87(4): 2625-2634. DOI:10.1007/s11071-016-3215-1 (  0) 0) |
| [9] |
Chen L, Pan W, Wu R, et al. New result on finite-time stability of fractional-order nonlinear delayed systems. Journal of Computational and Nonlinear Dynamics, 2015, 10(6): 064504. DOI:10.1115/1.4029784 (  0) 0) |
| [10] |
Velmurugan G, Rakkiyappan R. Hybrid projective synchronization of fractional-order chaotic complex nonlinear systems with time delays. Journal of Computational and Nonlinear Dynamics, 2016, 11(3): 031016. DOI:10.1115/1.4031860 (  0) 0) |
| [11] |
Babakhani A, Baleanu D, Khanbabaie R. Hopf bifurcation for a class of fractional differential equations with delay. Nonlinear Dynamics, 2012, 69(3): 721-729. DOI:10.1007/s11071-011-0299-5 (  0) 0) |
| [12] |
Xiao M, Zheng W X, Cao J. Hopf bifurcation of an (n+1)-neuron bidirectional associative memory neural network model with delays. IEEE Transactions on Neural Networks and Learning Systems, 2013, 24(1): 118-132. DOI:10.1109/TNNLS.2012.2224123 (  0) 0) |
| [13] |
Leung A Y T, Yang H X, Zhu P. Periodic bifurcation of Duffing-van der Pol oscillators having fractional derivatives and time delay. Communications in Nonlinear Science and Numerical Simulation, 2014, 19(4): 1142-1155. DOI:10.1016/j.cnsns.2013.08.020 (  0) 0) |
| [14] |
Huang C, Cao J, Ma Z. Delay-induced bifurcation in a tri-neuron fractional neural network. International Journal of Systems Science, 2015, 47(15): 1-10. DOI:10.1080/00207721.2015.1110641 (  0) 0) |
| [15] |
Baleanu D, Magin R L, Bhaleka S, et al. Chaos in the fractional order nonlinear bloch equation with delay. Communications in Nonlinear Science and Numerical Simulation, 2015, 25(1): 41-49. DOI:10.1016/j.cnsns.2015.01.004 (  0) 0) |
| [16] |
Wu G C, Baleanu D. Discrete chaos in fractional delayed logistic maps. Nonlinear Dynamics, 2015, 80(4): 1697-1703. DOI:10.1007/s11071-014-1250-3 (  0) 0) |
| [17] |
Ding Dawei, Qian Xin, Hu Wei, et al. Chaos and bopf bifurcation control in a fractional-order memristor-based chaotic system with time delay. The European Physical Journal Plus, 2017, 132: 447. DOI:10.1140/epjp/i2017-11699-9 (  0) 0) |
| [18] |
Hu Wei, Ding Dawei, Wang Nian. Nonlinear dynamic analysis of a simplest fractional-order delayed memristive chaotic system. Journal of Computational and Nonlinear Dynamics, 2017, 12(4): 041003. DOI:10.1115/1.4035412 (  0) 0) |
| [19] |
Muthuswamy B. Implementing memristor based chaotic circuits. International Journal of Bifurcation and Chaos, 2010, 20(5): 1335-1350. DOI:10.1142/S0218127410026514 (  0) 0) |
| [20] |
Charef A, Sun H H, Tsao Y Y, et al. Fractal system as represented by singularity function. IEEE Transactions on Automatic Control, 1992, 37(9): 1465-1470. DOI:10.1109/9.159595 (  0) 0) |
| [21] |
Ahmad W M, Sprott J C. Chaos in fractional-order autonomous nonlinear systems. Chaos, Solitons and Fractals, 2003, 16(2): 339-351. DOI:10.1016/S0960-0779(02)00438-1 (  0) 0) |
| [22] |
Oustaloup A, Levron F, Mathieu B, et al. Frequency-band complex noninteger differentiator: Characterization and synthesis. IEEE Transactions on Circuits and Systems Ⅰ: Fundamental Theory and Applications, 2000, 47(1): 25-39. DOI:10.1109/81.817385 (  0) 0) |
| [23] |
Wang F Q, Ma X K. Transfer function modeling and analysis of the open-loop Buck converter using the fractional calculus. Chinese Phys. B, 2013, 22(3): 232-239. (  0) 0) |
| [24] |
Biswas D, Banerjee T. A simple chaotic and hyperchaotic time-delay system: Design and electronic circuit implementation. Nonlinear Dynamics, 2016, 83(4): 2331-2347. DOI:10.1007/s11071-015-2484-4 (  0) 0) |
| [25] |
Sedra A S, Smith K C. Microelectronic Circuits. Oxford: Oxford Univ. Press, 2003.
(  0) 0) |
| [26] |
Banerjee T, Biswas D, Sarkar B C. Design and analysis of a first order time-delayed chaotic system. Nonlinear Dynamics, 2012, 70(1): 721-734. DOI:10.1007/s11071-012-0490-3 (  0) 0) |
| [27] |
Banerjee T, Biswas D. Theory and experiment of a firstorder chaotic delay dynamical system. International Journal Bifurcation and Chaos, 2013, 23(6): 1330020. DOI:10.1142/S0218127413300206 (  0) 0) |
| [28] |
Pham V T, Vaidyanathan S, Volos C K, et al. A novel memristive time-delay chaotic system without equilibrium points. The European Physical Journal Special Topics, 2016, 225(1): 127-136. DOI:10.1140/epjst/e2016-02625-8 (  0) 0) |
| [29] |
Pham V T, Buscarino A, Fortuna L, et al. Simple memristive time-delay chaotic systems. International Journal Bifurcation and Chaos, 2013, 23(4): 1350073. DOI:10.1142/S0218127413500739 (  0) 0) |
| [30] |
Bhalekar S A. Necessary condition for the existence of chaos in fractional order delay differential equations. International Journal of Mathematical and Computational Sciences, 2013, 7(3): 28-32. DOI:10.5281/zenodo.1087915 (  0) 0) |
 2020, Vol. 27
2020, Vol. 27


