2. Shanghai YS Information Technology Co., Ltd., Shanghai 200240, China
Actuators made of smart materials have increasingly wide range of applications due to their excellent performance in structural controls. Macro Fiber Composite (MFC) is such a smart material that has been widely used in shape and vibration controlling, health monitoring, structural morphing, energy harvesting, etc. The MFC actuator was first invented in 1996 and later commercialized in 2002. One important application of the MFC actuator is to maintain desired geometries for high precision space structures[1]. A typical MFC actuator consists of rectangular Lead Zirconium Titanate rods sandwiched by epoxy layers, interspaced copper electrodes, and Kapton films. One of its advantages is that the MFC actuator can provide low cost and in-situ actuation with high flexibility[2].
The beam-actuator system consisting of a CFRP composite and an MFC actuator can be widely used in airfoils, blades, and adaptive truss structures for shape control and vibration control problems. Ro et al.[3] used MFC actuators to control the vibration of a hollow cylindrical rod. Vadiraja[4] et al. investigated the optimal vibration control of rotating pre-twisted thin-walled composite beams with MFC actuators and sensors. Kumar et al.[5] studied the vibration control of a deep composite cylindrical shell using MFC actuators by finite element method. Wu et al.[6] designed PD and fuzzy controllers for vibration control of a panel reflection antenna using MFC actuators. When an MFC actuator is bonded onto the surface of a structure, the piezoelectric induced strain of the actuator produces a complex deflection that combines axial, bending and shear deformations. An analytical model needs to be developed to predict the surface deflections. Lots of researchers have investigated the relationship between the electric potential acting on a piezoelectric actuator and the deformation of the structure. Saravanos[7] used finite element method to analyze the static and free vibration of composite beams with embedded piezoelectric sensors and actuators. Benjeddou[8] presented a finite element model for adaptive sandwich beams to deal with either extension or shear actuation mechanism. Wang[9] studied the free vibration of a sandwich beam coupled with a piezoelectric layer based on Euler-Bernoulli beam model. Kapuria[10] presented a one-dimensional finite element with electric degrees of freedom for the dynamic analysis of hybrid piezoelectric beams based on layerwise (zigzag) theory. Robbin and Reddy[11] investigated the static and dynamic interactions between a bonded piezoelectric actuator and the host beam. Tzou and Tseng[12] using classical laminated plate theory developed a piezoelectric isotropic plate element with internal degrees of freedom. Koconis et al.[13-14] investigated the changes in shapes of composite beams, plates, and shells introduced by embedded piezoelectric actuators. Portela[15] used non-linear FEM to analyze a multi stable structure actuated by piezoelectric patches. Huang[16] used FEM with four node plate elements to model a partially bonded piezoelectric actuator on a composite laminates. Frequency and transient responses of the structure were obtained in his study.
Although numerical methods like FEM are widely used in analyzing piezoelectric structures, analytical solutions still need to be developed. Most analytical methods in the literature are just for static analysis. Using truncated series or admissible functions to form the solutions are complicated and constrained by the boundary conditions. It is difficult to extend them to solve large adaptive truss systems. Thus, a simple but effective method to get the analytical solutions for structures composed of beam-actuator components is desired.
As a study case for this paper, an MFC actuator was bonded onto the surface of a CFRP laminates to form a partially bonded beam-actuator system. Governing equations associated to this beam-actuator system were derived by this study. Shear deformation and active stiffening effects are included in the governing equations.
A novel analytical modeling method which distributes transfer function formulation is proposed to derive the analytic solution. The advantages of the proposed method include conciseness, effectiveness, and involving no truncated series or admissible functions at arbitrary boundary conditions. Compared with FEM, the proposed method provides closed-form analytical solutions and needs much fewer elements. It is very convenient to perform optimization analyses and feedback controls for complex systems composed of piezoelectric beam components. Numerical solutions of FEM were used to compare with the analytical solutions. An experiment was also conducted to verify the results of analyses.
2 Governing EquationsFor general piezoelectric materials, the constitution equations are given as[17]
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\varepsilon }} = {\mathit{\boldsymbol{s}}^E}\mathit{\boldsymbol{\sigma }} + \mathit{\boldsymbol{dE}}\\ \mathit{\boldsymbol{D}} = \mathit{\boldsymbol{d\sigma }} + {\mathit{\boldsymbol{e}}^{\rm{T}}}E \end{array} \right. $ | (1) |
where ε and σ stand for strain and stress vectors. sEand ddenote the compliance and piezoelectric constant matrices. D and E are electric displacement and electric field vectors. For free strain condition, i.e., σ=0, εΛ= dE is the strain induced by MFC actuator.
The concept of a piezoelectric composite beam is shown in Fig. 1.
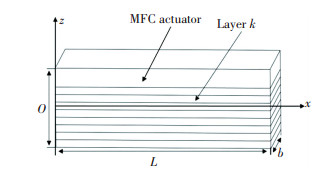
|
Fig.1 CFRP laminates with an MFC actuator |
The MFC actuator is bonded on the top surface of the CFRP composite beam. The x-direction is the direction of the length and the x axis is in the mid-plane. The origin point is located at the end of the beam. L is the length of the composite beam. The fiber direction of the MFC actuator is along the x-direction. Let εx denote axial strain of mid-plane points, u0 denote the axial displacement of the points in the mid-plane, γzx denote the first order of shear strain, φ denote the rotation angle of the actuator-beam structure. εΛ is the actuator induced strain vector. The relationship of them can be written as
| $ \left[ {\begin{array}{*{20}{c}} {{\varepsilon _x}}\\ {{\gamma _{zx}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {u_0}}}{{\partial x}}}\\ {\frac{{\partial w}}{{\partial x}} + \phi } \end{array}} \right] - z\left[ {\begin{array}{*{20}{c}} { - \frac{{\partial \phi }}{{\partial x}}}\\ 0 \end{array}} \right] + {\varepsilon _\Lambda } $ | (2) |
where
| $ {\mathit{\boldsymbol{\varepsilon }}_\Lambda } = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_1}}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{d_{11}}{\mathit{\boldsymbol{E}}^1} + {d_{31}}{\mathit{\boldsymbol{E}}^3}}\\ {{d_{15}}{\mathit{\boldsymbol{E}}^1}} \end{array}} \right] $ | (3) |
where εΛ is the strain vector induced by the MFC actuator with different voltages, dij is the piezoelectric constants. i denotes the direction of electric field and j denotes the direction of induced strain. Λ1, Λ2 stand for the induced axial and shear strains. Vectors E1 and E3 denote the electric field where the superscripts 1 and 3 stand for the directions of the electric fields. The axial force, internal moment, and the shear force can be written as
| $ \begin{array}{l} \mathit{\boldsymbol{N}}\left( x \right) = b\int_{ - h/2}^{h/2} {\sigma \left( z \right){\rm{d}}z = } \\ \;\;\;\;\;\;b\int_{ - h/2}^{h/2} {\mathit{\boldsymbol{E}}\left( z \right)\left[ {\varepsilon _x^0 - z\left( { - \frac{{\partial \phi }}{{\partial x}}} \right) + {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_1}} \right]{\rm{d}}z} \end{array} $ | (4) |
| $ \begin{array}{l} \mathit{\boldsymbol{M}}\left( x \right) = - b\int_{ - h/2}^{h/2} {\sigma \left( z \right)z{\rm{d}}z = } \\ \;\;\;\;\;\;\;\;\; - b\int_{ - h/2}^{h/2} {\mathit{\boldsymbol{E}}\left( z \right)\left( {\varepsilon _x^0 - z\left( { - \frac{{\partial \phi }}{{\partial x}}} \right) + {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_1}} \right)z{\rm{d}}z} \end{array} $ | (5) |
| $ \begin{array}{l} \mathit{\boldsymbol{Q}}\left( x \right) = b\int_{ - h/2}^{h/2} {{\tau _{zx}}\left( z \right)z{\rm{d}}z = } \\ \;\;\;\;\;\;b\int_{ - h/2}^{h/2} {\kappa \mathit{\boldsymbol{G}}\left( z \right)\left[ {\left( {\frac{{\partial w}}{{\partial x}} + \phi } \right) + {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_2}} \right]{\rm{d}}z} \end{array} $ | (6) |
where E(z) and G(z) denote the elastic modulus and shear modulus of the layers. κ is a shear correction factor and is usually taken as 5/6. For a laminated actuator-beam system, the relationship between the generalized internal forces and the strain vectors can be written as a matrix form
| $ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{N}}\left( x \right)}\\ {\mathit{\boldsymbol{M}}\left( x \right)}\\ {\mathit{\boldsymbol{Q}}\left( x \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} A&B&0\\ B&C&0\\ 0&0&D \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\varepsilon _x^0}\\ { - \phi \prime }\\ {w\prime + \phi } \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{N}}_\Lambda }}\\ {{\mathit{\boldsymbol{M}}_\Lambda }}\\ {{\mathit{\boldsymbol{Q}}_\Lambda }} \end{array}} \right] $ | (7) |
where A, B, C, D are constants related to the materials and fiber orientations of the laminates. NΛ, MΛ, and QΛ are the forces and moments induced by the MFC actuator. They are defined in Appendix (Ⅰ). Let U denote the total energy including piezoelectric strain energy and K denote the kinetic energy. The total strain energy of the piezoelectric composite laminates including normal strain and shear strain energy can be expressed as
| $ \begin{array}{l} U = \frac{1}{2}\sum\limits_{k = 1}^n {\left[ {\int\limits_L {\int\limits_{{z_{k - 1}}}^{{z_k}} {\left( {{\varepsilon _x}{\sigma _x} + {\tau _{zx}}{\gamma _{zx}}} \right){\rm{d}}z{\rm{d}}x} } } \right]} = \\ \;\;\;\;\;\;\frac{1}{2}\sum\limits_{k = 1}^n {\left\{ {\int\limits_L {\int\limits_{{z_{k - 1}}}^{{z_k}} {\left[ {{\mathit{\boldsymbol{E}}_k}{{\left( {u_0^\prime + z{\phi ^\prime } + {\mathit{\Lambda} _1}} \right)}^2} + } \right.} } } \right.} \\ \;\;\;\;\;\;\;\left. {\left. {{G_k}{{\left( {\left( {{w^\prime } + \phi } \right) + {\mathit{\Lambda} _2}} \right)}^2}} \right]{\rm{d}}z{\rm{d}}x} \right\} \end{array} $ | (8) |
| $ K = \frac{1}{2}\int\limits_S {{\rho _k}b} \left( {{{\dot u}^2} + {{\dot w}^2}} \right){\rm{d}}z{\rm{d}}x $ | (9) |
where symbols "'" and "˙" denote the derivatives with respect to x and t. zk and ρk denote the z-coordinate and density of the k-th layer.b is the width of the actuator-beam system. L and n denote the length and the total layers of the actuator-beam system. Variations of U and K can be written as
| $\begin{array}{l} \delta U = - \int\limits_L {[\left( {Au'' - B\phi ''} \right)\delta u - \left( {Bu'' - C\phi '' - D(w\prime + } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\left. {\phi )} \right)\delta \phi - D\left( {w'' + \phi \prime } \right)\delta w]{\rm{d}}x + N\left( x \right)\delta u|_0^L - \\ \;\;\;\;\;\;\;\;\;\;\;M\left( x \right)\delta \phi |_0^L + Q\left( x \right)\delta w|_0^L \end{array} $ | (10) |
and
| $ \begin{array}{l} \delta K = \frac{1}{2}\delta \int\limits_S {{\rho _k}b\left( {{{\dot u}^2} + {{\dot w}^2}} \right){\rm{d}}z{\rm{d}}x = \int\limits_S {{\rho _k}b} [{{\dot u}_0}\delta {{\dot u}_0} + } \\ \;\;\;\;\;z\left( {\dot \phi \delta {{\dot u}_0} + {{\dot u}_0}\delta \dot \phi } \right) + {z^2}\dot \phi \delta \dot \phi + \dot w\delta \dot w]{\rm{d}}z{\rm{d}}x \end{array} $ | (11) |
Let
| $ {I_0} = b\sum\limits_{k = 1}^n {\int\limits_{{z_{k - 1}}}^{{z_k}} {{\rho _k}{\rm{d}}z} } $ | (12) |
| $ {I_1} = b\sum\limits_{k = 1}^n {\int\limits_{{z_{k - 1}}}^{{z_k}} {z{\rho _k}{\rm{d}}z} } $ | (13) |
and
| $ {I_2} = b\sum\limits_{k = 1}^n {\int\limits_{{z_{k - 1}}}^{{z_k}} {{z^2}{\rho _k}{\rm{d}}z} } $ | (14) |
then the variation of K can be simplified as
| $ \delta K = \int\limits_L {\left[ {\left( {{I_0}\dot u + {I_1}\dot \phi } \right)\delta \dot u + I\left( {_1\dot u + {I_2}\dot \phi } \right)\delta \dot \phi + {I_0}\dot w\delta \dot w} \right]{\rm{d}}x} $ | (15) |
The variation of external work can be expressed as
| $ \begin{array}{l} \delta W = \int\limits_L {\left( {q - Pw''} \right)\delta w{\rm{d}}x + {N_{{\rm{ext}}}}\delta {u_t} + {M_{{\rm{ext}}}}\delta {\phi _t} + } \\ \;\;\;\;\;\;\;\;\;{Q_{{\rm{ext}}}}\delta {w_t} \end{array} $ | (16) |
where q is the distributed force of the actuator-beam system, Next, Mext, and Qext are the external axial force, moment, and shear force. They take zeros in this paper. The stretching force P can be represented as
| $ P = {N_{{\rm{ext}}}} + {N_\Lambda } $ | (17) |
According to the generalized Hamilton's principle
| $\int\limits_{{t_1}}^{{t_2}} {\delta \left( {U - K + W} \right){\rm{d}}t = 0} $ | (18) |
substitute Eqs. (10), (15), and (16) into Eq. (18) to get
| $ \begin{array}{*{20}{l}} {\int\limits_{{t_1}}^{{t_2}} {\int\limits_L {\left[ {\left( { - Au'' + B\phi '' + {I_0}\ddot u + {I_1}\ddot \phi } \right)\delta u + \left( {Bu'' - C\phi '' + } \right.} \right.} } }\\ {\left. {\quad D\left( {{w^\prime } + \phi } \right) + {I_1}\ddot u + {I_2}\ddot u} \right)\delta \phi + D\left( {w'' + {\phi ^\prime } - } \right.}\\ {\left. {\left. {\quad Pw'' - {I_0}\ddot w} \right)\delta w} \right]{\rm{d}}x{\rm{d}}t = 0} \end{array} $ | (19) |
Due to the arbitrariness of variation, the terms before the variations must be zeros. Governing equations of the actuator-beam system can thus be derived as
| $ \left\{ {\begin{array}{*{20}{l}} {A{u^{\prime \prime }} - B{\phi ^{\prime \prime }} = {I_0}\ddot u + {I_1}\ddot \phi }\\ { - B{u^{\prime \prime }} + C{\phi ^{\prime \prime }} - D\left( {{w^\prime } + \phi } \right) = {I_1}\ddot u + {I_2}\ddot \phi }\\ {D\left( {{w^{\prime \prime }} + {\phi ^\prime }} \right) - P{w^{\prime \prime }} = {I_0}\ddot w} \end{array}} \right. $ | (20) |
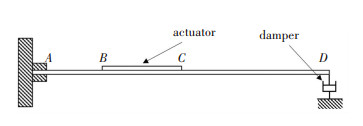
The boundary equations are determined by the boundary conditions. The piezoelectric composite beam can be divided into three elements as shown in Fig. 2.
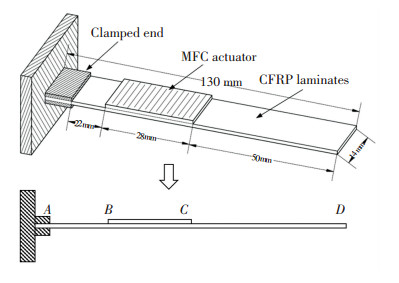
|
Fig.2 Geometric schematic of the beam-actuator system |
The nodes are A, B, C and D. The displacement boundary equations of the system are
| $ \left\{\begin{array}{l} \left.u\right|_{A}=u(0, t), \left.w\right|_{A}=w(0, t), \left.\phi\right|_{A}=\phi(0, t) \\ \left.u\right|_{B}=u(l, t), \left.w\right|_{B}=w(l, t), \left.\phi\right|_{B}=\phi(l, t) \end{array}\right. $ | (21) |
The distributed transfer function formulation is applied to derive the solution of the governing equation and boundary conditions. Take Laplace transformation to Eq.(20) with zero initial disturbances, thus the partial differential equations can be transferred to algebraic equations in the s domain. Through Gauss elimination method, the governing equations and boundary conditions can be transferred to a state space form as
| $\left\{ \begin{array}{l} \frac{{\rm{d}}}{{{\rm{d}}x}}\mathit{\boldsymbol{\eta }}\left( {x, s} \right) = \mathit{\boldsymbol{F}}\left( s \right)\mathit{\boldsymbol{\eta }}\left( {x, s} \right) + \mathit{\boldsymbol{q}}\left( {x, s} \right)\\ {\mathit{\boldsymbol{M}}_b}\left( s \right)\mathit{\boldsymbol{\eta }}\left( {0, s} \right) + {\mathit{\boldsymbol{N}}_b}\left( s \right)\mathit{\boldsymbol{\eta }}\left( {L, s} \right) = r\left( s \right) \end{array} \right. $ | (22) |
Eq.(19) are the state space equations for each element. Here η(x, s) is the state vector, F(s) respresents system matrix, Mb and Nb represent boundary matrices, q(x, s) stands for the distributed force in s domain and here it is zero, r(s) stands for the displacements vector at the element boundary nodes. In Eq.(22), the state vector, displacement vector, and the boundary vector are defined as
| $ \boldsymbol{\eta}(x, s)=\left[\begin{array}{lll} u(x, s) & w(x, s) & \phi(x, s) \\ u^{\prime}(x, s) & \phi^{\prime}(x, s) & w^{\prime \prime \prime}(x, s) \end{array}\right]^{\mathrm{T}} $ | (23) |
| $ \mathit{\boldsymbol{\alpha }}\left( {x, s} \right) = {\left[ {u\left( {x, s} \right)\;\;\;w\left( {x, s} \right)\;\;\;\phi \left( {x, s} \right)} \right]^{\rm{T}}} $ | (24) |
| $ \mathit{\boldsymbol{r}}\left( s \right) = {[\alpha \left( {0, s} \right)\;\;\;\alpha \left( {{L^e}, s} \right)]^{\rm{T}}} $ | (25) |
where Le is the length of the actuator-beam element. F(s), Mb(s) and Nb(s) can be written as
| $ \begin{array}{l} \boldsymbol{F}(s)= \\ {\left[\begin{array}{cccccc} 0 & 0 & 0 & 1 & 0 & 0 \\ \lambda_{1}(s) & 0 & \lambda_{2}(s) & 0 & 0 & \lambda_{3}(s) \\ 0 & 0 & 0 & 0 & 1 & 0 \\ \mathit{\Psi}_{1}(s) & 0 & \mathit{\Psi}_{2}(s) & 0 & 0 & \mathit{\Psi}_{3}(s) \\ K_{1}(s) & 0 & K_{2}(s) & 0 & 0 & K_{3}(s) \\ 0 & F_{1}(s) & 0 & F_{2}(s) & F_{3}(s) & 0 \end{array}\right]} \end{array} $ | (26) |
| $ \boldsymbol{M}_{b}=\left[\begin{array}{cccccc} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right] $ | (27) |
| $ \boldsymbol{N}_{b}=\left[\begin{array}{cccccc} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \end{array}\right] $ | (28) |
The parameters in F(s) are shown in Appendix(Ⅱ). The closed form solution of Eq.(22) is unique and can be formulated as
| $ \mathit{\boldsymbol{\eta }}\left( {x, s} \right) = \int_0^L {\mathit{\boldsymbol{G}}\left( {x, \zeta , s} \right)\mathit{\boldsymbol{q}}\left( {\zeta , s} \right){\rm{d}}\zeta + \mathit{\boldsymbol{H}}\left( {x, s} \right)\mathit{\boldsymbol{r}}\left( s \right)} $ | (29) |
where
| $ \mathit{\boldsymbol{G}}\left( {x, \zeta , s} \right) = \left\{ {\begin{array}{*{20}{l}} {{e^{F\left( s \right)x}}{{\left( {\mathit{\boldsymbol{M}} + \mathit{\boldsymbol{N}}{\mathit{\boldsymbol{e}}^{F\left( s \right)L}}} \right)}^{ - 1}}\mathit{\boldsymbol{M}}{\mathit{\boldsymbol{e}}^{ - F\left( s \right)\zeta }}, }&{\zeta \le x}\\ { - {e^{F\left( s \right)x}}{{\left( {\mathit{\boldsymbol{M}} + \mathit{\boldsymbol{N}}{\mathit{\boldsymbol{e}}^{F\left( s \right)L}}} \right)}^{ - 1}}\mathit{\boldsymbol{N}}{\mathit{\boldsymbol{e}}^{ - F\left( s \right)(L - \zeta )}}, }&{\zeta \ge x} \end{array}} \right. $ | (30) |
and
| $ \mathit{\boldsymbol{H}}\left( {x, s} \right) = {e^{F\left( s \right)x}}{(\mathit{\boldsymbol{M}} + \mathit{\boldsymbol{N}}{\mathit{\boldsymbol{e}}^{F\left( s \right)L}})^{ - 1}} $ | (31) |
where G(x, ζ, s) is called the Green's function matrix for this boundary value problem (BVP). H(x, s) are called transfer function matrix. Here, they are 6 by 6 matrices shown as
| $ \mathit{\boldsymbol{G}}\left( {x, \xi , s} \right) = \left[ {\begin{array}{*{20}{c}} {{g_{1, 1}}\left( {x, \xi , s} \right)}& \ldots &{{g_{1, 6}}\left( {x, \xi , s} \right)}\\ \vdots &{}& \vdots \\ {{g_{6, 1}}\left( {x, \xi , s} \right)}& \ldots &{{g_{6, 6}}\left( {x, \xi , s} \right)} \end{array}} \right] $ | (32) |
| $ \mathit{\boldsymbol{H}}\left( {x, s} \right) = \left[ {\begin{array}{*{20}{c}} {{h_{1, 1}}\left( {x, \xi , s} \right)}& \ldots &{{h_{1, 6}}\left( {x, \xi , s} \right)}\\ \vdots &{}& \vdots \\ {{h_{6, 1}}\left( {x, \xi , s} \right)}& \ldots &{{h_{6, 6}}\left( {x, \xi , s} \right)} \end{array}} \right] $ | (33) |
Using expression (29), the element stiffness matrix in s domain can be easily obtained analytically. The generalized external force vector can be written as
| $ \mathit{\boldsymbol{\sigma }}\left( {x, s} \right) = {\left[ {\mathit{\boldsymbol{N}}\left( {x, s} \right)\;\;\;\mathit{\boldsymbol{M}}\left( {x, s} \right)\;\;\;\mathit{\boldsymbol{Q}}\left( {x, s} \right)} \right]^{\rm{T}}} $ | (34) |
where N(x, s), M(x, s), and Q(x, s) are axial force, bending moment, and shear force. According to Eq.(7), the generalized force vector σ(x, s) can be signified as
| $ \mathit{\boldsymbol{\sigma }}\left( {x, s} \right) = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{N}}\left( {x, s} \right)}\\ {\mathit{\boldsymbol{M}}\left( {x, s} \right)}\\ {\mathit{\boldsymbol{Q}}\left( {x, s} \right)} \end{array}} \right] = \mathit{\boldsymbol{\bar E}}\eta \left( {x, s} \right) + {\mathit{\boldsymbol{F}}_\Lambda }\left( s \right) $ | (35) |
where
| $ \overline{\boldsymbol{E}}=\left[\begin{array}{cccc} A & B & 0 & 0 \\ B & C & 0 & 0 \\ 0 & 0 & D & D-P \end{array}\right]\left[\begin{array}{cccccc} 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & -1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ \lambda_{1} & 0 & \lambda_{2} & 0 & 0 & \lambda_{3} \end{array}\right] $ | (36) |
and
| $ {\mathit{\boldsymbol{F}}_\Lambda }\left( s \right) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{N}}_\Lambda }\left( s \right)}\\ {{\mathit{\boldsymbol{M}}_\Lambda }\left( s \right)}\\ {{\mathit{\boldsymbol{Q}}_\Lambda }\left( s \right)} \end{array}} \right] $ | (37) |
give the relationship of the generalized mechanical forces and state vector. FΛ denotes the generalized actuator induced forces. Substituting Eq. (29) into Eq. (35) yields
| $ \begin{array}{l} \mathit{\boldsymbol{\sigma }}\left( {x, s} \right) = \mathit{\boldsymbol{\bar E}}\int\limits_0^{{L^e}} {\mathit{\boldsymbol{G}}\left( {x, \zeta , s} \right)\mathit{\boldsymbol{q}}\left( {\xi , s} \right){\rm{d}}\xi + \mathit{\boldsymbol{\bar EH}}\left( {x, s} \right)r\left( s \right) + } \\ \;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{F}}_\Lambda }\left( {x, s} \right) \end{array} $ | (38) |
Considering an element of the beam-actuator system, the equilibrium equation can be denoted as
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} { - \mathit{\boldsymbol{\sigma }}\left( {0, s} \right)}\\ {\mathit{\boldsymbol{\sigma }}\left( {{L^e}, s} \right)} \end{array}} \right] = {\left[ { - \mathit{\boldsymbol{\bar EH}}\left( {0, s} \right)\;\;\;\;\mathit{\boldsymbol{\bar EH}}\left( {{L^e}, s} \right)} \right]^{\rm{T}}}\cdot\\ \;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\alpha }}\left( {0, s} \right)}\\ {\mathit{\boldsymbol{\alpha }}\left( {{L^e}, s} \right)} \end{array}} \right] + \mathit{\boldsymbol{\bar E}}\int\limits_0^{{L^e}} {{{\left[ { - \mathit{\boldsymbol{G}}\left( {0, \zeta , s} \right)\;\;\;\;\mathit{\boldsymbol{G}}\left( {{L^e}, \zeta , s} \right)} \right]}^{\rm{T}}}\cdot} \\ \;\;\;\;\;\;\mathit{\boldsymbol{q}}\left( {\xi , s} \right){\rm{d}}\xi + \left[ {\begin{array}{*{20}{c}} { - {\mathit{\boldsymbol{F}}_\Lambda }\left( {0, s} \right)}\\ {{\mathit{\boldsymbol{F}}_\Lambda }\left( {{L^e}, s} \right)} \end{array}} \right] \end{array} $ | (39) |
In Eq.(39),
| $ {\mathit{\boldsymbol{K}}^e} = \left[ { - \mathit{\boldsymbol{\bar EH}}\left( {0, s} \right)\;\;\;\;\mathit{\boldsymbol{\bar EH}}\left( {{L^e}, s} \right)} \right] $ | (40) |
and
| $\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{f}}\left( {0, s} \right)}\\ {\mathit{\boldsymbol{f}}\left( {{L^e}, s} \right)} \end{array}} \right] = \mathit{\boldsymbol{\bar E}}\int\limits_0^{{L^e}} {{{\left[ { - \mathit{\boldsymbol{G}}\left( {0, \zeta , s} \right)\;\;\;\;\mathit{\boldsymbol{G}}\left( {{L^e}, \zeta , s} \right)} \right]}^{\rm{T}}}\mathit{\boldsymbol{q}}\left( {\xi , s} \right){\rm{d}}\xi } $ | (41) |
are called generalized element stiffness matrix and distributed transfer loads. The studied actuator-beam system is divided into three elements. Via Eq. (39), the external nodes forces, displacement, and element stiffness matrixes can be assembled. The relationship among global displacements, forces, and stiffness matrix can be expressed as
| $ \mathit{\boldsymbol{K}}\left( s \right)\mathit{\boldsymbol{U}}\left( s \right) = {\mathit{\boldsymbol{F}}_{\rm{T}}}\left( s \right) $ | (42) |
where K(s), U(s), and FT(s) are global stiffness matrix, global displacement vector, and global force vector in s domain. Here, for the beam-actuator system, the K(s), U(s), and FT(s) can be denoted as
| $ \mathit{\boldsymbol{K}}\left( s \right) = \left[ {\begin{array}{*{20}{c}} {{k_{1, 1}}\left( s \right)}& \ldots &{{k_{12, 1}}\left( s \right)}\\ \vdots &{}& \vdots \\ {{k_{12, 1}}\left( s \right)}& \ldots &{{k_{12, 12}}\left( s \right)} \end{array}} \right] $ | (43) |
| $ \mathit{\boldsymbol{U}}\left( s \right) = {[{u_1}\left( s \right)\;{u_2}\left( s \right)\; \ldots \;{u_{11}}\left( s \right)\;{u_{12}}\left( s \right)]^{\rm{T}}} $ | (44) |
| $ {\mathit{\boldsymbol{F}}_{\rm{T}}}\left( s \right) = [{F_{{\rm{T}}, 1}}\left( s \right)\;{F_{{\rm{T}}, 2}}\left( s \right)\; \ldots \;{F_{{\rm{T}}, 11}}\left( s \right)\;{F_{{\rm{T}}, 12}}\left( s \right)] $ | (45) |
The static deformations, natural frequencies, mode shapes, and frequency response can be obtained through Eq. (42).
4 Static Deformation AnalysisDeflections and deflection angles of different voltages were calculated by the proposed method analytically. Results of FEM were also used to compare with that of the analytical solution. A finite element models with different numbers of elements were developed.
The material properties of the actuator-beam system are given in Table 1.
| Table 1 Material properties |
According to Eq.(42), the global nodal displacements can be written as
| $ \mathit{\boldsymbol{U}}\left( s \right) = {\left[ {\mathit{\boldsymbol{K}}\left( s \right)} \right]^{ - 1}}{F_{\rm{T}}}\left( s \right) $ | (46) |
Set the Laplace parameter s to be zero. Static deflections and displacements of the actuator-beam system at different voltages can be readily obtained. Numerical results of FEM were also used to compare with the analytical results. To show the accuracy of the results calculated by the proposed distributed transfer function method (DTFM), different element number by the finite element method were used in the static deformation analysis. The comparison of deflections of the free end when the voltage is 500 V are shown in Table 2.
| Table 2 Deflections of the free end (500 V) |
It can be observed from Table 2 that the results of FEM are a little smaller than that of the proposed method. As the number of the finite elements increase, the deflections calculating by FEM are closer to that of the analytical result. This is because the result of FEM finally converges to the analytical result as the number of elements increase. The deflections of the actuator-beam system at different voltages are given in Fig. 3.
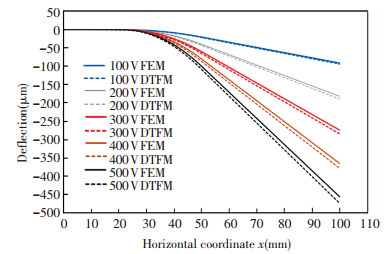
|
Fig.3 Deflections calculated by DTFM and FEM |
The element number of finite element model used in Fig. 3 is 30. It can be observed that the analytical results are close to numerical results at different voltages. The maximum deviation occurs at node D when the voltage is 500 V. The deflection calculated by the proposed method is -473.1 μ m and the numerical result is -462.6 μ m. The relative deviation is about 2.2%. The comparison of rotation angles calculated by two methods is shown in Fig. 4.

|
Fig.4 The calculated rotation angles |
They are also very close to each other. The absolute value of numerical result is a little smaller than that of analytical results. The deflection angles at segment AB are closed to zero and it does not change in segment CD. The deflection angles of the free end at different voltages are shown in Table 3.
| Table 3 Deflection angles of the free end |
To verify the results calculated by the two methods, an experimental study was conducted. The MFC actuator is 2814-P1 type. The piezoelectric beam structure was clamped by a fixture which is installed on an optical platform. A DC controller was used to apply voltage to the MFC actuator.
A laser displacement sensor was installed on a 2 DOF fine-adjustment linear stage. The experiment set up is shown in Fig. 5. The voltages applied to the MFC actuator varies from 50 V to 300 V. There are 20 measuring points evenly distributed along the mid-line of the piezoelectric composite beam. The deflections of the free end at the corresponding voltages 50 V, 100 V, 150 V, 200 V, 250 V and 300 V are 40.5 μ m, 93.9 μ m, 130.4 μ m, 192.9 μ m, 267.8 μ m, and 300.8 μ m, respectively. The free end deflection increases proportionally to the voltage. The deflections obtained by the proposed method, FEM, and experiment at the voltages of 100 V, 200 V and 300 V are compared in Fig. 6. The element number of finite element model used in Fig. 6 is 30.

|
Fig.5 Test set up |
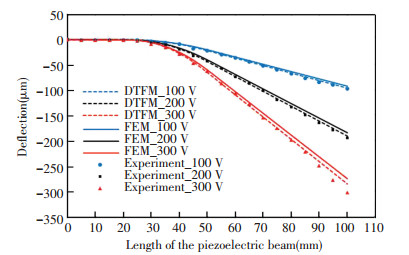
|
Fig.6 Deflections by analyses and experiment |
The relative deviation between the analytical result and the experimental result at the voltage of 100 V is smaller than that at the voltage of 200 V and 300 V. The relative deviation of free end deflection by DTFM and experiment are 2.4 % and 5.7 % at the voltages of 200 V and 300 V, respectively.
5 Vibration Analysis 5.1 Mode Shape and Natural FrequencyThe mode shapes and natural frequencies of the beam-actuator system can be obtained analytically. The voltage acting on the MFC actuator produces a stretching or compression deformation. It changes the natural frequencies and mode shapes of the system. The value of voltage and actuator location influences the results. It is convenient to calculate the modal shapes and natural frequencies of the beam-actuator system with different voltages and actuator locations by the proposed method. In Eq. (42), K(s) is the global stiffness matrix. Let
| $ s = {\rm{j}}\omega , \;\;\;{\rm{j}} = \sqrt { - 1} $ | (47) |
The natural frequencies of the actuator-beam system at different boundary conditions can be obtained through calculating the determinant of the global stiffness matrix. It can be written as
| $ {\rm{det}}\left( {\mathit{\boldsymbol{K}}\left( {{\rm{j}}\omega } \right)} \right) = 0 $ | (48) |
where K(jω) is the global stiffness matrix. It depends on the structure and the boundary condition. Eq.(48) is a transcendental equation, and its roots are infinity. Natural frequencies can be obtained by roots searching methods to get ω1, ω2, …, ωi …. Also, the results of finite element method were used to compare with that of the proposed method. Under the cantilever boundary condition without any voltage acting on MFC actuator, FEM with different number of elements was used to calculate the first five modal frequencies. The comparisons are shown in Table 4.
| Table 4 Frequencies for cantilever beam-actuator system |
It can be seen from Table 4, the natural frequencies calculated by the proposed method are smaller than that of FEM. As the element number increases, the results of FEM are closer to that of the analytical solution. The results of the two methods are closer for lower frequency modes. For the fifth modal frequency, the relative error was no more than 5% when the element number is up to 400. The natural frequencies under the boundary conditions of simple support and two-end fixed can also be calculated with different K(jω). Table 5 gives the results of two methods. The element number of FEM is 500.
| Table 5 Natural frequencies of different conditions |
As shown in Table 5, the natural frequencies calculated by the two methods are closer in lower modes, which means the proposed method have higher accuracy than FEM in calculation of high-order natural frequency. The normalized modal shapes can also be obtained by calculating nontrivial solution of the equation
| $ \mathit{\boldsymbol{K}}\left( {{\rm{j}}{\omega _i}} \right)\mathit{\boldsymbol{U}} = 0 $ | (49) |
It gives the nodal deformations and rotations of the i-th mode. The displacement vector at any point other than nodes can be determined by plugging nodal displacement vector U into Eq.(29). Here, the first six normalized mode shapes of the cantilever actuator-beam system by the proposed method are presented in Fig. 7.
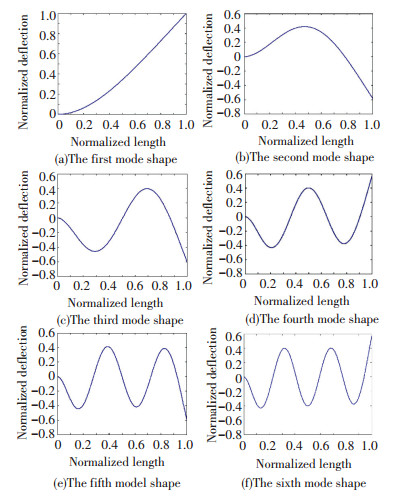
|
Fig.7 The first six modal shapes |
If there is a voltage applied to the MFC actuator, the actuator induced force will cause the variation of natural frequencies and the mode shapes of the actuator-beam system. Positive voltage stretches the beam and makes the beam stiffer. On the other hand, negative voltage compresses the beam and decreases the stiffness of the beam. The stress-introduced stiffness variation is called active stiffness. Using FEM to analyze the natural frequencies usually takes two steps, the first step is to calculate the stress distribution and the active stiffness, the second step is to add the active stiffness to the original stiffness matrix and to perform an eigenvalue analysis, which is a complicated process. The proposed method is more suitable for such problems because it does not induce any extra efforts.
The location of the MFC actuator and the value of voltage are considered in the analyses. Define a variable
| $ \delta = {d_1}/L $ | (50) |
where d1 is the distance between the clamped end and MFC actuator. It equals to the distance from point A to point B as shown in Fig. 2. L is the length of the whole actuator-beam system. Fig. 8 (a) shows the relationship between voltage and natural frequency when the δ=0.22. Results of the analytical method and FEM are both provided. Here the element number of FEM is 100. Fig. 8 (b) shows the relationship between δ and natural frequency when the voltage is 200 V with the proposed method.
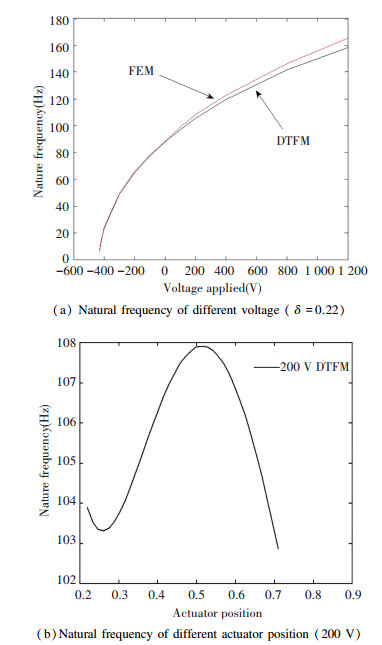
|
Fig.8 Natural frequencies under different conditions |
From Fig. 8 (a), we can see that the relationship between the first modal frequency and the applying voltage is nonlinear. As the voltage increases, the natural frequency increases. When the voltage decreases to -429.5 V, the natural frequency reaches zero, which means the cantilever actuator-beam system reaches to buckling point. From Fig. 8 (b), we can see that the natural frequency reaches to maximum value when δ≈0.5 while the voltage is 200 V. The voltage and the actuator location also impact the mode shapes. The first modal shapes with different voltages and actuator locations were calculated by the proposed method. Fig. 9 (a) presents first mode shapes of the cantilever actuator-beam system when δ≈0.22. Fig. 9 (b) shows the mode shapes of different actuator positions when the voltage equals to 200 V.
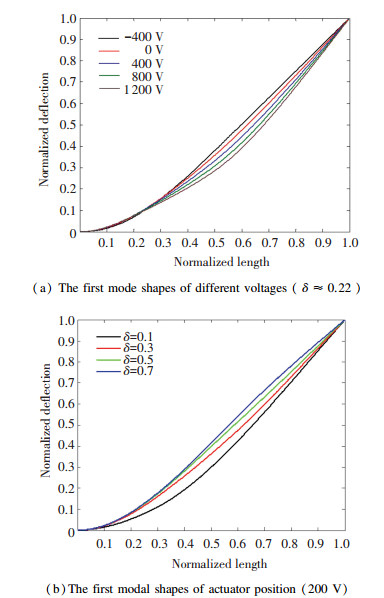
|
Fig.9 The first mode shapes under different conditions |
5.2 Frequencies Response
Frequency response of the actuator-beam system can also be obtained by the proposed method.Assuming that the excitation is a pulse voltage applied to the MFC actuator, the response at any point of the actuator-beam system can easily be obtained analytically. Eq. (42) can be rewritten as
| $ \mathit{\boldsymbol{U}}\left( s \right) = \mathit{\boldsymbol{K}}{\left( s \right)^{ - 1}}{\mathit{\boldsymbol{F}}_{\rm{T}}}\left( s \right) $ | (51) |
The matrix G(s)= K(s)-1 is the transfer function matrix between external forces or actuator induced forces and the displacements. In Eq.(51), let s=jω and the frequency response U(jω) can be obtained as a function of frequency. The velocity response can be obtained by multiplying s to the displacement response and the acceleration response can be obtained by multiplying s to the velocity response. Assume that there is no time delay between the voltage applied to MFC actuator and the induced forces or moments, the relationship between displacement and the voltage can be written as
| $ \mathit{\boldsymbol{U}}\left( s \right) = \mathit{\boldsymbol{G}}\left( s \right)\mathit{\boldsymbol{KV}}\left( s \right) $ | (52) |
where FT(s)= KV (s). The V(s) is the voltage applied to MFC actuator and the K is a constant matrix between F(s) and V(s) and it can be obtained by Eq.(7). Thus the frequency response between the voltage and the displacement can be written as a matrix form:
| $ \mathit{\boldsymbol{H}}\left( {{\rm{j}}\omega } \right) = \frac{{\mathit{\boldsymbol{U}}\left( {{\rm{j}}\omega } \right)}}{{\mathit{\boldsymbol{V}}\left( {{\rm{j}}\omega } \right)}} = \mathit{\boldsymbol{G}}\left( {{\rm{j}}\omega } \right)\mathit{\boldsymbol{K}} $ | (53) |
As a study case, a damper is added to the free end as shown in Fig. 10.
|
Fig.10 Actuator-beam system with a damper |
The damping coefficient of the damper is 0.002. The excitation is a pulse voltage acting on the MFC actuator. The response point is point D in Fig. 10. The frequency response amplitude is denoted by the unit dB which 1 dB equals 20lg(A). A is the amplitude of frequency response. The frequency of calculation varies from 0 Hz to 3 000 Hz. Results of FEM (500 elements) were compared with the analytical results. The magnitude of the deflection and axial displacement frequency responses are shown in Fig. 11 (a) and (b). The velocity and acceleration responses are shown in Fig. 11 (c) and (d).
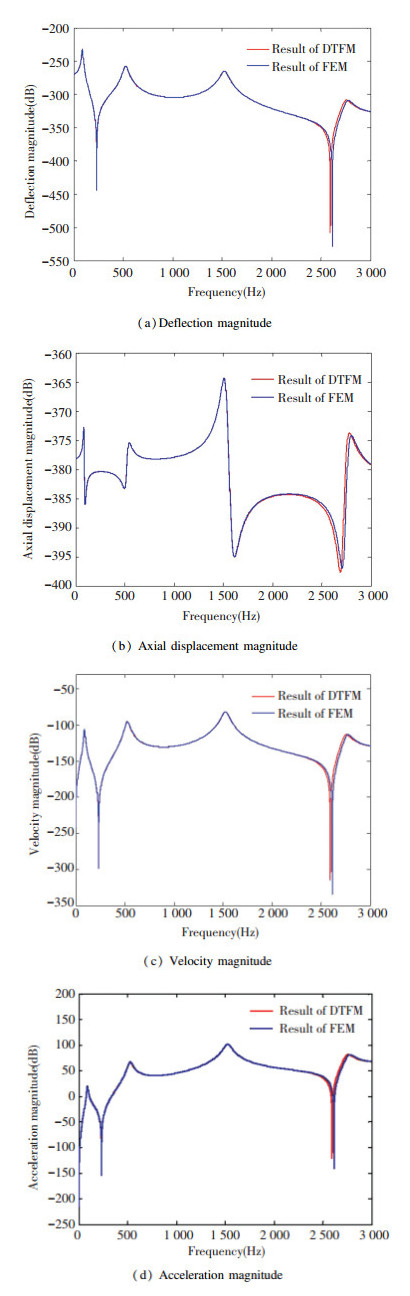
|
Fig.11 Frequency responses |
The results of FEM are almost identical to that of the proposed method in lower frequency range. There is a little difference between the results of the two methods in higher frequency range. This example demonstrates that the proposed method is very convenient to compute the frequency response of the actuator-beam system with arbitrary boundary conditions. It can be easily extended to calculate the frequency response of large adaptive truss structures.
6 ConclusionsIn this paper, an MFC actuator was bonded to a CFRP beam to form an actuator-beam system. Based on FSTD, a mathematical relationship between generalized internal forces, strains, and actuator induced forces was developed. The dynamic governing equations considering active stiffening effect was derived via generalized Hamilton principle. A novel distributed transfer function formulation was proposed to formulate the governing equations and boundary conditions and then to obtain closed form analytical solutions. Static deformations, natural frequencies, mode shapes, and frequency responses can easily be obtained by this method. Compared with FEM, the proposed method has the following advantages:
1) It yields analytical solution;
2) The calculation is efficient and does not use any infinite series;
3) It has higher accuracy and efficiency than FEM in calculating the high natural frequency and frequency response;
4) It can be conveniently applied to obtain the transfer function for shape control or vibration control problems.
Appendix(Ⅰ) The formulations of parameter A, B, C, D, NΛ, MΛand QΛ are
| $ \begin{array}{l} A = b\sum\limits_{k = 1}^n {\int\limits_{{z_{k - 1}}}^{{z_k}} {{E_k}} } {\rm{d}}z = b\sum\limits_{k = 1}^n {{E_k}} \left( {{z_k} - {z_{k - 1}}} \right)({\rm{N}})\\ B = - b\sum\limits_{k = 1}^n {\int\limits_{{z_{k - 1}}}^{{z_k}} {{E_k}} } z{\rm{d}}z = \\ \;\;\;\;\;\;\; - \frac{1}{2}b\sum\limits_{k = 1}^n {{E_k}} \left( {z_k^2 - z_{k - 1}^2} \right)({\rm{N}} \cdot {\rm{m}})\\ C = b\sum\limits_{k = 1}^n {\int\limits_{ - h/2}^{h/2} {{E_k}} } {z^2}{\rm{d}}z = \frac{1}{3}b\sum\limits_{k = 1}^n {{E_k}} \left( {z_k^3 - z_{k - 1}^3} \right)\left( {{\rm{N}} \cdot {{\rm{m}}^2}} \right)\\ D = b\sum\limits_{k = 1}^n {\int\limits_{ - h/2}^{h/2} {{G_k}} } {\rm{d}}z = b\sum\limits_{k = 1}^n {{G_k}} \left( {{z_k} - {z_{k - 1}}} \right)({\rm{N}})\\ {N_\Lambda } = b\sum\limits_{k = 1}^n {\int\limits_{{z_{k - 1}}}^{{z_k}} {{E_k}} } \left( {{d_{11}}{E^1} + {d_{31}}{E^3}} \right){\rm{d}}z = \\ \;\;\;\;\;\;\;\;\;b\sum\limits_{k = 1}^n {{E_k}} \left( {{z_k} - {z_{k - 1}}} \right)\left( {{d_{11}}{E^1} + {d_{31}}{E^3}} \right)({\rm{N}})\\ {M_\Lambda } = b\sum\limits_{k = 1}^n {\int\limits_{{z_{k - 1}}}^{{z_k}} {{E_k}} } \left( {{d_{11}}{E^1} + {d_{31}}{E^3}} \right)z{\rm{d}}z = \\ \;\;\;\;\;\;\;\;\;\frac{1}{2}b\sum\limits_{k = 1}^n {{E_k}} \left( {z_k^2 - z_{k - 1}^2} \right)\left( {{d_{11}}{E^1} + {d_{31}}{E^3}} \right)({\rm{N}} \cdot {\rm{m}})\\ {Q_\Lambda } = b\sum\limits_{k = 1}^n {\int\limits_{{z_{k - 1}}}^{{z_k}} {{G_k}} } \left( {{d_{15}}{E^1}} \right){\rm{d}}z = \\ \;\;\;\;\;\;\;\;\;\;b\sum\limits_{k = 1}^n \kappa {G_k}\left( {{z_k} - {z_{k - 1}}} \right)\left( {{d_{15}}{E^1}} \right)({\rm{N}}) \end{array} $ |
(Ⅱ) The parameters in the F(s) can be written as
| $ \begin{array}{l} {\lambda _1} = \frac{{ - \left( {{I_1} + B{I_0}/A} \right){s^2}}}{{D - \left( {C - {B^2}/A} \right){I_0}{s^2}/D}}\\ {\lambda _2} = - \frac{{D + \left( {{I_2} + B{I_1}/A} \right){s^2}}}{{D - \left( {C - {B^2}/A} \right){I_0}{s^2}/D}}\\ {\lambda _3} = - \frac{{K\left( {C - {B^2}/A} \right)}}{{D\left[ {D - \left( {C - {B^2}/A} \right){I_0}{s^2}/D} \right]}}\\ {\Psi _1} = \left( {1 + \frac{B}{D}{\lambda _1}} \right)\frac{{{I_0}{s^2}}}{A}\\ {\Psi _2} = \left( {\frac{{B{I_0}}}{D}{\lambda _2} + {I_1}} \right)\frac{{{s^2}}}{A}\\ {\Psi _3} = \frac{B}{A}\left( {\frac{{{I_0}}}{D}{\lambda _3}{s^2} - 1} \right)\\ {K_1} = \frac{{{I_0}{\lambda _1}{s^2}}}{D}, {K_2} = \frac{{{I_0}{\lambda _2}{s^2}}}{D}, {K_3} = \frac{{{I_0}{\lambda _3}{s^2} - K}}{D}\\ {F_1} = \frac{{{I_0}{s^2}}}{{{K^2}}}\left[ {\frac{{{D^2}}}{{\left( {{B^2}/A - C} \right)}} + {I_0}{s^2}} \right]\\ {F_2} = \frac{{D\left( {B{I_0}/A + {I_1}} \right){s^2}}}{{K\left( {{B^2}/A - C} \right)}}\\ {F_3} = \frac{D}{{{K^2}}}\left[ {\frac{{(D - P)\left( {B{I_1}/A + {I_2}} \right){s^2} + KD - {D^2}}}{{\left( {{B^2}/A - C} \right)}} - {I_0}{s^2}} \right] \end{array} $ |
where K=D-P.
| [1] |
Wu K, Fang H, Lan L, et al. Shape control of a CFRC reflector with PZT and MFC actuators. AIAA Spacecraft Structures Conference, 2018. AIAA 2018-1197. DOI: 10.2514/6.2018-1197.
(  0) 0) |
| [2] |
Hari Krishna S, Harursampath D. Macro-fiber composite (MFC) as a delamination sensor in antisymmetric laminates. Proceedings of SPIE - The International Society for Optical Engineering, 2007, 6414(1): 641414-1-641414-11. DOI:10.1117/12.695245 (  0) 0) |
| [3] |
Ro J J, Chien C C, Wei T Y, et al. Flexural vibration control of the circular handlebars of a bicycle by using MFC actuators. Journal of Vibration & Control, 2007, 13(7): 969-98. DOI:10.1177/1077546307078740 (  0) 0) |
| [4] |
Vadiraja D N, Sahasrabudhe A D. Vibration analysis and optimal control of rotating pre-twisted thin-walled beams using MFC actuators and sensors. Thin-Walled Structures, 2009, 47(5): 555-567. DOI:10.1016/j.tws.2008.10.004 (  0) 0) |
| [5] |
Kumar G V, Raja S, Prasanna K B, et al. Finite element analysis and vibration control of a deep composite cylindrical shell using MFC actuators. Smart Materials Research, 2012(2012): 123-136. DOI:10.1155/2012/513271 (  0) 0) |
| [6] |
Wu C, Xu M, Wu T, et al. Active vibration control of the panel reflection antenna by MFC sensors and actuators. International Journal of Applied Electromagnetics & Mechanics, 2016, 52(3): 1-9. DOI:10.3233/JAE-162157 (  0) 0) |
| [7] |
Saravanos D A, Heyliger P R. Coupled Layerwise analysis of composite beams with embedded piezoelectric sensors and actuators. Journal of Intelligent Material Systems & Structures, 1995, 6(3): 350-363. DOI:10.1177/1045389X9500600306 (  0) 0) |
| [8] |
Benjeddou A, Trindade M A, Ohayon R, et al. A unified beam finite element model for extension and shear piezoelectric actuation mechanisms. Journal of Intelligent Material Systems & Structures, 1997, 8(12): 1012-1025. DOI:10.1177/1045389X9700801202 (  0) 0) |
| [9] |
Wang Q, Quek S T. Flexural vibration analysis of sandwich beam coupled with piezoelectric actuator. Smart Materials & Structures, 2000, 9(1): 103. DOI:10.1088/0964-1726/9/1/311 (  0) 0) |
| [10] |
Kapuria S, Alam N. Efficient layerwise finite element model for dynamic analysis of laminated piezoelectric beams. Computer Methods in Applied Mechanics & Engineering, 2006, 195(19-22): 2742-2760. DOI:10.1016/j.cma.2005.06.008 (  0) 0) |
| [11] |
Robbins D H, Reddy J N. Analysis of piezoelectrically actuated beams using a layer-wise displacement theory. Computers & Structures, 1991, 41(2): 265-279. DOI:10.1016/0045-7949(91)90430-T (  0) 0) |
| [12] |
Tzou H S, Tseng C I. Distributed piezoelectric sensor/actuator design for dynamic measurement/ control of distributed parameter systems: A piezoelectric finite element approach. Journal of Sound & Vibration, 1990, 138(1): 17-34. DOI:10.1016/0022-460X(90)90701-Z (  0) 0) |
| [13] |
Koconis D B, Kollar L P, Springer G S. Shape control of composite plates and shells with embedded actuators. I. Voltages Specified. Journal of Composite Materials, 1994, 28(5): 415-458. DOI:10.1177/002199839402800503 (  0) 0) |
| [14] |
Koconis D B, Kollar L P, Springer G S. Shape control of composite plates and shells with embedded actuators. Ⅱ. Desired shape specified. Journal of Composite Materials, 1994, 28(5): 459-482. DOI:10.1177/002199839402800504 (  0) 0) |
| [15] |
Portela P, Camanho P, Weaver P, et al. Analysis of morphing, multi stable structures actuated by piezoelectric patches. Computers & Structures, 2008, 86(3-5): 347-356. DOI:10.1016/j.compstruc.2007.01.032 (  0) 0) |
| [16] |
Huang B, Kim H S, Yoon G H. Modeling of a partiallydebonded piezoelectric actuator in smart composite laminates. Smart Materials & Structures, 2015, 24(7). DOI:10.1088/0964-1726/24/7/075013 (  0) 0) |
| [17] |
Inman D J. Smartstructures theory. AIAA Journal, 2014, 52(11): 2624-2624. DOI:10.2514/1.J053653 (  0) 0) |
 2020, Vol. 27
2020, Vol. 27


