2. Key Laboratory of Intelligent Computing and Signal Processing, Ministry of Education, Hefei 230601, China
Memristor is one of the four basic electronic components in a circuit. In the early 1970s[1], Leon Chua[2] tried to build six different mathematical relationships connecting four pairs of basic circuit variables, such as the voltage v, the current i, the charge q, and the flux φ. Chua found that five of these relationships are well known:
| $ v = \frac{{{\rm{d}}\varphi }}{{{\rm{d}}t}},i = \frac{{{\rm{d}}q}}{{{\rm{d}}t}},R = \frac{{{\rm{d}}v}}{{{\rm{d}}i}},L = \frac{{{\rm{d}}\varphi }}{{{\rm{d}}i}},C = \frac{{{\rm{d}}q}}{{{\rm{d}}v}} $ |
while one is undefined, which is the relation between the flux φ and the charge q. According to his seminal paper published in 1971, he assumed that the fourth basic circuit element should exist, which is characterized by a q(φ) curve. Then, memristor was named as the abbreviation of "memory resistor"[3].
Fractional calculus is a mathematical subject with a history of more than 300 years, which acts as the generalization of integer calculus. It has attracted more and more researchers' attention in the last few years[4-5]. Many systems can be expressed as fractional differential equations, for example, economic system[6], biological population model[7], financial system[8], chaotic and hyper-chaotic systems[9-12].
Time-delay usually exists in a variety of engineering systems, such as biology, chemical processes, and economical systems, while their forms are not the same. For example, when the feedback delay occurs in a closed-loop system, it manifests as transportation and communication lag. The dynamic behavior of the system is usually affected by such a tiny delay. Thus, more and more researchers have studied systems with time-delay, such as biology[13], economy[14], system control[15-17], and so on.
In addition, delayed fractional system is proved useful in signal processing[18], financial system[19], and biology[20], so that the research of fractional time-delay system must be considered. The fractional order delayed system has been studied by a lot of investigators[21-26]. In Ref. [22], the fractional delayed Hopfield neural networks were discussed, and two types of them were studied. In Ref. [23], the existence of solutions near the equilibrium point for fractional differential equations with time-delay was analyzed. In Ref. [24], explicit formulas and stability of bifurcation periodic solutions were derived based on central manifold reduction. Additionally, chaotic behavior of fractional time-delay systems has become one of the research hotspots[27-29]. In Ref. [27], the chaotic phenomena in Bloch model with time-delay were discussed. It was found that the delay has an effect on the stability of the system. The Hopf bifurcation of fractional memristor chaotic delayed systems was studied by taking the time-delay and fractional order as bifurcation parameters in Ref. [28]. In Ref. [29], the chaotic dynamics of fractional order logistic maps with delays were analyzed, and a discrete chaotic attractor was found.
On the other hand, sliding mode control (SMC) is such an effective nonlinear control technology that a large number of SMC methods have been developed in the past few decades. For many fractional order system control schemes, impulsive control[30], active control[31], passive control[32], pinning adaptive control[33], and generalized projective control[34] are included. Main characteristics of SMC are that it is insensitive to the changes or disturbances of the system parameters and it has rapid transient response. Therefore, scholars have studied the sliding mode control strategy in the last few years[35-38]. The control of the fractional systems was studied by SMC.
With the above discussions, the innovation of this paper lies in the combination of sliding mode technology and fractional calculus theory, where fractional sliding mode controller is designed to control chaos of fractional memristor time-delay system. Therefore, a fractional sliding mode method based on Lyapunov stability theory is proposed and a suitable control structure is designed. Although many studies have discussed the application of sliding mode controllers in fractional chaotic systems, few have studied them in fractional memristor delayed chaotic systems. The controller makes the state of the system asymptotically stable, and there are external disturbances in the systems of commensurate and non-commensurate order.
The organizational structures of the article are as follows: the second section gives the definitions for fractional calculus and memristor model. In the third section, a delayed chaotic system based on fractional memristor is discussed. On the basis of the sliding mode control strategy theory, the controller of fractional chaotic time-delay system is designed in the fourth section, and the design process of fractional sliding mode approximation is introduced. The simulation results are given in the fifth section. At last, the sixth section gives some conclusions.
2 Basic Definitions and Preliminaries 2.1 DefinitionsDefinition 1 The fractional Caputo derivative of fractional q is defined as[39]
| $ D_t^qf(t) = \frac{1}{{\Gamma (m - q)}}\int_0^t {\frac{{{f^m}(\tau )}}{{{{(t - \tau )}^{q + 1 - m}}}}} {\rm{d}}\tau ,m - 1 < q < m $ | (1) |
where Γ is a gamma function,
| $ {\Gamma (z) = \int_0^\infty {{e^{ - t}}} {t^{z - 1}}{\rm{d}}t} $ | (2) |
| $ {\Gamma (z + 1) = z\Gamma (z)} $ | (3) |
Definition 2 The Laplace transform of Caputo derivative is defined as[40]
| $ L\{ D_t^qf(t)\} = {s^q}F(s) - \sum\limits_{k = 0}^{m - 1} {{s^{q - 1 - k}}} {f^{(k)}}(0),m - 1 < q < m $ | (4) |
where F(s) is the Laplace transform of f(t), fk(0), k=1, 2, ...n, are the initial conditions. If fk(0)=0, k=1, 2, ...n, then L{Dtqf(t)}=sqF(s).
2.2 MemristorsThe memristor is a circuit component used to display the relationship between flux (φ) and charge (z). The forms of memristor are as follows:
Firstly, flux-controlled memristor is defined as
| $ \left\{ {\begin{array}{*{20}{l}} {{i_M} = W(\varphi ){v_M}}\\ {W(\varphi ) = \frac{{{\rm{d}}z(\varphi )}}{{{\rm{d}}\varphi }}} \end{array}} \right. $ | (5) |
where W(φ) is the memductance.
Secondly, charge-controlled memristor is defined as
| $ \left\{ {\begin{array}{*{20}{l}} {{v_M} = M(z){i_M}}\\ {M(z) = \frac{{{\rm{d}}\varphi (z)}}{{{\rm{d}}z}}} \end{array}} \right. $ | (6) |
where M(z) is the memristance, and vM, iM, z, and φ are the voltage, current, charge, and flux in the memristor, respectively.
3 Description of Fractional Order Delayed SystemThe memristor-based chaotic delayed system has been investigated in Ref.[41]. The circuit system includes nonlinear active memristor with time-delay and capacitor, as depicted in Fig. 1. The following equations describe the system:

|
Fig.1 Chaotic circuit system based on delayed memristor |
| $ \left\{ {\begin{array}{*{20}{l}} {\dot x = f({x_\tau },{v_M},t) = a{x_\tau } + b|{x_\tau }| + c{v_M}}\\ {{i_M} = G(x,{v_M},t){v_M} = (\alpha + \beta x){v_M}} \end{array}} \right. $ | (7) |
Then, Kirchhoff's circuit law was applied to the system (Fig. 1) and the following circuit equations were obtained:
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}x(t)}}{{{\rm{d}}t}} = ax(t - \tau ) + b|x(t - \tau )| + c{v_C}(t)}\\ {C\frac{{{\rm{d}}{v_C}(t)}}{{{\rm{d}}t}} = - \alpha {v_C}(t) - \beta x(t){v_C}(t)} \end{array}} \right. $ | (8) |
where x is the state variable through memristor, τ is the time-delay, and a, b, c, α, and β are all constants. The equations were derived as follows:
| $ \left\{ {\begin{array}{*{20}{l}} {\dot x = a{x_\tau } + b|{x_\tau }| + cy}\\ {\dot y = my + nxy} \end{array}} \right. $ | (9) |
where y=vC(t), xτ=x(t-τ), m=-α/C, and n=-β/C.
Therefore, the time-delay system based on fractional memristor can be expressed by equations
| $ \left\{ {\begin{array}{*{20}{l}} {D_t^{{q_1}}x = ax(t - \tau ) + b|x(t - \tau )| + cy}\\ {D_t^{{q_2}}y = my + nxy} \end{array}} \right. $ | (10) |
where q1 and q2 are fractional order of memristor M and capacitor C.
The analyses of chaotic dynamic based on the Lyapunov exponent are presented in Ref.[28].
4 Design of Fractional SMCIn order to stabilize the fractional memristor-based chaotic delayed system, control input u(t) was added to Eq.(10) and the controlled system can be rewritten as
| $ \left\{ {\begin{array}{*{20}{l}} {D_t^{{q_1}}x = ax(t - \tau ) + b|x(t - \tau )| + cy}\\ {D_t^{{q_2}}y = my + nxy + u(t)} \end{array}} \right. $ | (11) |
Then, fractional sliding mode controller was designed. First of all, fractional sliding mode surface was constructed, which indicates required system dynamics. Therefore, the following sliding mode surface was selected:
| $ s(t) = {D^{{q_2} - 1}}y(t) + {D^{ - 1}}\psi (t) = {D^{{q_2} - 1}}y(t) + \int_0^t \psi (\tau ){\rm{d}}\tau $ | (12) |
where ψ(t) is a function:
| $ \psi (t) = my + nxy $ | (13) |
The sliding mode surface and the derivative should meet the following conditions, which are on the basis of the sliding mode method:
| $ s(t) = 0,\dot s(t) = 0 $ | (14) |
Thus, this conclusion is drawn:
| $ \begin{array}{*{20}{c}} {\dot s(t) = \frac{{\rm{d}}}{{{\rm{d}}t}}s(t) = \frac{{\rm{d}}}{{{\rm{d}}t}}[{D^{{q_2} - 1}}y(t) + \int_0^t \psi (\tau ){\rm{d}}\tau ] = }\\ {\frac{{\rm{d}}}{{{\rm{d}}t}}{D^{{q_2} - 1}}y(t) + \frac{{\rm{d}}}{{{\rm{d}}t}}\int_0^t \psi (\tau ){\rm{d}}\tau = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {D^{{q_2}}}y(t) + \psi (t) = 0 \Rightarrow {D^{{q_2}}}y(t) = - \psi (t)} \end{array} $ | (15) |
The next step was to develop a switching control method and drive any external state to the surface in a finite time[42-43]. The equivalent control law was deduced as
| $ \begin{array}{l} {u_{ep}}(t) = \frac{{{{\rm{d}}^{{q_2}}}y}}{{{\rm{d}}{t^{{q_2}}}}} - my - nxy = - my - nxy - my - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} nxy = - 2my - 2nxy \end{array} $ | (16) |
The system was kept on a sliding manifold by using the switching control. In order to meet the sliding condition, the method of discontinuous reaching was selected as
| $ {u_r}(t) = {K_r}{\rm{sign}}(s) $ | (17) |
where Kr is the controller's gain, and
| $ {\rm sign} (s) = \left\{ {\begin{array}{*{20}{c}} { + 1,}&{s > 0}\\ {0,}&{s = 0}\\ { - 1,}&{s < 0} \end{array}} \right. $ | (18) |
Thus, the total control method can be written as
| $ u(t) = {u_{eq}}(t) + {u_r}(t) = - 2my - 2nxy + {K_r} {\rm{sign}} (s) $ | (19) |
Theorem 1 Considering the chaotic time-delay system based on fractional order memristor (11) and the control law (19), the system is asymptotically stable when the controller's gain satisfies Kr < 0.
Proof Choose Lyapunov candidate as
| $ V = \frac{1}{2}{s^2} $ | (20) |
Therefore, the time derivative is calculated as follows:
| $ \begin{array}{l} \dot V = s \cdot \dot s = s \cdot [{D^{{q_2}}}y(t) + \psi (t)] = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} s \cdot [my + nxy + u(t) + my + nxy] = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} s \cdot [2my + 2nxy + u(t)] = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} s \cdot [2my + 2nxy - 2my - 2nxy + {K_r} {\rm{sign}} (s)] = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} s \cdot {K_r} {\rm{sign}} (s) = {K_r}|s| < 0 \end{array} $ | (21) |
It can be clearly concluded that when Kr < 0 and s(t)≠0, then
Theorem 2 If the controlled system (11) is disturbed by external interference, it can be expressed as follows:
| $ \left\{ {\begin{array}{*{20}{l}} {D_t^{{q_1}}x = ax(t - \tau ) + b|x(t - \tau )| + cy}\\ {D_t^{{q_2}}y = my + nxy + \varDelta f(x,y) + \xi (t) + u(t)} \end{array}} \right. $ | (22) |
where Δf(x, y) and ξ(t) are bounded that |Δf(x, y)|≤ h1 and |ξ(t)|≤h2. Under the sliding mode control (19), the chaotic system is asymptotically stable when Kr < -(h1+h2).
Proof When the Lyapunov candidate (20) is chosen, the floowing expression is obtained:
| $ \begin{array}{l} \dot V = s \cdot \dot s = s \cdot [{D^{{q_2}}}y(t) + \psi (t)] = s \cdot [my + nxy + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varDelta f(x,y) + \xi (t) + u(t) + my + nxy] = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} s \cdot [2my + 2nxy + \varDelta f(x,y) + \xi (t) + u(t)] = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} s \cdot [\Delta f(x,y) + \xi (t) + {K_r} {\rm{sign}} (s)] \le \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} |s|({h_1} + {h_2} + {K_r}) < 0 \end{array} $ | (23) |
Thus, considering the uncertainties and disturbances, when the controller's gain Kr < -(h1+h2), the controller (19) can stabilize the system asymptotically.
Therefore, the two theorems are thoroughly proved.
5 Simulation ResultsThe dynamical behaviors and chaotic states of an uncontrolled fractional order memristor delayed system (10) in Ref. [28] were analyzed. Parameters for the system (10) are as follows: a=1, b=-2, c=5, m=0.5, n=-0.9. In this part, four cases are presented to prove the correctness of sliding mode control scheme. According to the improved Adams-Bashforth-Moulton predictor algorithm[44], the numerical simulation was carried out in this paper.
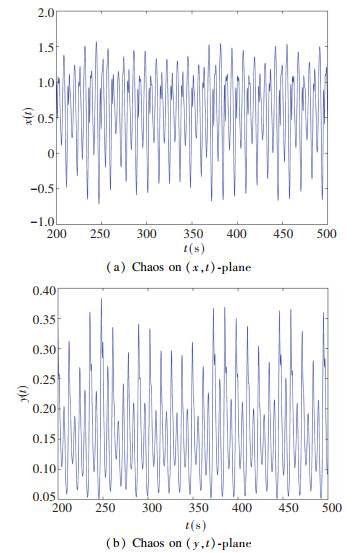
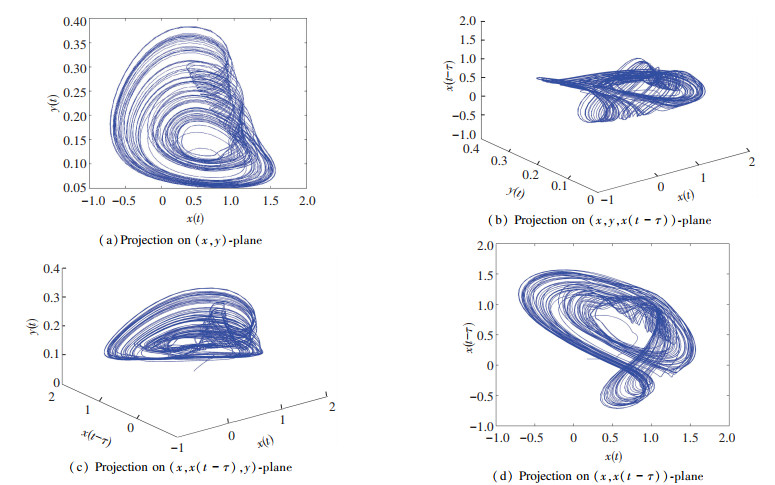
5.1 System without Uncertainties and Disturbances 5.1.1 Commensurate order system without uncertainties and disturbancesWhen it supposes the same derivative order in Eq.(10), i.e., q1=q2=q, a commensurate order system can be obtained. The time-delay system based on fractional memristor is chaotic in case: q1=q2=0.88, (Figs. 2-3).
|
Fig.2 Time domain plot of chaotic delayed system (10) when q1=q2=0.88, τ =2 without controller |
|
Fig.3 Chaotic attractor of delayed system (10) when q1=q2=0.88, τ=2 without controller |
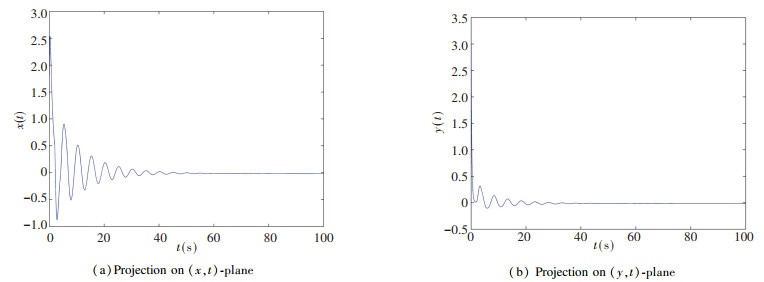
The controller's gain Kr=-1 was chosen in system (11) so as to satisfy Theorem 1. The control law (19) was used to stabilize the system, and the numerical simulations are shown in Fig. 4. It proved that the theoretical results obtained are feasible for the system based on fractional order controlled time-delay memristor.
|
Fig.4 Time diagram of controlled commensurate delayed system states |
However, when the gain of the controller Kr=0.01 was chosen in the system (11), it did not meet the conditions in Theorem 1. Fig. 5 depicts the time domain of the delayed system under control, which is a mismatched control condition. It shows that the time domain curves are divergent. The counter example validated the feasibility of the designed control scheme.

|
Fig.5 Time domain of controlled chaotic delayed system (11) mismatching control condition |
5.1.2 Non-commensurate order system without uncertainties and disturbances
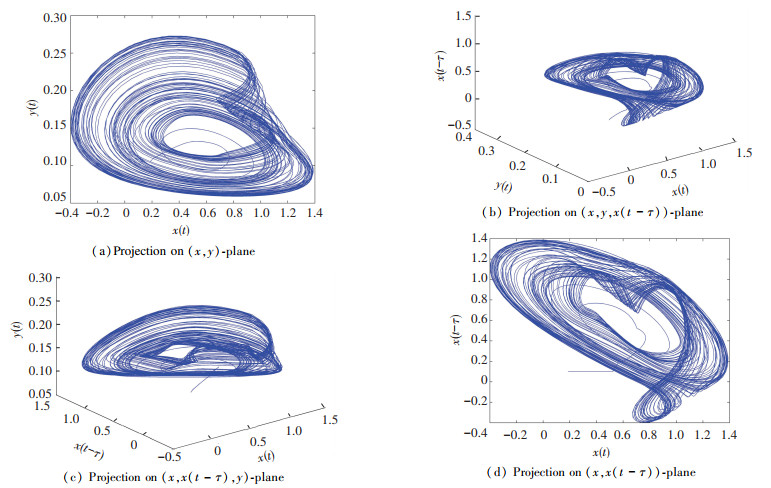
If the two orders of derivatives in Eq.(10) are different, for example, q1≠q2, then a non-commensurate order system is generally available. When the orders q1=0.80 and q2=0.85, Figs. 6-7 show some chaotic behaviors for the fractional memristor-based delayed system.

|
Fig.6 Time domain diagram of chaotic delayed system (10) when q1=0.80, q2=0.85, τ=2 without controller |
|
Fig.7 Chaotic attractor of delayed system (10) when q1=0.80, q2=0.85, τ=2 without controller |
When the controller's gain Kr=-1 was chosen in the system (11), it conformed to Theorem 1. The control law (19) was used to stabilize the system. Fig. 8 shows the numerical simulations. Its results show that the obtained theoretical conclusions are effective for fractional order memristor-based delayed system under control.
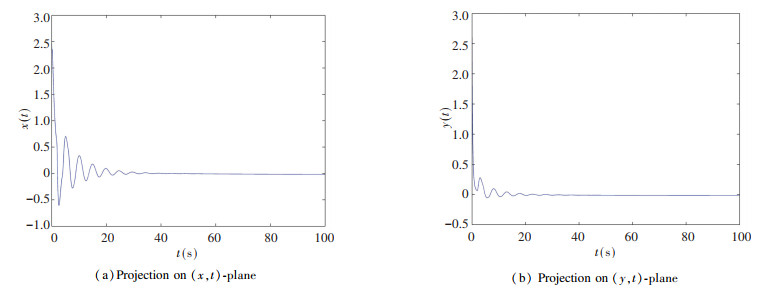
|
Fig.8 Time domain diagram of controlled non-commensurate chaotic delayed system |
In addition, controller's gain Kr=0.01 was chosen to prove the correctness of Theorem 1, but it did not meet Theorem 1. Fig. 9 depicts the time state for the chaotic delayed system under control, which does not match the given control conditions. It can be concluded that the time domain curves are unstable.
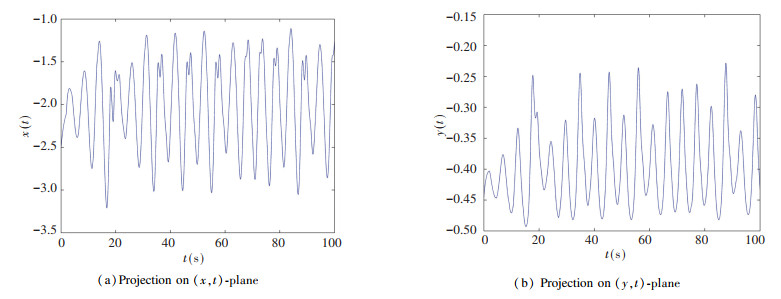
|
Fig.9 Time domain diagram of controlled chaotic delayed system mismatching control condition |
5.2 System with Uncertainties and Disturbances 5.2.1 Commensurate order system with uncertainties and disturbances
In this part, the memristor-based chaotic delayed system was disturbed by uncertainty Δf(x, y)=0.45sin(πx)cos(πy) and disturbance ξ(t)=0.5sin(πt), where |Δf(x, y)|≤h1=0.45 and |ξ(t)|≤h2=0.5. Fig. 10 depicts the system state response with the control law (19) when the controller's gain Kr=-1, and it satisfies Theorem 2.
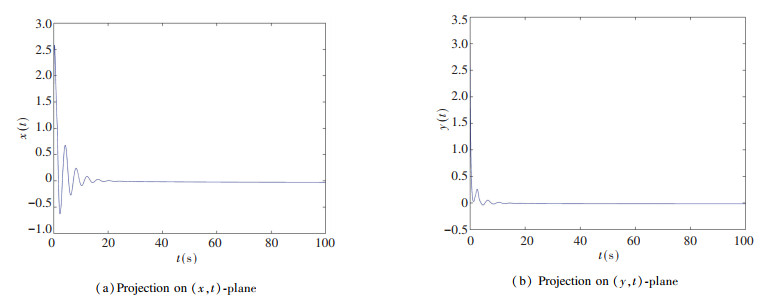
|
Fig.10 Time domain diagram of controlled commensurate order chaotic delayed system with uncertainties and disturbances |
5.2.2 Non-commensurate order system with uncertainties and disturbances
The memristor-based chaotic delayed system was disturbed by uncertainty Δf(x, y)=0.45sin(πx)·cos(πy) and disturbance ξ(t)=0.5sin(πt), where |Δf(x, y)|≤h1=0.45 and |ξ(t)|≤h2=0.5. In the case of control law (19), the system time response is depicted in Fig. 11 when the controller's gain Kr=-1, and it satisfies Theorem 2.

|
Fig.11 Time domain diagram of controlled non-commensurate order chaotic delayed system with uncertainties and disturbances |
6 Conclusions
This paper investigated the chaotic time-delay system based on fractional memristor. A fractional sliding mode control method was designed to control chaotic behavior of the system. On the basis of Lyapunov theorem, the proposed control scheme could make the fractional delayed memristor-based chaotic system asymptotically stable, which proves that the designed control scheme is theoretically sound and robust. In the case of uncertainties and disturbances, the method was also applicable to the commensurate and non-commensurate order systems. The simulation results indicate that sliding mode control scheme has anti-interference ability. Finally, numerical simulations show that the designed control scheme can make the fractional order memristor-based time-delay system stable in finite time. Two counterexamples were used to verify correctness of the designed sliding mode control scheme.
| [1] |
Scarabello M C, Messias M. Bifurcations leading to nonlinear oscillations in a 3D piecewise linear memristor oscillator. International Journal of Bifurcation & Chaos, 2014, 24(1): 023136. DOI:10.1142/S0218127414300018 (  0) 0) |
| [2] |
Chua L O. Memristor-the missing circuit element. IEEE Trans Circuit Theory, 1971, 18(5): 507-519. DOI:10.1109/TCT.1971.1083337 (  0) 0) |
| [3] |
Strukov D B, Snider G S, Stewart D R, et al. The missing memristor found. Nature, 2008, 453(7191): 80-83. DOI:10.1038/nature06932 (  0) 0) |
| [4] |
Shokooh A, Suárez L. A comparison of numerical methods applied to a fractional model of damping materials. Journal of Vibration & Control, 1999, 5(3): 331-354. DOI:10.1177/107754639900500301 (  0) 0) |
| [5] |
Shukla M K, Sharma B B. Backstepping based stabilization and synchronization of a class of fractional order chaotic systems. Chaos, Solitons & Fractals, 2017, 102: 274-284. DOI:10.1016/j.chaos.2017.05.015 (  0) 0) |
| [6] |
Wang Z, Huang X, Shen H. Control of an uncertain fractional order economic system via adaptive sliding mode. Neurocomputing, 2012, 83(6): 83-88. DOI:10.1016/j.neucom.2011.11.018 (  0) 0) |
| [7] |
Srivastava V K, Kumar S, Awasthi M K, et al. Two-dimensional time fractional-order biological population model and its analytical solution. Egyptian Journal of Basic & Applied Sciences, 2014, 1(1): 71-76. DOI:10.1016/j.ejbas.2014.03.001 (  0) 0) |
| [8] |
Xin B, Zhang J. Finite-time stabilizing a fractional-order chaotic financial system with market confidence. Nonlinear Dynamics, 2015, 79(2): 1399-1409. DOI:10.1007/s11071-014-1749-7 (  0) 0) |
| [9] |
Boulkroune A, Bouzeriba A, Bouden T, et al. Fuzzy Adaptive Synchronization of Uncertain Fractional-order Chaotic Systems. Azar A T. Vaidyanathan S. Advances in Chaos Theory and Intelligent Control. Berlin: Springer International Publishing, 2016. 1-16. DOI: 10.1007/978-3-319-30340-6.
(  0) 0) |
| [10] |
Mahmoud G M, Abed-Elhameed T M, Ahmed M E. Generalization of combination-combination synchronization of chaotic n-dimensional fractional-order dynamical systems. Nonlinear Dynamics, 2016, 83(4): 1885-1893. DOI:10.1007/s11071-015-2453-y (  0) 0) |
| [11] |
El-Sayed A M A, Nour H M, Elsaid A, et al. Dynamical behaviors, circuit realization, chaos control, and synchronization of a new fractional order hyperchaotic system. Applied Mathematical Modelling, 2016, 40(5-6): 3516-3534. DOI:10.1016/j.apm.2015.10.010 (  0) 0) |
| [12] |
Yang L, Jiang J. Complex dynamical behavior and modified projective synchronization in fractional-order hyper-chaotic complex Lü system. Chaos, Solitons & Fractals, 2015, 78: 267-276. DOI:10.1016/j.chaos.2015.08.006 (  0) 0) |
| [13] |
Matouk A E, Elsadany A A, Ahmed E, et al. Dynamical behavior of fractional-order Hastings-Powell food chain model and its discretization. Communications in Nonlinear Science & Numerical Simulation, 2015, 27(1-3): 153-167. DOI:10.1016/j.cnsns.2015.03.004 (  0) 0) |
| [14] |
Wang Z, Huang X, Shi G. Analysis of nonlinear dynamics and chaos in a fractional order financial system with time delay. Computers & Mathematics with Applications, 2011, 62(3): 1531-1539. DOI:10.1016/j.camwa.2011.04.057 (  0) 0) |
| [15] |
Almawlawe M, Mitić D, Antić D, et al. An approach to microcontroller-based realization of boost converter with quasi-sliding mode control. Journal of Circuits, Systems & Computers, 2017, 26(7): 1750106. DOI:10.1142/S0218126617501067 (  0) 0) |
| [16] |
Lin T C, Lee T Y. Chaos synchronization of uncertain fractional-order chaotic systems with time delay based on adaptive fuzzy sliding mode control. IEEE Transactions on Fuzzy Systems, 2011, 19(4): 623-635. DOI:10.1109/TFUZZ.2011.2127482 (  0) 0) |
| [17] |
Liu L, Pan F, Xue D. Fractional-order optimal fuzzy control for network delay. Optik - International Journal for Light and Electron Optics, 2014, 125(23): 7020-7024. DOI:10.1016/j.ijleo.2014.08.082 (  0) 0) |
| [18] |
Wang Z, Huang X, Li N, et al. Image encryption based on a delayed fractional-order chaotic logistic system. Chinese Physics B, 2012, 21(5): 107-112. DOI:10.1088/1674-1056/21/5/050506 (  0) 0) |
| [19] |
Cao J, Ma C, Xie H, et al. Nonlinear dynamics of Duffing system with fractional order damping. Journal of Computational and Nonlinear Dynamics, 2010, 5(4): 1003-1009. DOI:10.1115/1.4002092 (  0) 0) |
| [20] |
Rihan F A, Lakshmanan S, Hashish A H, et al. Fractional-order delayed predator-prey systems with Holling type-Ⅱ functional response. Nonlinear Dynamics, 2015, 80(1-2): 777-789. DOI:10.1007/s11071-015-1905-8 (  0) 0) |
| [21] |
Wen S F, Shen Y J, Yang S P, et al. Dynamical response of Mathieu-Duffing oscillator with fractional-order delayed feedback. Chaos, Solitons & Fractals, 2017, 94: 54-62. DOI:10.1016/j.chaos.2016.11.008 (  0) 0) |
| [22] |
Velmurugan G, Rakkiyappan R. Hybrid projective synchronization of fractional-order memristor-based neural networks with time delays. Nonlinear Dynamics, 2016, 83: 419-432. DOI:10.1007/s11071-015-2337-1 (  0) 0) |
| [23] |
Babakhani A, Baleanu D, Khanbabaie R. Hopf bifurcation for a class of fractional differential equations with delay. Nonlinear Dynamics, 2012, 69(3): 721-729. DOI:10.1007/s11071-011-0299-5 (  0) 0) |
| [24] |
Xiao M, Zheng W X, Cao J. Hopf bifurcation of an (n+1)-neuron bidirectional associative memory neural network model with delays. IEEE Transactions on Neural Networks & Learning Systems, 2013, 24(1): 118-132. DOI:10.1109/TNNLS.2012.2224123 (  0) 0) |
| [25] |
Leung A Y T, Yang H X, Zhu P. Periodic bifurcation of Duffing-van der Pol oscillators having fractional derivatives and time delay. Communications in Nonlinear Science & Numerical Simulation, 2014, 19(4): 1142-1155. DOI:10.1016/j.cnsns.2013.08.020 (  0) 0) |
| [26] |
Huang C, Cao J, Ma Z. Delay-induced bifurcation in a tri-neuron fractional neural network. International Journal of Systems Science, 2015, 47(15): 1-10. DOI:10.1080/00207721.2015.1110641 (  0) 0) |
| [27] |
Baleanu D, Magin R L, Bhalekar S, et al. Chaos in the fractional order nonlinear Bloch equation with delay. Communications in Nonlinear Science & Numerical Simulation, 2015, 25(1-3): 41-49. DOI:10.1016/j.cnsns.2015.01.004 (  0) 0) |
| [28] |
Hu W, Ding D, Zhang Y, et al. Hopf bifurcation and chaos in a fractional order delayed memristor-based chaotic circuit system. Optik - International Journal for Light and Electron Optics, 2017, 130: 189-200. DOI:10.1016/j.ijleo.2016.10.123 (  0) 0) |
| [29] |
Wu G C, Baleanu D. Discrete chaos in fractional delayed logistic maps. Nonlinear Dynamics, 2015, 80(4): 1607-1703. DOI:10.1007/s11071-014-1250-3 (  0) 0) |
| [30] |
Xi H, Yu S, Zhang R, et al. Adaptive impulsive synchronization for a class of fractional-order chaotic and hyperchaotic systems. Optik - International Journal for Light and Electron Optics, 2014, 125(9): 2036-2040. DOI:10.1016/j.ijleo.2013.12.002 (  0) 0) |
| [31] |
Agrawal S K, Srivastava M, Das S. Synchronization of fractional order chaotic systems using active control method. Chaos, Solitons & Fractals, 2012, 45(6): 737-752. DOI:10.1016/j.chaos.2012.02.004 (  0) 0) |
| [32] |
Kocamaz U E, Uyaroglu Y, Vaidyanathan S. Control of Shimizu-Morioka Chaotic System with Passive Vontrol, Sliding Mode Control and Backstepping Design Methods: A Comparative Analysis. Vaidyanathan S, Volos C. Advances and Applications in Chaotic Systems. Berbin: Springer International Publishing, 2016. 409-425. DOI: 10.1007/978-3-319-30279-9.
(  0) 0) |
| [33] |
Kuntanapreeda S. Adaptive control of fractional-order unified chaotic systems using a passivity-based control approach. Nonlinear Dynamics, 2016, 84(4): 2505-2515. DOI:10.1007/s11071-016-2661-0 (  0) 0) |
| [34] |
Boulkroune A, Bouzeriba A, Bouden T. Fuzzy generalized projective synchronization of incommensurate fractional-order chaotic systems. Neurocomputing, 2016, 173: 606-614. DOI:10.1016/j.neucom.2015.08.003 (  0) 0) |
| [35] |
Lin T C, Lee T Y, Balas V E. Adaptive fuzzy sliding mode control for synchronization of uncertain fractional order chaotic systems. Chaos, Solitons & Fractals, 2011, 44(10): 791-801. DOI:10.1016/j.chaos.2011.04.005 (  0) 0) |
| [36] |
Guo B Z, Zhou H C, Al-Fhaid A S, et al. Stabilization of Euler-Bernoulli Beam equation with boundary moment control and disturbance by active disturbance rejection control and sliding mode control approaches. Journal of Dynamical & Control Systems, 2014, 20(4): 539-558. DOI:10.1007/s10883-014-9241-8 (  0) 0) |
| [37] |
Jiang B, Shi P, Mao Z. Sliding mode observer-based fault estimation for nonlinear networked control systems. Circuits Systems & Signal Processing, 2011, 30(1): 1-16. DOI:10.1007/s00034-010-9203-7 (  0) 0) |
| [38] |
Gao Z, Jiang B, Shi P, et al. Active fault tolerant control design for reusable launch vehicle using adaptive sliding mode technique. Journal of the Franklin Institute, 2012, 349(4): 1543-1560. DOI:10.1016/j.jfranklin.2011.11.003 (  0) 0) |
| [39] |
Liu F, Agrawal O P, Momani S, et al. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications. Cambridge: Academic Press, 1999.
(  0) 0) |
| [40] |
Wang S, Yu Y, Wen G. Hybrid projective synchronization of time-delayed fractional order chaotic systems. Nonlinear Analysis: Hybrid Systems, 2014, 11(1): 129-138. DOI:10.1016/j.nahs.2013.07.004 (  0) 0) |
| [41] |
Pham V T, Buscarino A, Fortuna L, et al. Simple memristive time-delay chaotic systems. International Journal of Bifurcation & Chaos, 2013, 23(4): 1350073. DOI:10.1142/S0218127413500739 (  0) 0) |
| [42] |
Dadras S, Momeni H R. Control of a fractional-order economical system via sliding mode. Physica A: Statistical Mechanics and its Applications, 2010, 389(12): 2434-2442. DOI:10.1016/j.physa.2010.02.025 (  0) 0) |
| [43] |
Azza H B, Moujahed M, Jemli M, et al. Implementation of improved sliding mode observer and fault tolerant control for a PMSM drive. Journal of Circuits, Systems and Computers, 2017, 26(2): 1413-1421. DOI:10.1142/S0218126617500323 (  0) 0) |
| [44] |
Bhalekar S, Daftardar-Gejji V. A predictor-corrector scheme for solving nonlinear delay differential equations of fractional order. Journal of Fractional Calculus and Applications, 2011, 1(5): 1-9. (  0) 0) |
 2020, Vol. 27
2020, Vol. 27


